Aprendizaje profundo

Capítulo 4. Principales arquitecturas de las redes profundas

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

El arte madre es la arquitectura. Sin una arquitectura propia no tenemos alma de civilización propia.

Frank Lloyd Wright

Ahora que hemos visto algunos de los componentes de las redes profundas, echemos un vistazo a las cuatro arquitecturas principales de las redes profundas y a cómo utilizamos las redes más pequeñas para construirlas. Anteriormente en el libro, presentamos cuatro arquitecturas de red principales:

• Redes Preentrenadas No Supervisadas (UPN)
• Redes neuronales convolucionales (CNN)
• Redes neuronales recurrentes
• Redes neuronales recursivas

En este capítulo, examinaremos con más detalle cada una de estas arquitecturas. En el Capítulo 2, te proporcionamos una comprensión más profunda de los algoritmos y las matemáticas que subyacen a las redes neuronales en general. En este capítulo, nos centramos más en la arquitectura de alto nivel de las distintas redes profundas, con el fin de construir una comprensión adecuada para aplicar estas redes en la práctica.

Cubriremos algunas redes más ligeramente que otras, pero nos centraremos sobre todo en las dos arquitecturas principales que verás en la naturaleza: Las CNN para el modelado de imágenes y las Redes de Memoria Larga a Corto Plazo (LSTM) (Redes Recurrentes) para el modelado de secuencias.

Redes preentrenadas no supervisadas

En este grupo abarca tres arquitecturas concretas:

• Autocodificadores
• Redes profundas de creencias (DBN)
• Redes Generativas Adversariales (GAN)

Nota sobre el papel de los autocodificadores

Como ya tratamos anteriormente en el Capítulo 3, los autocodificadores son estructuras fundamentales en las redes profundas porque a menudo se utilizan como parte de redes más grandes. Como muchas otras redes, cumplen esa función y luego también se utilizan como red independiente.

Como ya hemos tratado en profundidad los autocodificadores, pasaremos a examinar más de cerca las DBN y las GAN.

Redes de Creencias Profundas

Las DBN se componen de capas de Máquinas de Boltzmann Restringidas (RBM) para la fase de preentrenamiento y luego de una red feed-forward para la fase de ajuste fino. La Figura 4-1 muestra la arquitectura de red de una DBN.

Figura 4-1. Arquitectura de la DBN

En las secciones siguientes, explicamos más sobre cómo las DBN aprovechan los RBM para modelar mejor los datos de entrenamiento.

Extracción de rasgos con capas RBM

En utilizamos los RBM para extraer características de nivel superior de los vectores de entrada sin procesar. Para ello, queremos establecer los estados y pesos de las unidades ocultas de forma que, cuando mostremos al RBM un registro de entrada y le pidamos que lo reconstruya, genere algo bastante parecido al vector de entrada original. Hinton habla de este efecto en términos de cómo las máquinas "sueñan con datos".

El propósito fundamental de los RBM en el contexto del aprendizaje profundo y las DBN es aprender estas características de nivel superior de un conjunto de datos de forma no supervisada. Se descubrió que podíamos entrenar mejores redes neuronales dejando que los RBM aprendieran progresivamente características de nivel superior utilizando las características aprendidas de una capa de preentrenamiento RBM de nivel inferior como entrada a una capa de preentrenamiento RBM de nivel superior.

Aprendizaje automático de rasgos de orden superior

Aprender estas características de forma no supervisada se considera la fase de preentrenamiento de las DBN. Cada capa oculta de la RBM en la fase de preentrenamiento aprende características progresivamente más complejas a partir de la distribución de los datos. Estas características de orden superior se combinan progresivamente de forma no lineal para realizar una elegante ingeniería automatizada de características.

Para comprender visualmente la construcción de rasgos con capas de RRBMs, echa un vistazo a las Figuras 4-2, 4-3 y 4-4, que muestran la progresión de renders de activación en un RBM a medida que aprende los dígitos MNIST.

Figura 4-2. Render de activación al inicio del entrenamiento

Figura 4-3. Los rasgos emergen en el render de activación posterior

Figura 4-4. Porciones de dígitos MNIST emergen hacia el final del entrenamiento

Enel capítulo 6 se explica con más detalle cómo se producen estos renders. Podemos ver cómo una capa de RBM extrae fragmentos de dígitos a medida que se entrena. Estas características se combinan después en capas de nivel superior para construir características progresivamente más complejas (y no lineales).

A medida que estos datos brutos se modelan en el proceso de modelado generativo con cada capa del RBM, el sistema es capaz de extraer características de nivel cada vez más alto a partir de los datos de entrada brutos producidos por nuestro proceso de vectorización de entrada de referencia. Estas características avanzan a través de estas capas de RBM en una dirección, produciendo características más elaboradas en la capa superior.

Inicializar la red feed-forward

A continuación, en utilizamos estas capas de características como pesos iniciales en una red neuronal feed-forward tradicional impulsada por retropropagación.

Estos valores de inicialización ayudan al algoritmo de entrenamiento a guiar los parámetros de la red neuronal tradicional hacia mejores regiones del espacio de búsqueda de parámetros. Esta fase se conoce como fase de ajuste fino de las DBN.

Ajuste fino de una DBN con una red neuronal multicapa feed-forward

En la fase de ajuste fino de una DBN utilizamos la retropropagación normal con una tasa de aprendizaje más baja para hacer una retropropagación "suave". Consideramos que la fase de preentrenamiento es una búsqueda general del espacio de parámetros de forma no supervisada basada en datos brutos. En cambio, la fase de ajuste fino consiste en especializar la red y sus características para la tarea que realmente nos interesa (como la clasificación).

Retropropagación suave

La fase de preentrenamiento con RBM aprende características de orden superior a partir de los datos, que utilizamos como buenos valores iniciales de partida para nuestra red feed-forward. Queremos tomar estos pesos y afinarlos un poco más para encontrar buenos valores para nuestro modelo final de red neuronal.

La capa de salida

El objetivo normal de una red profunda es aprender un conjunto de características. La primera capa de una red profunda aprende a reconstruir el conjunto de datos original. Las capas siguientes aprenden a reconstruir las distribuciones de probabilidad de las activaciones de la capa anterior. La capa de salida de una red neuronal está vinculada al objetivo general. Suele ser una regresión logística, con un número de características igual al número de entradas de la capa final, y un número de salidas igual al número de clases.

Estado actual de las DBN

En no tratamos las DBN tan extensamente como las demás arquitecturas de red de este libro. Esto se debe a que en este campo las CNN se han apoderado en gran medida del espacio del modelado de imágenes y, por tanto, hemos optado por hacer más hincapié en esa arquitectura, como verás en la siguiente sección.

El papel de las DBN en el auge del aprendizaje profundo

Aunque en no hacemos tanto hincapié en las DBN en este libro, esta red desempeñó un papel no trivial en el auge del aprendizaje profundo. El equipo de Geoff Hinton de la Universidad de Toronto persistió durante mucho tiempo en el avance de las técnicas en el espacio del modelado de imágenes para producir grandes avances. Nos pareció importante señalar el papel que las DBN han desempeñado en la evolución de las redes profundas.

Redes Generativas Adversariales

Una red digna de mención es la GAN.¹ Se ha demostrado que las GAN son bastante adeptas a sintetizar nuevas imágenes novedosas basándose en otras imágenes de entrenamiento. Podemos ampliar este concepto para modelar otros dominios como los siguientes:

• Sonido
• Vídeo²
• Generar imágenes a partir de descripciones de texto³

Las GAN son un ejemplo de red que utiliza el aprendizaje no supervisado para entrenar dos modelos en paralelo. Un aspecto clave de las GAN (y de los modelos generativos en general) es que utilizan un número de parámetros significativamente menor de lo normal con respecto a la cantidad de datos sobre los que estamos entrenando la red. La red se ve obligada a representar eficientemente los datos de entrenamiento, lo que la hace más eficaz a la hora de generar datos similares a los de entrenamiento.

Entrenamiento de modelos generativos, aprendizaje no supervisado y GANs

Si tuviéramos un gran corpus de imágenes de entrenamiento (como el conjunto de datos ImageNet ), podríamos construir una red neuronal generativa que diera como salida imágenes (en lugar de clasificaciones). Consideraríamos estas imágenes de salida generadas como muestras del modelo. El modelo generativo de las GAN genera esas imágenes, mientras que una red secundaria "discriminadora" intenta clasificar esas imágenes generadas.

Esta red discriminadora secundaria intenta clasificar las imágenes de salida como reales o sintéticas. Al entrenar las GAN, queremos actualizar los parámetros de modo que la red genere imágenes de salida más creíbles basándose en los datos de entrenamiento. El objetivo aquí es hacer que las imágenes sean lo suficientemente realistas como para que la red discriminadora sea engañada hasta el punto de que no pueda distinguir la diferencia entre los datos de entrada reales y los sintéticos.

Un ejemplo de la eficacia de la representación del modelo en las GAN es cómo suelen tener alrededor de 100 millones de parámetros cuando modelan un conjunto de datos como ImageNet. En el transcurso del entrenamiento, un conjunto de datos de entrada como ImageNet (200 GB) se convierte en cerca de 100 MB de parámetros. Este proceso de aprendizaje intenta encontrar la forma más eficaz de representar las características de los datos, como grupos similares de píxeles, perímetros y otros patrones (como veremos con más detalle en "Redes neuronales convolucionales (CNN)").

La red discriminadora

Cuando modela imágenes, la red discriminadora suele ser una CNN estándar. Utilizar una red neuronal secundaria como red discriminadora permite a la GAN entrenar ambas redes en paralelo de forma no supervisada. Estas redes discriminadoras toman las imágenes como entrada y luego emiten una clasificación.

El gradiente de la salida de la red discriminadora respecto a los datos de entrada sintéticos indica cómo introducir pequeños cambios en los datos sintéticos para hacerlos más realistas.

La red generativa

La red generativa de las GAN genera datos (o imágenes) con un tipo especial de capa llamada capa deconvolucional (lee más sobre las redes y capas deconvolucionales en el siguiente recuadro).

Durante el entrenamiento, utilizamos la retropropagación en ambas redes para actualizar los parámetros de la red generadora y generar imágenes de salida más realistas. El objetivo aquí es actualizar los parámetros de la red generadora hasta el punto en que la red discriminadora sea suficientemente "engañada" por la red generadora porque la salida es muy realista en comparación con las imágenes reales de los datos de entrenamiento.

Redes deconvolucionales

Este tipo de red fue desarrollado por Matthew Zeiler y Rob Fergus de la Universidad de Nueva York como parte del desarrollo de ZF Net en el artículo "Visualizing and Understanding Convolutional Neural Networks" (2013). Una red deconvolucional nos ayuda a examinar diferentes activaciones de rasgos y su relación con el espacio de entrada(Figura 4-5).

Figura 4-5. Visualización de las capas deconvolucionales

Las capas deconvolucionales de una red deconvolucional ("deconvnet" para abreviar) asignan características a píxeles al modelar imágenes, como se ve en la Figura 4-5, que es lo contrario de lo que hace una capa convolucional normal. Este aspecto de las redes deconvolucionales es lo que nos permite generar imágenes como salida de las redes neuronales. Las redes deconvolucionales no están supervisadas y se entrenan por capas, de forma similar a una DBN. La red tiene varias capas deconvolucionales apiladas en las que cada capa se entrena con la entrada de la capa anterior. La idea general con la información que pasa por las capas es que la salida de cada capa es una representación dispersa de la entrada a la capa.

Construir modelos generativos y Redes Adversariales Generativas Convolucionales Profundas

Una variante de las GAN es la Red Adversarial Generativa Convolucional Profunda (DCGAN). La Figura 4-6 muestra imágenes de dormitorios generadas a partir de una DCGAN.

Figura 4-6. Imágenes generadas de dormitorios de una red DCGAN⁴

Esta red toma números aleatorios (de una distribución uniforme) y genera una imagen del modelo de red como salida. A medida que cambian los números aleatorios de entrada, vemos que el DCGAN genera distintos tipos de imágenes.

GAN condicionales

GAN condicionales⁵ también pueden utilizar la información de la etiqueta de clase, lo que les permite generar condicionalmente datos de una clase específica.

Comparación entre GAN y autocodificadores variacionales

Las GAN se centran en intentar clasificar los registros de entrenamiento como pertenecientes a la distribución del modelo o a la distribución real. Cuando el modelo discriminador hace una predicción en la que hay una diferencia entre las dos distribuciones, la red generadora ajusta sus parámetros. Finalmente, el generador converge en unos parámetros que reproducen la distribución real de los datos, y el discriminador es incapaz de detectar la diferencia.

Con los autocodificadores variacionales (VAE) estamos planteando este mismo problema con modelos gráficos probabilísticos para reconstruir la entrada de forma no supervisada, como se ha visto anteriormente en el Capítulo 3. Los VAE intentan maximizar un límite inferior en la probabilidad logarítmica de los datos, de modo que las imágenes generadas parezcan cada vez más reales.

Otra diferencia interesante entre las GAN y las VAE es cómo se generan las imágenes. Con las GAN básicas, la imagen se genera con un código arbitrario y no tenemos forma de generar una imagen con características específicas. Los VAE, en cambio, tienen un esquema específico de codificación/decodificación con el que podemos comparar la imagen generada con la imagen original. Esto nos da el efecto secundario de poder codificar para que se generen tipos específicos de imágenes.

Problemas con los modelos generativos

A veces con imágenes generadas también obtenemos un tipo diferente de ruido en la imagen de salida generada. El inconveniente de las imágenes generadas por VAE es que, debido a la forma en que se generan, a veces son ligeramente borrosas. Las imágenes generadas por GAN tienden a captar el estilo de los datos de entrada, pero a veces no componen la escena de forma coherente (por ejemplo, es una imagen de un perro, pero el perro no se ve del todo bien).

Redes neuronales convolucionales (CNN)

El objetivo de una CNN es aprender características de orden superior en los datos mediante convoluciones. Son muy adecuadas para el reconocimiento de objetos con imágenes y ocupan sistemáticamente los primeros puestos en los concursos de clasificación de imágenes. Pueden identificar caras, individuos, señales de tráfico, ornitorrincos y muchos otros aspectos de los datos visuales. Las CNN se solapan con el análisis de textos mediante el reconocimiento óptico de caracteres, pero también son útiles para analizar palabras⁶ como unidades textuales discretas. También son buenas analizando sonidos.

La eficacia de las CNN en el reconocimiento de imágenes es una de las principales razones por las que el mundo reconoce el poder del aprendizaje profundo. Como ilustra la Figura 4-7, las CNN son buenas construyendo características invariantes de posición y (en cierto modo) de rotación a partir de datos de imágenes sin procesar.

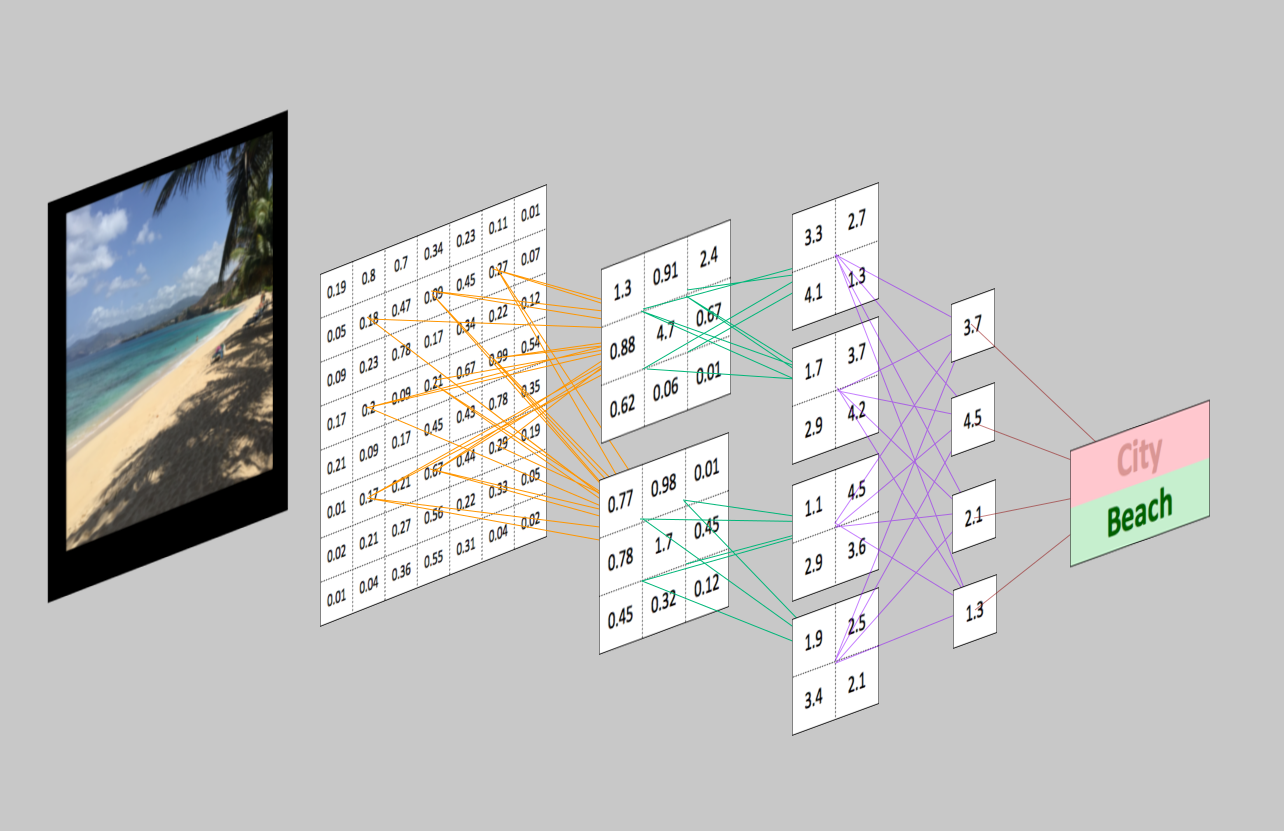
Figura 4-7. Las CNN y la visión por ordenador

Las CNN están impulsando importantes avances en visión artificial, lo que tiene aplicaciones obvias para los coches autoconducidos, la robótica, los drones y los tratamientos para los discapacitados visuales.

Las CNN y la estructura de los datos

Las CNN suelen ser más útiles cuando hay cierta estructura en los datos de entrada. Un ejemplo sería cómo se relacionan espacialmente las imágenes y los datos de audio que tienen un conjunto específico de patrones repetitivos y valores de entrada próximos entre sí. Por el contrario, los datos en columnas exportados de un sistema de gestión de bases de datos relacionales (RDBMS) tienden a no tener relaciones estructurales espacialmente. Las columnas contiguas simplemente se materializan de esa forma en la vista materializada exportada de la base de datos.

Las CNN también se han utilizado en otras tareas, como la traducción/generación de lenguaje natural⁷ y el análisis de sentimientos.⁸ Una convolución es un concepto poderoso para ayudar a construir un espacio de características más robusto basado en una señal.

Inspiración biológica

La inspiración biológica de las CNN es la corteza visual de los animales.⁹ Las células de la corteza visual son sensibles a pequeñas subregiones de la entrada. A esto lo llamamos campo visual (o campo receptivo). Estas subregiones más pequeñas se agrupan en mosaico para cubrir todo el campo visual. Las células están bien adaptadas para explotar la fuerte correlación espacial local que se encuentra en los tipos de imágenes que procesa nuestro cerebro, y actúan como filtros locales sobre el espacio de entrada. Hay dos clases de células en esta región del cerebro. Las células simples se activan cuando detectan patrones similares a perímetros, y las células más complejas se activan cuando tienen un campo receptivo mayor y son invariables a la posición del patrón.

Intuición

Las redes neuronales multicapa Feed-forward toman la entrada como un único vector unidimensional y transforman los datos con una o más capas ocultas (totalmente conectadas). A continuación, la red da un resultado a partir de la capa de salida. El problema que nos encontramos con las redes neuronales multicapa tradicionales y los datos de imágenes es que estas redes no escalan bien con datos de imágenes como entrada. Un ejemplo sería modelar el conjunto de datos CIFAR-10 (véase el próximo recuadro). Las imágenes sobre las que se entrena tienen sólo 32 píxeles de ancho por 32 píxeles de alto, con 3 canales de información RGB. Sin embargo, esto crea 3.072 pesos por neurona en la primera capa oculta, y probablemente querremos más de una neurona en esa capa oculta. En muchos casos, querremos varias capas ocultas en nuestra red neuronal multicapa, lo que multiplicará también esos pesos.

¿Qué es el conjunto de datos CIFAR-10?

El conjunto de datos CIFAR-10 es un conocido conjunto de datos de referencia de clasificación de imágenes recopilado por Alex Krizhevsky, Vinod Nair y Geoffrey Hinton. El conjunto de datos tiene 60.000 imágenes en color con 10 clases diferentes que comprenden 6.000 imágenes por clase. Las imágenes tienen 32 × 32 píxeles cada una. Hay 50.000 imágenes de entrenamiento y 10.000 imágenes de prueba. La Figura 4-8 muestra las clases de imágenes del conjunto de datos.

Figura 4-8. El conjunto de datos CIFAR-10

Las clases no se solapan, lo que significa que una imagen de un camión sólo contendrá una imagen de un camión. El conjunto de datos tiene un tamaño de unos 170 MB.

Una imagen normal podría tener fácilmente 300 píxeles de ancho por 300 de alto, con 3 canales de información RGB. Esto crearía 270.000 pesos de conexión por neurona oculta. Esto demuestra lo rápido que una red multicapa totalmente conectada crea un número masivo de conexiones al modelar datos de imagen. La estructura de los datos de imagen nos permite cambiar la arquitectura de una red neuronal de forma que podamos aprovechar esta estructura. Con las CNN, podemos disponer las neuronas en una estructura tridimensional para la que tenemos lo siguiente:

• Anchura
• Altura
• Profundidad

Estos atributos de la entrada coinciden con una estructura de imagen para la que tenemos:

• Anchura de la imagen en píxeles
• Altura de la imagen en píxeles
• canales RGB como profundidad

Podemos considerar esta estructura como un volumen tridimensional de neuronas. Un aspecto significativo de cómo evolucionaron las CNN a partir de las variantes anteriores de alimentación hacia delante es cómo lograron la eficiencia computacional con nuevos tipos de capas. Trataremos esta disposición con más profundidad momentáneamente. Echemos ahora un vistazo a la arquitectura general de alto nivel de las CNN.

Visión general de la arquitectura de la CNN

Las CNN transforman los datos de entrada de la capa de entrada a través de todas las capas conectadas en un conjunto de puntuaciones de clase dadas por la capa de salida. Existen muchas variaciones de la arquitectura de las CNN, pero se basan en el patrón de capas, como se muestra en la Figura 4-9.

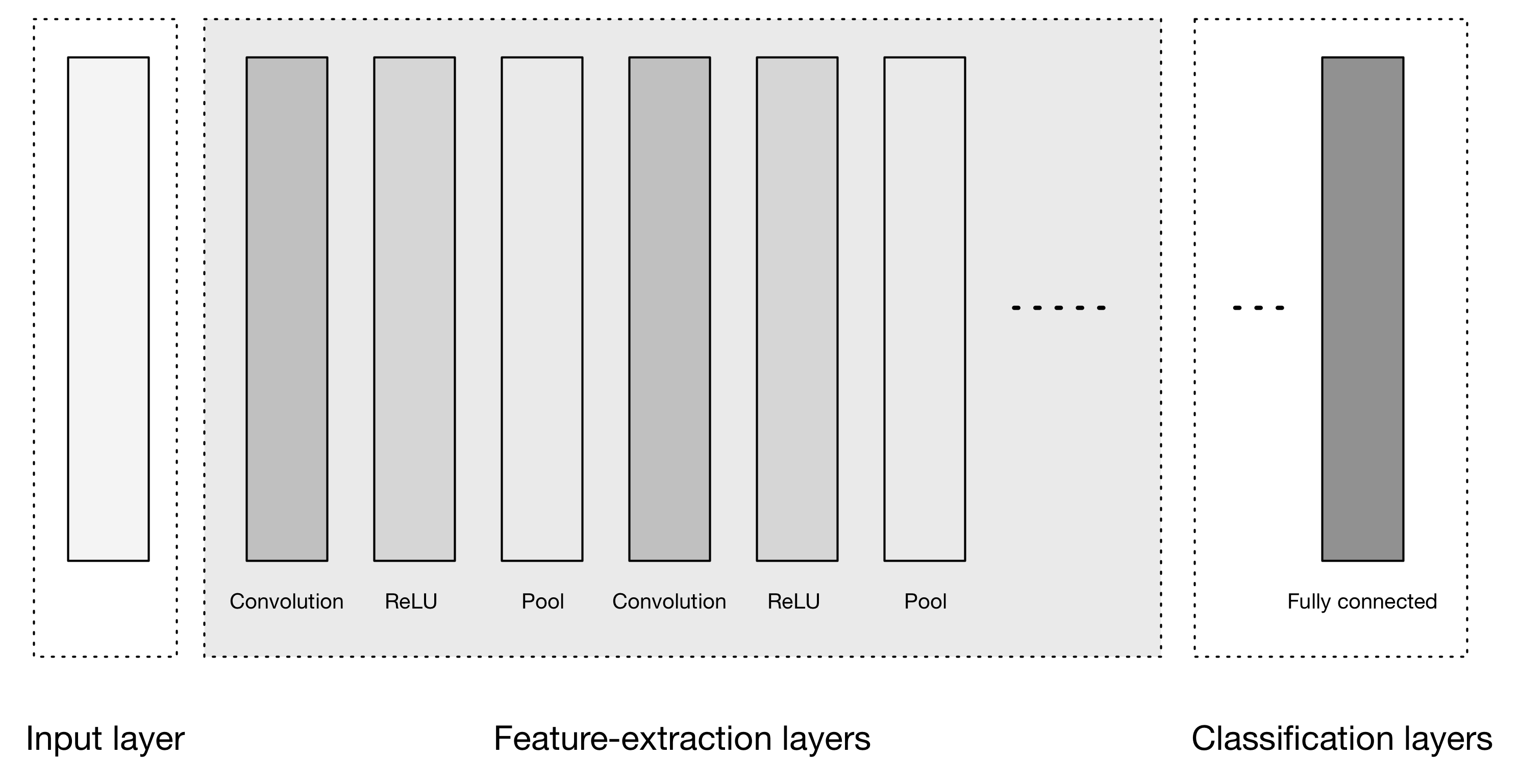
Figura 4-9. Arquitectura general de alto nivel de la CNN

La Figura 4-9 muestra tres grandes grupos:

1. Capa de entrada
2. Capas de extracción de rasgos (aprendizaje)
3. Capas de clasificación

La capa de entrada acepta la entrada tridimensional, generalmente en la forma espacial del tamaño (anchura × altura) de la imagen, y tiene una profundidad que representa los canales de color (generalmente tres para los canales de color RGB).

El minilote como cuarta dimensión

Cuando agrupamos los ejemplos por lotes en un minilote para el entrenamiento, acabamos teniendo cuatro dimensiones: una dimensión más para indexar el ejemplo dentro del minilote. Así, en DL4J, las matrices de datos de entrenamiento de imágenes tienen cuatro dimensiones, no sólo tres.

Las capas de extracción de rasgos tienen un patrón general de repetición de la secuencia:

1. Capa de convolución

   Expresamos aquí la función de activación Unidad Lineal Rectificada (ReLU) como una capa en el diagrama, para que coincida con otra bibliografía.

2. Capa de agrupamiento

Estas capas encuentran una serie de características en las imágenes y construyen progresivamente características de orden superior. Esto se corresponde directamente con el tema actual del aprendizaje profundo, según el cual las características se aprenden automáticamente, en lugar de diseñarse a mano tradicionalmente.

Por último, tenemos las capas de clasificación, en las que tenemos una o varias capas totalmente conectadas para tomar las características de orden superior y producir probabilidades de clase o puntuaciones. Estas capas están totalmente conectadas a todas las neuronas de la capa anterior, como su nombre indica. La salida de estas capas produce normalmente una salida bidimensional de las dimensiones[b × N], donde b es el número de ejemplos del minilote y N es el número de clases que nos interesa puntuar.

Disposición espacial de las neuronas

Recuerda que en las redes neuronales multicapa tradicionales, las capas están totalmente conectadas y cada neurona de una capa está conectada a cada neurona de la capa siguiente. Las neuronas de las capas de una CNN están dispuestas en tres dimensiones para coincidir con los volúmenes de entrada. Aquí, profundidad significa la tercera dimensión del volumen de activación, no el número de capas, como en una red neuronal multicapa.

Evolución de las conexiones entre capas

Otro cambio es cómo conectamos las capas en una arquitectura convolucional. Las neuronas de una capa sólo están conectadas a una pequeña región de neuronas de la capa anterior. Las CNN conservan una arquitectura orientada a capas, como en las redes multicapa tradicionales, pero tienen distintos tipos de capas. Cada capa transforma el volumen de entrada 3D de la capa anterior en un volumen de salida 3D de activaciones neuronales con alguna función diferenciable que puede o no tener parámetros, como se muestra en la Figura 4-10.

Capas de entrada

Capas de entrada es donde cargamos y almacenamos los datos de entrada brutos de la imagen para procesarlos en la red. Estos datos de entrada especifican la anchura, la altura y el número de canales. Normalmente, el número de canales es tres, para los valores RGB de cada píxel.

Figura 4-10. Volumen 3D de la capa de entrada

Capas convolucionales

Las capas convolucionales se consideran los componentes básicos de las arquitecturas CNN. Como ilustra la Figura 4-11, las capas convolucionales transforman los datos de entrada utilizando un parche de neuronas conectadas localmente de la capa anterior. La capa calculará un producto punto entre la región de las neuronas de la capa de entrada y los pesos a los que están conectadas localmente en la capa de salida.

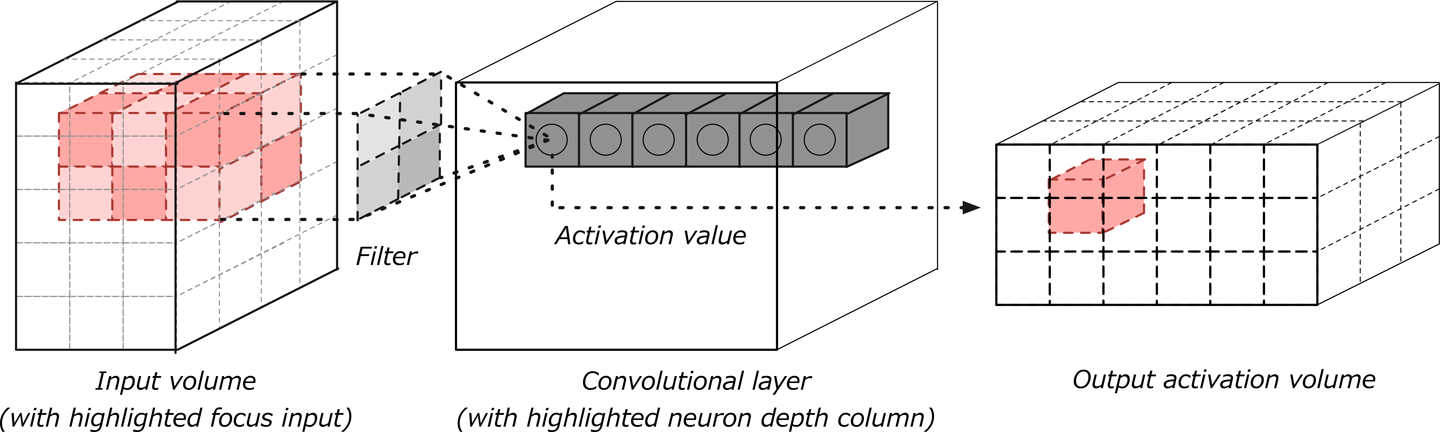
Figura 4-11. Capa de convolución con volúmenes de entrada y salida

La salida resultante suele tener las mismas dimensiones espaciales (o dimensiones espaciales menores), pero a veces aumenta el número de elementos en la tercera dimensión de la salida (dimensión de profundidad). Veamos más detenidamente un concepto clave de estas capas, llamado convolución.

Convolución

Una convolución se define como una operación matemática que describe una regla para fusionar dos conjuntos de información. Es importante tanto en física como en matemáticas y define un puente entre el dominio espacio/tiempo y el dominio de la frecuencia mediante el uso de las transformadas de Fourier. Toma una entrada, aplica un núcleo de convolución y nos da un mapa de características como salida.

La operación de convolución , mostrada en la Figura 4-12, se conoce como el detector de características de una CNN. La entrada de una convolución pueden ser datos sin procesar o un mapa de características resultante de otra convolución. A menudo se interpreta como un filtro en el que el núcleo filtra los datos de entrada para determinados tipos de información; por ejemplo, un núcleo de perímetro sólo deja pasar la información del borde de una imagen.

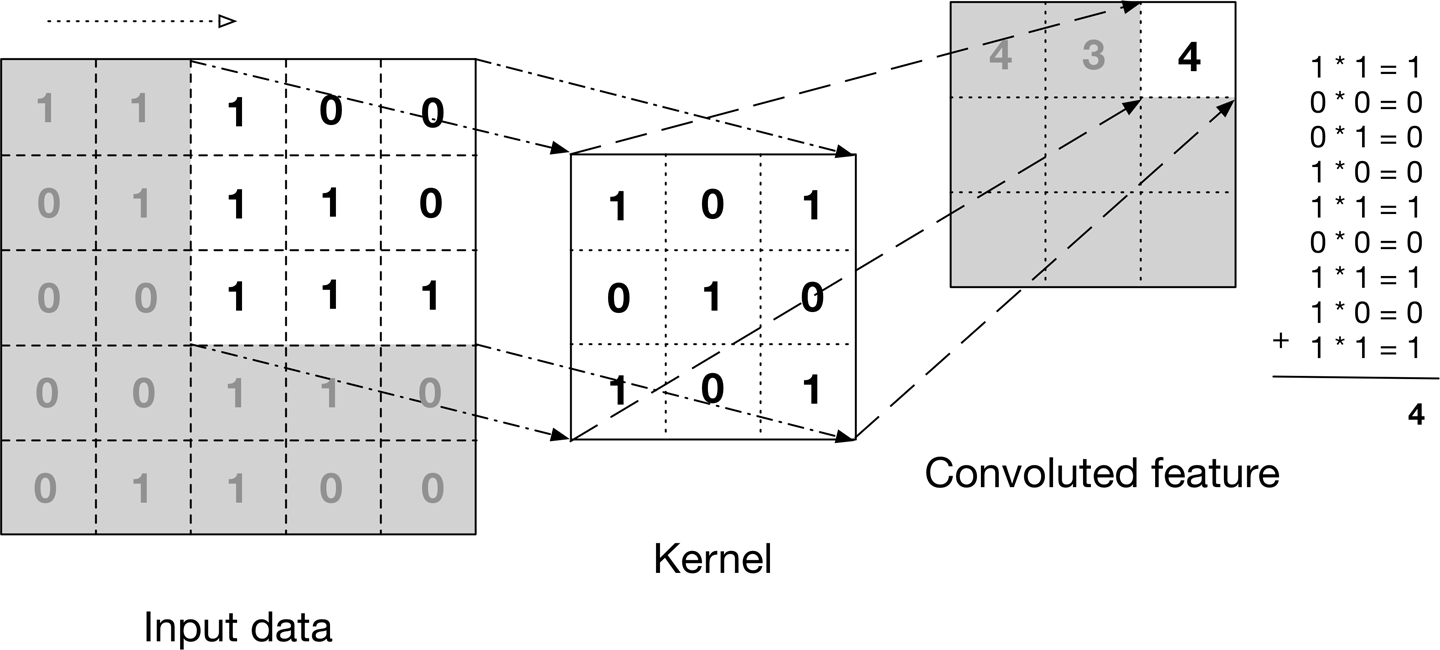
Figura 4-12. La operación de convolución

La figura ilustra cómo se desliza el núcleo a través de los datos de entrada para producir los datos de características convolucionadas (de salida). En cada paso, el núcleo se multiplica por los valores de los datos de entrada dentro de sus límites, creando una única entrada en el mapa de características de salida. En la práctica, la salida es grande si la característica que buscamos se detecta en la entrada.

Solemos referirnos a los conjuntos de pesos de una capa convolucional como un filtro (o núcleo). Este filtro se convoluciona con la entrada y el resultado es un mapa de características (o mapa de activación). Las capas convolucionales realizan transformaciones en el volumen de datos de entrada que son una función de las activaciones en el volumen de entrada y los parámetros (pesos y sesgos de las neuronas). El mapa de activación de cada filtro se apila a lo largo de la dimensión de profundidad para construir el volumen de salida 3D.

Las capas convolucionales tienen parámetros para la capa e hiperparámetros adicionales. El descenso gradiente se utiliza para entrenar los parámetros de esta capa de forma que las puntuaciones de clase sean coherentes con las etiquetas del conjunto de entrenamiento. A continuación se describen los principales componentes de las capas convolucionales:

• Filtros
• Mapas de activación
• Compartir parámetros
• Hiperparámetros específicos de capa

Veamos los detalles de cada componente.

Filtros

Los parámetros de una capa convolucional configuran el conjunto de filtros de la capa. Los filtros son una función que tiene una anchura y una altura menores que la anchura y la altura del volumen de entrada.

Tamaños de filtro en aplicaciones de procesamiento del lenguaje natural

Nosotros podemos tener un tamaño de filtro igual al volumen de entrada, pero normalmente sólo en una dimensión, no en ambas. Esto sería algo a tener en cuenta para los casos en que aplicaríamos las CNN a casos de uso en el Procesamiento del Lenguaje Natural (PLN).

Los filtros (por ejemplo, las convoluciones) se aplican a lo ancho y alto del volumen de entrada en forma de ventana deslizante, como se muestra en la Figura 4-12. También se aplican filtros para cada profundidad del volumen de entrada. Calculamos la salida del filtro produciendo el producto punto del filtro y la región de entrada.

Mapas de recuento y activación de filtros

El resultado de aplicar un filtro al volumen de entrada se conoce como mapa de activación (a veces denominado mapa de características) de ese filtro. En muchos diagramas de CNN, a menudo vemos montones de pequeños mapas de activación; cómo se producen a veces puede resultar confuso.

El recuento de filtros es un valor de hiperparámetro para cada capa convolucional. Este hiperparámetro también controla cuántos mapas de activación se producen desde la capa convolucional como entrada en la capa siguiente y se considera la tercera dimensión (número de mapas de activación) en el volumen de activación de salida de la capa 3D. El hiperparámetro de recuento de filtros puede elegirse libremente, aunque algunos valores funcionarán mejor que otros.

La arquitectura de las CNN se configura de modo que los filtros aprendidos produzcan la activación más fuerte ante patrones de entrada espacialmente locales. Esto significa que se aprenden filtros que se activarán sobre patrones (o características) sólo cuando los patrones se den en los datos de entrenamiento en su campo respectivo. A medida que avanzamos en capas en una CNN, nos encontramos con filtros que pueden reconocer combinaciones no lineales de rasgos y son cada vez más globales en su forma de detectar patrones. Las arquitecturas convolucionales de alto rendimiento (que veremos más adelante en esta sección) han demostrado que la profundidad de la red es un factor importante en las CNN.

Mapas de activación

Recuerda del Capítulo 1 que una activación es un resultado numérico si una neurona decide dejar pasar información. Es una función de las entradas a la función de activación, los pesos en las conexiones (para las entradas, y el tipo de función de activación en sí). Cuando decimos que el filtro "se activa", queremos decir que el filtro deja pasar información a través de él desde el volumen de entrada al volumen de salida.

Deslizamos cada filtro a través de las dimensiones espaciales (anchura, altura) del volumen de entrada durante el paso hacia delante de la información a través de la CNN. Esto produce una salida bidimensional denominada mapa de activación para ese filtro concreto. La Figura 4-13 muestra cómo se relaciona este mapa de activación con el concepto de característica convoluta que hemos introducido anteriormente.

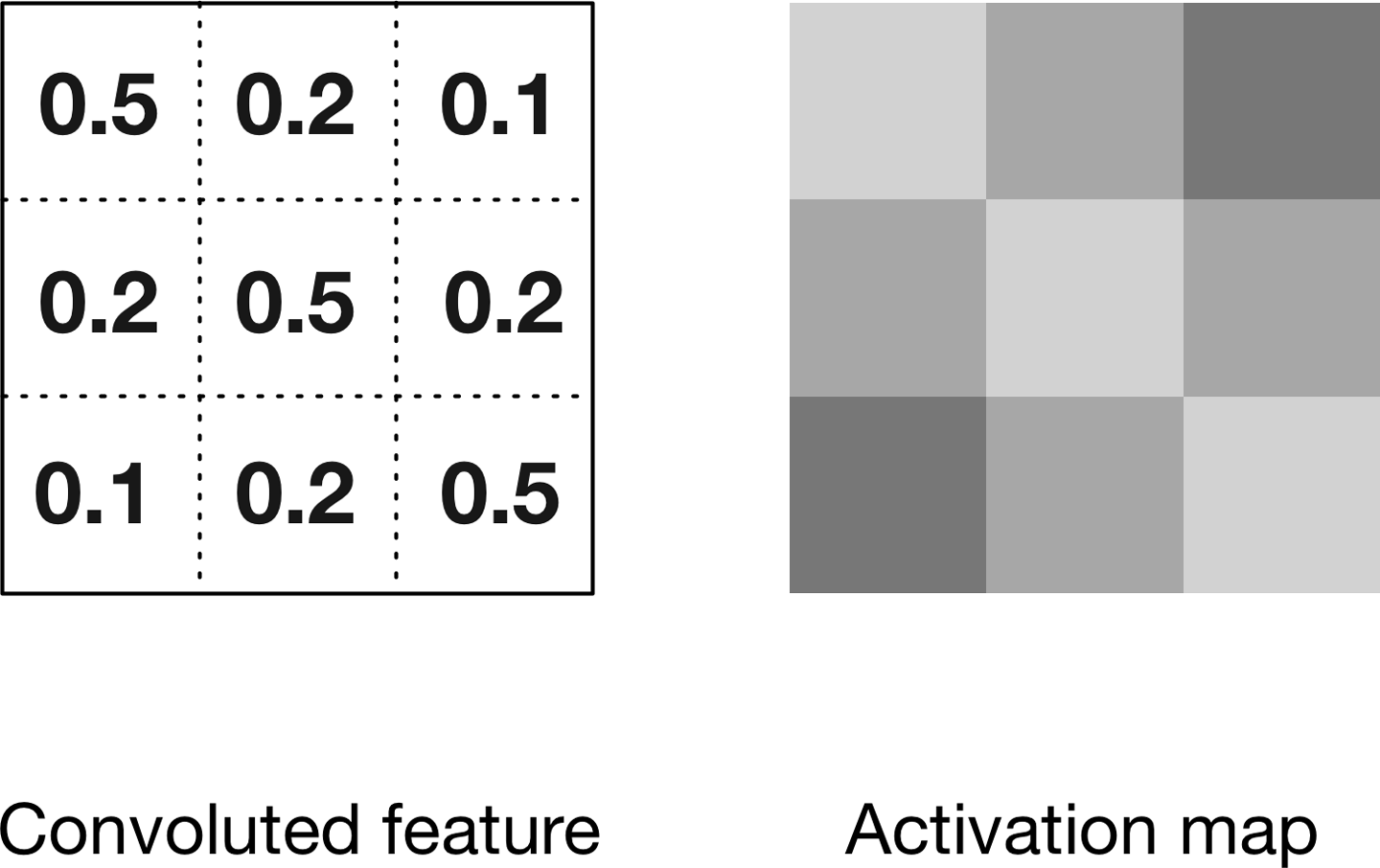
Figura 4-13. Convoluciones y mapas de activación

El mapa de activación de la derecha de la Figura 4-13 se representa de forma diferente para ilustrar cómo se representan habitualmente los mapas de activación convolucionales en la bibliografía.

Mapas de activación

En algunas publicaciones, la salida del mapa de activación se denomina mapa de características, pero en este texto nos referiremos a él como mapa de activación.

Para calcular el mapa de activación, deslizamos el filtro por el corte de profundidad del volumen de entrada. Calculamos el producto punto entre las entradas del filtro y el volumen de entrada. El filtro representa los pesos que se multiplican por la ventana móvil (subconjunto) de activaciones de entrada. Las redes aprenden filtros que se activan cuando ven determinados tipos de características en los datos de entrada en una posición espacial específica.

Creamos el volumen de salida tridimensional para la capa de convolución apilando estos mapas de activación a lo largo de la dimensión de profundidad en la salida, como se muestra en la Figura 4-14. El volumen de salida tendrá entradas que consideramos la salida de una neurona que mira sólo una pequeña ventana del volumen de entrada.

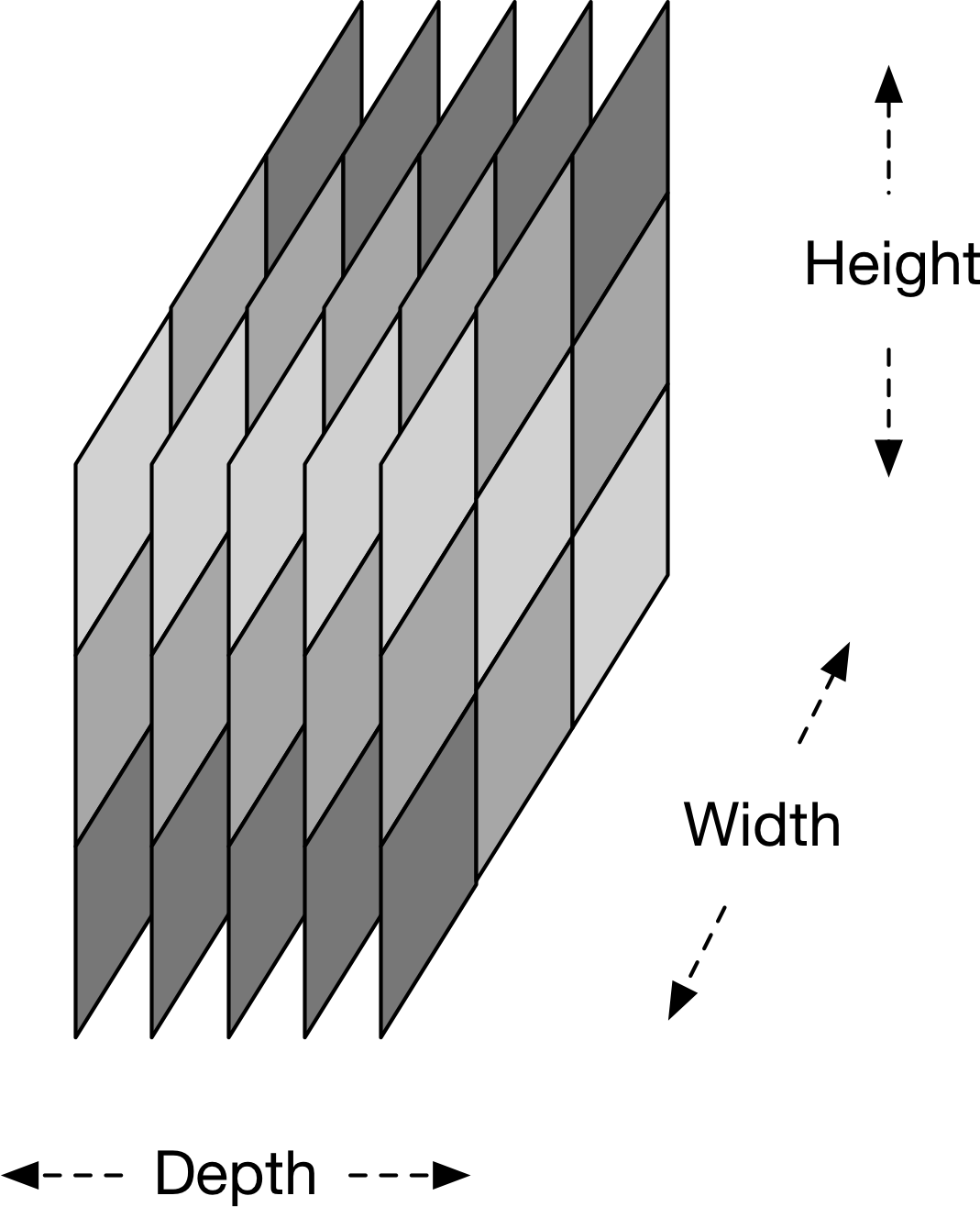
Figura 4-14. Salida del volumen de activación de la capa convolucional

En algunos casos, esta salida será el resultado de parámetros compartidos con neuronas del mismo mapa de activación. Cada neurona que genera el volumen de salida está conectada sólo a una región local del volumen de entrada, como se muestra en la Figura 4-15.

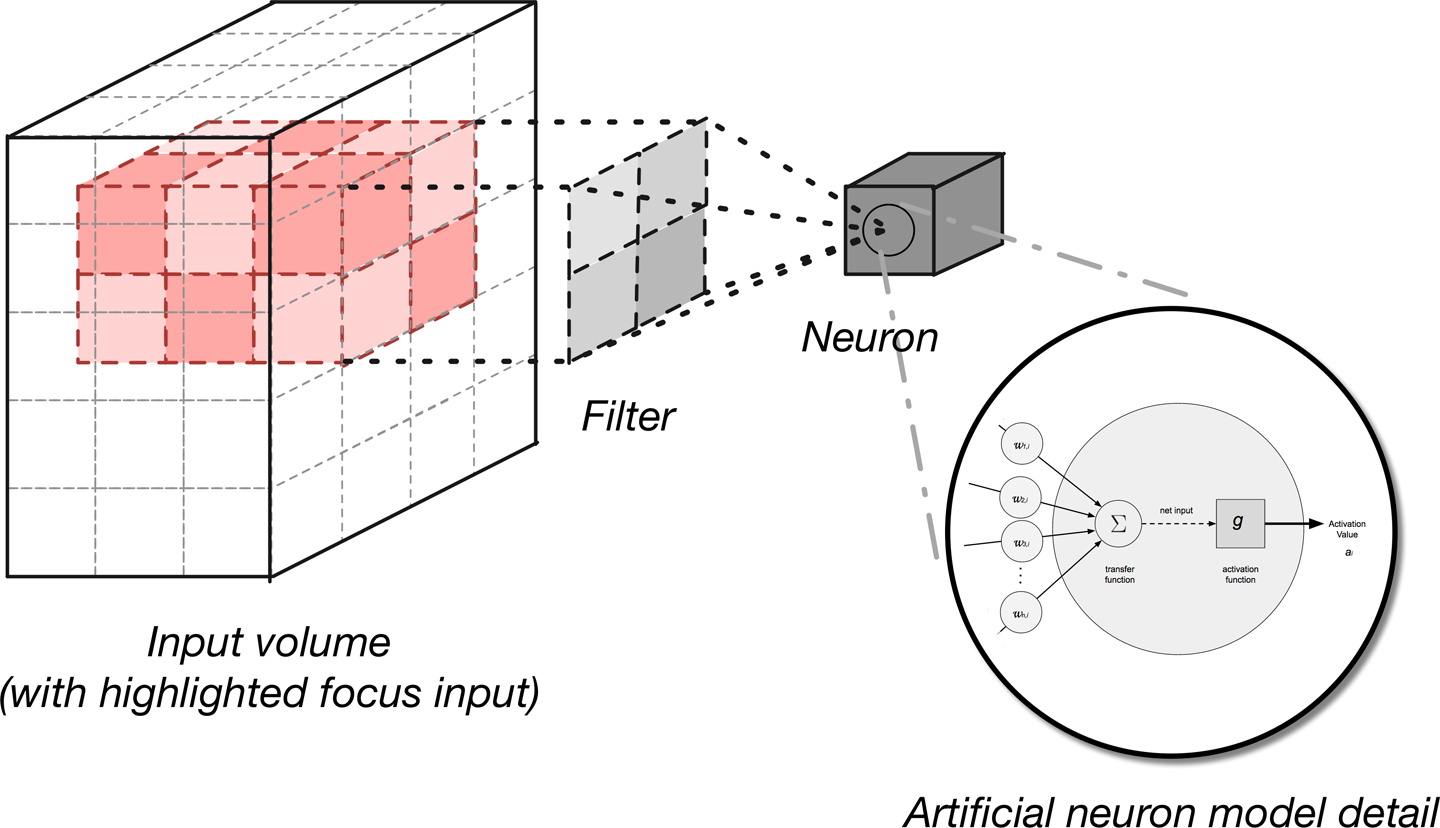
Figura 4-15. Generar un volumen de salida de activación

Nosotros controlamos la conectividad local de este proceso con el hiperparámetro llamado campo receptivo, que controla qué parte de la anchura y la altura del volumen de entrada mapea nuestro filtro.

Control de la conectividad local con el campo receptivo

Las neuronas de una capa están conectadas a una región más pequeña del volumen de entrada a lo largo de las dimensiones espaciales (anchura y altura), pero la conectividad a lo largo del eje de profundidad es siempre igual a la profundidad del volumen de entrada. Esto significa que siempre tenemos conectividad completa a lo largo de la profundidad del volumen de entrada. Veamos un ejemplo de esto basado en los datos de entrada CIFAR-10(imagen RGB) que viste en "¿Qué es el conjunto de datos CIFAR-10?".

En esta situación, el volumen de entrada tiene el tamaño 32 × 32 × 3 y nuestro hiperparámetro de campo receptivo se establece en 5 × 5. Cada neurona de la capa convolucional tendrá pesos para una región de 5 × 5 × 3 en el volumen de entrada. Esto nos da 5 * 5 * 3 = 75 pesos para cada neurona de nuestra capa convolucional.

Observamos que la profundidad del volumen de entrada es 3, que es siempre la profundidad de la conectividad del peso en la capa de convolución. La región a la que se conecta la neurona es menor que la anchura y la altura de la imagen, pero la profundidad siempre es la misma.

Nuestra conectividad en las capas convolucionales puede ser local, pero las neuronas en sí no cambian. Seguimos calculando un producto punto de los pesos con la entrada mediante una función no lineal.

La única diferencia ahora es que la neurona está conectada sólo a un subconjunto de la entrada y no a todas las neuronas de la capa anterior, como en las redes neuronales multicapa tradicionales. Consideraríamos que esta conectividad es de profundidad total pero espacialmente local.

Los filtros definen una región delimitada más pequeña para generar mapas de activación a partir de los volúmenes de entrada. Están conectados sólo a un subconjunto del volumen de entrada mediante la dinámica de conectividad local descrita anteriormente. Esto nos permite seguir teniendo una extracción de rasgos de calidad, a la vez que reducimos el número de parámetros por capa que necesitamos entrenar. Las capas convolucionales reducen aún más el número de parámetros mediante una técnica llamada compartir parámetros.

Compartir parámetros

Las CNN utilizan un esquema de parámetros compartidos para controlar el número total de parámetros. Esto ayuda al tiempo de entrenamiento porque utilizaremos menos recursos para aprender el conjunto de datos de entrenamiento. Para aplicar el reparto de parámetros en las CNN, primero denotamos un único corte bidimensional de profundidad como "corte de profundidad". Luego obligamos a las neuronas de cada corte de profundidad a utilizar los mismos pesos y sesgos. Esto nos proporciona un número significativamente menor de parámetros (o pesos) para una capa convolucional determinada.

No podemos aprovechar la compartición de parámetros cuando las imágenes de entrada sobre las que entrenamos tienen una estructura centrada específica. Vemos este efecto en los rostros cuando siempre esperamos que una característica específica aparezca en un lugar concreto (para rostros centrados). En este caso, probablemente no utilizaríamos la compartición de parámetros. La compartición de parámetros es lo que también confiere a las CNN invariancia a la traslación/posición.

Filtros y renders aprendidos

Figura 4-16 presenta un ejemplo de los 96 filtros aprendidos de tamaño 11 × 11 × 3. Con el esquema de parámetros compartidos, vemos que la detección de un perímetro horizontal es útil en muchos lugares de la imagen debido a la naturaleza invariante traslacional de las imágenes. Esto significa que podemos aprender el perímetro horizontal en un lugar y luego no preocuparnos de aprenderlo como característica en todas las posiciones de la imagen.

Figura 4-16. Ejemplo de filtros aprendidos por Krizhevsky et al.¹⁰ (96 filtros, 11 × 11 × 3)

Rompiendo un poco esto, pensemos en una imagen 2D. Si subdividimos una imagen en cuatro secciones, la red neuronal aprenderá características de la imagen invariantes respecto a la posición. La razón de que sean invariantes respecto a la posición es el modo en que la red subdivide los datos en cuadrantes. Luego aprende porciones de la imagen cada vez y agrupa los resultados. Esto permite a la red neuronal aprender una representación global que no es local a ningún conjunto concreto de características. Hablaremos más sobre la generación de renders de filtro en el Capítulo 6.

Invarianza de rotación en las características de las CNN

Las características aprendidas en son invariantes de posición por diseño, pero no son (en general) invariantes de rotación. Sin embargo, puedes conseguir cierto nivel de invariancia de rotación con un aumento adecuado de los datos.

Funciones de activación ReLU como capas

En las CNN de , a menudo vemos que se utilizan capas ReLU. La capa ReLU aplicará una función de activación por elementos sobre los datos de entrada, umbralizando -por ejemplo, max(0,x)- en cero, lo que nos dará la misma dimensión de salida que la entrada a la capa.

DL4J, tipos de capas y funciones de activación

En DL4J, identificamos las capas con el tipo de función de activación de su neurona (pero esto no siempre se refleja en los nombres de las clases de capas). DL4J tiene funciones de activación integradas en las propias capas. Otras bibliotecas, como Caffe, utilizan capas de activación independientes.

Al ejecutar esta función sobre el volumen de entrada, cambiarán los valores de los píxeles, pero no cambiarán las dimensiones espaciales de los datos de entrada en la salida. Las capas ReLU no tienen parámetros ni hiperparámetros adicionales.

Hiperparámetros de la capa convolucional

A continuación están los hiperparámetros¹¹ que dictan la disposición espacial y el tamaño del volumen de salida de una capa convolucional son:

• Tamaño del filtro (o núcleo) (tamaño del campo)
• Profundidad de salida
• Zancada
• Sin relleno

Más información sobre el dimensionamiento de las capas convolucionales en el capítulo 7

En esta sección explicamos cómo funcionan estos hiperparámetros. En el Capítulo 7, exponemos la mecánica de ajuste de las capas de la CNN.

Tamaño del filtro

Cada filtro de es pequeño espacialmente con respecto a la anchura y la altura del tamaño del filtro. Un ejemplo de esto es cómo la primera capa convolucional podría tener un filtro de tamaño 5 × 5 × 3. Esto significaría que el filtro tiene 5 píxeles de ancho por 5 de alto, con 3 representando los canales de color, suponiendo que la imagen de entrada estuviera en color RGB de 3 canales.

Profundidad de salida

En podemos elegir manualmente la profundidad del volumen de salida. El hiperparámetro profundidad controla el número de neuronas de la capa convolucional que están conectadas a la misma región del volumen de entrada.

Perímetros y activación

Diferentes neuronas a lo largo de la dimensión de profundidad aprenden a activarse cuando se las estimula con datos de entrada creados (por ejemplo, color o perímetros).

Consideramos un conjunto de neuronas que miran todas a la misma región del volumen de entrada como una columna de profundidad.

Zancada

Stride configura hasta dónde se moverá nuestra ventana de filtro deslizante por aplicación de la función de filtro. Cada vez que aplicamos la función de filtro a la columna de entrada, creamos una nueva columna de profundidad en el volumen de salida. Los ajustes más bajos para el paso (por ejemplo, 1 especifica sólo un paso unitario) asignarán más columnas de profundidad en el volumen de salida. Esto también producirá campos receptivos más solapados entre las columnas, lo que dará lugar a volúmenes de salida mayores. Lo contrario ocurre cuando especificamos valores de zancada más altos. Estos valores de zancada más altos nos dan menos solapamiento y volúmenes de salida más pequeños espacialmente.

Sin relleno

El último hiperparámetro es el relleno cero, con el que podemos controlar el tamaño espacial de los volúmenes de salida. Querríamos hacer esto para los casos en los que queramos mantener el tamaño espacial del volumen de entrada en el volumen de salida.

Normalización por lotes y capas

Para acelerar el entrenamiento en las CNN podemos normalizar las activaciones de la capa anterior en cada lote.¹² Esta técnica aplica una transformación que mantiene la activación media próxima a 0,0, al tiempo que mantiene la desviación típica de la activación próxima a 1,0.

Se ha demostrado que la normalización por lotes en las CNN acelera el entrenamiento haciendo que la normalización forme parte de la arquitectura de la red. Aplicando la normalización a cada minilote de entrenamiento de registros de entrada, podemos utilizar tasas de aprendizaje mucho más altas. La normalización por lotes también reduce la sensibilidad del entrenamiento a la inicialización de pesos y actúa como regularizador (reduciendo la necesidad de otros tipos de regularización). La normalización por lotes también se ha aplicado a las redes LSTM¹³ que es otro tipo de red profunda que trataremos más adelante en el capítulo.

Agrupar capas

Las capas de agrupamiento suelen insertarse entre capas convolucionales sucesivas. Queremos seguir las capas convolucionales con capas de agrupamiento para reducir progresivamente el tamaño espacial (anchura y altura) de la representación de los datos. Las capas de agrupamiento reducen la representación de los datos progresivamente a lo largo de la red y ayudan a controlar el sobreajuste. La capa de agrupamiento opera independientemente en cada corte de profundidad de la entrada.

Operaciones comunes de reducción de la muestra

La operación de muestreo descendente más habitual es la operación máx. La siguiente operación más habitual es la agrupación de medias.

La capa de agrupación utiliza la operación max() para redimensionar espacialmente los datos de entrada (anchura, altura). Esta operación se denomina agrupación máxima. Con un tamaño de filtro de 2 × 2, la operación max() consiste en tomar el mayor de los cuatro números del área de filtrado. Esta operación no afecta a la dimensión de profundidad.

Las capas de agrupamiento utilizan filtros para realizar el proceso de reducción de la muestra en el volumen de entrada. Estas capas realizan operaciones de reducción a lo largo de la dimensión espacial de los datos de entrada. Esto significa que si la imagen de entrada tuviera 32 píxeles de ancho por 32 píxeles de alto, la imagen de salida sería más pequeña en anchura y altura (por ejemplo, 16 píxeles de ancho por 16 píxeles de alto). La configuración más habitual para una capa de agrupación es aplicar filtros 2 × 2 con un paso de 2. Esto reducirá la muestra de cada corte de profundidad en el volumen de entrada en un factor de dos en las dimensiones espaciales (anchura y altura). Esta operación de reducción de la muestra hará que se descarten el 75% de las activaciones.

Las capas de agrupamiento no tienen parámetros para la capa, pero sí hiperparámetros adicionales. Esta capa no tiene parámetros, porque calcula una función fija del volumen de entrada. No es habitual utilizar el relleno cero para las capas de agrupamiento.

Capas totalmente conectadas

En utilizamos esta capa para calcular las puntuaciones de las clases que utilizaremos como salida de la red (por ejemplo, la capa de salida al final de la red). Las dimensiones del volumen de salida son [ 1 × 1 × N ], donde N es el número de clases de salida que estamos evaluando. En el caso del conjunto de datos CIFAR que hemos comentado antes, N sería 10 para las 10 clases de objetos del conjunto de datos. Esta capa tiene una conexión entre todas sus neuronas y cada neurona de la capa anterior.

Las capas totalmente conectadas tienen los parámetros normales de la capa y los hiperparámetros. Las capas totalmente conectadas realizan transformaciones en el volumen de datos de entrada que son función de las activaciones en el volumen de entrada y de los parámetros (pesos y sesgos de las neuronas).

Varias capas totalmente conectadas

Hay algunas arquitecturas CNN que utilizan varias capas totalmente conectadas al final de la red. AlexNet es un ejemplo de ello; tiene dos capas totalmente conectadas seguidas de una capa softmax al final.

Otras aplicaciones de las CNN

Más allá de datos de imágenes bidimensionales normales, también vemos CNN aplicadas a conjuntos de datos tridimensionales. He aquí algunos ejemplos de estos usos alternativos:

• Datos de RMN¹⁴
• Datos de forma 3D¹⁵
• Datos gráficos¹⁶
• Aplicaciones de la PNL¹⁷

La naturaleza invariante de posición de las CNN ha demostrado su utilidad en estos dominios, porque no estamos limitados a codificar a mano nuestras características para que aparezcan en determinados "puntos" del vector de características.

CNNs de interés

En encontrarás una lista de algunas de las arquitecturas de CNN más populares.

• LeNet¹⁸

  • Un de las primeras arquitecturas exitosas de CNNs
  • Desarrollado por Yann Lecun
  • Originalmente se utilizaba para leer dígitos en imágenes

• AlexNet¹⁹

  • Ayudó a a popularizar las CNN en visión por ordenador
  • Desarrollado por Alex Krizhevsky, Ilya Sutskever y Geoff Hinton
  • Ganó el ILSVRC 2012

• Red ZF²⁰

  • Ganó el ILSVRC 2013
  • Desarrollado por Matthew Zeiler y Rob Fergus
  • Introducido el concepto de visualización de la Red Deconvolucional

• GoogLeNet²¹

  • Ganó el ILSVRC 2014
  • Desarrollado por Christian Szegedy y su equipo en Google
  • Con el nombre en clave "Inception", una variante tiene 22 capas

• VGGNet²²

  • Subcampeón en la ILSVRC 2014
  • Desarrollado por Karen Simonyan y Andrew Zisserman
  • Demostró que la profundidad de la red era un factor crítico para un buen rendimiento

• ResNet²³

  • Entrenado en redes muy profundas (hasta 1.200 capas)
  • Ganó el primer puesto en la tarea de clasificación de la ILSVRC 2015

Resumen

Las CNN evolucionaron debido a la necesidad de extraer características especializadas de los datos de las imágenes. Vimos capas que son buenas para encontrar características independientemente de por dónde "vaguen" a través de las columnas. Vimos cómo las capas convolucionales, las capas de agrupamiento y las capas normales totalmente conectadas trabajaban juntas para realizar la clasificación de imágenes. Ahora, pasemos a una arquitectura de red neuronal centrada en modelar el dominio temporal: Las Redes Neuronales Recurrentes.

Redes neuronales recurrentes

Las Redes Neuronales Recurrentes pertenecen a la familia de las redes neuronales feed-forward. Se diferencian de otras redes feed-forward en su capacidad para enviar información a través de pasos temporales. Aquí tienes una interesante explicación de las Redes Neuronales Recurrentes del destacado investigador Juergen Schmidhuber:

Las [Redes Neuronales Recurrentes] permiten tanto el cálculo paralelo como el secuencial, y en principio pueden calcular cualquier cosa que pueda calcular un ordenador tradicional. Sin embargo, a diferencia de los ordenadores tradicionales, las Redes Neuronales Recurrentes son similares al cerebro humano, que es una gran red de retroalimentación de neuronas conectadas que, de alguna manera, puede aprender a traducir un flujo de entrada sensorial de toda la vida en una secuencia de salidas motoras útiles. El cerebro es un modelo extraordinario, ya que puede resolver muchos problemas que las máquinas actuales aún no pueden resolver.

Históricamente, estas redes han sido difíciles de entrenar, pero más recientemente, los avances en la investigación (optimización, arquitecturas de red, paralelismo y unidades de procesamiento gráfico [GPU]) las han hecho más accesibles para el profesional.

Las redes neuronales recurrentes toman cada vector de una secuencia de vectores de entrada y los modelan de uno en uno. Esto permite a la red conservar el estado mientras modela cada vector de entrada a lo largo de la ventana de vectores de entrada. Modelar la dimensión temporal es una característica distintiva de las Redes Neuronales Recurrentes.

Modelar la dimensión temporal

Recurrente Las Redes Neuronales se consideran Turing completas y pueden simular programas arbitrarios (con pesos). Si vemos las redes neuronales como optimización sobre funciones, podemos considerar las Redes Neuronales Recurrentes como "optimización sobre programas". Las redes neuronales recurrentes son muy adecuadas para modelar funciones para las que la entrada y/o la salida se componen de vectores que implican una dependencia temporal entre los valores. Las redes neuronales recurrentes modelan el aspecto temporal de los datos creando ciclos en la red (de ahí la parte "recurrente" del nombre).

Perdido en el tiempo

Muchas herramientas de clasificación (máquinas de vectores de soporte, regresión logística y redes regulares feed-forward) se han aplicado con éxito sin modelar la dimensión temporal, asumiendo la independencia. Otras variaciones de estas herramientas capturan la dinámica temporal modelando una ventana deslizante de la entrada (por ejemplo, la entrada anterior, la actual y la siguiente juntas como un único vector de entrada).

Un inconveniente de estas herramientas es que suponer la independencia en la conexión temporal entre las entradas del modelo no permite que nuestro modelo capte las dependencias temporales de largo alcance. Las técnicas de ventana deslizante tienen un ancho de ventana limitado y no captarán ningún efecto mayor que el tamaño de ventana fijo. Un gran ejemplo de esto es modelar cómo funcionan las conversaciones y hacer que las máquinas comprendan cómo responder de forma coherente a medida que la conversación evoluciona en el tiempo. Una Red Neuronal Recurrente bien entrenada podría competir, por ejemplo, en el famoso Test de Turing de Alan Turing, que intenta engañar a un humano haciéndole creer que está hablando con una persona real.

Retroalimentación temporal y bucles en las conexiones

Las Redes Neuronales Recurrentes pueden tener bucles en las conexiones. Esto les permite modelar el comportamiento temporal ganando precisión en dominios como las series temporales, el lenguaje, el audio y el texto.

Nota sobre las conexiones desde la salida a las capas ocultas

En la práctica, vemos este esquema de conectividad con menos frecuencia que otros. DL4J tampoco utiliza este esquema. Sin embargo, nos ha parecido importante señalar esta variante para contextualizar el material. Lo más frecuente es que veamos conexiones entre neuronas de un paso temporal al siguiente en cada capa recurrente.

Los datos en estos dominios están inherentemente ordenados y son sensibles al contexto, donde los valores posteriores dependen de los anteriores. El cableado de una Red Neuronal Recurrente permite la retroalimentación de forma que sea posible captar estos efectos temporales. Principalmente vemos arquitecturas de Redes Neuronales Recurrentes aplicadas en dominios de series temporales para aplicaciones.

Una Red Neuronal Recurrente incluye un bucle de realimentación que utiliza para aprender de secuencias, incluidas secuencias de longitudes variables. Las Redes Neuronales Recurrentes contienen una matriz de parámetros adicional para las conexiones entre pasos temporales, que se utilizan/entrenan para captar las relaciones temporales en los datos.

Las Redes Neuronales Recurrentes se entrenan para generar secuencias, en las que la salida en cada paso temporal se basa tanto en la entrada actual como en la entrada de todos los pasos temporales anteriores. Las Redes Neuronales Recurrentes normales calculan un gradiente con un algoritmo llamado retropropagación en el tiempo (BPTT). Más adelante entraremos en detalles sobre la BPTT.

Secuencias y series temporales de datos

En encontramos datos secuenciales en muchos ámbitos problemáticos de la industria para los que nuestro modelo necesita dar salida a una secuencia de vectores:

• Pie de foto
• Síntesis de voz²⁴
• Generación de música²⁵
• Jugar a videojuegos
• Modelado lingüístico
• Modelos de generación de texto a nivel de carácter

En otros dominios, necesitamos una secuencia de vectores de entrada:

• Predicción de series temporales
• Videoanálisis
• Recuperación de información musical

Y luego tenemos dominios que requieren tanto una serie de vectores de entrada como de salida:

• Traducción en lenguaje natural²⁶
• Entablar un diálogo
• Control robótico

Las Redes Neuronales Recurrentes contrastan con otras redes profundas en el tipo de entrada que pueden modelar (entrada no fija):

• Pasos de cálculo no fijos
• Tamaño de salida no fijo
• Puede operar sobre secuencias de vectores, como fotogramas de vídeo

Una faceta importante de las Redes Neuronales Recurrentes es cómo podemos trabajar con la entrada y la salida de formas únicas.

Comprender la entrada y salida del modelo

El aprendizaje automático tradicional opera sobre el concepto de un único vector de entrada de tamaño fijo. En las actividades de modelado tradicionales, normalmente vemos una relación entrada-salida de tamaño fijo de entrada a tamaño fijo de salida.

Éste suele ser el patrón de modelado en la construcción de clasificadores para la clasificación de imágenes o la clasificación de datos columnares.

Las Redes Neuronales Recurrentes cambian esta dinámica de entrada para incluir múltiples vectores de entrada, uno para cada paso temporal, y cada vector puede tener muchas columnas. La siguiente lista ofrece ejemplos de cómo operan las Redes Neuronales Recurrentes con secuencias de vectores de entrada y salida:

• De uno a muchos: salida de secuencias. Por ejemplo, el subtitulado de imágenes toma una imagen y produce una secuencia de palabras.
• Muchos a uno: entrada secuencial. Por ejemplo, el análisis de sentimientos, en el que se introduce una frase determinada.
• De muchos a muchos: Por ejemplo, clasificación de vídeos: etiqueta cada fotograma.

Ahora que hemos visto las variaciones de los datos de entrada y salida, veamos cómo se representan esos datos de entrada.

Entrada volumétrica 3D

La entrada en las Redes Neuronales Recurrentes implica más dimensiones que la entrada estándar del modelado de aprendizaje automático. Esto es conceptualmente similar a las CNN. Tenemos tres dimensiones para la entrada:

1. Tamaño del minilote
2. Número de columnas de nuestro vector por paso de tiempo
3. Número de pasos temporales

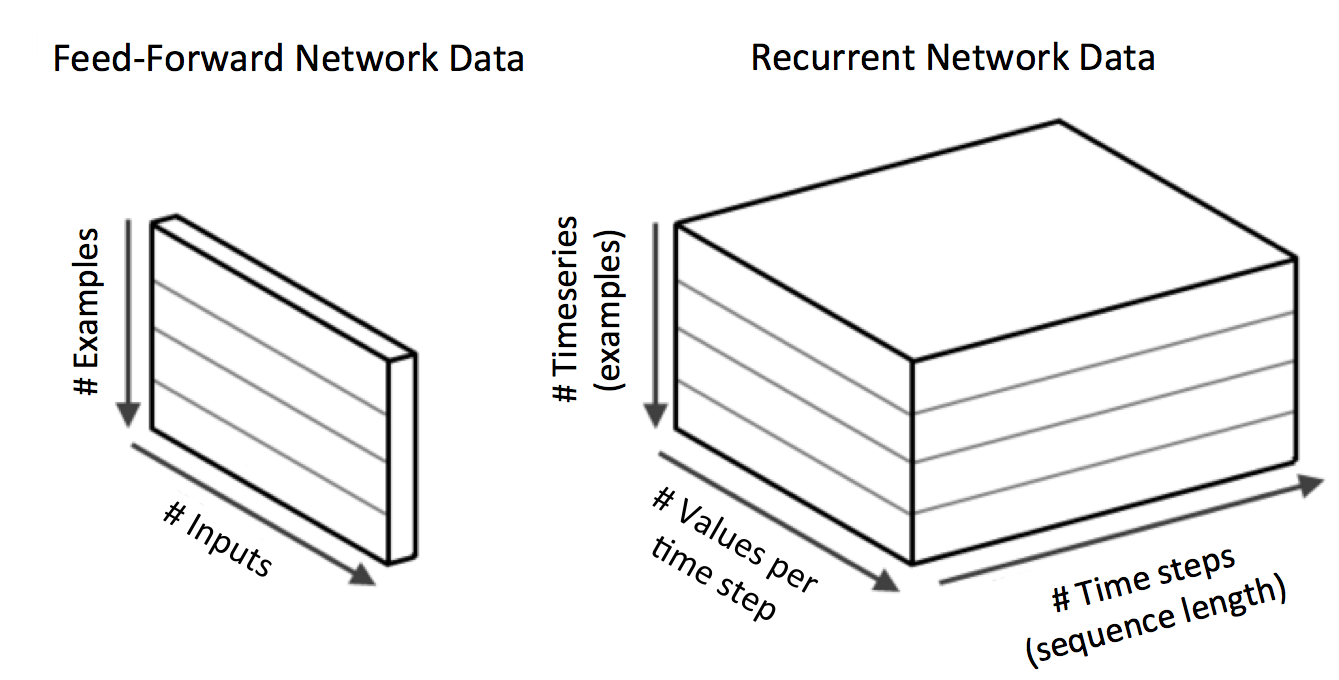
Figura 4-17. Vectores de entrada normales comparados con la entrada de las redes neuronales recurrentes

Mini-lote El tamaño es el número de registros de entrada (colecciones de puntos de series temporales para una única entidad fuente) que queremos modelizar por lote. El número de columnas coincide con el recuento tradicional de columnas de características de un vector de entrada normal. El número de pasos temporales es la forma en que representamos el cambio en el vector de entrada a lo largo del tiempo. Éste es el aspecto de serie temporal de los datos de entrada. En la terminología de la sección anterior, consideraríamos que cualquier recuento de pasos temporales superior a 1 es "múltiple" en términos de arquitectura de entrada y salida.

Series temporales desiguales y enmascaramiento

En hemos descrito anteriormente cómo con la entrada de la Red Neuronal Recurrente tenemos el concepto de pasos de tiempo además de características en nuestro vector de entrada. La Figura 4-18 ofrece una representación visual.

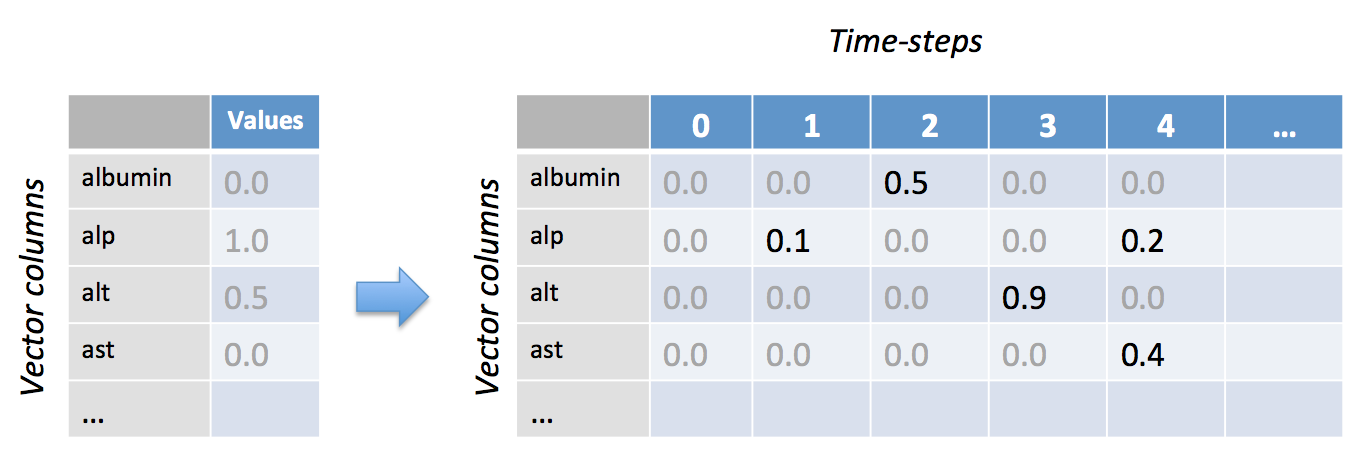
Figura 4-18. El aspecto del paso del tiempo de la entrada de la Red Neuronal Recurrente

Es probable que no todos los valores de columna se den en todos los pasos temporales, especialmente en el caso de que estemos mezclando datos de descriptores (por ejemplo, columnas de una tabla de base de datos estática) con datos de series temporales (por ejemplo, mediciones del ritmo cardíaco de un paciente de la UCI cada minuto). Para los casos en los que tenemos valores de pasos temporales "irregulares", necesitamos utilizar el enmascaramiento para que DL4J sepa dónde se encuentran nuestros datos reales en el vector. Para ello, proporcionamos una matriz adicional para la máscara que indica los pasos temporales que tienen datos de entrada para al menos una columna, como se muestra en la Figura 4-19.

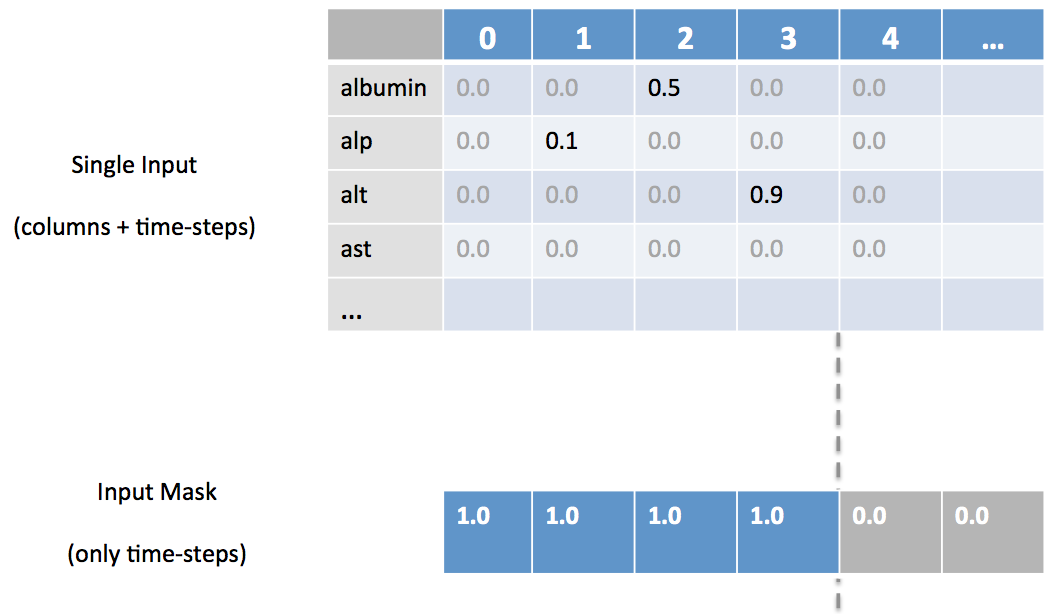
Figura 4-19. Enmascarar pasos temporales específicos

El capítulo 3 proporciona ejemplos de código real que muestran cómo configuramos estas máscaras.

¿Por qué no modelos de Markov?

Cuando trata la dimensión temporal en nuestros modelos, naturalmente podríamos considerar los modelos de Markov como una opción. Los modelos de Markov son otra clase de modelos de aprendizaje automático que se han utilizado ampliamente para modelar secuencias. El factor limitante de los modelos de Markov es que, a medida que su ventana de contexto aumenta de tamaño, estos modelos acaban resultando poco prácticos desde el punto de vista computacional para modelar dependencias de largo alcance.

Las Redes Neuronales Recurrentes (modelos conexionistas) son mejores que los modelos de Markov (y otros modelos limitados por la ventana temporal) porque pueden captar las dependencias temporales de largo alcance en los datos de entrada. Las Redes Neuronales Recurrentes lo consiguen porque su estado oculto capta información de una ventana de contexto arbitrariamente larga y no tiene la limitación de las otras técnicas. Además, el número de estados que pueden modelar está representado por la capa oculta de nodos, y estos estados crecen exponencialmente con el número de nodos de la capa. Esto hace que las Redes Neuronales Recurrentes sean excepcionales para captar mucha información relevante en la dimensión temporal a través de muchos vectores de entrada.

Redes neuronales recurrentes, capas ocultas y número de estados

Si la entrada fueran sólo valores binarios (0,1), la red podría representar ^2N estados, donde N es el número de nodos de la capa oculta. Si la salida fueran números de 64 bits con valores reales, una sola capa oculta de estos nodos puede representar $2^{{64}^N}$ estados diferentes.

El entrenamiento de estas redes crece sólo cuadráticamente con el número de nodos ocultos, mientras que la potencia expresiva de la red crece exponencialmente con el número de nodos ocultos.

Arquitectura general de la red neuronal recurrente

Las Redes Neuronales Recurrentes son un superconjunto de las redes neuronales feed-forward, pero añaden el concepto de conexiones recurrentes. Estas conexiones (o perímetros recurrentes) abarcan pasos temporales adyacentes (por ejemplo, un paso temporal anterior), dando al modelo el concepto de tiempo. Las conexiones convencionales no contienen ciclos en las redes neuronales recurrentes. Sin embargo, las conexiones recurrentes pueden formar ciclos que incluyan conexiones de vuelta a las propias neuronas originales en futuros pasos temporales.

Arquitectura y pasos temporales de las Redes Neuronales Recurrentes

En cada paso de tiempo de envío de entrada a través de una red recurrente, los nodos que reciben la entrada a lo largo de los perímetros recurrentes reciben activaciones de entrada del vector de entrada actual y de los nodos ocultos del estado anterior de la red.

La salida se calcula a partir del estado oculto en el paso de tiempo dado. El vector de entrada anterior en el paso de tiempo anterior puede influir en la salida actual en el paso de tiempo actual a través de las conexiones recurrentes.

Podemos encadenar capas de estas neuronas recurrentes especializadas para construir modelos mejores. Conectamos la salida de la capa anterior a la entrada de la capa siguiente de forma similar a como conectaríamos las redes neuronales multicapa feed-forward.

Problema del gradiente evanescente

Se sabe que las Redes Neuronales Recurrentes tienen problemas con el "problema del gradiente evanescente". Este problema se produce cuando los gradientes se hacen demasiado grandes o demasiado pequeños y dificultan el modelado de dependencias de largo alcance (10 pasos temporales o más) en la estructura del conjunto de datos de entrada. La forma más eficaz de evitar este problema es utilizar la variante LSTM de las Redes Neuronales Recurrentes que admite DL4J.

Redes LSTM

Las redes LSTM son la variante más utilizada de las Redes Neuronales Recurrentes. Las redes LSTM fueron introducidas en 1997 por Hochreiter y Schmidhuber.²⁷

El componente crítico de la LSTM²⁸ es la célula de memoria y las compuertas (incluida la compuerta de olvido²⁹ pero también la puerta de entrada). El contenido de la célula de memoria está modulado por las puertas de entrada y las puertas del olvido.³⁰ Suponiendo que ambas puertas estén cerradas, el contenido de la célula de memoria permanecerá inalterado entre un paso temporal y el siguiente. La estructura de compuertas permite que la información se retenga a lo largo de muchos pasos temporales y, en consecuencia, también permite que los gradientes fluyan a lo largo de muchos pasos temporales. Esto permite que el modelo LSTM supere el problema del gradiente evanescente que se produce con la mayoría de los modelos de Redes Neuronales Recurrentes.

Propiedades de las redes LSTM

Los LSTMs son conocidos por lo siguiente:

• Mejores ecuaciones de actualización
• Mejor retropropagación

En encontrarás algunos ejemplos de uso de las LSTM:

• Generar frases (por ejemplo, modelos lingüísticos a nivel de caracteres)
• Clasificar series temporales
• Reconocimiento de voz
• Reconocimiento de escritura
• Modelado de música polifónica

Las arquitecturas LSTM y las Redes Neuronales Recurrentes Bidireccionales (BRNN) han demostrado ser líderes en la industria en los últimos años en tareas como las siguientes:

• Pie de foto
• Traducción de idiomas
• Reconocimiento de escritura

Las redes LSTM están formadas por muchas células LSTM conectadas y tienen un buen rendimiento durante el aprendizaje.

Una nota sobre la complejidad del entrenamiento en las LSTM

La complejidad computacional de las operaciones de paso hacia delante y hacia atrás escala linealmente con el número de pasos temporales de la secuencia de entrada.

En las secciones siguientes, ofrecemos una visión general de la arquitectura y los componentes de la LSTM.

Arquitectura de la red LSTM

Para que comprenda mejor la compleja disposición de las conexiones entre unidades y capas en las redes LSTM, basémonos en algunos conceptos anteriores.

Anteriormente en este libro, desarrollamos el concepto de red neuronal multicapa feed-forward, como se muestra en la Figura 4-20.

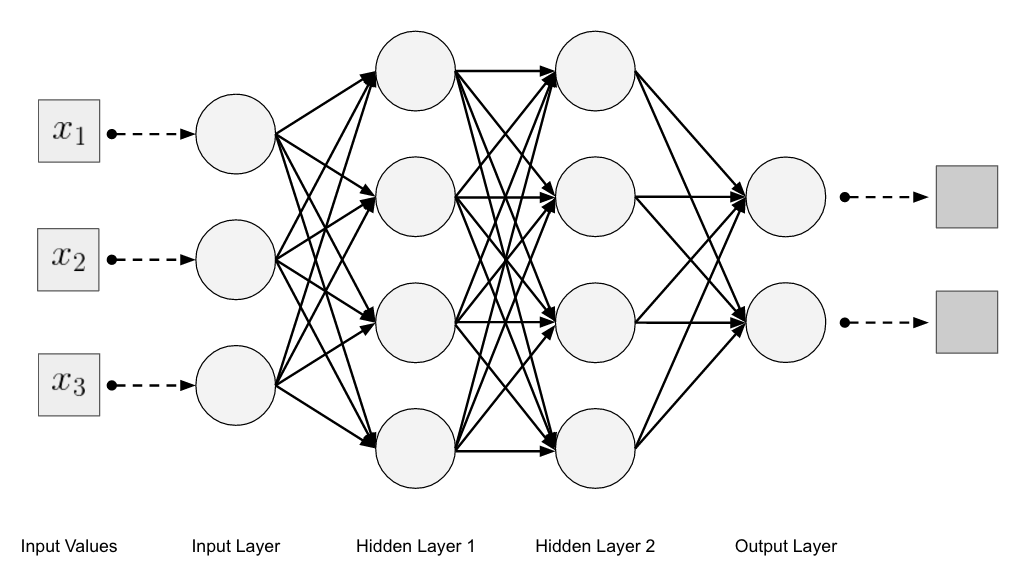
Figura 4-20. Arquitectura de la red neuronal multicapa de alimentación hacia delante

Si mostráramos cada capa de la red mostrada en la Figura 4-20 como un único nodo en una representación aplanada, tendría el aspecto de la Figura 4-21.

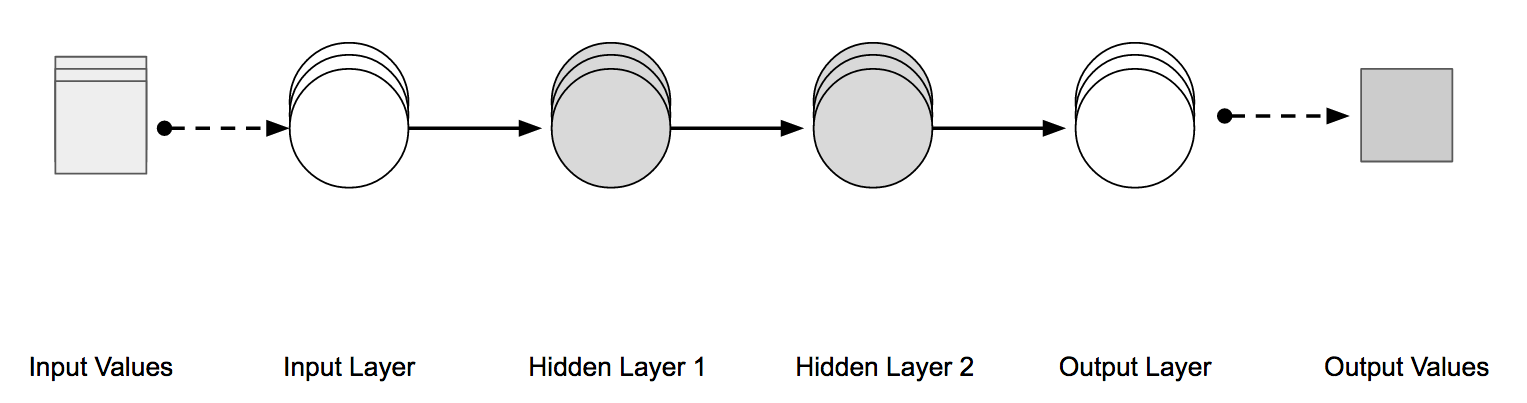
Figura 4-21. Red multicapa de avance visual

Con las Redes Neuronales Recurrentes, introducimos la idea de un tipo de conexión que conecta la salida de una neurona de capa oculta como entrada a la misma neurona de capa oculta. Con esta conexión recurrente, podemos tomar la entrada del paso temporal anterior en la neurona como parte de la información entrante.

La Figura 4-22 demuestra que aplanando la red mostrada en la Figura 4-21, podemos visualizar más fácilmente las conexiones recurrentes en una LSTM.

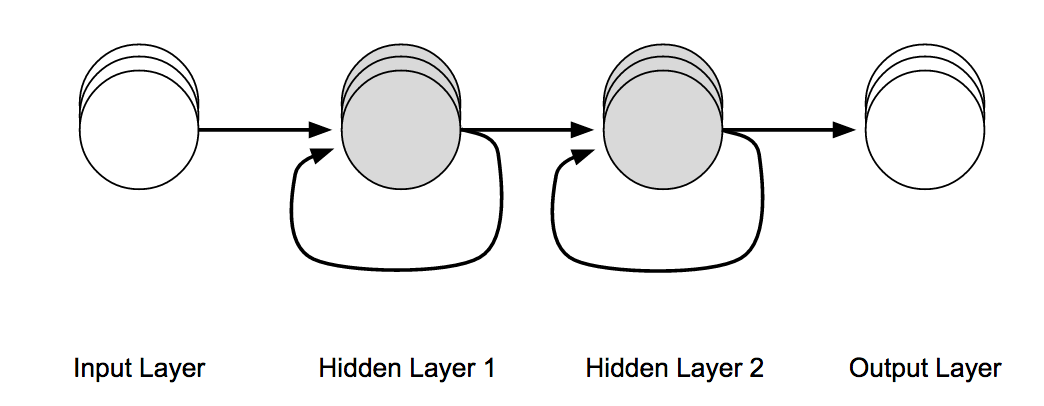
Figura 4-22. Muestra las conexiones recurrentes en los nodos de la capa oculta

La Figura 4-23 ilustra cómo podemos entender esto visualmente "desenrollando" el diagrama de red de la Figura 4-22 para mostrar cómo "fluye" la información a través de la red de una manera "feed-forward" y "a través del tiempo".

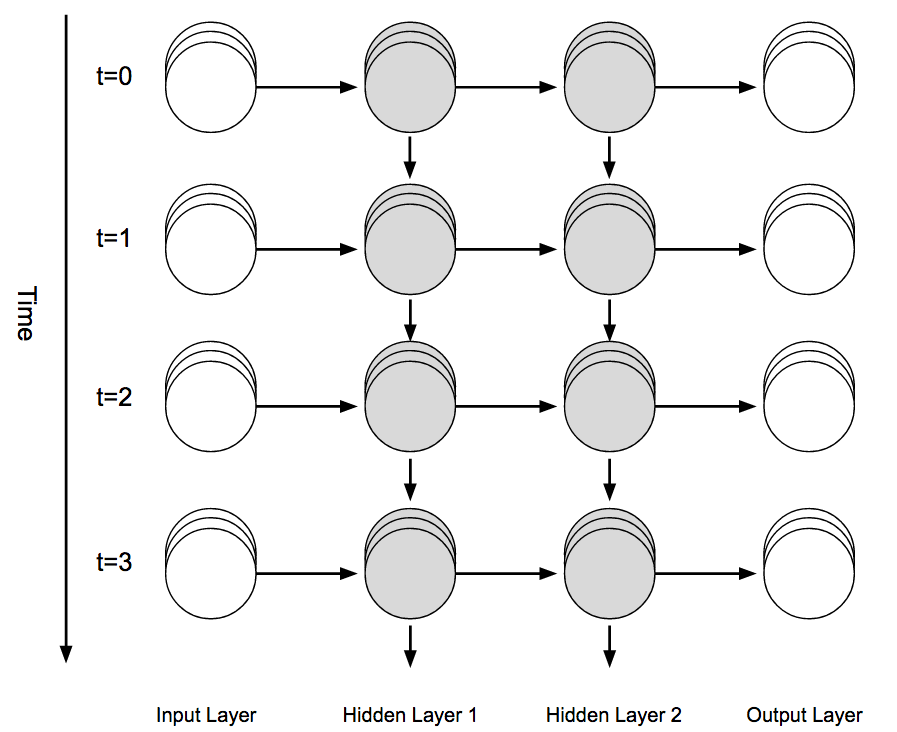
Figura 4-23. Red neuronal recurrente desenrollada a lo largo del eje temporal

Las redes LSTM pasan más información a través de la conexión recurrente que las redes neuronales recurrentes tradicionales, como veremos en la siguiente sección.

Unidades LSTM

Las unidades de las capas de las Redes Neuronales Recurrentes son una variación de la neurona artificial clásica.

Cada unidad LSTM tiene dos tipos de conexiones:

• Conexiones del paso temporal anterior (salidas de esas unidades)
• Conexiones de la capa anterior

La célula de memoria de una red LSTM es el concepto central que permite a la red mantener el estado a lo largo del tiempo. El cuerpo principal de la unidad LSTM se denomina bloque LSTM, como se muestra en la Figura 4-24.

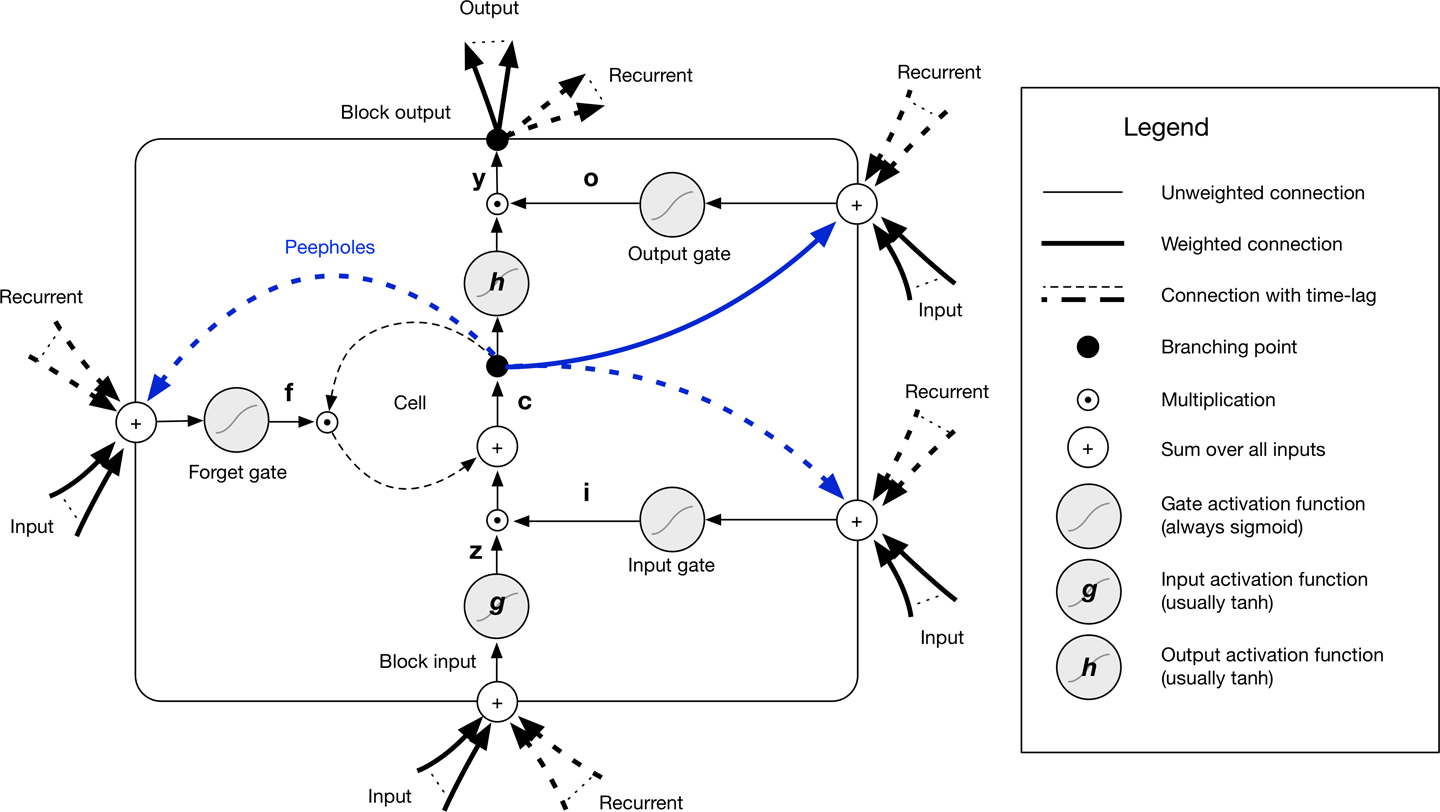
Figura 4-24. Diagrama de bloques LSTM

Estos son los componentes de una unidad LSTM:

• Tres puertas
  • puerta de entrada (puerta de modulación de entrada)
  • puerta de olvido
  • puerta de salida
• Entrada en bloque
• Célula de memoria (el carrusel de errores constantes)
• Función de activación de salida
• Conexiones de mirilla

Hay tres unidades de compuerta, que aprenden a proteger la unidad lineal de señales engañosas:

• La puerta de entrada protege a la unidad de eventos de entrada irrelevantes.
• La puerta de olvido ayuda a la unidad a olvidar el contenido de la memoria anterior.
• La puerta de salida expone (o no) el contenido de la celda de memoria a la salida de la unidad LSTM.

La salida del bloque LSTM es recurrente conectada de nuevo a la entrada del bloque y a todas las puertas del bloque LSTM. Las puertas de entrada, olvido y salida de una unidad LSTM tienen funciones de activación sigmoideas para la restricción [0, 1]. La función de activación de entrada y salida del bloque LSTM (normalmente) es una función de activación tanh.

Nota sobre la Puerta del Olvido

Una salida de activación de 1,0 significa "recuérdalo todo" y una salida de activación de 0,0 significa "olvídalo todo". Desde otra perspectiva, ¡un nombre mejor para la puerta del olvido podría ser "puerta del recuerdo"!

Teniendo esto en cuenta, solemos inicializar el sesgo de la puerta del olvido con un valor grande para permitir el aprendizaje de las dependencias a largo plazo (donde valor grande == 1,0 por defecto en DL4J).

Utilizando la notación de Greff et al,³¹ la Figura 4-25 presenta las fórmulas vectoriales para el paso hacia delante de una capa LSTM.

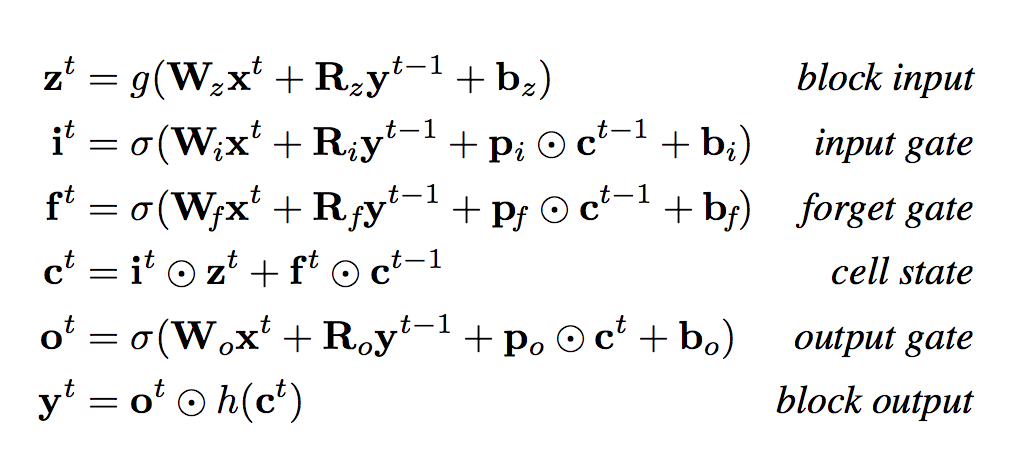
Figura 4-25. Fórmulas vectoriales para el paso hacia delante de la capa LSTM

La Tabla 4-1 enumera las variables individuales de las ecuaciones de la Figura 4-25.

Tabla 4-1. Descripción de las variables de las fórmulas vectoriales LSTM

Nombre de la variable	Descripción
xt	Vector de entrada en el momento t
W	Matrices de pesos de entrada rectangulares
R	Matrices de pesos recurrentes cuadradas
p	Vectores de peso de la mirilla
b	Vectores de sesgo

La conexión autorrecurrente tiene un peso fijo de 1,0 (excepto cuando está modulada) para superar los problemas con los gradientes evanescentes. Esta unidad central permite a las unidades LSTM descubrir eventos de mayor alcance en las secuencias. Estos sucesos pueden abarcar hasta 1.000 pasos temporales discretos, en comparación con las antiguas arquitecturas recurrentes, que sólo podían modelar sucesos en unos 10 pasos temporales.

Para más variantes de LSTMs...

Consulta el artículo "LSTM: Una odisea del espacio de búsqueda".

Unidades Recurrentes Cerradas (GRU)

Otra unidad recurrente similar a la LSTM es la Unidad Recurrente Cerrada (GRU).³² La GRU tiene una puerta de reinicio y una puerta de actualización, similares a las puertas de olvido/entrada de la unidad LSTM. La principal diferencia es que la GRU expone completamente su contenido de memoria utilizando sólo la integración con fugas (pero con una constante de tiempo adaptativa controlada por la puerta de actualización). La GRU se inspira en la unidad LSTM, pero se considera más sencilla de calcular e implementar.

Capas LSTM

Una capa básica acepta un vector de entrada x (no fijo) y da la salida y. La salida y está influida por la entrada x y el historial de todas las entradas. La capa está influida por el historial de entradas a través de las conexiones recurrentes. La RNN tiene un estado interno que se actualiza cada vez que introducimos un vector en la capa. El estado consiste en un único vector oculto.

Formación

Las redes LSTM utilizan el aprendizaje supervisado para actualizar los pesos de la red. Se entrenan con un vector de entrada cada vez en una secuencia de vectores. Los vectores son de valor real y se convierten en secuencias de activaciones de los nodos de entrada. Cada unidad no de entrada calcula su activación actual en cualquier paso temporal. Este valor de activación se calcula como la función no lineal de la suma ponderada de las activaciones de todas las unidades de las que recibe conexiones.

Para cada vector de entrada de la secuencia de entrada, el error es igual a la suma de las desviaciones de todas las señales objetivo respecto a las activaciones correspondientes calculadas por la red. Veamos ahora la variante BPTT de la retropropagación utilizada con las Redes Neuronales Recurrentes, incluidas las LSTM.

BPTT y BPTT truncada

El entrenamiento de la Red Neuronal Recurrente puede ser costoso desde el punto de vista informático. La opción tradicional es utilizar BPTT.

Nota

BPTT es fundamentalmente igual que la retropropagación estándar: aplicamos la regla de la cadena para calcular las derivadas (gradientes) basándonos en la estructura de conexiones de la red. Es a través del tiempo en el sentido de que algunos de esos gradientes/señales de error también fluirán hacia atrás desde los pasos de tiempo futuros hacia los pasos de tiempo actuales, no sólo desde la capa superior (como ocurre en la retropropagación estándar).

Cuando nuestra red recurrente se enfrenta a secuencias largas con muchos pasos temporales, recomendamos utilizar alternativamente la BPTT truncada. La BPTT truncada reduce la complejidad computacional de cada actualización de parámetros en una Red Neuronal Recurrente.

Redes neuronales recurrentes y retropropagación

Calcular el gradiente de una Red Neuronal Recurrente en una secuencia de longitud 1.000 tiene el mismo coste computacional que hacer un paso adelante y atrás en una red perceptrón multicapa que tenga 1.000 capas.

Realizar actualizaciones más frecuentes de los parámetros acelera el entrenamiento de la red neuronal recurrente. Recomendamos el BPTT truncado cuando tus secuencias de entrada tengan más de unos cientos de pasos temporales.

Para comprender mejor los conceptos implicados en la BPTT truncada, consideremos lo que ocurre cuando entrenamos una red con series temporales de entrada de longitud 12 (pasos temporales). En este caso, tenemos que hacer una pasada hacia delante de 12 pasos y luego calcular el error de la red. A continuación, haz una pasada hacia atrás de los 12 pasos temporales, como se muestra en la Figura 4-26.

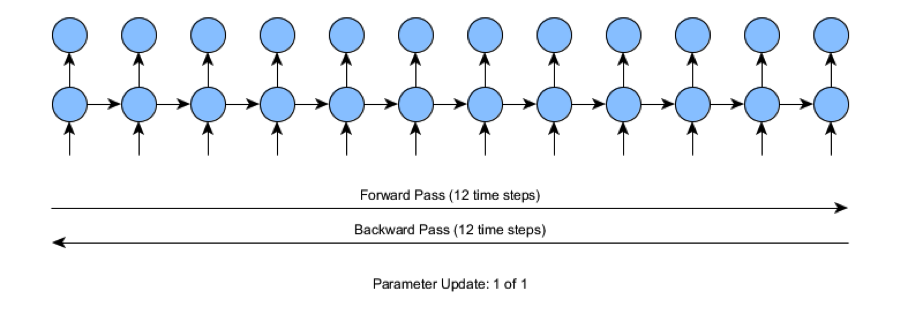
Figura 4-26. BPTT estándar

En la figura, los 12 pasos temporales no son tan difíciles para el proceso de entrenamiento. A medida que pasamos a modelos que se entrenan con datos de series temporales de unos cientos de pasos o más, nos encontramos con que el entrenamiento es más difícil. Si el número de pasos en la entrada de la serie temporal fuera de 1.000 pasos, el entrenamiento de retropropagación estándar requeriría 1.000 pasos de tiempo para cada pasada hacia delante y hacia atrás (para cada actualización individual de los parámetros). Esto se vuelve rápidamente costoso desde el punto de vista informático y es la razón por la que buscamos métodos de entrenamiento alternativos, como el BPTT y el BPTT truncado.

El BPTT truncado separa los pases hacia delante y hacia atrás en operaciones más pequeñas. El BPTT truncado que se muestra en la Figura 4-27 realiza una pasada hacia delante más pequeña, hace una pasada hacia atrás igualmente pequeña y, a continuación, actualiza el parámetro previsto. Este tamaño de pase más pequeño es un hiperparámetro configurado por el usuario. En la figura podemos ver que el tamaño de pasada del BPTT truncado es de cuatro pasos de tiempo.

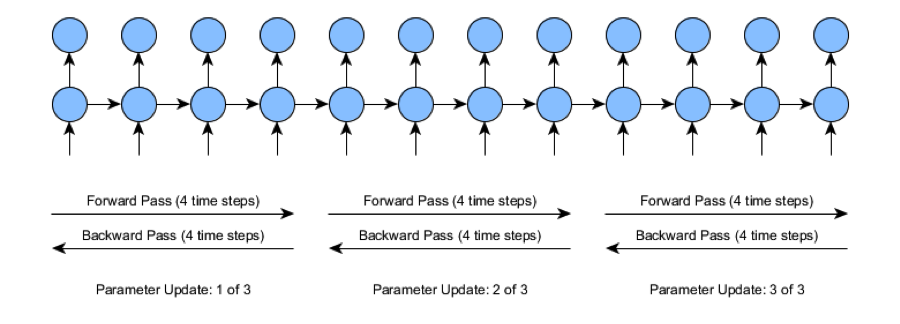
Figura 4-27. BPTT truncado

La BPTT truncada se considera el método actual más práctico para entrenar Redes Neuronales Recurrentes. Con la BPTT truncada, podemos captar las dependencias a largo plazo con menos carga computacional que con la BPTT normal.

La complejidad global de la BPTT estándar y de la BPTT truncada es similar y requiere el mismo número de pasos temporales durante el entrenamiento. Sin embargo, obtenemos más actualizaciones de los parámetros por aproximadamente el mismo esfuerzo computacional (aunque hay cierta sobrecarga por cada actualización de los parámetros). Como ocurre con todas las aproximaciones, vemos un pequeño inconveniente al utilizar el BPTT truncado; la longitud de las relaciones aprendidas en el BPTT truncado puede acabar siendo más corta que los resultados del algoritmo BPTT completo. En la práctica, esta compensación de velocidad suele merecer la pena, siempre que las longitudes BPTT truncadas se establezcan correctamente.

Aplicaciones específicas de dominio y redes combinadas

Como ya ha mencionado , las Redes Neuronales Recurrentes realizan muchas aplicaciones específicas de dominio, como la transcripción de voz a texto, la traducción automática y la generación de texto manuscrito. Las Redes Neuronales Recurrentes han demostrado ser adeptas en el mundo de la visión por ordenador y pueden hacer lo siguiente:

• Análisis de vídeo a nivel de fotograma³³
• Pie de foto
• Subtítulos de vídeo³⁴
• Respuesta visual a preguntas³⁵

Otra área emergente de investigación en visión por ordenador con Redes Neuronales Recurrentes es una red que puede extraer información de una imagen procesando sólo una pequeña región cada vez y se llama Modelos Recurrentes de Atención Visual.³⁶ Estos modelos son eficaces para trabajar con imágenes que están abarrotadas de múltiples objetos y son más difíciles de clasificar para las CNN. Estas redes combinan las CNN para la percepción en bruto y las Redes Neuronales Recurrentes para el modelado en el dominio temporal.

Otra red CNN + RNN híbrida digna de mención es el trabajo de Andrej Karpathy y Li Fei-Fei, en el que la red genera descripciones en lenguaje natural de las imágenes y sus regiones.³⁷ El modelo es capaz de generar pies de foto para imágenes utilizando conjuntos de datos de imágenes y su frase correspondiente, como se muestra en la Figura 4-28.

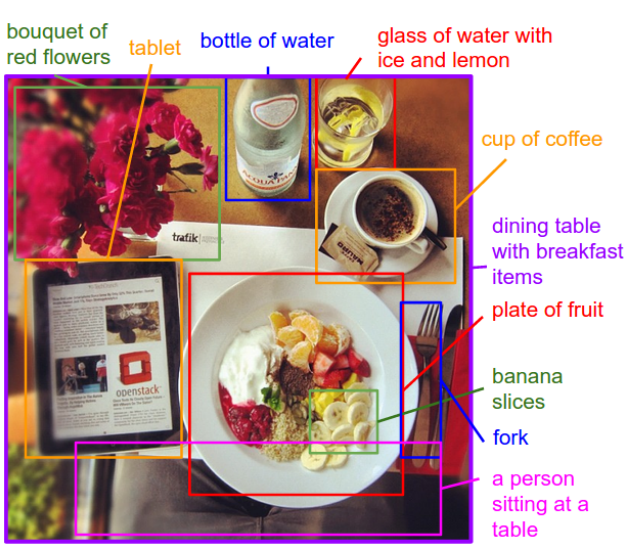
Figura 4-28. Etiquetado de imágenes con una CNN/Red Neuronal Recurrente combinada³⁸

Este tipo de red es una combinación de una CNN y una BRNN.

Redes neuronales recursivas

Las Redes Neuronales Recursivas , al igual que las Redes Neuronales Recurrentes, pueden tratar con entradas de longitud variable. La principal diferencia es que las Redes Neuronales Recurrentes tienen la capacidad de modelar las estructuras jerárquicas del conjunto de datos de entrenamiento. Las imágenes suelen tener una escena compuesta por muchos objetos. La deconstrucción de escenas suele ser un problema de interés, pero no es trivial. La naturaleza recursiva de esta deconstrucción nos reta no sólo a identificar los objetos de la escena, sino también cómo se relacionan los objetos para formar la escena.

Arquitectura de red

Una arquitectura de Red Neuronal Recursiva se compone de una matriz de pesos compartidos y una estructura de árbol binario que permite a la red recursiva aprender secuencias variables de palabras o partes de una imagen. Es útil como analizador sintáctico de frases y escenas. Las Redes Neuronales Recursivas utilizan una variación de la retropropagación llamada retropropagación a través de la estructura (BPTS). El paso feed-forward se produce de abajo arriba, y la retropropagación es de arriba abajo. Piensa que el objetivo es la parte superior del árbol, mientras que las entradas son la parte inferior.

Variedades de redes neuronales recursivas

Las redes neuronales recursivas se presentan en algunas variedades. Una es el autocodificador recursivo. Al igual que su primo alimentador, los autocodificadores recursivos aprenden a reconstruir la entrada. En el caso de la PNL, aprenden a reconstruir contextos. Un autocodificador recursivo semisupervisado aprende la probabilidad de ciertas etiquetas en cada contexto.

Otra variación de es una red neuronal supervisada, llamada red neuronal tensorial recursiva, que calcula un objetivo supervisado en cada nodo del árbol. La parte tensorial significa que calcula el gradiente de forma algo diferente, teniendo en cuenta más información en cada nodo aprovechando otra dimensión de la información mediante un tensor (una matriz de tres o más dimensiones).

Aplicaciones de las redes neuronales recursivas

Tanto Redes Neuronales Recursivas como Recurrentes comparten muchos de los mismos casos de uso. Las Redes Neuronales Recurrentes se utilizan tradicionalmente en PNL por sus vínculos con los árboles binarios, los contextos y los analizadores sintácticos basados en el lenguaje natural. Por ejemplo, los analizadores sintácticos constitutivos son capaces de descomponer una frase en un árbol binario, segmentándola según las propiedades lingüísticas de la frase. En el caso de las Redes Neuronales Recursivas, es una restricción que utilicemos un analizador sintáctico que construya la estructura de árbol (normalmente el analizador sintáctico de constituyentes).

Las redes neuronales recursivas pueden recuperar tanto la estructura granular como la estructura jerárquica de nivel superior en conjuntos de datos como imágenes o frases. Las aplicaciones de las redes neuronales recursivas son las siguientes:

• Descomposición de la escena de la imagen
• PNL
• Transcripción de audio a texto

Dos configuraciones de red concretas que vemos en la práctica son los autocodificadores recursivos y los tensores neuronales recursivos. Utilizamos autocodificadores recursivos para dividir frases en segmentos para la PNL. Utilizamos tensores neuronales recursivos para dividir una imagen en los objetos que la componen y etiquetar semánticamente los objetos de la escena.

Las Redes Neuronales Recurrentes tienden a ser más rápidas de entrenar, por lo que solemos utilizarlas en aplicaciones más temporales, pero se ha demostrado que también funcionan bien en dominios basados en la PLN, como el análisis de sentimientos.

Resumen y debate

En hemos revisado en este capítulo las principales arquitecturas más recientes del aprendizaje profundo. En resumen, para agrupar y resumir estas arquitecturas, señalamos lo siguiente:

• Para generar datos (por ejemplo, imágenes, audio o texto), utilizaríamos
  • GANs
  • VAEs
  • Redes Neuronales Recurrentes
• Para modelar imágenes, probablemente utilizaríamos
  • CNNs
  • DBNs
• Para modelar datos de secuencias, probablemente utilizaríamos
  • Redes neuronales recurrentes/LSTMs

En los capítulos siguientes, presentamos ejemplos de código del mundo real de la mayoría de estas redes y cubrimos consideraciones sobre el entrenamiento y el ajuste de diferentes tipos de redes neuronales. En el Capítulo 5 vemos cómo se unen estos conceptos en ejemplos de API en los que vemos en acción la biblioteca de aprendizaje profundo DL4J. Antes de pasar a más ejemplos, vamos a tratar algunos temas que surgen con frecuencia en el contexto del aprendizaje profundo.

¿Hará obsoleto el aprendizaje profundo a otros algoritmos?

El debate sobre si el aprendizaje profundo hace obsoletos otros algoritmos de modelado surge muchas veces en los tablones de anuncios de Internet. La respuesta hoy es "no", porque para muchas aplicaciones de aprendizaje automático más sencillas, vemos que algoritmos mucho más simples funcionan perfectamente para la precisión requerida del modelo. Los modelos como la regresión logística también son más fáciles de trabajar, por lo que necesitamos calibrar el nivel de esfuerzo frente a la precisión requerida en el dominio a la hora de tomar esta decisión. Sin embargo, los algoritmos de aprendizaje profundo tienden a funcionar bien cuando entendemos poco sobre el dominio aplicado y nos esforzamos por hacer una construcción artesanal avanzada de características.

Diferentes problemas tienen diferentes mejores métodos

En general, el aprendizaje automático consiste en aplicar el enfoque correcto en la situación adecuada. Aún no hemos llegado al punto en que una única técnica domine el panorama, por lo que debemos evaluar el espacio del problema y los datos cada vez que busquemos el mejor modelo para aplicar. Esto se basa en el "teorema de que no hay almuerzo gratis".

Teorema de la no gratuidad

El "teorema de la comida gratis" afirma que no hay un modelo que funcione para todos los problemas. Los supuestos de un gran modelo para un problema pueden no ser válidos para otro problema. Es habitual en el aprendizaje automático probar varios modelos y encontrar el que mejor funciona para un problema concreto.

Todo método de aprendizaje automático tiene cierto sesgo y varianza. Cuanto más se acerque nuestro modelo al verdadero modelo subyacente, mejor nos irá de media con nuestro algoritmo de aprendizaje.

Otra forma de entenderlo es considerarlo desde el punto de vista de un ejemplo práctico. Si los datos son claramente lineales, como se ve en las visualizaciones, ¿intentarías ajustarlos con un modelo no lineal (por ejemplo, un perceptrón multicapa)? No, probablemente abordarías el problema con algo más sencillo, como la regresión logística. En las competiciones Kaggle, el método que obtiene mejores resultados varía de una competición a otra. Sin embargo, los bosques aleatorios y los métodos de conjunto suelen ser los ganadores cuando no gana el aprendizaje profundo.

El tamaño del conjunto de datos de entrada puede ser otro factor que influya en la idoneidad del aprendizaje profundo para un problema determinado. Los resultados empíricos de los últimos años han demostrado que el aprendizaje profundo proporciona el mejor poder predictivo cuando el conjunto de datos es lo suficientemente grande. Esto significa que los resultados del aprendizaje profundo mejoran a medida que aumenta el tamaño del conjunto de datos. Las redes neuronales tienen mayor capacidad de representación que los modelos lineales y pueden explotar mejor los datos. Una buena regla general es que un profesional debería ser capaz de entrenar una red neuronal con al menos 5.000 ejemplos etiquetados de entrada de entrenamiento.

¿Cuándo necesito aprendizaje profundo?

Para terminar este capítulo, queremos dejarte con un sencillo conjunto de reglas que te ayudarán a responder a la pregunta: ¿necesita este proyecto utilizar el aprendizaje profundo?

Cuándo utilizar el aprendizaje profundo

Tú deberías utilizar el aprendizaje profundo cuando...

• Los modelos más sencillos (regresión logística) no alcanzan el nivel de precisión que necesita tu caso de uso
• Tienes que enfrentarte a una compleja concordancia de patrones en imágenes, PNL o audio
• Tienes datos de alta dimensionalidad
• Tienes la dimensión del tiempo en tus vectores (secuencias)

Cuándo seguir con el aprendizaje automático tradicional

Tú deberías utilizar un modelo de aprendizaje automático tradicional cuando...

• Tienes datos de alta calidad y baja dimensión; por ejemplo, datos en columnas procedentes de la exportación de una base de datos
• No intentas encontrar patrones complejos en datos de imágenes

Obtendrás malos resultados con ambos métodos cuando los datos estén incompletos y/o sean de mala calidad.

¹ Goodfellow et al. 2014. "Redes Generativas Adversariales".

² Vondrick, Pirsiavash y Torralba. 2016. "Generación de vídeos con dinámica de escena".

³ Zhang et al. 2016. "StackGAN: Síntesis de texto a imagen fotorrealista con redes generativas adversariales apiladas".

⁴ La imagen procede del repositorio GitHub de los autores de DCGAN.

⁵ Mirza y Osindero. 2014. "Redes Adversariales Generativas Condicionales".

⁶ Kalchbrenner et al. 2016. "Traducción automática neuronal en tiempo lineal".

⁷ Gehring et al. 2016. "Un modelo de codificador convolucional para la traducción automática neuronal".

⁸ Nogueira dos Santos y Gatti. 2014. "Redes Neuronales Convolucionales Profundas para el Análisis de Sentimiento de Textos Cortos".

⁹ Eickenberg et al. 2017. "Verlo todo: Las capas de redes convolucionales mapean la función del sistema visual humano".

¹⁰ Krizhevsky et al. 2012. "Clasificación de ImageNet con redes neuronales convolucionales profundas".

¹¹ Otro hiperparámetro habitual en las CNN es la dilatación. Actualmente, DL4J no admite la dilatación a partir de la versión 0.7.

¹² Ioffe y Szegedy. 2015. "Normalización por lotes: Acelerar el entrenamiento de redes profundas reduciendo el desplazamiento interno de covariables".

¹³ Cooijmans et al. 2016. "Normalización recurrente por lotes".

¹⁴ Milletari, Navab y Ahmadi. 2016. "V-Net: Redes neuronales totalmente convolucionales para la segmentación volumétrica de imágenes médicas".

¹⁵ Maturana y Scherer. 2015. "VoxNet: Una red neuronal convolucional 3D para el reconocimiento de objetos en tiempo real".

¹⁶ Henaff, Bruna y LeCun. 2015. "Redes convolucionales profundas sobre datos estructurados en grafos".

¹⁷ Conneau et al. 2016. "Redes convolucionales muy profundas para la clasificación de textos".

¹⁸ LeCun et al. 1998. "Aprendizaje basado en gradientes aplicado al reconocimiento de documentos".

¹⁹ Krizhevsky, Sutskever y Hinton. 2012. "Clasificación de ImageNet con redes neuronales convolucionales profundas".

²⁰ Zeiler y Fergus. 2013. "Visualizar y comprender las redes convolucionales".

²¹ Szegedy et al. 2015. "Profundizando con las convoluciones".

²² Simonyan y Zisserman. 2015. "Redes convolucionales muy profundas para el reconocimiento de imágenes a gran escala".

²³ He et al. 2015. "Aprendizaje residual profundo para el reconocimiento de imágenes".

²⁴ Graves y Jaitly. 2014. "Hacia el reconocimiento del habla de extremo a extremo con redes neuronales recurrentes".

²⁵ Nayebi y Vitelli. 2015. "GRUV: Generación algorítmica de música mediante redes neuronales recurrentes".

²⁶ Sutskever, Vinyals y Le. 2014. "Aprendizaje de secuencia a secuencia con redes neuronales".

²⁷ Hochreiter y Schmidhuber. 1997. "Memoria a largo plazo".

²⁸ Graves. 2012. "Etiquetado supervisado de secuencias con redes neuronales recurrentes".

²⁹ Gers, Schmidhuber y Cummins. 1999. "Aprender a olvidar: Predicción continua con LSTM".

³⁰ Graves. 2012. "Etiquetado supervisado de secuencias con redes neuronales recurrentes".

³¹ Greff et al. 2015. "LSTM: una odisea en el espacio de búsqueda".

³² Cho et al. 2014. "Aprendizaje de representaciones de frases mediante codificador-decodificador RNN para traducción automática estadística".

³³ Srivastava, Mansimov y Salakhutdinov. 2015. "Aprendizaje no supervisado de representaciones de vídeo mediante LSTMs".

³⁴ Venugopalan et al. 2014. "Traducir vídeos a lenguaje natural utilizando redes neuronales recurrentes profundas".

³⁵ Wu et al. 2016. "Subtitulado de imágenes y respuesta a preguntas visuales basadas en atributos y conocimiento externo".

³⁶ Mnih et al. 2014. "Modelos recurrentes de atención visual".

³⁷ Karpathy y Fei-Fei. 2014. "Alineaciones visuales-semánticas profundas para generar descripciones de imágenes".

³⁸ La imagen procede de Karpathy y Fei-Fei. 2014. "Alineaciones visuales-semánticas profundas para generar descripciones de imágenes".