Capítulo 1. Una revisión del aprendizaje automático
Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: translation-feedback@oreilly.com
Condensar los hechos a partir del vapor de los matices
Neal Stephenson, Snow Crash
Las máquinas de aprender
El interés por el aprendizaje automático se ha disparado en la última década. El aprendizaje automático aparece casi a diario en los programas de informática, en las conferencias del sector y en el Wall Street Journal. Por mucho que se hable del aprendizaje automático, muchos confunden lo que puede hacer con lo que desearían que pudiera hacer. Fundamentalmente, el aprendizaje automático consiste en utilizar algoritmos para extraer información de datos brutos y representarla en algún tipo de modelo. Utilizamos este modelo para inferir cosas sobre otros datos que aún no hemos modelado.
Redes neuronales son un tipo de modelo para el aprendizaje automático; existen desde hace al menos 50 años. La unidad fundamental de una red neuronal es un nodo, que se basa vagamente en la neurona biológica del cerebro de los mamíferos. Las conexiones entre neuronas también se modelan a partir de cerebros biológicos, al igual que la forma en que estas conexiones se desarrollan con el tiempo (con el "entrenamiento"). Profundizaremos en el funcionamiento de estos modelos en los dos próximos capítulos.
En a mediados de los 80 y principios de los 90, se hicieron muchos avances arquitectónicos importantes en las redes neuronales. Sin embargo, la cantidad de tiempo y datos necesarios para obtener buenos resultados ralentizó su adopción, por lo que el interés se enfrió. A principios de la década de 2000, la potencia computacional aumentó exponencialmente y la industria asistió a una "explosión cámbrica" de técnicas computacionales que antes no eran posibles. El aprendizaje profundo emergió del explosivo crecimiento computacional de esa década como un serio contendiente en el campo, ganando muchas competiciones importantes de aprendizaje automático. El interés no se ha enfriado en 2017; hoy en día, vemos que se menciona el aprendizaje profundo en todos los rincones del aprendizaje automático.
Trataremos nuestra definición de aprendizaje profundo con mayor profundidad en la sección siguiente. Este libro está estructurado de forma que tú, el profesional, puedas cogerlo de la estantería y hacer lo siguiente:
- Repasar las partes básicas relevantes del álgebra lineal y el aprendizaje automático
- Repasa los fundamentos de las redes neuronales
- Estudia las cuatro arquitecturas principales de las redes profundas
- Utiliza los ejemplos del libro para probar variaciones de redes profundas prácticas
Esperamos que encuentres el material práctico y accesible. Comencemos el libro con una rápida introducción sobre qué es el aprendizaje automático y algunos de los conceptos básicos que necesitarás para comprender mejor el resto del libro.
¿Cómo pueden aprender las máquinas?
Para definir en cómo pueden aprender las máquinas, tenemos que definir qué entendemos por "aprendizaje". En el lenguaje cotidiano, cuando decimos aprender, queremos decir algo así como "adquirir conocimientos mediante el estudio, la experiencia o la enseñanza". Afinando un poco nuestro enfoque, podemos pensar en el aprendizaje automático como el uso de algoritmos para adquirir descripciones estructurales a partir de ejemplos de datos. Un ordenador aprende algo sobre las estructuras que representan la información en los datos brutos. Las descripciones estructurales son otro término para los modelos que construimos para contener la información extraída de los datos brutos, y podemos utilizar esas estructuras o modelos para predecir datos desconocidos. Las descripciones estructurales (o modelos) pueden adoptar muchas formas, como las siguientes:
- Árboles de decisión
- Regresión lineal
- Pesos de la red neuronal
Cada tipo de modelo tiene una forma distinta de aplicar reglas a datos conocidos para predecir datos desconocidos. Los árboles de decisión crean un conjunto de reglas en forma de estructura de árbol y los modelos lineales crean un conjunto de parámetros para representar los datos de entrada.
Las redes neuronales tienen lo que se denomina un vector de parámetros que representa los pesos de las conexiones entre los nodos de la red. Describiremos los detalles de este tipo de modelo más adelante en este capítulo.
Arthur Samuel, pionero de la inteligencia artificial (IA) en IBM y Stanford, definió el aprendizaje automático de la siguiente manera:
[Campo de estudio que confiere a los ordenadores la capacidad de aprender sin ser programados explícitamente.
Samuel creó un software que podía jugar a las damas y adaptar su estrategia a medida que aprendía a asociar la probabilidad de ganar y perder con determinadas disposiciones del tablero. Ese esquema fundamental de búsqueda de patrones que conducen a la victoria o a la derrota y, a continuación, de reconocimiento y refuerzo de los patrones exitosos, sustenta el aprendizaje automático y la IA hasta nuestros días.
El concepto de máquinas que pueden aprender a alcanzar objetivos por sí mismas nos ha cautivado durante décadas. Quizá lo expresaron mejor los abuelos modernos de la IA, Stuart Russell y Peter Norvig, en su libro Inteligencia Artificial: Un Enfoque Moderno:
¿Cómo es posible que un cerebro lento y diminuto, ya sea biológico o electrónico, perciba, comprenda, prediga y manipule un mundo mucho más grande y complicado que él mismo?
Esta cita alude a ideas sobre cómo los conceptos de aprendizaje se inspiraron en procesos y algoritmos descubiertos en la naturaleza. Para contextualizar visualmente el aprendizaje profundo, la Figura 1-1 ilustra nuestra concepción de la relación entre IA, aprendizaje automático y aprendizaje profundo.
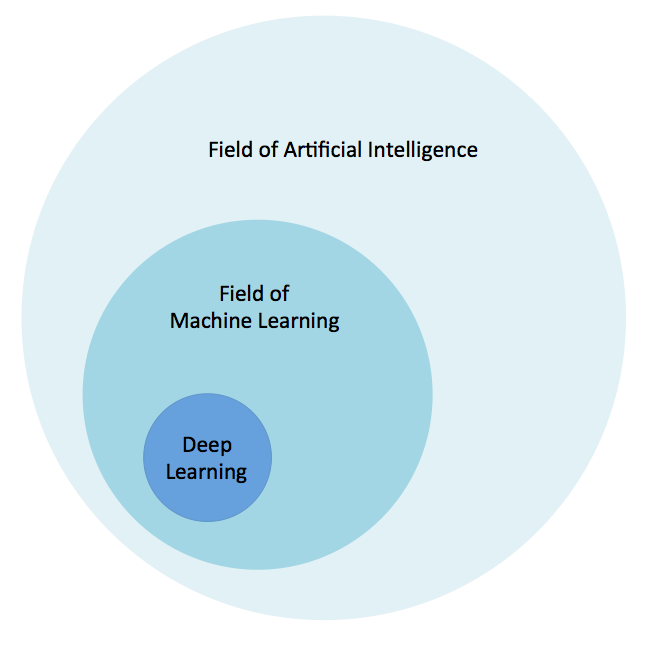
Figura 1-1. La relación entre la IA y el aprendizaje profundo
El campo de la IA es amplio y existe desde hace mucho tiempo. El aprendizaje profundo es un subconjunto del campo del aprendizaje automático, que es un subcampo de la IA. Echemos ahora un rápido vistazo a otra de las raíces del aprendizaje profundo: cómo las redes neuronales se inspiran en la biología.
Inspiración biológica
Biológico las redes neuronales (cerebros) están compuestas por unos 86.000 millones de neuronas conectadas a muchas otras neuronas.
Conexiones totales en el cerebro humano
Los investigadores estiman de forma conservadora que hay más de 500 billones de conexiones entre neuronas en el cerebro humano. Ni siquiera las mayores redes neuronales artificiales actuales se acercan a esta cifra.
Desde el punto de vista del procesamiento de la información, una neurona biológica es una unidad excitable que puede procesar y transmitir información mediante señales eléctricas y químicas. En el cerebro biológico, una neurona se considera un componente principal del cerebro, de la médula espinal del sistema nervioso central y de los ganglios del sistema nervioso periférico. Como veremos más adelante en este capítulo, las redes neuronales artificiales son mucho más simples en su estructura comparativa.
Comparar lo biológico con lo artificial
¡Las redes neuronales biológicas son considerablemente más complejas (varios órdenes de magnitud) que las versiones de redes neuronales artificiales!
Hay dos propiedades principales de las redes neuronales artificiales que siguen la idea general de cómo funciona el cerebro. La primera es que la unidad más básica de la red neuronal es la neurona artificial (o nodo en abreviatura). Las neuronas artificiales se modelan a partir de las neuronas biológicas del cerebro y, al igual que las neuronas biológicas, se estimulan mediante entradas. Estas neuronas artificiales transmiten parte -pero no toda- la información que reciben a otras neuronas artificiales, a menudo con transformaciones. A medida que avancemos en este capítulo, entraremos en detalle en qué consisten estas transformaciones en el contexto de las redes neuronales.
En segundo lugar, del mismo modo que se puede entrenar a las neuronas del cerebro para que sólo transmitan señales útiles para alcanzar los objetivos generales del cerebro, podemos entrenar a las neuronas de una red neuronal para que sólo transmitan señales útiles. A medida que avancemos en este capítulo, nos basaremos en estas ideas y veremos cómo las redes neuronales artificiales son capaces de modelar a sus homólogas biológicas mediante bits y funciones.
¿Qué es el aprendizaje profundo?
El aprendizaje profundo ha sido un reto de definir para muchos porque ha cambiado de forma lentamente durante la última década. Una definición útil especifica que el aprendizaje profundo trata de una "red neuronal con más de dos capas". El aspecto problemático de esta definición es que hace que el aprendizaje profundo suene como si existiera desde la década de 1980. Creemos que las redes neuronales tuvieron que trascender arquitectónicamente desde los estilos de red anteriores (junto con mucha más potencia de procesamiento) antes de mostrar los espectaculares resultados que se han visto en años más recientes. A continuación se exponen algunas de las facetas de esta evolución de las redes neuronales:
- Más neuronas que las redes anteriores
- Formas más complejas de conectar capas/neuronas en las NNs
- Explosión de la cantidad de potencia informática disponible para entrenar
- Extracción automática de rasgos
A efectos de este libro, definiremos el aprendizaje profundo como redes neuronales con un gran número de parámetros y capas en una de las cuatro arquitecturas de red fundamentales:
- Redes preentrenadas no supervisadas
- Redes neuronales convolucionales
- Redes neuronales recurrentes
- Redes neuronales recursivas
También existen algunas variaciones de las arquitecturas mencionadas -una red neuronal convolucional y recurrente híbrida, por ejemplo-. A efectos de este libro, nos centraremos en las cuatro arquitecturas enumeradas.
La extracción automática de características de es otra de las grandes ventajas que tiene el aprendizaje profundo sobre los algoritmos tradicionales de aprendizaje automático. Por extracción de características, entendemos el proceso de la red de decidir qué características de un conjunto de datos pueden utilizarse como indicadores para etiquetar esos datos de forma fiable. Históricamente, los profesionales del aprendizaje automático han dedicado meses, años y, a veces, décadas de su vida a crear manualmente conjuntos exhaustivos de características para la clasificación de datos. En el momento del Big Bang del aprendizaje profundo, que comenzó en 2006, los algoritmos de aprendizaje automático más avanzados habían absorbido décadas de esfuerzo humano mientras acumulaban características relevantes con las que clasificar la entrada. El aprendizaje profundo ha superado a esos algoritmos convencionales en precisión para casi todos los tipos de datos con un ajuste y un esfuerzo humano mínimos. Estas redes profundas pueden ayudar a los equipos de ciencia de datos a ahorrar su sangre, sudor y lágrimas para tareas más significativas.
Bajando por la madriguera del conejo
El aprendizaje profundo ha penetrado en la conciencia de la informática más allá de la mayoría de las técnicas de la historia reciente. Esto se debe en parte a que no sólo ha demostrado una precisión de primer orden en el modelado del aprendizaje automático, sino que también ha demostrado una mecánica generativa que fascina incluso a los no informáticos. Un ejemplo de ello serían las demostraciones de generación de arte, en las que se entrenó una red profunda en las obras de un pintor famoso concreto, y la red fue capaz de renderizar otras fotografías con el estilo único del pintor, como se demuestra en la Figura 1-2.

Figura 1-2. Imágenes estilizadas de Gatys et al., 20152
Esto empieza a entrar en muchas discusiones filosóficas, como "¿pueden ser creativas las máquinas?" y luego "¿qué es la creatividad?". Dejaremos esas preguntas para que reflexiones sobre ellas más adelante. El aprendizaje automático ha evolucionado a lo largo de los años, como cambian las estaciones: sutil pero constantemente, hasta que un día te levantas y una máquina se ha convertido en campeona de Jeopardy o ha vencido a un Gran Maestro de Go.
¿Pueden las máquinas ser inteligentes y asumir una inteligencia de nivel humano? ¿Qué es la IA y cuán poderosa puede llegar a ser? Estas preguntas aún no tienen respuesta y no la tendrán por completo en este libro. Simplemente pretendemos ilustrar algunas de las esquirlas de inteligencia de las máquinas con las que podemos imbuir nuestro entorno actual mediante la práctica del aprendizaje profundo.
Para un debate ampliado sobre la IA
Si quieres leer más sobre la IA, echa un vistazo al Apéndice A.
Formular las preguntas
Los fundamentos de la aplicación del aprendizaje automático se comprenden mejor planteando las preguntas correctas para empezar. Esto es lo que tenemos que definir:
- ¿Cuáles son los datos de entrada de los que queremos extraer información (modelo)?
- ¿Qué tipo de modelo es el más adecuado para estos datos?
- ¿Qué tipo de respuesta nos gustaría obtener de los nuevos datos basados en este modelo?
Si podemos responder a estas tres preguntas, podremos establecer un flujo de trabajo de aprendizaje automático que construya nuestro modelo y produzca las respuestas deseadas. Para apoyar mejor este flujo de trabajo, repasemos algunos de los conceptos básicos que debemos conocer para practicar el aprendizaje automático. Más adelante, volveremos sobre cómo se combinan en el aprendizaje automático y utilizaremos esa información para comprender mejor tanto las redes neuronales como el aprendizaje profundo.
Las matemáticas detrás del aprendizaje automático: Álgebra lineal
Lineal álgebra es la base del aprendizaje automático y del aprendizaje profundo. El álgebra lineal nos proporciona los fundamentos matemáticos para resolver las ecuaciones que utilizamos para construir modelos.
Nota
Un excelente manual de álgebra lineal es Matrix Algebra, de James E. Gentle : Teoría, Cálculos y Aplicaciones en Estadística, de James E. Gentle.
Veamos algunos conceptos básicos de este campo antes de seguir adelante, empezando por el concepto básico llamado escalar.
Escaras
En las matemáticas de , cuando se menciona el término escalar, se trata de elementos de un vector. Un escalar es un número real y un elemento de un campo utilizado para definir un espacio vectorial.
En informática, el término escalar es sinónimo del término variable y es un lugar de almacenamiento asociado a un nombre simbólico. Este lugar de almacenamiento contiene una cantidad desconocida de información llamada valor.
Vectores
Para nuestro uso, definimos un vector como sigue:
Para un número entero positivo n, un vector es una n-tupla, (multi)conjunto ordenado o matriz de n números, llamados elementos o escalares.
Lo que estamos diciendo es que queremos crear una estructura de datos llamada vector mediante un proceso llamado vectorización. El número de elementos del vector se denomina "orden" (o "longitud") del vector. Los vectores también pueden representar puntos en un espacio n-dimensional. En el sentido espacial, la distancia euclidiana desde el origen hasta el punto representado por el vector nos da la "longitud" del vector.
En los textos matemáticos, a menudo vemos los vectores escritos de la siguiente manera:
O:
Hay muchas formas distintas de manejar la vectorización, y puedes aplicar muchos pasos de preprocesamiento, lo que nos dará distintos grados de eficacia en los modelos de salida. Trataremos más a fondo el tema de la conversión de datos brutos en vectores más adelante en este capítulo y después, de forma más completa, en el Capítulo 5.
Matrices
Considera que una matriz es un conjunto de vectores que tienen todos la misma dimensión (número de columnas). De este modo, una matriz es una matriz bidimensional para la que tenemos filas y columnas.
Si decimos que nuestra matriz es una matriz n × m, significa que tiene n filas y m columnas. La Figura 1-3 muestra una matriz de 3 × 3 que ilustra las dimensiones de una matriz. Las matrices son una estructura fundamental en álgebra lineal y aprendizaje automático, como mostraremos a medida que avancemos en este capítulo.

Figura 1-3. Una matriz 3 x 3
Tensores
Un tensor es una matriz multidimensional al nivel más fundamental. Es una estructura matemática más general que un vector. Podemos considerar un vector simplemente como una subclase de los tensores.
En los tensores, las filas se extienden a lo largo del eje y y las columnas a lo largo del eje x. Cada eje es una dimensión, y los tensores tienen dimensiones adicionales. Los tensores también tienen un rango. Comparativamente, un escalar es de rango 0 y un vector es de rango 1. También vemos que una matriz es de rango 2. Cualquier entidad de rango 3 o superior se considera un tensor.
Hiperplanos
Otro objeto del álgebra lineal de que debes conocer es el hiperplano. En el campo de la geometría, el hiperplano es un subespacio de una dimensión menos que su espacio ambiente. En un espacio tridimensional, los hiperplanos tendrían dos dimensiones. En un espacio bidimensional, consideramos que una recta unidimensional es un hiperplano.
Un hiperplano es una construcción matemática que divide un espacio n-dimensional en "partes" separadas y, por tanto, es útil en aplicaciones como la clasificación. Optimizar los parámetros del hiperplano es un concepto básico en la modelización lineal, como verás más adelante en este capítulo.
Operaciones matemáticas relevantes
En esta sección repasamos brevemente las operaciones comunes del álgebra lineal que debes conocer.
Producto de puntos
Una operación básica del álgebra lineal que vemos a menudo en el aprendizaje automático es el producto punto. El producto punto se denomina a veces "producto escalar" o "producto interior". El producto punto toma dos vectores de la misma longitud y devuelve un único número. Esto se hace emparejando las entradas de los dos vectores, multiplicándolas y sumando los productos así obtenidos. Sin ponernos demasiado matemáticos (inmediatamente), es importante mencionar que este único número codifica mucha información.
Para empezar , el producto punto es una medida de lo grandes que son los elementos individuales de cada vector. Dos vectores con valores bastante grandes pueden dar resultados bastante grandes, y dos vectores con valores bastante pequeños pueden dar valores bastante pequeños. Cuando los valores relativos de estos vectores se tienen en cuenta matemáticamente con algo llamado normalización, el producto punto es una medida de lo similares que son estos vectores. Esta noción matemática del producto escalar de dos vectores normalizados se denomina similitud coseno.
Producto por elementos
Otra operación de álgebra lineal habitual que vemos en la práctica es el producto elemento-sabio (o "producto de Hadamard"). Esta operación toma dos vectores de la misma longitud y produce un vector de la misma longitud con cada elemento correspondiente multiplicado a partir de los dos vectores de origen.
Convertir datos en vectores
En el curso de trabajo en aprendizaje automático y ciencia de datos necesitamos analizar todos los tipos de datos. Un requisito clave es poder tomar cada tipo de dato y representarlo como un vector. En el aprendizaje automático utilizamos muchos tipos de datos (por ejemplo, texto, series temporales, audio, imágenes y vídeo).
Entonces, ¿por qué no podemos simplemente alimentar con datos brutos a nuestro algoritmo de aprendizaje y dejar que se encargue de todo? La cuestión es que el aprendizaje automático se basa en el álgebra lineal y la resolución de conjuntos de ecuaciones. Estas ecuaciones esperan números en coma flotante como entrada, así que necesitamos una forma de traducir los datos brutos en conjuntos de números en coma flotante. Conectaremos estos conceptos en la siguiente sección sobre la resolución de estos conjuntos de ecuaciones. Un ejemplo de datos brutos sería el conjunto de datos canónicos del iris:
5.1,3.5,1.4,0.2,Iris-setosa 4.9,3.0,1.4,0.2,Iris-setosa 4.7,3.2,1.3,0.2,Iris-setosa 7.0,3.2,4.7,1.4,Iris-versicolor 6.4,3.2,4.5,1.5,Iris-versicolor 6.9,3.1,4.9,1.5,Iris-versicolor 5.5,2.3,4.0,1.3,Iris-versicolor 6.5,2.8,4.6,1.5,Iris-versicolor 6.3,3.3,6.0,2.5,Iris-virginica 5.8,2.7,5.1,1.9,Iris-virginica 7.1,3.0,5.9,2.1,Iris-virginica
Otro ejemplo podría ser un documento de texto sin formato:
Go, Dogs. Go! Go on skates or go by bike.
Ambos casos implican datos brutos de distintos tipos, pero ambos necesitan cierto nivel de vectorización para tener la forma que necesitamos para hacer aprendizaje automático. En algún momento, queremos que nuestros datos de entrada tengan la forma de una matriz, pero podemos convertir los datos a representaciones intermedias (por ejemplo, el formato de archivo "svmlight", que se muestra en el ejemplo de código que sigue). Queremos que los datos de entrada de nuestro algoritmo de aprendizaje automático se parezcan más al formato de vector disperso serializado svmlight, como se muestra en el siguiente ejemplo:
1.0 1:0.7500000000000001 2:0.41666666666666663 3:0.702127659574468 4:0. 5652173913043479 2.0 1:0.6666666666666666 2:0.5 3:0.9148936170212765 4:0.6956521739130436 2.0 1:0.45833333333333326 2:0.3333333333333336 3:0.8085106382978723 4:0 .7391304347826088 0.0 1:0.1666666666666665 2:1.0 3:0.021276595744680823 2.0 1:1.0 2:0.5833333333333334 3:0.9787234042553192 4:0.8260869565217392 1.0 1:0.3333333333333333 3:0.574468085106383 4:0.47826086956521746 1.0 1:0.7083333333333336 2:0.7500000000000002 3:0.6808510638297872 4:0 .5652173913043479 1.0 1:0.916666666666667 2:0.6666666666666667 3:0.7659574468085107 4:0 .5652173913043479 0.0 1:0.08333333333333343 2:0.5833333333333334 3:0.021276595744680823 2.0 1:0.6666666666666666 2:0.8333333333333333 3:1.0 4:1.0 1.0 1:0.9583333333333335 2:0.7500000000000002 3:0.723404255319149 4:0 .5217391304347826 0.0 2:0.7500000000000002
Este formato puede leerse rápidamente en una matriz y un vector de columnas para las etiquetas (el primer número de cada fila en el ejemplo anterior). El resto de los números indexados de la fila se insertan en la ranura adecuada de la matriz como "características" en tiempo de ejecución para prepararlos para diversas operaciones de álgebra lineal durante el proceso de aprendizaje automático. Trataremos el proceso de vectorización con más detalle en el Capítulo 8.
He aquí una pregunta muy común: "¿por qué los algoritmos de aprendizaje automático quieren que los datos se representen (típicamente) como una matriz (dispersa)?". Para entenderlo, demos un rápido rodeo por los fundamentos de la resolución de sistemas de ecuaciones.
Resolución de sistemas de ecuaciones
En el mundo del álgebra lineal, nos interesa resolver sistemas de ecuaciones lineales de la forma:
- Ax = b
donde A es una matriz de nuestro conjunto de vectores fila de entrada y b es el vector columna de etiquetas de cada vector de la matriz A. Si tomamos las tres primeras filas de la salida dispersa serializada del ejemplo anterior y colocamos los valores en su forma de álgebra lineal, queda así:
|
Columna 1 |
Columna 2 |
Columna 3 |
Columna 4 |
|
0.7500000000000001 |
0.41666666666666663 |
0.702127659574468 |
0.5652173913043479 |
|
0.6666666666666666 |
0.5 |
0.9148936170212765 |
0.6956521739130436 |
|
0.45833333333333326 |
0.3333333333333336 |
0.8085106382978723 |
0.7391304347826088 |
Esta matriz de números es nuestra variable A en nuestra ecuación, y cada valor independiente o valor de cada fila se considera una característica de nuestros datos de entrada.
Queremos encontrar coeficientes para cada columna de una fila dada para una función predictora que nos dé la salida b, o la etiqueta de cada fila. Las etiquetas de los vectores dispersos serializados que hemos visto antes serían las siguientes:
|
Etiquetas |
|
1.0 |
|
2.0 |
|
2.0 |
Los coeficientes mencionados anteriormente se convierten en el vector de columnas x (también llamado vector de parámetros) que se muestra en la Figura 1-4.

Figura 1-4. Visualización de la ecuación Ax = b
Se dice que este sistema es "coherente" si existe un vector de parámetros x tal que la solución de esta ecuación puede escribirse directamente de la siguiente manera:
Es importante delimitar la expresión x = A-1b del método para calcular realmente la solución. Esta expresión sólo representa la solución en sí. La variable A-1 es la matriz A invertida y se calcula mediante un proceso llamado inversión matricial. Dado que no todas las matrices pueden invertirse, nos gustaría disponer de un método para resolver esta ecuación que no implique la inversión matricial. Un método es la descomposición matricial. Un ejemplo de descomposición matricial en la resolución de sistemas de ecuaciones lineales es utilizar la descomposición inferior superior (LU) para resolver la matriz A. Más allá de la descomposición matricial, echemos un vistazo a los métodos generales para resolver conjuntos de ecuaciones lineales.
Métodos para resolver sistemas de ecuaciones lineales
En existen dos métodos generales para resolver un sistema de ecuaciones lineales. El primero se denomina "método directo", en el que sabemos algorítmicamente que hay un número fijo de cálculos. El otro enfoque es una clase de métodos conocidos como métodos iterativos, en los que mediante una serie de aproximaciones y un conjunto de condiciones de terminación podemos derivar el vector de parámetros x. La clase de métodos directos es especialmente eficaz cuando podemos ajustar todos los datos de entrenamiento(A y b) en la memoria de un solo ordenador. Ejemplos bien conocidos del método directo de resolución de conjuntos de ecuaciones lineales son la Eliminación de Gauss y las Ecuaciones Normales.
Métodos iterativos
La clase de métodos iterativos es especialmente eficaz cuando nuestros datos no caben en la memoria principal de un solo ordenador, y recorrer en bucle registros individuales desde el disco nos permite modelizar una cantidad de datos mucho mayor. El ejemplo canónico de los métodos iterativos más habituales en el aprendizaje automático actual es el Descenso Gradiente Estocástico (SGD ), del que hablaremos más adelante en este capítulo. Otras técnicas en este espacio son los Métodos de Gradiente Conjugado y los Mínimos Cuadrados Alternos (tratados más adelante en el Capítulo 3). Los métodos iterativos también han demostrado su eficacia en los métodos de escalado, en los que no sólo hacemos un bucle a través de los registros locales, sino que todo el conjunto de datos se desmenuza en un clúster de máquinas, y periódicamente el vector de parámetros se promedia en todos los agentes y luego se actualiza en cada agente de modelado local (se describe con más detalle en el Capítulo 9).
Métodos iterativos y álgebra lineal
A nivel matemático, queremos poder operar sobre nuestro conjunto de datos de entrada con estos algoritmos. Esta restricción nos obliga a convertir nuestros datos de entrada brutos en la matriz de entrada A. Este rápido repaso del álgebra lineal nos da el "por qué" de tomarnos la molestia de vectorizar los datos. A lo largo de este libro, mostramos ejemplos de código para convertir los datos de entrada brutos en la matriz de entrada A, dándote el "cómo". La mecánica de cómo vectorizamos nuestros datos también afecta a los resultados del proceso de aprendizaje. Como veremos más adelante en el libro, la forma en que manejamos los datos en la etapa de preprocesamiento antes de la vectorización puede crear modelos más precisos.
Las matemáticas detrás del aprendizaje automático: Estadística
Vamos a repasar en la estadística suficiente para que este capítulo avance. Debemos destacar algunos conceptos básicos de estadística, como los siguientes:
- Probabilidades
- Distribuciones
- Probabilidad
También hay otras relaciones básicas que nos gustaría destacar en la estadística descriptiva y la estadística inferencial. Las estadísticas descriptivas incluyen lo siguiente:
- Histogramas
- Gráficos de caja
- Gráficos de dispersión
- Media
- Desviación típica
- Coeficiente de correlación
Esto contrasta con el modo en que la estadística inferencial se ocupa de las técnicas para generalizar de una muestra a una población. He aquí algunos ejemplos de estadística inferencial:
- valores p
- intervalos de credibilidad
La relación entre probabilidad y estadística inferencial:
- Razona la probabilidad desde la población a la muestra (razonamiento deductivo)
- La estadística inferencial razona de la muestra a la población
Antes de poder entender lo que una muestra concreta nos dice sobre la población de origen, tenemos que comprender la incertidumbre asociada a la toma de una muestra de una población determinada.
En cuanto a la estadística general, no nos detendremos en lo que es un tema inherentemente amplio ya tratado en profundidad por otros libros. Esta sección no pretende en modo alguno servir como un verdadero repaso de estadística; más bien, está diseñada para dirigirte hacia temas relevantes que puedes investigar con mayor profundidad en otros recursos. Una vez aclarado esto, empecemos definiendo la probabilidad en estadística.
Probabilidad
En definimos la probabilidad de un suceso E como un número siempre comprendido entre 0 y 1. En este contexto, el valor 0 infiere que el suceso E no tiene ninguna posibilidad de ocurrir, y el valor 1 significa que el suceso E ocurrirá con toda seguridad. Muchas veces veremos esta probabilidad expresada como un número de coma flotante, pero también podemos expresarla como un porcentaje entre 0 y 100%; no veremos probabilidades válidas inferiores a 0% y superiores a 100%. Un ejemplo sería una probabilidad de 0,35 expresada como 35 por ciento (por ejemplo, 0,35 x 100 == 35 por ciento).
El ejemplo canónico de medir la probabilidad es observar cuántas veces sale cara o cruz al lanzar una moneda justa (por ejemplo, 0,5 para cada cara). La probabilidad del espacio muestral es siempre 1, porque el espacio muestral representa todos los resultados posibles para un ensayo determinado. Como podemos ver con los dos resultados ("cara" y su complemento, "cruz") para la moneda lanzada al aire, 0,5 + 0,5 == 1,0 porque la probabilidad total del espacio muestral siempre debe sumar 1. Expresamos la probabilidad de un suceso de la siguiente manera:
- P( E ) = 0,5
Y leemos esto así
La probabilidad de un suceso E es 0,5
La probabilidad está en el centro de las redes neuronales y el aprendizaje profundo debido a su papel en la extracción de características y la clasificación, dos de las principales funciones de las redes neuronales profundas. Para una revisión más amplia de la estadística, consulta Statistics in a Nutshell de O'Reilly : A Desktop Quick Reference de Boslaugh y Watters.
Probabilidades condicionales
Cuando en queremos conocer la probabilidad de que se produzca un suceso determinado en función de la presencia de otro suceso, lo expresamos como probabilidad condicional. En la literatura se expresa de la forma
- P( E | F )
donde:
E es el acontecimiento cuya probabilidad nos interesa.
F es el acontecimiento que ya se ha producido.
Un ejemplo sería expresar cómo una persona con una frecuencia cardiaca saludable tiene una menor probabilidad de morir en la UCI durante una visita al hospital:
P(Muerte en UCI | Frecuencia cardiaca baja) > P(Muerte en UCI | Frecuencia cardiaca sana)
A veces, oiremos referirse al segundo suceso, F, como la "condición". La probabilidad condicional es interesante en el aprendizaje automático y el aprendizaje profundo porque a menudo nos interesa saber cuándo ocurren varias cosas y cómo interactúan. Nos interesan las probabilidades condicionales en el aprendizaje automático en el contexto en el que aprenderíamos un clasificador aprendiendo
- P ( E | F )
donde E es nuestra etiqueta y F es una serie de atributos sobre la entidad para la que estamos prediciendo E. Un ejemplo sería predecir la mortalidad (aquí, E) dadas las mediciones tomadas en la UCI para cada paciente (aquí, F).
Probabilidad posterior
En Estadística bayesiana, llamamos probabilidad posterior del suceso aleatorio a la probabilidad condicional que asignamos después de considerar las pruebas. La distribución de probabilidad posterior se define como la distribución de probabilidad de una cantidad desconocida condicional a las pruebas recogidas de un experimento tratado como una variable aleatoria. Vemos este concepto en acción con las funciones de activación softmax (explicadas más adelante en este capítulo), en las que los valores de entrada brutos se convierten en probabilidades posteriores.
Distribuciones
Una distribución de probabilidad es una especificación de la estructura estocástica de las variables aleatorias. En estadística, nos basamos en hacer suposiciones sobre cómo se distribuyen los datos para hacer inferencias sobre ellos. Queremos una fórmula que especifique la frecuencia de los valores de las observaciones en la distribución y los valores que pueden tomar los puntos de la distribución. Una distribución habitual es la distribución normal (también llamada distribución de Gauss o curva de campana). Nos gusta ajustar un conjunto de datos a una distribución porque si el conjunto de datos se aproxima razonablemente a la distribución, podemos hacer suposiciones basadas en la distribución teórica en la forma en que operamos con los datos.
En clasificamos las distribuciones en continuas o discretas. Una distribución discreta tiene datos que sólo pueden asumir determinados valores. En una distribución continua, los datos pueden tener cualquier valor dentro del intervalo. Un ejemplo de distribución continua sería la distribución normal. Un ejemplo de distribución discreta sería la distribución binomial.
La distribución normal nos permite suponer que las distribuciones muestrales de los estadísticos (por ejemplo, la "media muestral") se distribuyen normalmente en condiciones especificadas. La distribución normal (ver Figura 1-5), o distribución gaussiana, debe su nombre al matemático y físico del siglo XVIII Karl Gauss. La distribución normal se define por su media y su desviación típica, y suele tener la misma forma en todas las variaciones.
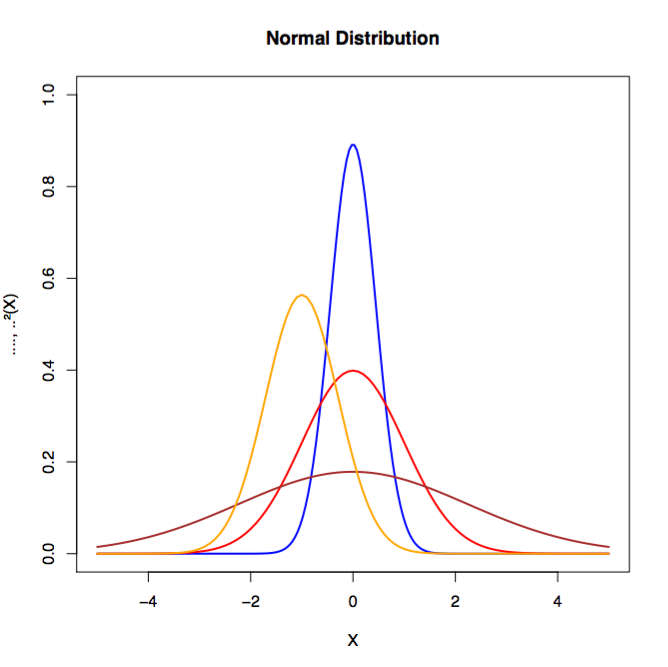
Figura 1-5. Ejemplos de distribuciones normales
Otras distribuciones relevantes en el aprendizaje automático son las siguientes:
- Distribución binomial
- Distribución gaussiana inversa
- Distribución logarítmica normal
La distribución de los datos de entrenamiento en el aprendizaje automático es importante para comprender cómo vectorizar los datos para el modelado.
Una distribución de cola larga (como las distribuciones de Zipf, leyes de potencia y Pareto) es un escenario en el que a una población de alta frecuencia le sigue una población de baja frecuencia que disminuye gradualmente de forma asintótica. Estas distribuciones fueron descubiertas por Benoit Mandelbrot en la década de 1950 y posteriormente popularizadas por el escritor Chris Anderson en su libro The Long Tail: Why the Future of Business is Selling Less of More.
Un ejemplo sería clasificar los artículos que vende un minorista entre los cuales unos pocos artículos son excepcionalmente populares y luego vemos un gran número de artículos únicos con cantidades vendidas relativamente pequeñas. Esta distribución rango-frecuencia (principalmente de popularidad o "cuántos se vendieron") suele formar leyes de potencia. Desde esta perspectiva, podemos considerarlas distribuciones de cola larga.
Vemos que estas distribuciones de cola larga se manifiestan en lo siguiente:
- Daños por terremoto
-
Los daños se agravan a medida que aumenta la magnitud del seísmo, por lo que el peor de los casos se desplaza.
- Rendimiento de los cultivos
-
A veces vemos acontecimientos fuera del registro histórico, mientras que nuestro modelo tiende a ajustarse en torno a la media.
- Predicción de la mortalidad tras la visita a la UCI
-
Puede haber acontecimientos muy ajenos a lo que ocurre dentro de la visita a la UCI que afecten a la mortalidad.
Estos ejemplos son relevantes en el contexto de este libro para los problemas de clasificación, porque la mayoría de los modelos estadísticos dependen de la inferencia a partir de muchos datos. Si los sucesos más interesantes ocurren en la cola de la distribución y no tenemos esto representado en los datos de la muestra de entrenamiento, nuestro modelo podría funcionar de forma impredecible. Este efecto puede potenciarse en modelos no lineales, como las redes neuronales. Consideraríamos esta situación como el caso especial del problema "dentro de la muestra/fuera de la muestra". Incluso un experto en aprendizaje automático puede sorprenderse de lo bien que funciona un modelo en una muestra de datos de entrenamiento sesgada, pero no generaliza bien en la población de datos más amplia.
Las distribuciones de cola larga se ocupan de la posibilidad real de que se produzcan sucesos cinco veces superiores a la desviación típica. Debemos tener cuidado de obtener una representación decente de los sucesos en nuestros datos de entrenamiento para evitar el sobreajuste de los datos de entrenamiento. Examinaremos con más detalle las formas de hacerlo más adelante, cuando hablemos del sobreajuste, y luego en el Capítulo 4 sobre el ajuste.
Muestras frente a población
Una población de datos se define como todas las unidades que queremos estudiar o modelizar en nuestro experimento. Un ejemplo sería definir nuestra población de estudio como "todos los programadores Java del estado de Tennessee".
Una muestra de datos es un subconjunto de la población de datos que, con suerte, representa la distribución exacta de los datos sin introducir sesgos de muestreo (p. ej., sesgar la distribución de la muestra en función de cómo hayamos muestreado la población).
Métodos de remuestreo
Bootstrapping y la validación cruzada son dos métodos habituales de remuestreo en estadística que resultan útiles a los profesionales del aprendizaje automático. En el contexto del aprendizaje automático con bootstrapping, estamos extrayendo muestras aleatorias de otra muestra para generar una nueva muestra que tenga un equilibrio entre el número de muestras por clase. Esto es útil cuando queremos modelizar un conjunto de datos con clases muy desequilibradas.
Validación cruzada (también llamada estimación de rotación) es un método para estimar lo bien que generaliza un modelo en un conjunto de datos de entrenamiento. En la validación cruzada dividimos el conjunto de datos de entrenamiento en un número N de divisiones y, a continuación, separamos las divisiones en grupos de entrenamiento y de prueba. Nos entrenamos en el grupo de entrenamiento y luego probamos el modelo en el grupo de prueba. Rotamos las divisiones entre los dos grupos muchas veces hasta que hayamos agotado todas las variaciones. No existe un número fijo para el número de divisiones a utilizar, pero los investigadores han descubierto que 10 divisiones funcionan bien en la práctica. También es habitual ver que se utiliza una parte separada de los datos retenidos como conjunto de datos de validación durante el entrenamiento.
Sesgo de selección
En sesgo de selección nos enfrentamos a un método de muestreo que no tiene una aleatorización adecuada y sesga la muestra de tal manera que ésta no es representativa de la población que queremos modelizar. Tenemos que ser conscientes del sesgo de selección cuando volvamos a muestrear conjuntos de datos, para no introducir sesgos en nuestros modelos que reduzcan la precisión de nuestro modelo en los datos de la población más amplia.
Probabilidad
Cuando en hablamos de la probabilidad de que se produzca un acontecimiento sin referirnos específicamente a su probabilidad numérica, estamos utilizando el término informal probabilidad. Normalmente, cuando utilizamos este término, estamos hablando de un acontecimiento que tiene una probabilidad razonable de ocurrir, pero que aún así podría no ocurrir. También puede haber factores aún no observados que influyan en el suceso. Informalmente, verosimilitud también se utiliza como sinónimo de probabilidad.
¿Cómo funciona el aprendizaje automático?
En una sección anterior sobre la resolución de sistemas de ecuaciones lineales, introdujimos los fundamentos de la resolución de Ax = b. Fundamentalmente, el aprendizaje automático se basa en técnicas algorítmicas para minimizar el error en esta ecuación mediante la optimización.
En la optimización, nos centramos en cambiar los números del vector de columnas x (vector de parámetros) hasta que encontremos un buen conjunto de valores que nos proporcione los resultados más próximos a los valores reales. Cada peso de la matriz de pesos se ajustará después de que la función de pérdida calcule el error (basado en el resultado real, como se ha mostrado antes, como vector de columna b ) producido por la red. Una matriz de error que atribuya una parte de la pérdida a cada peso se multiplicará por los propios pesos.
Más adelante en este capítulo hablaremos del SGD como uno de los principales métodos para realizar optimizaciones de aprendizaje automático, y luego conectaremos estos conceptos con otros algoritmos de optimización a medida que avance el libro. También cubriremos los aspectos básicos de los hiperparámetros, como la regularización y la tasa de aprendizaje.
Regresión
Regresión se refiere a las funciones que intentan predecir un valor real de salida. Este tipo de función estima la variable dependiente conociendo la variable independiente. La clase más común de regresión es la regresión lineal, basada en los conceptos que hemos descrito anteriormente en el modelado de sistemas de ecuaciones lineales. La regresión lineal intenta dar con una función que describa la relación entre x e y y, para valores conocidos de x, prediga valores de y que resulten exactos.
Configurar el modelo
La predicción de un modelo de regresión lineal es la combinación lineal de los coeficientes (del vector de parámetros x) y luego las variables de entrada (características del vector de entrada). Podemos modelizarlo mediante la siguiente ecuación:
- y = a + Bx
donde a es la intersección y, B son las características de entrada y x es el vector de parámetros.
Esta ecuación se expande a lo siguiente
Un ejemplo sencillo de un problema que resuelve la regresión lineal sería predecir cuánto gastaríamos al mes en gasolina en función de la longitud de nuestro trayecto al trabajo. En este caso, lo que pagas en el depósito es función de la distancia que recorres. El coste de la gasolina es la variable dependiente y la longitud del trayecto es la variable independiente. Es razonable llevar la cuenta de estas dos cantidades y luego definir una función, así:
- coste = f (distancia)
Esto nos permite predecir razonablemente nuestro gasto en gasolina basándonos en el kilometraje. En este ejemplo, consideraríamos la distancia como nuestra variable independiente y el coste como la variable dependiente en nuestro modelo f.
Aquí tienes otros ejemplos de modelos de regresión lineal:
- Predicción del peso en función de la altura
- Predecir el precio de venta de una casa en función de sus metros cuadrados
Visualizar la regresión lineal
Visualmente, podemos representar la regresión lineal como la búsqueda de una línea que se acerque al mayor número posible de puntos en un diagrama de dispersión de datos, como se muestra en la Figura 1-6.
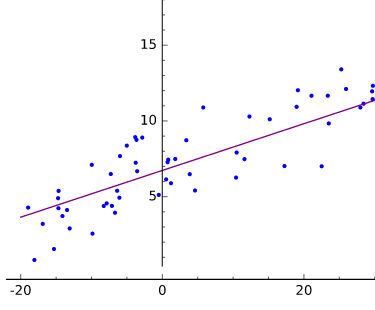
Figura 1-6. Regresión lineal trazada
Elajuste es definir una función f(x) que produzca valores ypróximos a los valores y medidos o del mundo real. La recta producida por y = f(x) se aproxima a las coordenadas dispersas, los pares de variables dependiente e independiente.
Relacionar el modelo de regresión lineal
En podemos relacionar esta función con la ecuación anterior, Ax = b, donde A son las características (por ejemplo, "peso" o "metros cuadrados") de todos los ejemplos de entrada que queremos modelar. Cada registro de entrada es una fila de la matriz A. El vector columna b son los resultados de todos los registros de entrada de la matriz A. Utilizando una función de error y un método de optimización (por ejemplo, SGD), podemos encontrar un conjunto de parámetros x tal que minimicemos el error en todas las predicciones frente a los resultados verdaderos.
Utilizando SGD, como hemos comentado antes, tendríamos tres componentes para resolver nuestro vector parámetro x:
- Una hipótesis sobre los datos
-
El producto interno del vector de parámetros x y las características de entrada (como se muestra arriba)
- Una función de costes
-
Error al cuadrado (predicción - real) de la predicción
- Una función de actualización
-
La derivada de la función de pérdida de error al cuadrado (función de coste)
Mientras que la regresión lineal se ocupa de las líneas rectas, el ajuste no lineal de curvas se ocupa de todo lo demás, sobre todo de las curvas que se ocupan de x a exponentes superiores a 1. (Por eso a veces oímos describir el aprendizaje automático como "ajuste de curvas".) Un ajuste absoluto daría con todos los puntos de un diagrama de dispersión. Irónicamente, el ajuste absoluto suele ser un resultado muy pobre, porque significa que tu modelo se ha entrenado con demasiada perfección en el conjunto de entrenamiento, y casi no tiene poder predictivo más allá de los datos que ha visto (por ejemplo, no generaliza bien), como ya hemos comentado.
Clasificación
Clasificación es el modelado basado en la delimitación de clases de resultados a partir de un conjunto de características de entrada. Si la regresión nos da un resultado de"cuánto", la clasificación nos da un resultado de"qué clase". La variable dependiente y es categórica en lugar de numérica.
La forma más básica de clasificación es un clasificador binario que sólo tiene una única salida con dos etiquetas (dos clases: 0 y 1, respectivamente). La salida también puede ser un número de coma flotante entre 0,0 y 1,0 para indicar una clasificación por debajo de la certeza absoluta. En este caso, tenemos que determinar un umbral (normalmente 0,5) a partir del cual delimitamos entre las dos clases. En la bibliografía, estas clases suelen denominarse clasificaciones positivas (por ejemplo, 1,0) y negativas (por ejemplo, 0,0). Hablaremos más de esto en "Evaluación de modelos".
Algunos ejemplos de clasificación binaria son
- Clasificar si alguien tiene una enfermedad o no
- Clasificar un correo electrónico como spam o no spam
- Clasificar una transacción como fraudulenta o nominal
Más allá de dos etiquetas, podemos tener modelos de clasificación que tengan N etiquetas para las que puntuaríamos cada una de las etiquetas de salida, y luego la etiqueta con la puntuación más alta sería la etiqueta de salida. Hablaremos más de esto cuando hablemos de las redes neuronales con múltiples salidas frente a las redes neuronales con una única salida (clasificación binaria). También hablaremos más de la clasificación en este capítulo cuando hablemos de la regresión logística y luego nos sumerjamos en la arquitectura completa de las redes neuronales.
Recomendación
Recomendación es el proceso de sugerir artículos a los usuarios de un sistema basándose en otros usuarios similares u otros artículos que hayan mirado antes. Una de las variantes más famosas de los algoritmos de recomendación es el llamado Filtrado Colaborativo, que se hizo famoso gracias a Amazon.com.
Agrupación
Agrupación es una técnica de aprendizaje no supervisado que consiste en utilizar una medida de distancia y acercar iterativamente los elementos similares. Al final del proceso, los elementos agrupados más densamente en torno a n centroides se consideran clasificados en ese grupo. La agrupación de K-means es una de las variantes más famosas de la agrupación en el aprendizaje automático.
Infraadaptación y sobreadaptación
Como hemos mencionado antes en , los algoritmos de optimización primero intentan resolver el problema del ajuste insuficiente, es decir, de tomar una línea que no se aproxima bien a los datos y hacer que se aproxime mejor a ellos. Una línea recta que corta un diagrama de dispersión curvo sería un buen ejemplo de ajuste insuficiente, como se ilustra en la Figura 1-7.
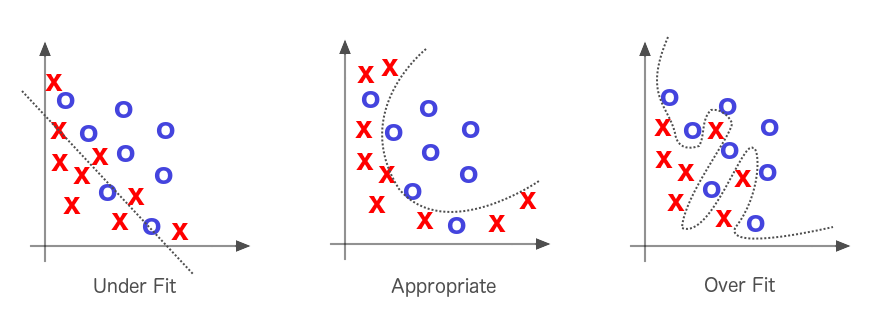
Figura 1-7. Ajuste insuficiente y ajuste excesivo en el aprendizaje automático
Si la recta se ajusta demasiado bien a los datos, tenemos el problema contrario, llamado "sobreajuste". Resolver el infraajuste es la prioridad, pero gran parte del esfuerzo en el aprendizaje automático se dedica a intentar no sobreajustar la recta a los datos. Cuando decimos que un modelo se ajusta demasiado a un conjunto de datos, nos referimos a que puede tener una tasa de error baja para los datos de entrenamiento, pero no generaliza bien a la población general de datos en la que estamos interesados.
Otra forma de explicar el sobreajuste es pensar en las distribuciones probables de los datos. El conjunto de datos de entrenamiento sobre el que intentamos trazar una recta es sólo una muestra de un conjunto mayor desconocido, y la recta que tracemos tendrá que ajustarse igualmente bien al conjunto mayor si queremos que tenga algún poder predictivo. Debemos suponer, por tanto, que nuestra muestra es vagamente representativa de un conjunto mayor.
Optimización
El proceso antes mencionado de ajustar las ponderaciones para producir conjeturas cada vez más precisas sobre los datos se conoce como optimización de parámetros. Puedes pensar en este proceso como en un método científico. Formulas una hipótesis, la contrastas con la realidad y refinas o sustituyes esa hipótesis una y otra vez para describir mejor los acontecimientos del mundo.
Cada conjunto de pesos representa una hipótesis específica sobre lo que significan las entradas; es decir, cómo se relacionan con los significados contenidos en las etiquetas propias. Los pesos representan conjeturas sobre las correlaciones entre las entradas de las redes y las etiquetas objetivo que pretenden adivinar. Todos los pesos posibles y sus combinaciones pueden describirse como el espacio de hipótesis de este problema. Nuestro intento de formular la mejor hipótesis es una cuestión de búsqueda a través de ese espacio de hipótesis, y lo hacemos utilizando algoritmos de error y optimización. Cuantos más parámetros de entrada tengamos, mayor será el espacio de búsqueda de nuestro problema. Gran parte del trabajo de aprendizaje consiste en decidir qué parámetros ignorar y cuáles escuchar.
El límite de decisión y los hiperplanos
Cuando en mencionamos el "límite de decisión", estamos hablando del hiperplano n-dimensional creado por el vector de parámetros en la modelización lineal.
Ajustar las líneas a los datos midiendo su coste (es decir, su distancia a los puntos de los datos reales) es el centro del aprendizaje automático. La recta debe ajustarse más o menos a los datos, y lo hace minimizando la distancia agregada de todos los puntos a la recta. Minimizas la suma de la diferencia entre la línea en el punto x y el punto objetivo y al que corresponde. En un espacio tridimensional, puedes imaginar el paisaje de error de colinas y valles, e imaginar tu algoritmo como un excursionista ciego que va tanteando la pendiente. Un algoritmo de optimización, como el descenso de pendiente, es el que informa a la excursionista de qué dirección es cuesta abajo para que sepa dónde pisar.
El objetivo es encontrar los pesos que minimicen la diferencia entre lo que predice tu red (o el producto punto de A y x) y lo que tu conjunto de pruebas sabe que es cierto(b), como vimos anteriormente en la Figura 1-4. El vector de parámetros(x) anterior es donde encontrarías los pesos. La precisión de una red es función de su entrada y sus parámetros, y la velocidad a la que se vuelve precisa es función de sus hiperparámetros.
Hiperparámetros
En el aprendizaje automático de , tenemos tanto parámetros de modelo como parámetros que afinamos para que las redes entrenen mejor y más rápido. Estos parámetros de ajuste se llaman hiperparámetros, y se ocupan de controlar la función de optimización y la selección del modelo durante el entrenamiento con nuestro algoritmo de aprendizaje.
Convergencia
Convergencia se refiere a que un algoritmo de optimización encuentre valores para un vector de parámetros que den a nuestro algoritmo de optimización el menor error posible en todos los ejemplos de entrenamiento. Se dice que el algoritmo de optimización "converge" en la solución de forma iterativa después de probar varias variaciones diferentes de los parámetros.
En encontrarás las tres funciones importantes que intervienen en la optimización del aprendizaje automático:
- Parámetros
-
Transformar la entrada para ayudar a determinar las clasificaciones que infiere una red
- Función de pérdida
- Función de optimización
-
La guía hacia los puntos de menor error
Ahora veamos más de cerca una subclase de optimización llamada optimización convexa.
Optimización convexa
En optimización convexa, los algoritmos de aprendizaje tratan con funciones de coste convexas. Si el eje x representa un único peso, y el eje y representa ese coste, el coste descenderá hasta 0 en un punto del eje x y aumentará exponencialmente a ambos lados a medida que el peso se aleje de su ideal en dos direcciones.
La Figura 1-8 demuestra que también podemos darle la vuelta a la idea de función de costes.
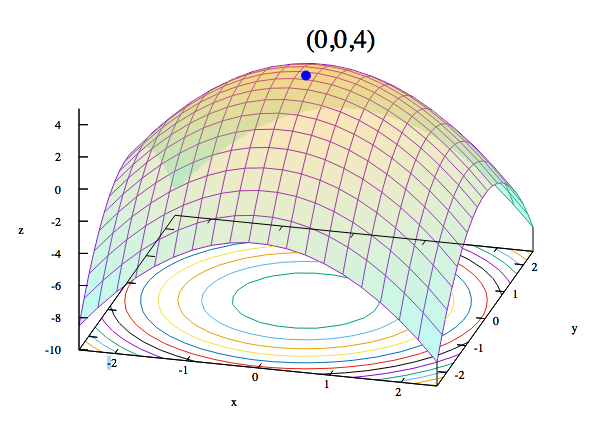
Figura 1-8. Visualización de funciones convexas
Otra forma de relacionar los parámetros con los datos es con una estimación de máxima verosimilitud, o MLE. La MLE traza una parábola cuyos perímetros apuntan hacia abajo, con la probabilidad medida en el eje vertical, y un parámetro en el horizontal. Cada punto de la parábola mide la verosimilitud de los datos, dado un determinado conjunto de parámetros. El objetivo del MLE es iterar sobre los posibles parámetros hasta encontrar el conjunto que hace más probables los datos dados.
En cierto sentido, la máxima verosimilitud y el mínimo coste son dos caras de la misma moneda. El cálculo de la función de coste de dos pesos frente al error (que nos sitúa en un espacio tridimensional) producirá algo que se parece más a una hoja sujeta por cada esquina y que cae convexamente en el centro: una función con forma de cuenco. Las pendientes de estas curvas convexas dan a nuestro algoritmo una pista sobre la dirección en la que debe dar el siguiente paso de parámetro, como veremos en el algoritmo de optimización por descenso de gradiente del que hablaremos a continuación.
Descenso Gradiente
En descenso gradiente, podemos imaginar la calidad de las predicciones de nuestra red (en función de los valores de los pesos/parámetros) como un paisaje. Las colinas representan ubicaciones (valores de parámetros o pesos) que dan mucho error de predicción; los valles representan ubicaciones con menos error. Elegimos un punto de ese paisaje en el que colocar nuestro peso inicial. A continuación, podemos seleccionar el peso inicial basándonos en el conocimiento del dominio (si estamos entrenando una red para clasificar una especie de flor, sabemos que la longitud de los pétalos es importante, pero el color no). O, si dejamos que la red haga todo el trabajo, podemos elegir los pesos iniciales al azar.
El objetivo es mover ese peso cuesta abajo, hacia zonas de menor error, lo más rápidamente posible. Un algoritmo de optimización como el descenso por gradiente puede percibir la pendiente real de las colinas con respecto a cada peso; es decir, sabe qué dirección es hacia abajo. El descenso gradiente mide la pendiente (el cambio en el error causado por un cambio en el peso) y lleva el peso un paso hacia el fondo del valle. Lo hace tomando una derivada de la función de pérdida para producir el gradiente. El gradiente da al algoritmo la dirección para el siguiente paso en el algoritmo de optimización, como se muestra en la Figura 1-9.
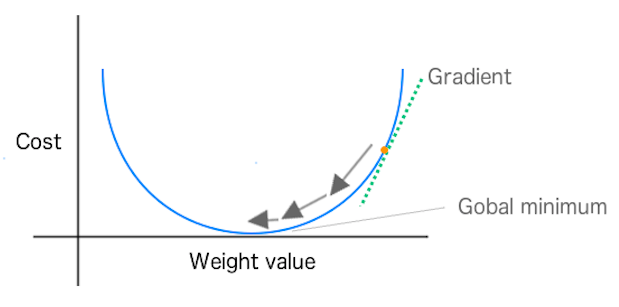
Figura 1-9. Muestra los cambios de peso hacia el mínimo global en SGD
La derivada mide la "velocidad de cambio" de una función. En la optimización convexa, buscamos el punto en el que la derivada es igual a 0 para la función. Este punto también se conoce como punto estacionario de la función o punto mínimo. En optimización, consideramos que optimizar una función es minimizar una función (al margen de invertir la función de coste).
Este proceso de medir la pérdida y cambiar el peso un paso en la dirección de menor error se repite hasta que el peso llega a un punto más allá del cual no puede bajar más. Se detiene en el valle, el punto de mayor precisión. Cuando se utiliza una función de pérdida convexa (normalmente en modelización lineal), vemos una función de pérdida que sólo tiene un mínimo global.
Puedes pensar en la modelización lineal en términos de tres componentes para resolver nuestro vector de parámetros x:
- Una hipótesis sobre los datos; por ejemplo, "la ecuación que utilizamos para hacer una predicción en el modelo".
- Una función de coste. También llamada función de pérdida; por ejemplo, "suma de errores al cuadrado".
- Una función de actualización; tomamos la derivada de la función de pérdida.
Nuestra hipótesis es la combinación de los parámetros aprendidos x y los valores de entrada (características) que nos da una salida de clasificación o de valor real (regresión). La función de coste nos dice lo lejos que estamos del mínimo global de la función de pérdida, y utilizamos la derivada de la función de pérdida como función de actualización para cambiar el vector de parámetros x.
Tomar la derivada de la función de pérdida indica para cada parámetro en x el grado en que necesitamos ajustar el parámetro para acercarnos al punto 0 en las curvas de pérdida. Examinaremos más detenidamente estas ecuaciones más adelante en este capítulo, cuando mostremos cómo funcionan tanto para la regresión lineal como para la regresión logística (clasificación).
Sin embargo, en otros problemas no lineales no siempre obtenemos una curva de pérdida tan limpia. El problema con estos otros paisajes hipotéticos no lineales es que puede haber varios valles, y el mecanismo de descenso por gradiente para hacer descender el peso no puede saber si ha llegado al valle más bajo o simplemente al punto más bajo de un valle más alto, por así decirlo. El punto más bajo del valle más bajo se conoce como mínimo global, mientras que los nadires de todos los demás valles se conocen como mínimos locales. Si el descenso gradiente alcanza un mínimo local, queda atrapado de hecho, y éste es uno de los inconvenientes del algoritmo. Veremos formas de superar este problema en el Capítulo 6, cuando examinemos los hiperparámetros y la velocidad de aprendizaje.
Un segundo problema con el que se encuentra el descenso de gradiente es con las características no normalizadas. Cuando escribimos "características no normalizadas", nos referimos a características que pueden medirse con escalas muy diferentes. Si tienes una dimensión medida en millones y otra en decimales, el descenso de gradiente tendrá dificultades para encontrar la pendiente más pronunciada para minimizar el error.
Hacer frente a la normalización
En el capítulo 8 examinamos más detenidamente los métodos de normalización en el contexto de la vectorización e ilustramos algunas formas de abordar mejor esta cuestión.
Descenso Gradiente Estocástico
En descenso de gradiente calcularíamos la pérdida global en todos los ejemplos de entrenamiento antes de calcular el gradiente y actualizar el vector de parámetros. En SGD, calculamos el gradiente y actualizamos el vector de parámetros después de cada muestra de entrenamiento. Se ha demostrado que esto acelera el aprendizaje y también se paraleliza bien, como veremos más adelante en el libro. El SGD es una aproximación al descenso del gradiente "por lotes completos".
Formación en mini lotes y SGD
Otra variante del SGD consiste en utilizar más de un único ejemplo de entrenamiento para calcular el gradiente, pero menos que el conjunto completo de datos de entrenamiento. Esta variante se denomina tamaño de minilotes de entrenamiento con SGD y se ha demostrado que es más eficaz que utilizar un único ejemplo de entrenamiento. También se ha demostrado que la aplicación de minilotes al descenso de gradiente estocástico conduce a una convergencia más suave, ya que el gradiente se calcula en cada paso y utiliza más ejemplos de entrenamiento para calcular el gradiente.
A medida que aumenta el tamaño del minilote, el gradiente calculado se aproxima más al gradiente "verdadero" de todo el conjunto de entrenamiento. Esto también nos da la ventaja de una mayor eficiencia computacional. Si el tamaño de nuestro minilote es demasiado pequeño (por ejemplo, 1 registro de entrenamiento), no estamos utilizando el hardware con la eficacia que podríamos, especialmente en situaciones como las GPU. A la inversa, hacer que el tamaño del mini lote sea mayor (más allá de un punto) también puede ser ineficaz, porque podemos producir el mismo gradiente con menos esfuerzo computacional (en algunos casos) con el descenso de gradiente regular.
Métodos de Optimización Quasi-Newton
Quasi-Newton los métodos de optimización son algoritmos iterativos que implican una serie de "búsquedas de línea". Su característica distintiva respecto a otros métodos de optimización es cómo eligen la dirección de búsqueda. Estos métodos se tratan con más detalle en capítulos posteriores del libro.
Modelos Generativos Versus Discriminativos
Nosotros podemos generar distintos tipos de resultados a partir de un modelo, según el tipo de modelo que configuremos. Los dos tipos principales son los modelos generativos y los modelos discriminativos. Los modelos generativos comprenden cómo se crearon los datos para generar un tipo de respuesta o salida. Los modelos discriminativos no se preocupan de cómo se crearon los datos y se limitan a darnos una clasificación o categoría para una señal de entrada dada. Los modelos discriminativos se centran en modelar de cerca el límite entre clases y pueden dar una representación más matizada de este límite que un modelo generativo. Los modelos discriminatorios se suelen utilizar para la clasificación en el aprendizaje automático.
Un modelo generativo aprende la distribución de probabilidad conjunta p(x, y), mientras que un modelo discriminativo aprende la distribución de probabilidad condicional p(y|x). La distribución p(y|x) es la distribución natural para tomar una entrada x y producir una salida (o clasificación) y, de ahí el nombre de "modelo discriminativo". Con los modelos generativos que aprenden la distribuciónp(x,y), vemos que se utilizan para generar una salida probable, dada una determinada entrada. Los modelos generativos suelen configurarse como modelos gráficos probabilísticos que captan las relaciones sutiles de los datos.
Regresión logística
Regresión logística es un tipo de clasificación muy conocido en modelización lineal. Funciona tanto para la clasificación binaria como para etiquetas múltiples en forma de regresión logística multinomial. La regresión logística es un modelo de regresión (técnicamente) en el que la variable dependiente es categórica (por ejemplo, "clasificación"). El modelo logístico binario se utiliza para estimar la probabilidad de una respuesta binaria basada en un conjunto de una o más variables de entrada (variables independientes o "características"). El resultado es la probabilidad estadística de una categoría, dados ciertos predictores de entrada.
De forma similar a la regresión lineal, podemos expresar un problema de modelado de regresión logística de la forma Ax = b, donde A es la característica (por ejemplo, "peso" o "metros cuadrados") de todos los ejemplos de entrada que queremos modelar. Cada registro de entrada es una fila de la matriz A, y el vector columna b son los resultados de todos los registros de entrada de la matriz A. Mediante una función de coste y un método de optimización, podemos encontrar un conjunto de parámetros x que minimice el error de todas las predicciones frente a los resultados reales.
De nuevo, utilizaremos SGD para plantear este problema de optimización y tenemos tres componentes que resolver para nuestro vector de parámetros x:
- Una hipótesis sobre los datos
- Una función de costes
-
"estimación de máxima verosimilitud"
- Una función de actualización
-
Una derivada de la función de coste
En este caso, la entrada comprende variables independientes (por ejemplo, las columnas de entrada o "características"), mientras que la salida son las variables dependientes (por ejemplo, las "puntuaciones de las etiquetas"). Una forma fácil de pensar en ello es que la función de regresión logística empareja valores de entrada con pesos para determinar si un resultado es probable. Echemos un vistazo más de cerca a la función logística.
La función logística
En la regresión logística definimos la función logística ("hipótesis") de la siguiente manera:
Esta función es útil en la regresión logística porque toma cualquier entrada en el intervalo de infinito negativo a positivo y la asigna a una salida en el intervalo de 0,0 a 1,0. Esto nos permite interpretar el valor de salida como una probabilidad. La Figura 1-10 muestra un gráfico de la ecuación de la función logística.
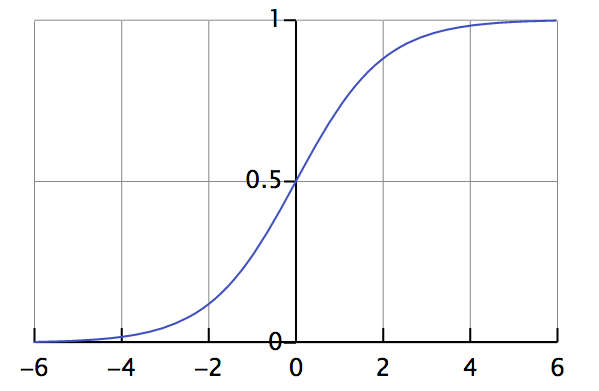
Figura 1-10. Gráfico de la función logística
Esta función se conoce como función log-sigmoidea continua con un intervalo de 0,0 a 1,0. Volveremos a ver esta función más adelante en "Funciones de activación".
Comprender los resultados de la regresión logística
La función logística se denota a menudo con la letra griega sigma, o σ, porque la relación entre x e y en un gráfico bidimensional se asemeja a una "s" alargada, soplada por el viento, cuyo máximo y mínimo se aproximan asintóticamente a 1 y 0, respectivamente.
Si y es una función de x, y esa función es sigmoidal o logística, cuanto más aumenta x, más nos acercamos a 1/1, porque e a la potencia de un número negativo infinitamente grande se aproxima a cero; por el contrario, cuanto más disminuye x por debajo de cero, más crece la expresión (1 + e-θx), reduciéndose todo el cociente. Como (1 + e-θx) está en el denominador, cuanto mayor sea, más se acercará a cero el propio cociente.
Con la regresión logística, f(x) representa la probabilidad de que y sea igual a 1 (es decir, que sea cierto) dada cada entrada x. Si intentamos estimar la probabilidad de que un correo electrónico sea spam, y resulta que f(x) es igual a 0,6, podríamos parafrasearlo diciendo que y tiene un 60% de probabilidades de ser 1, o que el correo electrónico tiene un 60% de probabilidades de ser spam, dada la entrada. Si definimos el aprendizaje automático como un método para inferir salidas desconocidas a partir de entradas conocidas, el vector de parámetros x en un modelo de regresión logística determina la fuerza y la certeza de nuestras deducciones.
La transformación Logit
La función logit es la inversa de la función logística ("transformación logística").
Evaluación de modelos
Evaluar los modelos es el proceso de comprender lo bien que dan la clasificación correcta y, a continuación, medir el valor de la predicción en un contexto determinado. A veces, sólo nos importa la frecuencia con la que un modelo acierta cualquier predicción; otras veces, es importante que el modelo acierte un determinado tipo de predicción más a menudo que los demás. En esta sección, tratamos temas como los malos positivos, los inofensivos negativos, las clases desequilibradas y los costes desiguales de las predicciones. Echemos un vistazo a la herramienta básica para evaluar modelos: la matriz de confusión.
La matriz de la confusión
La matriz de confusión (ver Figura 1-11) -también llamada tabla de confusión- esuna tabla de filas y columnas que representa las predicciones y los resultados reales (etiquetas) de un clasificador. Utilizamos esta tabla para comprender mejor el rendimiento del modelo o clasificador, basado en dar la respuesta correcta en el momento adecuado.
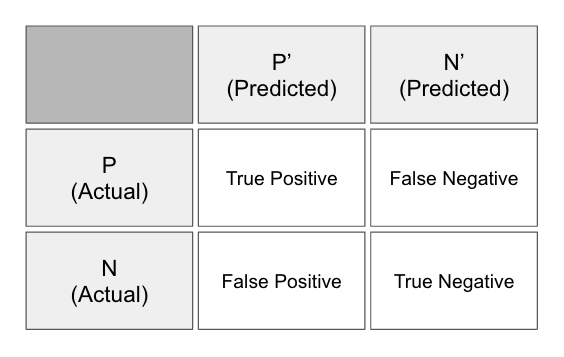
Figura 1-11. La matriz de confusión
Medimos estas respuestas contando el número de las siguientes:
- Verdaderos positivos
- Predicción positiva
- La etiqueta era positiva
- Falsos positivos
- Predicción positiva
- La etiqueta era negativa
- Verdaderos negativos
- Predicción negativa
- La etiqueta era negativa
- Falsos negativos
- Predicción negativa
- La etiqueta era positiva
En estadística tradicional, un falso positivo también se conoce como "error de tipo I" y un falso negativo como "error de tipo II". Mediante el seguimiento de estas métricas, podemos conseguir un análisis más detallado del rendimiento del modelo, más allá del porcentaje básico de conjeturas que fueron correctas. Podemos calcular distintas evaluaciones del modelo basadas en combinaciones de los cuatro recuentos mencionados en la matriz de confusión, como se muestra aquí:
Accuracy: 0.94 Precision: 0.8662 Recall: 0.8955 F1 Score: 0.8806
En el ejemplo anterior, podemos ver cuatro medidas diferentes habituales en la evaluación de los modelos de aprendizaje automático. Cubriremos cada una de ellas en breve, pero por ahora, empecemos por lo básico de la evaluación de la sensibilidad del modelo frente a la especificidad del modelo.
Sensibilidad frente a especificidad
Sensibilidad y especificidad son dos medidas diferentes de un modelo de clasificación binaria. La tasa de verdaderos positivos mide la frecuencia con la que clasificamos un registro de entrada como la clase positiva y su clasificación correcta. También se denomina sensibilidad o recuerdo; un ejemplo sería clasificar como enfermo a un paciente que en realidad lo estaba. La sensibilidad cuantifica lo bien que el modelo evita los falsos negativos.
- Sensibilidad = TP / (TP + FN)
Si nuestro modelo clasificara a una paciente del ejemplo anterior como no enferma y en realidad no lo estuviera, se consideraría un verdadero negativo (también llamado especificidad). La especificidad cuantifica lo bien que el modelo evita los falsos positivos.
- Especificidad = TN / (TN + FP)
Muchas veces necesitamos evaluar el compromiso entre sensibilidad y especificidad. Un ejemplo sería tener un modelo que detecta enfermedades graves en los pacientes con mayor frecuencia debido al elevado coste de diagnosticar mal a un paciente verdaderamente enfermo. Consideraríamos que este modelo tiene una especificidad baja. Una enfermedad grave podría suponer un peligro para la vida del paciente y para los demás que le rodean, por lo que nuestro modelo se consideraría que tiene una sensibilidad alta ante esta situación y sus implicaciones. En un mundo perfecto, nuestro modelo tendría una sensibilidad del 100% (es decir, se detectan todos los enfermos) y una especificidad del 100% (es decir, no se clasifica como enfermo a nadie que no lo esté).
Precisión
Precisión es el grado de aproximación de las mediciones de una magnitud al valor real de dicha magnitud.
- Precisión = (TP + TN) / (TP + FP + FN + TN)
La precisión puede inducir a error sobre la calidad del modelo cuando el desequilibrio de clases es alto. Si nos limitamos a clasificar todo como la clase más grande, nuestro modelo acertará automáticamente un gran número de sus conjeturas y nos proporcionará una puntuación de precisión alta, pero engañosa en cuanto al valor basado en una aplicación real del modelo (por ejemplo, nunca predecirá la clase más pequeña o el suceso raro).
Precisión
El grado en que las mediciones repetidas en las mismas condiciones nos dan los mismos resultados se denomina precisión en el contexto de la ciencia y la estadística. La precisión también se conoce como valor de predicción positivo. Aunque a veces se utiliza indistintamente con "precisión" en el uso coloquial, los términos se definen de forma diferente en el marco del método científico.
- Precisión = TP / (TP + FP)
Una medida puede ser exacta pero no precisa, no exacta pero precisa, ni exacta ni precisa, o exacta y precisa a la vez. Consideramos que una medición es válida si es exacta y precisa a la vez.
F1
En clasificación binaria consideramos que la puntuación F1 (o puntuación F, medida F) es una medida de la precisión de un modelo. La puntuación F1 es la media armónica de las medidas de precisión y recuperación (descritas anteriormente) en una única puntuación, como se define aquí:
- F1 = 2TP / (2TP + FP + FN)
Vemos puntuaciones para F1 entre 0,0 y 1,0, donde 0,0 es la peor puntuación y 1,0 es la mejor puntuación que nos gustaría ver. La puntuación F1 se utiliza normalmente en la recuperación de información para ver lo bien que un modelo recupera resultados relevantes. En el aprendizaje automático, la puntuación F1 se utiliza como puntuación general del rendimiento de nuestro modelo.
Contexto e interpretación de las puntuaciones
El contexto puede influir en cómo evaluamos nuestro modelo y dictar cuándo utilizamos distintos tipos de puntuaciones, como se ha descrito anteriormente en esta sección. El desequilibrio de clases puede desempeñar un papel importante a la hora de elegir la puntuación de evaluación, y en muchos conjuntos de datos nos encontraremos con que las clases o los recuentos de etiquetas no están bien equilibrados. He aquí algunos dominios típicos en los que vemos esto:
- Predicción de clics en la web
- Predicción de mortalidad en la UCI
- Detección del fraude
En estos contextos, una puntuación global de "porcentaje correcto" puede inducir a error sobre el valor global, en términos prácticos, del modelo. Un ejemplo de ello sería el conjunto de datos del Desafío PhysioNet de 2012.
El objetivo del reto era "predecir la mortalidad intrahospitalaria con la mayor precisión utilizando un clasificador binario". La dificultad y el reto de modelar este conjunto de datos es que predecir que un paciente vivirá es la parte fácil, porque la mayoría de los ejemplos del conjunto de datos tienen resultados en los que el paciente vive. Predecir la muerte con exactitud en este escenario es el objetivo; aquí es donde el modelo tiene más valor en el contexto de ser clínicamente relevante en el mundo real. En esta competición, las puntuaciones se calcularon de la siguiente manera:
- Puntuación = MIN(Precisión, Recall)
Esto se organizó de tal forma que los concursantes no se limitaron a predecir que el paciente viviría la mayor parte del tiempo y a obtener una buena puntuación F1, sino que se centraron en predecir cuándo moriría el paciente (manteniendo el enfoque en ser clínicamente relevante). Este es un gran ejemplo de cómo el contexto puede cambiar la forma en que evaluamos nuestros modelos.
Métodos para tratar el desequilibrio de clases
En el Capítulo 6 ilustramos formas prácticas de tratar el desequilibrio de clases. Examinamos más detenidamente las distintas facetas del desequilibrio de clases y las distribuciones de errores en el contexto de la clasificación y la regresión.
Comprender el aprendizaje automático
En este capítulo, hemos introducido los conceptos básicos necesarios para practicar el aprendizaje automático. Hemos visto los conceptos matemáticos básicos del modelado basado en la ecuación:
- Ax = b
También vimos las ideas básicas de introducir características en la matriz A, las formas de cambiar el vector de parámetros x y de establecer los resultados en el vector b. Ilustramos algunas formas básicas de cambiar el vector de parámetros x para minimizar la puntuación (o "pérdida") de la función objetivo.
A medida que avancemos en este libro, seguiremos ampliando estos conceptos clave. Veremos cómo las redes neuronales y el aprendizaje profundo se basan en estos fundamentos, pero añaden formas más complejas de crear la matriz A, cambiar el vector de parámetros x mediante métodos de optimización y medir la pérdida durante el entrenamiento. Pasemos ahora al Capítulo 2, donde profundizaremos en estos conceptos con los fundamentos de las redes neuronales.
1 Patterson. 2008. "TinyTermite: A Secure Routing Algorithm" y Sartipi y Patterson. 2009. "TinyTermite: Un algoritmo de enrutamiento seguro en la plataforma de red de sensores Intel Mote 2".
2 Gatys et. al, 2015. "Un algoritmo neuronal del estilo artístico".
Get Aprendizaje profundo now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

