Programming C# 12

Chapter 4. Generics

In Chapter 3, I showed how to write types and described the various kinds of members they can contain. However, there’s an extra dimension to classes, structs, interfaces, delegates, and methods that I did not show. They can define type parameters, placeholders that let you plug in different types at compile time. This allows you to write just one type and then produce multiple versions of it. A type that does this is called a generic type. For example, the runtime libraries define a generic class called List<T> that acts as a variable-length array. T is a type parameter here, and you can use almost any type as an argument, so List<int> is a list of integers, List<string> is a list of strings, and so on.¹ You can also write a generic method, which is a method that has its own type arguments, independently of whether its containing type is generic.

Generic types and methods are visually distinctive because they always have angle brackets (< and >) after the name. These contain a comma-separated list of parameters or arguments. The same parameter/argument distinction applies here as with methods: the declaration specifies a list of parameters, and then when you come to use the method or type, you supply arguments for those parameters. So List<T> defines a single type parameter, T, and List<int> supplies a type argument, int, for that parameter.

You can use any name you like for type parameters, within the usual constraints for identifiers in C#, but there are some popular conventions. It’s common (but not universal) to use T when there’s only one parameter. For multiparameter generics, you tend to see slightly more descriptive names. For example, the runtime libraries define the Dictionary<TKey, TValue> collection class. Sometimes you will see a descriptive name like that even when there’s just one parameter, but in any case, you will tend to see a T prefix so that the type parameters stand out when you use them in your code.

Generic Types

Classes, structs, records, and interfaces can all be generic, as can delegates, which we’ll be looking at in Chapter 9. Example 4-1 shows how to define a generic class. This happens to use C# 12.0’s new primary constructor syntax, so after the type parameter list (<T>) this example also has a primary constructor parameter list.

Example 4-1. Defining a generic class

public class NamedContainer<T>(T item, string name)
{
    public T Item { get; } = item;
    public string Name { get; } = name;
}

The syntax for structs, records, and interfaces is much the same: the type name is followed immediately by a type parameter list. Example 4-2 shows how to write a generic record similar to the class in Example 4-1.

Example 4-2. Defining a generic record

public record NamedContainer<T>(T Item, string Name);

Inside the definition of a generic type, I can use the type parameter T anywhere you would normally see a type name. In the first two examples, I’ve used it as the type of a constructor argument and as the Item property’s type. I could define fields of type T too. (In fact I have, albeit not explicitly. Automatic properties generate hidden fields, so my Item property will have an associated hidden field of type T.) You can also define local variables of type T. And you’re free to use type parameters as arguments for other generic types. My NamedContainer<T> could declare members of type List<T>, for example.

The types that Examples 4-1 and 4-2 define are, like any generic type, not complete types. A generic type declaration is unbound, meaning that there are type parameters that must be filled in to produce a complete type. Basic questions, such as how much memory a NamedContainer<T> instance will require, cannot be answered without knowing what T is—the hidden field for the Item property would need 4 bytes if T were an int but 16 bytes if it were a decimal. The CLR cannot produce executable code for a type if it does not know how the contents will be arranged in memory. So to use this, or any other generic type, we must provide type arguments. Example 4-3 shows how. When type arguments are supplied, the result is sometimes called a constructed type. (This has nothing to do with constructors, the special kind of member we looked at in Chapter 3. In fact, Example 4-3 uses those too—it invokes the constructors of a couple of constructed types.)

Example 4-3. Using a generic class

var a = new NamedContainer<int>(42, "The answer");
var b = new NamedContainer<int>(99, "Number of red balloons");
var c = new NamedContainer<string>("Programming C#", "Book title");

You can use a constructed generic type anywhere you would use a normal type. For example, you can use them as the types for method parameters and return values, properties, or fields. You can even use one as a type argument for another generic type, as Example 4-4 shows.

Example 4-4. Constructed generic types as type arguments

// ...where a, and b come from Example 4-3.
List<NamedContainer<int>> namedInts = [a, b];
var namedNamedItem = new NamedContainer<NamedContainer<int>>(a, "Wrapped");

Each different type I supply as an argument to NamedContainer<T> constructs a distinct type. (And for generic types with multiple type arguments, each distinct combination of type arguments would construct a distinct type.) This means that NamedContainer<int> is a different type than NamedContainer<string>. That’s why there’s no conflict in using NamedContainer<int> as the type argument for another NamedContainer, as the final line of Example 4-4 does—there’s no infinite recursion here.

Because each different set of type arguments produces a distinct type, in most cases there is no implied compatibility between different forms of the same generic type. You cannot assign a NamedContainer<int> into a variable of type Nam⁠ed​Con⁠tai⁠ner⁠<str⁠ing> or vice versa. It makes sense that those two types are incompatible, because int and string are quite different types. But what if we used object as a type argument? As Chapter 2 described, you can put almost anything in an object variable. If you write a method with a parameter of type object, it’s OK to pass a string, so you might expect a method that takes a NamedContainer<object> to be happy with a NamedContainer<string>. That won’t work, but some generic types (specifically, interfaces and delegates) can declare that they want this kind of compatibility relationship. The mechanisms that support this (called covariance and contravariance) are closely related to the type system’s inheritance mechanisms. Chapter 6 is all about inheritance and type compatibility, so I will discuss this aspect of generic types there.

The number of type parameters forms part of an unbound generic type’s identity. This makes it possible to introduce multiple types with the same name as long as they have different numbers of type parameters. (The technical term for number of type parameters is arity.)

So you could define a generic class called, say, Operation<T>, and then another class, Operation<T1, T2>, and also Operation<T1, T2, T3>, and so on, all in the same namespace, without introducing any ambiguity. When you are using these types, it’s clear from the number of arguments which type was meant—Operation<int> clearly uses the first, while Operation<string, double> uses the second, for example. And for the same reason, a nongeneric Operation class would be distinct from generic types of the same name.

My NamedContainer<T> example doesn’t do anything to instances of its type argument, T—it never invokes any methods or uses any properties or other members of T. All it does is accept a T as a constructor argument, which it stores away for later retrieval. This is also true of many generic types in the runtime libraries—I’ve mentioned some collection classes (and we’ll see more of these in Chapter 5), which are all variations on the same theme of containing data for later retrieval.

There is a reason for this: a generic class can find itself working with any type, so it can presume little about its type arguments. However, it doesn’t have to be this way. You can specify constraints for your type arguments.

Constraints

C# allows you to state that a type argument must fulfill certain requirements. For example, suppose you want to be able to create new instances of the type on demand. Example 4-5 shows a simple class that provides deferred construction—it makes an instance available through a static property but does not attempt to construct that instance until the first time you read the property.

Example 4-5. Creating a new instance of a parameterized type

// For illustration only. Consider using Lazy<T> in a real program.
public static class Deferred<T>
    where T : new()
{
    private static T? _instance;

    public static T Instance => _instance ??= new T();
}

Warning

You wouldn’t write a class like this in practice, because the runtime libraries offer Lazy<T>, which does the same job but with more flexibility. Lazy<T> can work correctly in multithreaded code, whereas Example 4-5 will not. Example 4-5 is just to illustrate how constraints work. Don’t use it!

For this class to do its job, it needs to be able to construct an instance of whatever type is supplied as the argument for T. The get accessor uses the new keyword, and since it passes no arguments, it clearly requires T to provide a parameterless constructor. But not all types do, so what happens if we try to use a type without a suitable constructor as the argument for Deferred<T>?

The compiler will reject it, because it violates a constraint that this generic type has declared for T. Constraints appear just before the class’s opening brace, and they begin with the where keyword. The new() constraint in Example 4-5 states that T is required to supply a zero-argument constructor.

If that constraint had not been present, the class in Example 4-5 would not compile—you would get an error on the line that attempts to construct a new T. A generic type (or method) is allowed to use only features of its type parameters that it has specified through constraints, or that are defined by the base object type. (The object type defines a ToString method, for example, so you can invoke that on instances of any type without needing to specify a constraint.)

C# offers only a very limited suite of constraints. You cannot demand a constructor that takes arguments, for example. In fact, C# supports only seven kinds of constraints on a type argument: a type constraint, a reference type constraint, a value type constraint, default, notnull, unmanaged, and the new() constraint. The default constraint only applies in inheritance scenarios, so we’ll look at that in Chapter 6, and we just saw how new() works, so now let’s look at the remaining five.

Type Constraints

You can constrain the argument for a type parameter to be compatible with a particular type. For example, you could use this to demand that the argument type implements a certain interface. Example 4-6 shows the syntax.

Example 4-6. Using a type constraint

public class GenericComparer<T> : IComparer<T>
    where T : IComparable<T>
{
    public int Compare(T? x, T? y)
    {
        if (x == null) { return y == null ? 0 : -1; }
        return x.CompareTo(y);
    }
}

I’ll just explain the purpose of this example before describing how it takes advantage of a type constraint. This class provides a bridge between two styles of value comparison that you’ll find in .NET. Some data types provide their own comparison logic, but at times, it can be more useful for comparison to be a separate function implemented in its own class. These two styles are represented by the IComparable<T> and IComparer<T> interfaces, which are both part of the runtime libraries. (They are in the System and System.Collections.Generics namespaces, respectively.) I showed IComparer<T> in Chapter 3—an implementation of this interface can compare two objects or values of type T. The interface defines a single Compare method that takes two arguments and returns either a negative number, 0, or a positive number if the first argument is, respectively, less than, equal to, or greater than the second. IComparable<T> is very similar, but its CompareTo method takes just a single argument, because with this interface, you are asking an instance to compare itself to some other instance.

Some of the runtime libraries’ collection classes require you to provide an IC⁠om​pa⁠re⁠r<T> to support ordering operations such as sorting. They use the model in which a separate object performs the comparison, because this offers two advantages over the IComparable<T> model. First, it enables you to use data types that don’t implement IComparable<T>. Second, it allows you to plug in different sorting orders. (For example, suppose you want to sort some strings with a case-insensitive order. The string type implements IComparable<string>, but it provides a case-sensitive, locale-specific order.) So IComparer<T> is the more flexible model. However, what if you are using a data type that implements IComparable<T>, and you’re perfectly happy with the order that provides? What would you do if you’re working with an API that demands an IComparer<T>?

Actually, the answer is that you’d probably just use the .NET feature designed for this very scenario: Comparer<T>.Default. If T implements IComparable<T>, that property will return an IComparer<T> that does precisely what you want. So in practice you wouldn’t need to write the code in Example 4-6, because Microsoft has already written it for you. However, it’s instructive to see how you’d write your own version, because it illustrates how to use a type constraint.

The line starting with the where keyword states that this generic class requires the argument for its type parameter T to implement IComparable<T>. Without this addition, the Compare method would not compile—it invokes the CompareTo method on an argument of type T. That method is not present on all objects, and the C# compiler allows this only because we’ve constrained T to be an implementation of an interface that does offer such a method.

Interface constraints are somewhat odd: at first glance, it may look like we really shouldn’t need them. If a method needs a particular argument to implement a particular interface, you would normally just use that interface as the argument’s type. However, Example 4-6 can’t do this. You can demonstrate this by trying Example 4-7. It won’t compile.

Example 4-7. Will not compile: interface not implemented

public class GenericComparer<T> : IComparer<T>
{
    public int Compare(IComparable<T>? x, T? y)
    {
        if (x == null) { return y == null ? 0 : -1; }
        return x.CompareTo(y);
    }
}

The compiler will complain that I’ve not implemented the IComparer<T> interface’s Compare method. Example 4-7 has a Compare method, but its signature is wrong—that first argument should be a T. I could also try the correct signature without specifying the constraint, as Example 4-8 shows.

Example 4-8. Will not compile: missing constraint

public class GenericComparer<T> : IComparer<T>
{
    public int Compare(T? x, T? y)
    {
        if (x == null) { return y == null ? 0 : -1; }
        return x.CompareTo(y);
    }
}

That will also fail to compile, because the compiler can’t find that CompareTo method I’m trying to use. It’s the constraint for T in Example 4-6 that enables the compiler to know what that method really is.

Type constraints don’t have to be interfaces, by the way. You can use any type. For example, you can require a particular type argument to derive from a particular base class. More subtly, you can also define one parameter’s constraint in terms of another type parameter. Example 4-9 requires the first type argument to derive from the second, for example.

Example 4-9. Constraining one argument to derive from another

public class Foo<T1, T2>
    where T1 : T2
...

Type constraints are fairly specific—they require either a particular inheritance relationship, or the implementation of certain interfaces. However, you can define slightly less specific constraints.

Reference Type Constraints

You can constrain a type argument to be a reference type. As Example 4-10 shows, this looks similar to a type constraint. You just put the keyword class instead of a type name. If you are in an enabled nullable annotation context, the meaning of this annotation changes: it requires the type argument to be a non-nullable reference type. If you specify class?, that allows the type argument to be either a nullable or a non-nullable reference type.

Example 4-10. Constraint requiring a reference type

public class Bar<T>
    where T : class
...

This constraint prevents the use of value types such as int, double, or any struct as the type argument. Its presence enables your code to do three things that would not otherwise be possible. First, it means that you can write code that tests whether variables of the relevant type are null.² If you’ve not constrained the type to be a reference type, there’s always a possibility that it’s a value type, and those can’t have null values. The second capability is that you can use it as the target type of the as operator, which we’ll look at in Chapter 6. This is just a variation on the first feature—the as keyword requires a reference type because it can produce a null result.

Note

Nullable types such as int? (or Nullable<int>, as the CLR calls it) add nullability to value types, so you might be wondering whether you can use these as the argument for a type parameter with a class constraint. You can’t, because although types such as int? allow comparison with null, they work quite differently than reference types, so the compiler often generates quite different code for nullable types than it does for a reference type.

The third feature that a reference type constraint enables is the ability to use certain other generic types. It’s often convenient for generic code to use one of its type arguments as an argument for another generic type, and if that other type specifies a constraint, you’ll need to put the same constraint on your own type parameter. So if some other type specifies a class constraint, this might require you to constrain one of your own arguments in the same way.

Of course, this does raise the question of why the type you’re using needs the constraint in the first place. It might be that it simply wants to test for null or use the as operator, but there’s another reason for applying this constraint. Sometimes, you just need a type argument to be a reference type—there are situations in which a generic method might be able to compile without a class constraint, but it will not work correctly if used with a value type.

One common scenario in which this comes up is with libraries that can create fake objects to be used as part of a test by generating code at runtime. Using faked stand-in objects can often reduce the amount of code any single test has to exercise, which can make it easier to verify the behavior of the object being tested. For example, a test might need to verify that my code sends messages to a server at the right moment. I don’t want to have to run a real server during a unit test, so I could provide an object that implements the same interface as the class that would transmit the message but that won’t really send the message. Since this combination of an object under test plus a fake is a common pattern, I might choose to write a reusable base class embodying the pattern. Using generics means that the class can work for any combination of the type being tested and the type being faked. Example 4-11 shows a simplified version of this kind of helper class.

Example 4-11. Constrained by another constraint

using Microsoft.VisualStudio.TestTools.UnitTesting;
using Moq;

public class TestBase<TSubject, TFake>
    where TSubject : new()
    where TFake : class
{
    public TSubject? Subject { get; private set; }
    public Mock<TFake>? Fake { get; private set; }

    [TestInitialize]
    public void Initialize()
    {
        Subject = new TSubject();
        Fake = new Mock<TFake>();
    }
}

There are various ways to build fake objects for test purposes. You could just write new classes that implement the same interface as your real objects, but there are also third-party libraries that can generate them. One such library is called Moq (an open source project), and that’s where the Mock<T> class in Example 4-11 comes from. It’s capable of generating a fake implementation of any interface or of any nonsealed class. (Chapter 6 describes the sealed keyword.) It will provide empty implementations of all members by default, and you can configure more interesting behaviors if necessary. You can also verify whether the code under test used the fake object in the way you expected.

How is that relevant to constraints? The Mock<T> class specifies a reference type constraint on its own type argument, T. This is due to the way in which it creates dynamic implementations of types at runtime; it’s a technique that can work only for reference types. Moq generates a type at runtime, and if T is an interface, that generated type will implement it, whereas if T is a class, the generated type will derive from it.³ There’s nothing useful it can do if T is a struct, because you cannot derive from a value type. That means that when I use Mock<T> in Example 4-11, I need to make sure that the type argument I pass is not a struct (i.e., it must be a reference type). But the type argument I’m using is one of my class’s type parameters: TFake. So I don’t know what type that will be—that’ll be up to whoever is using my TestBase class.

For my class to compile without error, I have to ensure that I have met the constraints of any generic types that I use. I have to guarantee that Mock<TFake> is valid, and the only way to do that is to add a constraint on my own type that requires TFake to be a reference type. And that’s what I’ve done on the third line of the class definition in Example 4-11. Without that, the compiler would report errors on the two lines that refer to Mock<TFake>.

To put it more generally, if you want to use one of your own type parameters as the type argument for a generic that specifies a constraint, you’ll need to specify the same constraint on your own type parameter.

Value Type Constraints

Just as you can constrain a type argument to be a reference type, you can instead constrain it to be a value type. As shown in Example 4-12, the syntax is similar to that for a reference type constraint but with the struct keyword.

Example 4-12. Constraint requiring a value type

public class Quux<T>
    where T : struct
...

Before now, we’ve seen the struct keyword only in the context of custom value types, but despite how it looks, this constraint permits bool, enum types, and any of the built-in numeric types such as int, as well as custom structs.

.NET’s Nullable<T> type imposes this constraint. Recall from Chapter 3 that Nullable<T> provides a wrapper for value types that allows a variable to hold either a value or no value. (We normally use the special syntax C# provides, so we’d write, say, int? instead of Nullable<int>.) The only reason this type exists is to provide nullability for types that would not otherwise be able to hold a null value. So it only makes sense to use this with a value type—reference type variables can already be set to null without needing this wrapper. The value type constraint prevents you from using Nu⁠ll​ab⁠le⁠<T> with types for which it is unnecessary.

Value Types All the Way Down with Unmanaged Constraints

You can specify unmanaged as a constraint, which requires that the type argument be a value type but also that it contains no references. All of the type’s fields must be value types, and if any of those fields is not a built-in primitive type, then its type must in turn contain only fields that are value types, and so on all the way down. In practice this means that all the actual data needs to be either one of a fixed set of built-in types (essentially, all the numeric types, bool, or a pointer) or an enum type. This is mainly of interest in interop scenarios, because types that match the unmanaged constraint can be passed safely and efficiently to unmanaged code. It can also be important if you are writing high-performance code that takes control of exactly where memory is allocated and when it is copied, using the techniques described in Chapter 18.

Not Null Constraints

If you use the nullable references feature described in Chapter 3 (which is enabled by default when you create new projects), you can specify a notnull constraint. This allows either value types or non-nullable reference types but not nullable reference types.

Other Special Type Constraints

Chapter 3 described various special kinds of types, including enumeration types (enum) and delegate types (covered in detail in Chapter 9). It is sometimes useful to constrain type arguments to be one of these kinds of types. There’s no special trick to this, though: you can just use type constraints. All delegate types derive from System.Delegate, and all enumeration types derive from System.Enum. As Example 4-13 shows, you can just write a type constraint requiring a type argument to derive from either of these.

Example 4-13. Constraints requiring delegate and enum types

public class RequireDelegate<T>
    where T : Delegate
{
}

public class RequireEnum<T>
    where T : Enum
{
}

Multiple Constraints

If you’d like to impose multiple constraints for a single type argument, you can just put them in a list, as Example 4-14 shows. There are some restrictions. You cannot combine the class, struct, notnull, or unmanaged constraints—these are mutually exclusive. If you do use one of these keywords, it must come first in the list. If the new() constraint is present, it must be last.

Example 4-14. Multiple constraints

public class Spong<T>
    where T : IEnumerable<T>, IDisposable, new()
...

When your type has multiple type parameters, you write one where clause for each type parameter you wish to constrain. In fact, we saw this earlier—Example 4-11 defines constraints for both of its parameters.

Zero-Like Values

There are certain features that all types support and that therefore do not require a constraint. This includes the set of methods defined by the object base class, covered in Chapters 3 and 6. But there’s a more basic feature that can sometimes be useful in generic code.

Variables of any type can be initialized to a default value. As you have seen in the preceding chapters, there are some situations in which the CLR does this for us. For example, all the fields in a newly constructed object will have a known value even if we don’t write field initializers and don’t supply values in the constructor. Likewise, a new array of any type will have all of its elements initialized to a known value. The CLR does this by filling the relevant memory with zeros. The exact meaning of this depends on the data type. For any of the built-in numeric types, the value will quite literally be the number 0, but for nonnumeric types, it’s something else. For bool, the default is false, and for a reference type, it is null.

Sometimes, it can be useful for generic code to be able to obtain this initial default zero-like value for one of its type parameters. But you cannot use a literal expression to do this in most situations. You cannot assign null into a variable whose type is specified by a type parameter unless that parameter has been constrained to be a reference type. And you cannot assign the literal 0 into any such variable (although .NET 7.0’s generic math feature makes it possible to constrain a type argument to be a numeric type, in which case you can write T.Zero).

Instead, you can request the zero-like value for any type using the default keyword. (This is the same keyword we saw inside a switch statement in Chapter 2 but used in a completely different way. C# keeps up the C-family tradition of defining multiple, unrelated meanings for each keyword.) If you write default(SomeType), where SomeType is either a specific type or a type parameter, you will get the default initial value for that type: 0 if it is a numeric type, and the equivalent for any other type. For example, the expression default(int) has the value 0, default(bool) is false, and default(string) is null. You can use this with a generic type parameter to get the default value for the corresponding type argument, as Example 4-15 shows.

Example 4-15. Getting the default (zero-like) value of a type argument

static void ShowDefault<T>()
{
    Console.WriteLine(default(T));
}

Inside a generic type or method that defines a type parameter T, the expression default(T) will produce the default, zero-like value for T—whatever T may be—without requiring constraints. So you could use the generic method in Example 4-15 to verify that the defaults for int, bool, and string are the values I stated.

Note

When the nullable references feature (described in Chapter 3) is enabled, the compiler will consider a default(T) to be a potentially null value, unless you’ve ruled out the use of reference types by applying the struct constraint.

In cases where the compiler is able to infer what type is required, you can use a simpler form. Instead of writing default(T), you can just write default. That wouldn’t work in Example 4-15. Console.WriteLine can accept pretty much anything, so the compiler can’t narrow it down to one option, but it will work in Example 4-16. There, the compiler can see that the generic method’s return type is T?, so this must need a default(T). Since it can infer that, it’s enough for us to write just default.

Example 4-16. Getting the default (zero-like) value of an inferred type

static T? GetDefault<T>() => default;

And since I’ve just shown you an example of one, this seems like a good time to talk about generic methods.

Generic Methods

As well as generic types, C# also supports generic methods. In this case, the generic type parameter list follows the method name and precedes the method’s normal parameter list. Example 4-17 shows a method with a single type parameter, T. It uses that parameter as its return type and also as the element type for an array to be passed in as the method’s argument. This method returns the final element in the array, and because it’s generic, it will work for any array element type.

Example 4-17. A generic method

public static T GetLast<T>(T[] items) => items[^1];

Note

You can define generic methods inside either generic types or nongeneric types. If a generic method is a member of a generic type, all of the type parameters from the containing type are in scope inside the method, as well as the type parameters specific to the method.

Just as with a generic type, you can use a generic method by specifying its name along with its type arguments, as Example 4-18 shows.

Example 4-18. Invoking a generic method

int[] values = [1, 2, 3];
int last = GetLast<int>(values);

Generic methods work in a similar way to generic types but with type parameters that are only in scope within the method declaration and body. You can specify constraints in much the same way as with generic types. The constraints appear after the method’s parameter list and before its body, as Example 4-19 shows.

Example 4-19. A generic method with a constraint

public static T MakeFake<T>()
    where T : class
{
    return new Mock<T>().Object;
}

There’s one significant way in which generic methods differ from generic types, though: you don’t always need to specify a generic method’s type arguments explicitly.

Type Inference

The C# compiler is often able to infer the type arguments for a generic method. I can modify Example 4-18 by removing the type argument list from the method invocation, as Example 4-20 shows. This doesn’t change the meaning of the code in any way.

Example 4-20. Generic method type argument inference

int[] values = [1, 2, 3];
int last = GetLast(values);

When presented with this sort of ordinary-looking method call, if there’s no nongeneric method of that name available, the compiler starts looking for suitable generic methods. If the method in Example 4-17 is in scope, it will be a candidate, and the compiler will attempt to deduce the type arguments. This is a pretty simple case. The method expects an array of some type T, and we’ve passed an array with elements of type int, so it’s not a massive stretch to work out that this code should be treated as a call to GetLast<int>.

It gets more complex with more intricate cases. The C# specification dedicates many pages to the type inference algorithm, but it’s all to support one goal: letting you leave out type arguments when they would be redundant. By the way, type inference is always performed at compile time, so it’s based on the static type of the method arguments.

With APIs that make extensive use of generics (such as LINQ, which is the topic of Chapter 10), explicitly listing every type argument can make the code very hard to follow, so it is common to rely on type inference. And if you use anonymous types, then type argument inference becomes essential because it is not possible to supply the type arguments explicitly.

Generic Math

One of the most significant new capabilities in C# 11.0 and .NET 7.0 is called generic math. This makes it possible to write generic methods that perform mathematical operations on variables declared with type parameters. To show why this required new language and runtime features, Example 4-21 shows a naive attempt to perform arithmetic in a generic method.

Example 4-21. A technique that doesn’t work in C# generics

public static T Add<T>(T x, T y)
{
    return x + y;  // Will not compile
}

The compiler will complain about the use of addition here because nothing stops someone from using this method with a type parameter that does not support addition. What should happen if we called this method passing arguments of type bool? We’d probably like the answer to be that such attempts would be blocked: we should only be allowed to call this Add<T> method if we use a type argument that supports addition.

This is exactly the kind of scenario that constraints are meant for. All we need to do is constrain the type parameter T to types that do implement addition. But up until C# 11.0, it was not possible to specify such a constraint. We can require a type argument to provide certain members by using an interface type constraint, but interfaces used to be unable to require implementations to define particular operators. When types implement operators such as +, these are static members. (They have a distinctive syntax but they are really just static methods.) And it wasn’t possible for an interface to define static virtual or abstract members. These keywords indicate, respectively, that a type either can or must define its own version of a particular member, and used to be applicable only in inheritance scenarios (described in Chapter 6) with nonstatic methods.

As you saw in Chapter 3, .NET 7.0 has extended the type system so that it is now possible for interfaces to require implementers to provide specific static members. C# 11.0 supports this with its new static abstract and static virtual syntax. This means that it is now possible to define interfaces that require implementers to offer, say, the + operator. The .NET runtime libraries now define such interfaces, meaning that we can define a constraint for a type parameter that requires it to support arithmetic. Example 4-22 does this, enabling it to use the + operator.

Example 4-22. Using generic math

public static T Add<T>(T x, T y)
    where T : INumber<T>
{
    return x + y; // No error, because INumber<T> requires + to be available
}

The INumber<T> interface is defined in the System.Numerics namespace and is implemented by all of the built-in numeric types. You can think of INumber<T> as saying that any type implementing this interface provides all common mathematical operations for type T. So int implements INumber<int>, float implements INumber<float>, and so on. The interface needs to be generic—it couldn’t just be INumber because it needs to specify the input and output types for operators. Example 4-23 shows the problem that would occur if we tried to define this kind of constraint interface without a generic type argument.

Example 4-23. Why operator constraint interfaces need to be generic

public interface IAdd
{
    static abstract int operator +(int x, int y); // Won't compile
}

This hypothetical IAdd interface attempts to state that any implementing type must support the addition operator by defining it as abstract. But operator declarations need to state their input and output types. This example chooses int, so this would be of no use for any other type. In fact, it won’t even compile—C# imposes a rule that when a type defines an operator member, at least one of the arguments must either have the same type as the declaring type, or it must derive from or implement that defining type. So MyType can define addition for a pair of MyType inputs, and it can also define addition for a MyType and an int, but it doesn’t get to define addition for a pair of int values. (That would create ambiguity—if MyType could define that, C# wouldn’t know whether to use that or the normal built-in behavior when adding two int values together.) The same rules apply to interfaces—at least one of the arguments in Example 4-23 would need to be IAdd. But as you’ll see in Chapter 7, declaring these arguments with an interface type would result in boxing when the underlying types are value types, which would result in heap allocations each time you performed basic arithmetic.

This is why INumber<T> takes a type argument. It plugs this in as the input and output types of the + operator. In fact, it doesn’t do that directly—each of the different operators is separated out into a distinct interface, and INumber<T> inherits them all. For example, INumber<T> inherits from IAdditionOperators<T,T,T>, and as Example 4-24 shows, that’s the interface that actually defines the operator members. The operator arguments here don’t use interface types, they use the actual type parameter (avoiding any boxing overhead), but the compiler is satisfied because a constraint on this type parameter requires it to implement the interface.

Example 4-24. The IAdditionOperators<TSelf, TOther, TResult> interface

public interface IAdditionOperators<TSelf, TOther, TResult>
    where TSelf : IAdditionOperators<TSelf, TOther, TResult>?
{
    static abstract TResult operator +(TSelf left, TOther right);
    static virtual TResult operator checked +(TSelf left, TOther right)
        => left + right;
}

This is more complex than the hypothetical IAdd shown in Example 4-23. It is generic for the reasons just described, but it has three type arguments, not just one. This is to make it possible to define constraints requiring addition with mixed inputs. There are some mathematical objects that are more complex than individual values (e.g., vectors, matrices) and which support common arithmetic operations (e.g., you can add two matrices together), and in some cases you might be able to apply operations with different input types. For example, you can multiply a matrix by an ordinary number (a scalar) and the result is a new matrix. The operator interfaces are able to represent this because they take separate type arguments for the inputs and outputs, so a mathematical library that wanted to represent this capability could represent it as IMultiplyOperators<double, Matrix, Matrix>.

You’ll notice that INumber<T> takes only one type argument. While the individual operator interfaces are able to represent hybrid operations, INumber<T> chooses not to exploit this—it passes its single type parameter in as all three type arguments to operator interfaces. So any type implementing INumber<T> implements IAd⁠dit⁠io⁠n​Ope⁠rat⁠or⁠s<T, T, T>, IMultiplyOperators<T, T, T>, and so on.

The other feature making Example 4-24 more complex is that it enables types to provide different implementations of addition for checked and unchecked contexts. As Chapter 2 described, C# does not emit code detecting arithmetic overflow by default, but inside blocks or expressions marked with the checked keyword, arithmetic operations producing results too large to fit in the target type will cause exceptions. Types providing custom implementations of arithmetic operators can supply a different method to be used in a checked context so that they can offer the same feature. This is optional, which is why IAdditionOperators<TSelf, TOther, TResult> defines the checked + operator as virtual (not abstract): it provides a default implementation that just calls the unchecked version. This is a suitable default for types that do not overflow, such as BigInteger. Types that can overflow tend to need specialized code to detect this, in which case they will override the checked operator.

Generic Math Interfaces

As you’ve just seen, System.Numerics defines multiple interfaces representing various mathematical capabilities. Very often we’ll just specify a constraint of INumber<T>, but sometimes we will need to be a bit more specific. Our code might need to be able to represent negative numbers, in which case INumber<T> is too broad: it is implemented by signed (e.g., int) and unsigned types (e.g., uint) types alike. If we specify ISignedNumber<T> as a constraint, that will prevent the use of unsigned types. Generic math defines four groups of interfaces representing different kinds of characteristics we might require:

• Numeric category (e.g., INumber<T>, ISignedNumber<T>, IFloatingPoint<T>)

• Operator (e.g., IAdditionOperators<TSelf, TOther, TResult>, IMu⁠lti⁠pl⁠y​Ope⁠rat⁠or⁠s<TSelf, TOther, TResult>)

• Function (e.g., IExponentialFunctions<TSelf, TOther, TResult> or ITrigonometricFunctions<TSelf, TOther, TResult>)

• Parsing and formatting

The following sections describe each of these groups.

Numeric Category Interfaces

The various numeric category interfaces represent certain kinds of characteristics that we might want from numeric types, not all of which are universal to all kinds of numbers. Some methods, such as the generic Add<T> method shown in Example 4-22, will be able to work with more or less any numeric type, so a constraint of INumber<T> is a reasonable choice. But some code might be able to work only with whole numbers, while other code might absolutely require floating point. Figure 4-1 shows the category interfaces that let us express various capabilities that our generic code might require. Each of .NET’s numeric types implements some but not all of these interfaces.

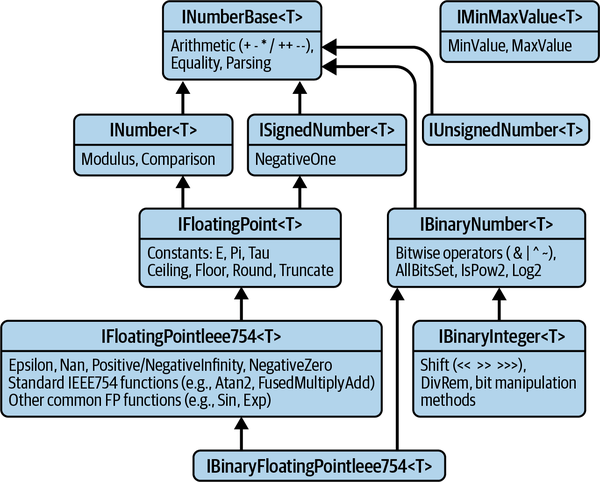
Figure 4-1. Numeric category interfaces

This figure shows inheritance relationships that define fixed relationships between some of the category interfaces. Chapter 6 describes inheritance in detail, but with interfaces it’s fairly straightforward: any type that implements an interface is required also to implement any inherited interfaces. For example, if a number implements IFloatingPoint<T>, it must also implement INumber<T>. There are other relationships that, while not strictly required, exist in practice in .NET’s numeric types. For example, although there is no absolute requirement that types implementing ISignedNumber<T> must also implement INumber<T>, all the types built into the .NET runtime libraries that implement the former implement the latter. (For example, int, double, and decimal all implement both.)

The .NET documentation generally encourages you to use INumber<T> as the constraint in code where you need common arithmetic operations but don’t have any particular requirements about the kind of number in use. However, you can see from Figure 4-1 that there is an even more general interface: INumberBase<T>. All of the interfaces in that diagram except for IMinMaxValue<T> inherit directly or indirectly from INumberBase<T> (and in practice, types that implement IMinMaxValue<T> usually implement INumberBase<T>), so if you want to write code that can work with the absolute widest range of types possible, INumberBase<T> is a better choice than INumber<T>. Example 4-22 could be modified to specify INumberBase<T> as a constraint, for example, and it would still work, because the basic arithmetic operators are available.

So what’s the difference? If you’re using the numeric types built into .NET, the only impact of specifying INumber<T> as a constraint instead of INumberBase<T> is that you won’t be able to use the Complex type. Complex numbers are two-dimensional, which means that for any two complex numbers, we can’t necessarily say which is larger—for any particular complex number there will be infinitely many other complex numbers with different values but the same magnitude. INumberBase<T> requires types to support comparison for equality (is x equal to y?) but does not require types to support comparison for ordering (is x greater than y?). INumber<T> requires types to support both. So Complex implements INumberBase<T> but cannot implement INumber<T>. Also, Complex does not provide a way to get the remainder of a division operation, and this is similarly absent from the INumberBase<T> interface (but it is present in INumber<T>). These are the only two differences between these two interfaces. So unless you need your numbers to be sortable, or you need to calculate remainders (with the % operator), using INumberBase<T> as a constraint is the simplest way to work with the widest possible range of numeric types.

INumberBase<T> doesn’t just define the basic arithmetic operators. It also defines properties called One and Zero. Example 4-25 uses Zero to provide an initial value for calculating the sum total of an array of values. Why not just write the literal 0? IL (the compiler’s output) uses different representations for literals of different types, and since T here is a generic type argument, it’s not possible for the compiler to generate code that creates a literal of type T.

Example 4-25. Using INumberBase<T>.Zero

static T Sum<T>(T[] values)
    where T : INumberBase<T>
{
    T total = T.Zero;
    foreach (T value in values)
    {
        total += value;
    }
    return total;
}

The Zero and One properties are available on any INumber<T>, but the interface also makes it possible to attempt conversions from other values. It defines a static CreateChecked<TOther>(TOther value) method, so instead of T.Zero, we could have written T.CreateChecked(0). This is a generic method, and it constrains the TOther type argument to implement INumberBase<TOther> so you can pass any numeric type, but the compiler won’t let you call T.CreateChecked("banana"), for example. However, not all conversions are guaranteed to succeed—if code passes a value to CreateChecked of some type with a larger range than the target type, the value could exceed the target type’s range, in which case the method will throw an OverflowException. For example, T.CreateChecked(uint.MaxValue) would fail if the generic method is invoked with a type argument of int. (This is why I’ve used T.Zero: that won’t throw exceptions under any circumstances.) INumber<T> also defines CheckedSaturating, which handles out-of-range values by returning the largest or smallest available value (depending on the direction in which you exceeded the range). For example, if the target is int, and you pass a value that is too high, CreateSaturating will return int.MaxValue. If you pass too large a negative number it will return int.MinValue. There is also CreateTruncating, which just discards higher-order bits. For example, if the input is a long and the target is int, CreateTruncating will use the bottom 32 bits of the value and will simply ignore the top 32 bits. (This is the same as the behavior when casting a long to an int in an unchecked context.)

INumberBase<T> also provides various utility methods you can use to ask about certain characteristics. For example, it requires all implementing types to define IsPositive, IsNegative, and IsInteger static methods.

The IBinaryNumber<T> interface is implemented by all types that have a defined binary representation. In practice, this means all of .NET’s native numeric types (integers and floating point) except for decimal, and it also includes BigInteger. It makes bitwise operators (such as & and |) available, and it defines IsPow2 and Log2 methods. IsPow2 enables you to discover whether the value has just a single nonzero binary digit (meaning it will be some power of two). Log2 essentially tells you how many binary digits are required to represent the value. IBinaryInteger<T> is more specialized, being implemented only by integer types (built-in and also BigInteger). It adds bit-shift and rotation operators, conversion to and from byte sequences in either big or little endian form, and some bit-counting functions.

There are various interfaces representing floating-point. One reason we can’t have a one-size-fits-all definition is that decimal is technically a kind of floating-point number, but it is very different from float, double, and System.Half, each of which implements the IEEE754 international standard for floating-point arithmetic. That means those types have a well-defined binary structure, and support a particular set of standard operations besides basic arithmetic. decimal does not have those features, but if all you need is the ability to represent non-whole numbers, it may be sufficient, and if you specify a constraint of IFloatingPoint<T>, that will allow any of the floating-point types, including decimal. You would specify IFloatingPoin⁠t​Ieee754<T> if you need the special values IEEE754 defines (such as NaN, the not a number value that can arise from some calculations, or its representations for positive and negative infinity) or if you need access to some of the standard IEEE754 operations such as trigonometric functions or exponentiation. Or you might specify this in order to exclude decimal because it has some very different characteristics around precision and error. It would be fairly rare to need the more specialized IBinary​Floa⁠tingPointIeee754<T>. This is implemented by all of the native .NET types that implement IFloatingPointIeee754<T>, and it makes it possible to use bitwise operations, but it’s relatively unusual to perform bit twiddling on floating-point values. In most cases, IFloatingPointIeee754<T> will be the most specific floating-point constraint you will need.

Figure 4-1 has one interface apparently sitting all on its own: IMinMaxValue<T>. In fact, almost all of the numeric types implement this—it makes MinValue and MaxValue properties available, reporting the highest and lowest values the type can represent. It only looks so isolated because none of the other numeric category interfaces requires IMinMaxValue<T>; it’s almost ubiquitous in practice. One exception is the Complex type, which does not implement this because, as already discussed, it doesn’t fully order its numbers, so there isn’t one single, highest value. BigInteger also does not implement this, because its defining feature is that it has no fixed upper limit.

There are two more interfaces that the .NET documentation puts in the numeric category group: IAdditiveIdentity<TSelf, TResult> and IMultiplicativeIdentity<TSelf, TResult>. I did not include these in Figure 4-1 because they are slightly different from the other category interfaces. These are closely associated with two of the operator interfaces described in the next section. Every type in the .NET runtime libraries that implements IAdditionOperators<TSelf, TOther, TResult> also implements IAdditiveIdentity<TSelf, TResult>, and likewise for IMultiplyOperators<TSelf, TOther, TResult> and IMultiplicativeIdentity<TSelf, TResult>. These each define a single property, AdditiveIdentity and MultiplicativeIdentity, respectively. If you use these values as one of the operands of their corresponding operation, the result will be the other operand. (In other words, x + T.AdditiveIdentity and x * T.MultiplicativeIdentity are both equal to x.) In practice, that means AdditiveIdentity is zero and MultiplicativeIdentity is one for all of the numeric types .NET supplies. So why not just use T.Zero and T.One? It’s because there are some less conventional mathematical objects that behave like numbers in certain ways, but which don’t correspond directly to normal numbers like one or zero. For example, some mathematicians like to do math with shapes, using rotation and reflection, and in some cases there may be behavior that is addition-like, but where the additive identity isn’t a simple number. Although none of the built-in numeric types enter this sort of territory, generic math was designed to make it possible to write libraries that do this kind of math.

Example 4-26 uses IAdditiveIdentity<TSelf, TResult> to implement an alternative to the Sum<T> method shown in Example 4-25. In theory this makes this method less constrained: it is able to work with any addable type, and does not require INumberBase<T>. All of the .NET runtime library types that are addable also implement INumberBase<T>, so this is of doubtful benefit, but if you are using a library representing more exotic mathematical objects, it might contain types that do not implement INumberBase<T> but which would work with this more precisely constrained method.

Example 4-26. Using AdditiveIdentity

public static T Sum<T>(T[] values)
    where T : IAdditionOperators<T, T, T>, IAdditiveIdentity<T, T>
{
    T total = T.AdditiveIdentity;
    foreach (T value in values)
    {
        total += value;
    }
    return total;
}

The somewhat complex and intricate taxonomy of numeric types represented by the numeric category interfaces makes it possible to define very specific constraints, which can enable generic code to work with the widest possible range of numeric types. However, as Example 4-26 shows, this comes at the cost of some complexity. The version of this code in Example 4-25 that used a constraint of INumberBase<T> is simpler, and doesn’t require developers reading the code to have committed Figure 4-1 to memory, or to be sufficiently familiar with mathematical terminology to understand exactly what an additive identity is. And since all of .NET’s numeric types implement INumberBase<T>, using that as a constraint will normally strike a better balance between ultimate flexibility and readability.

Operator Interfaces

You’ve already seen IAdditionOperators<TSelf, TOther, TResult>, which we can use as a constraint requiring the + operator to be available for a generic type parameter. This is one of a family of interfaces defining the availability of operators. Table 4-1 lists all the interfaces of this kind and shows which operators each interface defines.

Table 4-1. Operator interfaces

Interface	Operations	Available through
IAdditionOperators<TSelf,TOther,TResult>	x + y	INumberBase<T>
IBitwiseOperators<TSelf,TOther,TResult>	x & y, x | y, x ^ y, and ~x	IBinaryNumber<T>
IComparisonOperators<TSelf,TOther,​TRe⁠su⁠lt>	x < y, x > y, x <= y, and x >= y	INumber<T>
IDecrementOperators<TSelf>	--x and x--	INumberBase<T>
IDivisionOperators<TSelf,TOther,TResult>	x / y	INumberBase<T>
IEqualityOperators<TSelf,TOther,TResult>	x == y and x != y	INumberBase<T>
IIncrementOperators<TSelf>	++x and x++	INumberBase<T>
IModulusOperators<TSelf,TOther,TResult>	x % y	INumber<T>
IMultiplyOperators<TSelf,TOther,TResult>	x * y	INumberBase<T>
IShiftOperators<TSelf,TOther,TResult>	x << y, x >> y and x >>> y	IBinaryInteger<T>
ISubtractionOperators<TSelf,TOther,TResult>	x - y	INumberBase<T>
IUnaryNegationOperators<TSelf,TResult>	-x	INumberBase<T>
IUnaryPlusOperators<TSelf,TResult>	+x	INumberBase<T>

In practice we rarely express constraints directly in terms of these operator interfaces, because the various numeric category interfaces inherit from them and are less verbose. The final column of the table shows the most general category interface that inherits from that row’s operator interface. When a type implements an operator interface, it will usually also implement that corresponding numeric category interface. As the preceding section just discussed, although you could specify a constraint of IAdditionOperators<T, T, T>, all of the types in the runtime libraries that implement that also implement INumberBase<T>. Unless you’re using an unusual library that implements some operator interfaces but not the corresponding category interface, there’s no benefit in practice to being more specific, so when you need a particular operator, you’ll normally use the corresponding interface in the third column of Table 4-1 as the constraint.

Function Interfaces

Many common mathematical operations are expressed not as operators, but as functions. For most of .NET’s history, we have used the methods defined by the System.Math class, but that type predates generics. Generic math makes features such as trigonometric functions and exponentiation available through static abstract methods defined by the interfaces listed in Table 4-2.

Table 4-2. Function interfaces

Interface	Operations
IExponentialFunctions<TSelf>	Exponential functions such as T.Exp (ex) and T.Exp2 (2x)
IHyperbolicFunctions<TSelf>	Hyperbolic functions such as T.Sinh, T.Cosh, T.Asinh, and T.Acosh
ILogarithmicFunctions<TSelf>	Logarithmic functions such as T.Log and T.Log2
IPowerFunctions<TSelf>	Power function: T.Pow (xy)
IRootFunctions<TSelf>	Root functions such as T.Sqrt and T.Cbrt (square and cube roots)
ITrigonometricFunctions<TSelf>	Trigonometric functions such as T.Sin, T.Cos, T.Asin, and T.Acos

As with the operator interfaces, we don’t normally need to refer to these interfaces directly in constraints, because they are accessible through a numeric category. All of the .NET runtime library types that implement any of these interfaces also implement IFloatingPointIeee754<T>.

Parsing and Formatting

The final set of interfaces associated with generic math enables us to work with text representations of numbers. Strictly speaking, these four interfaces are not limited to working with just numeric types—DateTimeOffset implements all of them, for example. However, INumberBase<T> inherits from all of these, so they are available on types that support generic math.

IParsable<T> defines Parse and TryParse methods that enable you to convert a string to the target numeric type. There is also ISpanParsable<T>, which offers similar methods that can work with ReadOnlySpan<char>. Span types, which Chapter 18 describes in detail, make it possible to work with ranges of characters that are not necessarily full string objects in their own right. ISpanParsable<T> can parse text in subsections of an existing string, a char[], memory allocated on the stack, or even in a block of memory allocated by mechanisms outside of the .NET runtime’s control (e.g., through a system call, or by some external non-.NET library). There is also an IUtf8SpanParsable<T>, which can work directly with data encoded in UTF-8 format.

IFormattable<T>, ISpanFormattable<T>, and IUtf8SpanFormattable<T> go in the other direction: they are able to produce text representations of values. (These aren’t new—they have been around since .NET 6.0—but they are now associated with generic math because INumberBase<T> inherits from them.) IFormattable<T> defines an overload of ToString accepting the same kind of composite formatting as string.Format, along with an optional IFormatProvider argument controlling details that vary by language and culture (such as conventions for digit separators). ISpanFormattable<T> defines TryFormat, which provides the same service, but instead of returning a newly allocated string, it writes its output directly into a Span<char>, which may enable more complex strings to be built up with fewer allocations, reducing pressure on the garbage collector.

Generics and Tuples

C#’s lightweight tuples have a distinctive syntax, but as far as the runtime is concerned, there is nothing special about them. They are all just instances of a set of generic types. Look at Example 4-27. This uses (int, int) as the type of a local variable to indicate that it is a tuple containing two int values.

Example 4-27. Declaring a tuple variable in the normal way

(int, int) p = (42, 99);

Now look at Example 4-28. This uses the ValueTuple<int, int> type in the System namespace. But this is exactly equivalent to the declaration in Example 4-27. In Visual Studio or VS Code, if you hover the mouse over the p2 variable, it will report its type as (int, int).

Example 4-28. Declaring a tuple variable with its underlying type

ValueTuple<int, int> p2 = (42, 99);

One thing that C#’s special syntax for tuples adds is the ability to name the tuple elements. The ValueTuple family names its elements Item1, Item2, Item3, etc., but in C# we can pick other names. When you declare a local variable with named tuple elements, those names are a fiction maintained by C#—they have no runtime representation at all. However, when a method returns a tuple, as in Example 4-29, it’s different: the names need to be visible so that code consuming this method can use the same names. Even if this method is in some library component that my code has referenced, I want to be able to write Pos().X, instead of having to use Pos().Item1.

Example 4-29. Returning a tuple

public static (int X, int Y) Pos() => (10, 20);

To make this work, the compiler applies an attribute named TupleElementNames to the method’s return value, and this contains an array listing the property names to use. (Chapter 14 describes attributes.) You can’t actually write code that does this yourself: if you write a method that returns a ValueTuple<int, int> and you try to apply the TupleElementNamesAttribute as a return attribute, the compiler will produce an error telling you not to use this attribute directly and to use the tuple syntax instead. But that attribute is how the compiler reports the tuple element names.

Be aware that there’s another family of tuple types in the runtime libraries, Tuple<T>, Tuple<T1, T2>, and so on. These look almost identical to the ValueTuple family. The difference is that the Tuple family of generic types are all classes, whereas all the ValueTuple types are structs. The C# lightweight tuple syntax only uses the ValueTuple family. The Tuple family has been around in the runtime libraries for much longer, though, so you often see them used in older code that needed to bundle a set of values together without defining a new type just for that job.

Summary

Generics enable us to write types and methods with type parameters, which can be filled in at compile time to produce different versions of the types or methods that work with particular types. One of the most important use cases for generics back when they were first introduced was to make it possible to write type-safe collection classes such as List<T>. We will look at some of these collection types in the next chapter.

¹ When saying the names of generic types, the convention is to use the word of as in “List of T” or “List of int.”

² This is permitted even if you used the plain class constraint in an enabled nullable annotation context. This constraint does not provide watertight guarantees of non-nullness, so C# permits comparison with null.

³ Moq relies on the dynamic proxy feature from the Castle Project to generate this type. If you would like to use something similar in your code, you can find this at the Castle Project.