Chapter 4. Deep Q-Networks
Tabular reinforcement learning (RL) algorithms, such as Q-learning or SARSA, represent the expected value estimates of a state, or state-action pair, in a lookup table (also known as a Q-table or Q-values). You have seen that this approach works well for small, discrete states. But when the number of states increases the size of the table increases exponentially. The state space becomes infinitely large with continuous variables.
Actions have a similar problem. In an action-value version of Q-learning or SARSA the number of actions increases the table size. And again, if the actions are continuous then the table becomes infinite. But continuous actions are desirable in many applications. In the advertisement bidding example in “Industrial Example: Real-Time Bidding in Advertising”, it is better if the agent could suggest a bid value directly, rather than rely on a predefined set of discrete alterations.
The most common solution to these problems is to replace the table with an approximation function. Rather than attempting to store a map of how states and actions alter the expected return, you can build a function that approximates it. At each time step the agent looks at the current state-action pair and predicts the expected value. This is a regression problem.
You can choose from the wide variety of regression algorithms to solve this. But state-action pairs tend to be highly nonlinear and often discontinuous. For example, imagine the state space of the cliff environment. The expected values should converge so that states near the goal are high and states further away decrease in proportion to the discounting and reward scheme. But there will be a large discontinuity next to the cliff. If the agent uses a linear model to approximate the state-value function, then the large negative reward of the cliff acts like an outlier when compared to the rest of the state space and biases the model.
However, simple models are often preferred in industry because they are well understood, robust, and easy to interpret. If you wish to use a simple model, you must take steps to ensure your state space is representative. To achieve this you could randomly sample your environment and store the states. You can then perform regression offline to evaluate how well your model fits the data.
The most commonly used model is a deep artificial neural network. The network uses the state of the environment as an input and the output is the expected value of each action. The approximation is capable of handling huge and complex state spaces. I delay discussing continuous actions until later in the book.
Deep Learning Architectures
To create an artificial neural network (ANN, or NN for short) you can create a stack of linear approximators and mutate each with a nonlinear activation function. Then you train the network to find the optimal weights via regression. The result is a model that is capable of approximating any arbitrary function.
This is the promise of deep learning (DL), which is the moniker for “deep” stacks of ANNs. Alan Turing might have described them as one of his “universal computing machines.” By altering the structure and hyperparameters of the ANN, agents can model an arbitrary state space.
I will briefly review DL to set the context for deep RL. But this is not a book on deep learning or machine learning; if you wish to learn more please refer to the references in “Further Reading”.
Fundamentals
NNs are comprised of many interconnected functions, called neurons, that act in unison to solve classification or regression problems. A layer is a set of neurons with inputs and outputs. You can stack layers on top of each other to allow the ANN to learn abstractions of the data. The layer connected to the data is the input layer. The layer producing the outputs is the output layer. All layers in between are hidden layers.
The value of each connection, where a connection is between inputs, other neurons, or outputs, is multiplied by a weight. The neuron sums the products of the inputs and the weights (a dot product). You then train the weights to optimize an error function, which is the difference between the output of the ANN and the ground truth. Presented this way, ANNs are entirely linear. If you were performing classification then a simple ANN is a linear classifier. The same is true for regression.
The output of each neuron passes through a nonlinear activation function. The choice of function is a hyperparameter, but all activation functions are, by definition, nonlinear or discontinuous. This enables the ANN to approximate nonlinear functions or classify nonlinearly.
ANNs “learn” by changing the values of the weights. On each update, the training routine nudges the weights in proportion to the gradient of the error function. A key idea is that you update the weights iteratively by repeatedly stimulating the black box and correcting its estimate. Given enough data and time, the ANN will predict accurate values or classes.
Common Neural Network Architectures
Deep ANNs come in all shapes and sizes. All are fundamentally based on the idea of stacking neurons. Deep is a reference to large numbers of hidden layers that are required to model abstract concepts. But the specific architecture tends to be domain dependent.
Multilayer perceptrons (MLPs) are the simplest and traditional architecture for DL. Multiple layers of NNs are fully connected and feed-forward; the output of each neuron in the layer above is directed to every neuron in the layer below. The number of neurons in the input layer is the same as the size of the data. The size of the output layer is set to the number of classes and often provides a probability distribution over the classes by passing the neurons through a softmax function.
Deep belief networks (DBNs) are like MLPs, except that the connections between the top two (or more) layers are undirected; the information can pass back up from the second layer to the first. The undirected layers are restricted Boltzmann machines (RBMs). RBMs allow you to model the data and the MLP layers enable classification, based upon the model. This is beneficial because the model is capable of extracting latent information; information that is not directly observable. However, RBMs become more difficult to train in proportion to the network size.
Autoencoders have an architecture that tapers toward the middle, like an hourglass. The goal is to reproduce some input data as best as it can, given the constraint of the taper. For example, if there were two neurons in the middle and the corresponding reproduction was acceptable, then you could use the outputs of the two neurons to represent your data, instead of the raw data. In other words, it is a form of compression. Many architectures incorporate autoencoders as a form of automated feature extraction.
Convolutional NNs (CNNs) work well in domains where individual observations are locally correlated. For example, if one pixel in an image is black, then surrounding pixels are also likely to be black. This means that CNNs are well suited to images, natural language, and time series. The basic premise is that the CNN pre-processes the data through a set of filters, called convolutions. After going through several layers of filters the result is fed into an MLP. The training process optimizes the filters and the MLP for the problem at hand. The major benefit is that the filters allow the architecture as a whole to be time, rotation, and skew dependent, so long as those examples exist in the training data.
Recurrent NNs (RNNs) are a class of architectures that feed back the result of one time step into the input of the next. Given data that is temporally correlated, like text or time series, RNNs are able to “remember” the past and leverage this information to make decisions. RNNs are notoriously hard to train because of the feedback loop. Long short-term memory (LSTM) and gated recurrent units (GRUs) improve upon RNNs by incorporating gates to dump the previous “history” and cut the destructive feedback loop, like a blowoff valve in a turbocharged engine.
Echo state networks (ESNs) use a randomly initialized “pool” of RNNs to transform inputs into a higher number of dimensions. The major benefit of ESNs is that you don’t need to train the RNNs; you train the conversion back from the high dimensional space to your problem, possibly using something as simple as a logistic classifier. This removes all the issues relating to training RNNs and NNs.
Deep Learning Frameworks
I always recommend writing your own simple neural network library to help understanding, but for all industrial applications you should use a library. Intel, Mathworks, Wolfram, and others all have proprietary libraries. But I will focus on open source.
Open source DL libraries take two forms: implementation and wrapper. Implementation libraries are responsible for defining the NN (often as a directed acyclic graph [DAG]), optimizing the execution and abstracting the computation. Wrapper libraries introduce another layer of abstraction that allow you to define NNs in high-level concepts.
After years of intense competition, the most popular, actively maintained DL implementation frameworks include TensorFlow, PyTorch, and MXNet. TensorFlow is flexible enough to handle all NN architectures and use cases, but it is low-level, opinionated, and complex. It has a high barrier to entry, but is well supported and works everywhere you can think of. PyTorch has a lower barrier to entry and has a cool feature of being able to change the computation graph at any point during training. The API is reasonably high level, which makes it easier to use. MXNet is part of the Apache Foundation, unlike the previous two, which are backed by companies (Google and Facebook, respectively). MXNet has bindings in a range of languages and reportedly scales better than any other library.
Keras is probably the most famous wrapper library. You can write in a high-level API, where each line of code represents a layer in your NN, which you can then deploy to TensorFlow, Theano, or CNTK (the latter two are now defunct). A separate library allows you to use MXNet, too. PyTorch has its own set of wrapper libraries, Ignite and Skorch being the most popular general-purpose high-level APIs. Gluon is a wrapper for MXNet. Finally, ONNX is a different type of wrapper that aims to be a standardized format for NN models. It is capable of converting trained models from one framework into another for prediction. For example, you could train in PyTorch and serve in MXNet.
Tip
If you forced me to make a recommendation, I suggest starting with a wrapper like Keras or Gluon first then graduating to PyTorch (because it too has a high-level API). But TensorFlow has strong industrial credentials, so that is a good choice, too. And MXNet is becoming increasingly popular for performance reasons. Any library will do, then. ONNX could become a standard for models in the future due to this reason.
Deep Reinforcement Learning
How does deep learning fit into RL? Recall from the beginning of Chapter 4 that you need models to cope with complex state spaces (complex in the sense of being continuous or having a high number of dimensions).
Simple models, like linear models, can cope with simple environments where the expected value mapping varies linearly. But many environments are far more complicated. For example, consider the advertisement bidding environment in “Industrial Example: Real-Time Bidding in Advertising” again. If our state was the rate of spend over time, as it was in the example, then a linear model should be able to fit that well. But if you added a feature that was highly nonlinear, like information about the age of the person viewing the ads if your ad appealed to a very specific age range, then a linear model would fit poorly.
Using DL allows the agents to accept any form of information and delegate the modeling to the NN. What about if you have a state based upon an image? Not a problem for a model using CNNs. Time-series data? Some kind of RNN. High-dimensional multisensor data? MLP. DL effectively becomes a tool used to translate raw observations into actions. RL doesn’t replace machine learning, it augments it.
Using DL in RL is more difficult than using it for ML. In supervised machine learning you improve a model by optimizing a measure of performance against the ground truth. In RL, the agent often has to wait a long time to receive any feedback at all. DL is already notorious because it takes a lot of data to train a good model, but combine this with the fact that the agent has to randomly stumble across a reward and it could take forever. For this and many more reasons, researchers have developed a bag of tricks to help DL learn in a reasonable amount of time.
Deep Q-Learning
Before 2013, researchers realized that they needed function approximation to solve problems with large or complex state spaces. They had proven that using a linear approximation retained the same convergence guarantees as tabular methods. But they warned that using nonlinear function approximators may in fact diverge, rather than converge.1 So, much of the research focused on improving linear approximation methods.
Eventually the forbidden fruit that is DL proved too tempting for researchers and they designed a deep Q-network (DQN).2 They realized that the main problem was the moving goalpost. Imagine trying to swat a fly. The fly’s motion is so random and reactions so quick that only the Karate Kid could hope to catch it midair. If you wait until the fly is stationary, you have a much greater chance of predicting where the fly is going to be in 500 milliseconds and therefore have a better chance of hitting it. The agent has the same problem. Unless the data is stationary, it can find it very hard to converge. In some cases it can actually diverge because like in a destructive feedback loop, the next action might make matters worse.
In general, model optimizers like stochastic gradient descent assume that your data is independent and identically distributed (IID) random variables. When you sample close in time, the data is likely to be correlated. For example, the definition of the MDP says that the next observation is dependent on the previous state and the action taken. This violates the IID assumption and models can fail to converge.
Experience Replay
The initial solution to this problem was to use experience replay. This is a buffer of observations, actions, rewards, and subsequent observations that can be used to train the DL model. This allows you to use old data to train your model, making training more sample efficient, much like in “Eligibility Traces”. By taking a random subset when training, you break the correlation between consecutive observations.
The size of the experience replay buffer is important. Zhang and Sutton observed that a poorly tuned buffer size can have a large impact on performance.3 In the worst case, agents can “catastrophically forget” experiences when observations drop off the end of a first in, first out (FIFO) buffer, which can lead to a large change in policy. Ideally, the distribution of the training data should match that observed by the agent.4
Q-Network Clones
In an update to the original DQN algorithm, the same researchers proposed cloning the Q-network. This leads to two NNs: one online network that produces actions and one target network that continues to learn. After some number of iterations the prediction network copies the current weights from the target network. The researchers found that this made the algorithm more stable and less likely to oscillate or diverge. The reason is the same as before. The data obtained by the agent is then stationary for a limited time. The trick is to set this period small enough so that you can improve the model quickly, but long enough to keep the data stationary.5 You will also notice that this is the same as the idea presented in “Double Q-Learning”; two estimates are more stable than one.
Neural Network Architecture
Using randomly sampled experience replay and a target Q-network, DQN is stable enough to perform well in complex tasks. The primary driver is the choice of NN that models and maps the observations into actions. The original DQN paper played Atari games from video frames, so using a CNN is an obvious choice. But this does not prevent you from using other NN architectures. Choose an architecture that performs well in your domain.
Another interesting feature of DQN is the choice to predict the state-value function. Recall standard Q-learning (or SARSA) uses the action-value function; the Q-values hold both the state and the actions as parameters. The result is an expected value estimate for a state and a single action. You could train a single NN for each action. Instead, NNs can have several heads that predict the values of all actions at the same time. When training you can set the desired action to 1 and the undesired actions to 0, a one-hot encoding of the actions.
Implementing DQN
The equation representing the update rule for DQN is like “Q-Learning”. The major difference is that the Q-value is aproximated by a function, and that function has a set of parameters. For example, to choose the optimal action, pick the action that has the highest expected value like in Equation 4-1.
Equation 4-1. Choosing an action with DQN
In Equation 4-1, represents the function used to predict the action values from the NN and represents the parameters of the function. All other symbols are the same as in Equation 3-5.
To train the NN you need to provide a loss function. Remember that the goal is to predict the action-value function. So a natural choice of loss function is the squared difference between the actual action-value function and the prediction, as shown in Equation 4-2. This is typically implemented as the mean squared error (MSE), but any loss function is possible.
Equation 4-2. DQN loss function
NN optimizers use gradient descent to update the estimates of the parameters of the NN. They use knowledge of the gradient of the loss function to nudge the parameters in a direction that minimizes the loss function. The underlying DL framework handles the calculation of the gradient for you. But you could write it out by differentiating Equation 4-2 with respect to .
The implementation of DQN is much Q-learning from Algorithm 3-1. The differences are that the action is delivered directly from the NN, the experiences need buffering, and occasionally you need to transfer or train the target NN’s parameters. The devil is in the detail. Precisely how you implement experience replay, what NN architecture and hyperparameters you choose, and when you do the training can make the difference between super-human performance and an algorithmic blowup.
For the rest of this chapter I have chosen to use a library called Coach by Intel’s Nervana Systems. I like it for three reasons: I find the abstractions intuitive, it implements many algorithms, and it supports lots of environments.
Example: DQN on the CartPole Environment
To gain some experience with DQN I recommend you use a simple “toy” environment, like the CartPole environment from OpenAI Gym.
The environment simulates balancing a pole on a cart. The agent can nudge the cart left or right; these are the actions. It represents the state with a position on the x-axis, the velocity of the cart, the velocity of the tip of the pole, and the angle of the pole (0° is straight up). The agent receives a reward of 1 for every step taken. The episode ends when the pole angle is more than ±12°, the cart position is more than ±2.4 (the edge of the display), or the episode length is greater than 200 steps. To solve the environment you need an average reward greater than or equal to 195 over 100 consecutive trials.
Coach has a concept of presets, which are settings for algorithms that are known to work. The CartPole_DQN preset has a solution to solve the CartPole environment with a DQN. I took this preset and made a few alterations to leave the following parameters:
-
It copies the target weights to the online weights every 100 steps of the environment.
-
The discount factor is set to 0.99.
-
The maximum size of the memory is 40,000 experiences.
-
It uses a constant -greedy schedule of 0.05 (to make the plots consistent).
-
The NN uses an MSE-based loss, rather than the default Huber loss.
-
No environment “warmup” to prepopulate the memory (to obtain a result from the beginning).
Of all of these settings, it is the use of MSE loss (Equation 4-2) that makes the biggest difference. Huber loss clips the loss to be a linear error above a threshold and zero otherwise. In more complex environments absolute losses like the Huber loss help mitigate against outliers. If you are using MSE, then outliers get squared and the huge error overwhelms all other data. But in this case the environment is simple and there is no noise, so MSE, because of the squaring, helps the NN learn faster, because the errors really are large to begin with. For this reason Huber loss tends to be the default loss function used in RL.
Tip
In general I recommend that you should use an absolute loss in noisy environments and a squared loss for simpler, noise-free environments.
To provide a baseline for the DQN algorithm, I have implemented two new agents in Coach. The random agent picks a random action on every step. The Q-learning agent implements Q-learning as described in “Q-Learning”. Recall that tabular Q-learning cannot handle continuous states. I was able to solve the CartPole environment with Q-learning by multiplying all states by 10, rounding to the nearest whole number, and casting to an integer. I also only use the angle and the angular velocity of the pole (the third and fourth elements in the observation array, respectively). This results in approximately 150 states in the Q-value lookup table.
Figure 4-1 shows the episode rewards for the three agents. Both DQN and Q-learning are capable of finding an optimal policy. The random policy is able to achieve an average reward of approximately 25 steps. This is due to the environment physics. It takes that long for the pole to fall. The Q-learning agent initially performs better than the DQN. This is because the DQN needs a certain amount of data before it can train a reasonable model of the Q-values. The precise amount of data required depends on the complexity of the deep neural network and the size of the state space. The Q-learning agent sometimes performs poorly due to the -greedy random action. In contrast, DQN is capable of generalizing to states that it hasn’t seen before, so performance is more stable.
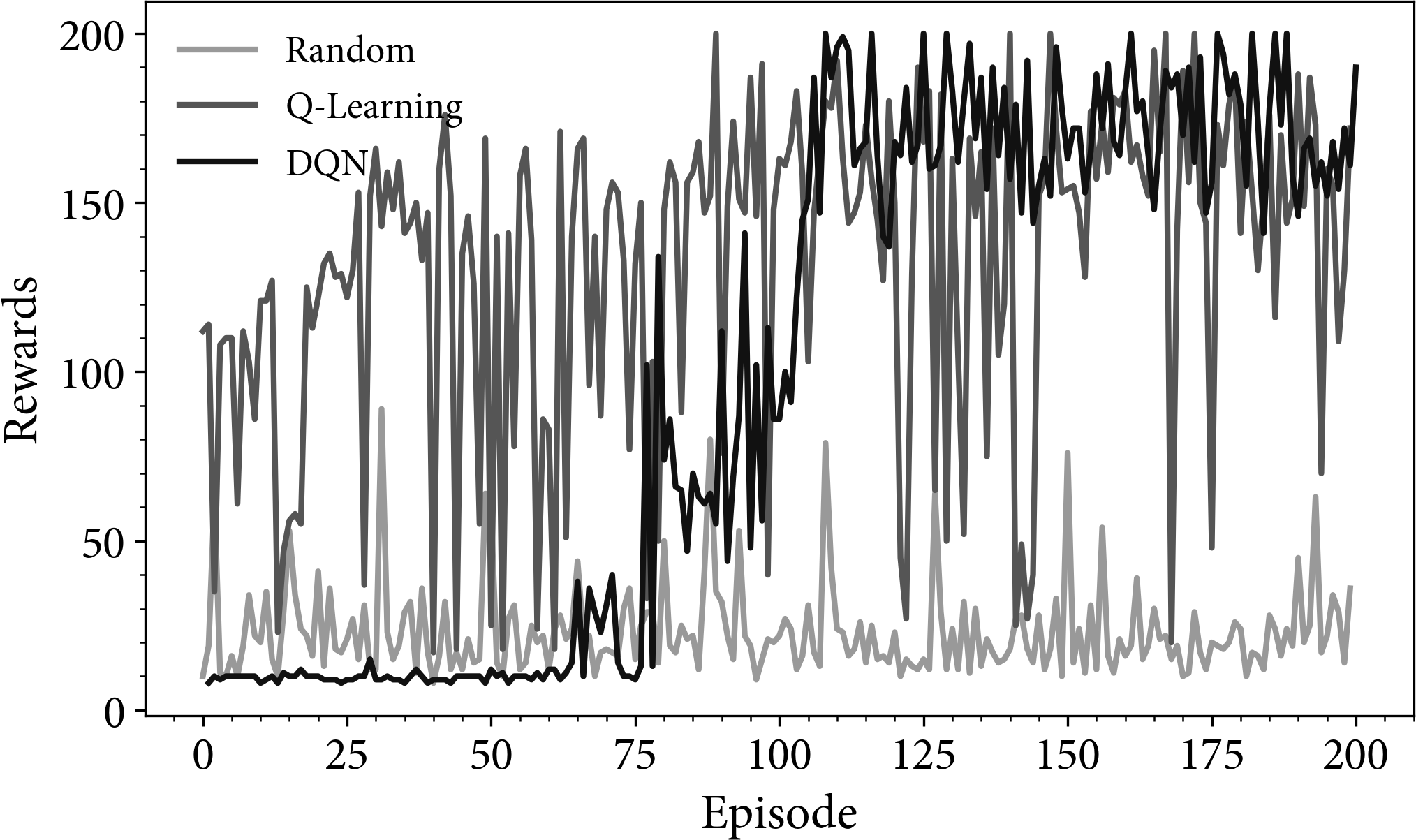
Figure 4-1. A plot of the episode rewards for random, Q-learning, and DQN agents. The results are noisy because they are not averaged.
Figures 4-2–4-4 show an example episode from the random, Q-learning, and DQN agents, respectively. Both the Q-learning and DQN examples last for 200 steps, which is the maximum for an episode.
Figure 4-2. An example of the random agent on the CartPole environment
Figure 4-3. An example of the Q-learning agent on the CartPole environment.
Figure 4-4. An example of the DQN agent on the CartPole environment.
Why train online?
At this point you might ask why you need to train online at all. You could generate and store 200 episodes’ worth of data from the environment and train a model offline in a supervised way. For simple environments this can work, albeit inefficiently. To generate the data the agent still needs to follow a policy. You could choose a random policy but this is unlikely to generate long episodes. Consider the CartPole environment. How many attempts do you think it will take a random policy to achieve 200 time steps? A lot. In most applications the agent needs to learn online so it can observe later states.
The second reason is that the agent must produce counterfactual actions (actions that might not be good) to confirm that it does have the best policy. This is at the heart of exploration. Actions produce new, unseen trajectories. One of them will be optimal. If you don’t have a sequential environment or you don’t need to explore to find optimal policies, then use standard machine learning. I discuss this further in “Learning from Offline Data”.
Which is better? DQN versus Q-learning
The results show that standard Q-learning is as good as DQN. And I haven’t applied any of the improvements to Q-learning seen in “Extensions to Q-Learning”. Why use DQN, given the complexities of adding an NN?
To make Q-learning work, I had to drastically reduce the amount of information. I removed half of the features and quantized the remaining to leave around 150 discrete values. To find those settings I had to perform feature engineering, which included trying many other combinations of features and quantization levels—effort that would take a book in itself. This might be worth the effort if you want to run models like this in production, because the simplicity will make decisions easier to explain, and the models will be more robust, more efficient, more stable, and so on.
With DQN I didn’t change anything. The NN was able to take the raw information, figure out which features were important, and tell me which action was optimal. The model can incorporate continuous values, making the result more fine-grained when compared to tabular methods. If your domain is more complex and feature engineering becomes difficult, NNs can be an efficient solution. But beware that all the usual NN caveats apply: they need a lot of data, are prone to overfitting, are sensitive to initial conditions and hyperparameters, are not resilient or robust, and are open to adversarial attack (see “Secure RL”).
Case Study: Reducing Energy Usage in Buildings
Around 40% of the European Union’s energy is spent on powering and heating buildings and this represents about 25% of the greenhouse gas emissions.6 There are a range of technologies that can help reduce building energy requirements, but many of them are invasive and expensive. However, fine-tuning the control of building heating, ventilation, and air conditioning (HVAC) is applicable to buildings of any age. Marantos et al. propose using RL inside a smart thermostat to improve the comfort and efficiency of building heating systems.7
They begin by defining the Markov decision process. The state is represented by a concatenation of outdoor weather sensors like the temperature and the amount of sunlight, indoor sensors like humidity and temperature, energy sensors to quantify usage, and an indication of thermal comfort.
The agent is able to choose from three actions: maintain temperature, increase temperature by one degree, or reduce temperature by one degree.
The reward is quantified through a combination of thermal comfort and energy usage that is scaled using a rolling mean and standard deviation, to negate the need for using arbitrary scaling parameters. Since this is largely a continuous problem, Marantos et al. introduce a terminal state to prevent the agent from going out of bounds: if the agent attempts to go outside of a predefined operating window then it is penalized.
Marantos et al. chose to use the neural fitted Q-iteration (NFQ) algorithm, which was a forerunner of DQN. DQN has the same ideas as NFQ, except that it also includes experience replay and the target network. They use a feed-forward multilayer perceptron as the state representation function to predict binary actions.
They evaluate their implementation using a simulation that is used in a variety of similar work. The simulation corresponds to an actual building located in Crete, Greece, using public weather information. Compared to a standard threshold-based thermostat, the agent is able to reduce average energy usage by up to 59%, depending on the level of comfort chosen.
One interesting idea that you don’t often see is that Marantos et al. implemented this algorithm in a Raspberry Pi Zero and demonstrated that even with the neural network, they have more than enough computational resources to train the model.
If I were to help improve this project the first thing I would consider is switching to DQN, or one of its derivatives, to improve algorithmic performance. NFQ is demonstrably weaker than DQN due to the experience replay and target network. This change would result in better sample efficiency and benefit from using an industry standard technique. I love the use of the embedded device to perform the computation and I would extend this by considering multiple agents throughout the building. In this multi-agent setting, agents could cooperate to optimize temperature comfort for different areas, like being cooler in bedrooms or turned off entirely overnight in living rooms.
Finally, this doesn’t just have to apply to heating. An agent could easily improve lighting efficiency, hot-water use, and electrical efficiency, all of which have documented case studies. You can find more on the accompanying website.
Rainbow DQN
Being a derivation of Q-learning, you can improve DQN using the extensions seen in “Extensions to Q-Learning”. In 2017, researchers created Rainbow DQN using six extensions that each addressed fundamental concerns with Q-learning and DQN. The researchers also ran experiments to see which improved performance most.8
You have already seen the first two improvements: double Q-learning (see “Double Q-Learning”), to mitigate the maximization bias and -step returns (see “n-Step Algorithms”), to accumulate the reward for multiple future steps.
Distributional RL
The most fundamental deviation from standard DQN is the reintroduction of probability into the agents. All Q-learning agents derive from the Bellman equation (Equation 2-10), which defines the optimal trajectory as the action that maximizes the expected reward. The key word here is expected. Q-learning implements this as an exponentially decaying average. Whenever you use a summary statistic you are implying assumptions about the underlying distribution. Usually, if you choose to use the mean as a summary statistic, you place an implicit assumption that the data is distributed according to a normal distribution. Is this correct?
For example, imagine you are balancing on the cliff in the Cliffworld environment. There is a large negative reward if you fall off the cliff. But there is also a much greater (but near zero) reward of walking along the cliff edge. “Q-Learning Versus SARSA” showed that SARSA followed the average “safe” path far away from the cliff. Q-learning took the risky path next to the cliff because the fewer number of steps to the goal resulted in a slightly greater expected return. All states in the Cliffworld environment lead to two outcomes. Both outcomes have their own distribution representing a small chance that some exploration may lead the agent to an alternative outcome. The expected return is not normally distributed. In general, rewards are multimodal.
Now imagine a Cliffworld-like environment where the difference between success and failure is not as dramatic. Imagine that the reward upon success is +1 and failure is –1. Then the expected return, for at least some states, will be close to zero. In these states, the average expected value yields actions that make no difference. This can lead to agents randomly wandering around meaningless states (compare this with gradient descent algorithms that plateau when the loss functions become too flat). This is shown in Figure 4-5. In general, reward distributions are much more complex.
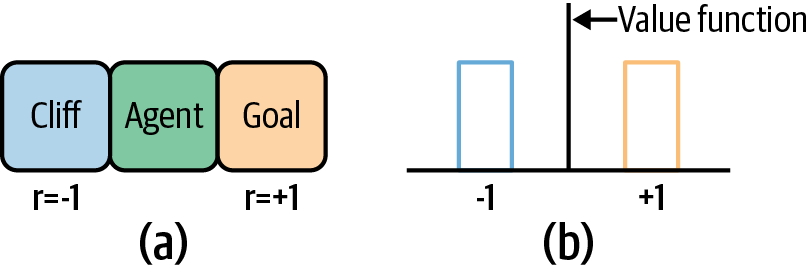
Figure 4-5. A depiction of multimodal rewards for a state. (a) presents a simple grid environment with a penalizing cliff on one side and a rewarding goal on the other. The reward distribution, shown in (b), has two opposite rewards and the mean, which is the same as the value function for that state, is zero.
In practice, this leads to convergence issues. The worst-case scenario is that the agent never converges. When it does, researchers often describe the agent as “chattering.” This is where the agent converges but never stabilizes. It can oscillate like in Figure 4-6 or can be more complex. Note that this is not the only cause of chattering.
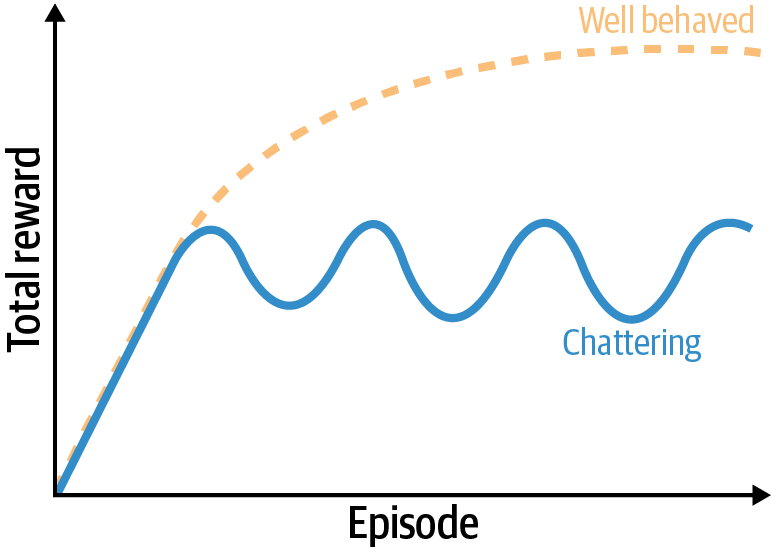
Figure 4-6. A depiction of chattering using a plot of the rewards during training.
Learning the distribution of rewards can lead to more stable learning.9 Bellemare et al. reformulate the Bellman equation to account for random rewards that you can see in Equation 4-3, where is the discount factor, and is a stochastic reward that depends on a state and action.
Equation 4-3. Distributional Bellman equation
Here I temporarily break from this book’s convention and use capital letters to denote stochastic variables. represents the distribution of rewards. The expectation of is the Q-value. Like the Q-value, should be updated recursively according to the received reward. The key difference is the emphasis that the expected return, , is a random variable distributed over all future states, , and future actions, . In other words, the policy is a mapping of state-action pairs to a distribution of expected returns. This representation preserves multimodality and Bellemare et al. suggest that this leads to more stable learning. I recommend that you watch this video to see an example of the distribution of rewards learned during a game of Space Invaders.
The first incarnation of this idea is an algorithm called C51. It asks two key questions. How do you represent the distribution? How do you create the update rule for Equation 4-3? The choice of distribution or function used to model the returns is important. C51 uses a discrete parametric distribution, in other words a histogram of returns. The “51” in C51 refers to the number of histogram bins chosen in the researchers’ implementation and suggests that performance is proportional to the numbers of bins, albeit with diminishing returns.
To produce an estimate of the distribution, Bellemare et al. built an NN with 51 output “bins.” When the environment produces a reward, which falls into one of the bins, the agent can train the NN to predict that bin. This is now a supervised classification problem and the agent can be trained using cross-entropy loss. The “C” in C51 refers to the fact that the agent is predicting classes, or categories.
Prioritized Experience Replay
The next set of improvements relate to the neural network. In DQN, transitions are sampled uniformly from the replay buffer (see “Deep Q-Learning”). The batch is likely to contain transitions that the agent has seen many times. It is better to include transitions from areas in which there is much to learn. Prioritized experience replay samples the replay buffer with a probability proportional to the absolute error of the temporal-difference update (see Equation 3-6).10 Schaul et al. alter this idea to incorporate the -step absolute error, instead of a single step.
Noisy Nets
In complex environments it may be difficult for the -greedy algorithm to stumble across a successful result. One idea, called noisy nets, is to augment the -greedy search by adding noise in the NN.11 Recall that the NN is a model of prospective actions for a given state: a policy. Applying noise directly to the NN enables a random search in the context of the current policy. The model will learn to ignore the noise (because it is random) when it experiences enough transitions for a given state. But new states will continue to be noisy, allowing context-aware exploration and automatic annealing (see “Improving the -greedy Algorithm”).
Dueling Networks
In Q-learning algorithms, the expected value estimates (the Q-values) are often very similar. It is often unnecessary to even calculate the expected value because both choices can lead to the same result. For example, in the CartPole environment, the first action won’t make much difference if it has learned to save the pole before it falls. Therefore, it makes sense to learn the state-value function, as opposed to the action-value function that I have been using since “Predicting Rewards with the Action-Value Function”. Then each observation can update an entire state, which should lead to faster learning. However, the agent still needs to choose an action.
Imagine for a second that you are able to accurately predict the state-value function. Recall that this is the expectation (the average) over all actions for that state. Therefore, I can represent the individual actions relative to that average. Researchers call this the advantage function and it is defined in Equation 4-4. To recover the action-value function required by Q-learning, you need to estimate the advantage function and the state-value function.
Equation 4-4. Advantage function
Dueling networks achieve this by creating a single NN with two heads, which are predictive outputs. One head is responsible for estimating the state-value function and the other the advantage function. The NN recombines these two heads to generate the required action-value function.12 The novelty is the special aggregator on the output of the two heads that allows the whole NN to be trained as one. The benefit is that the state-value function is quicker and easier to learn, which leads to faster convergence. Also, the effect of subtracting of the baseline in the advantage estimate improves stability. This is because the Q-learning maximization bias can cause large changes in individual action-value estimates.
Example: Rainbow DQN on Atari Games
The DQN paper popularized using the rewards of Atari games as a measure of agent performance. In this section I have re-created some of those results by training an agent to play two Atari games: Pong and Ms Pac-Man. I again use the Coach framework and its Atari presets.
The Atari environment is part of OpenAI Gym and exposes raw Atari 2600 frames. Each frame is a pixel image with an RGB 128-bit color palette. To reduce the computational complexity introduced by the large number of inputs, a pre-processing method converts the array by decimating, cropping, and converting it to grayscale. This reduces the number of input dimensions to . The agent clips the rewards at +/– 1 to unify the return of the Atari games.
The Atari games have lots of moving entities: bullets or ghosts, for example. The agent needs to be aware of the trajectory of these entities to react appropriately, to dodge a bullet or run away from a ghost. More advanced agents incorporate a time-dependent memory, often using recurrent neural networks. DQN and its derivatives do not, so instead agents typically stack multiple frames into a single observation by flattening the image and concatenating into one big array. This implementation merges four frames and the agent reuses the same action for the subsequent four frames.
Results
I chose to run two experiments due to the amount of time it took to train an agent. I used the default hyperparameter settings in the Coach library presets. These include annealing -greedy exploration for 250,000 frames and low ANN learning rates. I trained the agents on the Google Cloud Platform using n1-standard-4 virtual machines connected to a single Nvidia Tesla P4 GPU in the Netherlands.
The training times and approximate costs are described in Table 4-1. The DQN agent, on average, takes 4.8 hours and costs $5.80 to train upon one million frames. The Rainbow agent takes 7.6 hours and costs $8.50 to achieve a similar result. Note that these values are indicators. They are heavily affected by hyperparameters, which are different for the two agents. Research shows that Rainbow far exceeds the performance of DQN when looking at performance over all Atari games.
| Agent | Game | Millions of Frames | Time (hours) | Cost (approximate USD) |
|---|---|---|---|---|
DQN |
Pong |
2 |
10 |
12 |
DQN |
Ms. Pac-Man |
3 |
14 |
17 |
Rainbow |
Pong |
2.5 |
19 |
22 |
Rainbow |
Ms. Pac-Man |
3 |
23 |
26 |
These results highlight the exponential increase in complexity, which results in long training times. Despite proof that Rainbow results in better policies is less time, the context and circumstances are important. You must design the solution to fit within your specific requirements. For example, the improvement in performance obtained by using Rainbow may not justify the near doubling in computational cost. However, the training of the underlying ANN represents the bulk of the cost. If you can simplify, tune, or speed up the ANN architecture, the prices will drop dramatically.
Figure 4-7 shows the rewards obtained when training to play Pong. The Rainbow agent takes an extra 0.5 million frames to obtain a similar result to DQN. This could be due to the differing hyperparameter settings. The learning rate, , is set to for DQN. Rainbow is two-thirds of that value at 6.25e-5. DQN uses -greedy exploration, but Rainbow uses parameter noise exploration. I am confident that with similar hyperparameters Rainbow will perform at least as well as DQN in this example.
Figure 4-8 shows the rewards for the Ms. Pac-Man game. I have smoothed the reward with a moving average of 100 frames. This is because the reward is much noisier due to the random starting positions of the ghosts. For example, a single game could have a low reward because on that occasion the ghosts started in dangerous positions. On other games it might be high because the ghosts start in safe positions. I recommend that you consider the distributions of rewards when working in a stochastic environment.
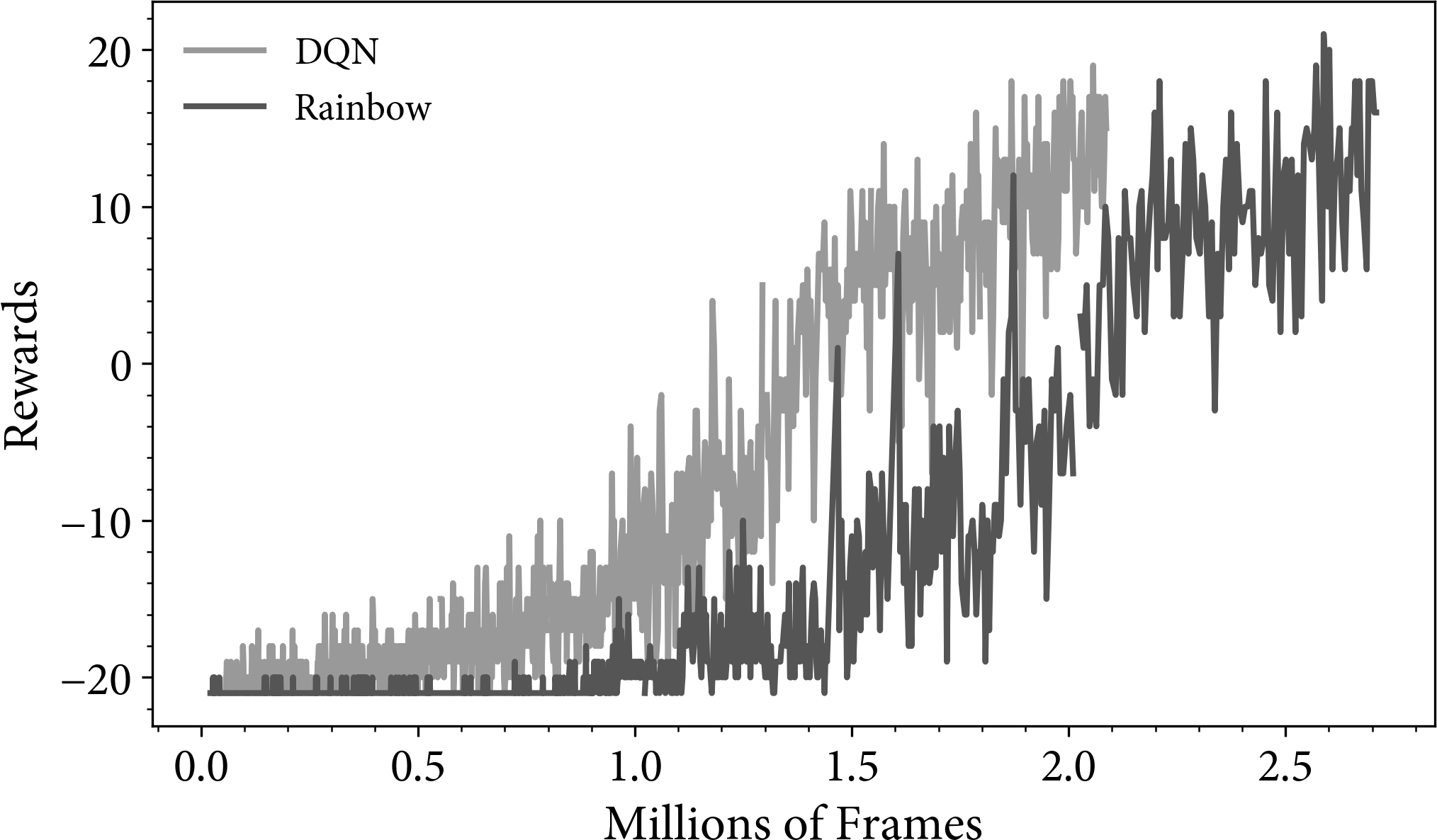
Figure 4-7. A plot of the rewards for DQN and Rainbow agents on the Atari game Pong.
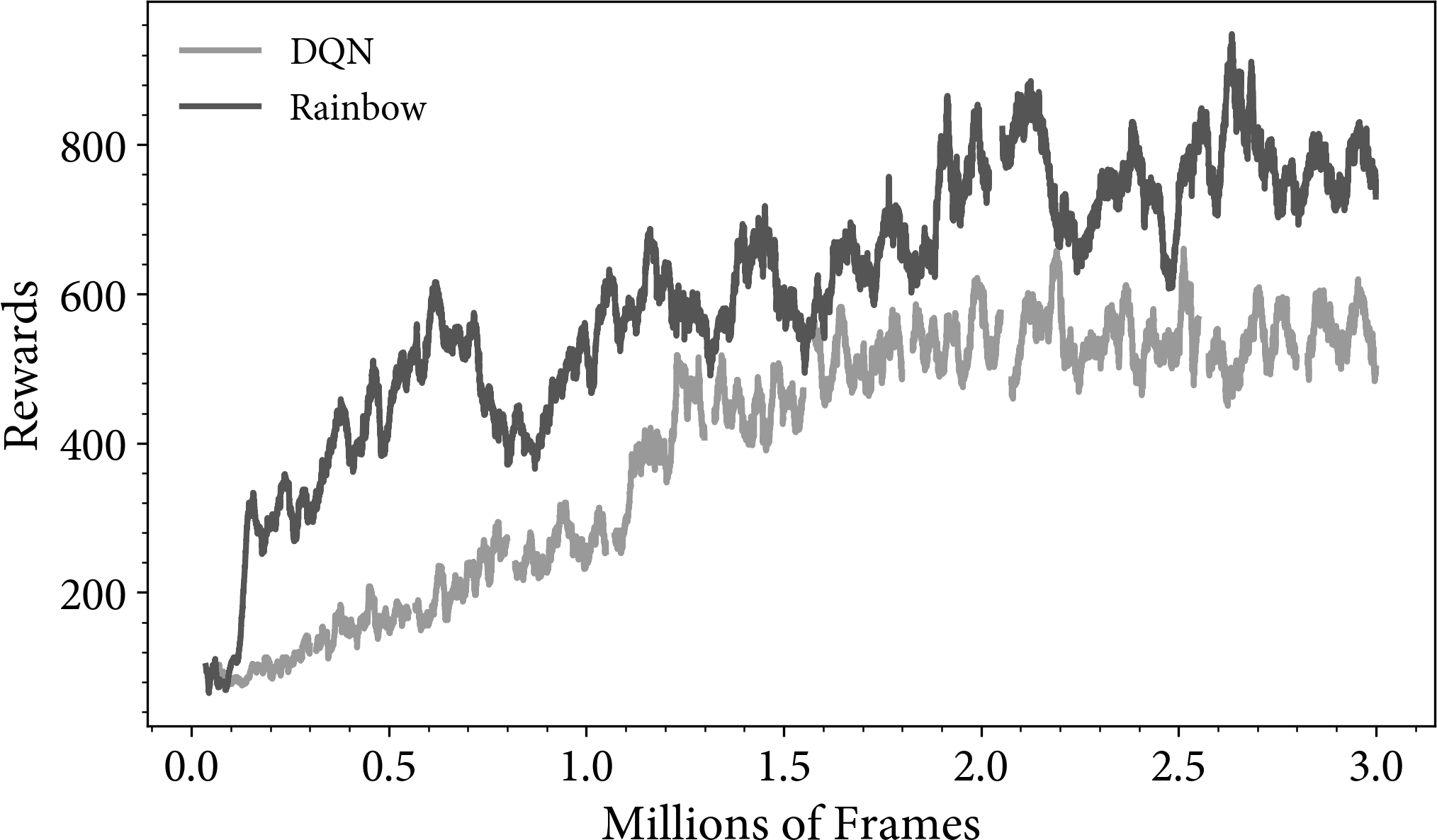
Figure 4-8. A plot of the rewards for DQN and Rainbow agents on the Atari game Ms. Pac-Man. The rewards have been smoothed using a 100-frame moving average.
Discussion
Figures 4-9 and 4-10 show a full episode from Pong for the DQN and Rainbow agents, respectively. Since these are single episodes and the hyperparameters used to train each agent differ, you must not to draw any firm conclusions from the result. But you can comment on the policy, from a human perspective.
Figure 4-9. An example of the trained DQN agent paying the Atari game Pong.
Figure 4-10. An example of the trained Rainbow agent paying the Atari game Pong.
When I first showed these videos to my wife, her initial reaction was “work, yeah right!” But after I explained that this was serious business, she noticed that the movement of the paddle was “agitated” when the ball wasn’t near. This is because the actions make no difference to the result; the Q-values are almost all the same and result in random movement. The agent responds quickly when the ball is close to the paddle because it has learned that it will lose if it is not close to the ball.
The two agents have subtle distinctions. DQN tends to bounce the ball on the corner of the paddle, whereas Rainbow tends to swipe at the ball. I suspect that these actions are artifacts of the early stopping of the training. If I ran these experiments for 20 million frames, I predict that the techniques would tend to converge, but that would be expensive, so I leave that as a reader exercise.
Figures 4-11 and 4-12 show a full episode from Ms. Pac-Man for the DQN and Rainbow agents, respectively. Both agents do a commendable job at avoiding ghosts, collecting pellets, and using the teleports that warp Ms. Pac-Man to the other side of the screen. But in general Rainbow seems to perform better than DQN. It has also learned to look for power pellets so it can eat the ghosts. Rainbow almost completes the first level and given more training time I’m certain it can. Neither agent has yet learned to eat fruits to gain extra points or actively hunt down ghosts after eating a power pellet, if indeed that is an optimal policy.
Figure 4-11. An example of the trained DQN agent paying the Atari game Ms. Pac-Man.
Figure 4-12. An example of the trained Rainbow agent paying the Atari game Ms. Pac-Man.
Other DQN Improvements
“Rainbow DQN” introduced six improvements to DQN. Each algorithm tackles a single impediment and generalizes three themes of research. (1) Neural networks should learn faster and produce results that are more informative. (2) Q-learning should not be unstable or biased. (3) RL should find an optimal policy efficiently. You can see that these refer to three different levels of abstraction. In Rainbow DQN, for example, prioritized experience replay attempts to improve the learning of the neural network, dual double Q-learning helps prevent the maximization bias in Q-learning, and distributional RL helps learn more realistic rewards in RL. In this section I will introduce other recent improvements that focus on DQN.
Improving Exploration
The -greedy exploration strategy is ubiquitous, designed to randomly sample small, finite state spaces. But dithering methods, where you randomly perturb the agent, are not practical in complex environments; they require exponentially increasing amounts of data. One way of describing this problem is to imagine the surface represented by the Q-values. If a Q-learning agent repeatedly chooses a suboptimal state-action pair, subsequent episodes will also choose this pair, like the agent is stuck in a local maxima. One alternative is to consider other sampling methods.
“Improving the -greedy Algorithm” introduced upper-confidence-bound (UCB) sampling, which biases actions toward undersampled states. This prevents the oversampling of initial optimal trajectories. Thompson sampling, often used in A/B testing (see “Multi-Arm Bandit Testing”), maintains distributions that represent the expected values. For Q-learning, this means each Q-value is a distribution, not an expectation. This is the same idea behind distributional RL (see “Distributional RL”). Bootstrapped DQN (BDQN) uses this idea and trains a neural network with multiple heads to simulate the distribution of Q-values, an ensemble of action-value estimates.13 This was superseded by distributional RL, which efficiently predicts the actual distribution, not a crude approximation. But Osband et al. cleverly continued to reuse the randomly selected policy to drive exploration in the future as well. This led to the idea of “deep exploration.” In complex environments, -greedy moves like a fly, often returning to states it has previously observed. It makes sense to push deeper to find new, unobserved states. You can see similarities here with noisy nets, too.
From a Bayesian perspective, modeling the Q-values as distributions is arguably the right way, but often computationally complex. If you treat each head of the neural network as independent estimates of the same policy, then you can combine them into an ensemble and obtain similar performance. To recap, an ensemble is a combination of algorithms that generates multiple hypotheses. The combination is generally more robust and less prone to overfitting. Following independent policies in a more efficient way, like via UCB sampling for example, is another way to achieve “deep exploration.” 14,15 Another major benefit is that you can follow the policy offered by one head to obtain the benefits of searching a deep, unexplored area in the state space, but then later share this learning to the other heads.16 More recent research has shown that although sharing speeds up learning, ultimate performance improves with more diverse heads.17
Improving Rewards
The previous section used separate policy estimates as a proxy for estimating the reward distribution. C51 (see “Distributional RL”) predicts a histogram of the distribution. Neither of these is as efficient as directly approximating the distribution, for example, picking the histogram bounds and the number of bins in C51.
A more elegant solution is to estimate the quantiles of the target distribution. After selecting the number of quantiles, which defines the resolution of the estimate and the number of heads in the neural network, the loss function minimizes the error between the predicted and actual quantiles. The major difference between bootstrapped DQN, C51, ensemble DQN, and this is the loss function. In Distributional RL with Quantile Regression, Dabney et al. replace the standard loss function used in RL (Huber loss) with a quantile equivalent. This results in higher performance on all the standard Atari games but, importantly, provides you with a high-resolution estimate of the reward distribution.18
Recent research is tending to agree that learning reward distributions is beneficial, but not for the reason you expect. Learning distributions should provide more information, which should lead to better policies. But researchers found that it has a regularizing effect on the neural network. In other words, distributional techniques may help to stabilize learning not because learning distributions is more data-efficient, but because it constrains the unwieldy neural network.19
Learning from Offline Data
Many industrial applications of RL need to learn from data that has already been collected. Batch RL is the task of learning a policy from a fixed dataset without further interaction from the environment. This is common in situations where interaction is costly, risky, or time consuming. Using a library of data can also speed up development. This problem is closely related to learning by example, which is also called imitation learning, and discussed in “Imitation RL”.
Most RL algorithms generate observations through interaction with an environment. The observations are then stored in buffers for later reuse. Could these algorithms also work without interaction and learn completely offline?
In one experiment, researchers trained two agents, one learning from interaction and another that only used the buffer of the first. In a surprising result, the buffer-trained agent performed significantly worse when trained with the same algorithm on the same dataset.
The reason for this, which comes from statistical learning theory, is that the training data does not match the testing data. The data generated by an agent is dependent on its policy at the time. The collected data is not necessarily representative of the entire state-action space. The first agent is capable of good performance because it has the power to self-correct through interaction. The buffer-trained agent cannot and requires truly representative data.
Prioritized experience replay, double Q-learning, and dueling Q-networks all help to mitigate this problem by making the data more representative in the first place, but they don’t tackle the core problem. Batch-constrained deep Q-learning (BCQ) provides a more direct solution. The implementation is quite complicated, but the key addition is a different way to provide experience. Rather than feeding the raw observations to the buffer-trained agent, the researchers train another neural network to generate prospective actions using a conditional variational autoencoder. This is a type of autoencoder that allows you to generate observations from specific classes. This has the effect of constraining the policy by only generating actions that lead to states in the buffer. They also include the ability to tune the model to generate random actions by adding noise to the actions, if desired. This helps to make the resulting policy more robust, by filling in the gaps left after sampling.
One final alteration is that they train two networks, like in double Q-learning, to obtain two independent estimates. They then clip these estimates to generate low variance Q-value updates, weighted by a hyperparameter.20
Figure 4-13 compares the results of two experiments on the CartPole environment, using Coach. First, I generate a buffer of transitions using a standard DQN agent. This buffer is then passed into a second agent that never explores. This simulates the situation where you have an algorithm running in production and you want to leverage logged data. When you train a second agent you will not be able to explore, because you cannot perform an action.
In the first experiment, I trained a DQN agent on the buffer data (the gray line). Note how the reward is poor in plot (a). The reason for this is that the agent is unstable, demonstrated by the diverging Q-values in plot (b). The agent will attempt to follow a policy to states that are not in the buffer. The maximization step in Q-learning will lead to an overly optimistic estimate of a Q-value. Because the agent cannot interact with the environment, it cannot retrieve evidence to suggest otherwise. The agent will keep following the bad Q-value and the value will keep on increasing. Recall that in an online environment, the agent can sample that state to verify the expected return. This constrains the Q-values.
In the second experiment, I trained a BCQ agent on the buffer data (the black line). Note the reward convergence in plot (a) and the stable Q-values in plot (b). This is primarily due to the generative model, which provides realistic return estimates via a simulation of the environment (a simulation of a simulation), but also, to a lesser extent, because of the low-variance sampling of independent Q-value estimates.
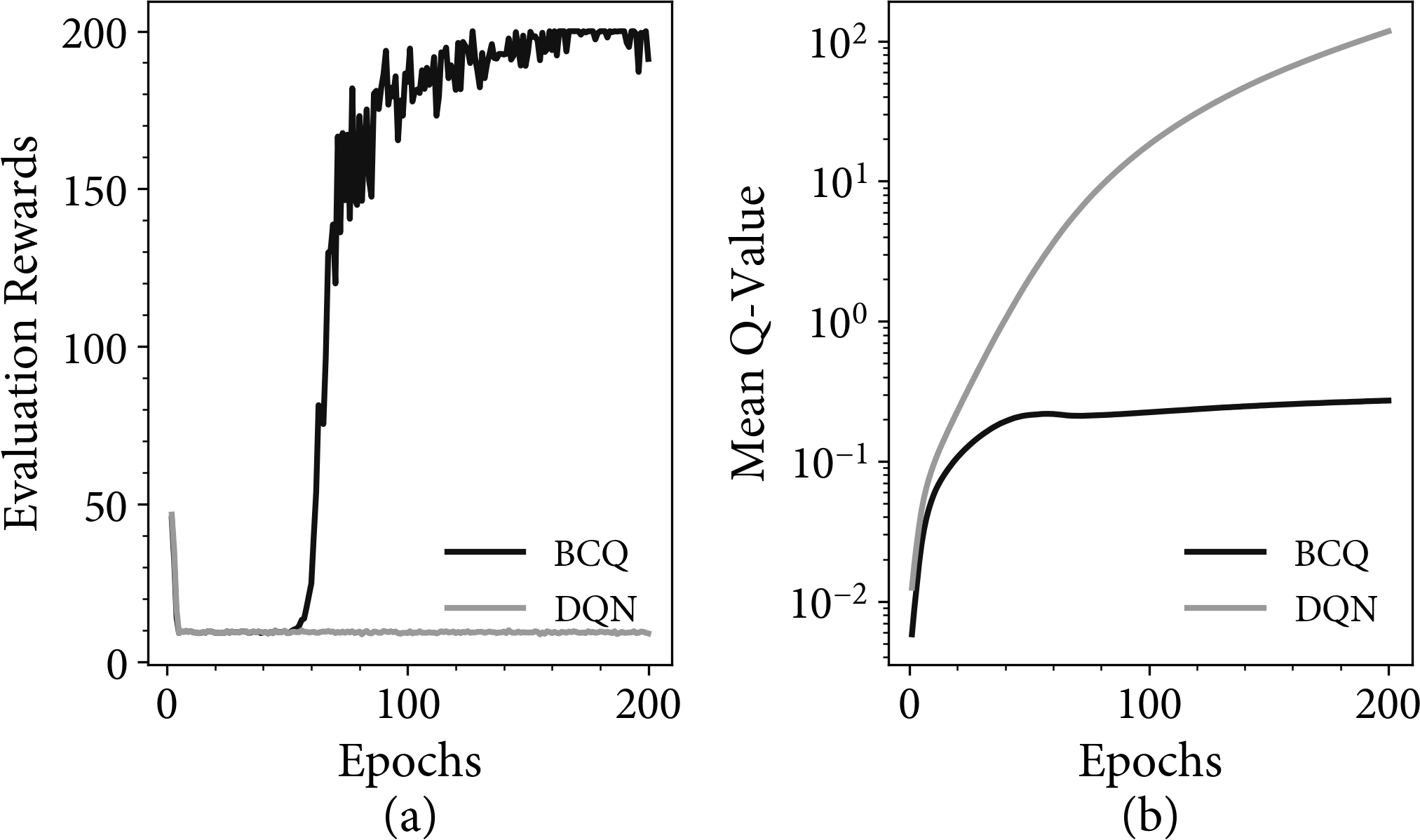
Figure 4-13. Results from an experiment to train BCQ and DQN agents with no interaction with the environment. (a) shows the rewards when evaluating inside the environment. (b) shows the mean Q-values (note the logarithmic y-axis).
Note that the use of the autoencoder adds complexity. In simpler agents like linear Q-learning, you could leverage simpler generative models, like k-nearest neighbors.21
Summary
In this whistle-stop tour, you can see how using deep neural networks as function approximators has revolutionized and reinvigorated Q-learning, the algorithm published in 1991. I thought it was useful to include a very brief overview of the main neural network architectures, but please refer yourself to a book on the subject in “Further Reading”.
Deep Q-networks was the breakthrough paper, but neural networks have been used in RL for a long time.22 Given the flexibility of neural networks, you can find as many improvements to DQN as the number of papers on deep learning. The key insight is that although nonlinear function approximators are unruly and may not converge, they have the incredible ability to approximate any function. This opens the door to applications that were previously deemed too complex.
This power was demonstrated by playing Atari games, but you can see more examples of industrial use cases every day. This chapter marks the end of your journey through basic tabular methods. In the next chapter I reformulate the problem of finding an optimal policy.
Further Reading
-
-
Provost, Foster, and Tom Fawcett. 2013. Data Science for Business: What You Need to Know about Data Mining and Data-Analytic Thinking. O’Reilly Media.
-
Raschka, Sebastian. 2015. Python Machine Learning. Packt Publishing Ltd.
-
-
Deep learning:
-
Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. MIT Press.
-
Chollet, François. 2017. Deep Learning with Python. Manning Publications Company.
-
-
Generative models (autoencoders and such):
-
Foster, David. 2019. Generative Deep Learning: Teaching Machines to Paint, Write, Compose, and Play. O’Reilly Media.
-
1 Tsitsiklis, J. N., and B. Van Roy. 1997. “An Analysis of Temporal-Difference Learning with Function Approximation”. IEEE Transactions on Automatic Control 42 (5): 674–90.
2 Mnih, Volodymyr, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller. 2013. “Playing Atari with Deep Reinforcement Learning”. ArXiv:1312.5602, December.
3 Zhang, Shangtong, and Richard S. Sutton. 2018. “A Deeper Look at Experience Replay”. ArXiv:1712.01275, April.
4 Isele, David, and Akansel Cosgun. 2018. “Selective Experience Replay for Lifelong Learning”. ArXiv:1802.10269, February.
5 Mnih, Volodymyr, et. al 2018. “Human-Level Control through Deep Reinforcement Learning”. Nature 518, 529–533.
6 “Shedding Light on Energy on the EU: How Are Emissions of Greenhouse Gases by the EU Evolving?”. n.d. Shedding Light on Energy on the EU. Accessed 12 September 2020.
7 Marantos, Charalampos, Christos P. Lamprakos, Vasileios Tsoutsouras, Kostas Siozios, and Dimitrios Soudris. 2018. “Towards Plug&Play Smart Thermostats Inspired by Reinforcement Learning”. In Proceedings of the Workshop on INTelligent Embedded Systems Architectures and Applications, 39–44. INTESA 2018. New York, NY, USA: Association for Computing Machinery.
8 Hessel, Matteo, Joseph Modayil, Hado van Hasselt, Tom Schaul, Georg Ostrovski, Will Dabney, Dan Horgan, Bilal Piot, Mohammad Azar, and David Silver. 2017. “Rainbow: Combining Improvements in Deep Reinforcement Learning”. ArXiv:1710.02298, October.
9 Bellemare, Marc G., Will Dabney, and Rémi Munos. 2017. “A Distributional Perspective on Reinforcement Learning”. ArXiv:1707.06887, July.
10 Schaul, Tom, John Quan, Ioannis Antonoglou, and David Silver. 2015. “Prioritized Experience Replay”. ArXiv:1511.05952, November.
11 Fortunato, Meire, Mohammad Gheshlaghi Azar, Bilal Piot, Jacob Menick, Ian Osband, Alex Graves, Vlad Mnih, et al. 2017. “Noisy Networks for Exploration”. ArXiv:1706.10295, June.
12 Wang, Ziyu, Tom Schaul, Matteo Hessel, Hado van Hasselt, Marc Lanctot, and Nando de Freitas. 2015. “Dueling Network Architectures for Deep Reinforcement Learning”. ArXiv:1511.06581, November.
13 Osband, Ian, Charles Blundell, Alexander Pritzel, and Benjamin Van Roy. 2016. “Deep Exploration via Bootstrapped DQN”. ArXiv:1602.04621, July.
14 Lu, Xiuyuan, and Benjamin Van Roy. 2017. “Ensemble Sampling”. ArXiv:1705.07347, November.
15 Chen, Richard Y., Szymon Sidor, Pieter Abbeel, and John Schulman. 2017. “UCB Exploration via Q-Ensembles”. ArXiv:1706.01502, November.
16 Menon, Rakesh R., and Balaraman Ravindran. 2017. “Shared Learning: Enhancing Reinforcement in Q-Ensembles”. ArXiv:1709.04909, September.
17 Jain, Siddhartha, Ge Liu, Jonas Mueller, and David Gifford. 2019. “Maximizing Overall Diversity for Improved Uncertainty Estimates in Deep Ensembles”. ArXiv:1906.07380, June.
18 Dabney, Will, Mark Rowland, Marc G. Bellemare, and Rémi Munos. 2017. “Distributional Reinforcement Learning with Quantile Regression”. ArXiv:1710.10044, October.
19 Lyle, Clare, Pablo Samuel Castro, and Marc G. Bellemare. 2019. “A Comparative Analysis of Expected and Distributional Reinforcement Learning”. ArXiv:1901.11084, February.
20 Fujimoto, Scott, David Meger, and Doina Precup. 2019. “Off-Policy Deep Reinforcement Learning without Exploration”. ArXiv:1812.02900, August.
21 Shah, Devavrat, and Qiaomin Xie. 2018. “Q-Learning with Nearest Neighbors”. ArXiv:1802.03900, October.
22 Gaskett, Chris, David Wettergreen, and Alexander Zelinsky. 1999. “Q-Learning in Continuous State and Action Spaces”. In Advanced Topics in Artificial Intelligence, edited by Norman Foo, 417–28. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer.
Get Reinforcement Learning now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

