Python for Algorithmic Trading

Chapter 4. Mastering Vectorized Backtesting

[T]hey were silly enough to think you can look at the past to predict the future.¹

The Economist

Developing ideas and hypotheses for an algorithmic trading program is generally the more creative and sometimes even fun part in the preparation stage. Thoroughly testing them is generally the more technical and time consuming part. This chapter is about the vectorized backtesting of different algorithmic trading strategies. It covers the following types of strategies (refer also to “Trading Strategies”):

Simple moving averages (SMA) based strategies

The basic idea of SMA usage for buy and sell signal generation is already decades old. SMAs are a major tool in the so-called technical analysis of stock prices. A signal is derived, for example, when an SMA defined on a shorter time window—say 42 days—crosses an SMA defined on a longer time window—say 252 days.

Momentum strategies

These are strategies that are based on the hypothesis that recent performance will persist for some additional time. For example, a stock that is downward trending is assumed to do so for longer, which is why such a stock is to be shorted.

Mean-reversion strategies

The reasoning behind mean-reversion strategies is that stock prices or prices of other financial instruments tend to revert to some mean level or to some trend level when they have deviated too much from such levels.

The chapter proceeds as follows. “Making Use of Vectorization” introduces vectorization as a useful technical approach to formulate and backtest trading strategies. “Strategies Based on Simple Moving Averages” is the core of this chapter and covers vectorized backtesting of SMA-based strategies in some depth. “Strategies Based on Momentum” introduces and backtests trading strategies based on the so-called time series momentum (“recent performance”) of a stock. “Strategies Based on Mean Reversion” finishes the chapter with coverage of mean-reversion strategies. Finally, “Data Snooping and Overfitting” discusses the pitfalls of data snooping and overfitting in the context of the backtesting of algorithmic trading strategies.

The major goal of this chapter is to master the vectorized implementation approach, which packages like NumPy and pandas allow for, as an efficient and fast backtesting tool. To this end, the approaches presented make a number of simplifying assumptions to better focus the discussion on the major topic of vectorization.

Vectorized backtesting should be considered in the following cases:

Simple trading strategies

The vectorized backtesting approach clearly has limits when it comes to the modeling of algorithmic trading strategies. However, many popular, simple strategies can be backtested in vectorized fashion.

Interactive strategy exploration

Vectorized backtesting allows for an agile, interactive exploration of trading strategies and their characteristics. A few lines of code generally suffice to come up with first results, and different parameter combinations are easily tested.

Visualization as major goal

The approach lends itself pretty well for visualizations of the used data, statistics, signals, and performance results. A few lines of Python code are generally enough to generate appealing and insightful plots.

Comprehensive backtesting programs

Vectorized backtesting is pretty fast in general, allowing one to test a great variety of parameter combinations in a short amount of time. When speed is key, the approach should be considered.

Making Use of Vectorization

Vectorization, or array programming, refers to a programming style where operations on scalars (that is, integer or floating point numbers) are generalized to vectors, matrices, or even multidimensional arrays. Consider a vector of integers $v={(1,2,3,4,5)}^T$ represented in Python as a list object v = [1, 2, 3, 4, 5]. Calculating the scalar product of such a vector and, say, the number 2 requires in pure Python a for loop or something similar, such as a list comprehension, which is just different syntax for a for loop:

In [1]: v = [1, 2, 3, 4, 5]

In [2]: sm = [2 * i for i in v]

In [3]: sm
Out[3]: [2, 4, 6, 8, 10]

In principle, Python allows one to multiply a list object by an integer, but Python’s data model gives back another list object in the example case containing two times the elements of the original object:

In [4]: 2 * v
Out[4]: [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

Vectorization with NumPy

The NumPy package for numerical computing (cf. NumPy home page) introduces vectorization to Python. The major class provided by NumPy is the ndarray class, which stands for n-dimensional array. An instance of such an object can be created, for example, on the basis of the list object v. Scalar multiplication, linear transformations, and similar operations from linear algebra then work as desired:

In [5]: import numpy as np  

In [6]: a = np.array(v)  

In [7]: a  
Out[7]: array([1, 2, 3, 4, 5])

In [8]: type(a)  
Out[8]: numpy.ndarray

In [9]: 2 * a  
Out[9]: array([ 2,  4,  6,  8, 10])

In [10]: 0.5 * a + 2  
Out[10]: array([2.5, 3. , 3.5, 4. , 4.5])

Imports the NumPy package.

Instantiates an ndarray object based on the list object.

Prints out the data stored as ndarray object.

Looks up the type of the object.

Achieves a scalar multiplication in vectorized fashion.

Achieves a linear transformation in vectorized fashion.

The transition from a one-dimensional array (a vector) to a two-dimensional array (a matrix) is natural. The same holds true for higher dimensions:

In [11]: a = np.arange(12).reshape((4, 3))  

In [12]: a
Out[12]: array([[ 0,  1,  2],
                [ 3,  4,  5],
                [ 6,  7,  8],
                [ 9, 10, 11]])

In [13]: 2 * a
Out[13]: array([[ 0,  2,  4],
                [ 6,  8, 10],
                [12, 14, 16],
                [18, 20, 22]])

In [14]: a ** 2  
Out[14]: array([[  0,   1,   4],
                [  9,  16,  25],
                [ 36,  49,  64],
                [ 81, 100, 121]])

Creates a one-dimensional ndarray object and reshapes it to two dimensions.

Calculates the square of every element of the object in vectorized fashion.

In addition, the ndarray class provides certain methods that allow vectorized operations. They often also have counterparts in the form of so-called universal functions that NumPy provides:

In [15]: a.mean()  
Out[15]: 5.5

In [16]: np.mean(a)  
Out[16]: 5.5

In [17]: a.mean(axis=0)  
Out[17]: array([4.5, 5.5, 6.5])

In [18]: np.mean(a, axis=1)  
Out[18]: array([ 1.,  4.,  7., 10.])

Calculates the mean of all elements by a method call.

Calculates the mean of all elements by a universal function.

Calculates the mean along the first axis.

Calculates the mean along the second axis.

As a financial example, consider the function generate_sample_data() in “Python Scripts” that uses an Euler discretization to generate sample paths for a geometric Brownian motion. The implementation makes use of multiple vectorized operations that are combined to a single line of code.

See the Appendix A for more details of vectorization with NumPy. Refer to Hilpisch (2018) for a multitude of applications of vectorization in a financial context.

The standard instruction set and data model of Python does not generally allow for vectorized numerical operations. NumPy introduces powerful vectorization techniques based on the regular array class ndarray that lead to concise code that is close to mathematical notation in, for example, linear algebra regarding vectors and matrices.

Vectorization with pandas

The pandas package and the central DataFrame class make heavy use of NumPy and the ndarray class. Therefore, most of the vectorization principles seen in the NumPy context carry over to pandas. The mechanics are best explained again on the basis of a concrete example. To begin with, define a two-dimensional ndarray object first:

In [19]: a = np.arange(15).reshape(5, 3)

In [20]: a
Out[20]: array([[ 0,  1,  2],
                [ 3,  4,  5],
                [ 6,  7,  8],
                [ 9, 10, 11],
                [12, 13, 14]])

For the creation of a DataFrame object, generate a list object with column names and a DatetimeIndex object next, both of appropriate size given the ndarray object:

In [21]: import pandas as pd  

In [22]: columns = list('abc')  

In [23]: columns
Out[23]: ['a', 'b', 'c']

In [24]: index = pd.date_range('2021-7-1', periods=5, freq='B')  

In [25]: index
Out[25]: DatetimeIndex(['2021-07-01', '2021-07-02', '2021-07-05',
          '2021-07-06',
                        '2021-07-07'],
                       dtype='datetime64[ns]', freq='B')

In [26]: df = pd.DataFrame(a, columns=columns, index=index)  

In [27]: df
Out[27]:              a   b   c
         2021-07-01   0   1   2
         2021-07-02   3   4   5
         2021-07-05   6   7   8
         2021-07-06   9  10  11
         2021-07-07  12  13  14

Imports the pandas package.

Creates a list object out of the str object.

A pandas DatetimeIndex object is created that has a “business day” frequency and goes over five periods.

A DataFrame object is instantiated based on the ndarray object a with column labels and index values specified.

In principle, vectorization now works similarly to ndarray objects. One difference is that aggregation operations default to column-wise results:

In [28]: 2 * df  
Out[28]:              a   b   c
         2021-07-01   0   2   4
         2021-07-02   6   8  10
         2021-07-05  12  14  16
         2021-07-06  18  20  22
         2021-07-07  24  26  28

In [29]: df.sum()  
Out[29]: a    30
         b    35
         c    40
         dtype: int64

In [30]: np.mean(df)  
Out[30]: a    6.0
         b    7.0
         c    8.0
         dtype: float64

Calculates the scalar product for the DataFrame object (treated as a matrix).

Calculates the sum per column.

Calculates the mean per column.

Column-wise operations can be implemented by referencing the respective column names, either by the bracket notation or the dot notation:

In [31]: df['a'] + df['c']  
Out[31]: 2021-07-01     2
         2021-07-02     8
         2021-07-05    14
         2021-07-06    20
         2021-07-07    26
         Freq: B, dtype: int64

In [32]: 0.5 * df.a + 2 * df.b - df.c  
Out[32]: 2021-07-01     0.0
         2021-07-02     4.5
         2021-07-05     9.0
         2021-07-06    13.5
         2021-07-07    18.0
         Freq: B, dtype: float64

Calculates the element-wise sum over columns a and c.

Calculates a linear transform involving all three columns.

Similarly, conditions yielding Boolean results vectors and SQL-like selections based on such conditions are straightforward to implement:

In [33]: df['a'] > 5  
Out[33]: 2021-07-01    False
         2021-07-02    False
         2021-07-05     True
         2021-07-06     True
         2021-07-07     True
         Freq: B, Name: a, dtype: bool

In [34]: df[df['a'] > 5]  
Out[34]:              a   b   c
         2021-07-05   6   7   8
         2021-07-06   9  10  11
         2021-07-07  12  13  14

Which element in column a is greater than five?

Select all those rows where the element in column a is greater than five.

For a vectorized backtesting of trading strategies, comparisons between two columns or more are typical:

In [35]: df['c'] > df['b']  
Out[35]: 2021-07-01    True
         2021-07-02    True
         2021-07-05    True
         2021-07-06    True
         2021-07-07    True
         Freq: B, dtype: bool

In [36]: 0.15 * df.a + df.b > df.c  
Out[36]: 2021-07-01    False
         2021-07-02    False
         2021-07-05    False
         2021-07-06     True
         2021-07-07     True
         Freq: B, dtype: bool

For which date is the element in column c greater than in column b?

Condition comparing a linear combination of columns a and b with column c.

Vectorization with pandas is a powerful concept, in particular for the implementation of financial algorithms and the vectorized backtesting, as illustrated in the remainder of this chapter. For more on the basics of vectorization with pandas and financial examples, refer to Hilpisch (2018, ch. 5).

While NumPy brings general vectorization approaches to the numerical computing world of Python, pandas allows vectorization over time series data. This is really helpful for the implementation of financial algorithms and the backtesting of algorithmic trading strategies. By using this approach, you can expect concise code, as well as a faster code execution, in comparison to standard Python code, making use of for loops and similar idioms to accomplish the same goal.

Strategies Based on Simple Moving Averages

Trading based on simple moving averages (SMAs) is a decades old strategy that has its origins in the technical stock analysis world. Brock et al. (1992), for example, empirically investigate such strategies in systematic fashion. They write:

The term “technical analysis” is a general heading for a myriad of trading techniques….In this paper, we explore two of the simplest and most popular technical rules: moving average-oscillator and trading-range break (resistance and support levels). In the first method, buy and sell signals are generated by two moving averages, a long period, and a short period….Our study reveals that technical analysis helps to predict stock changes.

Getting into the Basics

This sub-section focuses on the basics of backtesting trading strategies that make use of two SMAs. The example to follow works with end-of-day (EOD) closing data for the EUR/USD exchange rate, as provided in the csv file under the EOD data file. The data in the data set is from the Refinitiv Eikon Data API and represents EOD values for the respective instruments (RICs):

In [37]: raw = pd.read_csv('http://hilpisch.com/pyalgo_eikon_eod_data.csv',
                            index_col=0, parse_dates=True).dropna()  

In [38]: raw.info()  
         <class 'pandas.core.frame.DataFrame'>
         DatetimeIndex: 2516 entries, 2010-01-04 to 2019-12-31
         Data columns (total 12 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   AAPL.O  2516 non-null   float64
          1   MSFT.O  2516 non-null   float64
          2   INTC.O  2516 non-null   float64
          3   AMZN.O  2516 non-null   float64
          4   GS.N    2516 non-null   float64
          5   SPY     2516 non-null   float64
          6   .SPX    2516 non-null   float64
          7   .VIX    2516 non-null   float64
          8   EUR=    2516 non-null   float64
          9   XAU=    2516 non-null   float64
          10  GDX     2516 non-null   float64
          11  GLD     2516 non-null   float64
         dtypes: float64(12)
         memory usage: 255.5 KB

In [39]: data = pd.DataFrame(raw['EUR='])  

In [40]: data.rename(columns={'EUR=': 'price'}, inplace=True)  

In [41]: data.info()  
         <class 'pandas.core.frame.DataFrame'>
         DatetimeIndex: 2516 entries, 2010-01-04 to 2019-12-31
         Data columns (total 1 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   price   2516 non-null   float64
         dtypes: float64(1)
         memory usage: 39.3 KB

Reads the data from the remotely stored CSV file.

Shows the meta information for the DataFrame object.

Transforms the Series object to a DataFrame object.

Renames the only column to price.

Shows the meta information for the new DataFrame object.

The calculation of SMAs is made simple by the rolling() method, in combination with a deferred calculation operation:

In [42]: data['SMA1'] = data['price'].rolling(42).mean()  

In [43]: data['SMA2'] = data['price'].rolling(252).mean()  

In [44]: data.tail()  
Out[44]:              price      SMA1      SMA2
         Date
         2019-12-24  1.1087  1.107698  1.119630
         2019-12-26  1.1096  1.107740  1.119529
         2019-12-27  1.1175  1.107924  1.119428
         2019-12-30  1.1197  1.108131  1.119333
         2019-12-31  1.1210  1.108279  1.119231

Creates a column with 42 days of SMA values. The first 41 values will be NaN.

Creates a column with 252 days of SMA values. The first 251 values will be NaN.

Prints the final five rows of the data set.

A visualization of the original time series data in combination with the SMAs best illustrates the results (see Figure 4-1):

In [45]: %matplotlib inline
         from pylab import mpl, plt
         plt.style.use('seaborn')
         mpl.rcParams['savefig.dpi'] = 300
         mpl.rcParams['font.family'] = 'serif'

In [46]: data.plot(title='EUR/USD | 42 & 252 days SMAs',
                   figsize=(10, 6));

The next step is to generate signals, or rather market positionings, based on the relationship between the two SMAs. The rule is to go long whenever the shorter SMA is above the longer one and vice versa. For our purposes, we indicate a long position by 1 and a short position by –1.

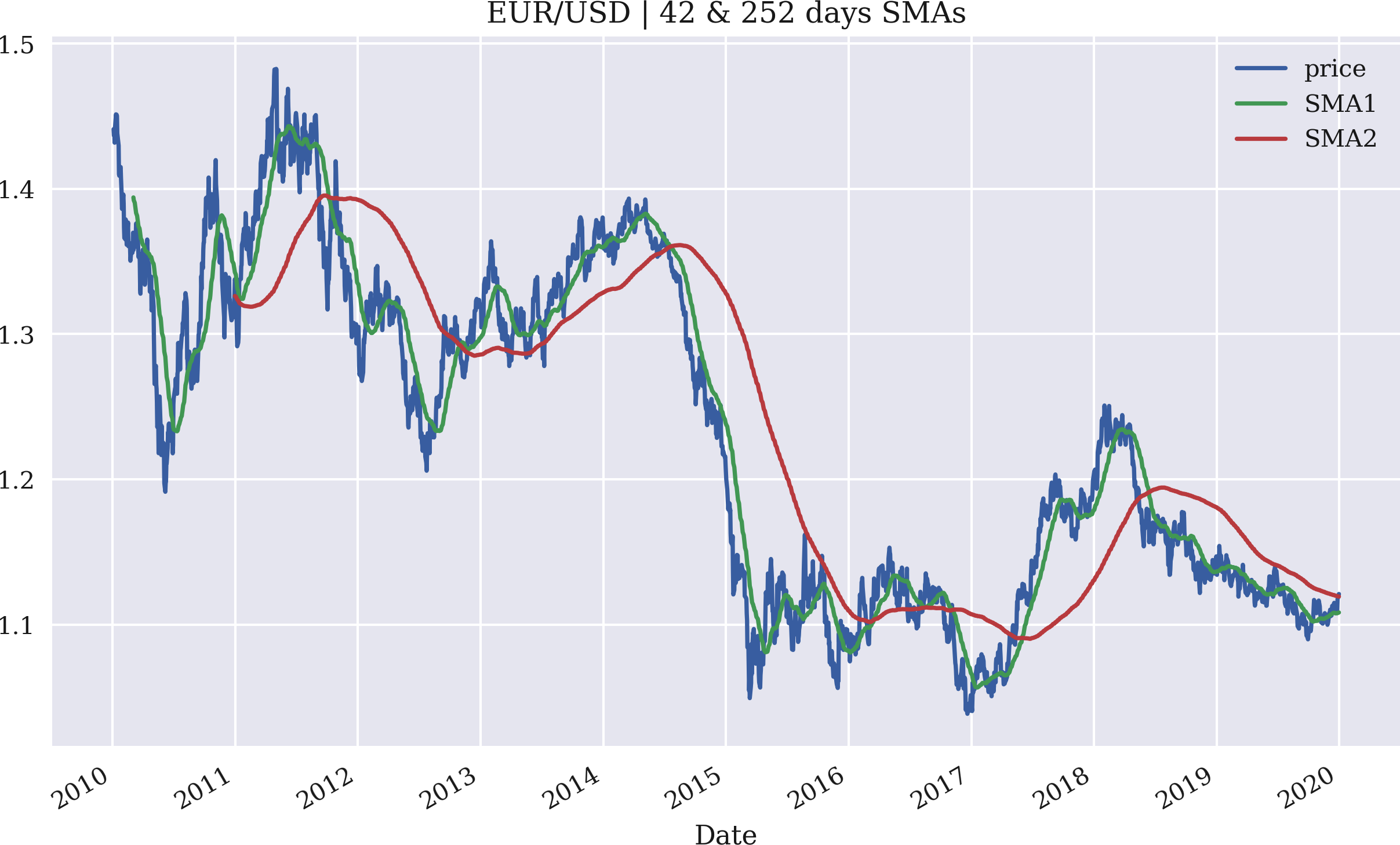
Figure 4-1. The EUR/USD exchange rate with two SMAs

Being able to directly compare two columns of the DataFrame object makes the implementation of the rule an affair of a single line of code only. The positioning over time is illustrated in Figure 4-2:

In [47]: data['position'] = np.where(data['SMA1'] > data['SMA2'],
                                     1, -1)  

In [48]: data.dropna(inplace=True)  

In [49]: data['position'].plot(ylim=[-1.1, 1.1],
                               title='Market Positioning',
                               figsize=(10, 6));  

Implements the trading rule in vectorized fashion. np.where() produces +1 for rows where the expression is True and -1 for rows where the expression is False.

Deletes all rows of the data set that contain at least one NaN value.

Plots the positioning over time.

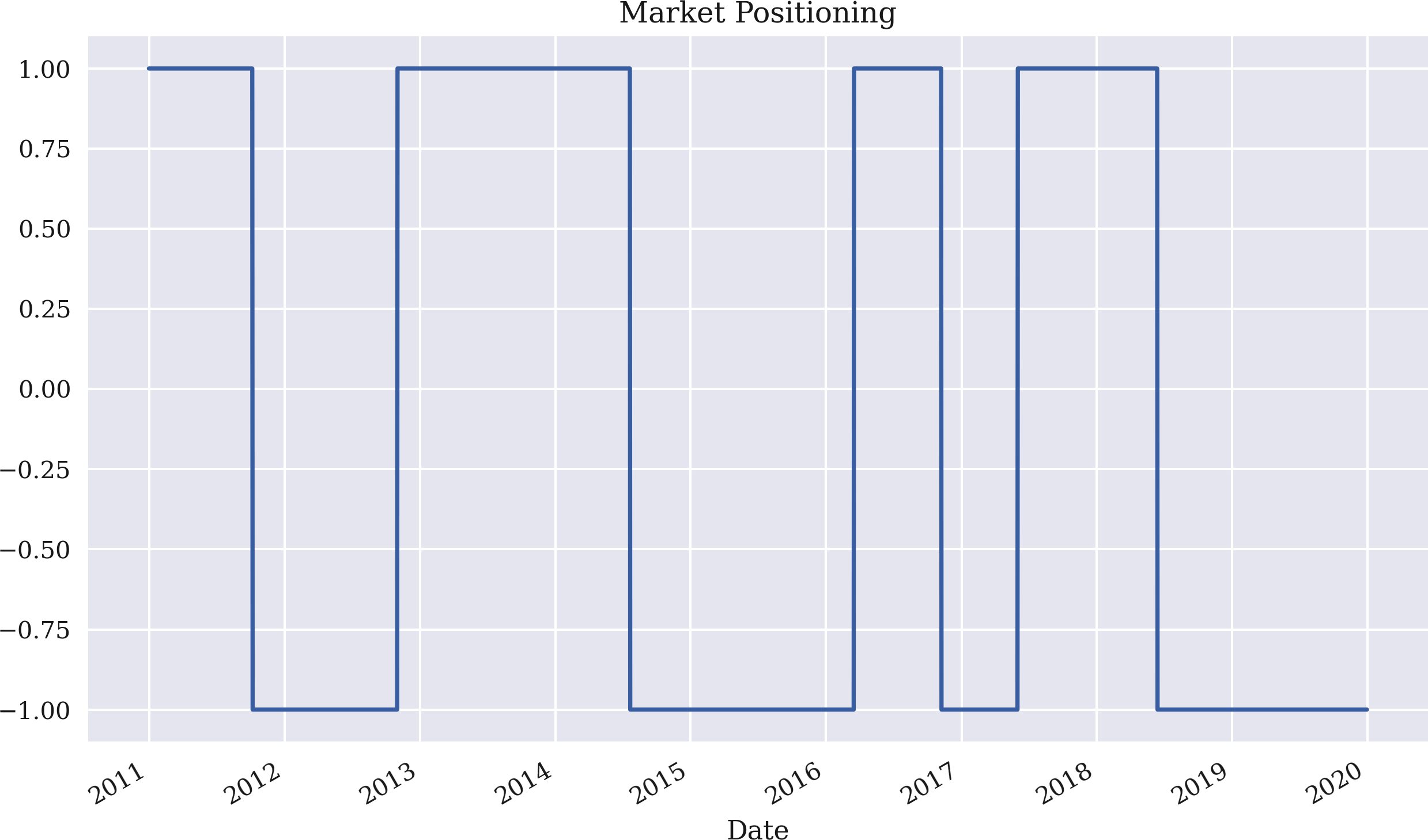
Figure 4-2. Market positioning based on the strategy with two SMAs

To calculate the performance of the strategy, calculate the log returns based on the original financial time series next. The code to do this is again rather concise due to vectorization. Figure 4-3 shows the histogram of the log returns:

In [50]: data['returns'] = np.log(data['price'] / data['price'].shift(1))  

In [51]: data['returns'].hist(bins=35, figsize=(10, 6));  

Calculates the log returns in vectorized fashion over the price column.

Plots the log returns as a histogram (frequency distribution).

To derive the strategy returns, multiply the position column—shifted by one trading day—with the returns column. Since log returns are additive, calculating the sum over the columns returns and strategy provides a first comparison of the performance of the strategy relative to the base investment itself.

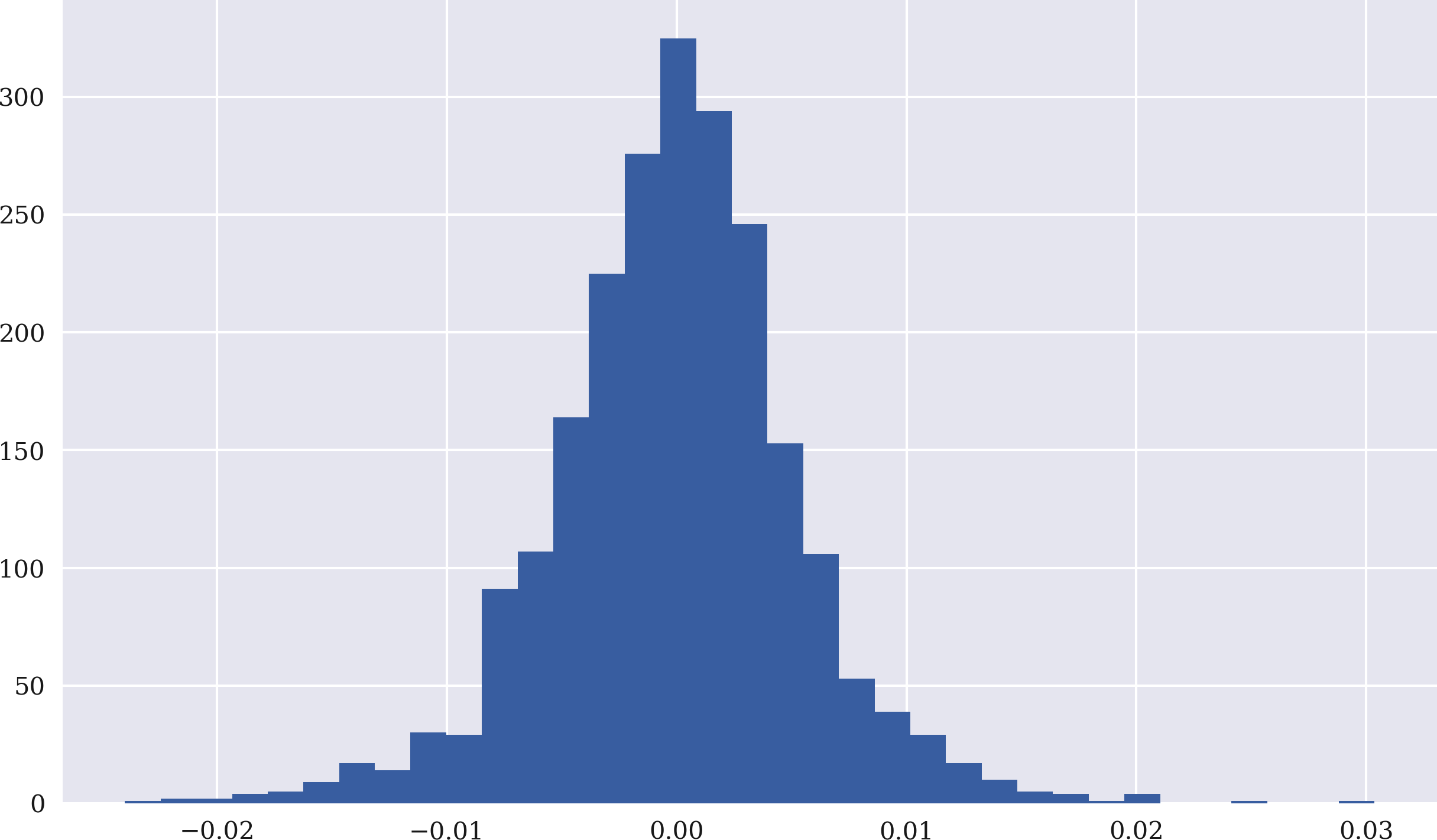
Figure 4-3. Frequency distribution of EUR/USD log returns

Comparing the returns shows that the strategy books a win over the passive benchmark investment:

In [52]: data['strategy'] = data['position'].shift(1) * data['returns']  

In [53]: data[['returns', 'strategy']].sum()  
Out[53]: returns    -0.176731
         strategy    0.253121
         dtype: float64

In [54]: data[['returns', 'strategy']].sum().apply(np.exp)  
Out[54]: returns     0.838006
         strategy    1.288039
         dtype: float64

Derives the log returns of the strategy given the positionings and market returns.

Sums up the single log return values for both the stock and the strategy (for illustration only).

Applies the exponential function to the sum of the log returns to calculate the gross performance.

Calculating the cumulative sum over time with cumsum and, based on this, the cumulative returns by applying the exponential function np.exp() gives a more comprehensive picture of how the strategy compares to the performance of the base financial instrument over time. Figure 4-4 shows the data graphically and illustrates the outperformance in this particular case:

In [55]: data[['returns', 'strategy']].cumsum(
                     ).apply(np.exp).plot(figsize=(10, 6));

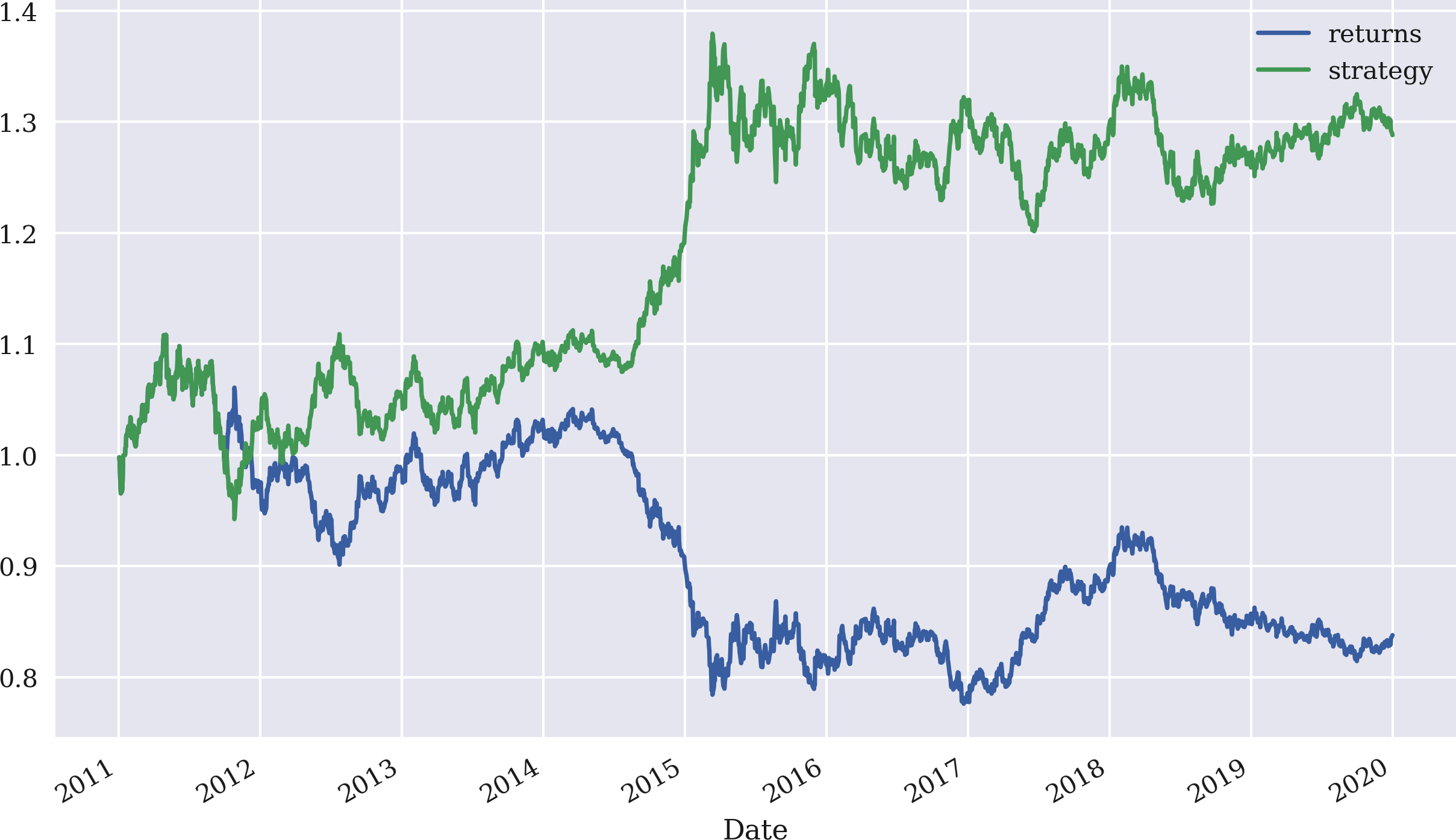
Figure 4-4. Gross performance of EUR/USD compared to the SMA-based strategy

Average, annualized risk-return statistics for both the stock and the strategy are easy to calculate:

In [56]: data[['returns', 'strategy']].mean() * 252  
Out[56]: returns    -0.019671
         strategy    0.028174
         dtype: float64

In [57]: np.exp(data[['returns', 'strategy']].mean() * 252) - 1  
Out[57]: returns    -0.019479
         strategy    0.028575
         dtype: float64

In [58]: data[['returns', 'strategy']].std() * 252 ** 0.5  
Out[58]: returns     0.085414
         strategy    0.085405
         dtype: float64

In [59]: (data[['returns', 'strategy']].apply(np.exp) - 1).std() * 252 ** 0.5  
Out[59]: returns     0.085405
         strategy    0.085373
         dtype: float64

Calculates the annualized mean return in both log and regular space.

Calculates the annualized standard deviation in both log and regular space.

Other risk statistics often of interest in the context of trading strategy performances are the maximum drawdown and the longest drawdown period. A helper statistic to use in this context is the cumulative maximum gross performance as calculated by the cummax() method applied to the gross performance of the strategy. Figure 4-5 shows the two time series for the SMA-based strategy:

In [60]: data['cumret'] = data['strategy'].cumsum().apply(np.exp)  

In [61]: data['cummax'] = data['cumret'].cummax()  

In [62]: data[['cumret', 'cummax']].dropna().plot(figsize=(10, 6));  

Defines a new column, cumret, with the gross performance over time.

Defines yet another column with the running maximum value of the gross performance.

Plots the two new columns of the DataFrame object.

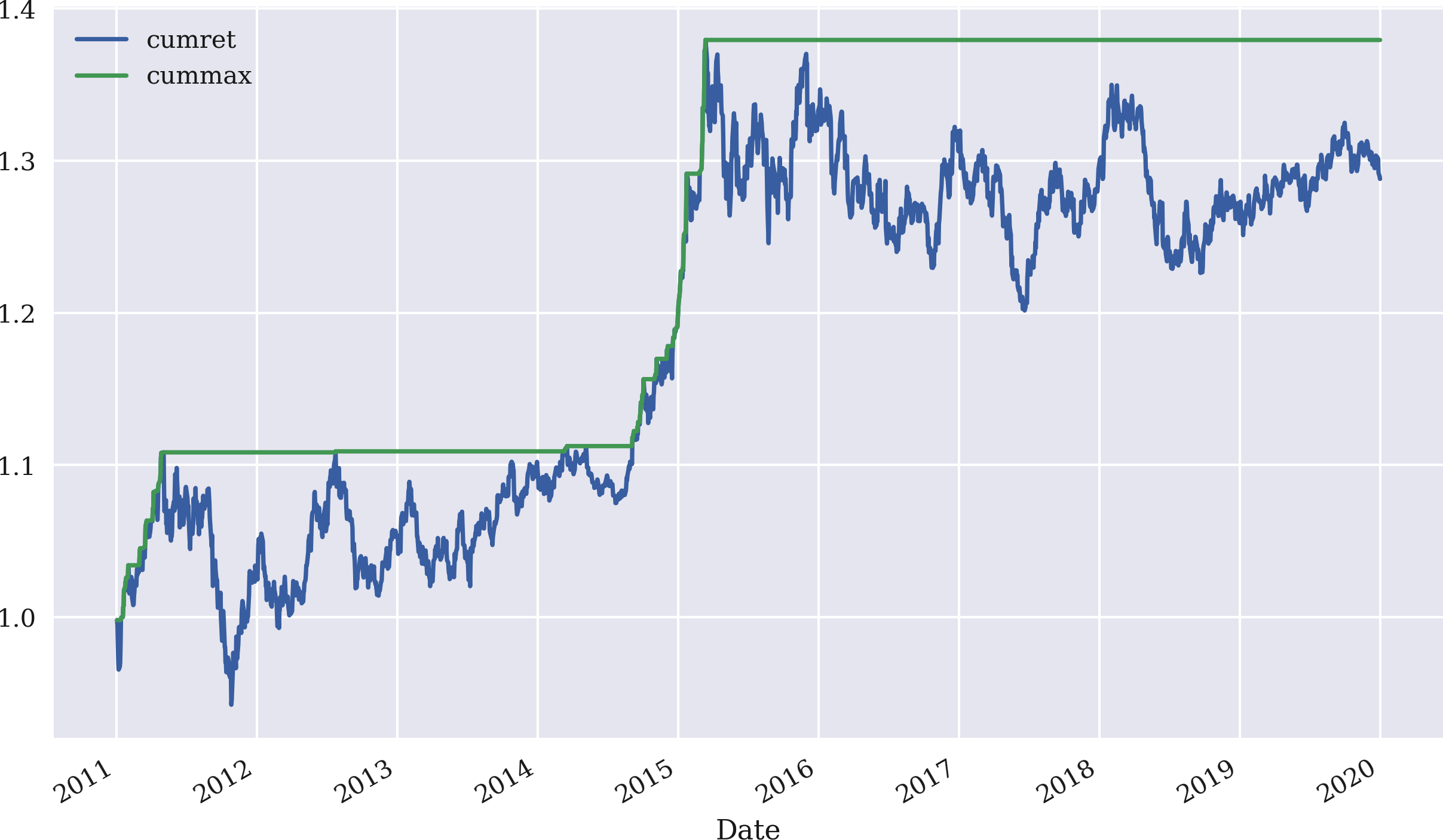
Figure 4-5. Gross performance and cumulative maximum performance of the SMA-based strategy

The maximum drawdown is then simply calculated as the maximum of the difference between the two relevant columns. The maximum drawdown in the example is about 18 percentage points:

In [63]: drawdown = data['cummax'] - data['cumret']  

In [64]: drawdown.max()  
Out[64]: 0.17779367070195917

Calculates the element-wise difference between the two columns.

Picks out the maximum value from all differences.

The determination of the longest drawdown period is a bit more involved. It requires those dates at which the gross performance equals its cumulative maximum (that is, where a new maximum is set). This information is stored in a temporary object. Then the differences in days between all such dates are calculated and the longest period is picked out. Such periods can be only one day long or more than 100 days. Here, the longest drawdown period lasts for 596 days—a pretty long period:²

In [65]: temp = drawdown[drawdown == 0]  

In [66]: periods = (temp.index[1:].to_pydatetime() -
                    temp.index[:-1].to_pydatetime())  

In [67]: periods[12:15]
Out[67]: array([datetime.timedelta(days=1), datetime.timedelta(days=1),
                datetime.timedelta(days=10)], dtype=object)

In [68]: periods.max()  
Out[68]: datetime.timedelta(days=596)

Where are the differences equal to zero?

Calculates the timedelta values between all index values.

Picks out the maximum timedelta value.

Vectorized backtesting with pandas is generally a rather efficient endeavor due to the capabilities of the package and the main DataFrame class. However, the interactive approach illustrated so far does not work well when one wishes to implement a larger backtesting program that, for example, optimizes the parameters of an SMA-based strategy. To this end, a more general approach is advisable.

pandas proves to be a powerful tool for the vectorized analysis of trading strategies. Many statistics of interest, such as log returns, cumulative returns, annualized returns and volatility, maximum drawdown, and maximum drawdown period, can in general be calculated by a single line or just a few lines of code. Being able to visualize results by a simple method call is an additional benefit.

Generalizing the Approach

“SMA Backtesting Class” presents a Python code that contains a class for the vectorized backtesting of SMA-based trading strategies. In a sense, it is a generalization of the approach introduced in the previous sub-section. It allows one to define an instance of the SMAVectorBacktester class by providing the following parameters:

• symbol: RIC (instrument data) to be used

• SMA1: for the time window in days for the shorter SMA

• SMA2: for the time window in days for the longer SMA

• start: for the start date of the data selection

• end: for the end date of the data selection

The application itself is best illustrated by an interactive session that makes use of the class. The example first replicates the backtest implemented previously based on EUR/USD exchange rate data. It then optimizes the SMA parameters for maximum gross performance. Based on the optimal parameters, it plots the resulting gross performance of the strategy compared to the base instrument over the relevant period of time:

In [69]: import SMAVectorBacktester as SMA  

In [70]: smabt = SMA.SMAVectorBacktester('EUR=', 42, 252,
                                         '2010-1-1', '2019-12-31')   

In [71]: smabt.run_strategy()  
Out[71]: (1.29, 0.45)

In [72]: %%time
         smabt.optimize_parameters((30, 50, 2),
                                   (200, 300, 2))  
         CPU times: user 3.76 s, sys: 15.8 ms, total: 3.78 s
         Wall time: 3.78 s

Out[72]: (array([ 48., 238.]), 1.5)

In [73]: smabt.plot_results()  

This imports the module as SMA.

An instance of the main class is instantiated.

Backtests the SMA-based strategy, given the parameters during instantiation.

The optimize_parameters() method takes as input parameter ranges with step sizes and determines the optimal combination by a brute force approach.

The plot_results() method plots the strategy performance compared to the benchmark instrument, given the currently stored parameter values (here from the optimization procedure).

The gross performance of the strategy with the original parametrization is 1.24 or 124%. The optimized strategy yields an absolute return of 1.44 or 144% for the parameter combination SMA1 = 48 and SMA2 = 238. Figure 4-6 shows the gross performance over time graphically, again compared to the performance of the base instrument, which represents the benchmark.

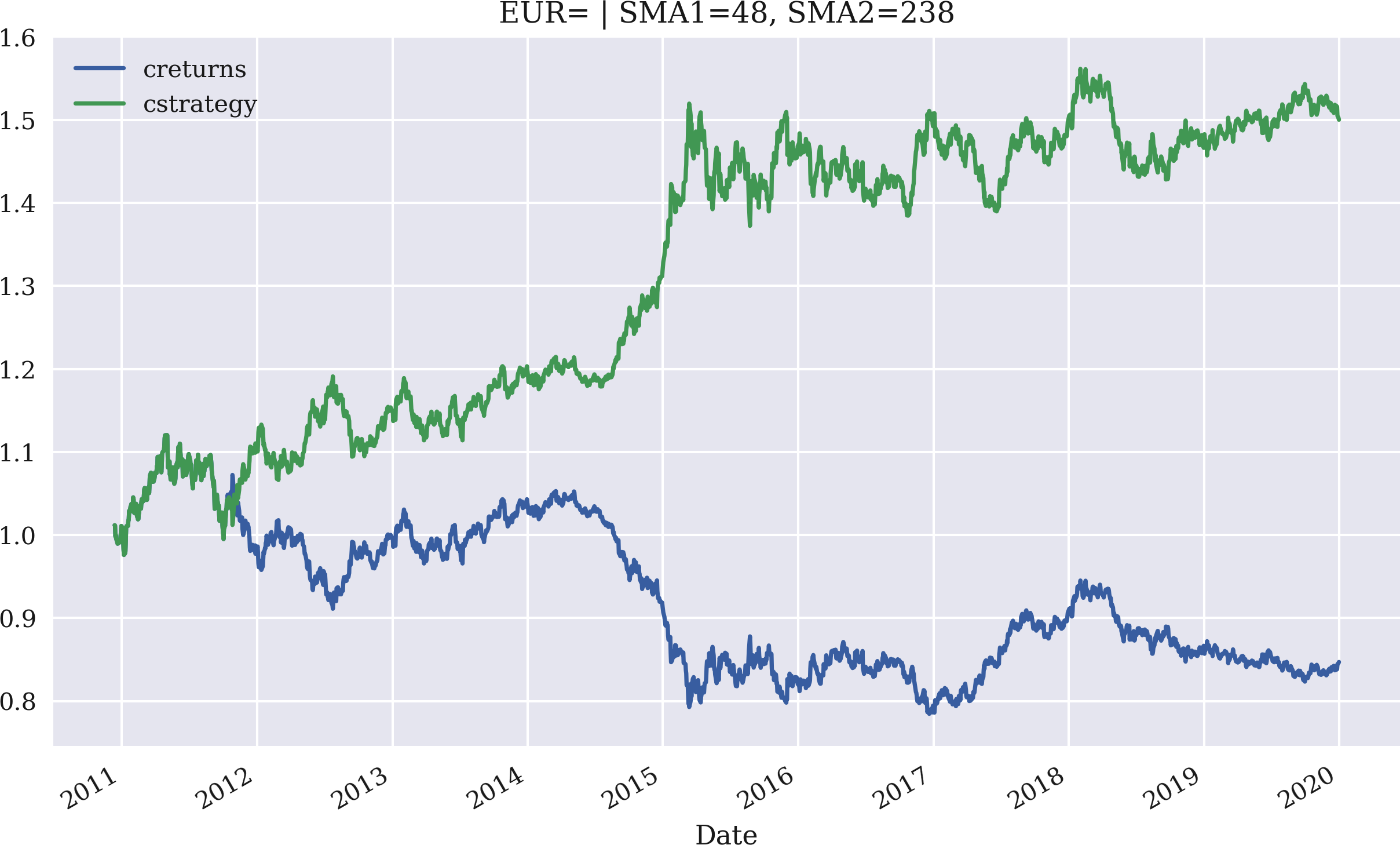
Figure 4-6. Gross performance of EUR/USD and the optimized SMA strategy

Strategies Based on Momentum

There are two basic types of momentum strategies. The first type is cross-sectional momentum strategies. Selecting from a larger pool of instruments, these strategies buy those instruments that have recently outperformed relative to their peers (or a benchmark) and sell those instruments that have underperformed. The basic idea is that the instruments continue to outperform and underperform, respectively—at least for a certain period of time. Jegadeesh and Titman (1993, 2001) and Chan et al. (1996) study these types of trading strategies and their potential sources of profit.

Cross-sectional momentum strategies have traditionally performed quite well. Jegadeesh and Titman (1993) write:

This paper documents that strategies which buy stocks that have performed well in the past and sell stocks that have performed poorly in the past generate significant positive returns over 3- to 12-month holding periods.

The second type is time series momentum strategies. These strategies buy those instruments that have recently performed well and sell those instruments that have recently performed poorly. In this case, the benchmark is the past returns of the instrument itself. Moskowitz et al. (2012) analyze this type of momentum strategy in detail across a wide range of markets. They write:

Rather than focus on the relative returns of securities in the cross-section, time series momentum focuses purely on a security’s own past return….Our finding of time series momentum in virtually every instrument we examine seems to challenge the “random walk” hypothesis, which in its most basic form implies that knowing whether a price went up or down in the past should not be informative about whether it will go up or down in the future.

Getting into the Basics

Consider end-of-day closing prices for the gold price in USD (XAU=):

In [74]: data = pd.DataFrame(raw['XAU='])

In [75]: data.rename(columns={'XAU=': 'price'}, inplace=True)

In [76]: data['returns'] = np.log(data['price'] / data['price'].shift(1))

The most simple time series momentum strategy is to buy the stock if the last return was positive and to sell it if it was negative. With NumPy and pandas this is easy to formalize; just take the sign of the last available return as the market position. Figure 4-7 illustrates the performance of this strategy. The strategy does significantly underperform the base instrument:

In [77]: data['position'] = np.sign(data['returns'])  

In [78]: data['strategy'] = data['position'].shift(1) * data['returns']  

In [79]: data[['returns', 'strategy']].dropna().cumsum(
                     ).apply(np.exp).plot(figsize=(10, 6));  

Defines a new column with the sign (that is, 1 or –1) of the relevant log return; the resulting values represent the market positionings (long or short).

Calculates the strategy log returns given the market positionings.

Plots and compares the strategy performance with the benchmark instrument.

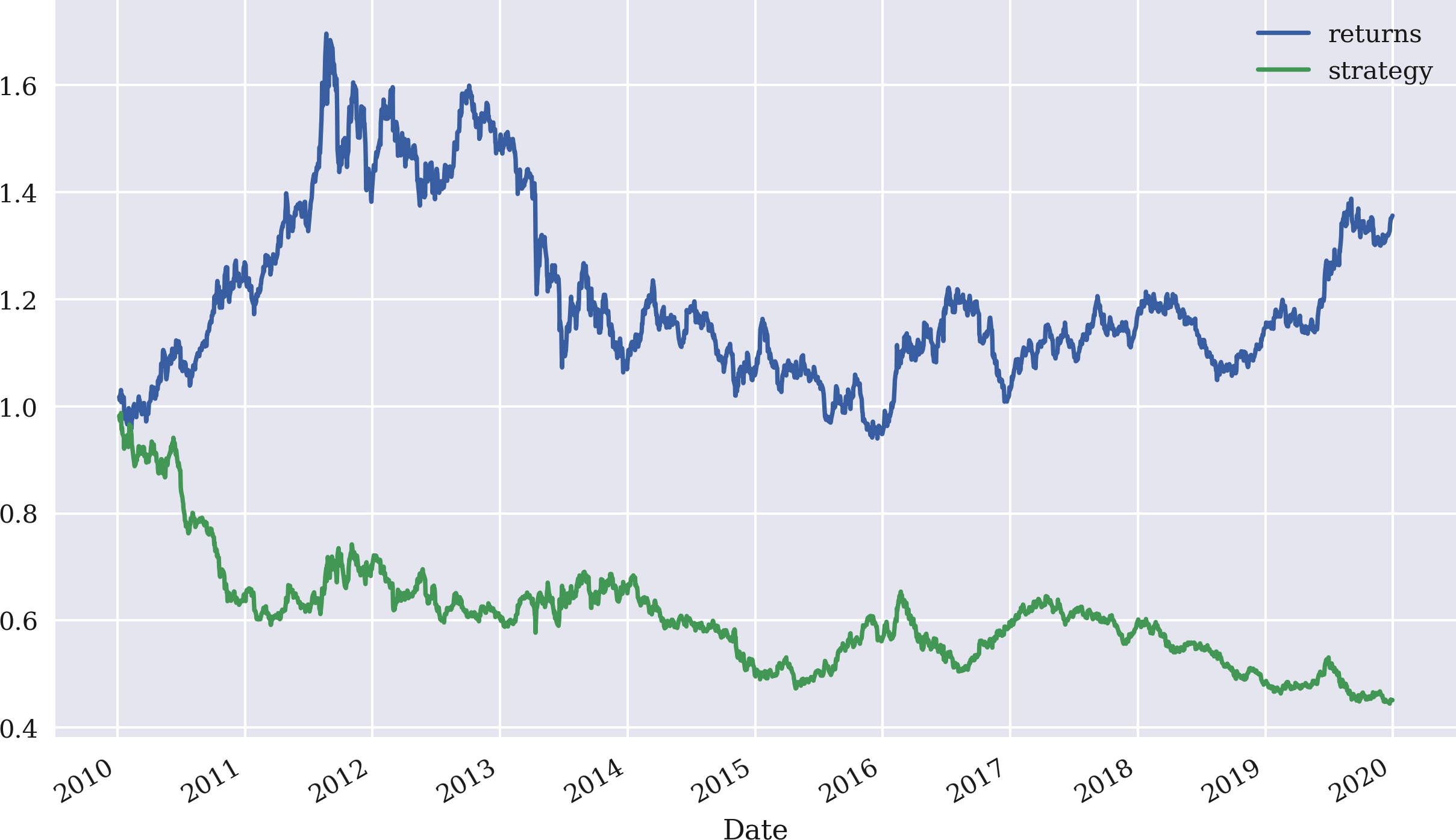
Figure 4-7. Gross performance of gold price (USD) and momentum strategy (last return only)

Using a rolling time window, the time series momentum strategy can be generalized to more than just the last return. For example, the average of the last three returns can be used to generate the signal for the positioning. Figure 4-8 shows that the strategy in this case does much better, both in absolute terms and relative to the base instrument:

In [80]: data['position'] = np.sign(data['returns'].rolling(3).mean())  

In [81]: data['strategy'] = data['position'].shift(1) * data['returns']

In [82]: data[['returns', 'strategy']].dropna().cumsum(
                 ).apply(np.exp).plot(figsize=(10, 6));

This time, the mean return over a rolling window of three days is taken.

However, the performance is quite sensitive to the time window parameter. Choosing, for example, the last two returns instead of three leads to a much worse performance, as shown in Figure 4-9.

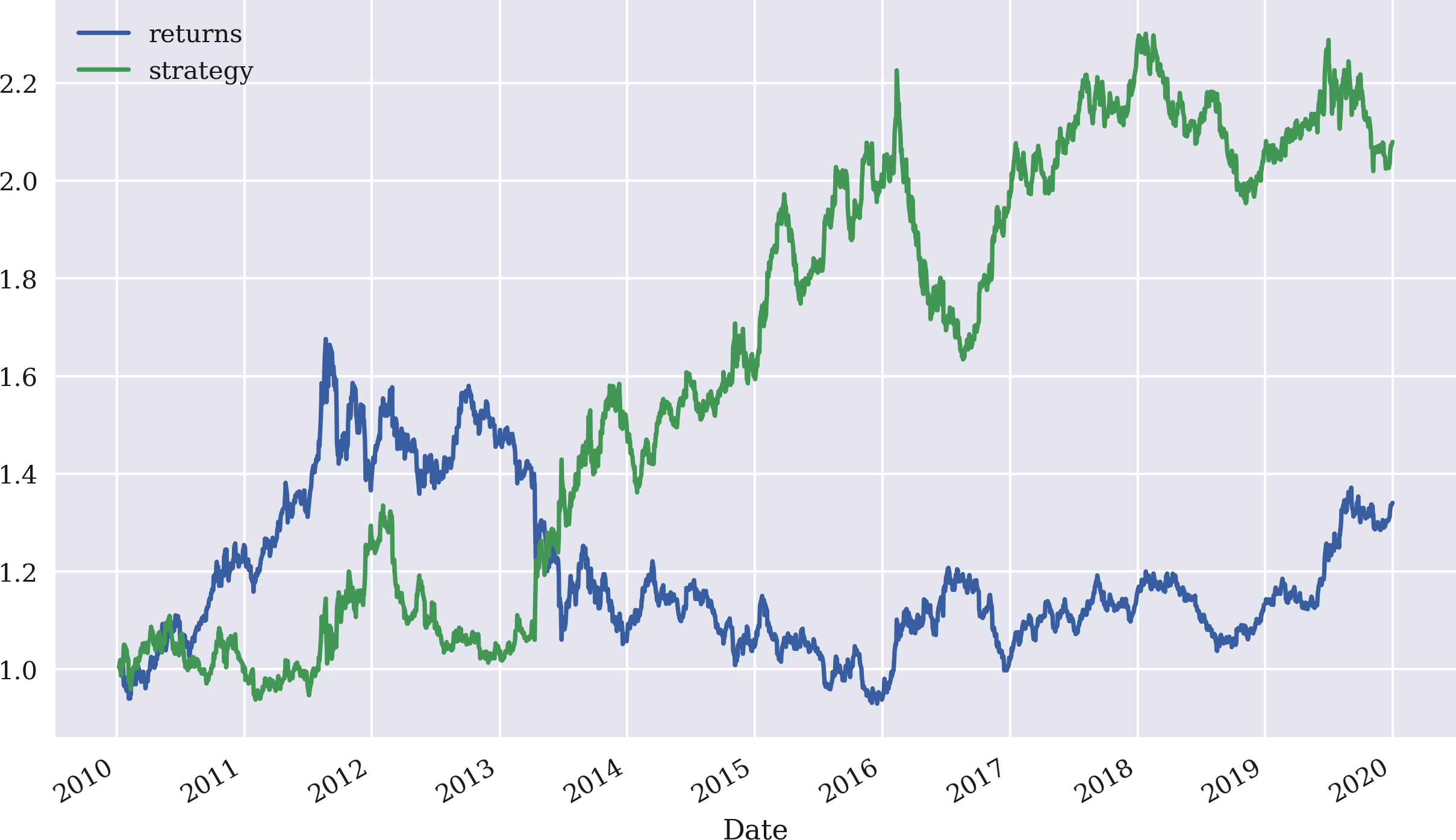
Figure 4-8. Gross performance of gold price (USD) and momentum strategy (last three returns)

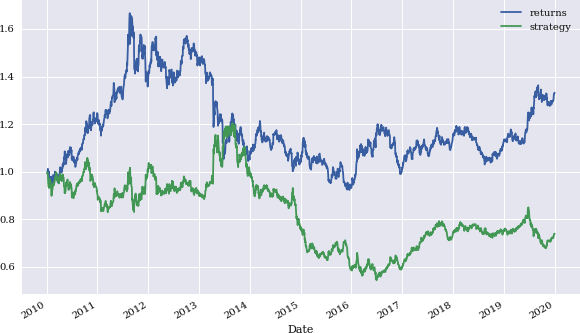
Figure 4-9. Gross performance of gold price (USD) and momentum strategy (last two returns)

Time series momentum might be expected intraday, as well. Actually, one would expect it to be more pronounced intraday than interday. Figure 4-10 shows the gross performance of five time series momentum strategies for one, three, five, seven, and nine return observations, respectively. The data used is intraday stock price data for Apple Inc., as retrieved from the Eikon Data API. The figure is based on the code that follows. Basically all strategies outperform the stock over the course of this intraday time window, although some only slightly:

In [83]: fn = '../data/AAPL_1min_05052020.csv'  
         # fn = '../data/SPX_1min_05052020.csv'  

In [84]: data = pd.read_csv(fn, index_col=0, parse_dates=True)  

In [85]: data.info()  
         <class 'pandas.core.frame.DataFrame'>
         DatetimeIndex: 241 entries, 2020-05-05 16:00:00 to 2020-05-05 20:00:00
         Data columns (total 6 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   HIGH    241 non-null    float64
          1   LOW     241 non-null    float64
          2   OPEN    241 non-null    float64
          3   CLOSE   241 non-null    float64
          4   COUNT   241 non-null    float64
          5   VOLUME  241 non-null    float64
         dtypes: float64(6)
         memory usage: 13.2 KB

In [86]: data['returns'] = np.log(data['CLOSE'] /
                                  data['CLOSE'].shift(1))  

In [87]: to_plot = ['returns']  

In [88]: for m in [1, 3, 5, 7, 9]:
             data['position_%d' % m] = np.sign(data['returns'].rolling(m).mean())  
             data['strategy_%d' % m] = (data['position_%d' % m].shift(1) *
                                        data['returns'])  
             to_plot.append('strategy_%d' % m)   

In [89]: data[to_plot].dropna().cumsum().apply(np.exp).plot(
             title='AAPL intraday 05. May 2020',
             figsize=(10, 6), style=['-', '--', '--', '--', '--', '--']);  

Reads the intraday data from a CSV file.

Calculates the intraday log returns.

Defines a list object to select the columns to be plotted later.

Derives positionings according to the momentum strategy parameter.

Calculates the resulting strategy log returns.

Appends the column name to the list object.

Plots all relevant columns to compare the strategies’ performances to the benchmark instrument’s performance.

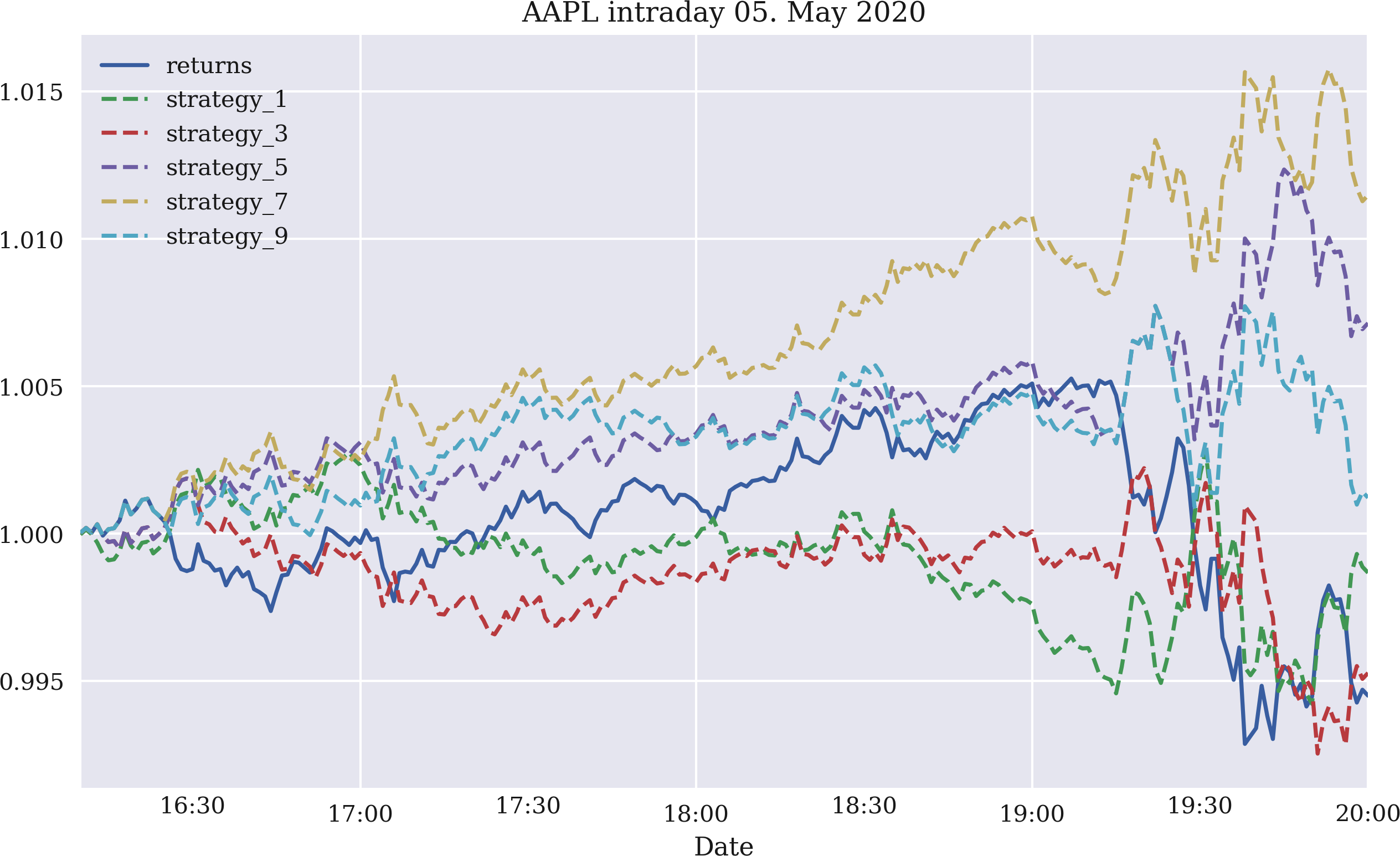
Figure 4-10. Gross intraday performance of the Apple stock and five momentum strategies (last one, three, five, seven, and nine returns)

Figure 4-11 shows the performance of the same five strategies for the S&P 500 index. Again, all five strategy configurations outperform the index and all show a positive return (before transaction costs).

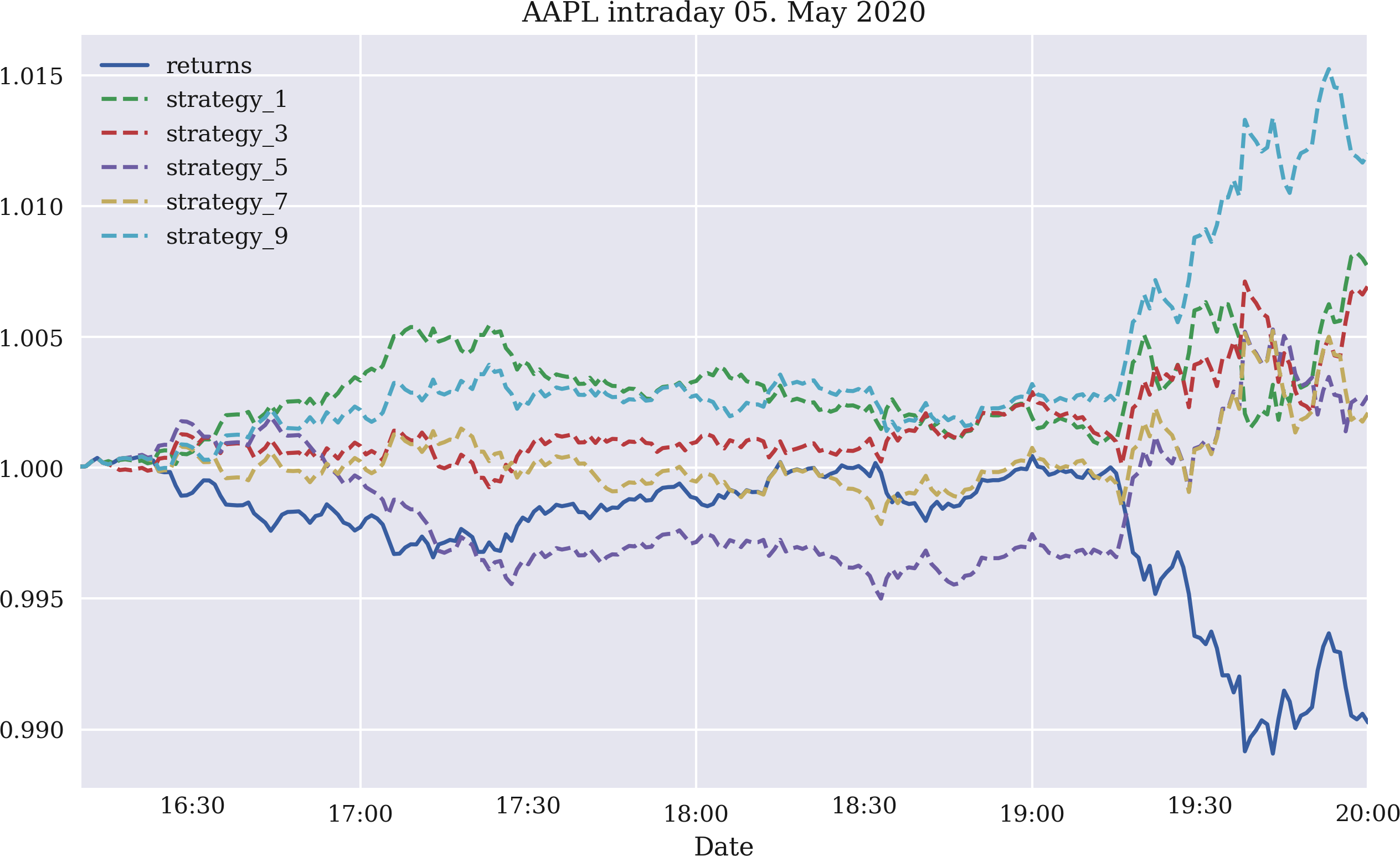
Figure 4-11. Gross intraday performance of the S&P 500 index and five momentum strategies (last one, three, five, seven, and nine returns)

Generalizing the Approach

“Momentum Backtesting Class” presents a Python module containing the MomVectorBacktester class, which allows for a bit more standardized backtesting of momentum-based strategies. The class has the following attributes:

• symbol: RIC (instrument data) to be used

• start: for the start date of the data selection

• end: for the end date of the data selection

• amount: for the initial amount to be invested

• tc: for the proportional transaction costs per trade

Compared to the SMAVectorBacktester class, this one introduces two important generalizations: the fixed amount to be invested at the beginning of the backtesting period and proportional transaction costs to get closer to market realities cost-wise. In particular, the addition of transaction costs is important in the context of time series momentum strategies that often lead to a large number of transactions over time.

The application is as straightforward and convenient as before. The example first replicates the results from the interactive session before, but this time with an initial investment of 10,000 USD. Figure 4-12 visualizes the performance of the strategy, taking the mean of the last three returns to generate signals for the positioning. The second case covered is one with proportional transaction costs of 0.1% per trade. As Figure 4-13 illustrates, even small transaction costs deteriorate the performance significantly in this case. The driving factor in this regard is the relatively high frequency of trades that the strategy requires:

In [90]: import MomVectorBacktester as Mom  

In [91]: mombt = Mom.MomVectorBacktester('XAU=', '2010-1-1',
                                         '2019-12-31', 10000, 0.0)  

In [92]: mombt.run_strategy(momentum=3)  
Out[92]: (20797.87, 7395.53)

In [93]: mombt.plot_results()
In [94]: mombt = Mom.MomVectorBacktester('XAU=', '2010-1-1',
                                         '2019-12-31', 10000, 0.001)  

In [95]: mombt.run_strategy(momentum=3)  
Out[95]: (10749.4, -2652.93)

In [96]: mombt.plot_results()

Imports the module as Mom

Instantiates an object of the backtesting class defining the starting capital to be 10,000 USD and the proportional transaction costs to be zero.

Backtests the momentum strategy based on a time window of three days: the strategy outperforms the benchmark passive investment.

This time, proportional transaction costs of 0.1% are assumed per trade.

In that case, the strategy basically loses all the outperformance.

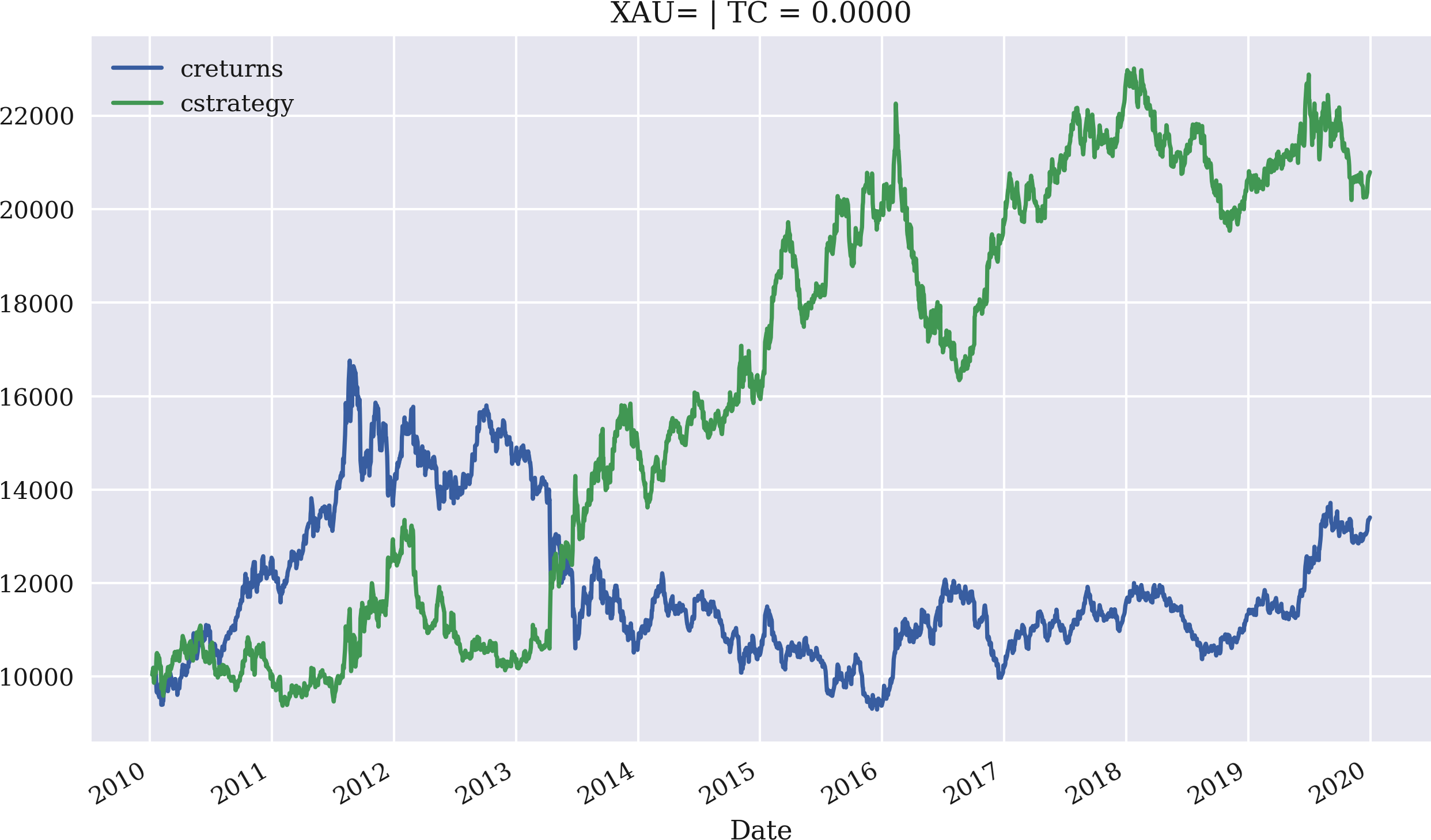
Figure 4-12. Gross performance of the gold price (USD) and the momentum strategy (last three returns, no transaction costs)

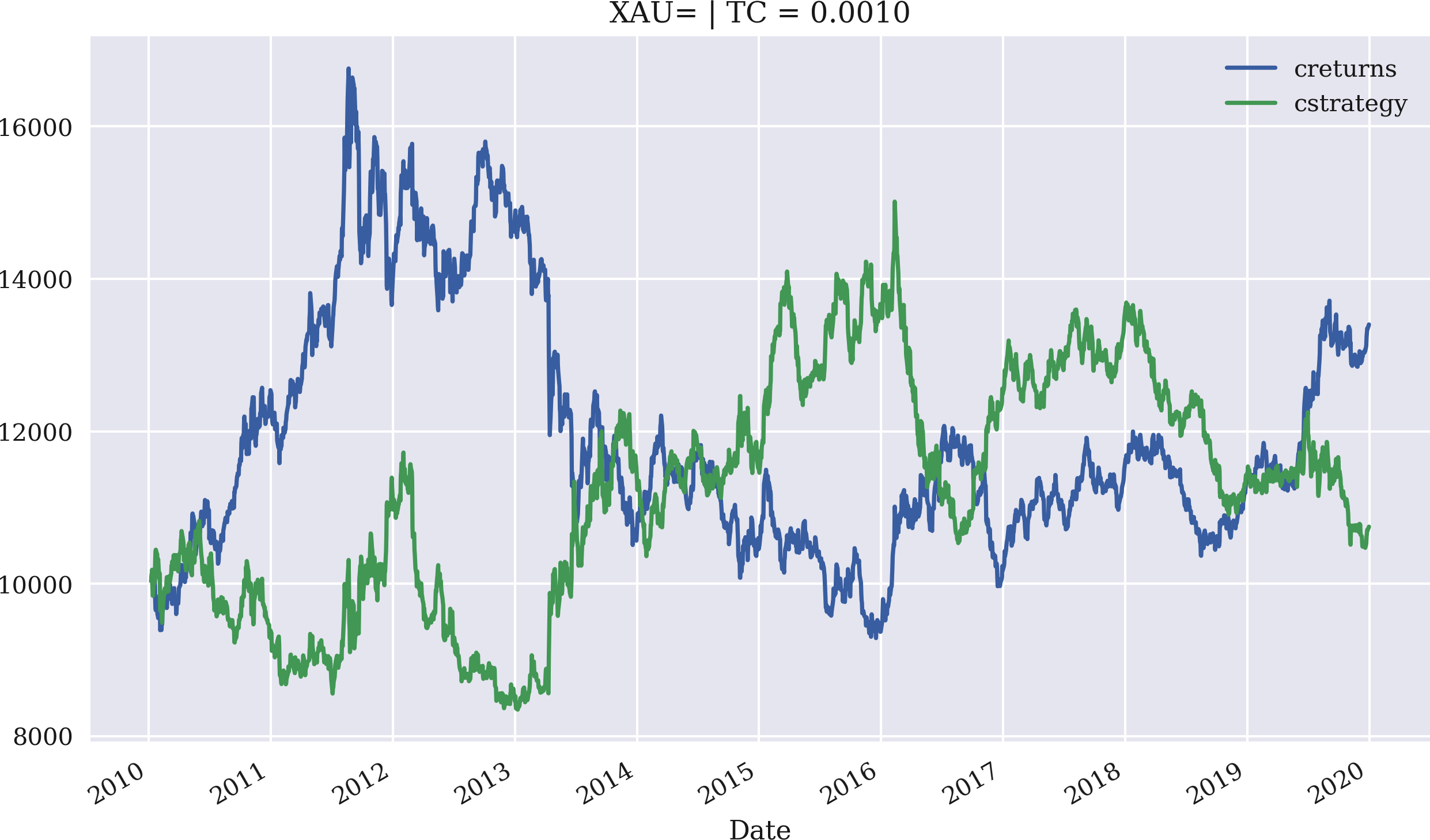
Figure 4-13. Gross performance of the gold price (USD) and the momentum strategy (last three returns, transaction costs of 0.1%)

Strategies Based on Mean Reversion

Roughly speaking, mean-reversion strategies rely on a reasoning that is the opposite of momentum strategies. If a financial instrument has performed “too well” relative to its trend, it is shorted, and vice versa. To put it differently, while (time series) momentum strategies assume a positive correlation between returns, mean-reversion strategies assume a negative correlation. Balvers et al. (2000) write:

Mean reversion refers to a tendency of asset prices to return to a trend path.

Working with a simple moving average (SMA) as a proxy for a “trend path,” a mean-reversion strategy in, say, the EUR/USD exchange rate can be backtested in a similar fashion as the backtests of the SMA- and momentum-based strategies. The idea is to define a threshold for the distance between the current stock price and the SMA, which signals a long or short position.

Getting into the Basics

The examples that follow are for two different financial instruments for which one would expect significant mean reversion since they are both based on the gold price:

• GLD is the symbol for SPDR Gold Shares, which is the largest physically backed exchange traded fund (ETF) for gold (cf. SPDR Gold Shares home page).

• GDX is the symbol for the VanEck Vectors Gold Miners ETF, which invests in equity products to track the NYSE Arca Gold Miners Index (cf. VanEck Vectors Gold Miners overview page).

The example starts with GDX and implements a mean-reversion strategy on the basis of an SMA of 25 days and a threshold value of 3.5 for the absolute deviation of the current price to deviate from the SMA to signal a positioning. Figure 4-14 shows the differences between the current price of GDX and the SMA, as well as the positive and negative threshold value to generate sell and buy signals, respectively:

In [97]: data = pd.DataFrame(raw['GDX'])

In [98]: data.rename(columns={'GDX': 'price'}, inplace=True)

In [99]: data['returns'] = np.log(data['price'] /
                                  data['price'].shift(1))

In [100]: SMA = 25  

In [101]: data['SMA'] = data['price'].rolling(SMA).mean()  

In [102]: threshold = 3.5  

In [103]: data['distance'] = data['price'] - data['SMA']  

In [104]: data['distance'].dropna().plot(figsize=(10, 6), legend=True)  
          plt.axhline(threshold, color='r')
          plt.axhline(-threshold, color='r')
          plt.axhline(0, color='r');

The SMA parameter is defined…

…and SMA (“trend path”) is calculated.

The threshold for the signal generation is defined.

The distance is calculated for every point in time.

The distance values are plotted.

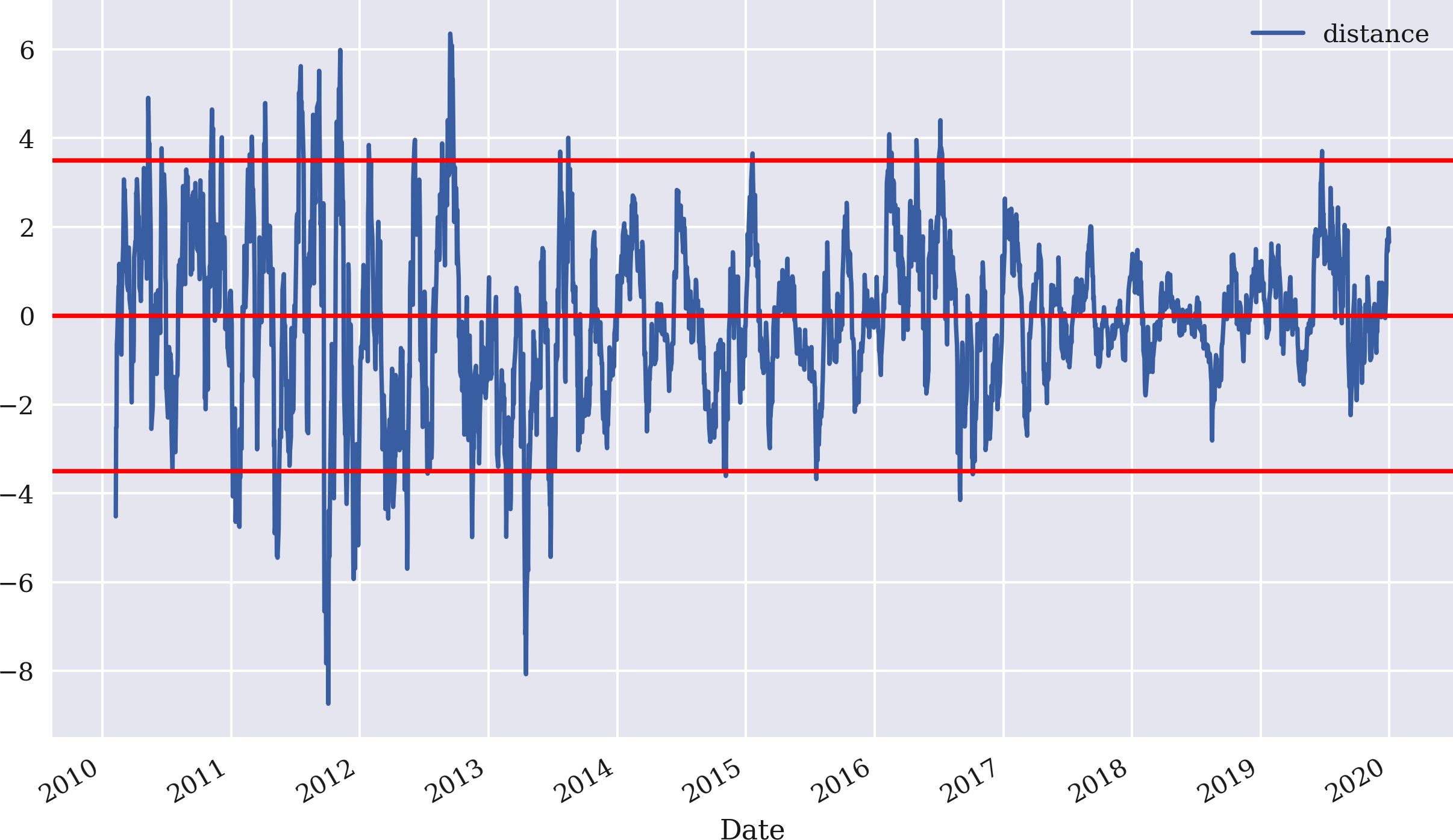
Figure 4-14. Difference between current price of GDX and SMA, as well as threshold values for generating mean-reversion signals

Based on the differences and the fixed threshold values, positionings can again be derived in vectorized fashion. Figure 4-15 shows the resulting positionings:

In [105]: data['position'] = np.where(data['distance'] > threshold,
                                      -1, np.nan)  

In [106]: data['position'] = np.where(data['distance'] < -threshold,
                                      1, data['position'])  

In [107]: data['position'] = np.where(data['distance'] *
                      data['distance'].shift(1) < 0, 0, data['position'])  

In [108]: data['position'] = data['position'].ffill().fillna(0)  

In [109]: data['position'].iloc[SMA:].plot(ylim=[-1.1, 1.1],
                                         figsize=(10, 6));  

If the distance value is greater than the threshold value, go short (set –1 in the new column position), otherwise set NaN.

If the distance value is lower than the negative threshold value, go long (set 1), otherwise keep the column position unchanged.

If there is a change in the sign of the distance value, go market neutral (set 0), otherwise keep the column position unchanged.

Forward fill all NaN positions with the previous values; replace all remaining NaN values by 0.

Plot the resulting positionings from the index position SMA on.

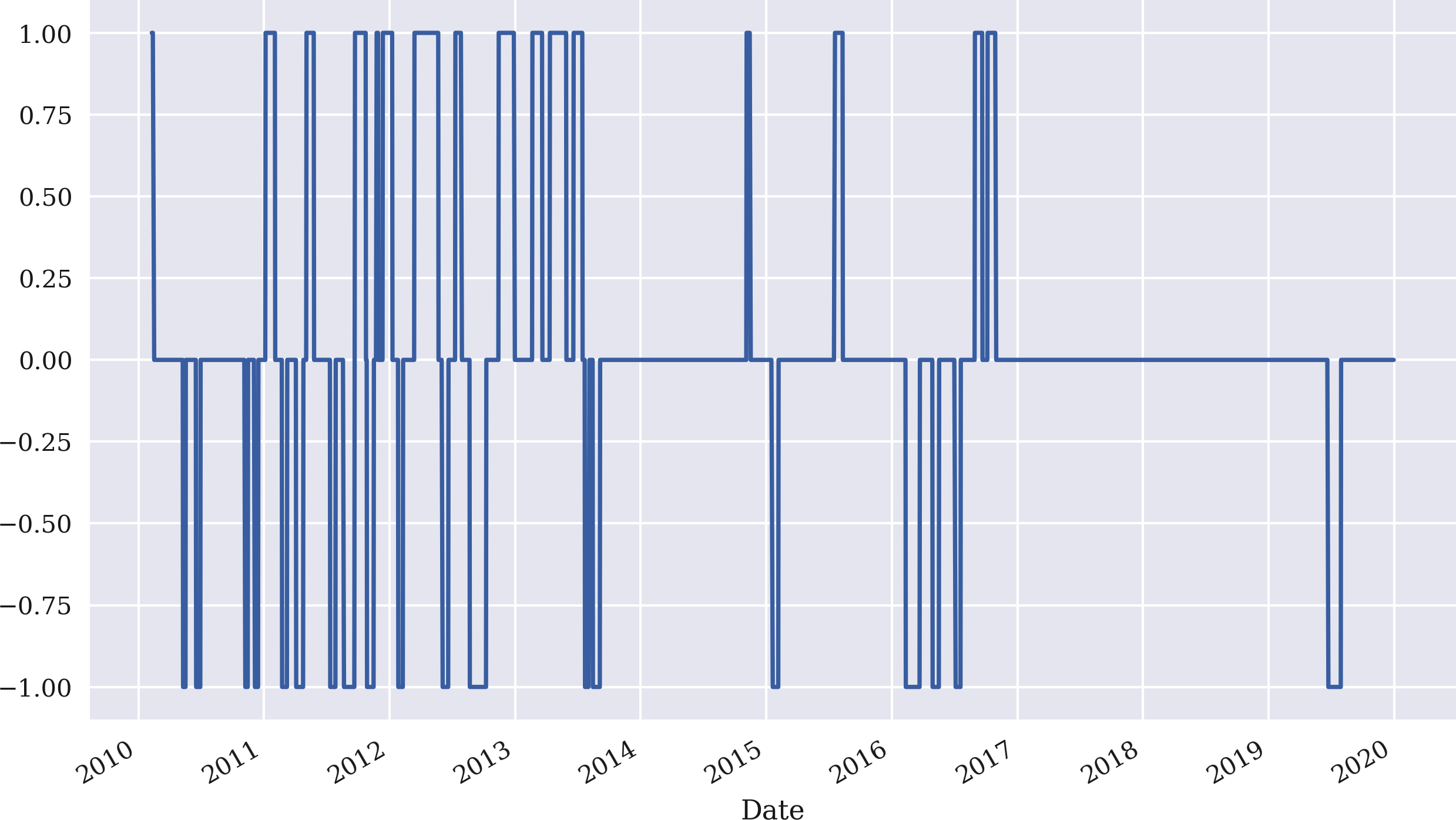
Figure 4-15. Positionings generated for GDX based on the mean-reversion strategy

The final step is to derive the strategy returns that are shown in Figure 4-16. The strategy outperforms the GDX ETF by quite a margin, although the particular parametrization leads to long periods with a neutral position (neither long or short). These neutral positions are reflected in the flat parts of the strategy curve in Figure 4-16:

In [110]: data['strategy'] = data['position'].shift(1) * data['returns']

In [111]: data[['returns', 'strategy']].dropna().cumsum(
                  ).apply(np.exp).plot(figsize=(10, 6));

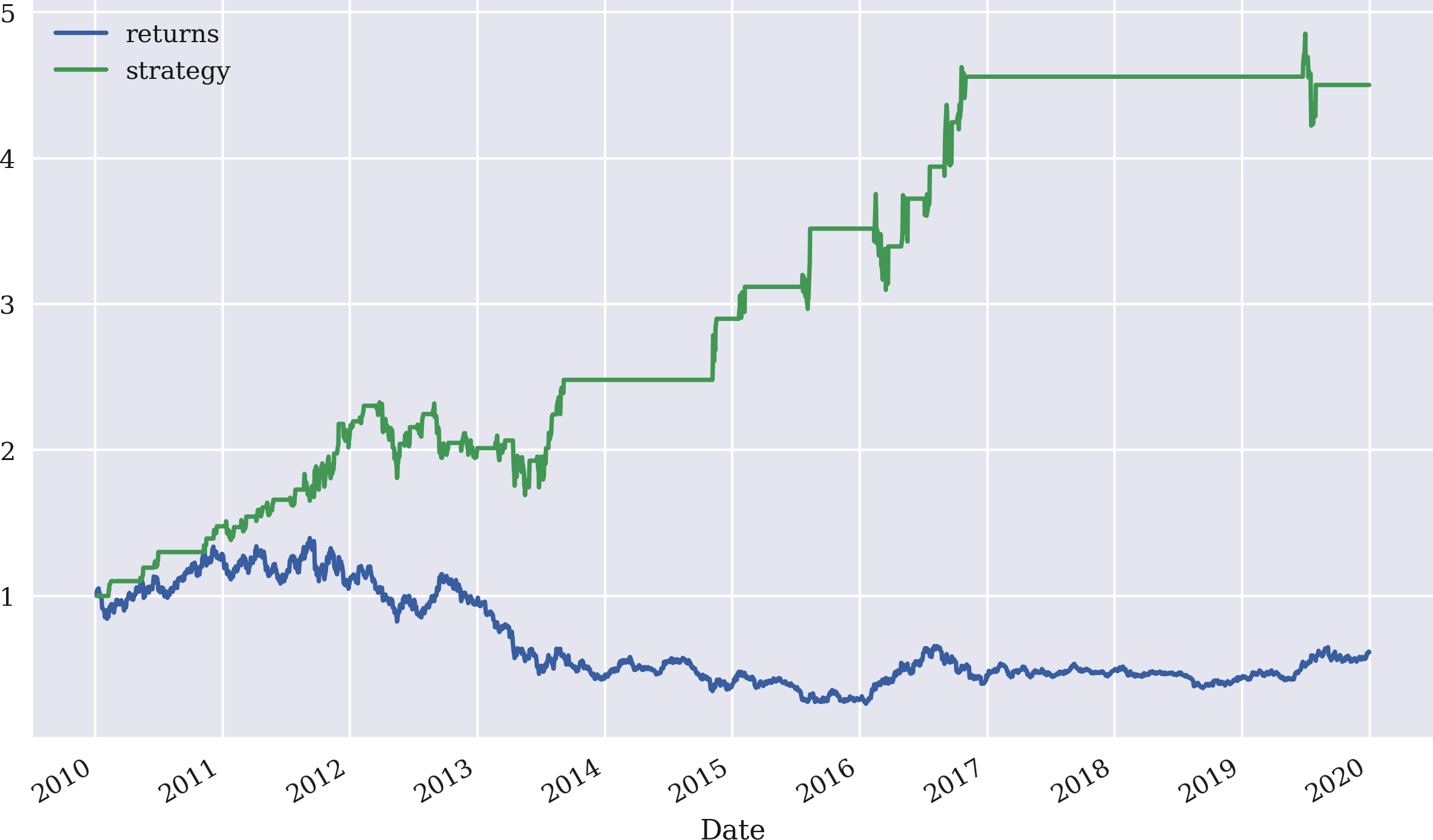
Figure 4-16. Gross performance of the GDX ETF and the mean-reversion strategy (SMA = 25, threshold = 3.5)

Generalizing the Approach

As before, the vectorized backtesting is more efficient to implement based on a respective Python class. The class MRVectorBacktester presented in “Mean Reversion Backtesting Class” inherits from the MomVectorBacktester class and just replaces the run_strategy() method to accommodate for the specifics of the mean-reversion strategy.

The example now uses GLD and sets the proportional transaction costs to 0.1%. The initial amount to invest is again set to 10,000 USD. The SMA is 43 this time, and the threshold value is set to 7.5. Figure 4-17 shows the performance of the mean-reversion strategy compared to the GLD ETF:

In [112]: import MRVectorBacktester as MR  

In [113]: mrbt = MR.MRVectorBacktester('GLD', '2010-1-1', '2019-12-31',
                                       10000, 0.001)  

In [114]: mrbt.run_strategy(SMA=43, threshold=7.5)  
Out[114]: (13542.15, 646.21)

In [115]: mrbt.plot_results()  

Imports the module as MR.

Instantiates an object of the MRVectorBacktester class with 10,000 USD initial capital and 0.1% proportional transaction costs per trade; the strategy significantly outperforms the benchmark instrument in this case.

Backtests the mean-reversion strategy with an SMA value of 43 and a threshold value of 7.5.

Plots the cumulative performance of the strategy against the base instrument.

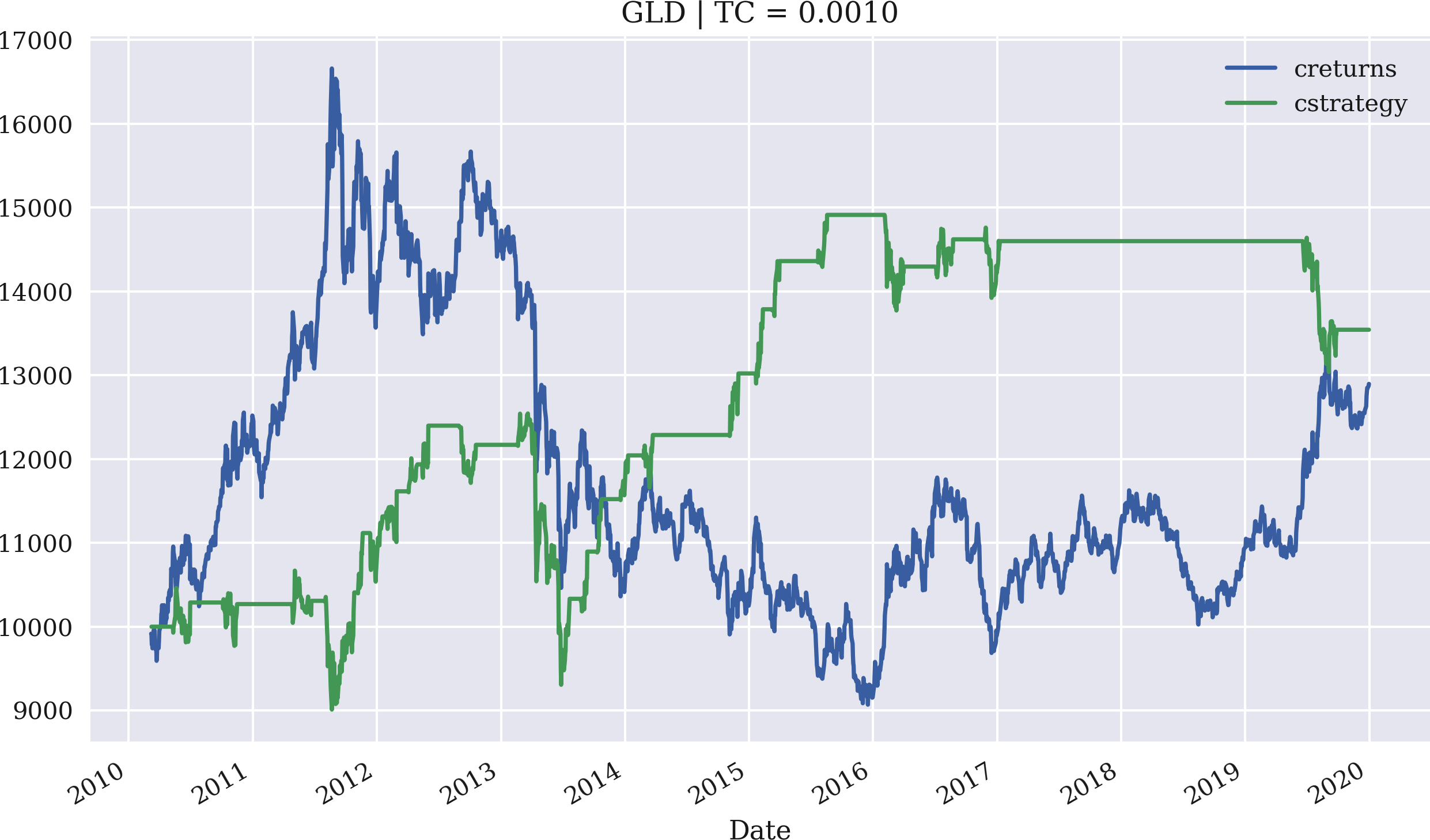
Figure 4-17. Gross performance of the GLD ETF and the mean-reversion strategy (SMA = 43, threshold = 7.5, transaction costs of 0.1%)

Data Snooping and Overfitting

The emphasis in this chapter, as well as in the rest of this book, is on the technological implementation of important concepts in algorithmic trading by using Python. The strategies, parameters, data sets, and algorithms used are sometimes arbitrarily chosen and sometimes purposefully chosen to make a certain point. Without a doubt, when discussing technical methods applied to finance, it is more exciting and motivating to see examples that show “good results,” even if they might not generalize on other financial instruments or time periods, for example.

The ability to show examples with good results often comes at the cost of data snooping. According to White (2000), data snooping can be defined as follows:

Data snooping occurs when a given set of data is used more than once for purposes of inference or model selection.

In other words, a certain approach might be applied multiple or even many times on the same data set to arrive at satisfactory numbers and plots. This, of course, is intellectually dishonest in trading strategy research because it pretends that a trading strategy has some economic potential that might not be realistic in a real-world context. Because the focus of this book is the use of Python as a programming language for algorithmic trading, the data snooping approach might be justifiable. This is in analogy to a mathematics book which, by way of an example, solves an equation that has a unique solution that can be easily identified. In mathematics, such straightforward examples are rather the exception than the rule, but they are nevertheless frequently used for didactical purposes.

Another problem that arises in this context is overfitting. Overfitting in a trading context can be described as follows (see the Man Institute on Overfitting):

Overfitting is when a model describes noise rather than signal. The model may have good performance on the data on which it was tested, but little or no predictive power on new data in the future. Overfitting can be described as finding patterns that aren’t actually there. There is a cost associated with overfitting—an overfitted strategy will underperform in the future.

Even a simple strategy, such as the one based on two SMA values, allows for the backtesting of thousands of different parameter combinations. Some of those combinations are almost certain to show good performance results. As Bailey et al. (2015) discuss in detail, this easily leads to backtest overfitting with the people responsible for the backtesting often not even being aware of the problem. They point out:

Recent advances in algorithmic research and high-performance computing have made it nearly trivial to test millions and billions of alternative investment strategies on a finite dataset of financial time series….[I]t is common practice to use this computational power to calibrate the parameters of an investment strategy in order to maximize its performance. But because the signal-to-noise ratio is so weak, often the result of such calibration is that parameters are chosen to profit from past noise rather than future signal. The outcome is an overfit backtest.

The problem of the validity of empirical results, in a statistical sense, is of course not constrained to strategy backtesting in a financial context.

Ioannidis (2005), referring to medical publications, emphasizes probabilistic and statistical considerations when judging the reproducibility and validity of research results:

There is increasing concern that in modern research, false findings may be the majority or even the vast majority of published research claims. However, this should not be surprising. It can be proven that most claimed research findings are false….As has been shown previously, the probability that a research finding is indeed true depends on the prior probability of it being true (before doing the study), the statistical power of the study, and the level of statistical significance.

Against this background, if a trading strategy in this book is shown to perform well given a certain data set, combination of parameters, and maybe a specific machine learning algorithm, this neither constitutes any kind of recommendation for the particular configuration nor allows it to draw more general conclusions about the quality and performance potential of the strategy configuration at hand.

You are, of course, encouraged to use the code and examples presented in this book to explore your own algorithmic trading strategy ideas and to implement them in practice based on your own backtesting results, validations, and conclusions. After all, proper and diligent strategy research is what financial markets will compensate for, not brute-force driven data snooping and overfitting.

Conclusions

Vectorization is a powerful concept in scientific computing, as well as for financial analytics, in the context of the backtesting of algorithmic trading strategies. This chapter introduces vectorization both with NumPy and pandas and applies it to backtest three types of trading strategies: strategies based on simple moving averages, momentum, and mean reversion. The chapter admittedly makes a number of simplifying assumptions, and a rigorous backtesting of trading strategies needs to take into account more factors that determine trading success in practice, such as data issues, selection issues, avoidance of overfitting, or market microstructure elements. However, the major goal of the chapter is to focus on the concept of vectorization and what it can do in algorithmic trading from a technological and implementation point of view. With regard to all concrete examples and results presented, the problems of data snooping, overfitting, and statistical significance need to be considered.

References and Further Resources

For the basics of vectorization with NumPy and pandas, refer to these books:

• McKinney, Wes. 2017. Python for Data Analysis. 2nd ed. Sebastopol: O’Reilly.

• VanderPlas, Jake. 2016. Python Data Science Handbook. Sebastopol: O’Reilly.

For the use of NumPy and pandas in a financial context, refer to these books:

• Hilpisch, Yves. 2015. Derivatives Analytics with Python: Data Analysis, Models, Simulation, Calibration, and Hedging. Wiley Finance.

• ⸻. 2017. Listed Volatility and Variance Derivatives: A Python-Based Guide. Wiley Finance.

• ⸻. 2018. Python for Finance: Mastering Data-Driven Finance. 2nd ed. Sebastopol: O’Reilly.

For the topics of data snooping and overfitting, refer to these papers:

• Bailey, David, Jonathan Borwein, Marcos López de Prado, and Qiji Jim Zhu. 2015. “The Probability of Backtest Overfitting.” Journal of Computational Finance 20, (4): 39-69. https://oreil.ly/sOHlf.

• Ioannidis, John. 2005. “Why Most Published Research Findings Are False.” PLoS Medicine 2, (8): 696-701.

• White, Halbert. 2000. “A Reality Check for Data Snooping.” Econometrica 68, (5): 1097-1126.

For more background information and empirical results about trading strategies based on simple moving averages, refer to these sources:

• Brock, William, Josef Lakonishok, and Blake LeBaron. 1992. “Simple Technical Trading Rules and the Stochastic Properties of Stock Returns.” Journal of Finance 47, (5): 1731-1764.

• Droke, Clif. 2001. Moving Averages Simplified. Columbia: Marketplace Books.

The book by Ernest Chan covers in detail trading strategies based on momentum, as well as on mean reversion. The book is also a good source for the pitfalls of backtesting trading strategies:

• Chan, Ernest. 2013. Algorithmic Trading: Winning Strategies and Their Rationale. Hoboken et al: John Wiley & Sons.

These research papers analyze characteristics and sources of profit for cross-sectional momentum strategies, the traditional approach to momentum-based trading:

• Chan, Louis, Narasimhan Jegadeesh, and Josef Lakonishok. 1996. “Momentum Strategies.” Journal of Finance 51, (5): 1681-1713.

• Jegadeesh, Narasimhan, and Sheridan Titman. 1993. “Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency.” Journal of Finance 48, (1): 65-91.

• Jegadeesh, Narasimhan, and Sheridan Titman. 2001. “Profitability of Momentum Strategies: An Evaluation of Alternative Explanations.” Journal of Finance 56, (2): 599-720.

The paper by Moskowitz et al. provides an analysis of so-called time series momentum strategies:

• Moskowitz, Tobias, Yao Hua Ooi, and Lasse Heje Pedersen. 2012. “Time Series Momentum.” Journal of Financial Economics 104: 228-250.

These papers empirically analyze mean reversion in asset prices:

• Balvers, Ronald, Yangru Wu, and Erik Gilliland. 2000. “Mean Reversion across National Stock Markets and Parametric Contrarian Investment Strategies.” Journal of Finance 55, (2): 745-772.

• Kim, Myung Jig, Charles Nelson, and Richard Startz. 1991. “Mean Reversion in Stock Prices? A Reappraisal of the Empirical Evidence.” Review of Economic Studies 58: 515-528.

• Spierdijk, Laura, Jacob Bikker, and Peter van den Hoek. 2012. “Mean Reversion in International Stock Markets: An Empirical Analysis of the 20th Century.” Journal of International Money and Finance 31: 228-249.

Python Scripts

This section presents Python scripts referenced and used in this chapter.

SMA Backtesting Class

The following presents Python code with a class for the vectorized backtesting of strategies based on simple moving averages:

#
# Python Module with Class
# for Vectorized Backtesting
# of SMA-based Strategies
#
# Python for Algorithmic Trading
# (c) Dr. Yves J. Hilpisch
# The Python Quants GmbH
#
import numpy as np
import pandas as pd
from scipy.optimize import brute


class SMAVectorBacktester(object):
    ''' Class for the vectorized backtesting of SMA-based trading strategies.

    Attributes
    ==========
    symbol: str
        RIC symbol with which to work
    SMA1: int
        time window in days for shorter SMA
    SMA2: int
        time window in days for longer SMA
    start: str
        start date for data retrieval
    end: str
        end date for data retrieval

    Methods
    =======
    get_data:
        retrieves and prepares the base data set
    set_parameters:
        sets one or two new SMA parameters
    run_strategy:
        runs the backtest for the SMA-based strategy
    plot_results:
        plots the performance of the strategy compared to the symbol
    update_and_run:
        updates SMA parameters and returns the (negative) absolute performance
    optimize_parameters:
        implements a brute force optimization for the two SMA parameters
    '''

    def __init__(self, symbol, SMA1, SMA2, start, end):
        self.symbol = symbol
        self.SMA1 = SMA1
        self.SMA2 = SMA2
        self.start = start
        self.end = end
        self.results = None
        self.get_data()

    def get_data(self):
        ''' Retrieves and prepares the data.
        '''
        raw = pd.read_csv('http://hilpisch.com/pyalgo_eikon_eod_data.csv',
                          index_col=0, parse_dates=True).dropna()
        raw = pd.DataFrame(raw[self.symbol])
        raw = raw.loc[self.start:self.end]
        raw.rename(columns={self.symbol: 'price'}, inplace=True)
        raw['return'] = np.log(raw / raw.shift(1))
        raw['SMA1'] = raw['price'].rolling(self.SMA1).mean()
        raw['SMA2'] = raw['price'].rolling(self.SMA2).mean()
        self.data = raw

    def set_parameters(self, SMA1=None, SMA2=None):
        ''' Updates SMA parameters and resp. time series.
        '''
        if SMA1 is not None:
            self.SMA1 = SMA1
            self.data['SMA1'] = self.data['price'].rolling(
                self.SMA1).mean()
        if SMA2 is not None:
            self.SMA2 = SMA2
            self.data['SMA2'] = self.data['price'].rolling(self.SMA2).mean()

    def run_strategy(self):
        ''' Backtests the trading strategy.
        '''
        data = self.data.copy().dropna()
        data['position'] = np.where(data['SMA1'] > data['SMA2'], 1, -1)
        data['strategy'] = data['position'].shift(1) * data['return']
        data.dropna(inplace=True)
        data['creturns'] = data['return'].cumsum().apply(np.exp)
        data['cstrategy'] = data['strategy'].cumsum().apply(np.exp)
        self.results = data
        # gross performance of the strategy
        aperf = data['cstrategy'].iloc[-1]
        # out-/underperformance of strategy
        operf = aperf - data['creturns'].iloc[-1]
        return round(aperf, 2), round(operf, 2)

    def plot_results(self):
        ''' Plots the cumulative performance of the trading strategy
        compared to the symbol.
        '''
        if self.results is None:
            print('No results to plot yet. Run a strategy.')
        title = '%s | SMA1=%d, SMA2=%d' % (self.symbol,
                                               self.SMA1, self.SMA2)
        self.results[['creturns', 'cstrategy']].plot(title=title,
                                                     figsize=(10, 6))

    def update_and_run(self, SMA):
        ''' Updates SMA parameters and returns negative absolute performance
        (for minimazation algorithm).

        Parameters
        ==========
        SMA: tuple
            SMA parameter tuple
        '''
        self.set_parameters(int(SMA[0]), int(SMA[1]))
        return -self.run_strategy()[0]

    def optimize_parameters(self, SMA1_range, SMA2_range):
        ''' Finds global maximum given the SMA parameter ranges.

        Parameters
        ==========
        SMA1_range, SMA2_range: tuple
            tuples of the form (start, end, step size)
        '''
        opt = brute(self.update_and_run, (SMA1_range, SMA2_range), finish=None)
        return opt, -self.update_and_run(opt)


if __name__ == '__main__':
    smabt = SMAVectorBacktester('EUR=', 42, 252,
                                '2010-1-1', '2020-12-31')
    print(smabt.run_strategy())
    smabt.set_parameters(SMA1=20, SMA2=100)
    print(smabt.run_strategy())
    print(smabt.optimize_parameters((30, 56, 4), (200, 300, 4)))

Momentum Backtesting Class

The following presents Python code with a class for the vectorized backtesting of strategies based on time series momentum:

#
# Python Module with Class
# for Vectorized Backtesting
# of Momentum-Based Strategies
#
# Python for Algorithmic Trading
# (c) Dr. Yves J. Hilpisch
# The Python Quants GmbH
#
import numpy as np
import pandas as pd


class MomVectorBacktester(object):
    ''' Class for the vectorized backtesting of
    momentum-based trading strategies.

    Attributes
    ==========
    symbol: str
       RIC (financial instrument) to work with
    start: str
        start date for data selection
    end: str
        end date for data selection
    amount: int, float
        amount to be invested at the beginning
    tc: float
        proportional transaction costs (e.g., 0.5% = 0.005) per trade

    Methods
    =======
    get_data:
        retrieves and prepares the base data set
    run_strategy:
        runs the backtest for the momentum-based strategy
    plot_results:
        plots the performance of the strategy compared to the symbol
    '''

    def __init__(self, symbol, start, end, amount, tc):
        self.symbol = symbol
        self.start = start
        self.end = end
        self.amount = amount
        self.tc = tc
        self.results = None
        self.get_data()

    def get_data(self):
        ''' Retrieves and prepares the data.
        '''
        raw = pd.read_csv('http://hilpisch.com/pyalgo_eikon_eod_data.csv',
                          index_col=0, parse_dates=True).dropna()
        raw = pd.DataFrame(raw[self.symbol])
        raw = raw.loc[self.start:self.end]
        raw.rename(columns={self.symbol: 'price'}, inplace=True)
        raw['return'] = np.log(raw / raw.shift(1))
        self.data = raw

    def run_strategy(self, momentum=1):
        ''' Backtests the trading strategy.
        '''
        self.momentum = momentum
        data = self.data.copy().dropna()
        data['position'] = np.sign(data['return'].rolling(momentum).mean())
        data['strategy'] = data['position'].shift(1) * data['return']
        # determine when a trade takes place
        data.dropna(inplace=True)
        trades = data['position'].diff().fillna(0) != 0
        # subtract transaction costs from return when trade takes place
        data['strategy'][trades] -= self.tc
        data['creturns'] = self.amount * data['return'].cumsum().apply(np.exp)
        data['cstrategy'] = self.amount * \
            data['strategy'].cumsum().apply(np.exp)
        self.results = data
        # absolute performance of the strategy
        aperf = self.results['cstrategy'].iloc[-1]
        # out-/underperformance of strategy
        operf = aperf - self.results['creturns'].iloc[-1]
        return round(aperf, 2), round(operf, 2)

    def plot_results(self):
        ''' Plots the cumulative performance of the trading strategy
        compared to the symbol.
        '''
        if self.results is None:
            print('No results to plot yet. Run a strategy.')
        title = '%s | TC = %.4f' % (self.symbol, self.tc)
        self.results[['creturns', 'cstrategy']].plot(title=title,
                                                     figsize=(10, 6))


if __name__ == '__main__':
    mombt = MomVectorBacktester('XAU=', '2010-1-1', '2020-12-31',
                                10000, 0.0)
    print(mombt.run_strategy())
    print(mombt.run_strategy(momentum=2))
    mombt = MomVectorBacktester('XAU=', '2010-1-1', '2020-12-31',
                                10000, 0.001)
    print(mombt.run_strategy(momentum=2))

Mean Reversion Backtesting Class

The following presents Python code with a class for the vectorized backtesting of strategies based on mean reversion:.

#
# Python Module with Class
# for Vectorized Backtesting
# of Mean-Reversion Strategies
#
# Python for Algorithmic Trading
# (c) Dr. Yves J. Hilpisch
# The Python Quants GmbH
#
from MomVectorBacktester import *


class MRVectorBacktester(MomVectorBacktester):
    ''' Class for the vectorized backtesting of
    mean reversion-based trading strategies.

    Attributes
    ==========
    symbol: str
        RIC symbol with which to work
    start: str
        start date for data retrieval
    end: str
        end date for data retrieval
    amount: int, float
        amount to be invested at the beginning
    tc: float
        proportional transaction costs (e.g., 0.5% = 0.005) per trade

    Methods
    =======
    get_data:
        retrieves and prepares the base data set
    run_strategy:
        runs the backtest for the mean reversion-based strategy
    plot_results:
        plots the performance of the strategy compared to the symbol
    '''

    def run_strategy(self, SMA, threshold):
        ''' Backtests the trading strategy.
        '''
        data = self.data.copy().dropna()
        data['sma'] = data['price'].rolling(SMA).mean()
        data['distance'] = data['price'] - data['sma']
        data.dropna(inplace=True)
        # sell signals
        data['position'] = np.where(data['distance'] > threshold,
                                    -1, np.nan)
        # buy signals
        data['position'] = np.where(data['distance'] < -threshold,
                                    1, data['position'])
        # crossing of current price and SMA (zero distance)
        data['position'] = np.where(data['distance'] *
                                    data['distance'].shift(1) < 0,
                                    0, data['position'])
        data['position'] = data['position'].ffill().fillna(0)
        data['strategy'] = data['position'].shift(1) * data['return']
        # determine when a trade takes place
        trades = data['position'].diff().fillna(0) != 0
        # subtract transaction costs from return when trade takes place
        data['strategy'][trades] -= self.tc
        data['creturns'] = self.amount * \
            data['return'].cumsum().apply(np.exp)
        data['cstrategy'] = self.amount * \
            data['strategy'].cumsum().apply(np.exp)
        self.results = data
        # absolute performance of the strategy
        aperf = self.results['cstrategy'].iloc[-1]
        # out-/underperformance of strategy
        operf = aperf - self.results['creturns'].iloc[-1]
        return round(aperf, 2), round(operf, 2)


if __name__ == '__main__':
    mrbt = MRVectorBacktester('GDX', '2010-1-1', '2020-12-31',
                              10000, 0.0)
    print(mrbt.run_strategy(SMA=25, threshold=5))
    mrbt = MRVectorBacktester('GDX', '2010-1-1', '2020-12-31',
                              10000, 0.001)
    print(mrbt.run_strategy(SMA=25, threshold=5))
    mrbt = MRVectorBacktester('GLD', '2010-1-1', '2020-12-31',
                              10000, 0.001)
    print(mrbt.run_strategy(SMA=42, threshold=7.5))

¹ Source: “Does the Past Predict the Future?” The Economist, September 23, 2009.

² For more on the datetime and timedelta objects, refer to Appendix C of Hilpisch (2018).