Python for Algorithmic Trading

Chapter 1. Python and Algorithmic Trading

At Goldman [Sachs] the number of people engaged in trading shares has fallen from a peak of 600 in 2000 to just two today.¹

The Economist

This chapter provides background information for, and an overview of, the topics covered in this book. Although Python for algorithmic trading is a niche at the intersection of Python programming and finance, it is a fast-growing one that touches on such diverse topics as Python deployment, interactive financial analytics, machine and deep learning, object-oriented programming, socket communication, visualization of streaming data, and trading platforms.

For a quick refresher on important Python topics, read the Appendix A first.

Python for Finance

The Python programming language originated in 1991 with the first release by Guido van Rossum of a version labeled 0.9.0. In 1994, version 1.0 followed. However, it took almost two decades for Python to establish itself as a major programming language and technology platform in the financial industry. Of course, there were early adopters, mainly hedge funds, but widespread adoption probably started only around 2011.

One major obstacle to the adoption of Python in the financial industry has been the fact that the default Python version, called CPython, is an interpreted, high-level language. Numerical algorithms in general and financial algorithms in particular are quite often implemented based on (nested) loop structures. While compiled, low-level languages like C or C++ are really fast at executing such loops, Python, which relies on interpretation instead of compilation, is generally quite slow at doing so. As a consequence, pure Python proved too slow for many real-world financial applications, such as option pricing or risk management.

Python Versus Pseudo-Code

Although Python was never specifically targeted towards the scientific and financial communities, many people from these fields nevertheless liked the beauty and conciseness of its syntax. Not too long ago, it was generally considered good tradition to explain a (financial) algorithm and at the same time present some pseudo-code as an intermediate step towards its proper technological implementation. Many felt that, with Python, the pseudo-code step would not be necessary anymore. And they were proven mostly correct.

Consider, for instance, the Euler discretization of the geometric Brownian motion, as in Equation 1-1.

Equation 1-1. Euler discretization of geometric Brownian motion

$$S_T=S_{0}exp((r-0.5{\sigma }^2)T+\sigma z\sqrt{T})$$

For decades, the LaTeX markup language and compiler have been the gold standard for authoring scientific documents containing mathematical formulae. In many ways, Latex syntax is similar to or already like pseudo-code when, for example, laying out equations, as in Equation 1-1. In this particular case, the Latex version looks like this:

S_T = S_0 \exp((r - 0.5 \sigma^2) T + \sigma z \sqrt{T})

In Python, this translates to executable code, given respective variable definitions, that is also really close to the financial formula as well as to the Latex representation:

S_T = S_0 * exp((r - 0.5 * sigma ** 2) * T + sigma * z * sqrt(T))

However, the speed issue remains. Such a difference equation, as a numerical approximation of the respective stochastic differential equation, is generally used to price derivatives by Monte Carlo simulation or to do risk analysis and management based on simulation.² These tasks in turn can require millions of simulations that need to be finished in due time, often in almost real-time or at least near-time. Python, as an interpreted high-level programming language, was never designed to be fast enough to tackle such computationally demanding tasks.

NumPy and Vectorization

In 2006, version 1.0 of the NumPy Python package was released by Travis Oliphant. NumPy stands for numerical Python, suggesting that it targets scenarios that are numerically demanding. The base Python interpreter tries to be as general as possible in many areas, which often leads to quite a bit of overhead at run-time.³ NumPy, on the other hand, uses specialization as its major approach to avoid overhead and to be as good and as fast as possible in certain application scenarios.

The major class of NumPy is the regular array object, called ndarray object for n-dimensional array. It is immutable, which means that it cannot be changed in size, and can only accommodate a single data type, called dtype. This specialization allows for the implementation of concise and fast code. One central approach in this context is vectorization. Basically, this approach avoids looping on the Python level and delegates the looping to specialized NumPy code, generally implemented in C and therefore rather fast.

Consider the simulation of 1,000,000 end of period values $S_T$ according to Equation 1-1 with pure Python. The major part of the following code is a for loop with 1,000,000 iterations:

In [1]: %%time
        import random
        from math import exp, sqrt

        S0 = 100  
        r = 0.05  
        T = 1.0  
        sigma = 0.2  

        values = []  

        for _ in range(1000000):  
            ST = S0 * exp((r - 0.5 * sigma ** 2) * T +
                            sigma * random.gauss(0, 1) * sqrt(T))  
            values.append(ST)  
        CPU times: user 1.13 s, sys: 21.7 ms, total: 1.15 s
        Wall time: 1.15 s

The initial index level.

The constant short rate.

The time horizon in year fractions.

The constant volatility factor.

An empty list object to collect simulated values.

The main for loop.

The simulation of a single end-of-period value.

Appends the simulated value to the list object.

With NumPy, you can avoid looping on the Python level completely by the use of vectorization. The code is much more concise, more readable, and faster by a factor of about eight:

In [2]: %%time
        import numpy as np

        S0 = 100
        r = 0.05
        T = 1.0
        sigma = 0.2

        ST = S0 * np.exp((r - 0.5 * sigma ** 2) * T +
                            sigma * np.random.standard_normal(1000000) *
                            np.sqrt(T))  
        CPU times: user 375 ms, sys: 82.6 ms, total: 458 ms
        Wall time: 160 ms

This single line of NumPy code simulates all the values and stores them in an ndarray object.

Vectorization is a powerful concept for writing concise, easy-to-read, and easy-to-maintain code in finance and algorithmic trading. With NumPy, vectorized code does not only make code more concise, but it also can speed up code execution considerably (by a factor of about eight in the Monte Carlo simulation, for example).

It’s safe to say that NumPy has significantly contributed to the success of Python in science and finance. Many other popular Python packages from the so-called scientific Python stack build on NumPy as an efficient, performing data structure to store and handle numerical data. In fact, NumPy is an outgrowth of the SciPy package project, which provides a wealth of functionality frequently needed in science. The SciPy project recognized the need for a more powerful numerical data structure and consolidated older projects like Numeric and NumArray in this area into a new, unifying one in the form of NumPy.

In algorithmic trading, a Monte Carlo simulation might not be the most important use case for a programming language. However, if you enter the algorithmic trading space, the management of larger, or even big, financial time series data sets is a very important use case. Just think of the backtesting of (intraday) trading strategies or the processing of tick data streams during trading hours. This is where the pandas data analysis package comes into play.

pandas and the DataFrame Class

Development of pandas began in 2008 by Wes McKinney, who back then was working at AQR Capital Management, a big hedge fund operating out of Greenwich, Connecticut. As with for any other hedge fund, working with time series data is of paramount importance for AQR Capital Management, but back then Python did not provide any kind of appealing support for this type of data. Wes’s idea was to create a package that mimics the capabilities of the R statistical language (http://r-project.org) in this area. This is reflected, for example, in naming the major class DataFrame, whose counterpart in R is called data.frame. Not being considered close enough to the core business of money management, AQR Capital Management open sourced the pandas project in 2009, which marks the beginning of a major success story in open source–based data and financial analytics.

Partly due to pandas, Python has become a major force in data and financial analytics. Many people who adopt Python, coming from diverse other languages, cite pandas as a major reason for their decision. In combination with open data sources like Quandl, pandas even allows students to do sophisticated financial analytics with the lowest barriers of entry ever: a regular notebook computer with an internet connection suffices.

Assume an algorithmic trader is interested in trading Bitcoin, the cryptocurrency with the largest market capitalization. A first step might be to retrieve data about the historical exchange rate in USD. Using Quandl data and pandas, such a task is accomplished in less than a minute. Figure 1-1 shows the plot that results from the following Python code, which is (omitting some plotting style related parameterizations) only four lines. Although pandas is not explicitly imported, the Quandl Python wrapper package by default returns a DataFrame object that is then used to add a simple moving average (SMA) of 100 days, as well as to visualize the raw data alongside the SMA:

In [3]: %matplotlib inline
        from pylab import mpl, plt  
        plt.style.use('seaborn')  
        mpl.rcParams['savefig.dpi'] = 300  
        mpl.rcParams['font.family'] = 'serif'  

In [4]: import configparser  
        c = configparser.ConfigParser()  
        c.read('../pyalgo.cfg')  
Out[4]: ['../pyalgo.cfg']

In [5]: import quandl as q  
        q.ApiConfig.api_key = c['quandl']['api_key']  
        d = q.get('BCHAIN/MKPRU')  
        d['SMA'] = d['Value'].rolling(100).mean()  
        d.loc['2013-1-1':].plot(title='BTC/USD exchange rate',
                                figsize=(10, 6));  

Imports and configures the plotting package.

Imports the configparser module and reads credentials.

Imports the Quandl Python wrapper package and provides the API key.

Retrieves daily data for the Bitcoin exchange rate and returns a pandas DataFrame object with a single column.

Calculates the SMA for 100 days in vectorized fashion.

Selects data from the 1st of January 2013 on and plots it.

Obviously, NumPy and pandas measurably contribute to the success of Python in finance. However, the Python ecosystem has much more to offer in the form of additional Python packages that solve rather fundamental problems and sometimes specialized ones. This book will make use of packages for data retrieval and storage (for example, PyTables, TsTables, SQLite) and for machine and deep learning (for example, scikit-learn, TensorFlow), to name just two categories. Along the way, we will also implement classes and modules that will make any algorithmic trading project more efficient. However, the main packages used throughout will be NumPy and pandas.

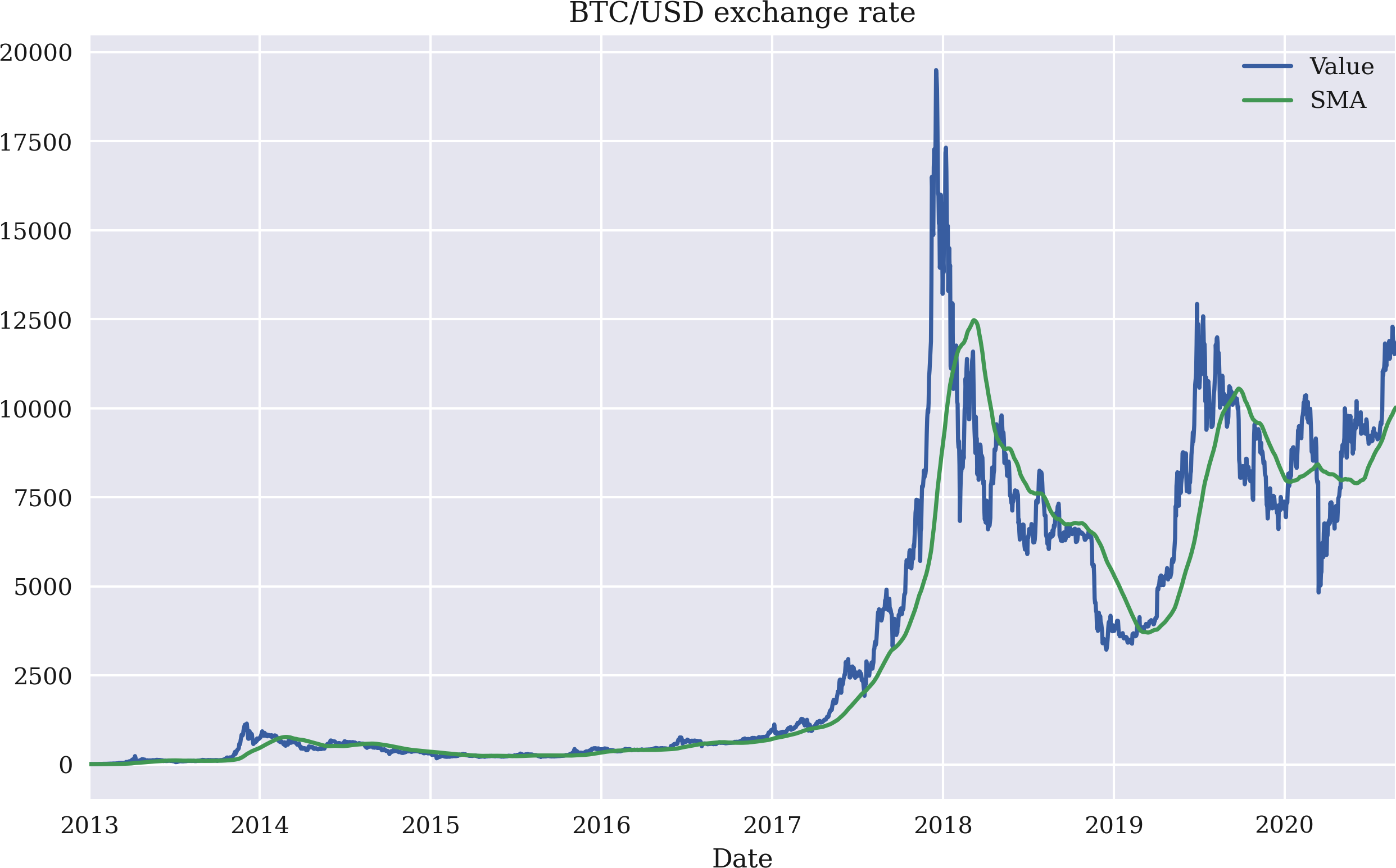
Figure 1-1. Historical Bitcoin exchange rate in USD from the beginning of 2013 until mid-2020

While NumPy provides the basic data structure to store numerical data and work with it, pandas brings powerful time series management capabilities to the table. It also does a great job of wrapping functionality from other packages into an easy-to-use API. The Bitcoin example just described shows that a single method call on a DataFrame object is enough to generate a plot with two financial time series visualized. Like NumPy, pandas allows for rather concise, vectorized code that is also generally executed quite fast due to heavy use of compiled code under the hood.

Algorithmic Trading

The term algorithmic trading is neither uniquely nor universally defined. On a rather basic level, it refers to the trading of financial instruments based on some formal algorithm. An algorithm is a set of operations (mathematical, technical) to be conducted in a certain sequence to achieve a certain goal. For example, there are mathematical algorithms to solve a Rubik’s Cube.⁴ Such an algorithm can solve the problem at hand via a step-by-step procedure, often perfectly. Another example is algorithms for finding the root(s) of an equation if it (they) exist(s) at all. In that sense, the objective of a mathematical algorithm is often well specified and an optimal solution is often expected.

But what about the objective of financial trading algorithms? This question is not that easy to answer in general. It might help to step back for a moment and consider general motives for trading. In Dorn et al. (2008) write:

Trading in financial markets is an important economic activity. Trades are necessary to get into and out of the market, to put unneeded cash into the market, and to convert back into cash when the money is wanted. They are also needed to move money around within the market, to exchange one asset for another, to manage risk, and to exploit information about future price movements.

The view expressed here is more technical than economic in nature, focusing mainly on the process itself and only partly on why people initiate trades in the first place. For our purposes, a nonexhaustive list of financial trading motives of people and financial institutions managing money of their own or for others includes the following:

Beta trading

Earning market risk premia by investing in, for instance, exchange traded funds (ETFs) that replicate the performance of the S&P 500.

Alpha generation

Earning risk premia independent of the market by, for example, selling short stocks listed in the S&P 500 or ETFs on the S&P 500.

Static hedging

Hedging against market risks by buying, for example, out-of-the-money put options on the S&P 500.

Dynamic hedging

Hedging against market risks affecting options on the S&P 500 by, for example, dynamically trading futures on the S&P 500 and appropriate cash, money market, or rate instruments.

Asset-liability management

Trading S&P 500 stocks and ETFs to be able to cover liabilities resulting from, for example, writing life insurance policies.

Market making

Providing, for example, liquidity to options on the S&P 500 by buying and selling options at different bid and ask prices.

All these types of trades can be implemented by a discretionary approach, with human traders making decisions mainly on their own, as well as based on algorithms supporting the human trader or even replacing them completely in the decision-making process. In this context, computerization of financial trading of course plays an important role. While in the beginning of financial trading, floor trading with a large group of people shouting at each other (“open outcry”) was the only way of executing trades, computerization and the advent of the internet and web technologies have revolutionized trading in the financial industry. The quotation at the beginning of this chapter illustrates this impressively in terms of the number of people actively engaged in trading shares at Goldman Sachs in 2000 and in 2016. It is a trend that was foreseen 25 years ago, as Solomon and Corso (1991) point out:

Computers have revolutionized the trading of securities and the stock market is currently in the midst of a dynamic transformation. It is clear that the market of the future will not resemble the markets of the past.

Technology has made it possible for information regarding stock prices to be sent all over the world in seconds. Presently, computers route orders and execute small trades directly from the brokerage firm’s terminal to the exchange. Computers now link together various stock exchanges, a practice which is helping to create a single global market for the trading of securities. The continuing improvements in technology will make it possible to execute trades globally by electronic trading systems.

Interestingly, one of the oldest and most widely used algorithms is found in dynamic hedging of options. Already with the publication of the seminal papers about the pricing of European options by Black and Scholes (1973) and Merton (1973), the algorithm, called delta hedging, was made available long before computerized and electronic trading even started. Delta hedging as a trading algorithm shows how to hedge away all market risks in a simplified, perfect, continuous model world. In the real world, with transaction costs, discrete trading, imperfectly liquid markets, and other frictions (“imperfections”), the algorithm has proven, somewhat surprisingly maybe, its usefulness and robustness, as well. It might not allow one to perfectly hedge away market risks affecting options, but it is useful in getting close to the ideal and is therefore still used on a large scale in the financial industry.⁵

This book focuses on algorithmic trading in the context of alpha generating strategies. Although there are more sophisticated definitions for alpha, for the purposes of this book, alpha is seen as the difference between a trading strategy’s return over some period of time and the return of the benchmark (single stock, index, cryptocurrency, etc.). For example, if the S&P 500 returns 10% in 2018 and an algorithmic strategy returns 12%, then alpha is +2% points. If the strategy returns 7%, then alpha is -3% points. In general, such numbers are not adjusted for risk, and other risk characteristics, such as maximal drawdown (period), are usually considered to be of second order importance, if at all.

This book focuses on alpha-generating strategies, or strategies that try to generate positive returns (above a benchmark) independent of the market’s performance. Alpha is defined in this book (in the simplest way) as the excess return of a strategy over the benchmark financial instrument’s performance.

There are other areas where trading-related algorithms play an important role. One is the high frequency trading (HFT) space, where speed is typically the discipline in which players compete.⁶ The motives for HFT are diverse, but market making and alpha generation probably play a prominent role. Another one is trade execution, where algorithms are deployed to optimally execute certain nonstandard trades. Motives in this area might include the execution (at best possible prices) of large orders or the execution of an order with as little market and price impact as possible. A more subtle motive might be to disguise an order by executing it on a number of different exchanges.

An important question remains to be addressed: is there any advantage to using algorithms for trading instead of human research, experience, and discretion? This question can hardly be answered in any generality. For sure, there are human traders and portfolio managers who have earned, on average, more than their benchmark for investors over longer periods of time. The paramount example in this regard is Warren Buffett. On the other hand, statistical analyses show that the majority of active portfolio managers rarely beat relevant benchmarks consistently. Referring to the year 2015, Adam Shell writes:

Last year, for example, when the Standard & Poor’s 500-stock index posted a paltry total return of 1.4% with dividends included, 66% of “actively managed” large-company stock funds posted smaller returns than the index…The longer-term outlook is just as gloomy, with 84% of large-cap funds generating lower returns than the S&P 500 in the latest five year period and 82% falling shy in the past 10 years, the study found.⁷

In an empirical study published in December 2016, Harvey et al. write:

We analyze and contrast the performance of discretionary and systematic hedge funds. Systematic funds use strategies that are rules‐based, with little or no daily intervention by humans….We find that, for the period 1996‐2014, systematic equity managers underperform their discretionary counterparts in terms of unadjusted (raw) returns, but that after adjusting for exposures to well‐known risk factors, the risk‐adjusted performance is similar. In the case of macro, systematic funds outperform discretionary funds, both on an unadjusted and risk‐adjusted basis.

Table 1-0 reproduces the major quantitative findings of the study by Harvey et al. (2016).⁸ In the table, factors include traditional ones (equity, bonds, etc.), dynamic ones (value, momentum, etc.), and volatility (buying at-the-money puts and calls). The adjusted return appraisal ratio divides alpha by the adjusted return volatility. For more details and background, see the original study.

The study’s results illustrate that systematic (“algorithmic”) macro hedge funds perform best as a category, both in unadjusted and risk-adjusted terms. They generate an annualized alpha of 4.85% points over the period studied. These are hedge funds implementing strategies that are typically global, are cross-asset, and often involve political and macroeconomic elements. Systematic equity hedge funds only beat their discretionary counterparts on the basis of the adjusted return appraisal ratio (0.35 versus 0.25).

	Systematic macro	Discretionary macro	Systematic equity	Discretionary equity
Return average	5.01%	2.86%	2.88%	4.09%
Return attributed to factors	0.15%	1.28%	1.77%	2.86%
Adj. return average (alpha)	4.85%	1.57%	1.11%	1.22%
Adj. return volatility	0.93%	5.10%	3.18%	4.79%
Adj. return appraisal ratio	0.44	0.31	0.35	0.25

Compared to the S&P 500, hedge fund performance overall was quite meager for the year 2017. While the S&P 500 index returned 21.8%, hedge funds only returned 8.5% to investors (see this article in Investopedia). This illustrates how hard it is, even with multimillion dollar budgets for research and technology, to generate alpha.

Python for Algorithmic Trading

Python is used in many corners of the financial industry but has become particularly popular in the algorithmic trading space. There are a few good reasons for this:

Data analytics capabilities

A major requirement for every algorithmic trading project is the ability to manage and process financial data efficiently. Python, in combination with packages like NumPy and pandas, makes life easier in this regard for every algorithmic trader than most other programming languages do.

Handling of modern APIs

Modern online trading platforms like the ones from FXCM and Oanda offer RESTful application programming interfaces (APIs) and socket (streaming) APIs to access historical and live data. Python is in general well suited to efficiently interact with such APIs.

Dedicated packages

In addition to the standard data analytics packages, there are multiple packages available that are dedicated to the algorithmic trading space, such as PyAlgoTrade and Zipline for the backtesting of trading strategies and Pyfolio for performing portfolio and risk analysis.

Vendor sponsored packages

More and more vendors in the space release open source Python packages to facilitate access to their offerings. Among them are online trading platforms like Oanda, as well as the leading data providers like Bloomberg and Refinitiv.

Dedicated platforms

Quantopian, for example, offers a standardized backtesting environment as a Web-based platform where the language of choice is Python and where people can exchange ideas with like-minded others via different social network features. From its founding until 2020, Quantopian has attracted more than 300,000 users.

Buy- and sell-side adoption

More and more institutional players have adopted Python to streamline development efforts in their trading departments. This, in turn, requires more and more staff proficient in Python, which makes learning Python a worthwhile investment.

Education, training, and books

Prerequisites for the widespread adoption of a technology or programming language are academic and professional education and training programs in combination with specialized books and other resources. The Python ecosystem has seen a tremendous growth in such offerings recently, educating and training more and more people in the use of Python for finance. This can be expected to reinforce the trend of Python adoption in the algorithmic trading space.

In summary, it is rather safe to say that Python plays an important role in algorithmic trading already and seems to have strong momentum to become even more important in the future. It is therefore a good choice for anyone trying to enter the space, be it as an ambitious “retail” trader or as a professional employed by a leading financial institution engaged in systematic trading.

Focus and Prerequisites

The focus of this book is on Python as a programming language for algorithmic trading. The book assumes that the reader already has some experience with Python and popular Python packages used for data analytics. Good introductory books are, for example, Hilpisch (2018), McKinney (2017), and VanderPlas (2016), which all can be consulted to build a solid foundation in Python for data analysis and finance. The reader is also expected to have some experience with typical tools used for interactive analytics with Python, such as IPython, to which VanderPlas (2016) also provides an introduction.

This book presents and explains Python code that is applied to the topics at hand, like backtesting trading strategies or working with streaming data. It cannot provide a thorough introduction to all packages used in different places. It tries, however, to highlight those capabilities of the packages that are central to the exposition (such as vectorization with NumPy).

The book also cannot provide a thorough introduction and overview of all financial and operational aspects relevant for algorithmic trading. The approach instead focuses on the use of Python to build the necessary infrastructure for automated algorithmic trading systems. Of course, the majority of examples used are taken from the algorithmic trading space. However, when dealing with, say, momentum or mean-reversion strategies, they are more or less simply used without providing (statistical) verification or an in-depth discussion of their intricacies. Whenever it seems appropriate, references are given that point the reader to sources that address issues left open during the exposition.

All in all, this book is written for readers who have some experience with both Python and (algorithmic) trading. For such a reader, the book is a practical guide to the creation of automated trading systems using Python and additional packages.

This book uses a number of Python programming approaches (for example, object oriented programming) and packages (for example, scikit-learn) that cannot be explained in detail. The focus is on applying these approaches and packages to different steps in an algorithmic trading process. It is therefore recommended that those who do not yet have enough Python (for finance) experience additionally consult more introductory Python texts.

Trading Strategies

Throughout this book, four different algorithmic trading strategies are used as examples. They are introduced briefly in the following sections and in some more detail in Chapter 4. All these trading strategies can be classified as mainly alpha seeking strategies, since their main objective is to generate positive, above-market returns independent of the market direction. Canonical examples throughout the book, when it comes to financial instruments traded, are a stock index, a single stock, or a cryptocurrency (denominated in a fiat currency). The book does not cover strategies involving multiple financial instruments at the same time (pair trading strategies, strategies based on baskets, etc.). It also covers only strategies whose trading signals are derived from structured, financial time series data and not, for instance, from unstructured data sources like news or social media feeds. This keeps the discussions and the Python implementations concise and easier to understand, in line with the approach (discussed earlier) of focusing on Python for algorithmic trading.⁹

The remainder of this chapter gives a quick overview of the four trading strategies used in this book.

Simple Moving Averages

The first type of trading strategy relies on simple moving averages (SMAs) to generate trading signals and market positionings. These trading strategies have been popularized by so-called technical analysts or chartists. The basic idea is that a shorter-term SMA being higher in value than a longer term SMA signals a long market position and the opposite scenario signals a neutral or short market position.

Momentum

The basic idea behind momentum strategies is that a financial instrument is assumed to perform in accordance with its recent performance for some additional time. For example, when a stock index has seen a negative return on average over the last five days, it is assumed that its performance will be negative tomorrow, as well.

Mean Reversion

In mean-reversion strategies, a financial instrument is assumed to revert to some mean or trend level if it is currently far enough away from such a level. For example, assume that a stock trades 10 USD under its 200 days SMA level of 100. It is then expected that the stock price will return to its SMA level sometime soon.

Machine and Deep Learning

With machine and deep learning algorithms, one generally takes a more black box approach to predicting market movements. For simplicity and reproducibility, the examples in this book mainly rely on historical return observations as features to train machine and deep learning algorithms to predict stock market movements.

This book does not introduce algorithmic trading in a systematic fashion. Since the focus lies on applying Python in this fascinating field, readers not familiar with algorithmic trading should consult dedicated resources on the topic, some of which are cited in this chapter and the chapters that follow. But be aware of the fact that the algorithmic trading world in general is secretive and that almost everyone who is successful is naturally reluctant to share their secrets in order to protect their sources of success (that is, their alpha).

Conclusions

Python is already a force in finance in general and is on its way to becoming a major force in algorithmic trading. There are a number of good reasons to use Python for algorithmic trading, among them the powerful ecosystem of packages that allows for efficient data analysis or the handling of modern APIs. There are also a number of good reasons to learn Python for algorithmic trading, chief among them the fact that some of the biggest buy- and sell-side institutions make heavy use of Python in their trading operations and constantly look for seasoned Python professionals.

This book focuses on applying Python to the different disciplines in algorithmic trading, like backtesting trading strategies or interacting with online trading platforms. It cannot replace a thorough introduction to Python itself nor to trading in general. However, it systematically combines these two fascinating worlds to provide a valuable source for the generation of alpha in today’s competitive financial and cryptocurrency markets.

References and Further Resources

Books and papers cited in this chapter:

• Black, Fischer, and Myron Scholes. 1973. “The Pricing of Options and Corporate Liabilities.” Journal of Political Economy 81 (3): 638-659.

• Chan, Ernest. 2013. Algorithmic Trading: Winning Strategies and Their Rationale. Hoboken et al: John Wiley & Sons.

• Dorn, Anne, Daniel Dorn, and Paul Sengmueller. 2008. “Why Do People Trade?” Journal of Applied Finance (Fall/Winter): 37-50.

• Harvey, Campbell, Sandy Rattray, Andrew Sinclair, and Otto Van Hemert. 2016. “Man vs. Machine: Comparing Discretionary and Systematic Hedge Fund Performance.” The Journal of Portfolio Management White Paper, Man Group.

• Hilpisch, Yves. 2015. Derivatives Analytics with Python: Data Analysis, Models, Simulation, Calibration and Hedging. Wiley Finance. Resources under http://dawp.tpq.io.

• ⸻. 2018. Python for Finance: Mastering Data-Driven Finance. 2nd ed. Sebastopol: O’Reilly. Resources under https://py4fi.pqp.io.

• ⸻. 2020. Artificial Intelligence in Finance: A Python-Based Guide. Sebastopol: O’Reilly. Resources under https://aiif.pqp.io.

• Kissel, Robert. 2013. The Science of Algorithmic Trading and Portfolio Management. Amsterdam et al: Elsevier/Academic Press.

• Lewis, Michael. 2015. Flash Boys: Cracking the Money Code. New York, London: W.W. Norton & Company.

• McKinney, Wes. 2017. Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython. 2nd ed. Sebastopol: O’Reilly.

• Merton, Robert. 1973. “Theory of Rational Option Pricing.” Bell Journal of Economics and Management Science 4: 141-183.

• Narang, Rishi. 2013. Inside the Black Box: A Simple Guide to Quantitative and High Frequency Trading. Hoboken et al: John Wiley & Sons.

• Solomon, Lewis, and Louise Corso. 1991. “The Impact of Technology on the Trading of Securities: The Emerging Global Market and the Implications for Regulation.” The John Marshall Law Review 24 (2): 299-338.

• VanderPlas, Jake. 2016. Python Data Science Handbook: Essential Tools for Working with Data. Sebastopol: O’Reilly.

¹ “Too Squid to Fail.” The Economist, 29. October 2016.

² For details, see Hilpisch (2018, ch. 12).

³ For example, list objects are not only mutable, which means that they can be changed in size, but they can also contain almost any other kind of Python object, like int, float, tuple objects or list objects themselves.

⁴ See The Mathematics of the Rubik’s Cube or Algorithms for Solving Rubik’s Cube.

⁵ See Hilpisch (2015) for a detailed analysis of delta hedging strategies for European and American options using Python.

⁶ See the book by Lewis (2015) for a non-technical introduction to HFT.

⁷ Source: “66% of Fund Managers Can’t Match S&P Results.” USA Today, March 14, 2016.

⁸ Annualized performance (above the short-term interest rate) and risk measures for hedge fund categories comprising a total of 9,000 hedge funds over the period from June 1996 to December 2014.

⁹ See the book by Kissel (2013) for an overview of topics related to algorithmic trading, the book by Chan (2013) for an in-depth discussion of momentum and mean-reversion strategies, or the book by Narang (2013) for a coverage of quantitative and HFT trading in general.