Optical Communications, 2nd Edition

2.3 DETECTOR FIELD EXPANSIONS

Earlier in Section 1.6, the notion of an orthogonal spatial expansion of an optical field over a collecting area was introduced. This led to the idea of considering fields as sums of modulated orthogonal spatial functions. It can now be shown that a similar expansion can be made for the focused detector field. As might be expected, the latter can be directly related to the received field expansion.

Let the received field f_r(t, r) be expanded into orthonormal spatial functions as in Eq. (1.6.5),

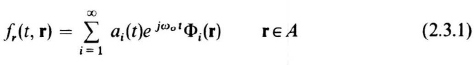
Then the focused field, via Fourier transformations, must have an associated expansion

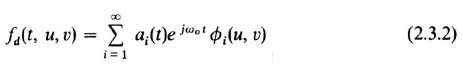
where ø_i(u, ν) is the focused field corresponding to Φ_i(x, y). That is,

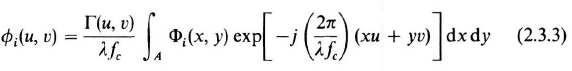
The focal-plane functions {ø_i(u, ν)} are the diffracted versions of the receiver functions {Φ_i(x, y)} and therefore are obtained by its Fourier transform. Using Parceval's theorem in Eq. (2.2.1), we can easily show that these focal-plane functions are themselves orthogonal, since the {Φ_i(x, y)} are orthogonal. Hence Eq. (2.3.2) itself represents an orthogonal expansion of the focused field over the focal plane, having the same coordinate time functions as the receiver field expansion. This means the focal-plane ...