Dominar Python para Bioinformática

Capítulo 4. Creación de la Secuencia de Fibonacci: Escribir, probar y comparar algoritmos

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

Escribir una implementación de la secuencia de Fibonacci es otro paso en el viaje del héroe para convertirse en codificador.La descripción de Rosalind Fibonacci señala que la génesis de la secuencia fue una simulación matemática de la cría de conejos que se basa en algunas suposiciones importantes (y poco realistas):

• El primer mes comienza con una pareja de conejos recién nacidos.

• Los conejos pueden reproducirse al cabo de un mes.

• Cada mes, cada conejo en edad reproductiva se aparea con otro conejo en edad reproductiva.

• Exactamente un mes después de que dos conejos se apareen, producen una camada del mismo tamaño.

• Los conejos son inmortales y nunca dejan de aparearse.

La secuencia comienza siempre con los números 0 y 1. Los números siguientes pueden generarse ad infinitum sumando los dos valores inmediatamente anteriores de la lista, como se muestra en la Figura 4-1.

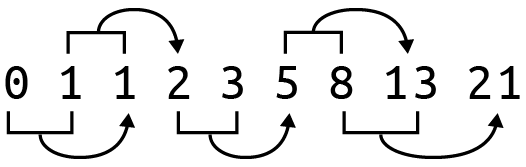
Figura 4-1. Los ocho primeros números de la secuencia de Fibonacci: tras el 0 y el 1 iniciales, los números siguientes se crean sumando los dos números anteriores.

Si buscas soluciones en Internet, encontrarás docenas de formas diferentes de generar la secuencia. Quiero centrarme en tres enfoques bastante diferentes. La primera solución utiliza un enfoque imperativo en el que el algoritmo define estrictamente cada paso.La siguiente solución utiliza una función generadora, y la última se centrará en una solución recursiva. La recursividad, aunque interesante, se ralentiza drásticamente a medida que intento generar más secuencia, pero resulta que los problemas de rendimiento pueden resolverse utilizando la memoria caché.

Aprenderás:

• Cómo validar manualmente los argumentos y lanzar errores

• Cómo utilizar una lista como pila

• Cómo escribir una función generadora

• Cómo escribir una función recursiva

• Por qué las funciones recursivas pueden ser lentas y cómo solucionarlo con la memoización

• Cómo utilizar los decoradores de funciones

Cómo empezar

El código y las pruebas de este capítulo se encuentran en el directorio 04_fib. Empieza copiando la primera solución en fib.py:

$ cd 04_fib/
$ cp solution1_list.py fib.py

Puedes utilizar n y k, pero yo opté por utilizar los nombres generations y litter:

$ ./fib.py -h
usage: fib.py [-h] generations litter

Calculate Fibonacci

positional arguments:
  generations  Number of generations
  litter       Size of litter per generation

optional arguments:
  -h, --help   show this help message and exit

Este será el primer programa que acepte argumentos que no sean cadenas. El reto Rosalind indica que el programa debe aceptar dos valores enteros positivos:

• n ≤ 40 que representa el número de generaciones

• k ≤ 5 que representa el tamaño de la camada producida por las parejas

Intenta pasar valores no enteros y observa cómo falla el programa:

$ ./fib.py foo
usage: fib.py [-h] generations litter
fib.py: error: argument generations: invalid int value: 'foo'

No se nota, pero además de imprimir el breve uso y un útil mensaje de error, el programa también generó un valor de salida distinto de cero. En la línea de comandos de Unix, un valor de salida de 0 indica éxito. Yo lo veo como "cero errores". En el intérprete de comandos bash, puedo inspeccionar la variable $? para ver el estado de salida del proceso más reciente. Por ejemplo, el comando echo Hello debería salir con un valor de 0, y de hecho lo hace:

$ echo Hello
Hello
$ echo $?
0

Vuelve a intentar el comando que falló anteriormente y, a continuación, inspecciona $?:

$ ./fib.py foo
usage: fib.py [-h] generations litter
fib.py: error: argument generations: invalid int value: 'foo'
$ echo $?
2

Que el estado de salida sea 2 no es tan importante como el hecho de que el valor no sea cero. Éste es un programa que se comporta bien porque rechaza un argumento no válido, imprime un mensaje de error útil y sale con un estado distinto de cero. Si este programa formara parte de una cadena de pasos de procesamiento de datos (como un Makefile, del que se habla en el Apéndice A), un valor de salida distinto de cero haría que todo el proceso se detuviera, lo cual es bueno. Los programas que aceptan silenciosamente valores no válidos y fallan silenciosamente o no fallan en absoluto pueden dar lugar a resultados irreproducibles. Es de vital importancia que los programas validen adecuadamente los argumentos y fallen de forma muy convincente cuando no puedan continuar.

El programa es muy estricto incluso con el tipo de número que acepta. Los valores deben ser enteros. También rechazará cualquier valor en coma flotante:

$ ./fib.py 5 3.2
usage: fib.py [-h] generations litter
fib.py: error: argument litter: invalid int value: '3.2'

Todos los argumentos de la línea de comandos del programa se reciben técnicamente como cadenas. Aunque 5 en la línea de comandos parezca el número 5, es el carácter "5". En esta situación, confío en que argparse intente convertir el valor de una cadena a un número entero. Cuando eso falla, argparse genera estos útiles mensajes de error.

Además, el programa rechaza valores para los parámetros generations y litter que no estén dentro de los rangos permitidos. Observa que el mensaje de error incluye el nombre del argumento y el valor infractor para proporcionar al usuario información suficiente para que puedas solucionarlo:

$ ./fib.py -3 2
usage: fib.py [-h] generations litter
fib.py: error: generations "-3" must be between 1 and 40 
$ ./fib.py 5 10
usage: fib.py [-h] generations litter
fib.py: error: litter "10" must be between 1 and 5 

El argumento generations de -3 no está en el rango de valores indicado.

El argumento litter de 10 es demasiado elevado.

Mira la primera parte de la solución para ver cómo hacer que esto funcione:

import argparse
from typing import NamedTuple


class Args(NamedTuple):
    """ Command-line arguments """
    generations: int 
    litter: int 


def get_args() -> Args:
    """ Get command-line arguments """

    parser = argparse.ArgumentParser(
        description='Calculate Fibonacci',
        formatter_class=argparse.ArgumentDefaultsHelpFormatter)

    parser.add_argument('gen', 
                        metavar='generations',
                        type=int, 
                        help='Number of generations')

    parser.add_argument('litter', 
                        metavar='litter',
                        type=int,
                        help='Size of litter per generation')

    args = parser.parse_args() 

    if not 1 <= args.gen <= 40: 
        parser.error(f'generations "{args.gen}" must be between 1 and 40') 

    if not 1 <= args.litter <= 5: 
        parser.error(f'litter "{args.litter}" must be between 1 and 5') 

    return Args(generations=args.gen, litter=args.litter) 

El campo generations debe ser un int.

El campo litter también debe ser un int.

El parámetro posicional gen se define primero, por lo que recibirá el primer valor posicional.

El type=int indica la clase requerida del valor. Observa que int indica la clase en sí, no el nombre de la clase.

El parámetro posicional litter se define en segundo lugar, por lo que recibirá el segundo valor posicional.

Intenta analizar los argumentos. Cualquier fallo provocará mensajes de error y la salida del programa con un valor distinto de cero.

El valor args.gen es ahora un valor real int, por lo que es posible realizar comparaciones numéricas con él. Comprueba si está dentro del rango aceptable.

Utiliza la función parser.error() para generar un error y salir del programa.

Comprueba también el valor del argumento args.litter.

Genera un error que incluya la información que el usuario necesita para solucionar el problema.

Si el programa llega a este punto, entonces los argumentos son valores enteros válidos dentro del rango aceptado, por lo que devuelve el Args.

Podría comprobar que los valores generations y litter están en los rangos correctos en la función main(), pero prefiero hacer la mayor validación de argumentos posible dentro de la función get_args() para poder utilizar la función parser.error() para generar mensajes útiles y salir del programa con un valor distinto de cero.

Elimina el programa fib.py y empieza de nuevo con new.py o con el método que prefieras para crear un programa:

$ new.py -fp 'Calculate Fibonacci' fib.py
Done, see new script "fib.py".

Puedes sustituir la definición de get_args() por el código anterior, y luego modificar tu función main() del siguiente modo:

def main() -> None:
    args = get_args()
    print(f'generations = {args.generations}')
    print(f'litter = {args.litter}')

Ejecuta tu programa con entradas no válidas y verifica que ves los tipos de mensajes de error mostrados anteriormente. Prueba tu programa con valores aceptables y verifica que ves este tipo de salida:

$ ./fib.py 1 2
generations = 1
litter = 2

Ejecuta pytest para ver qué pasa y qué falla tu programa. Deberías pasar las cuatro primeras pruebas y fallar la quinta:

$ pytest -xv
========================== test session starts ==========================
...
tests/fib_test.py::test_exists PASSED                             [ 14%]
tests/fib_test.py::test_usage PASSED                              [ 28%]
tests/fib_test.py::test_bad_generations PASSED                    [ 42%]
tests/fib_test.py::test_bad_litter PASSED                         [ 57%]
tests/fib_test.py::test_1 FAILED                                  [ 71%] 

=============================== FAILURES ================================
________________________________ test_1 _________________________________

    def test_1():
        """runs on good input"""

        rv, out = getstatusoutput(f'{RUN} 5 3') 
        assert rv == 0
>       assert out == '19' 
E       AssertionError: assert 'generations = 5\nlitter = 3' == '19' 
E         - 19    
E         + generations = 5 
E         + litter = 3

tests/fib_test.py:60: AssertionError
======================== short test summary info ========================
FAILED tests/fib_test.py::test_1 - AssertionError: assert 'generations...
!!!!!!!!!!!!!!!!!!!!!!! stopping after 1 failures !!!!!!!!!!!!!!!!!!!!!!!
====================== 1 failed, 4 passed in 0.38s ======================

La primera prueba fallida. La prueba se detiene aquí debido a la bandera -x.

El programa se ejecuta con 5 para el número de generaciones y 3 para el tamaño de la camada.

La salida debe ser 19.

Esto indica que las dos cadenas comparadas no son iguales.

El valor esperado era 19.

Esta es la salida que se recibió.

La salida de pytest se esfuerza por señalar exactamente lo que salió mal. Muestra cómo se ejecutó el programa y lo que se esperaba frente a lo que se produjo. Se supone que el programa debe imprimir 19, que es el quinto número de la secuencia de Fibonacci cuando se utiliza un tamaño de camada de 3. Si quieres terminar el programa por tu cuenta, ponte manos a la obra. Deberías utilizar pytest para verificar que superas todas las pruebas. Además, ejecuta make test para comprobar tu programa utilizando pylint, flake8, y mypy. Si quieres un poco de orientación, te explicaré el primer enfoque que describí.

Un enfoque imperativo

La figura 4-2 representa el crecimiento de la secuencia de Fibonacci. Los conejos más pequeños indican parejas no reproductoras que deben madurar para convertirse en parejas reproductoras más grandes.

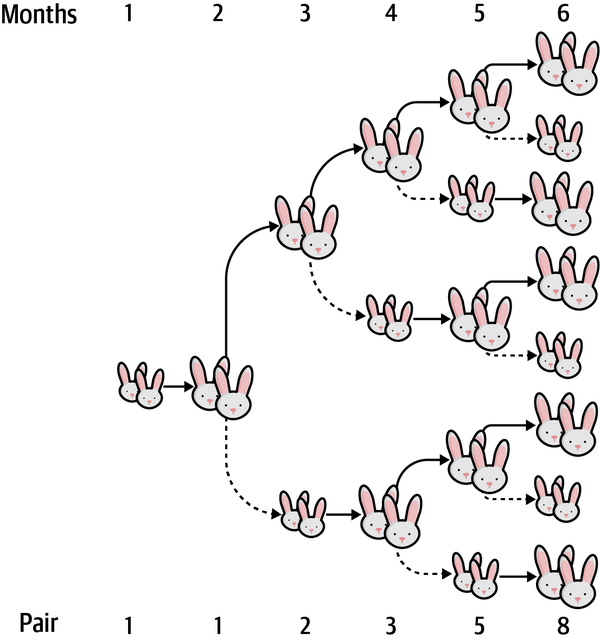
Figura 4-2. Visualización del crecimiento de la secuencia de Fibonacci a medida que se aparean parejas de conejos utilizando un tamaño de camada de 1

Puedes ver que para generar cualquier número después de los dos primeros, necesito conocer los dos números anteriores. Puedo utilizar esta fórmula para describir el valor de cualquier posición n de la sucesión de Fibonacci(F):

$$F_n=F_{n-1}+F_{n-2}$$

¿Qué tipo de estructura de datos en Python me permitiría mantener una secuencia de números en orden y referirme a ellos por su posición?Una lista. Empezaré con_F1 = 0 y _F2 = 1:

>>> fib = [0, 1]

El valor _F3 es _F2 +_F1 = 1 + 0 = 1. Al generar el siguiente número, siempre estaré haciendo referencia a los dos últimos elementos de la secuencia. Lo más fácil será utilizar la indexación negativa para indicar una posición desde el final de la lista.El último valor de una lista siempre está en la posición -1:

>>> fib[-1]
1

El penúltimo valor está en -2:

>>> fib[-2]
0

Tengo que multiplicar este valor por el tamaño de la camada para calcular el número de descendientes que creó esa generación. Para empezar, consideraré un tamaño de camada de 1:

>>> litter = 1
>>> fib[-2] * litter
0

Quiero sumar estos dos números y añadir el resultado a la lista:

>>> fib.append((fib[-2] * litter) + fib[-1])
>>> fib
[0, 1, 1]

Si vuelvo a hacerlo, veo que aparece la secuencia correcta:

>>> fib.append((fib[-2] * litter) + fib[-1])
>>> fib
[0, 1, 1, 2]

Necesito repetir esta acción generations veces. (Técnicamente será generations-1 veces porque Python utiliza indexación basada en 0.) Puedo utilizar la función range() de Python para generar una lista de números desde 0 hasta el valor final, pero sin incluirlo. Llamo a esta función únicamente por el efecto secundario de iterar un número determinado de veces, por lo que no necesito los valores producidos por la función range(). Es habitual utilizar la variable guión bajo (_) para indicar la intención de ignorar un valor:

>>> fib = [0, 1]
>>> litter = 1
>>> generations = 5
>>> for _ in range(generations - 1):
...     fib.append((fib[-2] * litter) + fib[-1])
...
>>> fib
[0, 1, 1, 2, 3, 5]

Esto debería bastarte para crear una solución que supere las pruebas. En la siguiente sección, trataré otras dos soluciones que ponen de relieve algunas partes muy interesantes de Python.

Soluciones

Todas las soluciones siguientes comparten la misma get_args() mostrada anteriormente.

Solución 1: Una solución imperativa utilizando una lista como pila

He aquí cómo escribí mi solución imperativa.Estoy utilizando una lista como una especie de pila para llevar la cuenta de los valores pasados. No necesito todos los valores, sólo los dos últimos, pero es bastante fácil hacer crecer la lista y referirse a los dos últimos valores:

def main() -> None:
    args = get_args()

    fib = [0, 1] 
    for _ in range(args.generations - 1): 
        fib.append((fib[-2] * args.litter) + fib[-1]) 

    print(fib[-1]) 

Comienza con 0 y 1.

Utiliza la función range() para crear el número adecuado de bucles.

Añade el siguiente valor a la secuencia.

Imprime el último número de la secuencia.

He utilizado el nombre de variable _ en el bucle for para indicar que no tengo intención de utilizar la variable. El guión bajo es un identificador válido de Python, y también es una convención utilizarlo para indicar un valor desechable. Las herramientas de linting, por ejemplo, podrían ver que he asignado algún valor a una variable pero que nunca la he utilizado, lo que normalmente indicaría un posible error. El guión bajo en la variable indica que no tengo intención de utilizar el valor. En este caso, estoy utilizando la función únicamente por el efecto secundario de crear el número de bucles necesarios. range()

Esto se considera una solución imperativa porque el código codifica directamente cada instrucción del algoritmo.Cuando leas la solución recursiva, verás que el algoritmo puede escribirse de forma más declarativa, lo que también tiene consecuencias imprevistas que debo manejar.

Una ligera variación de esto sería colocar este código dentro de una función que llamaré fib(). Ten en cuenta que en Python es posible declarar una función dentro de otra función, como aquí que crearé fib() dentro de main(). Hago esto para poder hacer referencia al parámetro args.litter, creando un cierre porque la función está capturando el valor en tiempo de ejecución del tamaño de la camada:

def main() -> None:
    args = get_args()

    def fib(n: int) -> int: 
        nums = [0, 1] 
        for _ in range(n - 1): 
            nums.append((nums[-2] * args.litter) + nums[-1]) 
        return nums[-1] 

    print(fib(args.generations)) 

Crea una función llamada fib() que acepte un parámetro entero n y devuelva un entero.

Este es el mismo código que antes. Observa que esta lista se llama nums para que no choque con el nombre de la función.

Utiliza la función range() para iterar las generaciones. Utiliza _ para ignorar los valores.

La función hace referencia al parámetro args.litter y crea así un cierre.

Utiliza return para devolver el valor final a la persona que llama.

Llama a la función fib() con el parámetro args.generations.

El ámbito de la función fib() del ejemplo anterior se limita a la función main().El ámbito se refiere a la parte del programa en la que es visible o legal un determinado nombre de función o variable.

No tengo que utilizar un cierre. He aquí cómo puedo expresar la misma idea con una función estándar:

def main() -> None:
    args = get_args()

    print(fib(args.generations, args.litter)) 

def fib(n: int, litter: int) -> int: 
    nums = [0, 1]
    for _ in range(n - 1):
        nums.append((nums[-2] * litter) + nums[-1])

    return nums[-1]

La función fib() debe llamarse con dos argumentos.

La función requiere tanto el número de generaciones como el tamaño de la camada. El cuerpo de la función es esencialmente el mismo.

En el código anterior, ves que debo pasar dos argumentos a fib(), mientras que el cierre sólo requería un argumento porque se capturaba litter. Vincular valores y reducir el número de parámetros es una razón válida para crear un cierre. Otra razón para escribir un cierre es limitar el alcance de una función. La definición de cierre de fib() sólo es válida dentro de la función main(), pero la versión anterior es visible en todo el programa. Ocultar una función dentro de otra dificulta su comprobación. En este caso, la función fib() es casi todo el programa, por lo que las pruebas ya se han escrito en tests/fib_test.py.

Solución 2: Crear una función generadora

En la solución anterior, generé la secuencia de Fibonacci hasta el valor solicitado y luego me detuve; sin embargo, la secuencia es infinita. ¿Podría crear una función que generara todos los números de la secuencia? Técnicamente, sí, pero nunca terminaría, con lo de ser infinita y todo eso.

Python tiene una forma de suspender una función que genera una secuencia posiblemente infinita. Puedo utilizar yield para devolver un valor de una función, abandonando temporalmente la función más tarde para reanudarla en el mismo estado cuando se solicite el siguiente valor.Este tipo de función se denomina generador, y he aquí cómo puedo utilizarla para generar la secuencia:

def fib(k: int) -> Generator[int, None, None]: 
    x, y = 0, 1 
    yield x 

    while True: 
        yield y 
        x, y = y * k, x + y 

La firma del tipo indica que la función toma el parámetro k (tamaño de la camada), que debe ser un int. Devuelve una función especial del tipo Generator que produce valores int y no tiene tipos de envío ni de retorno.

Sólo necesito hacer un seguimiento de las dos últimas generaciones, que inicializo a 0 y 1.

Cede el 0.

Crea un bucle infinito.

Cede la última generación.

Establece x (dos generaciones atrás) en la generación actual multiplicada por el tamaño de la camada. Establece y (una generación atrás) en la suma de las dos generaciones actuales.

Un generador actúa como un iterador, produciendo valores según lo solicite el código hasta que se agote.Puesto que este generador sólo generará valores de rendimiento, los tipos de envío y retorno son None. Por lo demás, este código hace exactamente lo mismo que la primera versión del programa, sólo que dentro de una función generadora de lujo. Mira la Figura 4-3 para ver cómo funciona la función para dos tamaños de camada diferentes.

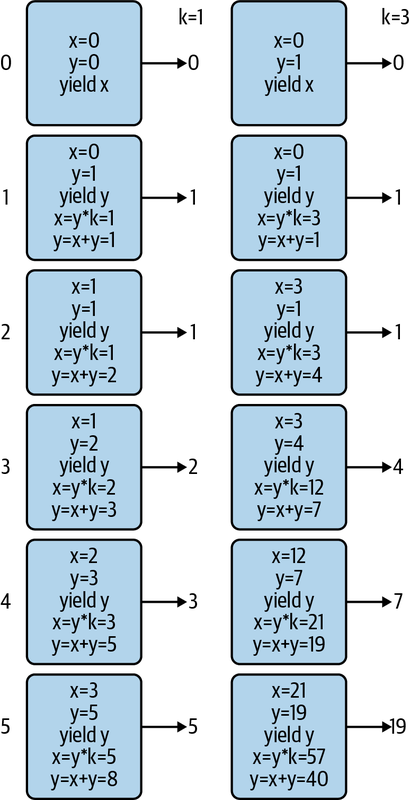
Figura 4-3. Representación de cómo cambia el estado del generador fib() a lo largo del tiempo (n=5) para dos tamaños de camada (k=1 y k=3)

La firma de tipos de Generator parece un poco complicada, ya que define tipos para yield, send y return. No necesito profundizar en ello aquí, pero te recomiendo que leas la documentación del módulo typing .

A continuación te explicamos cómo utilizarlo:

def main() -> None:
    args = get_args()
    gen = fib(args.litter) 
    seq = [next(gen) for _ in range(args.generations + 1)] 
    print(seq[-1]) 

La función fib() toma como argumento el tamaño de la camada y devuelve un generador.

Utiliza la función next() para recuperar el siguiente valor de un generador. Utiliza una comprensión de lista para hacer esto el número correcto de veces para generar la secuencia hasta el valor solicitado.

Imprime el último número de la secuencia.

La función range() es diferente porque la primera versión ya tenía los valores 0 y 1. Aquí tengo que llamar al generador dos veces más para producir esos valores.

Aunque prefiero la comprensión de lista, no necesito toda la lista, sólo me importa el valor final, así que podría haberlo escrito así:

def main() -> None:
    args = get_args()
    gen = fib(args.litter)
    answer = 0 
    for _ in range(args.generations + 1): 
        answer = next(gen) 
    print(answer) 

Inicializa la respuesta en 0.

Crea el número correcto de bucles.

Obtén el valor de la generación actual.

Imprime la respuesta.

Resulta que es bastante habitual llamar repetidamente a una función para generar una lista, por lo que existe una función que lo hace por nosotros. La función itertools.islice() "Crea un iterador que devuelve los elementos seleccionados de la iterable". He aquí cómo puedo utilizarla:

def main() -> None:
    args = get_args()
    seq = list(islice(fib(args.litter), args.generations + 1)) 
    print(seq[-1]) 

El primer argumento de islice() es la función a la que se llamará, y el segundo argumento es el número de veces que se llamará. La función es perezosa, así que utilizo list() para coaccionar los valores.

Imprime el último valor.

Como sólo utilizo la variable seq una vez, podría prescindir de esa asignación. Si la evaluación comparativa demostrara que la siguiente es la versión que mejor funciona, podría estar dispuesto a escribir una de una línea:

def main() -> None:
    args = get_args()
    print(list(islice(fib(args.litter), args.generations + 1))[-1])

El código inteligente es divertido, pero puede volverse ilegible.¹ Estás avisado.

Los generadores son geniales, pero más complejos que generar una lista. Son la forma adecuada de generar una secuencia de valores muy grande o potencialmente infinita porque son perezosos, sólo calculan el siguiente valor cuando tu código lo requiere.

Solución 3: Utilizar la Recursión y la Memoización

Aunque hay muchas más formas divertidas de escribir un algoritmo para producir una serie infinita de números, te mostraré sólo una más utilizando la recursividad, que es cuando una función se llama a sí misma:

def main() -> None:
    args = get_args()

    def fib(n: int) -> int: 
        return 1 if n in (1, 2) \ 
            else fib(n - 2) * args.litter + fib(n - 1) 

    print(fib(args.generations)) 

Define una función llamada fib() que tome el número de la generación deseada como un int y devuelva un int.

Si la generación es 1 o 2, devuelve 1. Este es el caso base que no hace una llamada recursiva.

Para todos los demás casos, llama a la función fib() dos veces, una para dos generaciones atrás y otra para la generación anterior. Factoriza el tamaño de la camada como antes.

Imprime los resultados de la función fib() para las generaciones dadas.

Aquí tienes otro ejemplo en el que defino una función fib() como cierre dentro de la función main() para utilizar el valor args.litter dentro de la función fib(). Esto es para cerrar alrededor de args.litter, vinculando efectivamente ese valor a la función. Si hubiera definido la función fuera de la función main(), habría tenido que pasar el argumento args.litter en las llamadas recursivas.

Esta es una solución realmente elegante que se enseña en casi todas las clases de iniciación a la informática. Es divertido estudiarla, pero resulta ser endiabladamente lenta porque acabo llamando a la función muchas veces. Es decir, fib(5) necesita llamar a fib(4) y fib(3) para sumar esos valores. A su vez, fib(4) necesita llamar a fib(3) y fib(2), y así sucesivamente.La Figura 4-4 muestra que fib(5) da lugar a 14 llamadas a la función para producir 5 valores distintos. Por ejemplo, fib(2) se calcula tres veces, pero sólo necesitamos calcularlo una vez.

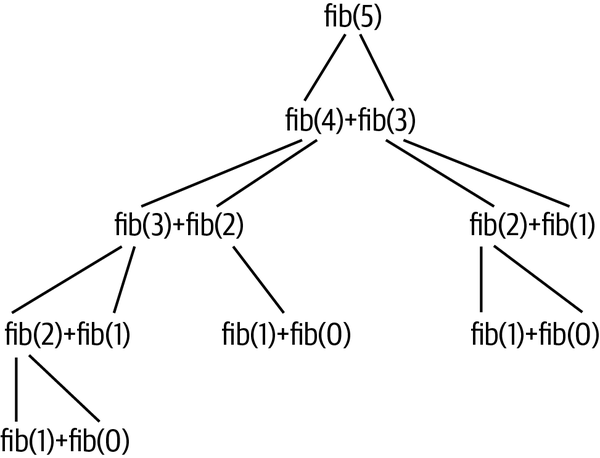
Figura 4-4. La pila de llamadas de fib(5) da lugar a muchas llamadas recursivas a la función, cuyo número aumenta aproximadamente de forma exponencial a medida que aumenta el valor de entrada

Para ilustrar el problema, tomaré una muestra de lo que tarda este programa en terminar hasta el máximo n de 40. De nuevo, utilizaré un bucle for en bash para mostrarte cómo se compara habitualmente un programa de este tipo en la línea de comandos:

$ for n in 10 20 30 40;
> do echo "==> $n <==" && time ./solution3_recursion.py $n 1
> done
==> 10 <==
55

real	0m0.045s
user	0m0.032s
sys	0m0.011s
==> 20 <==
6765

real	0m0.041s
user	0m0.031s
sys	0m0.009s
==> 30 <==
832040

real	0m0.292s
user	0m0.281s
sys	0m0.009s
==> 40 <==
102334155

real	0m31.629s
user	0m31.505s
sys	0m0.043s

El salto de 0,29s para n=30 a 31s para n=40 es enorme. Imagina llegar a 50 y más. Tengo que encontrar una forma de acelerar esto o abandonar toda esperanza de recursividad. La solución es almacenar en caché los resultados calculados previamente. Esto se llama memoización, y hay muchas formas de implementarla. El siguiente es un método. Ten en cuenta que necesitarás importar typing.Callable:

def memoize(f: Callable) -> Callable: 
    """ Memoize a function """

    cache = {} 

    def memo(x): 
        if x not in cache: 
            cache[x] = f(x) 
        return cache[x] 

    return memo 

Define una función que tome una función (algo que sea invocable) y devuelva una función.

Utiliza un diccionario para almacenar valores en caché.

Define memo() como un cierre alrededor de la caché. La función tomará algún parámetro x cuando sea llamada.

Comprueba si el valor del argumento está en la caché.

Si no, llama a la función con el argumento y establece la caché para ese valor del argumento en el resultado.

Devuelve el valor en caché del argumento.

Devuelve la nueva función.

Observa que la función memoize() devuelve una nueva función. En Python, las funciones se consideran objetos de primera clase, lo que significa que pueden utilizarse como otros tipos de variables: puedes pasarlas como argumentos y sobrescribir sus definiciones. La función memoize() es un ejemplo de función de orden superior (HOF) porque toma otras funciones como argumentos. Utilizaré otras HOF, como filter() y map(), a lo largo del libro.

Para utilizar la función memoize(), definiré fib() y luego la redefiniré con la versión memoizada. Si ejecutas esto, verás un resultado casi instantáneo, independientemente de lo alto que llegue n:

def main() -> None:
    args = get_args()

    def fib(n: int) -> int:
        return 1 if n in (1, 2) else fib(n - 2) * args.litter + fib(n - 1)

    fib = memoize(fib) 

    print(fib(args.generations))

Sobrescribe la definición existente de fib() con la función memoizada.

Un método preferido para conseguirlo utiliza un decorador, que es una función que modifica otra función:

def main() -> None:
    args = get_args()

    @memoize 
    def fib(n: int) -> int:
        return 1 if n in (1, 2) else fib(n - 2) * args.litter + fib(n - 1)

    print(fib(args.generations))

Decora la función fib() con la función memoize().

Por muy divertido que sea escribir funciones de memoización, de nuevo resulta que ésta es una necesidad tan común que otros ya nos la han resuelto. Puedo eliminar la función memoize() y, en su lugar, importar la función functools.lru_cache (caché de uso menos reciente):

from functools import lru_cache

Decora la función fib() con la función lru_cache() para conseguir la memoización con la mínima distracción:

def main() -> None:
    args = get_args()

    @lru_cache() 
    def fib(n: int) -> int:
        return 1 if n in (1, 2) else fib(n - 2) * args.litter + fib(n - 1)

    print(fib(args.generations))

Memoiza la función fib() mediante la decoración con la función lru_cache(). Ten en cuenta que Python 3.6 requiere los paréntesis, pero 3.8 y versiones posteriores no.

Evaluación comparativa de las soluciones

¿Cuál es la solución más rápida? Te he mostrado cómo utilizar un bucle for en bash con el comando time para comparar los tiempos de ejecución de los comandos:

$ for py in ./solution1_list.py ./solution2_generator_islice.py \
./solution3_recursion_lru_cache.py; do echo $py && time $py 40 5; done
./solution1_list.py
148277527396903091

real	0m0.070s
user	0m0.043s
sys	0m0.016s
./solution2_generator_islice.py
148277527396903091

real	0m0.049s
user	0m0.033s
sys	0m0.013s
./solution3_recursion_lru_cache.py
148277527396903091

real	0m0.041s
user	0m0.030s
sys	0m0.010s

Parece que la solución recursiva que utiliza la memoria caché LRU es la más rápida, pero de nuevo tengo muy pocos datos: sólo una ejecución por programa. Además, tengo que calcular a ojo estos datos y averiguar cuál es la más rápida.

Hay una forma mejor. He instalado una herramienta llamada hyperfine para ejecutar cada comando varias veces y comparar los resultados:

$ hyperfine -L prg ./solution1_list.py,./solution2_generator_islice.py,\
./solution3_recursion_lru_cache.py '{prg} 40 5' --prepare 'rm -rf __pycache__'
Benchmark #1: ./solution1_list.py 40 5
  Time (mean ± σ):      38.1 ms ±   1.1 ms    [User: 28.3 ms, System: 8.2 ms]
  Range (min … max):    36.6 ms …  42.8 ms    60 runs

Benchmark #2: ./solution2_generator_islice.py 40 5
  Time (mean ± σ):      38.0 ms ±   0.6 ms    [User: 28.2 ms, System: 8.1 ms]
  Range (min … max):    36.7 ms …  39.2 ms    66 runs

Benchmark #3: ./solution3_recursion_lru_cache.py 40 5
  Time (mean ± σ):      37.9 ms ±   0.6 ms    [User: 28.1 ms, System: 8.1 ms]
  Range (min … max):    36.6 ms …  39.4 ms    65 runs

Summary
  './solution3_recursion_lru_cache.py 40 5' ran
    1.00 ± 0.02 times faster than './solution2_generator_islice.py 40 5'
    1.01 ± 0.03 times faster than './solution1_list.py 40 5'

Parece que hyperfine ejecutó cada comando 60-66 veces, hizo una media de los resultados y descubrió que el programa solution3_recursion_lru_cache.py es quizás ligeramente más rápido. Otra herramienta de evaluación comparativa que puede resultarte útil es bench, pero puedes buscar otras herramientas de evaluación comparativa en Internet que quizá se adapten más a tus gustos.Sea cual sea la herramienta que utilices, la evaluación comparativa junto con las pruebas es vital para cuestionar las suposiciones sobre tu código.

He utilizado la opción --prepare para indicar a hyperfine que elimine el directorio pycache antes de ejecutar los comandos. Se trata de un directorio creado por Python para almacenar en caché el código de bytes del programa. Si el código fuente de un programa no ha cambiado desde la última vez que se ejecutó, Python puede saltarse la compilación y utilizar la versión del código de bytes que existe en el directorio pycache. Necesitaba eliminar esto porque hyperfine detectaba valores estadísticos atípicos al ejecutar los comandos, probablemente debido a los efectos de la caché.

Probando lo bueno, lo malo y lo feo

Para cada reto, espero que dediques parte de tu tiempo a leer las pruebas.Aprender a diseñar y escribir pruebas es tan importante como todo lo que te estoy mostrando. Como ya he dicho, mis primeras pruebas comprueban que el programa esperado existe y que producirá declaraciones de uso a petición. Después de eso, suelo dar entradas no válidas para asegurarme de que el programa falla. Me gustaría destacar las pruebas de los parámetros n y k incorrectos. Son esencialmente iguales, así que sólo mostraré la primera, ya que demuestra cómo seleccionar aleatoriamente un valor entero no válido, posiblemente negativo o demasiado alto:

def test_bad_n():
    """ Dies when n is bad """

    n = random.choice(list(range(-10, 0)) + list(range(41, 50))) 
    k = random.randint(1, 5) 
    rv, out = getstatusoutput(f'{RUN} {n} {k}') 
    assert rv != 0 
    assert out.lower().startswith('usage:') 
    assert re.search(f'n "{n}" must be between 1 and 40', out) 

Une las dos listas de rangos de números no válidos y selecciona un valor al azar.

Selecciona un número entero aleatorio en el intervalo comprendido entre 1 y 5 (ambos límites inclusive).

Ejecuta el programa con los argumentos y captura la salida.

Asegúrate de que el programa informó de un fallo (valor de salida distinto de cero).

Comprueba que la salida comienza con una declaración de uso.

Busca un mensaje de error que describa el problema con el argumento n.

A menudo me gusta utilizar valores no válidos seleccionados aleatoriamente cuando realizo pruebas. Esto se debe en parte a que escribo pruebas para estudiantes para que no escriban programas que fallen con una sola entrada incorrecta, pero también me ayuda a no codificar accidentalmente para un valor de entrada específico. Todavía no he cubierto el módulo random, pero te ofrece una forma de realizar elecciones pseudoaleatorias. Primero, tienes que importar el módulo:

>>> import random

Por ejemplo, puedes utilizar random.randint() para seleccionar un único número entero de un rango determinado:

>>> random.randint(1, 5)
2
>>> random.randint(1, 5)
5

O utiliza la función random.choice() para seleccionar aleatoriamente un único valor de alguna secuencia. Aquí quería construir un rango discontinuo de números negativos separados de un rango de números positivos:

>>> random.choice(list(range(-10, 0)) + list(range(41, 50)))
46
>>> random.choice(list(range(-10, 0)) + list(range(41, 50)))
-1

Todas las pruebas que siguen proporcionan buenas entradas al programa. Por ejemplo:

def test_2():
    """ Runs on good input """

    rv, out = getstatusoutput(f'{RUN} 30 4') 
    assert rv == 0 
    assert out == '436390025825' 

Estos son los valores que me dieron al intentar resolver el reto Rosalind.

El programa no debe fallar con esta entrada.

Esta es la respuesta correcta según Rosalind.

Las pruebas, como la documentación, son una carta de amor a tu yo futuro. Por muy tediosas que parezcan las pruebas, agradecerás que fallen cuando intentes añadir una función y acabes rompiendo accidentalmente algo que antes funcionaba. Escribir y ejecutar pruebas con asiduidad puede evitar que despliegues programas rotos.

Ejecutar el conjunto de pruebas en todas las soluciones

Has visto que en cada capítulo escribo varias soluciones para explorar diversas formas de resolver los problemas. Confío plenamente en mis pruebas para asegurarme de que mis programas son correctos. Puede que tengas curiosidad por ver cómo he automatizado el proceso de comprobación de cada solución. Mira el Makefile y busca el objetivo all:

$ cat Makefile
.PHONY: test

test:
	python3 -m pytest -xv --flake8 --pylint --mypy fib.py tests/fib_test.py

all:
    ../bin/all_test.py fib.py

El programa all_test.py sobrescribirá el programa fib.py con cada una de las soluciones antes de ejecutar el conjunto de pruebas. Esto podría sobrescribir tu solución. Asegúrate de confirmar tu versión en Git o al menos haz una copia antes de ejecutar make all o podrías perder tu trabajo.

Lo que sigue es el programa all_test.py que ejecuta el objetivo all. Lo dividiré en dos partes, empezando por la primera hasta llegar a get_args(). La mayor parte ya debería resultarte familiar:

#!/usr/bin/env python3
""" Run the test suite on all solution*.py """

import argparse
import os
import re
import shutil
import sys
from subprocess import getstatusoutput
from functools import partial
from typing import NamedTuple


class Args(NamedTuple):
    """ Command-line arguments """
    program: str 
    quiet: bool 


# --------------------------------------------------
def get_args() -> Args:
    """ Get command-line arguments """

    parser = argparse.ArgumentParser(
        description='Run the test suite on all solution*.py',
        formatter_class=argparse.ArgumentDefaultsHelpFormatter)

    parser.add_argument('program', metavar='prg', help='Program to test') 

    parser.add_argument('-q', '--quiet', action='store_true', help='Be quiet') 

    args = parser.parse_args()

    return Args(args.program, args.quiet)

El nombre del programa a probar, que en este caso es fib.py.

Un valor booleano de True o False para crear más o menos salida.

El tipo por defecto es str.

El action='store_true' lo convierte en una bandera booleana. Si la bandera está presente, el valor será True, y será False en caso contrario.

La función main() es donde se realizan las pruebas:

def main() -> None:
    args = get_args()
    cwd = os.getcwd() 
    solutions = list( 
        filter(partial(re.match, r'solution.*\.py'), os.listdir(cwd))) 

    for solution in sorted(solutions): 
        print(f'==> {solution} <==')
        shutil.copyfile(solution, os.path.join(cwd, args.program)) 
        subprocess.run(['chmod', '+x', args.program], check=True) 
        rv, out = getstatusoutput('make test') 
        if rv != 0: 
            sys.exit(out) 

        if not args.quiet: 
            print(out)

    print('Done.') 

Obtiene el directorio de trabajo actual, que será el directorio 04_fib si estás en ese directorio cuando ejecutes el comando.

Busca todos los archivos solution*.py en el directorio actual.

Tanto filter() como partial() son HOF; lo explicaré a continuación.

Los nombres de los archivos estarán en orden aleatorio, así que itera por los archivos ordenados.

Copia el archivo solution*.py en el nombre del archivo de pruebas.

Haz que el programa sea ejecutable.

Ejecuta el comando make test, y captura el valor de retorno y la salida.

Comprueba si el valor de retorno no es 0.

Sal de este programa mientras imprime la salida de la prueba y devuelve un valor distinto de cero.

A menos que se suponga que el programa es silencioso, imprime la salida de la prueba.

Haz saber al usuario que el programa finaliza normalmente.

En el código anterior, estoy utilizando sys.exit() para detener inmediatamente el programa, imprimir un mensaje de error y devolver un valor de salida distinto de cero. Si consultas la documentación, verás que puedes invocar sys.exit() sin argumentos, con un valor entero o con un objeto como una cadena, que es lo que estoy utilizando:

exit(status=None, /)
    Exit the interpreter by raising SystemExit(status).

    If the status is omitted or None, it defaults to zero (i.e., success).
    If the status is an integer, it will be used as the system exit status.
    If it is another kind of object, it will be printed and the system
    exit status will be one (i.e., failure).

El programa anterior también utiliza las funciones filter() o partial(), de las que aún no he hablado. Ambas son HOF. Te explicaré cómo y por qué las utilizo. Para empezar, la función os.listdir() devolverá todo el contenido de un directorio, incluidos archivos y directorios:

>>> import os
>>> files = os.listdir()

Hay mucho ahí, así que importaré la función pprint() del módulo pprint para imprimir esto de forma bonita:

>>> from pprint import pprint
>>> pprint(files)
['solution3_recursion_memoize_decorator.py',
 'solution2_generator_for_loop.py',
 '.pytest_cache',
 'Makefile',
 'solution2_generator_islice.py',
 'tests',
 '__pycache__',
 'fib.py',
 'README.md',
 'solution3_recursion_memoize.py',
 'bench.html',
 'solution2_generator.py',
 '.mypy_cache',
 '.gitignore',
 'solution1_list.py',
 'solution3_recursion_lru_cache.py',
 'solution3_recursion.py']

Quiero filtrarlos a nombres que empiecen por solución y terminen por .py.En la línea de comandos, haría coincidir este patrón utilizando un glob de archivo como solution*.py, donde * significa cero o más de cualquier carácter y . es un punto literal. Una versión de expresión regular de este patrón es la ligeramente más complicada solution.*\.py, donde . (punto) es un metacarácter regex que representa cualquier carácter, y * (estrella o asterisco) significa cero o más (ver Figura 4-5). Para indicar un punto literal, necesito escaparlo con una barra invertida (\.). Ten en cuenta que es prudente utilizar la cadena r( cadenasin procesar ) para encerrar este patrón.

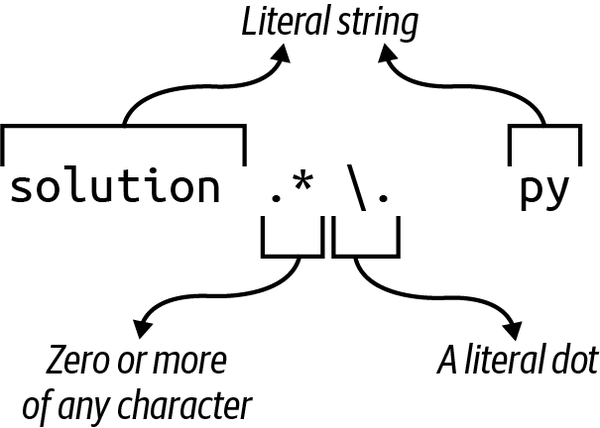
Figura 4-5. Una expresión regular para buscar archivos que coincidan con el archivo glob solution*.py

Cuando la coincidencia es correcta, se devuelve un objeto re.Match:

>>> import re
>>> re.match(r'solution.*\.py', 'solution1.py')
<re.Match object; span=(0, 12), match='solution1.py'>

Cuando falla una coincidencia, se devuelve el valor None. Aquí tengo que utilizar type() porque el valor None no se muestra en el REPL:

>>> type(re.match(r'solution.*\.py', 'fib.py'))
<class 'NoneType'>

Quiero aplicar esta coincidencia a todos los archivos devueltos por os.listdir(). Puedo utilizar filter() y la palabra clave lambda para crear una función anónima. Cada nombre de archivo de files se pasa como argumento name utilizado en la coincidencia. La función filter() sólo devolverá los elementos que devuelvan un valor verdadero de la función dada, por lo que se excluirán los nombres de archivo que devuelvan None al no coincidir:

>>> pprint(list(filter(lambda name: re.match(r'solution.*\.py', name), files)))
['solution3_recursion_memoize_decorator.py',
 'solution2_generator_for_loop.py',
 'solution2_generator_islice.py',
 'solution3_recursion_memoize.py',
 'solution2_generator.py',
 'solution1_list.py',
 'solution3_recursion_lru_cache.py',
 'solution3_recursion.py']

Verás que la función re.match() toma dos argumentos: un patrón y una cadena que debe coincidir. La función partial() me permite aplicar parcialmente la función, y el resultado es una nueva función.Por ejemplo, la función operator.add() espera dos valores y devuelve su suma:

>>> import operator
>>> operator.add(1, 2)
3

Puedo crear una función que añada 1 a cualquier valor, así:

>>> from functools import partial
>>> succ = partial(op.add, 1)

La función succ() requiere un argumento, y devolverá el sucesor:

>>> succ(3)
4
>>> succ(succ(3))
5

Del mismo modo, puedo crear una función f() que aplique parcialmente la función re.match() con su primer argumento, un patrón de expresión regular:

>>> f = partial(re.match, r'solution.*\.py')

La función f() está esperando una cadena para aplicar la coincidencia:

>>> type(f('solution1.py'))
<class 're.Match'>
>>> type(f('fib.py'))
<class 'NoneType'>

Si lo llamas sin argumento, obtendrás una excepción:

>>> f()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: match() missing 1 required positional argument: 'string'

Puedo sustituir lambda por la función aplicada parcialmente como primer argumento de filter():

>>> pprint(list(filter(f, files)))
['solution3_recursion_memoize_decorator.py',
 'solution2_generator_for_loop.py',
 'solution2_generator_islice.py',
 'solution3_recursion_memoize.py',
 'solution2_generator.py',
 'solution1_list.py',
 'solution3_recursion_lru_cache.py',
 'solution3_recursion.py']

Mi estilo de programación se basa en gran medida en ideas de programación puramente funcional, que me parece como jugar con ladrillos de LEGO: las funciones pequeñas, bien definidas y probadas pueden componer programas más grandes que funcionen bien.

Ir más lejos

Hay muchos estilos diferentes de programación, como la procedimental, la funcional, la orientada a objetos, etc. Incluso dentro de un lenguaje orientado a objetos como Python, puedo utilizar enfoques muy diferentes para escribir código. La primera solución podría considerarse un enfoque de programación dinámica, porque intentas resolver el problema más grande resolviendo primero problemas más pequeños. Si te interesan las funciones recursivas, el problema de la Torre de Hanoi es otro ejercicio clásico. Los lenguajes puramente funcionales como Haskell evitan en su mayoría construcciones como los bucles for y se basan en gran medida en la recursividad y las funciones de orden superior.Tanto los lenguajes orales como los de programación conforman nuestra forma de pensar, y te animo a que intentes resolver este problema utilizando otros lenguajes que conozcas para ver cómo podrías escribir soluciones diferentes.

Revisa

Puntos clave de este capítulo:

• Dentro de la función get_args(), puedes realizar una validación manual de los argumentos y utilizar la función parser.error() para generar manualmente errores argparse.

• Puedes utilizar una lista como una pila, introduciendo y extrayendo elementos.

• Utilizar yield en una función la convierte en un generador. Cuando la función produce un valor, éste se devuelve y el estado de la función se conserva hasta que se solicita el siguiente valor. Los generadores pueden utilizarse para crear un flujo potencialmente infinito de valores.

• Una función recursiva se llama a sí misma, y la recursión puede causar graves problemas de rendimiento. Una solución es utilizar la memoización para almacenar valores en caché y evitar el recálculo.

• Las funciones de orden superior son funciones que toman otras funciones como argumentos.

• Los decoradores de funciones de Python aplican HOFs a otras funciones.

• La evaluación comparativa es una técnica importante para determinar el algoritmo de mejor rendimiento. Las herramientas hyperfine y bench te permiten comparar los tiempos de ejecución de los comandos a lo largo de muchas iteraciones.

• El módulo random ofrece muchas funciones para la selección pseudoaleatoria de valores.

¹ Como observaron los legendarios David St. Hubbins y Nigel Tufnel: "Hay una línea muy fina entre lo estúpido y lo inteligente".