Vorstoß in die Analytik

Kapitel 4. Korrelation und Regression

Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: [e-mail]

Hast du schon gehört, dass der Konsum von Eiscreme mit Haiangriffen in Verbindung gebracht wird? Offenbar hat Jaws einen tödlichen Appetit auf Mint Chocolate Chip. Abbildung 4-1 veranschaulicht diesen vermuteten Zusammenhang.

Abbildung 4-1. Der vorgeschlagene Zusammenhang zwischen Eiscremekonsum und Hai-Angriffen

"Das stimmt nicht", wirst du vielleicht erwidern. "Das bedeutet nicht unbedingt, dass Haiangriffe durch den Verzehr von Eiscreme ausgelöst werden."

"Es könnte sein", schlussfolgerst du, "dass bei steigenden Außentemperaturen mehr Eiscreme konsumiert wird. Außerdem halten sich die Menschen bei warmem Wetter mehr am Meer auf, und das führt zu mehr Haiangriffen."

"Korrelation bedeutet nicht gleich Ursache"

Du hast wahrscheinlich schon oft gehört, dass "Korrelation nicht gleichbedeutend mit Kausalität ist".

In Kapitel 3 hast du gelernt, dass Kausalität in der Statistik ein heikler Begriff ist. Wir verwerfen eigentlich nur die Nullhypothese, weil wir einfach nicht alle Daten haben, um die Kausalität mit Sicherheit behaupten zu können. Abgesehen von diesem semantischen Unterschied: Hat Korrelation etwas mit Kausalität zu tun? Der Standardausdruck vereinfacht die Beziehung etwas zu sehr; du wirst in diesem Kapitel sehen, warum, wenn du die Werkzeuge der Inferenzstatistik verwendest, die du bereits kennengelernt hast.

Dieses letzte Kapitel wird hauptsächlich in Excel durchgeführt. Danach hast du das Grundgerüst der Analytik so weit verstanden, dass du dich mit R und Python beschäftigen kannst.

Die Einführung der Korrelation

Bis jetzt haben wir meistens nur eine Variable nach der anderen analysiert: Wir haben zum Beispiel die durchschnittliche Leseleistung oder die Varianz der Immobilienpreise ermittelt. Dies ist als univariate Analyse bekannt.

Wir haben auch eine bivariate Analyse durchgeführt. Zum Beispiel haben wir die Häufigkeiten von zwei kategorialen Variablen mit einer Zwei-Wege-Häufigkeitstabelle verglichen. Wir haben auch eine kontinuierliche Variable analysiert, wenn sie nach mehreren Stufen einer kategorialen Variable gruppiert wurde, und haben für jede Gruppe eine deskriptive Statistik erstellt.

Wir werden nun ein bivariates Maß für zwei kontinuierliche Variablen mithilfe der Korrelation berechnen. Genauer gesagt werden wir den Korrelationskoeffizienten nach Pearson verwenden, um die Stärke der linearen Beziehung zwischen zwei Variablen zu messen. Ohne eine lineare Beziehung ist die Pearson-Korrelation ungeeignet.

Wie können wir also wissen, dass unsere Daten linear sind? Es gibt strengere Methoden zur Überprüfung, aber wie immer ist eine Visualisierung ein guter Anfang. Wir werden ein Streudiagramm verwenden, um alle Beobachtungen anhand ihrer x- und y-Koordinaten darzustellen.

Wenn es den Anschein hat, dass eine Linie durch das Streudiagramm gezogen werden kann, die das Gesamtmuster zusammenfasst, dann handelt es sich um eine lineare Beziehung und die Pearson-Korrelation kann verwendet werden. Wenn du eine Kurve oder eine andere Form brauchst, um das Muster zusammenzufassen, ist das Gegenteil der Fall. In Abbildung 4-2 sind eine lineare und zwei nichtlineare Beziehungen dargestellt.

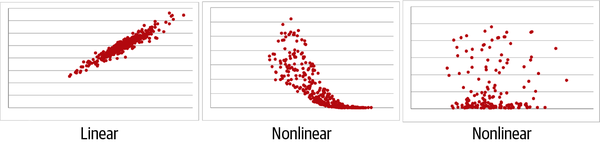
Abbildung 4-2. Lineare versus nichtlineare Beziehungen

Abbildung 4-2 zeigt ein Beispiel für eine positive lineare Beziehung: Wenn die Werte auf der x-Achse steigen, steigen auch die Werte auf der y-Achse (mit einer linearen Rate).

Es ist auch möglich, eine negative Korrelation zu haben, bei der eine negative Linie die Beziehung zusammenfasst, oder überhaupt keine Korrelation, bei der eine flache Linie die Beziehung zusammenfasst. Diese verschiedenen Arten von linearen Beziehungen sind in Abbildung 4-3 dargestellt. Erinnere dich daran, dass es sich um lineare Beziehungen handeln muss, damit eine Korrelation vorliegt.

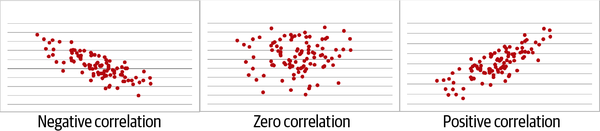
Abbildung 4-3. Negative, Null- und positive Korrelationen

Sobald wir festgestellt haben, dass die Daten linear sind, können wir den Korrelationskoeffizienten ermitteln. Er nimmt immer einen Wert zwischen -1 und 1 an, wobei -1 für eine perfekte negative lineare Beziehung, 1 für eine perfekte positive lineare Beziehung und 0 für gar keine lineare Beziehung steht. Tabelle 4-1 zeigt einige Faustregeln für die Bewertung der Stärke eines Korrelationskoeffizienten. Es handelt sich dabei keineswegs um offizielle Standards, sondern um einen nützlichen Anhaltspunkt für die Interpretation.

Tabelle 4-1. Interpretation der Korrelationskoeffizienten

Korrelationskoeffizient	Interpretation
-1.0	Perfektes negatives lineares Verhältnis
-0.7	Starke negative Beziehung
-0.5	Mäßig negative Beziehung
-0.3	Schwache negative Beziehung
0	Keine lineare Beziehung
+0.3	Schwache positive Beziehung
+0.5	Mäßig positive Beziehung
+0.7	Starke positive Beziehung
+1.0	Perfekte positive lineare Beziehung

Mit dem grundlegenden konzeptionellen Rahmen für Korrelationen im Hinterkopf, wollen wir nun eine Analyse in Excel durchführen. Wir werden einen Datensatz für den Kilometerstand von Fahrzeugen verwenden; du findest mpg.xlsx im Unterordner mpg des Ordners datasets des Buches. Dies ist ein neuer Datensatz, also nimm dir etwas Zeit, um ihn kennenzulernen: Mit welchen Variablen arbeiten wir? Fasse sie zusammen und visualisiere sie mit den in Kapitel 1 behandelten Tools. Um die spätere Analyse zu erleichtern, vergiss nicht, eine Indexspalte hinzuzufügen und den Datensatz in eine Tabelle zu konvertieren, die ich mpg nennen werde.

Excel enthält die Funktion CORREL() zur Berechnung des Korrelationskoeffizienten zwischen zwei Arrays:

CORREL(array1, array2)

Verwenden wir diese Funktion, um die Korrelation zwischen weight undmpg in unserem Datensatz zu finden:

=CORREL(mpg[weight], mpg[mpg])

Das ergibt tatsächlich einen Wert zwischen -1 und 1: -0,832. (Erinnerst du dich, wie das zu interpretieren ist?)

Eine Korrelationsmatrix stellt die Korrelationen zwischen allen Variablenpaaren dar. Wir erstellen eine solche Matrix mit dem Data Analysis ToolPak. Gehe im Menüband zu Daten → Datenanalyse → Korrelation.

Erinnere dich daran, dass es sich hier um ein Maß für die lineare Beziehung zwischen zweikontinuierlichen Variablen handelt. Deshalb sollten wir kategorische Variablen wie die Herkunft und diskrete Variablen wie Zylinder oder Modell.Jahr mit Bedacht einbeziehen. Das ToolPak besteht darauf, dass alle Variablen in einem zusammenhängenden Bereich liegen, also schließe ich vorsichtig Zylinder ein. Abbildung 4-4 zeigt, wie das ToolPak-Quellmenü aussehen sollte.

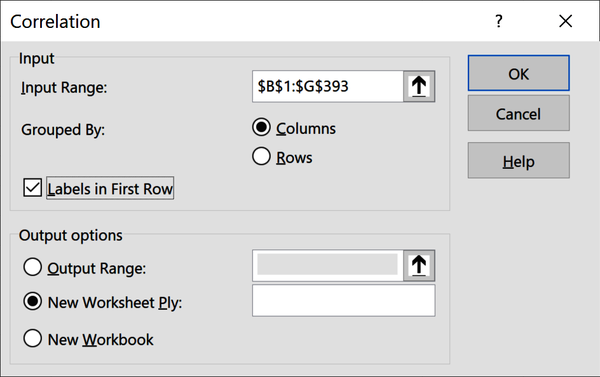
Abbildung 4-4. Einfügen einer Korrelationsmatrix in Excel

Daraus ergibt sich eine Korrelationsmatrix wie in Abbildung 4-5 dargestellt.

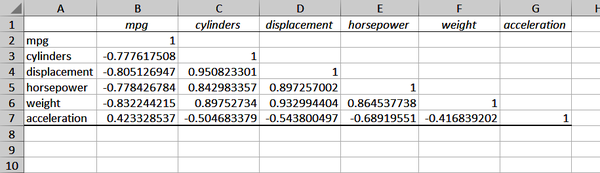
Abbildung 4-5. Korrelationsmatrix in Excel

Wir können die -0,83 in Zelle B6 sehen: Das ist der Schnittpunkt von Gewicht undmpg. Wir würden denselben Wert auch in der Zelle F2 sehen, aber Excel hat diese Hälfte der Matrix leer gelassen, da es sich um überflüssige Informationen handelt. Alle Werte entlang der Diagonale sind 1, da jede Variable perfekt mit selbst korreliert ist.

Warnung

Der Korrelationskoeffizient nach Pearson ist nur dann ein geeignetes Maß, wenn die Beziehung zwischen den beiden Variablen linear ist.

Wir haben einen großen Sprung in unseren Annahmen über unsere Variablen gemacht, indem wir ihre Korrelationen analysiert haben. Kannst du dir vorstellen, was das ist? Wir haben angenommen, dass ihre Beziehung linear ist. Lass uns diese Annahme mit Streudiagrammen überprüfen. Leider gibt es in Excel keine Möglichkeit, Streudiagramme für jedes Variablenpaar auf einmal zu erstellen. Um zu üben, solltest du sie alle aufstellen, aber wir versuchen es mit den Variablen Gewicht und Benzinverbrauch. Markiere diese Daten, gehe dann zum Menüband und klicke auf Einfügen → Streuung.

Ich werde einen benutzerdefinierten Diagrammtitel hinzufügen und die Achsen neu beschriften, um die Interpretation zu erleichtern. Um den Titel des Diagramms zu ändern, doppelklicke auf ihn. Um die Achsen neu zu beschriften, klickst du auf den Rand des Diagramms und wählst dann das Pluszeichen, das erscheint, um das Menü Diagrammelemente zu erweitern. (Auf dem Mac klickst du in das Diagramm und dann auf Diagrammdesign → Diagrammelement hinzufügen. Abbildung 4-6 zeigt das entstehende Streudiagramm. Es ist keine schlechte Idee, die Achsen mit Maßeinheiten zu versehen, damit Außenstehende die Daten besser verstehen können.

Abbildung 4-6 sieht im Grunde wie eine negative lineare Beziehung aus, mit einer größeren Streuung bei niedrigeren Gewichten und höheren Fahrleistungen. Standardmäßig hat Excel die erste Variable in unserer Datenauswahl entlang der x-Achse und die zweite entlang der y-Achse aufgetragen. Aber warum nicht andersherum? Versuche, die Reihenfolge dieser Spalten in deinem Arbeitsblatt so zu ändern, dass das Gewicht in der Spalte E und der Kilometerstand in der Spalte F steht, und füge dann ein neues Streudiagramm ein.

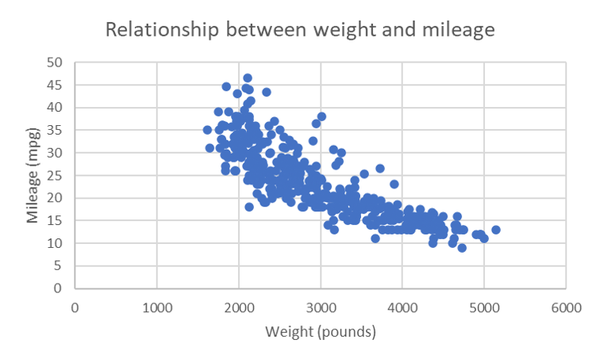
Abbildung 4-6. Streudiagramm von Gewicht und Kilometerstand

Abbildung 4-7 zeigt ein Spiegelbild der Beziehung. Excel ist ein großartiges Werkzeug, aber wie bei jedem Werkzeug musst du ihm sagen, was es tun soll. Excel berechnet Korrelationen unabhängig davon, ob die Beziehung linear ist. Es erstellt dir auch ein Streudiagramm, ohne sich darum zu kümmern, welche Variable auf welche Achse gehört.

Welches Streudiagramm ist also "richtig"? Ist das wichtig? Gemäß der Konvention von wird die unabhängige Variable auf der x-Achse und die abhängige Variable auf der y-Achse dargestellt. Nimm dir einen Moment Zeit, um zu überlegen, was was ist. Wenn du dir nicht sicher bist, erinnere dich daran, dass die unabhängige Variable in der Regel diejenige ist, die zuerst gemessen wurde.

Unsere unabhängige Variable ist das Gewicht, weil es durch die Konstruktion und den Bau des Autos bestimmt wurde. Der Benzinverbrauch ist die abhängige Variable, weil wir davon ausgehen, dass er durch das Gewicht des Autos beeinflusst wird. Damit liegt das Gewichtauf der x-Achse und der Benzinverbrauch auf der y-Achse.

In der Geschäftsanalytik ist es unüblich, Daten nur um der statistischen Analyse willen gesammelt zu haben; die Autos in unseremmpg-Datensatz wurden zum Beispiel gebaut, um Einnahmen zu generieren, nicht für eine Forschungsstudie über den Einfluss des Gewichts auf den Kilometerstand. Da es nicht immer klare unabhängige und abhängige Variablen gibt, müssen wir uns umso mehr bewusst sein, was diese Variablen messen und wie sie gemessen werden. Deshalb ist es so wichtig, dass du dich in dem Bereich auskennst, den du untersuchst, oder zumindest deine Variablen beschreibst und weißt, wie deine Beobachtungen gesammelt wurden .

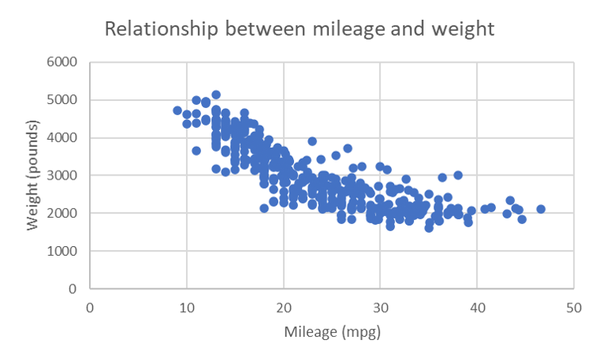
Abbildung 4-7. Streudiagramm von Kilometerstand und Gewicht

Von der Korrelation zur Regression

Obwohl es üblich ist, die unabhängige Variable auf der x-Achse zu platzieren, macht das keinen Unterschied für den Korrelationskoeffizienten. Allerdings gibt es hier einen großen Vorbehalt, der sich auf die frühere Idee bezieht, eine Linie zu verwenden, um die durch das Streudiagramm gefundene Beziehung zusammenzufassen. Diese Methode weicht von der Korrelation ab und ist dir vielleicht schon bekannt: die lineare Regression.

Die Korrelation ist unabhängig davon, welche Variable du als unabhängig und welche du als abhängig bezeichnest; das spielt bei ihrer Definition als "das Ausmaß, in dem sich zwei Variablen linear zueinander bewegen", keine Rolle.

Andererseits ist die lineare Regression von Natur aus von dieser Beziehung betroffen, da sie "die geschätzte Auswirkung einer Einheitsänderung der unabhängigen Variable X auf die abhängige Variable Y" darstellt.

Du wirst sehen, dass die Linie, die wir durch unser Streudiagramm ziehen, als Gleichung ausgedrückt werden kann. Anders als der Korrelationskoeffizient hängt diese Gleichung davon ab, wie wir unsere unabhängigen und abhängigen Variablen definieren.

Lineare Regression und lineare Modelle

Du wirst oft hören, dass die lineare Regression als lineares Modell bezeichnet wird, was nur eines von vielen statistischen Modellen ist. Genau wie ein Modellzug, den du bauen könntest, dient ein statistisches Modell als praktikable Annäherung an einen realen Sachverhalt. Wir verwenden statistische Modelle insbesondere, um die Beziehung zwischen abhängigen und unabhängigen Variablen zu verstehen. Modelle können zwar nicht alles erklären, was sie darstellen, aber das heißt nicht, dass sie nicht hilfreich sein können. Aber wie der britische Mathematiker George Box schon sagte: "Alle Modelle sind falsch, aber einige sind nützlich."

Wie die Korrelation geht auch die lineare Regression davon aus, dass eine lineare Beziehung zwischen den beiden Variablen besteht. Es gibt noch weitere Annahmen, die bei der Modellierung von Daten zu berücksichtigen sind. Wir wollen zum Beispiel keine extremen Beobachtungen haben, die den Gesamttrend der linearen Beziehung unverhältnismäßig stark beeinflussen könnten.

Für die Zwecke unserer Demonstration lassen wir diese und andere Annahmen erst einmal außer Acht. Diese Annahmen lassen sich mit Excel oft nur schwer überprüfen; deine Kenntnisse in statistischer Programmierung werden dir bei der Untersuchung der tieferen Aspekte der linearen Regression gute Dienste leisten.

Atme tief durch; es ist Zeit für eine weitere Gleichung:

Gleichung 4-1. Die Gleichung für die lineare Regression

$$Y={\beta }_0+{\beta }_1\times X+ϵ$$

Das Ziel von Gleichung 4-1 ist die Vorhersage unserer abhängigen Variable Y. Das ist die linke Seite. Vielleicht erinnerst du dich noch aus der Schule daran, dass eine Linie in ihrenAchsenabschnitt und ihre Steigung zerlegt werden kann. Das ist der Punkt, an dem ${\beta }_0$ und${\beta }_1\times X_i$ein. Im zweiten Term multiplizieren wir unsere unabhängige Variable mit einem Steigungskoeffizienten.

Schließlich gibt es einen Teil der Beziehung zwischen unserer unabhängigen und abhängigen Variable, der nicht durch das Modell an sich, sondern durch einen externen Einfluss erklärt werden kann. Dies ist bekannt als der Modellfehler und wird angegeben durch ${\epsilon }_i$.

Zuvor haben wir den t-Test für unabhängige Stichproben verwendet, um einen signifikanten Unterschied der Mittelwerte zwischen zwei Gruppen zu untersuchen. Hier messen wir den linearen Einfluss einer kontinuierlichen Variable auf eine andere. Dazu untersuchen wir, ob sich die Steigung der angepassten Regressionslinie statistisch von Null unterscheidet. Das bedeutet, dass unser Hypothesentest in etwa so funktionieren wird:

H0: Es gibt keinen linearen Einfluss unserer unabhängigen Variable auf unsere abhängige Variable. (Die Steigung der Regressionsgeraden ist gleich Null.)

Ha: Es gibt einen linearen Einfluss unserer unabhängigen Variable auf unsere abhängige Variable. (Die Steigung der Regressionsgeraden ist ungleich Null.)

Abbildung 4-8 zeigt einige Beispiele dafür, wie signifikante und unbedeutende Steigungen aussehen können.

Denke daran, dass uns nicht alle Daten vorliegen, sodass wir nicht wissen, wie die "wahre" Steigung für die Population aussehen würde. Stattdessen schließen wir daraus, ob sich diese Steigung in unserer Stichprobe statistisch von Null unterscheiden würde. Um die Signifikanz der Steigung zu schätzen, können wir dieselbe p-Wert-Methode anwenden wie bei der Ermittlung des Unterschieds zwischen den Mittelwerten von zwei Gruppen. Wir werden weiterhin zweiseitige Tests mit einem Konfidenzintervall von 95% durchführen. Beginnen wir nun mit der Ermittlung der Ergebnisse mit Excel.

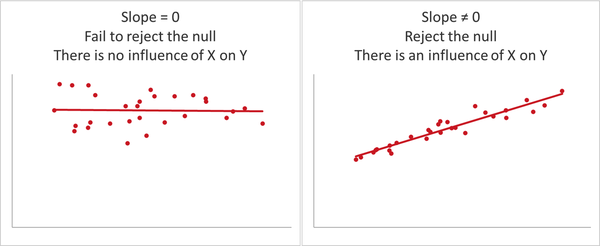
Abbildung 4-8. Regressionsmodelle mit signifikanten und insignifikanten Steigungen

Lineare Regression in Excel

In dieser Demo der linearen Regression auf den mpg-Datensatz in Excel testen wir, ob das Gewicht eines Autos einen signifikanten Einfluss auf den Kilometerstand(mpg) hat. Das bedeutet, dass unsere Hypothesen lauten werden:

H0: Es gibt keinen linearen Einfluss des Gewichts auf die Kilometerleistung.

Ha: Es gibt einen linearen Einfluss des Gewichts auf die Kilometerleistung.

Bevor du anfängst, solltest du die Regressionsgleichung mit den spezifischen Variablen von Interesse aufstellen, wie ich es in Gleichung 4-2 getan habe:

Gleichung 4-2. Unsere Regressionsgleichung zur Schätzung der Kilometerleistung

$$mpg={\beta }_0+{\beta }_1\times weight+ϵ$$

Beginnen wir mit der Visualisierung der Regressionsergebnisse: Wir haben bereits das Streudiagramm aus Abbildung 4-6, jetzt müssen wir nur noch die Regressionslinie darüberlegen oder "einpassen". Klicke auf den Rand des Diagramms, um das Menü "Diagrammelemente" zu öffnen. Klicke auf "Trendlinie" und dann auf "Weitere Optionen" an der Seite. Klicke unten auf dem Bildschirm "Trendlinie formatieren" auf das Optionsfeld "Gleichung im Diagramm anzeigen".

Klicken wir nun auf die resultierende Gleichung im Diagramm, um sie fett zu formatieren und die Schriftgröße auf 14 zu erhöhen. Wir färben die Trendlinie einfarbig schwarz und geben ihr eine Breite von 2,5 Punkten, indem wir sie im Diagramm anklicken und dann auf das Farbeimer-Symbol oben im Menü Trendlinie formatieren gehen. Jetzt haben wir die lineare Regression erstellt. Unser Streudiagramm mit Trendlinie sieht wie in Abbildung 4-9 aus. Excel enthält auch die gesuchte Regressionsgleichung aus Gleichung 4-2, mit der wir den Kilometerstand eines Autos anhand seines Gewichts schätzen können.

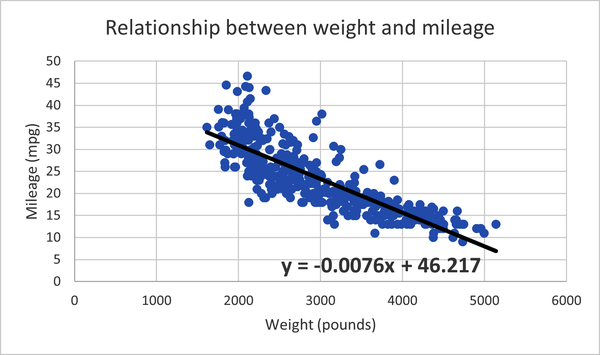
Abbildung 4-9. Streudiagramm mit Trendlinie und Regressionsgleichung für den Einfluss des Gewichts auf die Kilometerleistung

Wir können den Achsenabschnitt vor die Steigung in unserer Gleichung setzen, um Gleichung 4-3 zu erhalten.

Gleichung 4-3. Gleichung 4-3. Unsere angepasste Regressionsgleichung zur Schätzung der Kilometerleistung

$$mpg=46.217-0.0076\times weight$$

Beachte, dass Excel den Fehlerterm nicht in die Regressionsgleichung mit einbezieht. Nachdem wir die Regressionsgerade angepasst haben, haben wir die Differenz zwischen den Werten, die wir aus der Gleichung erwarten, und den Werten, die wir in den Daten finden, quantifiziert. Diese Differenz wird als Residuum bezeichnet und wir werden später in diesem Kapitel darauf zurückkommen. Zunächst einmal kommen wir zurück zu dem, was wir vorhatten: statistische Signifikanz zu ermitteln.

Es ist toll, dass Excel die Linie für uns angepasst hat und uns die resultierende Gleichung liefert. Aber das gibt uns nicht genug Informationen, um den Hypothesentest durchzuführen: Wir wissen immer noch nicht, ob die Steigung der Linie statistisch von Null verschieden ist. Um diese Informationen zu erhalten, verwenden wir erneut das Analysis ToolPak. Gehe im Menüband zu Daten → Datenanalyse → Regression. Du wirst aufgefordert, deine Y- und X-Bereiche auszuwählen; das sind deine abhängigen bzw. unabhängigen Variablen. Achte darauf, dass deine Eingaben Beschriftungen enthalten, wie in Abbildung 4-10 gezeigt.

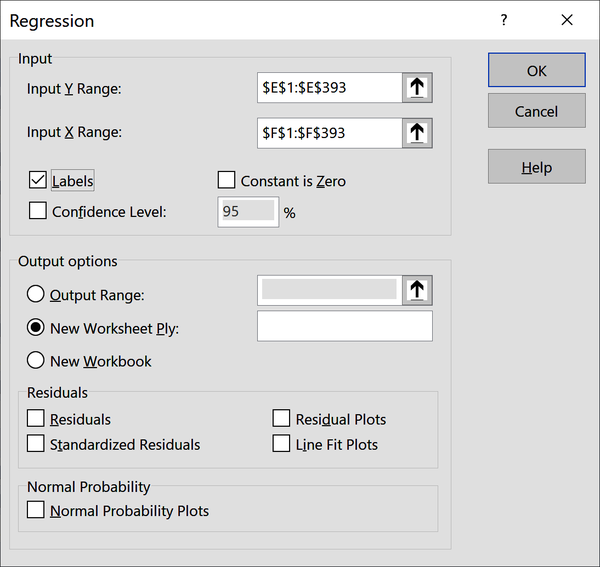
Abbildung 4-10. Menüeinstellungen für die Ableitung einer Regression mit dem ToolPak

Daraus ergibt sich eine ganze Menge an Informationen, die in Abbildung 4-11 zu sehen sind. Gehen wirsie Schritt für Schrittdurch.

Ignoriere den ersten Abschnitt in den Zellen A3:B8 für den Moment; wir werden später darauf zurückkommen. Unser zweiter Abschnitt in A10:F14 ist mit ANOVA (kurz für Varianzanalyse) beschriftet. Er zeigt uns, ob unsere Regression mit dem Koeffizienten der Steigung signifikant besser abschneidet als mit dem Achsenabschnitt.

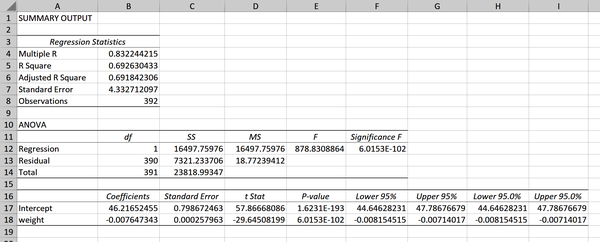
Abbildung 4-11. Regressionsausgabe

Tabelle 4-2 zeigt, wie die konkurrierenden Gleichungen aussehen.

Tabelle 4-2. Reines Intercept-Modell versus vollständiges Regressionsmodell

Incercept-only-Modell	Modell mit Koeffizienten
mpg = 46.217	mpg = 46,217 - 0,0076 × Gewicht

Ein statistisch signifikantes Ergebnis zeigt, dass unsere Koeffizienten das Modell verbessern. Wir können das Ergebnis des Tests anhand des p-Werts in Zelle F12in Abbildung 4-11 ermitteln. Erinnere dich daran, dass dies eine wissenschaftliche Schreibweise ist, also lies den p-Wert als 6,01 mal 10 hoch -102: viel kleiner als 0,05. Daraus können wir schließen, dass es sich lohnt, das Gewicht als Koeffizienten im Regressionsmodell zu behalten.

Das bringt uns zum dritten Bereich in den Zellen A16:I18; hier finden wir das, wonach wir ursprünglich gesucht haben. Dieser Bereich enthält eine Menge Informationen, also gehen wir spaltenweise vor, beginnend mit den Koeffizienten in den Zellen B17:B18. Diese sollten uns bekannt vorkommen wie der Schnittpunkt und die Steigung der Linie, die wir in Gleichung 4-3 angegeben haben.

Als Nächstes: der Standardfehler in C17:C18. Wir haben in Kapitel 3 darüber gesprochen: Er ist ein Maß für die Variabilität über wiederholte Stichproben hinweg und kann in diesem Fall als Maß für die Genauigkeit unserer Koeffizienten angesehen werden.

Dann haben wir das, was Excel die "t-Statistik" nennt, auch bekannt als t-Statistik oder Teststatistik, in D17:D18; diese kann abgeleitet werden, indem der Koeffizient durch den Standardfehler geteilt wird. Wir können diesen Wert mit dem kritischen Wert von 1,96 auf vergleichen, um die statistische Signifikanz mit 95%iger Sicherheit festzustellen.

Üblicher ist es jedoch, den p-Wert zu interpretieren und zu berichten, der die gleiche Information liefert. Wir haben zwei p-Werte zu interpretieren. Erstens den Koeffizienten des Achsenabschnitts in E17. Dieser sagt uns, ob der Abschnittswert signifikant von Null verschieden ist. DieSignifikanz des Achsenabschnitts ist nicht Teil unseres Hypothesentests, daher ist diese Information irrelevant. (Dies ist ein weiteres gutes Beispiel dafür, warum wir die Excel-Ausgaben nicht immer für bare Münze nehmen können).

Warnung

Die meisten Statistikpakete (einschließlich Excel) geben zwar den p-Wert des Achsenabschnitts an, aber das ist normalerweise keine relevante Information.

Stattdessen wollen wir den p-Wert des Gewichts in der Zelle E18: Dieser steht in Zusammenhang mit der Steigung der Linie. Der p-Wert liegt deutlich unter 0,05, so dass wir die Null zurückweisen und zu dem Schluss kommen, dass das Gewicht wahrscheinlich die Kilometerleistung beeinflusst. Mit anderen Worten: Die Steigung der Linie ist signifikant verschieden von Null. Genau wie bei unseren früheren Hypothesentests werden wir uns davor hüten, den Schluss zu ziehen, dass wir einen Zusammenhang "bewiesen" haben oder dass mehr Gewicht eine geringere Kilometerleistung verursacht. Auch hier wir anhand einer Stichprobe Rückschlüsse auf eine Grundgesamtheit gezogen, was mit Unsicherheiten verbunden ist.

Die Ausgabe gibt uns auch das 95%-Konfidenzintervall für unseren Achsenabschnitt und die Steigung in den Zellen F17:I18 an. Standardmäßig wird dies zweimal angegeben: Hätten wir im Eingabemenü nach einem anderen Konfidenzintervall gefragt, hätten wir hier beide erhalten.

Jetzt, wo du weißt, wie du die Regressionsergebnisse interpretieren kannst, versuchen wir eine Punktschätzung auf der Grundlage der Gleichungslinie: Wie hoch ist der erwartete Kilometerstand für ein Auto, das 3.021 Pfund wiegt? Setze dies in unsere Regressionsgleichung in Gleichung 4-4 ein:

Gleichung 4-4. Gleichung 4-4. Erstellen einer Punktschätzung auf der Grundlage unserer Gleichung

$$mpg=46.217-0.0076\times 3021$$

Anhand von Gleichung 4-4 erwarten wir, dass ein Auto mit einem Gewicht von 3.021 Pfund 23,26 Meilen pro Gallone erreicht. Wirf einen Blick auf den Quelldatensatz: Es gibt eine Beobachtung mit einem Gewicht von 3.021 Pfund (Ford Maverick, Zeile 101 im Datensatz) und er schafft 18 Meilen pro Gallone und nicht 23,26. Woran liegt das?

Diese Diskrepanz ist das Residuum, das bereits erwähnt wurde: Es ist die Differenz zwischen den Werten, die wir in der Regressionsgleichung geschätzt haben, und denen, die in den tatsächlichen Daten zu finden sind. Ich habe diese und einige andere Beobachtungen in Abbildung 4-12 eingefügt. Die Streuungspunkte stellen die tatsächlichen Werte im Datensatz dar und die Linie zeigt die Werte, die wir mit der Regression vorhergesagt haben.

Es liegt auf der Hand, dass wir die Differenz zwischen diesen Werten minimieren wollen. Excel und die meisten Regressionsprogramme verwenden dazu die Methode der gewöhnlichen kleinsten Quadrate (OLS). Unser Ziel bei OLS ist es, die Residuen, genauer gesagt die Summe der quadrierten Residuen, zu minimieren, sodass negative und positive Residuen gleichermaßen gemessen werden. Je niedriger die Summe der quadrierten Residuen ist, desto geringer ist der Unterschied zwischen den tatsächlichen und den erwarteten Werten und desto besser kann unsere Regressionsgleichung Schätzungen vornehmen.

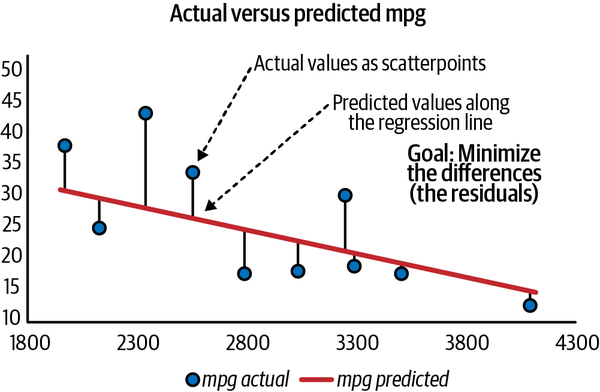
Abbildung 4-12. Residuen als Unterschiede zwischen tatsächlichen und vorhergesagten Werten

Aus dem p-Wert unserer Steigung haben wir gelernt, dass es eine signifikante Beziehung zwischen der unabhängigen und der abhängigen Variablen gibt. Das sagt uns aber nicht, wie viel der Variabilität unserer abhängigen Variable durch unsere unabhängige Variable erklärt wird.

Erinnere dich daran, dass die Variabilität der Kern dessen ist, was wir als Analytiker untersuchen; Variablen variieren und wir wollen untersuchen , warum sie variieren. Mit Experimenten können wir das tun, indem wir die Beziehung zwischen einer unabhängigen und einer abhängigen Variable verstehen. Aber wir werden nicht alles über unsere abhängige Variable mit unserer unabhängigen Variable erklären können. Es wird immer einen unerklärten Fehler geben.

R-Quadrat oder das Bestimmtheitsmaß (in Excel als R-Quadrat bezeichnet) drückt in Prozent aus, wie viel Variabilität in der abhängigen Variable durch unser Regressionsmodell erklärt wird. Ein R-Quadrat von 0,4 bedeutet zum Beispiel, dass 40 % der Variabilität von Y durch das Modell erklärt werden kann. Das bedeutet, dass 1 minus R-Quadrat die Variabilität ist, die nicht durch das Modell erklärt werden kann. Wenn das R-Quadrat 0,4 beträgt, bleiben 60 % der Variabilität von Y unberücksichtigt.

Excel berechnet das R-Quadrat für uns im ersten Feld der Regressionsausgabe; sieh dir die Zelle B5 in Abbildung 4-11 an. Die Quadratwurzel von R-Quadrat ist das Vielfache von R, das auch in der Zelle B4 der Ausgabe zu sehen ist. Das bereinigte R-Quadrat (Zelle B6) wird als konservativere Schätzung des R-Quadrats für ein Modell mit mehreren unabhängigen Variablen verwendet. Dieses Maß ist von Interesse, wenn eine multiple lineare Regression durchführt, was den Rahmen dieses Buches sprengen würde.

Multiple lineare Regression

In diesem Kapitel haben wir uns auf die univariate lineare Regression konzentriert, also auf den Einfluss einer unabhängigen auf eine abhängige Variable. Es ist auch möglich, multiple oder multivariate Regressionsmodelle zu erstellen, um den Einfluss mehrerer unabhängiger Variablen auf eine abhängige Variable zu schätzen. Diese unabhängigen Variablen können kategorische (nicht nur kontinuierliche) Variablen, Wechselwirkungen zwischen Variablen und mehr enthalten. Einen detaillierten Einblick in die Durchführung komplexer linearer Regressionen in Excel erhältst du in Conrad Carlbergs Regression Analysis Microsoft Excel (Que).

Es gibt noch andere Möglichkeiten als R-Quadrat, um die Leistung einer Regression zu messen: Excel fügt eine davon, den Standardfehler der Regression, in seine Ausgabe ein (Zelle B7 in Abbildung 4-11). Dieses Maß gibt an, wie weit die beobachteten Werte im Durchschnitt von der Regressionslinie abweichen. Einige Analysten bevorzugen dieses oder ein anderes Maß zur Bewertung von Regressionsmodellen anstelle von R-Quadrat, obwohl R-Quadrat nach wie vor die vorherrschende Wahl ist. Unabhängig von den Präferenzen ergibt sich die beste Bewertung oft aus der Auswertung mehrerer Zahlen in ihrem richtigen Kontext, so dass es keinen Grund gibt, auf ein bestimmtes Maß zu schwören oder es zu verwerfen.

Glückwunsch: Du hast eine vollständige Regressionsanalyse durchgeführt und interpretiert.

Unsere Ergebnisse überdenken: Unwahrscheinliche Zusammenhänge

Ausgehend von ihrer zeitlichen Reihenfolge und unserer eigenen Logik ist es in unserem Beispiel für den Kilometerstand fast zwingend, dass das Gewicht die unabhängige Variable und der Kilometerstand die abhängige Variable sein sollte. Aber was passiert, wenn wir die Regressionsgerade mit den umgekehrten Variablen anpassen? Probiere es einfach mit dem ToolPak aus. Die resultierende Regressionsgleichung ist in Gleichung 4-5 dargestellt.

Gleichung 4-5. Gleichung 4-5. Eine Regressionsgleichung zur Schätzung des Gewichts auf Basis der gefahrenen Kilometer

$$weight=5101.1-90.571\times mpg$$

Wir können unsere unabhängigen und abhängigen Variablen umdrehen und erhalten denselben Korrelationskoeffizienten. Aber wenn wir sie für die Regression ändern, ändern sich unsere Koeffizienten.

Wenn wir herausfinden würden, dass der Benzinverbrauch und das Gewicht gleichzeitig von einer äußeren Variable beeinflusst werden, wäre keines dieser Modelle korrekt. Das ist das gleiche Szenario wie beim Eiscremekonsum und den Haiattacken. Es ist albern zu behaupten, dass der Eiscremekonsum einen Einfluss auf Haiangriffe hat, denn beides wird von der Temperatur beeinflusst, wie Abbildung 4-13 zeigt.

Abbildung 4-13. Speiseeis-Konsum und Hai-Angriffe: ein falscher Zusammenhang

Das nennt man eine unechte Beziehung. Sie kommt in Daten häufig vor und ist vielleicht nicht so offensichtlich wie in diesem Beispiel. Ein gewisses Fachwissen über die Daten, die du untersuchst, kann von unschätzbarem Wert sein, um falsche Beziehungen zu erkennen.

Warnung

Variablen können korreliert sein; es könnte sogar Hinweise auf einen kausalen Zusammenhang geben. Die Beziehung könnte aber auch durch eine Variable bedingt sein, die du noch gar nicht berücksichtigt hast.

Fazit

Erinnerst du dich an diese alte Redewendung?

Korrelation bedeutet nicht gleich Kausalität.

Analytik ist in hohem Maße schrittweise: Normalerweise bauen wir ein Konzept auf das nächste auf, um immer komplexere Analysen zu erstellen. So beginnen wir zum Beispiel immer mit deskriptiven Statistiken der Stichprobe, bevor wir versuchen, auf Parameter der Grundgesamtheit zu schließen. Korrelation bedeutet zwar nicht unbedingt Kausalität, aber Kausalität basiert auf der Grundlage von Korrelation. Das bedeutet, dass man die Beziehung besser zusammenfassen könnte:

Korrelation ist eine notwendige, aber nicht hinreichende Bedingung für Kausalität.

Wir haben in diesem und den vorherigen Kapiteln nur an der Oberfläche der Inferenzstatistik gekratzt. Es gibt eine ganze Reihe von Tests, aber alle basieren auf demselben Rahmen von Hypothesentests, den wir hier verwendet haben. Wenn du diesen Prozess verinnerlicht hast, kannst du alle möglichen Beziehungen zwischen den Daten testen.

Aufsteigen in die Programmierung

Ich hoffe, du hast gesehen und stimmst mir zu, dass Excel ein fantastisches Werkzeug ist, um Statistik und Analytik zu lernen. Du hast einen praktischen Einblick in die statistischen Prinzipien bekommen, auf denen ein Großteil dieser Arbeit beruht, und gelernt, wie man Beziehungen in echten Datensätzen untersucht und testet.

Allerdings kann Excel bei fortgeschrittenen Analysen immer weniger Erfolg haben. Wir haben zum Beispiel mithilfe von Visualisierungen Eigenschaften wie Normalität und Linearität überprüft. Das ist ein guter Anfang, aber es gibt robustere Methoden, um sie zu testen (oft sogar mit statistischen Schlussfolgerungen). Diese Verfahren beruhen oft auf Matrixalgebra und anderen rechenintensiven Operationen, deren Ableitung in Excel mühsam sein kann. Es gibt zwar Add-Ins, die diese Mängel ausgleichen, aber sie können teuer sein und es fehlt ihnen an bestimmten Funktionen. R und Python hingegen sind als Open-Source-Tools kostenlos und enthalten viele app-ähnliche Funktionen, die Pakete genannt werden und für fast jeden Anwendungsfall geeignet sind. In dieser Umgebung kannst du dich auf die konzeptionelle Analyse deiner Daten konzentrieren und nicht auf die reine Berechnung, aber du musst programmieren lernen. Diese Tools und das Analyse-Toolkit im Allgemeinen werden im Mittelpunkt von Kapitel 5 stehen.

Übungen

Übe deine Korrelations- und Regressionsfähigkeiten, indem du auf den ais-Datensatz analysierst, der sich im Ordner " Datasets" des Buches befindet. Dieser Datensatz enthält Größe, Gewicht und Blutwerte von männlichen und weiblichen australischen Sportlern aus verschiedenen Sportarten.

Probiere mit dem Datensatz Folgendes aus:

1. Erstelle eine Korrelationsmatrix der relevanten Variablen in diesem Datensatz.

2. Veranschauliche das Verhältnis von Körpergröße und Gewicht. Ist es eine lineare Beziehung? Wenn ja, ist sie negativ oder positiv?

3. Welche der beiden Variablen - Körpergröße und Gewicht- ist deiner Meinung nach die unabhängige und die abhängige Variable?

   • Gibt es einen signifikanten Einfluss der unabhängigen Variable auf die abhängige Variable?

   • Wie ist die Steigung deiner angepassten Regressionslinie?

   • Wie viel Prozent der Varianz in der abhängigen Variable wird durch die unabhängige Variable erklärt?

4. Dieser Datensatz enthält eine Variable für den Body-Mass-Index, bmi. Wenn du mit dieser Kennzahl nicht vertraut bist, nimm dir einen Moment Zeit, um herauszufinden, wie sie berechnet wird. Würdest du mit diesem Wissen die Beziehung zwischen Körpergröße und BMI analysieren wollen? Zögere nicht, dich dabei auf den gesunden Menschenverstand zu verlassen und nicht nur auf statistische Überlegungen.