VLSI Digital Signal Processing Systems: Design and Implementation

4.3    SOLVING SYSTEMS OF INEQUALITIES

Given a set of M inequalities in N variables, where each inequality has the form r_i − r_j ≤ k for integer values of k, one of the shortest path algorithms in Appendix A can be used to determine if a solution exists and to find a solution if one does indeed exist. This is done using the following procedure.

1. Draw a constraint graph.

   (a)    Draw the node i for each of the N variables r_i, i = 1, 2, … , N.

   (b)    Draw the node N + 1.

   (c)    For each inequality r_i − r_j ≤ k, draw the edge j → i from node j to node i with length k.

   (d)    For each node i, i = 1, 2, … , n, draw the edge N + 1 → i from the node N + 1 to the node i with length 0.

   

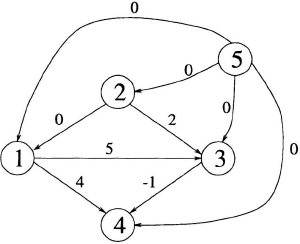
   Fig. 4.3    The constraint graph for Example 4.3.1.

2. Solve using a shortest path algorithm.

   (a)  The system of inequalities has a solution if and only if the constraint graph contains no negative cycles.

   (b)  If a solution exists, one solution is where r_i is the minimum-length path from the node N + 1 to the node i.

Example 4.3.1    In this example we demonstrate how shortest path algorithms can be used to solve a system of M = 5 inequalities

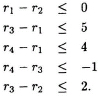
in N = 4 variables. The 1st step is to draw the constraint graph, which is shown in Fig. 4.3.

Using the Bellman-Ford algorithm (described in Section A.2 of Appendix A