VLSI Digital Signal Processing Systems: Design and Implementation

2.3    LOOP BOUND AND ITERATION BOUND

A loop is a directed path that begins and ends at the same node, such as the path A → B → A in Fig. 2.1(b). The terms “loop” and “cycle” are used interchangeably to describe a directed cycle in a directed graph. The amount of time required to execute a loop can be determined from the precedence relations described by the edges of the DFG. For the DFG in Fig. 2.1(b), the

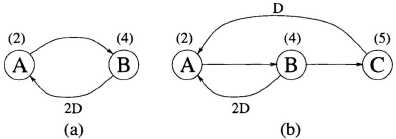
Fig. 2.3    (a) A DFG with one loop that has a loop bound of 6/2 = 3 u.t. The iteration bound for this DFG is 3 u.t. (b) A DFG with iteration bound T_∞ = max{6/2, 11/1} = 11 u.t.

edges describe the precedence constraints

A₀ → B₀ ⇒ A₁ → B₁ ⇒ A₂ → B₂ ⇒ A₃ → ···

where single arrows (→) represent intra-iteration precedence constraints and double arrows (⇒) represent inter-iteration precedence constraints. According to these precedence constraints, iteration k of the loop consists of the sequential execution of A_k and B_k. Given that the execution times of nodes A and B are 2 and 4 u.t., respectively, one iteration of the loop requires 6 u.t. This is the loop bound, which represents the lower bound on the loop computation time. Formally, the loop bound of the l-th loop is defined as t_l/w_l, where t_l is the loop computation time and w_l is the number of delays in the loop. We can verify that the loop bound for the loop in Fig. 2.1(b) is 6/1 = 6 u.t.

The loop in Fig. 2.3(a) has two delays, ...