Qiskit Pocket Guide

Chapter 1. Quantum Circuits and Operations

In Qiskit, quantum programs are normally expressed with quantum circuits that contain quantum operations. Quantum circuits are represented by the QuantumCircuit class, and quantum operations are represented by subclasses of the class Instruction.

Constructing Quantum Circuits

A quantum circuit may be created by supplying an argument that indicates the number of desired quantum wires (qubits) for that circuit. This is often supplied as an integer:

from qiskit import QuantumCircuit
QuantumCircuit(2)

Optionally, the number of desired classical wires (bits) may also be specified. The first argument refers to the number of quantum wires, and the second argument the number of classical wires:

QuantumCircuit(2, 2)

The number of desired quantum and classical wires may also be expressed by supplying instances of QuantumRegister and ClassicalRegister as arguments to QuantumCircuit. These classes are addressed in “Using the QuantumRegister Class” and “Using the ClassicalRegister Class”.

Using the QuantumCircuit Class

The QuantumCircuit class contains a large number of methods and attributes. The purpose of many of its methods is to apply quantum operations to a quantum circuit. Most of its other methods and attributes either manipulate or report information about a quantum circuit.

Commonly used gates

Table 1-1 contains some commonly used single-qubit gates and code examples. The variable qc refers to an instance of QuantumCircuit that contains at least four quantum wires.

Table 1-1. Commonly used single-qubit gates in Qiskit

Names	Example	Notes
H, Hadamard	qc.h(0)	Applies H gate to qubit 0. See “HGate”.
I, Identity	qc.id(2) or qc.i(2)	Applies I gate to qubit 2. See “IGate”.
P, Phase	qc.p(math.pi/2,0)	Applies P gate with π/2 phase rotation to qubit 0. See “PhaseGate”.
RX	qc.rx(math.pi/4,2)	Applies RX gate with π/4 rotation to qubit 2. See “RXGate”.
RY	qc.ry(math.pi/8,0)	Applies RY gate with π/8 rotation to qubit 0. See “RYGate”.
RZ	qc.rz(math.pi/2,1)	Applies RZ gate with π/2 rotation to qubit 1. See “RZGate”.
S	qc.s(3)	Applies S gate to qubit 3. Equivalent to P gate with π/2 phase rotation. See “SGate”.
Sâ€	qc.sdg(3)	Applies S† gate to qubit 3. Equivalent to P gate with 3π/2 phase rotation. See “SdgGate”.
SX	qc.sx(2)	Applies SX (square root of X) gate to qubit 2. Equivalent to RX gate with π/2 rotation. See “SXGate”.
T	qc.t(1)	Applies T gate to qubit 1. Equivalent to P gate with π/4 phase rotation. See “TGate”.
Tâ€	qc.tdg(1)	Applies T† gate to qubit 1. Equivalent to P gate with 7π/4 phase rotation. See “TdgGate”.
U	qc.u(math.pi/2,0,math.pi,1)	Applies rotation with 3 Euler angles to qubit 1. See “UGate”.
X	qc.x(3)	Applies X gate to qubit 3. See “XGate”.
Y	qc.y([0,2,3])	Applies Y gates to qubits 0, 2, and 3. See “YGate”.
Z	qc.z(2)	Applies Z gate to qubit 2. Equivalent to P gate with π phase rotation. See “ZGate”.

Figure 1-1 contains a nonsensical circuit with all of the single-qubit gate examples from Table 1-1.

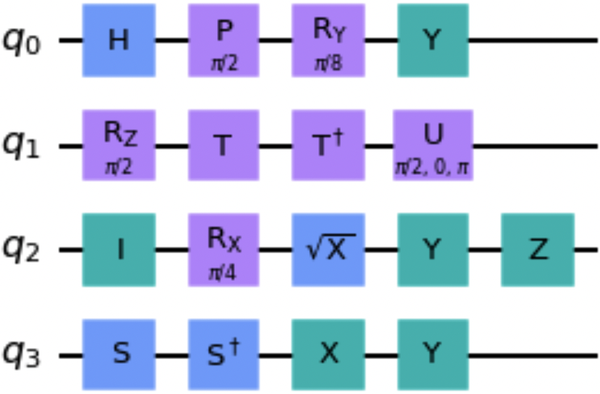
Figure 1-1. Nonsensical circuit with single-qubit gate examples

Table 1-2 contains some commonly used multiqubit gates and code examples. The variable qc refers to an instance of QuantumCircuit that contains at least four quantum wires.

Table 1-2. Commonly used multiqubit gates in Qiskit

Names	Example	Notes
CCX, Toffoli	qc.ccx(0,1,2)	Applies the X gate to quantum wire 2, subject to the state of the control qubits on wires 0 and 1. See “CCXGate”.
CH	qc.ch(0,1)	Applies the H gate to quantum wire 1, subject to the state of the control qubit on wire 0. See “CHGate”.
CP, Control-Phase	qc.cp(math.pi/4,0,1)	Applies the phase gate to quantum wire 1, subject to the state of the control qubit on wire 0. See “CPhaseGate”.
CRX, Control-RX	qc.crx(math.pi/2,2,3)	Applies the RX gate to quantum wire 3, subject to the state of the control qubit on wire 2. See “CRXGate”.
CRY, Control-RY	qc.cry(math.pi/8,2,3)	Applies the RY gate to quantum wire 3, subject to the state of the control qubit on wire 2. See “CRYGate”.
CRZ	qc.crz(math.pi/4,0,1)	Applies the RZ gate to quantum wire 1, subject to the state of the control qubit on wire 0. See “CRZGate”.
CSwap, Fredkin	qc.cswap(0,2,3) or qc.fredkin(0,2,3)	Swaps the qubit states of wires 2 and 3, subject to the state of the control qubit on wire 0. See “CSwapGate”.
CSX	qc.csx(0,1)	Applies the SX (square root of X) gate to quantum wire 1, subject to the state of the control qubit on wire 0. See “CSXGate”.
CU	qc.cu(math.pi/2,0,math.pi,0,0,1)	Applies the U gate with an additional global phase argument to quantum wire 1, subject to the state of the control qubit on wire 0. See “CUGate”.
CX, CNOT	qc.cx(2,3) or qc.cnot(2,3)	Applies the X gate to quantum wire 3, subject to the state of the control qubit on wire 2. See “CXGate”.
CY, Control-Y	qc.cy(2,3)	Applies the Y gate to quantum wire 3, subject to the state of the control qubit on wire 2. See “CYGate”.
CZ, Control-Z	qc.cz(1,2)	Applies the Z gate to quantum wire 2, subject to the state of the control qubit on wire 1. See “CZGate”.
DCX	qc.dcx(2,3)	Applies two CNOT gates whose control qubits are on wires 2 and 3. See “DCXGate”.
iSwap	qc.iswap(0,1)	Swaps the qubit states of wires 0 and 1, and changes the phase of the $|01〉$ and $|10〉$ amplitudes by i. See “iSwapGate”.
MCP, Multi-control phase	qc.mcp(math.pi/4, [0,1,2],3)	Applies the phase gate to quantum wire 3, subject to the state of the control qubits on wires 0, 1, and 2. See “MCPhaseGate”.
MCX, Multi-control X	qc.mcx([0,1,2],3)	Applies the X gate to quantum wire 3, subject to the state of the control qubits on wires 0, 1, and 2. See “MCXGate”.
Swap	qc.swap(2,3)	Swaps the qubit states of wires 2 and 3. See “SwapGate”.

Figure 1-2 contains a nonsensical circuit with all of the multi-qubit gate examples from Table 1-2.

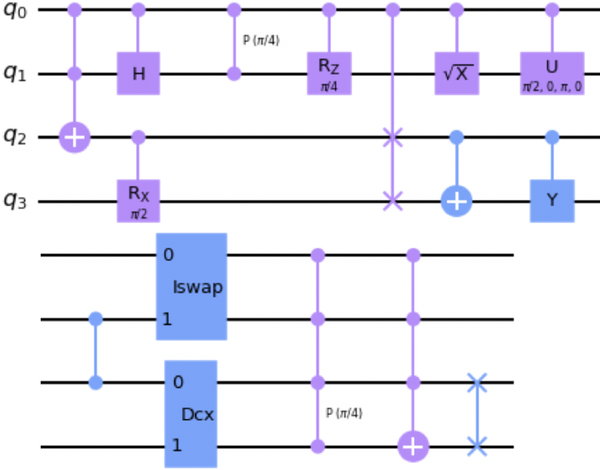
Figure 1-2. Nonsensical circuit with multiqubit gate examples

Drawing a quantum circuit

The draw() method draws a quantum circuit in various formats.

Using the draw() method

The following code snippet uses the draw() method in the default format:

qc = QuantumCircuit(3)
qc.h(0)
qc.cx(0, 1)
qc.cx(0, 2)
qc.draw()

Figure 1-3 shows the drawn circuit.

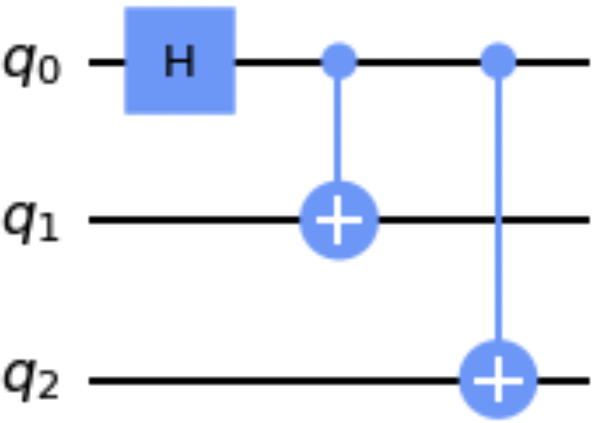
Figure 1-3. Example circuit visualization using the draw() method

Creating a barrier

The barrier() method places a barrier on a circuit (shown in Figure 1-4), providing both visual and functional separation between gates on a quantum circuit. Gates on either side of a barrier are not candidates for being optimized together as the circuit is converted to run on quantum hardware or a simulator.

Note

The set of gates expressed using Qiskit represents an abstraction for the actual gates implemented on a given quantum computer or simulator. Qiskit transpiles the gates into those implemented on the target platform, combining gates where possible to optimize the circuit.

Using the barrier() method

The barrier() method takes as an optional argument the qubit wires on which to place a barrier. If no argument is supplied, a barrier is placed across all of the quantum wires. This method creates a Barrier instance (see “Barrier”).

The following code snippet demonstrates using the barrier() method with and without arguments:

qc = QuantumCircuit(2)
qc.h([0,1])
qc.barrier()
qc.x(0)
qc.x(0)
qc.s(1)
qc.barrier([1])
qc.s(1)
qc.draw()

Figure 1-4 shows the resultant circuit.

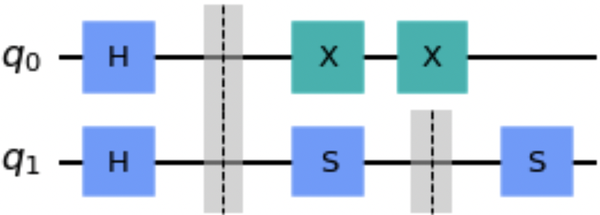
Figure 1-4. Example circuit using the barrier() method

Notice that the S gates in the circuit are separated by a barrier and therefore are not candidates to be combined into a Z gate. However, the X gates may be combined by removing both of them, as they cancel one another out.

Measuring a quantum circuit

The methods commonly used to measure quantum circuits are measure() and measure_all(). The former is useful when the quantum circuit contains classical wires on which to receive the result of a measurement. The latter is useful when the quantum circuit doesn’t have any classical wires. These methods create Measure instances (see “Measure”).

Using the measure() method

The measure() method takes two arguments:

• The qubit wires to be measured

• The classical wires on which to store the resulting bits

This code snippet uses the measure() method, and Figure 1-5 shows a drawing of the resultant circuit:

qc = QuantumCircuit(3, 3)
qc.h([0,1,2])
qc.measure([0,1,2], [0,1,2])
qc.draw()

Figure 1-5. Example circuit using the measure() method

Notice that the measure() method appended the requested measurement operations to the circuit.

Using the measure_all() method

The measure_all() method may be called with no arguments. This code snippet uses the measure_all() method, and Figure 1-6 shows a drawing of the resultant circuit:

qc = QuantumCircuit(3)
qc.h([0,1,2])
qc.measure_all()
qc.draw()

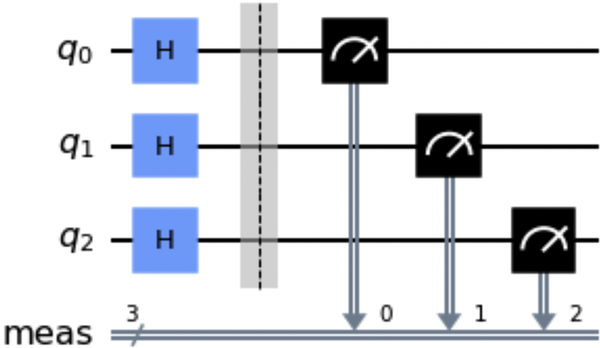
Figure 1-6. Example circuit using the measure_all() method

Notice that the measure_all() method created three classical wires and added a barrier to the circuit before appending the measurement operations.

Obtaining information about a quantum circuit

Methods commonly used to obtain information about a quantum circuit include depth(), size(), and width(). These are listed in Table 1-3. Note that the variable qc refers to an instance of QuantumCircuit.

Table 1-3. Methods commonly used to obtain information about a quantum circuit

Names	Example	Notes
depth	qc.depth()	Returns the depth (critical path) of a circuit if directives such as barrier were removed
size	qc.size()	Returns the total number of gate operations in a circuit
width	qc.width()	Returns the sum of qubits wires and classical wires in a circuit

Attributes commonly used to obtain information about a quantum circuit include clbits, data, global_phase, num_clbits, num_qubits, and qubits. These are listed in Table 1-4. Note that variable qc refers to an instance of QuantumCircuit.

Table 1-4. Attributes commonly used to obtain information about a quantum circuit

Names	Example	Notes
clbits	qc.clbits	Obtains the list of classical bits in the order that the registers were added
data	qc.data	Obtains a list of the operations (e.g., gates, barriers, and measurement operations) in the circuit
global_phase	qc.global_phase	Obtains the global phase of the circuit in radians
num_clbits	qc.num_clbits	Obtains the number of classical wires in the circuit
num_qubits	qc.num_qubits	Obtains the number of quantum wires in the circuit
qubits	qc.qubits	Obtains the list of quantum bits in the order that the registers were added

Manipulating a quantum circuit

Methods commonly used to manipulate quantum circuits include append(), bind_parameters(), compose(), copy(), decompose(), from_qasm_file(), from_qasm_str(), initialize(), reset(), qasm(), to_gate(), and to_instruction().

Using the append() method

The append() method appends an instruction or gate to the end of the circuit on specified wires, modifying the circuit in place. The following code snippet uses the append() method, and Figure 1-7 shows a drawing of the resultant circuit:

from qiskit.circuit.library import CXGate

qc = QuantumCircuit(2)
qc.h(1)
cx_gate = CXGate()
qc.append(cx_gate, [1,0])
qc.draw()

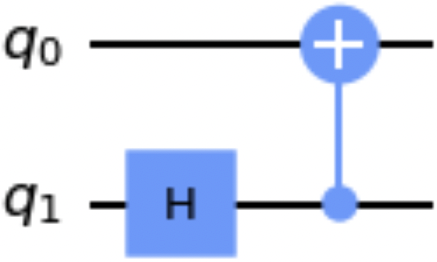
Figure 1-7. Example circuit resulting from the append() method

Note

The CXGate class (see “CXGate”) used here is one of the gates defined in the qiskit.circuit.library package. We advise you add the appropriate import statements to code snippets in this book.

Using the bind_parameters() method

The bind_parameters() method binds parameters (see “Creating a Parameter Instance”) to a quantum circuit. The following code snippet creates a circuit in which there are three parameterized phase gates. Note that the arguments to the Parameter constructors in this code snippet are strings, in this case ones that contain theta characters. Figure 1-8 shows a drawing of the circuit:

from qiskit.circuit import QuantumCircuit,\
                           Parameter

theta1 = Parameter('θ1')
theta2 = Parameter('θ2')
theta3 = Parameter('θ3')

qc = QuantumCircuit(3)
qc.h([0,1,2])
qc.p(theta1,0)
qc.p(theta2,1)
qc.p(theta3,2)

qc.draw()

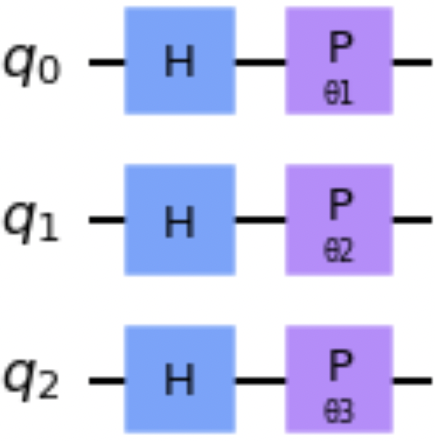
Figure 1-8. Example parameterized circuit

To bind the parameter values to a new circuit, we’ll pass a dictionary that contains the parameter references and desired values to the bind_parameters() method. The following code snippet uses this technique, and Figure 1-9 shows the bound circuit in which the phase gate parameters are replaced with the supplied values:

b_qc = qc.bind_parameters({theta1: math.pi/8,
                          theta2: math.pi/4,
                          theta3: math.pi/2})

b_qc.draw()

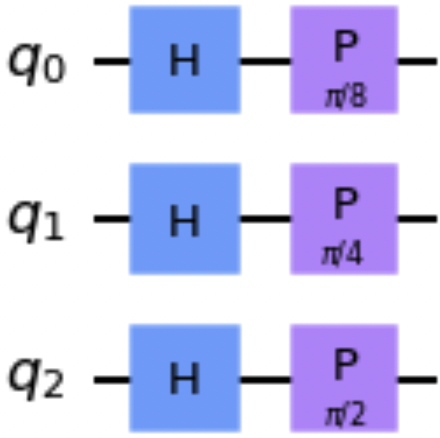
Figure 1-9. Example of bound circuit with the supplied phase gate rotation values

Using the compose() method

The compose() method returns a new circuit composed of the original and another circuit. The following code snippet uses the compose() method, and Figure 1-10 shows a drawing of the resultant circuit:

qc = QuantumCircuit(2,2)
qc.h(0)
another_qc = QuantumCircuit(2,2)
another_qc.cx(0,1)
bell_qc = qc.compose(another_qc)
bell_qc.draw()

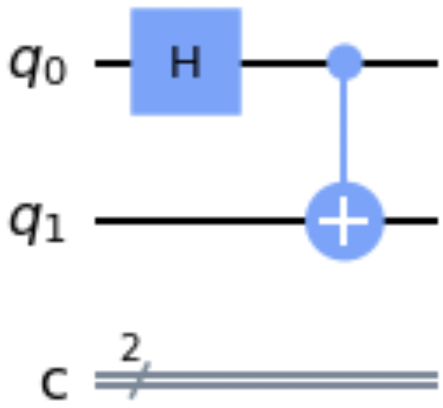
Figure 1-10. Example circuit resulting from the compose() method

Note that a circuit passed into the compose() method is allowed to have fewer quantum or classical wires than the original circuit.

Using the copy() method

The copy() method returns a copy of the original circuit. The following code snippet uses the copy() method:

qc = QuantumCircuit(3)
qc.h([0,1,2])
new_qc = qc.copy()

Using the decompose() method

The decompose() method returns a new circuit after decomposing the original circuit one level. The following code snippet uses the decompose() method. Figure 1-11 shows a drawing of the resultant circuit in which S, H, and X gates are decomposed into the more fundamental U gate operations (see “UGate”):

qc = QuantumCircuit(2)
qc.h(0)
qc.s(0)
qc.x(1)
decomposed_qc = qc.decompose()
decomposed_qc.draw()

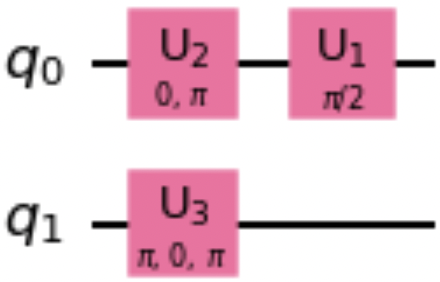
Figure 1-11. Example circuit resulting from the decompose() method

Using the from_qasm_file() method

The from_qasm_file() method returns a new circuit from a file that contains a quantum assembly-language (OpenQASM) program. The following code snippet uses the from_qasm_file() method:

new_qc = QuantumCircuit.from_qasm_file("file.qasm")

Using the from_qasm_str() method

The from_qasm_str() method returns a new circuit from a string that contains an OpenQASM program. The following code snippet uses the from_qasm_str() method, and Figure 1-12 shows a drawing of the resultant circuit:

qasm_str = """
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];
"""
new_qc = QuantumCircuit.from_qasm_str(qasm_str)
new_qc.draw()

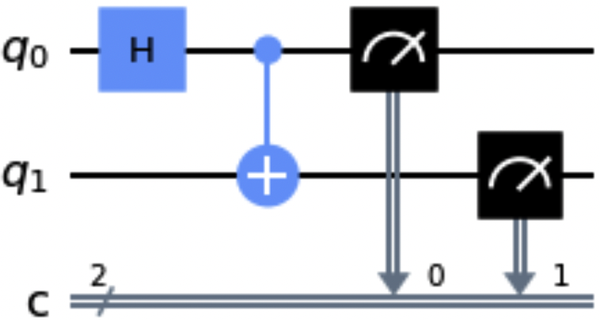
Figure 1-12. Example circuit resulting from the from_qasm_str() method

Using the initialize() method

The initialize() method initializes qubits of a quantum circuit to a given state and is not a unitary operation. The following code uses the initialize() method, and Figure 1-13 shows a drawing of the resultant circuit. In this code snippet, the circuit is initialized to the normalized statevector $|11〉$:

qc = QuantumCircuit(2)
qc.initialize([0, 0, 0, 1])
qc.draw()

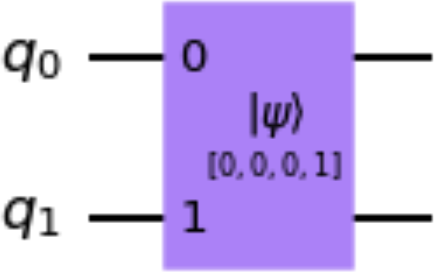
Figure 1-13. Example circuit resulting from the initialize() method

Using the reset() method

The reset() method resets a qubit in a quantum circuit to the $|0〉$ state and is not a unitary operation. The following code snippet uses the reset() method, and Figure 1-14 shows a drawing of the resultant circuit. Note that the qubit state is $|1〉$ before the reset operation. This method creates a Reset instance (see “Reset”):

qc = QuantumCircuit(1)
qc.x(0)
qc.reset(0)
qc.draw()

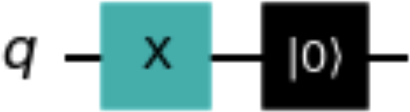
Figure 1-14. Example circuit resulting from using the reset() method

Using the qasm() method

The qasm() method returns an OpenQASM program that represents the quantum circuit. The following code snippet uses the qasm() method, and Example 1-1 shows the resultant OpenQASM program:

qc = QuantumCircuit(2, 2)
qc.h(0)
qc.cx(0, 1)
qasm_str = qc.qasm()
print(qasm_str)

Example 1-1. OpenQASM program resulting from the using the qasm() method

OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];

Using the to_gate() method

The to_gate() method creates a custom gate (see “The Gate Class”) from a quantum circuit. The following code snippet creates a circuit that will be converted to a gate, and Figure 1-15 shows a drawing of the circuit:

anti_cnot_qc = QuantumCircuit(2)
anti_cnot_qc.x(0)
anti_cnot_qc.cx(0,1)
anti_cnot_qc.x(0)

anti_cnot_qc.draw()

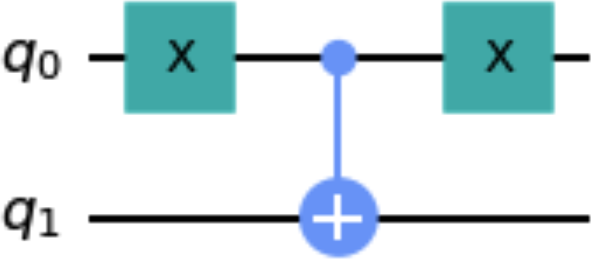
Figure 1-15. Example circuit that will be converted to a gate

This custom gate will implement an anticontrol NOT gate in which the X gate is applied only when the control qubit is $|0〉$. The following code snippet creates a circuit that uses this custom gate, and Figure 1-16 shows a decomposed drawing of this circuit:

anti_cnot_gate = anti_cnot_qc.to_gate()

qc = QuantumCircuit(3)
qc.x([0,1,2])
qc.append(anti_cnot_gate, [0,2])

qc.decompose().draw()

Note

A gate represents a unitary operation. To create a custom operation that isn’t unitary, use the to_instruction() method shown in “Using the to_instruction() method”.

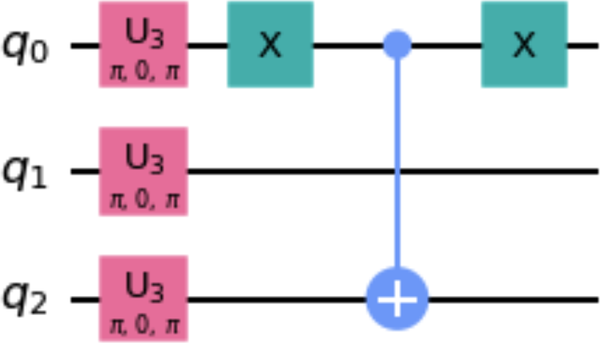
Figure 1-16. Decomposed circuit that uses a gate created by the to_gate() method

Using the to_instruction() method

The to_instruction() method creates a custom instruction (see “The Instruction Class”) from a quantum circuit. The following code snippet creates a circuit that will be converted to an instruction, and Figure 1-17 shows a drawing of the circuit:

reset_one_qc = QuantumCircuit(1)
reset_one_qc.reset(0)
reset_one_qc.x(0)

reset_one_qc.draw()

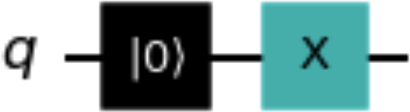
Figure 1-17. Example circuit that will be converted to an instruction

Note

An instruction represents an operation that isn’t necessarily unitary. To create a custom operation that is unitary, use the to_gate() method shown in “Using the to_gate() method”.

This custom instruction will reset a qubit and apply an X gate, in effect resetting the qubit to state $|1〉$. The following code snippet creates a circuit that uses this custom instruction, and Figure 1-18 shows a decomposed drawing of this circuit:

reset_one_inst = reset_one_qc.to_instruction()

qc = QuantumCircuit(2)
qc.h([0,1])
qc.reset(0)
qc.append(reset_one_inst, [1])

qc.decompose().draw()

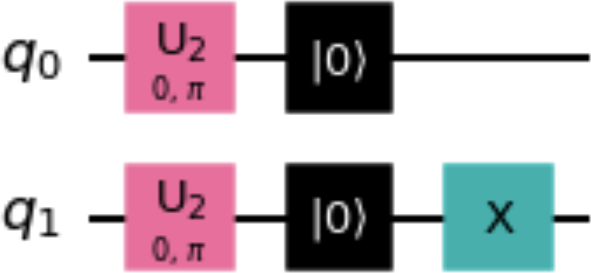
Figure 1-18. Circuit that uses an instruction created by the to_instruction() method

Saving state when running a circuit on AerSimulator

When running a circuit on an AerSimulator backend (see “Using the Aer Simulators”), the simulator state may be saved in the circuit instance by using the QuantumCircuit methods in Table 1-5. Please note that these methods are available after obtaining an AerSimulator backend.

Table 1-5. Methods used to save simulator state in a circuit instance

Method name	Description
save_state	Saves the simulator state as appropriate for the simulation method
save_density_matrix	Saves the simulator state as a density matrix
save_matrix_product_state	Saves the simulator state as a matrix product state tensor
save_stabilizer	Saves the simulator state as a Clifford stabilizer
save_statevector	Saves the simulator state as a statevector
save_superop	Saves the simulator state as a superoperator matrix of the run circuit
save_unitary	Saves the simulator state as a unitary matrix of the run circuit

Using the QuantumRegister Class

It is sometimes useful to treat groups of quantum or classical wires as a unit. For example, the control qubits of the CNOT gates in the quantum circuit expressed in the following code snippet, as well as in Figure 1-19, expect three qubits in equal superpositions. The additional quantum wire in the circuit is used as a scratch area whose output is disregarded:

from qiskit import QuantumRegister, \
                   ClassicalRegister

qr = QuantumRegister(3, 'q')
scratch = QuantumRegister(1, 'scratch')
cr = ClassicalRegister(3, 'c')
qc = QuantumCircuit(qr, scratch, cr)

qc.h(qr)
qc.x(scratch)
qc.h(scratch)
qc.cx(qr[0], scratch)
qc.cx(qr[2], scratch)
qc.barrier(qr)
qc.h(qr)
qc.measure(qr, cr)

qc.draw()

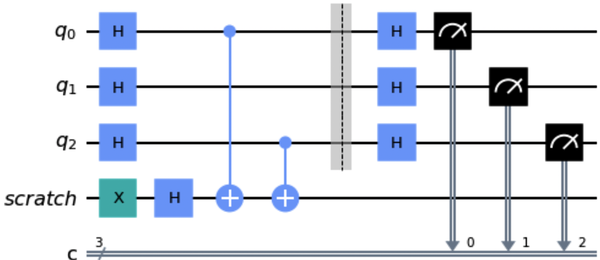
Figure 1-19. Example circuit using the QuantumRegister and ClassicalRegister classes

By defining a QuantumRegister consisting of three qubits, methods such as h(), barrier(), and measure() may be applied to all three wires by passing a QuantumRegister reference. Similarly, defining a ClassicalRegister (see “Using the ClassicalRegister Class”) consisting of three bits enables the measure() method to specify all three classical wires by passing a ClassicalRegister reference. Additionally, the names supplied to the QuantumRegister and ClassicalRegister constructors are displayed on the circuit drawing.

Using QuantumRegister Attributes

Commonly used QuantumRegister attributes include name and size. These are listed in Table 1-6. Note that the variable qr refers to an instance of QuantumRegister.

Table 1-6. Some QuantumRegister attributes

Names	Example	Notes
name	qr.name	Obtains the name of the quantum register
size	qr.size	Obtains the number of qubit wires in the quantum register

Using the ClassicalRegister Class

Please refer to “Using the QuantumRegister Class” for reasons to use the ClassicalRegister class.

Using ClassicalRegister Attributes

Commonly used ClassicalRegister attributes include name and size. These are listed in Table 1-7. Note that the variable cr refers to an instance of ClassicalRegister.

Table 1-7. Some ClassicalRegister attributes

Names	Example	Notes
name	cr.name	Obtains the name of the classical register
size	cr.size	Obtains the number of bit wires in the classical register

Instructions and Gates

In Qiskit, all operations that may be applied to a quantum circuit are derived from the Instruction class. Unitary operations are derived from the Gate class, which is a subclass of Instruction. Controlled-unitary operations are derived from the ControlledGate class, which is a subclass of Gate. These classes may be used to define new instructions, unitary gates, and controlled-unitary gates, respectively.

The Instruction Class

The nonunitary operations in Qiskit (such as Measure and Reset) are direct subclasses of Instruction. Although it is possible to define your own custom instructions by subclassing Instruction, another way is to use the to_instruction() method of the QuantumCircuit class (see an example of this in “Using the to_instruction() method”).

Methods in the Instruction class include copy(), repeat(), and reverse_ops(). These are listed in Table 1-8. Note that the variable inst refers to an instance of Instruction.

Table 1-8. Commonly used methods in the Instruction class

Names	Example	Notes
copy	inst.copy("My inst")	Returns a copy of the instruction, giving the supplied name to the copy
repeat	inst.repeat(2)	Returns an instruction with this instruction repeated a given number of times
reverse_ops	inst.reverse_ops()	Returns an instruction with its operations in reverse order

Commonly used attributes in the Instruction class include definition and params. These are listed in Table 1-9. Note that the variable inst refers to an instance of Instruction.

Table 1-9. Commonly used attributes in the Instruction class

Names	Example	Notes
definition	inst. definition	Returns the definition in terms of basic gates
params	inst.params	Obtains the parameters to the instruction

The Gate Class

The unitary operations in Qiskit (such as HGate and XGate) are subclasses of Gate. Although it is possible to define your own custom gates by subclassing Gate, another way is to use the to_gate() method of the QuantumCircuit class (see an example of this in “Using the to_gate() method”).

Commonly used methods in the Gate class include the Instruction methods listed in Table 1-8 as well as control(), inverse(), power(), and to_matrix(). These are all listed in Table 1-10. Note that the variable gate refers to an instance of Gate.

Table 1-10. Commonly used methods in the Gate class

Names	Example	Notes
control	gate.control(1)	Given a number of control qubits, returns a controlled version of the gate
copy	gate.copy("My gate")	Returns a copy of the gate, giving the supplied name to the copy
inverse	gate.inverse()	Returns the inverse of the gate
power	gate.power(2)	Returns the gate raised to a given floating-point power
repeat	gate.repeat(3)	Returns a gate with this gate repeated a given number of times
reverse_ops	gate.reverse_ops()	Returns a gate with its operations in reverse order
to_matrix	gate.to_matrix()	Returns an array for the gate’s unitary matrix

Commonly used attributes in the Gate class include the Instruction attributes listed in Table 1-9 as well as label. These are all listed in Table 1-11. Note that the variable gate refers to an instance of Gate.

Table 1-11. Commonly used attributes in the Gate class

Names	Example	Notes
definition	gate​.def⁠ini⁠tion	Returns the definition in terms of basic gates
label	gate.label	Obtains the label for the instruction
params	gate.params	Obtains the parameters to the instruction

The ControlledGate Class

The controlled-unitary operations in Qiskit (such as CZGate and CCXGate) are subclasses of ControlledGate, which is a subclass of Gate.

Commonly used methods in the ControlledGate class are the Gate methods listed in Table 1-10

Commonly used attributes in the ControlledGate class include the Gate attributes listed in Table 1-11 as well as num_ctrl_qubits and ctrl_state.

Using the num_ctrl_qubits attribute

The num_ctrl_qubits attribute holds an integer that represents the number of control qubits in a ControlledGate. The following code snippet, whose printed output would be 2, uses the num_ctrl_qubits attribute of a Toffoli gate:

from qiskit.circuit.library import CCXGate

toffoli = CCXGate()
print(toffoli.num_ctrl_qubits)

Using the ctrl_state() method

A ControlledGate may have one or more control qubits, each of which may actually be either control or anticontrol qubits (see the anticontrol example in “Using the to_gate() method”). The ctrl_state attribute holds an integer whose binary value represents which qubits are control qubits and which are anticontrol qubits. Specifically, the binary digit 1 represents a control qubit, and the binary digit 0 represents an anticontrol qubit.

The ctrl_state attribute supports both accessing and modifying its value. The following code snippet uses the ctrl_state attribute in which the binary value 10 causes the topmost control qubit to be an anticontrol qubit. Figure 1-20 shows a drawing of the resultant circuit:

toffoli = CCXGate()
toffoli.ctrl_state = 2

toffoli.definition.draw()

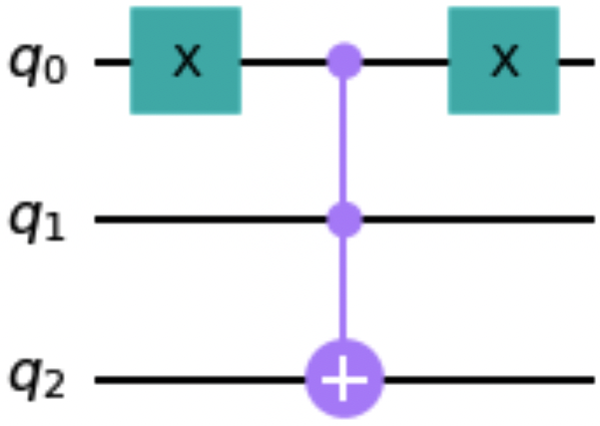
Figure 1-20. Toffoli gate with a control qubit and an anticontrol qubit

Defining a custom controlled gate

Although it is possible to define your own custom controlled gates by subclassing ControlledGate, another way is to follow these two steps:

1. Create a custom gate with the to_gate() method of the QuantumCircuit class (see an example of this in “Using the to_gate() method”).

2. Add control qubits to your custom gate by using the control() method shown in Table 1-10.

We’ll follow those two steps to define a custom controlled gate that applies a π/16 phase rotation when both of its control qubits are $|1〉$. First, the following code snippet defines a circuit that contains a π/16 P gate and converts it to a custom gate, with Figure 1-21 showing a drawing of the custom gate:

from qiskit import QuantumCircuit
import math

p16_qc = QuantumCircuit(1)
p16_qc.p(math.pi/16, 0)

p16_gate = p16_qc.to_gate()

p16_gate.definition.draw()

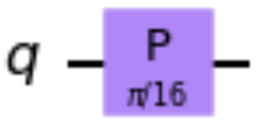
Figure 1-21. Custom π/16 phase gate drawing

Second, the following code snippet uses the control() method to create a ControlledGate from our custom gate, and Figure 1-22 shows a drawing of the custom controlled gate:

ctrl_p16 = p16_gate.control(2)

ctrl_p16.definition.draw()

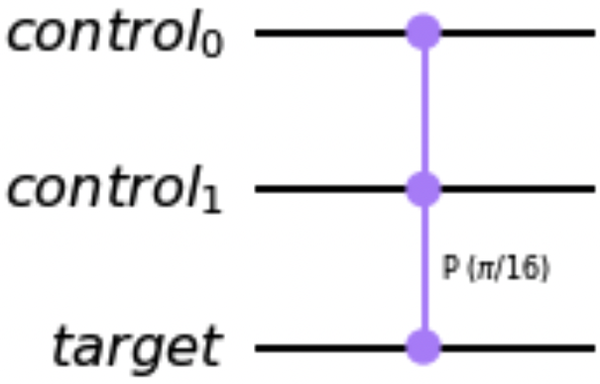
Figure 1-22. Custom controlled π/16 phase gate drawing

We’ll leverage the append() method (see “Using the append() method”) in the following code snippet to use our custom controlled gate in a quantum circuit. Figure 1-23 shows a drawing of the circuit:

qc = QuantumCircuit(4)
qc.h([0,1,2,3])
qc.append(ctrl_p16,[0,1,3])

qc.decompose().draw()

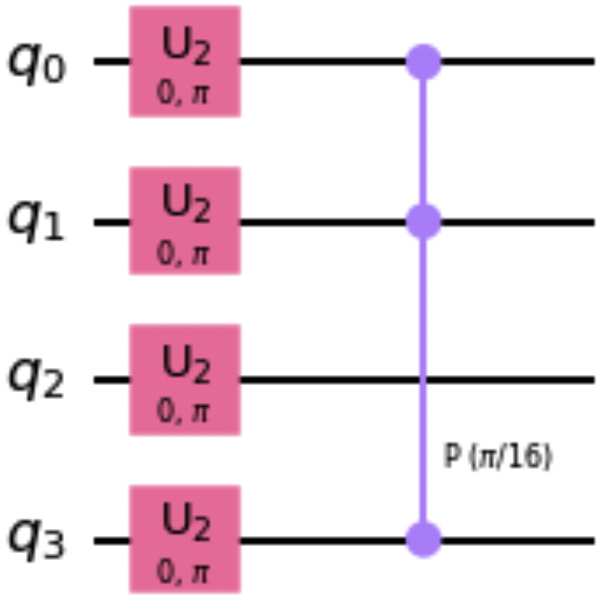
Figure 1-23. Decomposed circuit that uses the custom controlled gate

Parameterized Quantum Circuits

It is sometimes useful to create a quantum circuit in which values may be supplied at runtime. This capability is available in Qiskit using parameterized circuits, implemented in part by the Parameter and ParameterVector classes.

Creating a Parameter Instance

The Parameter class is used to represent a parameter in a quantum circuit. See “Using the bind_parameters() method” for an example of defining and using a parameterized circuit. As shown in that example, a parameter may be created by supplying a unicode string to its constructor as follows:

theta1 = Parameter("θ1")

The Parameter object reference named theta1 may subsequently be used in the bind_parameters() or alternatively the assign_parameters() method of the QuantumCircuit class.

Using the ParameterVector Class

The ParameterVector class may be leveraged to create and use parameters as a collection instead of individual variables. The following code snippet creates a circuit in which there are three parameterized phase gates. Figure 1-24 shows a drawing of the circuit:

from qiskit.circuit import QuantumCircuit,\
                           ParameterVector

theta = ParameterVector('θ', 3)

qc = QuantumCircuit(3)
qc.h([0,1,2])
qc.p(theta[0],0)
qc.p(theta[1],1)
qc.p(theta[2],2)

qc.draw()

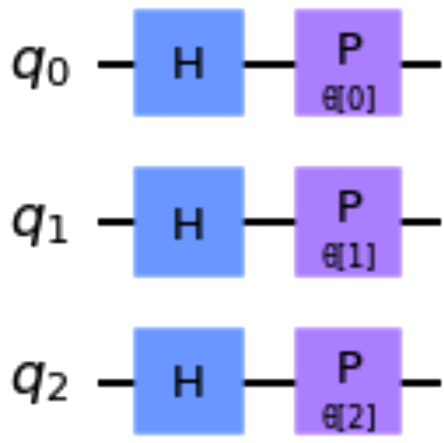
Figure 1-24. Example of a parameterized circuit leveraging ParameterVector

To bind the parameter values to a new circuit, we’ll pass a dictionary that contains the ParameterVector reference and desired list of values to the bind_parameters() method.

The following code snippet shows this technique, and Figure 1-25 shows the bound circuit in which the phase gate parameters are replaced with the supplied values:

import math

b_qc = qc.bind_parameters({theta: [math.pi/8,
                                   math.pi/4,
                                   math.pi/2]})

b_qc.draw()

Figure 1-25. Example of bound circuit with the supplied phase gate rotation values