Python für den algorithmischen Handel

Kapitel 4. Vektorisiertes Backtesting beherrschen

Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: [e-mail]

[Sie waren so dumm zu glauben, dass man aus der Vergangenheit die Zukunft vorhersagen kann.¹

Der Wirtschaftswissenschaftler

Die Entwicklung von Ideen und Hypothesen für ein algorithmisches Handelsprogramm ist in der Regel der kreativere und manchmal sogar lustigere Teil der Vorbereitungsphase. Sie gründlich zu testen ist in der Regel der technischere und zeitaufwändigere Teil. In diesem Kapitel geht es um das vektorisierte Backtesting von verschiedenen algorithmischen Handelsstrategien. Es behandelt die folgenden Arten von Strategien (siehe auch "Handelsstrategien"):

Auf einfachen gleitenden Durchschnitten (SMA) basierende Strategien

Die Grundidee der Verwendung von SMAs zur Generierung von Kauf- und Verkaufssignalen ist bereits Jahrzehnte alt. SMAs sind ein wichtiges Instrument in der sogenannten technischen Analyse von Aktienkursen. Ein Signal wird zum Beispiel abgeleitet, wenn ein SMA, der für ein kürzeres Zeitfenster definiert ist - zum Beispiel 42 Tage - einen SMA kreuzt, der für ein längeres Zeitfenster definiert ist - zum Beispiel 252 Tage.

Momentum-Strategien

Das sind Strategien, die auf der Annahme beruhen, dass die jüngste Entwicklung noch einige Zeit andauern wird. Bei einer Aktie, die sich in einem Abwärtstrend befindet, wird beispielsweise davon ausgegangen, dass dies noch länger der Fall sein wird, weshalb eine solche Aktie geshortet werden soll.

Mean-Reversion-Strategien

Mean-Reversion-Strategien beruhen darauf, dass die Aktienkurse oder die Preise anderer Finanzinstrumente dazu neigen, zu einem Mittelwert oder einem Trendniveau zurückzukehren, wenn sie zu stark von diesem Niveau abgewichen sind.

Das Kapitel geht wie folgt vor. In "Vektorisierung nutzen" wird die Vektorisierung als nützlicher technischer Ansatz zur Formulierung und zum Backtesting von Handelsstrategien vorgestellt. " Strategien, die auf einfachen gleitenden Durchschnitten basieren" ist der Kern dieses Kapitels und behandelt das vektorisierte Backtesting von SMA-basierten Strategien in aller Ausführlichkeit. " Strategien auf Basis von Momentum" stellt Handelsstrategien vor, die auf dem sogenannten Zeitreihenmomentum ("jüngste Performance") einer Aktie basieren, und führt ein Backtesting durch. "Strategien auf Basis von Mean Reversion" schließt das Kapitel mit der Behandlung von Mean-Reversion-Strategien ab. Schließlich werden in "Data Snooping and Overfitting" die Fallstricke von Data Snooping und Overfitting im Zusammenhang mit dem Backtesting von algorithmischen Handelsstrategien diskutiert.

Das Hauptziel dieses Kapitels ist es, den vektorisierten Implementierungsansatz, den Pakete wie NumPy und pandas ermöglichen, als effizientes und schnelles Backtesting-Tool zu beherrschen. Zu diesem Zweck werden in den vorgestellten Ansätzen einige vereinfachende Annahmen getroffen, um die Diskussion besser auf das Hauptthema der Vektorisierung zu konzentrieren.

Vektorisiertes Backtesting sollte in den folgenden Fällen in Betracht gezogen werden:

Einfache Handelsstrategien

Der vektorisierte Backtesting-Ansatz hat eindeutig seine Grenzen, wenn es um die Modellierung von algorithmischen Handelsstrategien geht. Viele beliebte, einfache Strategien lassen sich jedoch vektorisiert backtesten.

Interaktive Strategieerforschung

Vektorisiertes Backtesting ermöglicht eine agile, interaktive Erkundung von Handelsstrategien und ihren Eigenschaften. Ein paar Codezeilen reichen in der Regel aus, um erste Ergebnisse zu erzielen, und verschiedene Parameterkombinationen lassen sich leicht testen.

Visualisierung als Hauptziel

Der Ansatz eignet sich sehr gut für die Visualisierung der verwendeten Daten, Statistiken, Signale und Leistungsergebnisse. Ein paar Zeilen Python-Code reichen in der Regel aus, um ansprechende und aufschlussreiche Diagramme zu erstellen.

Umfassende Backtesting-Programme

Vektorisiertes Backtesting ist im Allgemeinen ziemlich schnell und ermöglicht es, eine Vielzahl von Parameterkombinationen in kurzer Zeit zu testen. Wenn Geschwindigkeit der Schlüssel ist, sollte dieser Ansatz in Betracht gezogen werden.

Nutzung der Vektorisierung

Vektorisierung oder Array-Programmierung bezeichnet einen Programmierstil, bei dem Operationen mit Skalaren (d.h. Ganzzahl- oder Fließkommazahlen) auf Vektoren, Matrizen oder sogar mehrdimensionale Arrays verallgemeinert werden. Betrachte einen Vektor aus ganzen Zahlen $v={(1,2,3,4,5)}^T$ wird in Python als list Objekt v = [1, 2, 3, 4, 5] dargestellt. Die Berechnung des Skalarprodukts eines solchen Vektors und z.B. der Zahl 2 erfordert in reinem Python eine for Schleife oder etwas Ähnliches, wie z.B. ein Listenverständnis, das nur eine andere Syntax für eine for Schleife ist:

In [1]: v = [1, 2, 3, 4, 5]

In [2]: sm = [2 * i for i in v]

In [3]: sm
Out[3]: [2, 4, 6, 8, 10]

Im Prinzip kann man mit Python ein list Objekt mit einer ganzen Zahl multiplizieren, aber das Datenmodell von Python gibt im Beispielfall ein anderes list Objekt zurück, das die doppelte Anzahl von Elementen des ursprünglichen Objekts enthält:

In [4]: 2 * v
Out[4]: [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

Vektorisierung mit NumPy

Das Paket NumPy für numerische Berechnungen (vgl. NumPy Homepage) führt die Vektorisierung in Python ein. Die wichtigste Klasse, die von NumPy bereitgestellt wird, ist die Klasse ndarray, die für n-dimensionales Array steht. Eine Instanz eines solchen Objekts kann z.B. auf der Grundlage des list Objekts v erstellt werden. Skalarmultiplikation, lineare Transformationen und ähnliche Operationen aus der linearen Algebra funktionieren dannwie gewünscht:

In [5]: import numpy as np  

In [6]: a = np.array(v)  

In [7]: a  
Out[7]: array([1, 2, 3, 4, 5])

In [8]: type(a)  
Out[8]: numpy.ndarray

In [9]: 2 * a  
Out[9]: array([ 2,  4,  6,  8, 10])

In [10]: 0.5 * a + 2  
Out[10]: array([2.5, 3. , 3.5, 4. , 4.5])

Importiert das Paket NumPy.

Instanziiert ein ndarray Objekt auf der Grundlage des list Objekts.

Druckt die als ndarray Objekt gespeicherten Daten aus.

Schaut nach dem Typ des Objekts.

Erzielt eine skalare Multiplikation auf vektorisierte Weise.

Erzielt eine lineare Transformation auf vektorisierte Weise.

Der Übergang von einem eindimensionalen Feld (einem Vektor) zu einem zweidimensionalen Feld (einer Matrix) ist ganz natürlich. Das Gleiche gilt für höhere Dimensionen:

In [11]: a = np.arange(12).reshape((4, 3))  

In [12]: a
Out[12]: array([[ 0,  1,  2],
                [ 3,  4,  5],
                [ 6,  7,  8],
                [ 9, 10, 11]])

In [13]: 2 * a
Out[13]: array([[ 0,  2,  4],
                [ 6,  8, 10],
                [12, 14, 16],
                [18, 20, 22]])

In [14]: a ** 2  
Out[14]: array([[  0,   1,   4],
                [  9,  16,  25],
                [ 36,  49,  64],
                [ 81, 100, 121]])

Erzeugt ein eindimensionales ndarray Objekt und formt es in zwei Dimensionen um.

Berechnet das Quadrat jedes Elements des Objekts auf vektorisierte Weise.

Darüber hinaus bietet die Klasse ndarray bestimmte Methoden, die vektorisierte Operationen ermöglichen. Sie haben oft auch Gegenstücke in Form von so genannten universellen Funktionen, die NumPy bereitstellt:

In [15]: a.mean()  
Out[15]: 5.5

In [16]: np.mean(a)  
Out[16]: 5.5

In [17]: a.mean(axis=0)  
Out[17]: array([4.5, 5.5, 6.5])

In [18]: np.mean(a, axis=1)  
Out[18]: array([ 1.,  4.,  7., 10.])

Berechnet den Mittelwert aller Elemente durch einen Methodenaufruf.

Berechnet den Mittelwert aller Elemente durch eine universelle Funktion.

Berechnet den Mittelwert entlang der ersten Achse.

Berechnet den Mittelwert entlang der zweiten Achse.

Ein Beispiel aus der Finanzwelt ist die Funktion generate_sample_data() in "Python Scripts", die eine Euler-Diskretisierung verwendet, um Musterpfade für eine geometrische Brownsche Bewegung zu erzeugen. Die Implementierung nutzt mehrere vektorisierte Operationen, die in einer einzigen Codezeile zusammengefasst sind.

Weitere Einzelheiten zur Vektorisierung mit NumPy findest du im Anhang A. In Hilpisch (2018) findest du eine Vielzahl von Anwendungen der Vektorisierung im Finanzkontext.

Der Standard-Befehlssatz und das Datenmodell von Python erlauben in der Regel keine vektorisierten numerischen Operationen. NumPy führt leistungsstarke Vektorisierungstechniken ein, die auf der regulären Array-Klasse ndarray basieren und zu prägnantem Code führen, der der mathematischen Notation beispielsweise in der linearen Algebra in Bezug auf Vektoren und Matrizen nahe kommt.

Vektorisierung mit Pandas

Das Paket pandas und die zentrale Klasse DataFrame machen viel Gebrauch von NumPy und der Klasse ndarray. Daher lassen sich die meisten Vektorisierungsprinzipien aus dem Kontext von NumPy auf pandas übertragen. Die Mechanismen lassen sich am besten anhand eines konkreten Beispiels erklären. Definiere zunächst ein zweidimensionales ndarray Objekt:

In [19]: a = np.arange(15).reshape(5, 3)

In [20]: a
Out[20]: array([[ 0,  1,  2],
                [ 3,  4,  5],
                [ 6,  7,  8],
                [ 9, 10, 11],
                [12, 13, 14]])

Für die Erstellung eines DataFrame -Objekts generierst du ein list -Objekt mit Spaltennamen und ein DatetimeIndex -Objekt, beide mit der passenden Größe für das ndarray -Objekt:

In [21]: import pandas as pd  

In [22]: columns = list('abc')  

In [23]: columns
Out[23]: ['a', 'b', 'c']

In [24]: index = pd.date_range('2021-7-1', periods=5, freq='B')  

In [25]: index
Out[25]: DatetimeIndex(['2021-07-01', '2021-07-02', '2021-07-05',
          '2021-07-06',
                        '2021-07-07'],
                       dtype='datetime64[ns]', freq='B')

In [26]: df = pd.DataFrame(a, columns=columns, index=index)  

In [27]: df
Out[27]:              a   b   c
         2021-07-01   0   1   2
         2021-07-02   3   4   5
         2021-07-05   6   7   8
         2021-07-06   9  10  11
         2021-07-07  12  13  14

Importiert das Paket pandas.

Erzeugt ein list Objekt aus dem str Objekt.

Es wird ein pandas DatetimeIndex Objekt erstellt, das eine "Werktags"-Frequenz hat und über fünf Perioden geht.

Ein DataFrame Objekt wird auf der Grundlage des ndarray Objekts a mit den angegebenen Spaltenbezeichnungen und Indexwerten instanziiert.

Im Prinzip funktioniert die Vektorisierung jetzt ähnlich wie die ndarray Objekte. Ein Unterschied ist, dass Aggregationsoperationen standardmäßig spaltenweise Ergebnisse liefern:

In [28]: 2 * df  
Out[28]:              a   b   c
         2021-07-01   0   2   4
         2021-07-02   6   8  10
         2021-07-05  12  14  16
         2021-07-06  18  20  22
         2021-07-07  24  26  28

In [29]: df.sum()  
Out[29]: a    30
         b    35
         c    40
         dtype: int64

In [30]: np.mean(df)  
Out[30]: a    6.0
         b    7.0
         c    8.0
         dtype: float64

Berechnet das Skalarprodukt für das Objekt DataFrame (behandelt als Matrix).

Berechnet die Summe pro Spalte.

Berechnet den Mittelwert pro Spalte.

Spaltenweise Operationen können durch Verweis auf die jeweiligen Spaltennamen durchgeführt werden, entweder durch die Klammer- oder die Punktschreibweise:

In [31]: df['a'] + df['c']  
Out[31]: 2021-07-01     2
         2021-07-02     8
         2021-07-05    14
         2021-07-06    20
         2021-07-07    26
         Freq: B, dtype: int64

In [32]: 0.5 * df.a + 2 * df.b - df.c  
Out[32]: 2021-07-01     0.0
         2021-07-02     4.5
         2021-07-05     9.0
         2021-07-06    13.5
         2021-07-07    18.0
         Freq: B, dtype: float64

Berechnet die elementweise Summe über die Spalten a und c.

Berechnet eine lineare Transformation, die alle drei Spalten umfasst.

Auch Bedingungen, die zu booleschen Ergebnisvektoren führen, und SQL-ähnliche Auswahlen, die auf solchen Bedingungen basieren, sind einfach zu implementieren:

In [33]: df['a'] > 5  
Out[33]: 2021-07-01    False
         2021-07-02    False
         2021-07-05     True
         2021-07-06     True
         2021-07-07     True
         Freq: B, Name: a, dtype: bool

In [34]: df[df['a'] > 5]  
Out[34]:              a   b   c
         2021-07-05   6   7   8
         2021-07-06   9  10  11
         2021-07-07  12  13  14

Welches Element in der Spalte a ist größer als fünf?

Wähle alle Zeilen aus, in denen das Element in der Spalte a größer als fünf ist.

Für ein vektorisiertes Backtesting von Handelsstrategien sind Vergleiche zwischen zwei oder mehr Spalten typisch:

In [35]: df['c'] > df['b']  
Out[35]: 2021-07-01    True
         2021-07-02    True
         2021-07-05    True
         2021-07-06    True
         2021-07-07    True
         Freq: B, dtype: bool

In [36]: 0.15 * df.a + df.b > df.c  
Out[36]: 2021-07-01    False
         2021-07-02    False
         2021-07-05    False
         2021-07-06     True
         2021-07-07     True
         Freq: B, dtype: bool

Für welches Datum ist das Element in der Spalte c größer als in der Spalte b?

Bedingung, die eine lineare Kombination der Spalten a und b mit der Spalte c vergleicht.

Die Vektorisierung mit pandas ist ein leistungsfähiges Konzept, insbesondere für die Implementierung von Finanzalgorithmen und das vektorisierte Backtesting, wie im weiteren Verlauf dieses Kapitels erläutert wird. Mehr über die Grundlagen der Vektorisierung mit pandas und Finanzbeispiele findest du in Hilpisch (2018, Kap. 5).

Während NumPy allgemeine Vektorisierungsansätze in die Welt der numerischen Berechnungen in Python bringt, ermöglicht pandas die Vektorisierung von Zeitreihendaten. Dies ist besonders hilfreich für die Implementierung von Finanzalgorithmen und das Backtesting von algorithmischen Handelsstrategien. Mit diesem Ansatz kannst du prägnanten Code und eine schnellere Codeausführung im Vergleich zu Standard-Python-Code erwarten, der for Schleifen und ähnliche Idiome verwendet, um das gleiche Ziel zu erreichen.

Strategien, die auf einfachen gleitenden Durchschnitten basieren

Der Handel auf Basis einfacher gleitender Durchschnitte (SMAs) ist eine jahrzehntealte Strategie, die ihren Ursprung in der technischen Aktienanalyse hat. Brock et al. (1992) zum Beispiel untersuchen solche Strategien empirisch und systematisch. Sie schreiben:

Der Begriff "technische Analyse" ist eine allgemeine Überschrift für eine Vielzahl von Handelstechniken....In diesem Beitrag untersuchen wir zwei der einfachsten und beliebtesten technischen Regeln: den gleitenden Durchschnitts-Oszillator und den Handelsbereichsbruch (Widerstands- und Unterstützungsniveaus). Bei der ersten Methode werden Kauf- und Verkaufssignale durch zwei gleitende Durchschnitte, eine lange und eine kurze Periode erzeugt....Unsere Studie zeigt, dass die technische Analyse hilft, Aktienveränderungen vorherzusagen.

Einstieg in die Grundlagen

In diesem Unterkapitel geht es um die Grundlagen des Backtestings von Handelsstrategien, die zwei SMAs verwenden. Das folgende Beispiel arbeitet mit Tagesabschlussdaten (EOD) für den EUR/USD-Wechselkurs, wie sie in der csv-Datei unter der EOD-Datendatei bereitgestellt werden. Die Daten im Datensatz stammen von der Refinitiv Eikon Data API und stellen EOD-Werte für die jeweiligen Instrumente dar (RICs):

In [37]: raw = pd.read_csv('http://hilpisch.com/pyalgo_eikon_eod_data.csv',
                            index_col=0, parse_dates=True).dropna()  

In [38]: raw.info()  
         <class 'pandas.core.frame.DataFrame'>
         DatetimeIndex: 2516 entries, 2010-01-04 to 2019-12-31
         Data columns (total 12 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   AAPL.O  2516 non-null   float64
          1   MSFT.O  2516 non-null   float64
          2   INTC.O  2516 non-null   float64
          3   AMZN.O  2516 non-null   float64
          4   GS.N    2516 non-null   float64
          5   SPY     2516 non-null   float64
          6   .SPX    2516 non-null   float64
          7   .VIX    2516 non-null   float64
          8   EUR=    2516 non-null   float64
          9   XAU=    2516 non-null   float64
          10  GDX     2516 non-null   float64
          11  GLD     2516 non-null   float64
         dtypes: float64(12)
         memory usage: 255.5 KB

In [39]: data = pd.DataFrame(raw['EUR='])  

In [40]: data.rename(columns={'EUR=': 'price'}, inplace=True)  

In [41]: data.info()  
         <class 'pandas.core.frame.DataFrame'>
         DatetimeIndex: 2516 entries, 2010-01-04 to 2019-12-31
         Data columns (total 1 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   price   2516 non-null   float64
         dtypes: float64(1)
         memory usage: 39.3 KB

Liest die Daten aus der per Fernzugriff gespeicherten Datei CSV.

Zeigt die Metainformationen für das Objekt DataFrame an.

Verwandelt das Series Objekt in ein DataFrame Objekt.

Benennt die einzige Spalte in price um.

Zeigt die Metainformationen für das neue DataFrame Objekt an.

Die Berechnung von SMAs wird durch die Methode rolling() in Kombination mit einer aufgeschobenen Berechnungsoperation vereinfacht:

In [42]: data['SMA1'] = data['price'].rolling(42).mean()  

In [43]: data['SMA2'] = data['price'].rolling(252).mean()  

In [44]: data.tail()  
Out[44]:              price      SMA1      SMA2
         Date
         2019-12-24  1.1087  1.107698  1.119630
         2019-12-26  1.1096  1.107740  1.119529
         2019-12-27  1.1175  1.107924  1.119428
         2019-12-30  1.1197  1.108131  1.119333
         2019-12-31  1.1210  1.108279  1.119231

Erzeugt eine Spalte mit 42 Tagen SMA-Werten. Die ersten 41 Werte werden NaN sein.

Erzeugt eine Spalte mit 252 Tagen SMA-Werten. Die ersten 251 Werte werden NaN sein.

Druckt die letzten fünf Zeilen des Datensatzes.

Eine Visualisierung der ursprünglichen Zeitreihendaten in Kombination mit den SMAs veranschaulicht die Ergebnisse am besten (siehe Abbildung 4-1):

In [45]: %matplotlib inline
         from pylab import mpl, plt
         plt.style.use('seaborn')
         mpl.rcParams['savefig.dpi'] = 300
         mpl.rcParams['font.family'] = 'serif'

In [46]: data.plot(title='EUR/USD | 42 & 252 days SMAs',
                   figsize=(10, 6));

Der nächste Schritt ist die Generierung von Signalen oder besser gesagt von Marktpositionierungen, die auf dem Verhältnis zwischen den beiden SMAs basieren. Die Regel lautet, dass wir immer dann kaufen, wenn die kürzere SMA über der längeren liegt und umgekehrt. Für unsere Zwecke kennzeichnen wir eine Long-Position mit 1 und eine Short-Position mit -1.

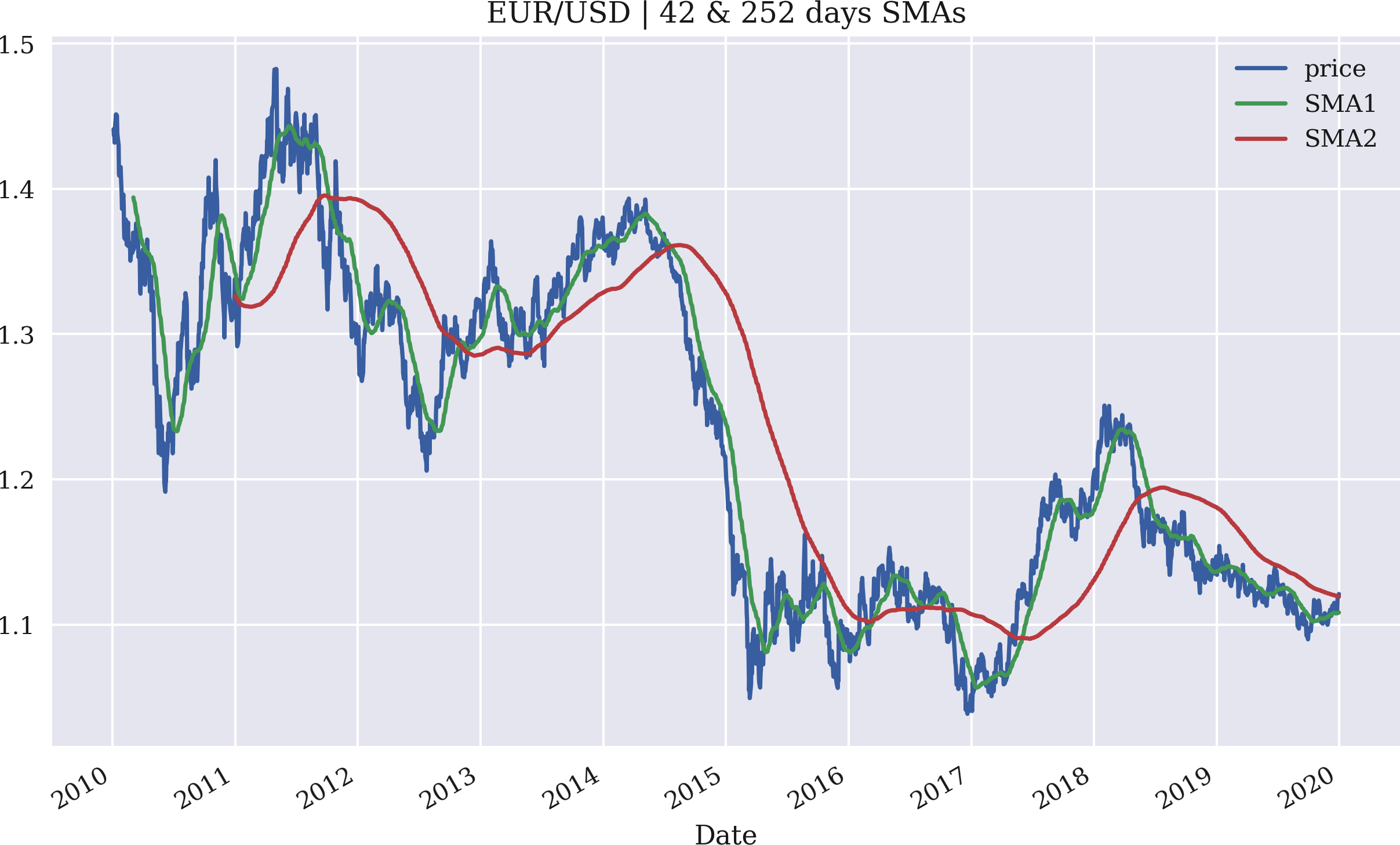
Abbildung 4-1. Der EUR/USD-Wechselkurs mit zwei SMAs

Die Möglichkeit, zwei Spalten des DataFrame Objekts direkt zu vergleichen, macht die Implementierung der Regel zu einer Angelegenheit von nur einer Codezeile. Die Positionierung über die Zeit ist in Abbildung 4-2 dargestellt:

In [47]: data['position'] = np.where(data['SMA1'] > data['SMA2'],
                                     1, -1)  

In [48]: data.dropna(inplace=True)  

In [49]: data['position'].plot(ylim=[-1.1, 1.1],
                               title='Market Positioning',
                               figsize=(10, 6));  

Implementiert die Handelsregel in vektorisierter Form. np.where() erzeugt +1 für Zeilen, in denen der Ausdruck True lautet und -1 für Zeilen, in denen der Ausdruck False lautet.

Löscht alle Zeilen des Datensatzes, die mindestens einen NaN Wert enthalten.

Stellt die Positionierung über die Zeit dar.

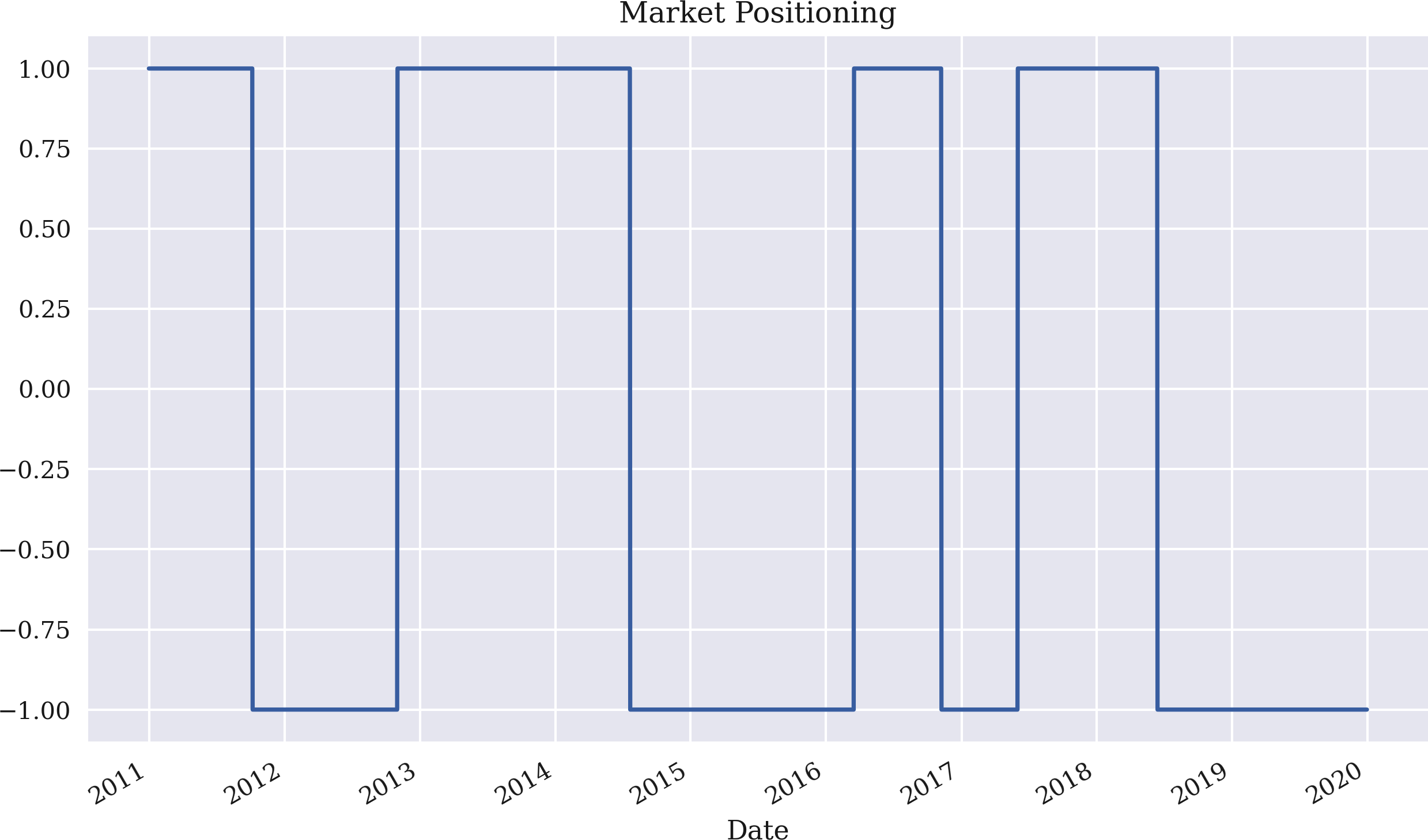
Abbildung 4-2. Marktpositionierung basierend auf der Strategie mit zwei SMAs

Um die Leistung der Strategie zu berechnen, berechnest du als Nächstes die logarithmischen Renditen auf der Grundlage der ursprünglichen Finanzzeitreihen. Der Code dafür ist dank der Vektorisierung wieder recht übersichtlich. Abbildung 4-3 zeigt das Histogramm der Log-Renditen:

In [50]: data['returns'] = np.log(data['price'] / data['price'].shift(1))  

In [51]: data['returns'].hist(bins=35, figsize=(10, 6));  

Berechnet die Log-Renditen in vektorisierter Form über die Spalte price.

Stellt die Log-Rückgaben als Histogramm (Häufigkeitsverteilung) dar.

Um die Rendite der Strategie zu ermitteln, multiplizierst du die Spalte position, die um einen Handelstag verschoben wurde, mit der Spalte returns. Da die logarithmischen Renditen additiv sind, liefert die Berechnung der Summe über die Spalten returns und strategy einen ersten Vergleich der Leistung der Strategie im Vergleich zur Basisinvestition selbst.

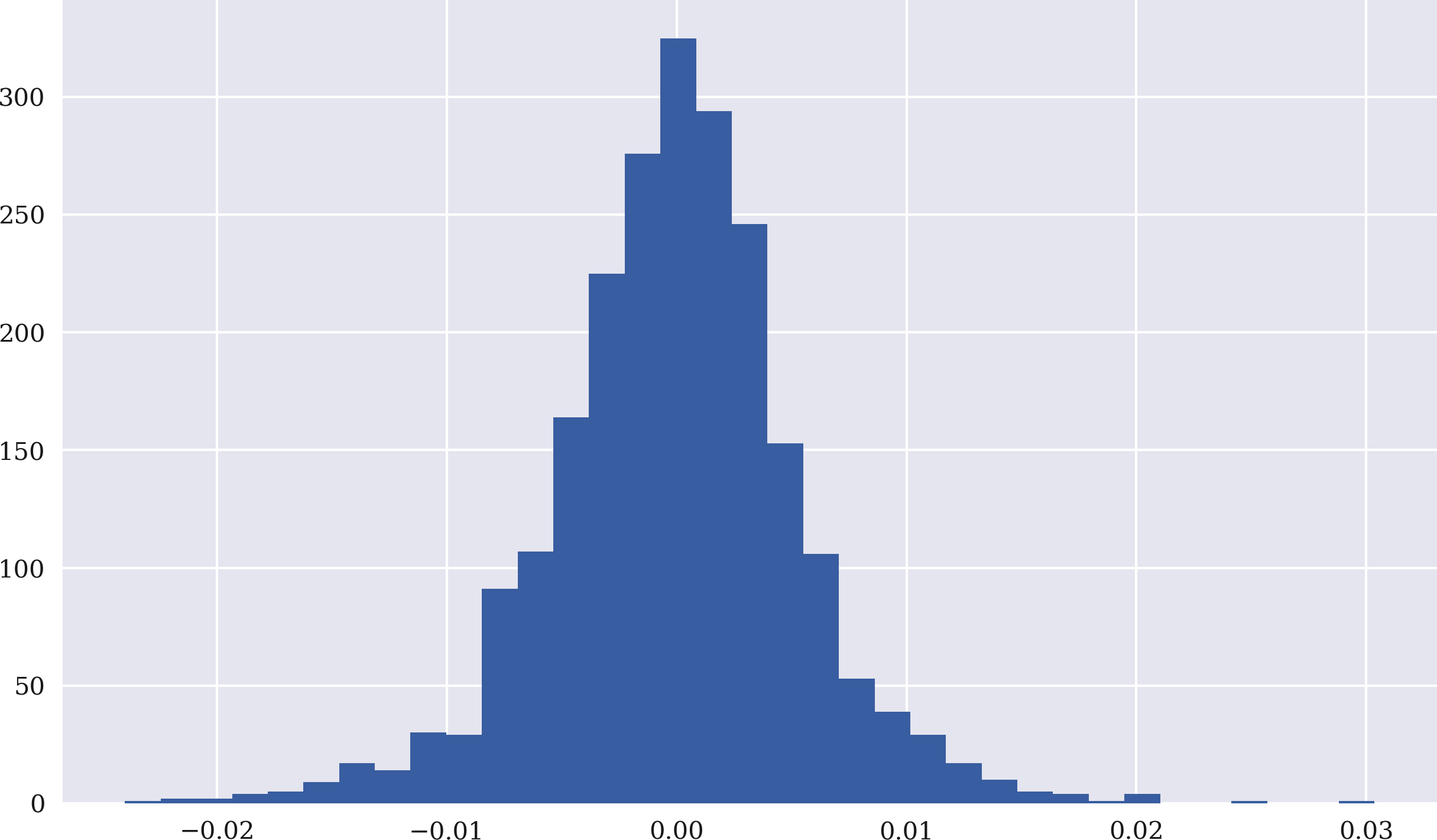
Abbildung 4-3. Häufigkeitsverteilung der EUR/USD-Log-Renditen

Der Vergleich der Renditen zeigt, dass die Strategie einen Gewinn gegenüber der passiven Benchmark-Anlage verbucht:

In [52]: data['strategy'] = data['position'].shift(1) * data['returns']  

In [53]: data[['returns', 'strategy']].sum()  
Out[53]: returns    -0.176731
         strategy    0.253121
         dtype: float64

In [54]: data[['returns', 'strategy']].sum().apply(np.exp)  
Out[54]: returns     0.838006
         strategy    1.288039
         dtype: float64

Ermittelt die logarithmischen Renditen der Strategie anhand der Positionierungen und der Marktrenditen.

Summiert die einzelnen logarithmischen Renditewerte sowohl für die Aktie als auch für die Strategie (nur zur Veranschaulichung).

Wendet die Exponentialfunktion auf die Summe der Log-Renditen an, um die Bruttoperformance zu berechnen.

Die Berechnung der kumulierten Summe über die Zeit mit cumsum und darauf aufbauend der kumulierten Renditen durch Anwendung der Exponentialfunktion np.exp() vermittelt ein umfassenderes Bild davon, wie die Strategie im Vergleich zur Performance des Basisfinanzinstruments im Laufe der Zeit abschneidet. Abbildung 4-4 zeigt die Daten grafisch und verdeutlicht die Outperformance in diesem speziellen Fall:

In [55]: data[['returns', 'strategy']].cumsum(
                     ).apply(np.exp).plot(figsize=(10, 6));

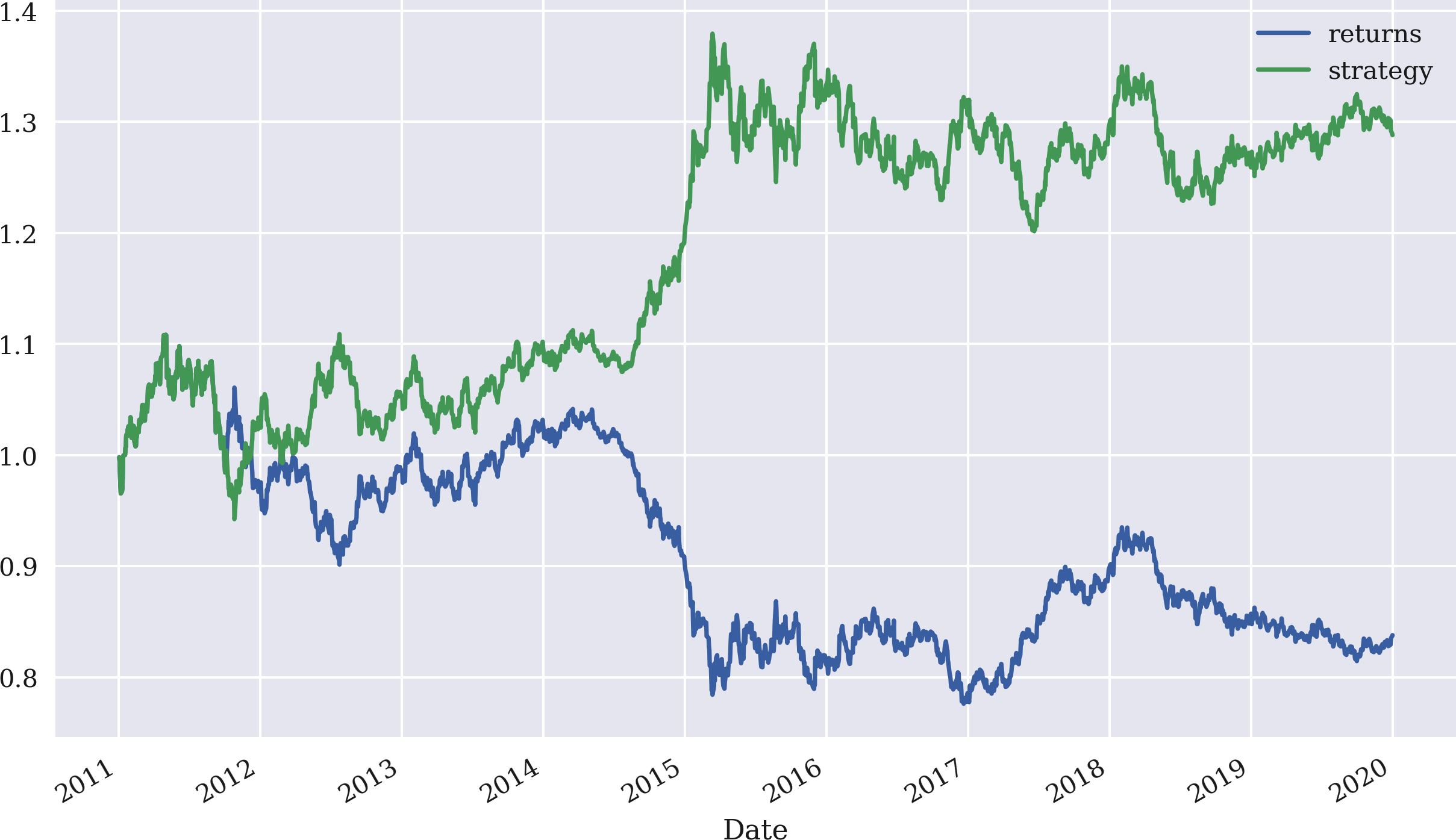
Abbildung 4-4. Bruttoperformance von EUR/USD im Vergleich zur SMA-basierten Strategie

Durchschnittliche, annualisierte Risiko-Rendite-Statistiken sowohl für die Aktie als auch für die Strategie sind leicht zu berechnen:

In [56]: data[['returns', 'strategy']].mean() * 252  
Out[56]: returns    -0.019671
         strategy    0.028174
         dtype: float64

In [57]: np.exp(data[['returns', 'strategy']].mean() * 252) - 1  
Out[57]: returns    -0.019479
         strategy    0.028575
         dtype: float64

In [58]: data[['returns', 'strategy']].std() * 252 ** 0.5  
Out[58]: returns     0.085414
         strategy    0.085405
         dtype: float64

In [59]: (data[['returns', 'strategy']].apply(np.exp) - 1).std() * 252 ** 0.5  
Out[59]: returns     0.085405
         strategy    0.085373
         dtype: float64

Berechnet den annualisierten Mittelwert der Rendite sowohl im logarithmischen als auch im regulären Raum.

Berechnet die annualisierte Standardabweichung sowohl im logarithmischen als auch im regulären Raum.

Andere Risikostatistiken, die im Zusammenhang mit der Performance von Handelsstrategien oft von Interesse sind, sind der maximale Drawdown und die längste Drawdown-Periode. Eine Hilfsstatistik, die in diesem Zusammenhang verwendet werden kann, ist die kumulative maximale Bruttoperformance, die mit der Methode cummax() berechnet und auf die Bruttoperformance der Strategie angewendet wird. Abbildung 4-5 zeigt die beiden Zeitreihen für die SMA-basierte Strategie:

In [60]: data['cumret'] = data['strategy'].cumsum().apply(np.exp)  

In [61]: data['cummax'] = data['cumret'].cummax()  

In [62]: data[['cumret', 'cummax']].dropna().plot(figsize=(10, 6));  

Definiert eine neue Spalte, cumret, mit der Bruttoleistung im Laufe der Zeit.

Definiert eine weitere Spalte mit dem laufenden Maximalwert derBruttoleistung.

Stellt die beiden neuen Spalten des DataFrame Objekts dar.

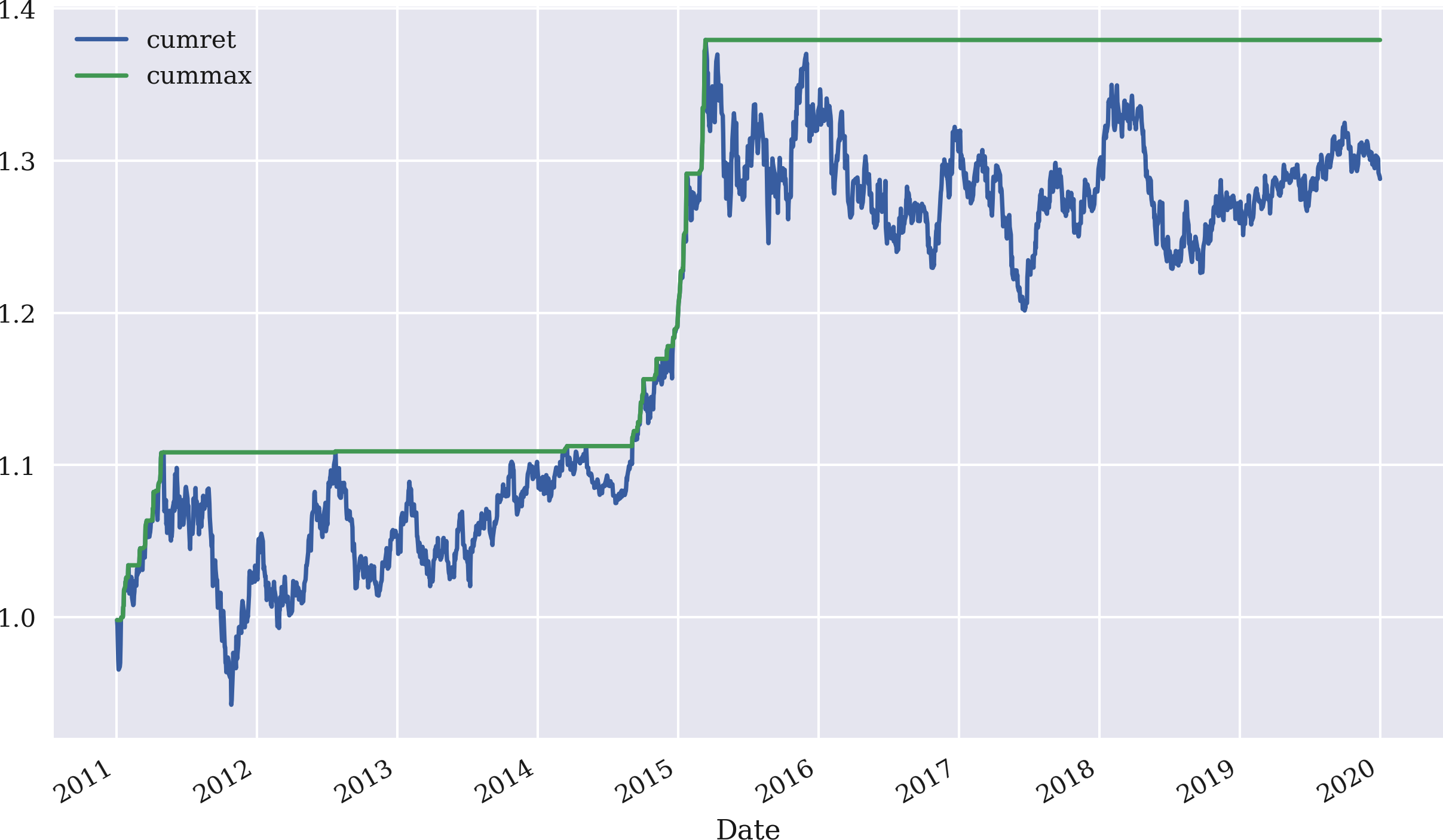
Abbildung 4-5. Bruttoperformance und kumulierte maximale Performance der SMA-basierten Strategie

Der maximale Drawdown wird dann einfach als das Maximum der Differenz zwischen den beiden relevanten Spalten berechnet. Der maximale Drawdown in diesem Beispiel beträgt etwa 18 Prozentpunkte:

In [63]: drawdown = data['cummax'] - data['cumret']  

In [64]: drawdown.max()  
Out[64]: 0.17779367070195917

Berechnet die elementweise Differenz zwischen den beiden Spalten.

Wählt den höchsten Wert aus allen Unterschieden aus.

Die Bestimmung der längsten Auszahlungsdauer ist etwas komplizierter. Dazu werden die Daten benötigt, an denen die Bruttowertentwicklung ihr kumulatives Maximum erreicht (d.h. an denen ein neues Maximum festgelegt wird). Diese Informationen werden in einem temporären Objekt gespeichert. Dann werden die Differenzen in Tagen zwischen all diesen Daten berechnet und der längste Zeitraum herausgesucht. Solche Zeiträume können nur einen Tag lang oder mehr als 100 Tage lang sein. Hier dauert der längste Zeitraum 596 Tage - ein ziemlich langer Zeitraum:²

In [65]: temp = drawdown[drawdown == 0]  

In [66]: periods = (temp.index[1:].to_pydatetime() -
                    temp.index[:-1].to_pydatetime())  

In [67]: periods[12:15]
Out[67]: array([datetime.timedelta(days=1), datetime.timedelta(days=1),
                datetime.timedelta(days=10)], dtype=object)

In [68]: periods.max()  
Out[68]: datetime.timedelta(days=596)

Wo sind die Differenzen gleich Null?

Berechnet die timedelta Werte zwischen allen Indexwerten.

Wählt den maximalen timedelta Wert aus.

Vektorisiertes Backtesting mit pandas ist aufgrund der Fähigkeiten des Pakets und der Hauptklasse DataFrame im Allgemeinen ein recht effizientes Unterfangen. Der bisher gezeigte interaktive Ansatz funktioniert jedoch nicht gut, wenn man ein größeres Backtesting-Programm implementieren möchte, das z. B. die Parameter einer SMA-basierten Strategie optimiert. Zu diesem Zweck ist ein allgemeinerer Ansatz ratsam.

pandas erweist sich als leistungsstarkes Werkzeug für die vektorielle Analyse von Handelsstrategien. Viele interessante Statistiken wie logarithmische Renditen, kumulative Renditen, annualisierte Renditen und Volatilität, maximaler Drawdown und maximale Drawdown-Periode können in der Regel mit einer einzigen oder wenigen Codezeilen berechnet werden. Ein zusätzlicher Vorteil ist, dass die Ergebnisse durch einen einfachen Methodenaufruf visualisiert werden können.

Verallgemeinerung des Ansatzes

"SMA Backtesting Class" präsentiert einen Python-Code, der eine Klasse für das vektorisierte Backtesting von SMA-basierten Handelsstrategien enthält. In gewisser Weise ist sie eine Verallgemeinerung des im vorherigen Unterabschnitt vorgestellten Ansatzes. Er ermöglicht es, eine Instanz der Klasse SMAVectorBacktester zu definieren, indem man die folgenden Parameter angibt:

• symbol RIC (Instrumentendaten) zu verwenden

• SMA1: für das Zeitfenster in Tagen für den kürzeren SMA

• SMA2: für das Zeitfenster in Tagen für den längeren SMA

• start: für das Startdatum der Datenauswahl

• end: für das Enddatum der Datenauswahl

Die Anwendung selbst wird am besten durch eine interaktive Sitzung veranschaulicht, in der die Klasse genutzt wird. Das Beispiel wiederholt zunächst den zuvor durchgeführten Backtest auf Basis der EUR/USD-Wechselkursdaten. Dann werden die SMA-Parameter für eine maximale Bruttoperformance optimiert. Auf der Grundlage der optimalen Parameter wird die resultierendeBruttoperformance der Strategie im Vergleich zum Basisinstrument über den entsprechenden Zeitraum dargestellt:

In [69]: import SMAVectorBacktester as SMA  

In [70]: smabt = SMA.SMAVectorBacktester('EUR=', 42, 252,
                                         '2010-1-1', '2019-12-31')   

In [71]: smabt.run_strategy()  
Out[71]: (1.29, 0.45)

In [72]: %%time
         smabt.optimize_parameters((30, 50, 2),
                                   (200, 300, 2))  
         CPU times: user 3.76 s, sys: 15.8 ms, total: 3.78 s
         Wall time: 3.78 s

Out[72]: (array([ 48., 238.]), 1.5)

In [73]: smabt.plot_results()  

Dies importiert das Modul als SMA.

Eine Instanz der Hauptklasse wird instanziiert.

Führt einen Backtest der SMA-basierten Strategie durch, wenn die Parameter bei der Instanziierung angegeben werden.

Die Methode optimize_parameters() nimmt als Eingabe Parameterbereiche mit Schrittgrößen und ermittelt die optimale Kombination durch einen Brute-Force-Ansatz.

Die Methode plot_results() stellt die Leistung der Strategie im Vergleich zum Benchmark-Instrument mit den aktuell gespeicherten Parameterwerten (hier aus dem Optimierungsverfahren) dar.

Die Bruttoperformance der Strategie mit der ursprünglichen Parametrisierung beträgt 1,24 oder 124%. Die optimierte Strategie erzielt eine absolute Rendite von 1,44 oder 144 % für die Parameterkombination SMA1 = 48 und SMA2 = 238. In Abbildung 4-6 ist die Bruttoperformance im Zeitverlauf grafisch dargestellt, wiederum im Vergleich zur Performance des Basisinstruments, das die Benchmark darstellt.

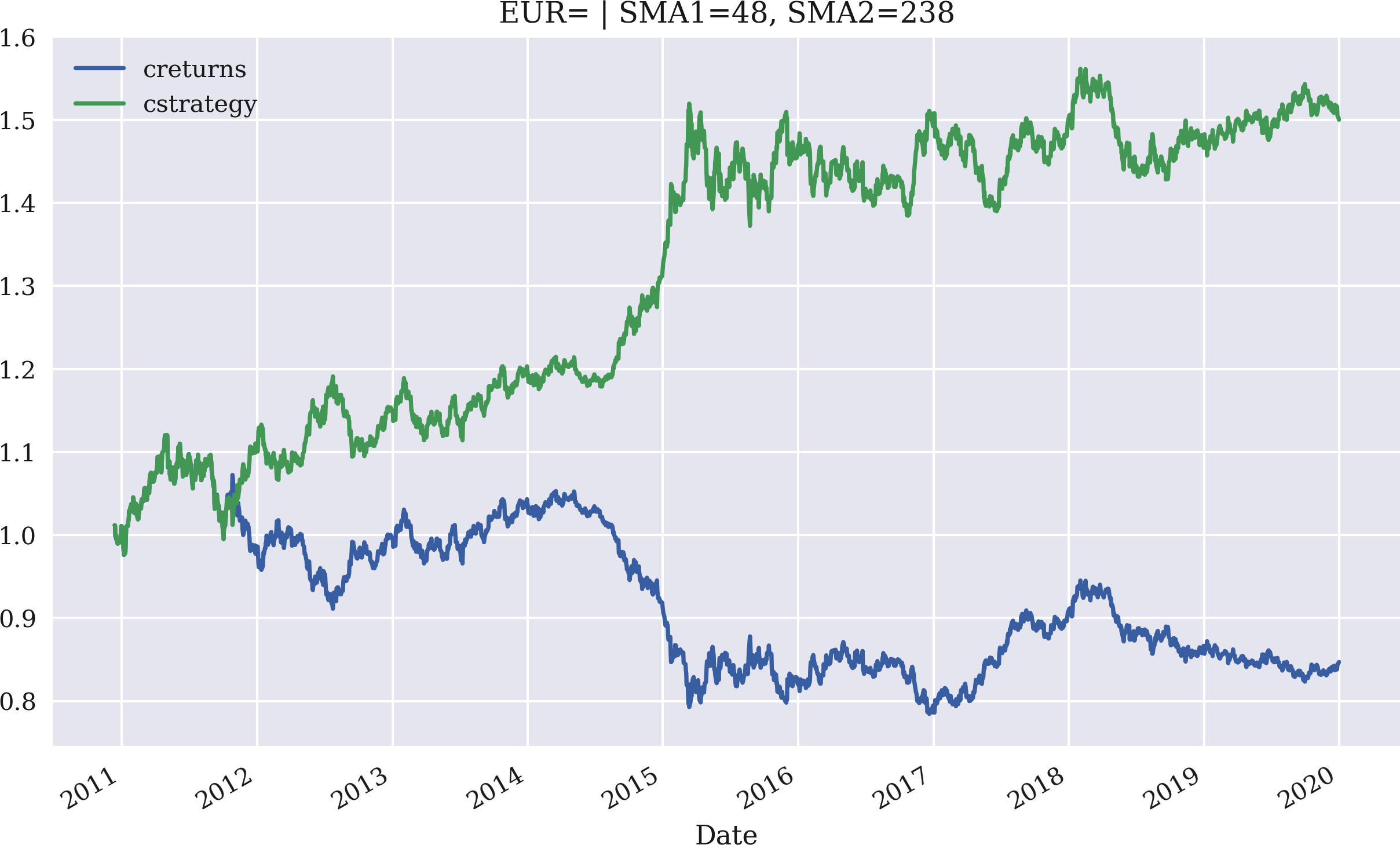
Abbildung 4-6. Bruttoperformance von EUR/USD und der optimierten SMA-Strategie

Strategien, die auf Momentum basieren

Es gibt zwei grundlegende Arten von Momentum-Strategien. Die erste Art sind Querschnittsmomentum-Strategien. Diese Strategien wählen aus einem größeren Pool von Instrumenten diejenigen aus, die sich in letzter Zeit im Vergleich zu ihren Konkurrenten (oder einer Benchmark) besser entwickelt haben, und verkaufen die Instrumente, die sich schlechter entwickelt haben. Der Grundgedanke ist, dass die Instrumente zumindest für einen bestimmten Zeitraum eine Outperformance bzw. eine Underperformance aufweisen. Jegadeesh und Titman (1993, 2001) und Chan et al. (1996) untersuchen diese Arten von Handelsstrategien und ihre potenziellen Gewinnquellen.

Querschnittliche Momentum-Strategien haben traditionell recht gut abgeschnitten. Jegadeesh und Titman (1993) schreiben:

Diese Studie belegt, dass Strategien, die Aktien kaufen, die in der Vergangenheit gut gelaufen sind, und Aktien verkaufen, die in der Vergangenheit schlecht gelaufen sind, über 3- bis 12-monatige Halteperioden deutlich positive Renditen erzielen.

Die zweite Art sind Zeitreihen-Momentumstrategien. Diese Strategien kaufen die Instrumente, die sich in letzter Zeit gut entwickelt haben, und verkaufen die Instrumente, die sich in letzter Zeit schlecht entwickelt haben. In diesem Fall ist die Benchmark die vergangene Rendite des Instruments selbst. Moskowitz et al. (2012) analysieren diese Art von Momentum-Strategie detailliert für eine Vielzahl von Märkten. Sie schreiben:

Anstatt sich auf die relativen Renditen von Wertpapieren im Querschnitt zu konzentrieren, konzentriert sich das Zeitreihenmomentum ausschließlich auf die Rendite eines Wertpapiers in der Vergangenheit....Unsere Erkenntnisse über das Zeitreihenmomentum bei praktisch allen von uns untersuchten Instrumenten scheinen die "Random-Walk"-Hypothese in Frage zu stellen, die in ihrer grundlegendsten Form besagt, dass das Wissen, ob ein Preis in der Vergangenheit gestiegen oder gefallen ist, nichts darüber aussagt, ob er in Zukunft steigen oder fallen wird.

Einstieg in die Grundlagen

Betrachte Tagesschlusskurse für den Goldpreis in USD (XAU=):

In [74]: data = pd.DataFrame(raw['XAU='])

In [75]: data.rename(columns={'XAU=': 'price'}, inplace=True)

In [76]: data['returns'] = np.log(data['price'] / data['price'].shift(1))

Die einfachste Zeitreihen-Momentumstrategie besteht darin, die Aktie zu kaufen, wenn die letzte Rendite positiv war, und sie zu verkaufen, wenn sie negativ war. Mit NumPy und pandas ist dies leicht zu formalisieren; nimm einfach das Vorzeichen der letzten verfügbaren Rendite als Marktposition. Abbildung 4-7 veranschaulicht die Leistung dieser Strategie. Die Strategie schneidet deutlich schlechter ab als das Basisinstrument:

In [77]: data['position'] = np.sign(data['returns'])  

In [78]: data['strategy'] = data['position'].shift(1) * data['returns']  

In [79]: data[['returns', 'strategy']].dropna().cumsum(
                     ).apply(np.exp).plot(figsize=(10, 6));  

Definiert eine neue Spalte mit dem Vorzeichen (d.h. 1 oder -1) der jeweiligen logarithmischen Rendite; die resultierenden Werte stellen die Marktpositionierungen (Long oder Short) dar.

Berechnet die logarithmischen Renditen der Strategie unter Berücksichtigung der Marktpositionierungen.

Stellt die Leistung der Strategie dar und vergleicht sie mit der des Benchmark-Instruments.

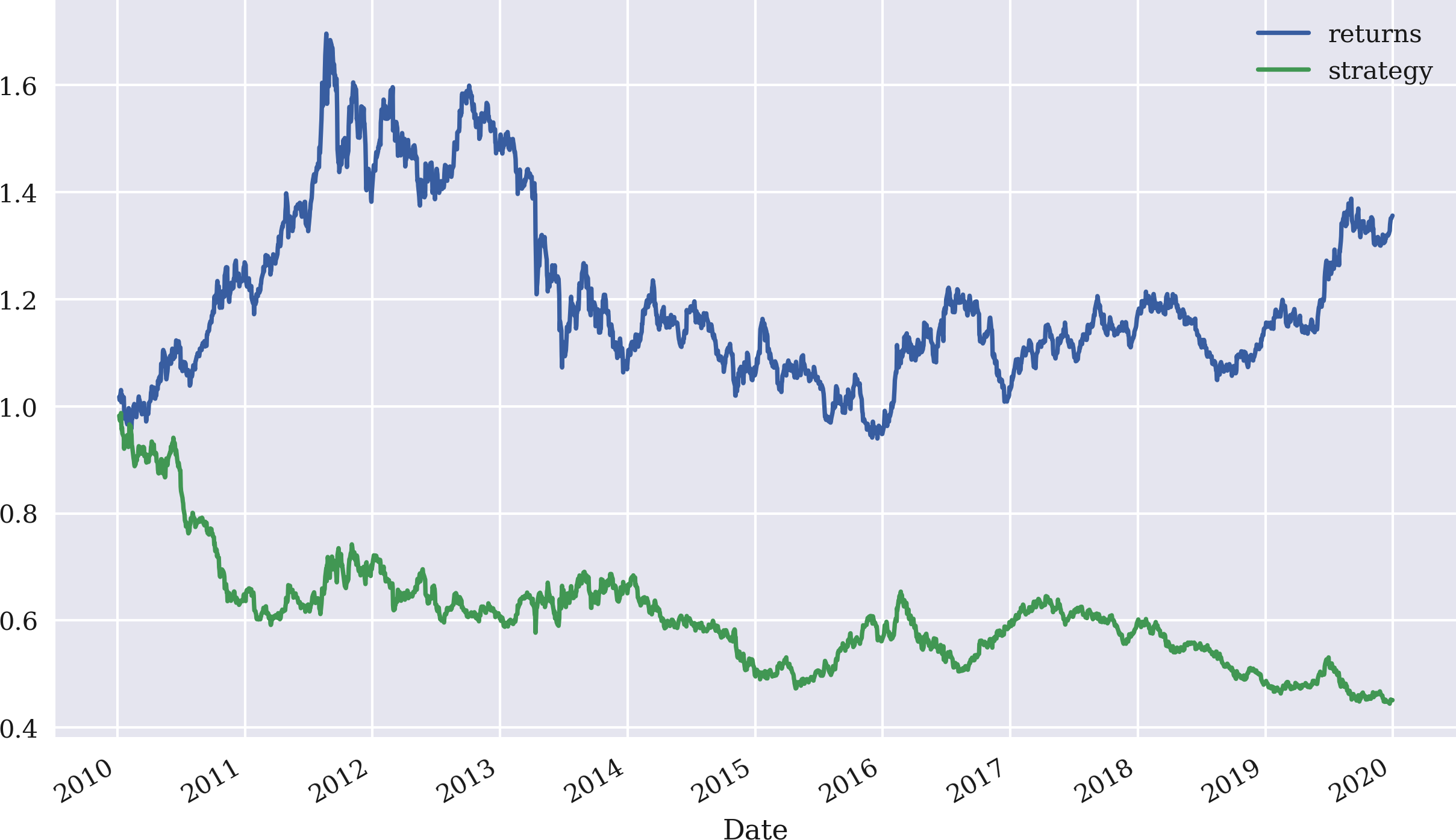
Abbildung 4-7. Bruttoperformance des Goldpreises (USD) und der Momentum-Strategie (nur letzte Rendite)

Mit einem rollierenden Zeitfenster kann die Zeitreihen-Momentumstrategie auf mehr als nur die letzte Rendite verallgemeinert werden. So kann zum Beispiel der Durchschnitt der letzten drei Renditen verwendet werden, um das Signal für die Positionierung zu erzeugen. Abbildung 4-8 zeigt, dass die Strategie in diesem Fall viel besser abschneidet, sowohl in absoluten Zahlen als auch relativ zumBasisinstrument:

In [80]: data['position'] = np.sign(data['returns'].rolling(3).mean())  

In [81]: data['strategy'] = data['position'].shift(1) * data['returns']

In [82]: data[['returns', 'strategy']].dropna().cumsum(
                 ).apply(np.exp).plot(figsize=(10, 6));

Dieses Mal wird die durchschnittliche Rendite über ein rollierendes Fenster von drei Tagen genommen.

Die Leistung hängt jedoch sehr stark vom Parameter Zeitfenster ab. Wenn du z. B. die letzten zwei statt drei Erträge auswählst, führt das zu einer deutlich schlechteren Leistung, wie in Abbildung 4-9 zu sehen ist.

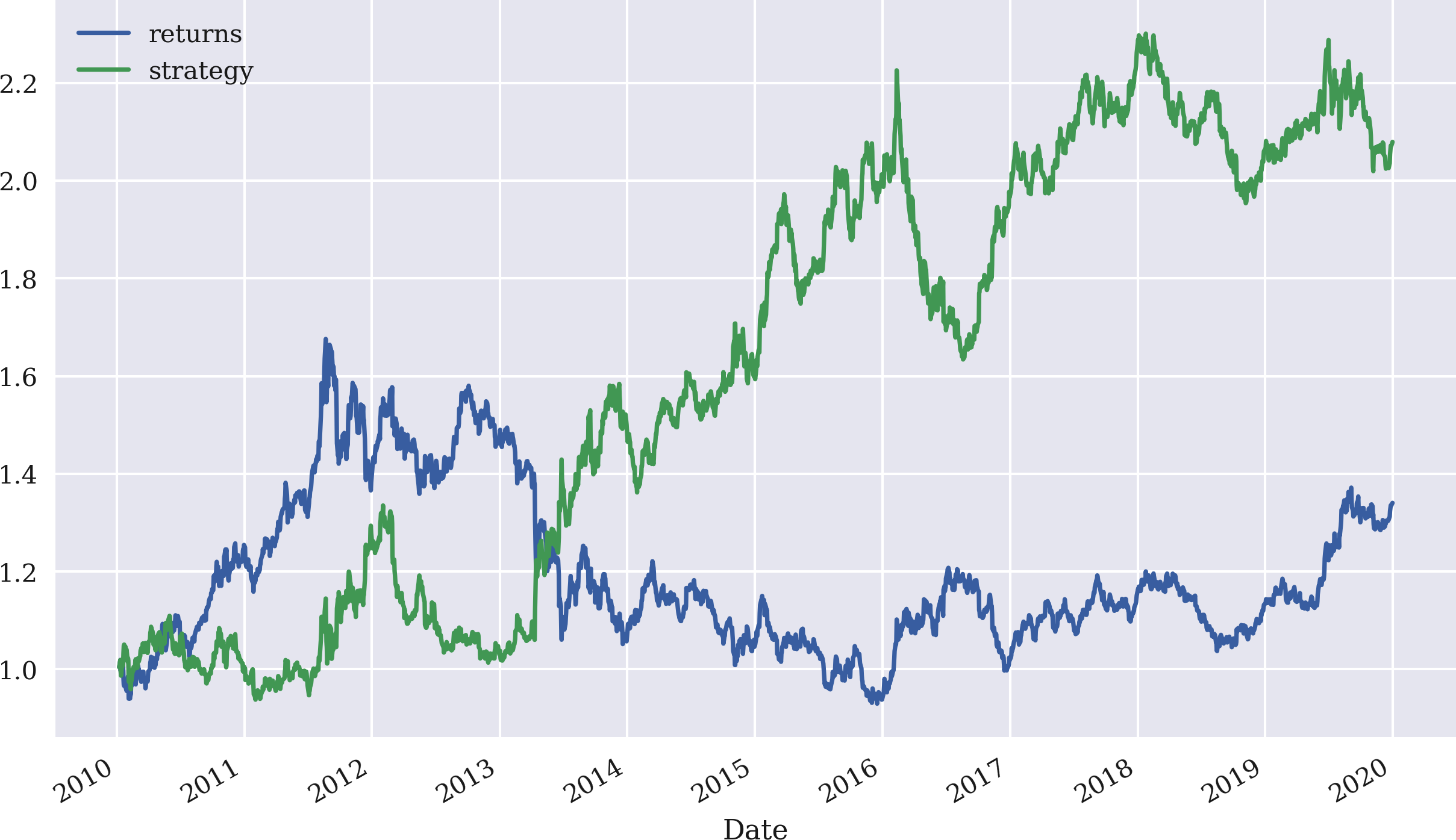
Abbildung 4-8. Bruttoperformance von Goldpreis (USD) und Momentum-Strategie (letzte drei Renditen)

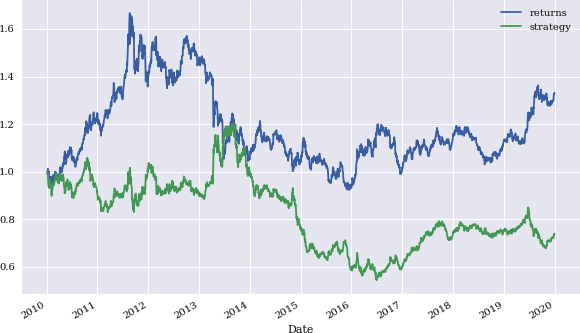
Abbildung 4-9. Bruttoperformance des Goldpreises (USD) und der Momentum-Strategie (letzte zwei Renditen)

Die Dynamik der Zeitreihe könnte auch innerhalb des Tages erwartet werden. Eigentlich würde man erwarten, dass sie intraday stärker ausgeprägt ist als interday. Abbildung 4-10 zeigt die Bruttoperformance von fünf Zeitreihen-Momentum-Strategien für eine, drei, fünf, sieben bzw. neun Renditebeobachtungen. Bei den verwendeten Daten handelt es sich um Intraday-Aktienkursdaten für Apple Inc., die von der Eikon Data API abgerufen wurden. Die Abbildung basiert auf dem folgenden Code. Grundsätzlich schneiden alle Strategien im Laufe dieses Intraday-Zeitfensters besser ab als die Aktie, wenn auch einige nur leicht:

In [83]: fn = '../data/AAPL_1min_05052020.csv'  
         # fn = '../data/SPX_1min_05052020.csv'  

In [84]: data = pd.read_csv(fn, index_col=0, parse_dates=True)  

In [85]: data.info()  
         <class 'pandas.core.frame.DataFrame'>
         DatetimeIndex: 241 entries, 2020-05-05 16:00:00 to 2020-05-05 20:00:00
         Data columns (total 6 columns):
          #   Column  Non-Null Count  Dtype
         ---  ------  --------------  -----
          0   HIGH    241 non-null    float64
          1   LOW     241 non-null    float64
          2   OPEN    241 non-null    float64
          3   CLOSE   241 non-null    float64
          4   COUNT   241 non-null    float64
          5   VOLUME  241 non-null    float64
         dtypes: float64(6)
         memory usage: 13.2 KB

In [86]: data['returns'] = np.log(data['CLOSE'] /
                                  data['CLOSE'].shift(1))  

In [87]: to_plot = ['returns']  

In [88]: for m in [1, 3, 5, 7, 9]:
             data['position_%d' % m] = np.sign(data['returns'].rolling(m).mean())  
             data['strategy_%d' % m] = (data['position_%d' % m].shift(1) *
                                        data['returns'])  
             to_plot.append('strategy_%d' % m)   

In [89]: data[to_plot].dropna().cumsum().apply(np.exp).plot(
             title='AAPL intraday 05. May 2020',
             figsize=(10, 6), style=['-', '--', '--', '--', '--', '--']);  

Liest die Intraday-Daten aus einer CSV Datei.

Berechnet die Intraday-Log-Renditen.

Definiert ein list Objekt, um die Spalten auszuwählen, die später geplottet werden sollen.

Leitet Positionierungen entsprechend dem Parameter der Momentumstrategie ab.

Berechnet die resultierenden Log-Renditen der Strategie.

Hängt den Spaltennamen an das list Objekt an.

Stellt alle relevanten Spalten dar, um die Leistung der Strategien mit der Leistung des Benchmark-Instruments zu vergleichen.

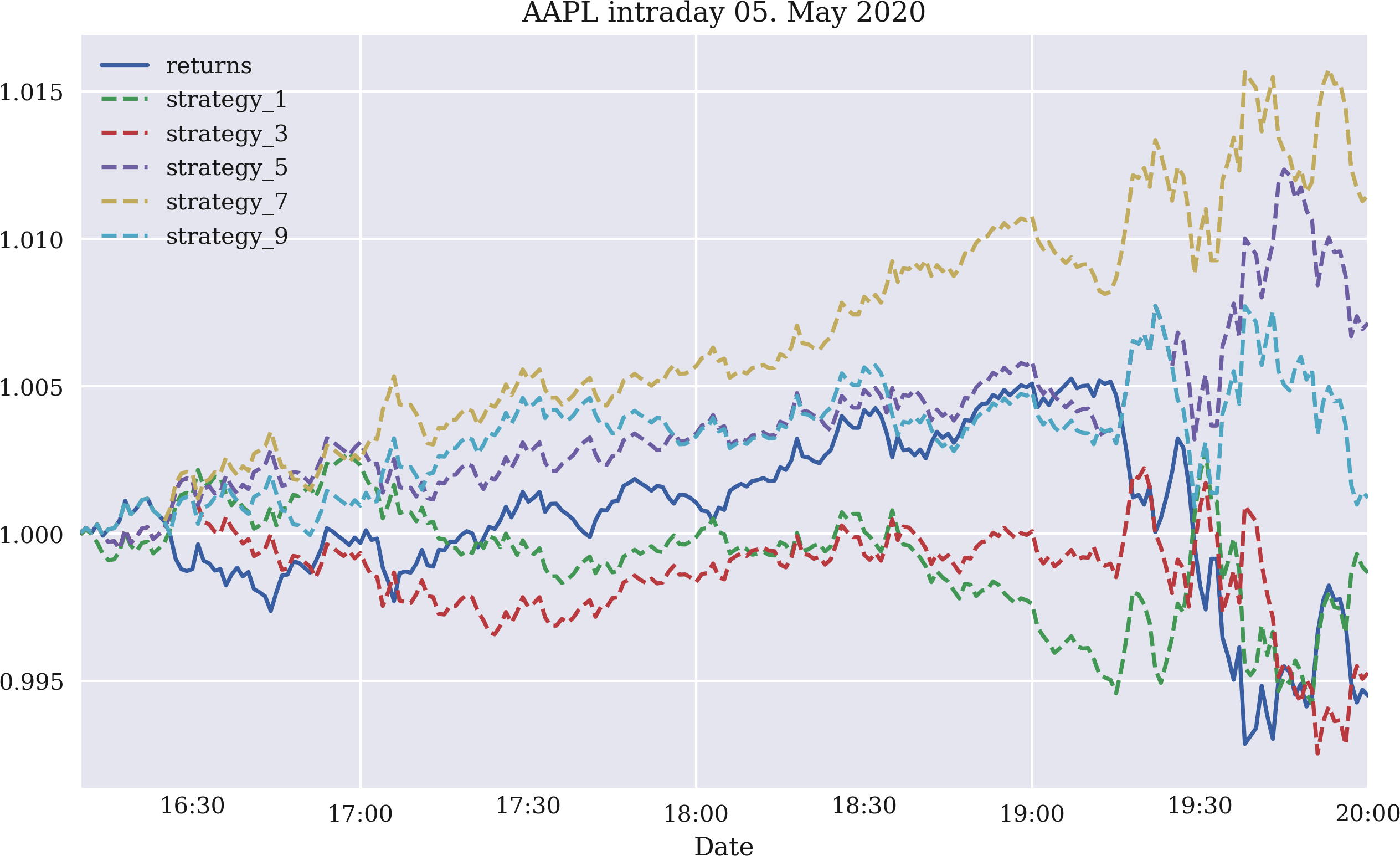
Abbildung 4-10. Brutto-Intraday-Performance der Apple-Aktie und fünf Momentum-Strategien (letzte ein, drei, fünf, sieben und neun Renditen)

Abbildung 4-11 zeigt die Leistung der gleichen fünf Strategien für den S&P 500 Index. Auch hier schneiden alle fünf Strategiekonfigurationen besser ab als der Index und weisen alle eine positive Rendite auf (vor Transaktionskosten).

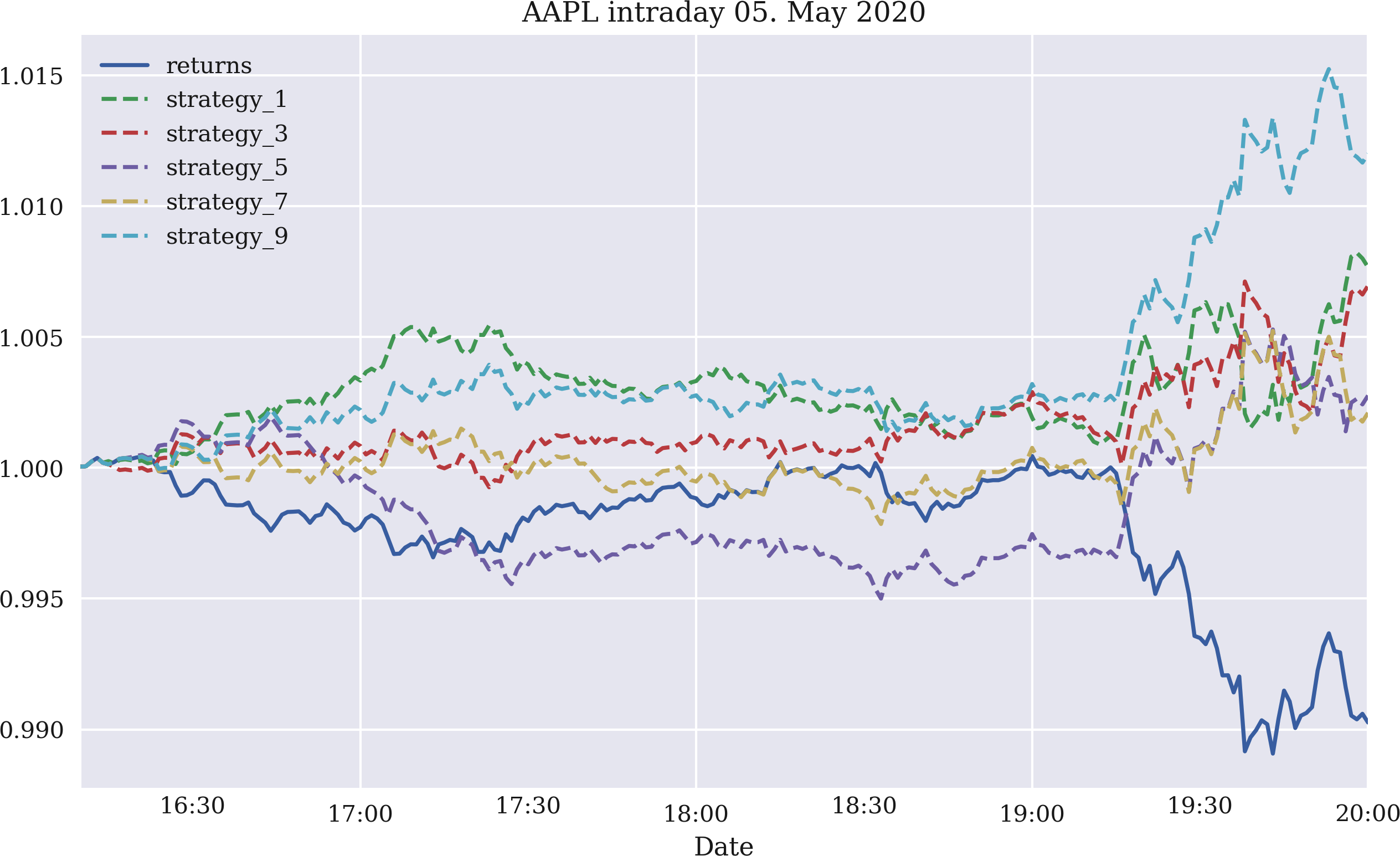
Abbildung 4-11. Brutto-Intraday-Performance des S&P 500 Index und fünf Momentum-Strategien (letzte ein, drei, fünf, sieben und neun Renditen)

Verallgemeinerung des Ansatzes

"Momentum Backtesting Class" stellt ein Python-Modul vor, das die Klasse MomVectorBacktester enthält, die ein etwas standardisierteres Backtesting von Momentum-basierten Strategien ermöglicht. Die Klasse hat die folgenden Eigenschaften:

• symbol RIC (Instrumentendaten) zu verwenden

• start: für das Startdatum der Datenauswahl

• end: für das Enddatum der Datenauswahl

• amount: für den zu investierenden Anfangsbetrag

• tc: für die proportionalen Transaktionskosten pro Handel

Im Vergleich zur Klasse SMAVectorBacktester führt diese Klasse zwei wichtige Verallgemeinerungen ein: den festen Betrag, der zu Beginn der Backtesting-Periode investiert werden muss, und die proportionalen Transaktionskosten, um kostenmäßig näher an die Marktrealitäten heranzukommen. Die Hinzufügung von Transaktionskosten ist insbesondere im Zusammenhang mit Zeitreihen-Momentumstrategien wichtig, die im Laufe der Zeit oft zu einer großen Anzahl von Transaktionen führen.

Die Anwendung ist genauso einfach und bequem wie zuvor. Das Beispiel wiederholt zunächst die Ergebnisse aus der interaktiven Sitzung zuvor, aber diesmal mit einer Anfangsinvestition von 10.000 USD. Abbildung 4-12 veranschaulicht die Leistung der Strategie, wobei der Mittelwert der letzten drei Renditen verwendet wird, um Signale für die Positionierung zu erzeugen. Der zweite Fall, der behandelt wird, ist einer mit proportionalen Transaktionskosten von 0,1 % pro Handel. Wie Abbildung 4-13 veranschaulicht, verschlechtern selbst geringe Transaktionskosten die Leistung in diesem Fall erheblich. Der treibende Faktor in dieser Hinsicht ist die relativ hohe Handelsfrequenz, die die Strategie erfordert:

In [90]: import MomVectorBacktester as Mom  

In [91]: mombt = Mom.MomVectorBacktester('XAU=', '2010-1-1',
                                         '2019-12-31', 10000, 0.0)  

In [92]: mombt.run_strategy(momentum=3)  
Out[92]: (20797.87, 7395.53)

In [93]: mombt.plot_results()
In [94]: mombt = Mom.MomVectorBacktester('XAU=', '2010-1-1',
                                         '2019-12-31', 10000, 0.001)  

In [95]: mombt.run_strategy(momentum=3)  
Out[95]: (10749.4, -2652.93)

In [96]: mombt.plot_results()

Importiert das Modul als Mom

Instanziiert ein Objekt der Backtesting-Klasse und legt das Startkapital auf 10.000 USD und die anteiligen Transaktionskosten auf Null fest.

Backtests der Momentum-Strategie auf Basis eines Zeitfensters von drei Tagen: Die Strategie übertrifft die passive Benchmark-Anlage.

Dieses Mal werden anteilige Transaktionskosten von 0,1% pro Handel angenommen.

In diesem Fall verliert die Strategie im Grunde die gesamte Outperformance.

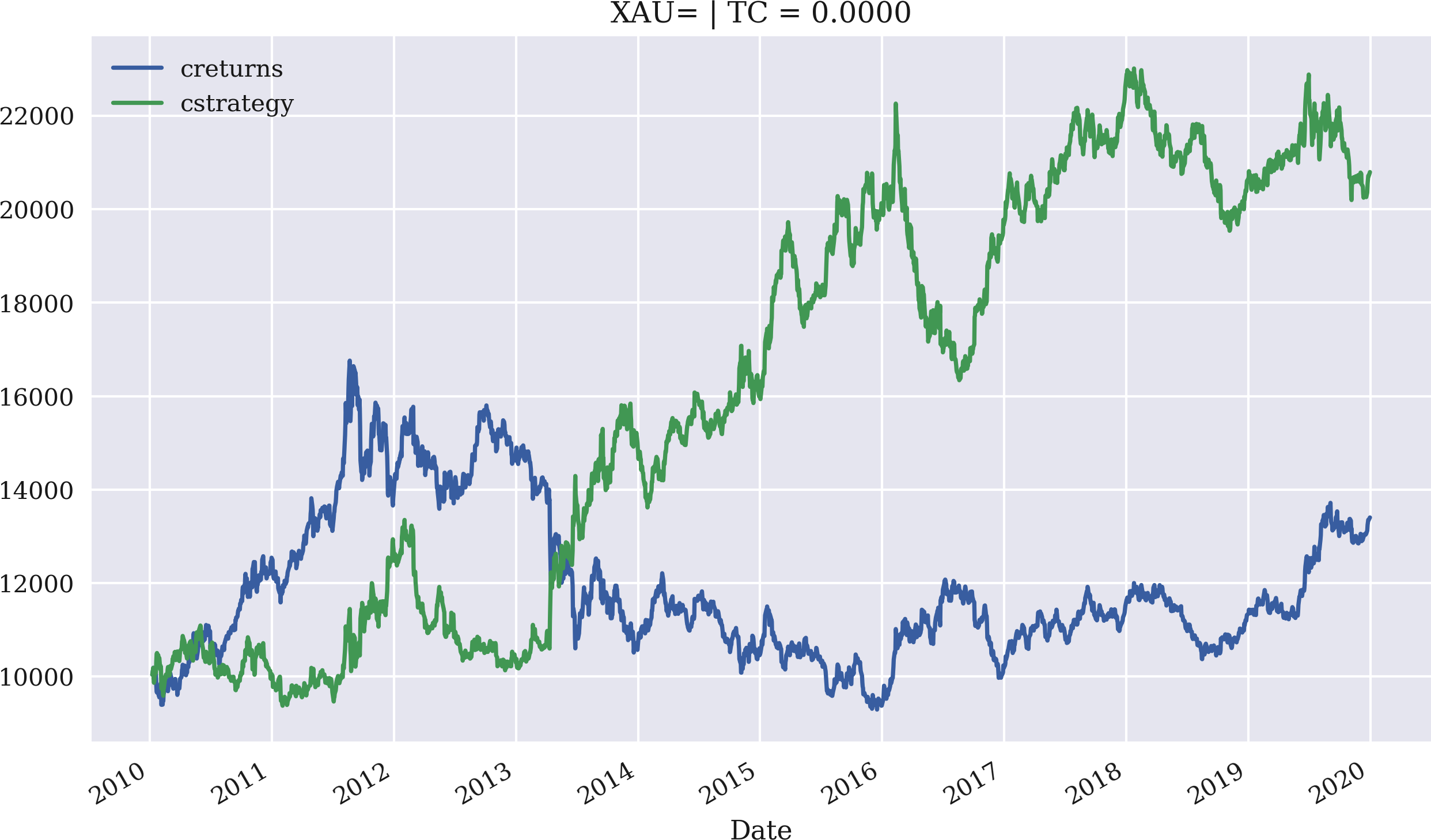
Abbildung 4-12. Bruttoperformance des Goldpreises (USD) und der Momentum-Strategie (letzte drei Renditen, ohne Transaktionskosten)

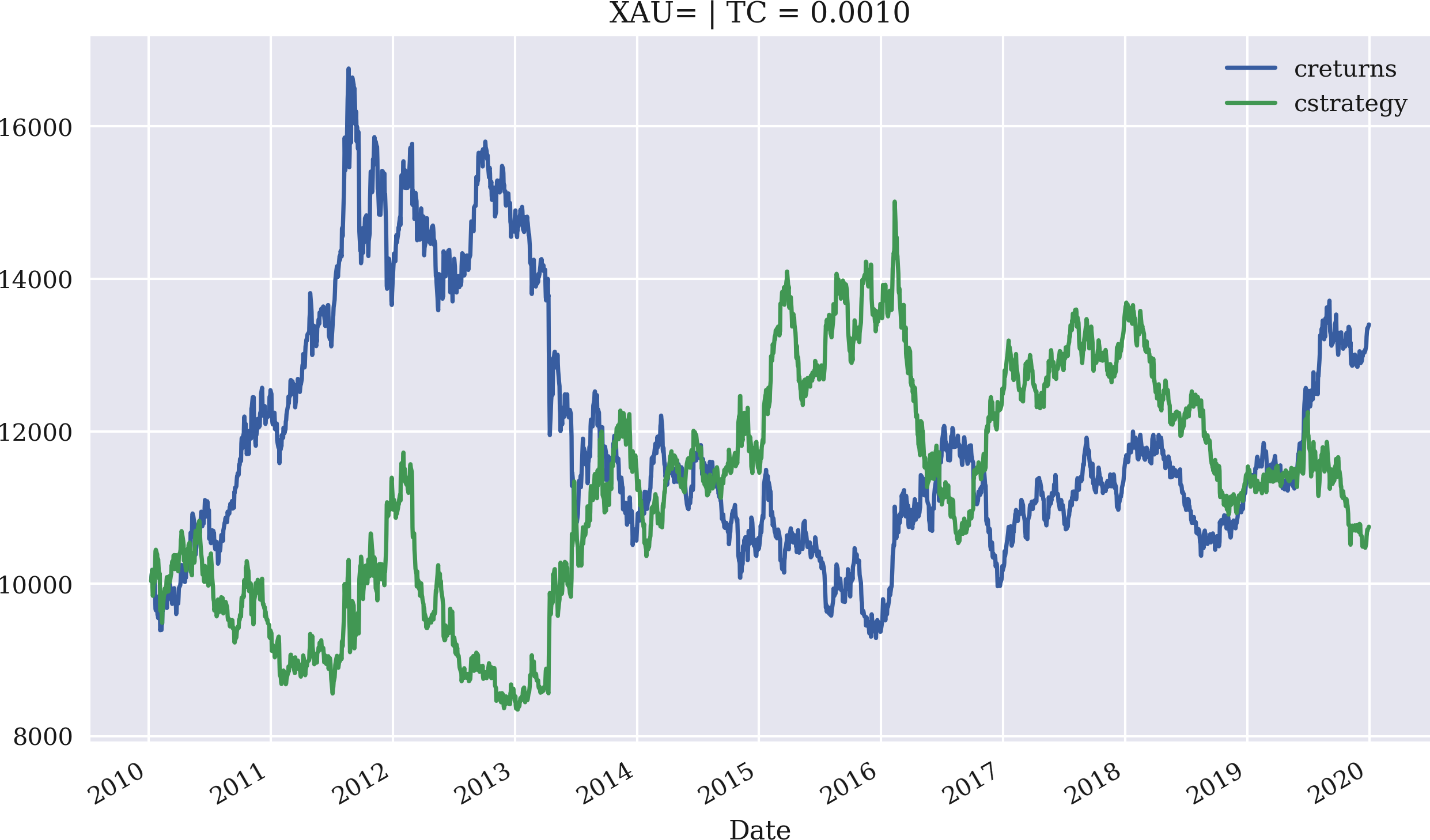
Abbildung 4-13. Bruttoperformance des Goldpreises (USD) und der Momentum-Strategie (letzte drei Renditen, Transaktionskosten von 0,1 %)

Strategien auf Basis von Mean Reversion

Grob gesagt beruhen Mean-Reversion-Strategien auf einer Überlegung, die das Gegenteil von Momentum-Strategien ist. Wenn sich ein Finanzinstrument im Vergleich zu seinem Trend "zu gut" entwickelt hat, wird es geshortet und umgekehrt. Anders ausgedrückt: Während (Zeitreihen-)Momentum-Strategien eine positive Korrelation zwischen den Renditen annehmen, gehen Mean-Reversion-Strategien von einer negativen Korrelation aus. Balvers et al. (2000) schreiben:

Mean Reversion bezeichnet die Tendenz von Vermögenspreisen, zu einem Trendpfad zurückzukehren.

Wenn du einen einfachen gleitenden Durchschnitt (SMA) als Stellvertreter für einen "Trendpfad" verwendest, kann eine Mean-Reversion-Strategie, z. B. für den EUR/USD-Wechselkurs, auf ähnliche Weise getestet werden wie die Backtests der SMA- und Momentum-basierten Strategien. Die Idee ist, einen Schwellenwert für den Abstand zwischen dem aktuellen Aktienkurs und dem SMA festzulegen, der eine Long- oder Short-Position signalisiert.

Einstieg in die Grundlagen

Die folgenden Beispiele beziehen sich auf zwei verschiedene Finanzinstrumente, für die man eine erhebliche Mittelwertumkehr erwarten würde, da sie beide auf dem Goldpreis basieren:

• GLD ist das Symbol für SPDR Gold Shares, den größten physisch besicherten börsengehandelten Fonds (ETF) für Gold (siehe Homepage von SPDR Gold Shares).

• GDX ist das Symbol für den VanEck Vectors Gold Miners ETF, der in Aktienprodukte investiert, um den NYSE Arca Gold Miners Index abzubilden (vgl. VanEck Vectors Gold Miners Übersichtsseite).

Das Beispiel beginnt mit GDX und implementiert eine Mean-Reversion-Strategie auf der Grundlage eines SMA von 25 Tagen und einem Schwellenwert von 3,5 für die absolute Abweichung des aktuellen Kurses vom SMA, um eine Positionierung zu signalisieren. Abbildung 4-14 zeigt die Abweichungen zwischen dem aktuellen Kurs von GDX und dem SMA sowie den positiven und negativen Schwellenwert, um Verkaufs- bzw. Kaufsignale zu erzeugen:

In [97]: data = pd.DataFrame(raw['GDX'])

In [98]: data.rename(columns={'GDX': 'price'}, inplace=True)

In [99]: data['returns'] = np.log(data['price'] /
                                  data['price'].shift(1))

In [100]: SMA = 25  

In [101]: data['SMA'] = data['price'].rolling(SMA).mean()  

In [102]: threshold = 3.5  

In [103]: data['distance'] = data['price'] - data['SMA']  

In [104]: data['distance'].dropna().plot(figsize=(10, 6), legend=True)  
          plt.axhline(threshold, color='r')
          plt.axhline(-threshold, color='r')
          plt.axhline(0, color='r');

Der SMA-Parameter ist definiert...

...und SMA ("Trendpfad") wird berechnet.

Der Schwellenwert für die Signalerzeugung wird festgelegt.

Die Entfernung wird für jeden Zeitpunkt berechnet.

Die Abstandswerte werden aufgezeichnet.

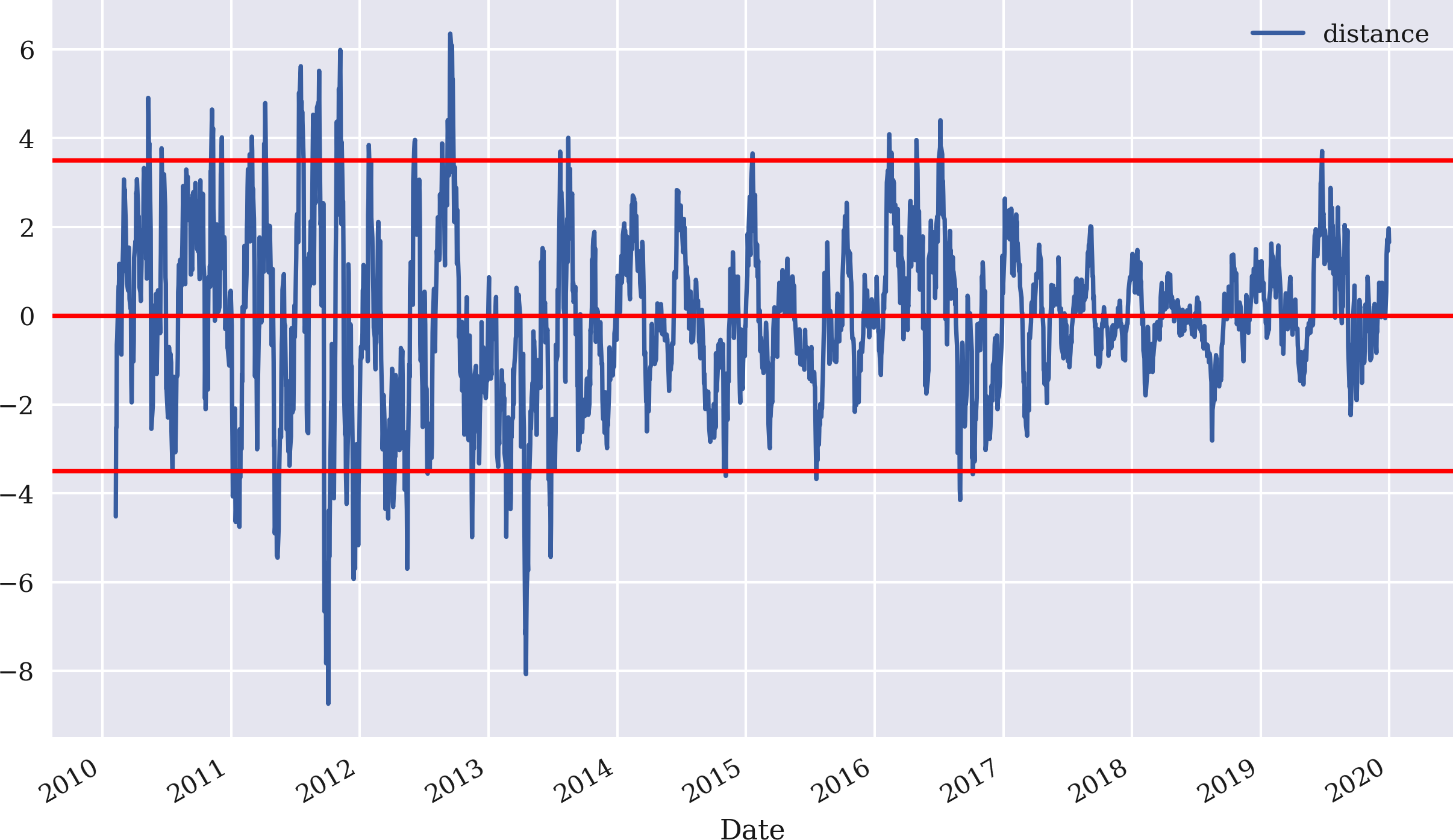
Abbildung 4-14. Differenz zwischen dem aktuellen Kurs von GDX und dem SMA sowie Schwellenwerte für die Erzeugung von Mean-Reversion-Signalen

Aus den Differenzen und den festgelegten Schwellenwerten lassen sich wiederum vektorisierte Positionierungen ableiten. Abbildung 4-15 zeigt die resultierenden Positionierungen:

In [105]: data['position'] = np.where(data['distance'] > threshold,
                                      -1, np.nan)  

In [106]: data['position'] = np.where(data['distance'] < -threshold,
                                      1, data['position'])  

In [107]: data['position'] = np.where(data['distance'] *
                      data['distance'].shift(1) < 0, 0, data['position'])  

In [108]: data['position'] = data['position'].ffill().fillna(0)  

In [109]: data['position'].iloc[SMA:].plot(ylim=[-1.1, 1.1],
                                         figsize=(10, 6));  

Wenn der Abstandswert größer als der Schwellenwert ist, gehst du short (setze -1 in der neuen Spalte position), ansonsten setze NaN.

Wenn der Abstandswert kleiner als der negative Schwellenwert ist, gehst du long (setze 1), ansonsten bleibt die Spalte position unverändert.

Wenn sich das Vorzeichen des Abstandswertes ändert, gehe marktneutral (setze 0), ansonsten lasse die Spalte position unverändert.

Fülle alle NaN Positionen mit den vorherigen Werten; ersetze alle verbleibenden NaN Werte durch 0.

Zeichne die resultierenden Positionierungen ab der Indexposition SMA auf.

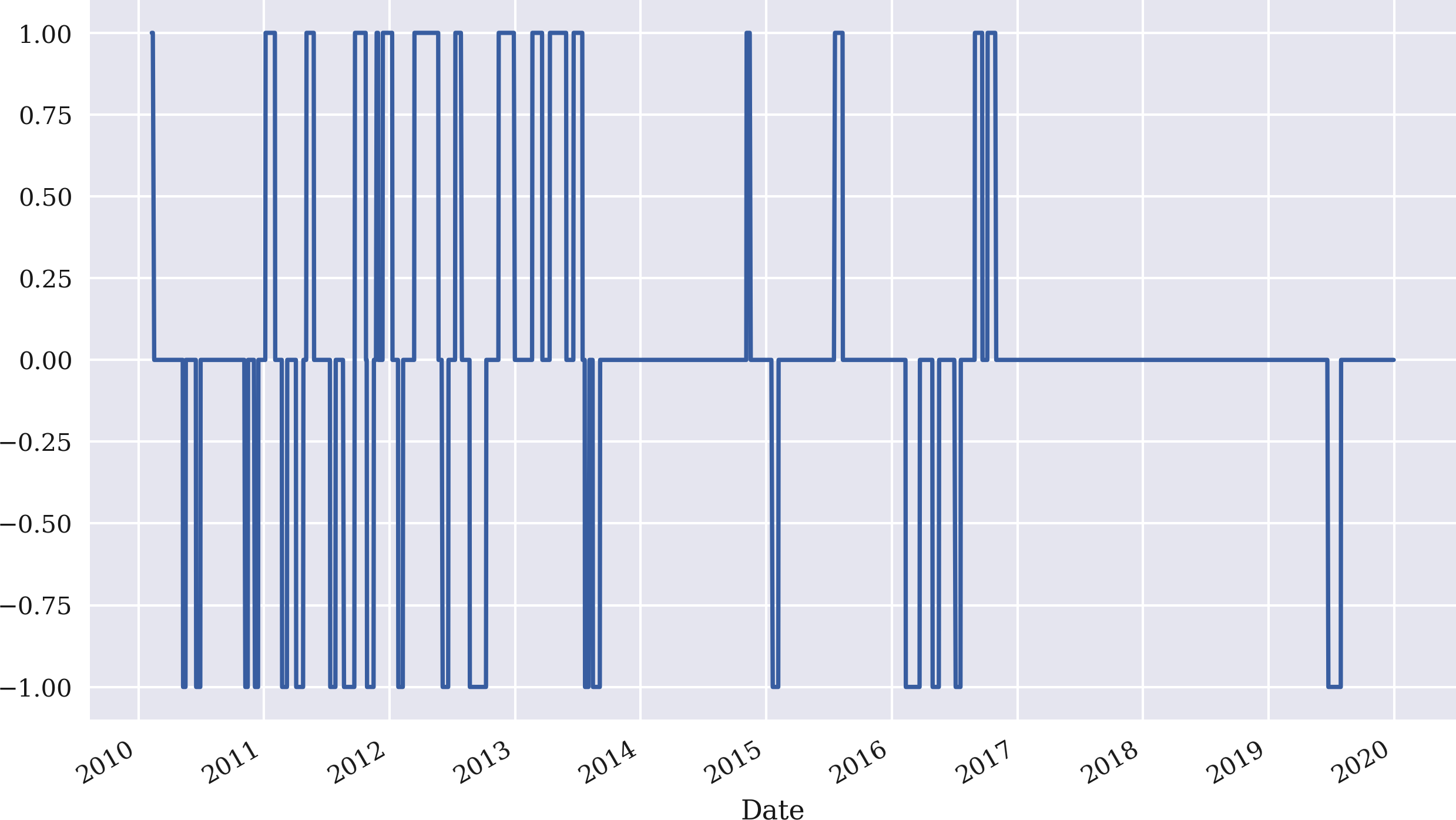
Abbildung 4-15. Positionierungen für GDX basierend auf der Strategie der Mittelwertumkehr

Der letzte Schritt besteht darin, die Renditen der Strategie abzuleiten, die in Abbildung 4-16 dargestellt sind. Die Strategie schneidet deutlich besser ab als der GDX ETF, obwohl die besondere Parametrisierung zu langen Perioden mit einer neutralen Position (weder long noch short) führt. Diese neutralen Positionen spiegeln sich in den flachen Teilen der Strategiekurve in Abbildung 4-16 wider:

In [110]: data['strategy'] = data['position'].shift(1) * data['returns']

In [111]: data[['returns', 'strategy']].dropna().cumsum(
                  ).apply(np.exp).plot(figsize=(10, 6));

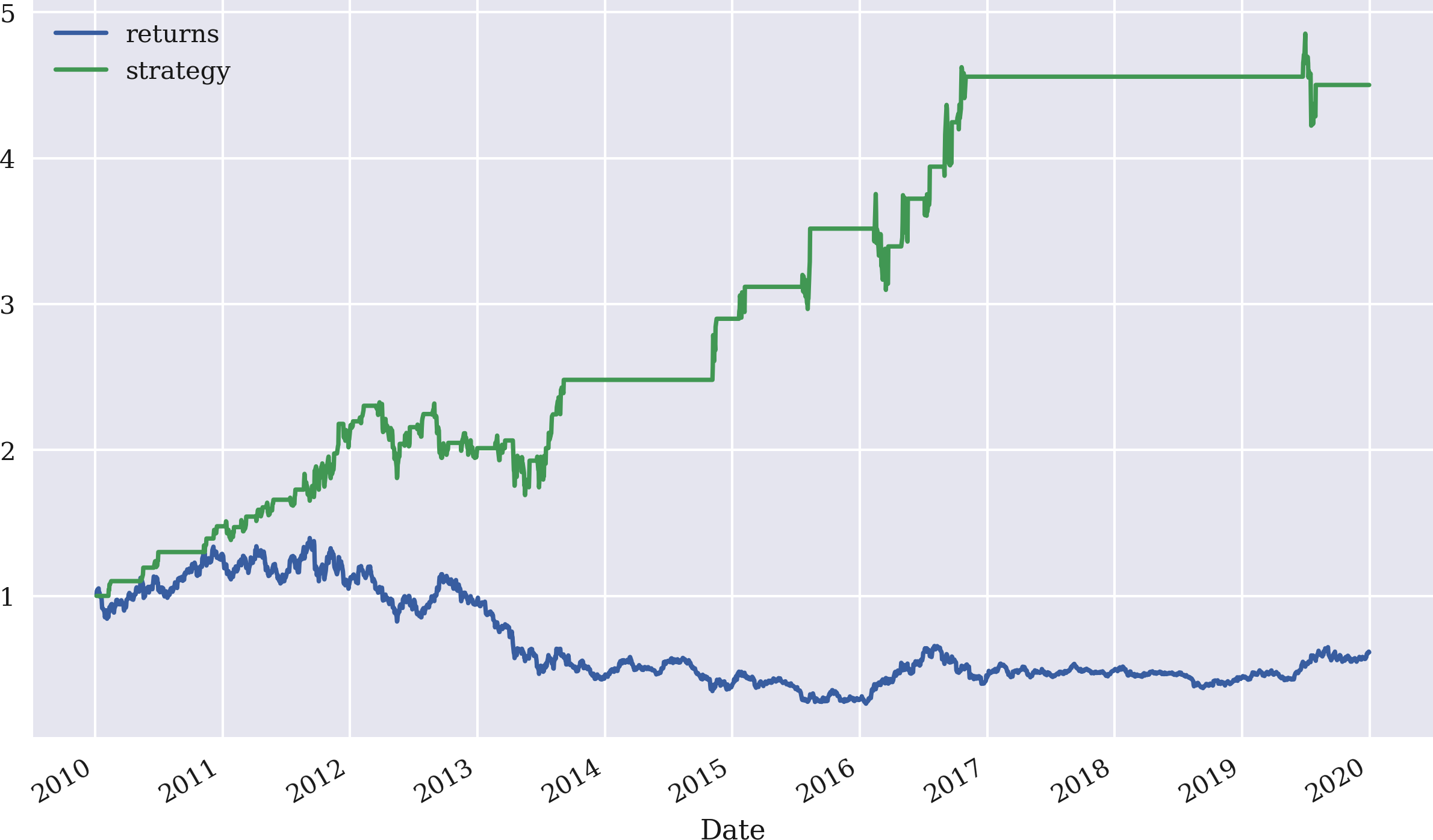
Abbildung 4-16. Bruttoperformance des GDX ETF und der Mean-Reversion-Strategie (SMA = 25, Schwellenwert = 3,5)

Verallgemeinerung des Ansatzes

Wie zuvor ist das vektorisierte Backtesting effizienter, wenn es mit einer entsprechenden Python-Klasse umgesetzt wird. Die Klasse MRVectorBacktester, die in "Mean Reversion Backtesting Class" vorgestellt wird, erbt von der Klasse MomVectorBacktester und ersetzt lediglich die Methode run_strategy(), um den Besonderheiten der Mean-Reversion-Strategie Rechnung zu tragen.

Das Beispiel verwendet nun GLD und setzt die anteiligen Transaktionskosten auf 0,1%. Der anfängliche Investitionsbetrag wird wieder auf 10.000 USD festgelegt. Der SMA beträgt dieses Mal 43 und der Schwellenwert wird auf 7,5 gesetzt. Abbildung 4-17 zeigt die Leistung der Mean-Reversion-Strategie im Vergleich zum GLD ETF:

In [112]: import MRVectorBacktester as MR  

In [113]: mrbt = MR.MRVectorBacktester('GLD', '2010-1-1', '2019-12-31',
                                       10000, 0.001)  

In [114]: mrbt.run_strategy(SMA=43, threshold=7.5)  
Out[114]: (13542.15, 646.21)

In [115]: mrbt.plot_results()  

Importiert das Modul als MR.

Instanziiert ein Objekt der Klasse MRVectorBacktester mit 10.000 USD Anfangskapital und 0,1 % anteiligen Transaktionskosten pro Handel; die Strategie schneidet in diesem Fall deutlich besser ab als das Referenzinstrument.

Backtests der Mean-Reversion-Strategie mit einem SMA Wert von 43 und einem threshold Wert von 7,5.

Stellt die kumulative Performance der Strategie gegenüber dem Basisinstrument dar.

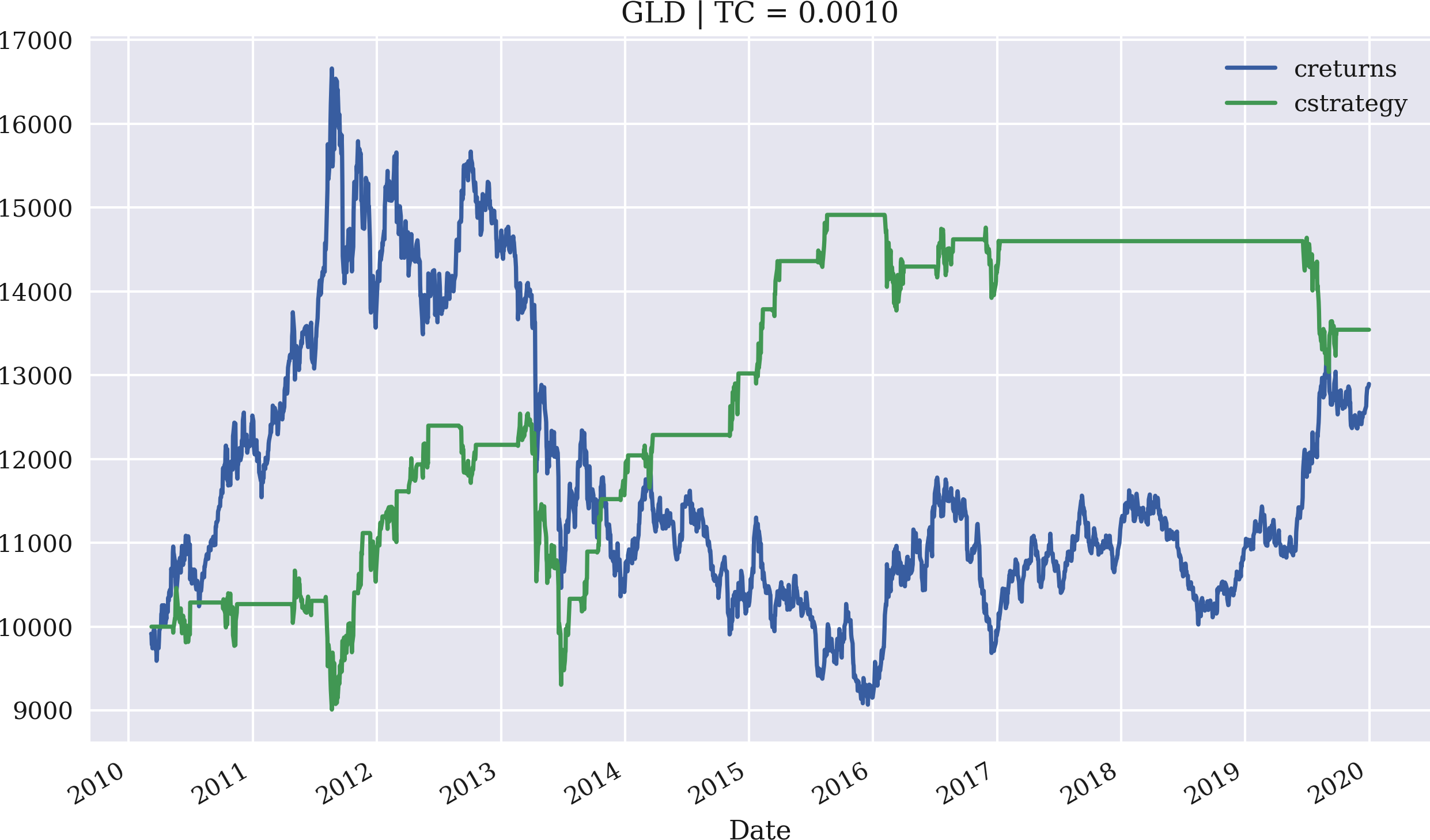
Abbildung 4-17. Bruttoperformance des GLD ETF und der Mean-Reversion-Strategie (SMA = 43, Schwellenwert = 7,5, Transaktionskosten von 0,1%)

Datenschnüffeln und Overfitting

Der Schwerpunkt in diesem Kapitel, wie auch im Rest des Buches, liegt auf der technischen Umsetzung wichtiger Konzepte im algorithmischen Handel mit Hilfe von Python. Die verwendeten Strategien, Parameter, Datensätze und Algorithmen sind manchmal willkürlich und manchmal absichtlich gewählt, um eine bestimmte Aussage zu treffen. Zweifelsohne ist es bei der Erörterung von technischen Methoden, die im Finanzbereich angewandt werden, spannender undmotivierender, Beispiele zu sehen, die "gute Ergebnisse" zeigen, auch wenn sie sich vielleicht nicht auf andere Finanzinstrumente oder Zeiträume verallgemeinern lassen, zum Beispiel.

Die Fähigkeit, Beispiele mit guten Ergebnissen zu zeigen, geht oft auf Kosten des Datenschnüffelns. Nach White (2000) kann Datenschnüffeln wie folgt definiert werden:

Daten-Snooping liegt vor, wenn ein bestimmter Datensatz mehr als einmal für Schlussfolgerungen oder die Modellauswahl verwendet wird.

Mit anderen Worten: Ein bestimmter Ansatz kann mehrfach oder sogar mehrmals auf denselben Datensatz angewendet werden, um zu zufriedenstellenden Zahlen und Diagrammen zu gelangen. Das ist in der Handelsstrategieforschung natürlich intellektuell unredlich, denn es wird so getan, als hätte eine Handelsstrategie ein wirtschaftliches Potenzial, das in der realen Welt möglicherweise nicht realistisch ist. Da der Schwerpunkt dieses Buches auf der Verwendung von Python als Programmiersprache für den algorithmischen Handel liegt, ist der Ansatz des Datenschnüffelns vielleicht vertretbar. Dies ist vergleichbar mit einem Mathematikbuch, in dem als Beispiel eine Gleichung gelöst wird, die eine eindeutige Lösung hat, die leicht zu identifizieren ist. In der Mathematik sind solche einfachen Beispiele eher die Ausnahme als die Regel, aber sie werden trotzdem häufig für didaktische Zwecke verwendet.

Ein weiteres Problem, das in diesem Zusammenhang auftritt, ist das Overfitting. Overfitting imHandelskontext kann wie folgt beschrieben werden (siehe Man Institute on Overfitting):

Überanpassung liegt vor, wenn ein Modell eher das Rauschen als das Signal beschreibt. Das Modell kann bei den Daten, mit denen es getestet wurde, eine gute Leistung erbringen, aber bei neuen Daten in der Zukunft wenig oder gar keine Vorhersagekraft haben. Überanpassung bedeutet, dass Muster gefunden werden, die es eigentlich gar nicht gibt. Die Überanpassung ist mit Kosten verbunden - eine überangepasste Strategie wird in der Zukunft schlechter abschneiden.

Selbst eine einfache Strategie, wie die, die auf zwei SMA-Werten basiert, ermöglicht das Backtesting tausender verschiedener Parameterkombinationen. Bei einigen dieser Kombinationen ist es fast sicher, dass sie gute Ergebnisse liefern. Wie Bailey et al. (2015) ausführlich darlegen, führt dies leicht zu einer Überanpassung der Backtests, ohne dass sich die für das Backtesting verantwortlichen Personen dieses Problems bewusst sind. Sie weisen darauf hin:

Die jüngsten Fortschritte in der Algorithmenforschung und im Hochleistungsrechnen haben es fast trivial gemacht, Millionen und Milliarden von alternativen Anlagestrategien auf einem endlichen Datensatz von Finanzzeitreihen zu testen....[I]n der Regel wird diese Rechenleistung genutzt, um die Parameter einer Anlagestrategie zu kalibrieren, um ihre Leistung zu maximieren. Aber weil das Signal-Rausch-Verhältnis so schwach ist, führt eine solche Kalibrierung oft dazu, dass die Parameter so gewählt werden, dass sie vom vergangenen Rauschen und nicht vom zukünftigen Signal profitieren. Das Ergebnis ist ein Overfit-Backtest.

Das Problem der Gültigkeit empirischer Ergebnisse im statistischen Sinne ist natürlich nicht auf das Strategie-Backtesting im Finanzkontext beschränkt.

Ioannidis (2005) betont in Bezug auf medizinische Veröffentlichungen probabilistische und statistische Überlegungen bei der Beurteilung der Reproduzierbarkeit und Validität von Forschungsergebnissen:

Es gibt zunehmend Bedenken, dass in der modernen Forschung falsche Ergebnisse die Mehrheit oder sogar die überwiegende Mehrheit der veröffentlichten Forschungsbehauptungen ausmachen könnten. Das sollte jedoch nicht überraschen. Es kann bewiesen werden, dass die meisten behaupteten Forschungsergebnisse falsch sind....Wie bereits gezeigt wurde, hängt die Wahrscheinlichkeit, dass ein Forschungsergebnis tatsächlich wahr ist, von der vorherigen Wahrscheinlichkeit, dass es wahr ist (vor der Durchführung der Studie), der statistischen Aussagekraft der Studie und dem Niveau der statistischen Signifikanz ab.

Wenn in diesem Buch gezeigt wird, dass eine Handelsstrategie bei einem bestimmten Datensatz, einer bestimmten Kombination von Parametern und vielleicht einem bestimmten maschinellen Lernalgorithmus gut abschneidet, stellt dies vor diesem Hintergrund weder eine Empfehlung für die jeweilige Konfiguration dar, noch lassen sich daraus allgemeinere Rückschlüsse auf die Qualität und das Leistungspotenzial der jeweiligen Strategiekonfiguration ziehen.

Du bist natürlich aufgefordert, den Code und die Beispiele in diesem Buch zu verwenden, um deine eigenen Ideen für algorithmische Handelsstrategien zu erforschen und sie auf der Grundlage deiner eigenen Backtesting-Ergebnisse, Validierungen und Schlussfolgerungen in die Praxis umzusetzen. Schließlich werden die Finanzmärkte für eine ordentliche und sorgfältige Strategierecherche entschädigt und nicht für brachiales Datenschnüffeln und Overfitting.

Schlussfolgerungen

Die Vektorisierung ist ein leistungsfähiges Konzept im wissenschaftlichen Rechnen und in der Finanzanalyse im Zusammenhang mit dem Backtesting von algorithmischen Handelsstrategien. In diesem Kapitel wird die Vektorisierung sowohl mit NumPy als auch mit pandas vorgestellt und zum Backtesting von drei Arten von Handelsstrategien angewendet: Strategien, die auf einfachen gleitenden Durchschnitten, Momentum und Mean Reversion basieren. Das Kapitel geht zugegebenermaßen von einigen vereinfachenden Annahmen aus, und ein rigoroses Backtesting von Handelsstrategien muss mehr Faktoren berücksichtigen, die in der Praxis über den Erfolg des Handels entscheiden, z. B. Datenprobleme, Auswahlprobleme, Vermeidung von Overfitting oder Elemente der Marktmikrostruktur. Das Hauptziel dieses Kapitels ist es jedoch, sich auf das Konzept der Vektorisierung zu konzentrieren und zu zeigen, was es im algorithmischen Handel aus technologischer Sicht und im Hinblick auf die Umsetzung leisten kann. Bei allen konkreten Beispielen und Ergebnissen, die vorgestellt werden, müssen die Probleme des Datenschnüffelns, des Overfittings und der statistischen Signifikanz berücksichtigt werden.

Referenzen und weitere Ressourcen

Die Grundlagen der Vektorisierung mit NumPy und pandas findest du in diesen Büchern:

• McKinney, Wes. 2017. Python for Data Analysis. 2nd ed. Sebastopol: O'Reilly.

• VanderPlas, Jake. 2016. Python Data Science Handbook. Sebastopol: O'Reilly.

Für die Verwendung von NumPy und pandas in einem finanziellen Kontext, siehe diese Bücher:

• Hilpisch, Yves. 2015. Derivative Analytics mit Python: Data Analysis, Models, Simulation, Calibration, and Hedging. Wiley Finance.

• ⸻. 2017. Listed Volatility and Variance Derivatives: A Python-Based Guide. Wiley Finance.

• ⸻. 2018. Python for Finance: Mastering Data-Driven Finance. 2nd ed. Sebastopol: O'Reilly.

Zu den Themen Datenschnüffelei und Overfitting siehe diese Artikel:

• Bailey, David, Jonathan Borwein, Marcos López de Prado, und Qiji Jim Zhu. 2015. "The Probability of Backtest Overfitting. Journal of Computational Finance 20, (4): 39-69. https://oreil.ly/sOHlf.

• Ioannidis, John. 2005. "Warum die meisten veröffentlichten Forschungsergebnisse falsch sind". PLoS Medicine 2, (8): 696-701.

• White, Halbert. 2000. "A Reality Check for Data Snooping". Econometrica 68, (5): 1097-1126.

Weitere Hintergrundinformationen und empirische Ergebnisse zu Handelsstrategien, die auf einfachen gleitenden Durchschnitten basieren, findest du in diesen Quellen:

• Brock, William, Josef Lakonishok, und Blake LeBaron. 1992. "Einfache technische Handelsregeln und die stochastischen Eigenschaften von Aktienrenditen". Journal of Finance 47, (5): 1731-1764.

• Droke, Clif. 2001. Gleitende Durchschnitte - vereinfacht. Columbia: Marketplace Books.

Das Buch von Ernest Chan behandelt im Detail Handelsstrategien, die auf Momentum und Mean Reversion basieren. Das Buch ist auch eine gute Quelle für die Fallstricke beim Backtesting von Handelsstrategien:

• Chan, Ernest. 2013. Algorithmischer Handel: Winning Strategies and Their Rationale. Hoboken et al: John Wiley & Sons.

Diese Forschungsarbeiten analysieren die Merkmale und Gewinnquellen von Cross-Sectional-Momentum-Strategien, dem traditionellen Ansatz des momentumbasierten Handels:

• Chan, Louis, Narasimhan Jegadeesh, und Josef Lakonishok. 1996. "Momentum-Strategien". Journal of Finance 51, (5): 1681-1713.

• Jegadeesh, Narasimhan, und Sheridan Titman. 1993. "Renditen beim Kauf von Gewinnern und Verkauf von Verlierern: Implications for Stock Market Efficiency". Journal of Finance 48, (1): 65-91.

• Jegadeesh, Narasimhan, und Sheridan Titman. 2001. "Rentabilität von Momentum-Strategien: An Evaluation of Alternative Explanations". Journal of Finance 56, (2): 599-720.

Die Arbeit von Moskowitz et al. bietet eine Analyse der sogenannten Zeitreihen-Momentumstrategien:

• Moskowitz, Tobias, Yao Hua Ooi, und Lasse Heje Pedersen. 2012. "Time Series Momentum". Journal of Financial Economics 104: 228-250.

Diese Arbeiten analysieren empirisch die Umkehrung des Mittelwerts bei Vermögenspreisen:

• Balvers, Ronald, Yangru Wu, und Erik Gilliland. 2000. "Mean Reversion across National Stock Markets and Parametric Contrarian Investment Strategies". Journal of Finance 55, (2): 745-772.

• Kim, Myung Jig, Charles Nelson, und Richard Startz. 1991. "Mean Reversion in Stock Prices? A Reappraisal of the Empirical Evidence". Review of Economic Studies 58: 515-528.

• Spierdijk, Laura, Jacob Bikker, und Peter van den Hoek. 2012. "Mean Reversion in internationalen Aktienmärkten: An Empirical Analysis of the 20th Century". Journal of International Money and Finance 31: 228-249.

Python-Skripte

In diesem Abschnitt werden die Python-Skripte vorgestellt, auf die in diesem Kapitel verwiesen wird.

SMA Backtesting Klasse

Im Folgenden wird Python-Code mit einer Klasse für das vektorisierte Backtesting von Strategien vorgestellt, die auf einfachen gleitenden Durchschnitten basieren:

#
# Python Module with Class
# for Vectorized Backtesting
# of SMA-based Strategies
#
# Python for Algorithmic Trading
# (c) Dr. Yves J. Hilpisch
# The Python Quants GmbH
#
import numpy as np
import pandas as pd
from scipy.optimize import brute


class SMAVectorBacktester(object):
    ''' Class for the vectorized backtesting of SMA-based trading strategies.

    Attributes
    ==========
    symbol: str
        RIC symbol with which to work
    SMA1: int
        time window in days for shorter SMA
    SMA2: int
        time window in days for longer SMA
    start: str
        start date for data retrieval
    end: str
        end date for data retrieval

    Methods
    =======
    get_data:
        retrieves and prepares the base data set
    set_parameters:
        sets one or two new SMA parameters
    run_strategy:
        runs the backtest for the SMA-based strategy
    plot_results:
        plots the performance of the strategy compared to the symbol
    update_and_run:
        updates SMA parameters and returns the (negative) absolute performance
    optimize_parameters:
        implements a brute force optimization for the two SMA parameters
    '''

    def __init__(self, symbol, SMA1, SMA2, start, end):
        self.symbol = symbol
        self.SMA1 = SMA1
        self.SMA2 = SMA2
        self.start = start
        self.end = end
        self.results = None
        self.get_data()

    def get_data(self):
        ''' Retrieves and prepares the data.
        '''
        raw = pd.read_csv('http://hilpisch.com/pyalgo_eikon_eod_data.csv',
                          index_col=0, parse_dates=True).dropna()
        raw = pd.DataFrame(raw[self.symbol])
        raw = raw.loc[self.start:self.end]
        raw.rename(columns={self.symbol: 'price'}, inplace=True)
        raw['return'] = np.log(raw / raw.shift(1))
        raw['SMA1'] = raw['price'].rolling(self.SMA1).mean()
        raw['SMA2'] = raw['price'].rolling(self.SMA2).mean()
        self.data = raw

    def set_parameters(self, SMA1=None, SMA2=None):
        ''' Updates SMA parameters and resp. time series.
        '''
        if SMA1 is not None:
            self.SMA1 = SMA1
            self.data['SMA1'] = self.data['price'].rolling(
                self.SMA1).mean()
        if SMA2 is not None:
            self.SMA2 = SMA2
            self.data['SMA2'] = self.data['price'].rolling(self.SMA2).mean()

    def run_strategy(self):
        ''' Backtests the trading strategy.
        '''
        data = self.data.copy().dropna()
        data['position'] = np.where(data['SMA1'] > data['SMA2'], 1, -1)
        data['strategy'] = data['position'].shift(1) * data['return']
        data.dropna(inplace=True)
        data['creturns'] = data['return'].cumsum().apply(np.exp)
        data['cstrategy'] = data['strategy'].cumsum().apply(np.exp)
        self.results = data
        # gross performance of the strategy
        aperf = data['cstrategy'].iloc[-1]
        # out-/underperformance of strategy
        operf = aperf - data['creturns'].iloc[-1]
        return round(aperf, 2), round(operf, 2)

    def plot_results(self):
        ''' Plots the cumulative performance of the trading strategy
        compared to the symbol.
        '''
        if self.results is None:
            print('No results to plot yet. Run a strategy.')
        title = '%s | SMA1=%d, SMA2=%d' % (self.symbol,
                                               self.SMA1, self.SMA2)
        self.results[['creturns', 'cstrategy']].plot(title=title,
                                                     figsize=(10, 6))

    def update_and_run(self, SMA):
        ''' Updates SMA parameters and returns negative absolute performance
        (for minimazation algorithm).

        Parameters
        ==========
        SMA: tuple
            SMA parameter tuple
        '''
        self.set_parameters(int(SMA[0]), int(SMA[1]))
        return -self.run_strategy()[0]

    def optimize_parameters(self, SMA1_range, SMA2_range):
        ''' Finds global maximum given the SMA parameter ranges.

        Parameters
        ==========
        SMA1_range, SMA2_range: tuple
            tuples of the form (start, end, step size)
        '''
        opt = brute(self.update_and_run, (SMA1_range, SMA2_range), finish=None)
        return opt, -self.update_and_run(opt)


if __name__ == '__main__':
    smabt = SMAVectorBacktester('EUR=', 42, 252,
                                '2010-1-1', '2020-12-31')
    print(smabt.run_strategy())
    smabt.set_parameters(SMA1=20, SMA2=100)
    print(smabt.run_strategy())
    print(smabt.optimize_parameters((30, 56, 4), (200, 300, 4)))

Momentum Backtesting Klasse

Im Folgenden wird Python-Code mit einer Klasse für das vektorisierte Backtesting von Strategien vorgestellt, die auf Zeitreihenmomentum basieren:

#
# Python Module with Class
# for Vectorized Backtesting
# of Momentum-Based Strategies
#
# Python for Algorithmic Trading
# (c) Dr. Yves J. Hilpisch
# The Python Quants GmbH
#
import numpy as np
import pandas as pd


class MomVectorBacktester(object):
    ''' Class for the vectorized backtesting of
    momentum-based trading strategies.

    Attributes
    ==========
    symbol: str
       RIC (financial instrument) to work with
    start: str
        start date for data selection
    end: str
        end date for data selection
    amount: int, float
        amount to be invested at the beginning
    tc: float
        proportional transaction costs (e.g., 0.5% = 0.005) per trade

    Methods
    =======
    get_data:
        retrieves and prepares the base data set
    run_strategy:
        runs the backtest for the momentum-based strategy
    plot_results:
        plots the performance of the strategy compared to the symbol
    '''

    def __init__(self, symbol, start, end, amount, tc):
        self.symbol = symbol
        self.start = start
        self.end = end
        self.amount = amount
        self.tc = tc
        self.results = None
        self.get_data()

    def get_data(self):
        ''' Retrieves and prepares the data.
        '''
        raw = pd.read_csv('http://hilpisch.com/pyalgo_eikon_eod_data.csv',
                          index_col=0, parse_dates=True).dropna()
        raw = pd.DataFrame(raw[self.symbol])
        raw = raw.loc[self.start:self.end]
        raw.rename(columns={self.symbol: 'price'}, inplace=True)
        raw['return'] = np.log(raw / raw.shift(1))
        self.data = raw

    def run_strategy(self, momentum=1):
        ''' Backtests the trading strategy.
        '''
        self.momentum = momentum
        data = self.data.copy().dropna()
        data['position'] = np.sign(data['return'].rolling(momentum).mean())
        data['strategy'] = data['position'].shift(1) * data['return']
        # determine when a trade takes place
        data.dropna(inplace=True)
        trades = data['position'].diff().fillna(0) != 0
        # subtract transaction costs from return when trade takes place
        data['strategy'][trades] -= self.tc
        data['creturns'] = self.amount * data['return'].cumsum().apply(np.exp)
        data['cstrategy'] = self.amount * \
            data['strategy'].cumsum().apply(np.exp)
        self.results = data
        # absolute performance of the strategy
        aperf = self.results['cstrategy'].iloc[-1]
        # out-/underperformance of strategy
        operf = aperf - self.results['creturns'].iloc[-1]
        return round(aperf, 2), round(operf, 2)

    def plot_results(self):
        ''' Plots the cumulative performance of the trading strategy
        compared to the symbol.
        '''
        if self.results is None:
            print('No results to plot yet. Run a strategy.')
        title = '%s | TC = %.4f' % (self.symbol, self.tc)
        self.results[['creturns', 'cstrategy']].plot(title=title,
                                                     figsize=(10, 6))


if __name__ == '__main__':
    mombt = MomVectorBacktester('XAU=', '2010-1-1', '2020-12-31',
                                10000, 0.0)
    print(mombt.run_strategy())
    print(mombt.run_strategy(momentum=2))
    mombt = MomVectorBacktester('XAU=', '2010-1-1', '2020-12-31',
                                10000, 0.001)
    print(mombt.run_strategy(momentum=2))

Mean Reversion Backtesting Klasse

Im Folgenden wird Python-Code mit einer Klasse für das vektorisierte Backtesting von Strategien auf Basis der Mean Reversion vorgestellt:.

#
# Python Module with Class
# for Vectorized Backtesting
# of Mean-Reversion Strategies
#
# Python for Algorithmic Trading
# (c) Dr. Yves J. Hilpisch
# The Python Quants GmbH
#
from MomVectorBacktester import *


class MRVectorBacktester(MomVectorBacktester):
    ''' Class for the vectorized backtesting of
    mean reversion-based trading strategies.

    Attributes
    ==========
    symbol: str
        RIC symbol with which to work
    start: str
        start date for data retrieval
    end: str
        end date for data retrieval
    amount: int, float
        amount to be invested at the beginning
    tc: float
        proportional transaction costs (e.g., 0.5% = 0.005) per trade

    Methods
    =======
    get_data:
        retrieves and prepares the base data set
    run_strategy:
        runs the backtest for the mean reversion-based strategy
    plot_results:
        plots the performance of the strategy compared to the symbol
    '''

    def run_strategy(self, SMA, threshold):
        ''' Backtests the trading strategy.
        '''
        data = self.data.copy().dropna()
        data['sma'] = data['price'].rolling(SMA).mean()
        data['distance'] = data['price'] - data['sma']
        data.dropna(inplace=True)
        # sell signals
        data['position'] = np.where(data['distance'] > threshold,
                                    -1, np.nan)
        # buy signals
        data['position'] = np.where(data['distance'] < -threshold,
                                    1, data['position'])
        # crossing of current price and SMA (zero distance)
        data['position'] = np.where(data['distance'] *
                                    data['distance'].shift(1) < 0,
                                    0, data['position'])
        data['position'] = data['position'].ffill().fillna(0)
        data['strategy'] = data['position'].shift(1) * data['return']
        # determine when a trade takes place
        trades = data['position'].diff().fillna(0) != 0
        # subtract transaction costs from return when trade takes place
        data['strategy'][trades] -= self.tc
        data['creturns'] = self.amount * \
            data['return'].cumsum().apply(np.exp)
        data['cstrategy'] = self.amount * \
            data['strategy'].cumsum().apply(np.exp)
        self.results = data
        # absolute performance of the strategy
        aperf = self.results['cstrategy'].iloc[-1]
        # out-/underperformance of strategy
        operf = aperf - self.results['creturns'].iloc[-1]
        return round(aperf, 2), round(operf, 2)


if __name__ == '__main__':
    mrbt = MRVectorBacktester('GDX', '2010-1-1', '2020-12-31',
                              10000, 0.0)
    print(mrbt.run_strategy(SMA=25, threshold=5))
    mrbt = MRVectorBacktester('GDX', '2010-1-1', '2020-12-31',
                              10000, 0.001)
    print(mrbt.run_strategy(SMA=25, threshold=5))
    mrbt = MRVectorBacktester('GLD', '2010-1-1', '2020-12-31',
                              10000, 0.001)
    print(mrbt.run_strategy(SMA=42, threshold=7.5))

¹ Quelle: "Sagt die Vergangenheit die Zukunft voraus?" The Economist, 23. September 2009.

² Weitere Informationen zu den Objekten datetime und timedelta findest du in Anhang C von Hilpisch (2018).