B.21 ZETA FUNCTION
Definition: Riemann Zeta Function The Riemann zeta function is
(B.115) 
where 
is a complex variable.
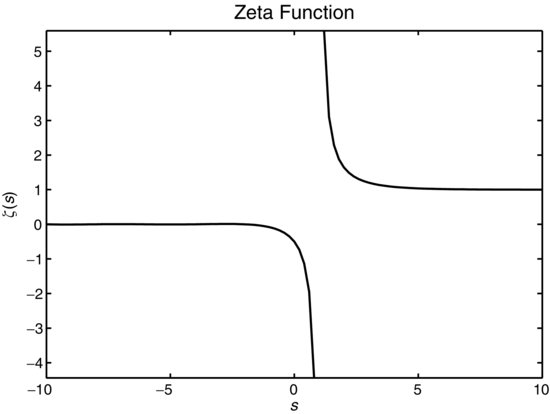
This series converges provided Re(s) = σ > 1. Figure B.18 shows a plot of 
for real values of s, which converges to zero for σ <0, converges to 1 for σ > 0, and has a pole at s = 1. The zeta function is used in the pmf of the zeta random variable with real-valued 
, which is a scale parameter of the distribution.
Figure B.18 Zeta function 
for real-valued s.
Get Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
