Probabilistisches maschinelles Lernen für Finanzen und Investieren

Kapitel 1. Der Bedarf an probabilistischem maschinellem Lernen

Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: [e-mail]

Im Grunde sind alle Modelle falsch, aber einige sind nützlich. Allerdings muss der ungefähre Charakter des Modells immer im Auge behalten werden.

-George Box, bedeutender Statistiker

Eine Karte ermöglicht es dir, von einem geografischen Ort zu einem anderen zu gelangen. Sie ist ein sehr nützliches mathematisches Modell, um sich in der physischen Welt zurechtzufinden. Noch nützlicher wird es, wenn du es mit Hilfe von Technologien der künstlichen Intelligenz (KI) zu einem GPS-System automatisierst. Doch weder das mathematische Modell noch das KI-System werden jemals in der Lage sein, die menschliche Erfahrung und den Reichtum des Geländes, das sie darstellen, zu erfassen. Das liegt daran, dass alle Modelle die Komplexität der realen Welt vereinfachen müssen, damit wir uns auf einige der Merkmale eines Phänomens konzentrieren können, die uns interessieren.

George Box, ein bedeutender Statistiker, hat einmal gesagt: "Alle Modelle sind falsch, aber einige sind nützlich." Dieser aufschlussreiche Spruch ist unser Mantra. Wir akzeptieren, dass alle Modelle falsch sind, weil sie die Realität nur unzureichend und unvollständig abbilden. Unser Ziel ist es, Finanzsysteme zu entwickeln, die auf Modellen und unterstützenden Technologien beruhen, die angesichts endemischer Ungewissheit, unvollständiger Informationen und ungenauer Messungen nützliche Schlüsse und Vorhersagen für die Entscheidungsfindung und das Risikomanagement ermöglichen.

Alle Finanzmodelle, ob theoretisch abgeleitet oder empirisch von Menschen und Maschinen entdeckt, sind nicht nur falsch, sondern auch drei Arten von Fehlern ausgeliefert. In diesem Kapitel erklären wir diese drei Arten von Fehlern anhand eines Beispiels aus dem Bereich der Verbraucherkredite und untersuchen sie mit Python-Code. Dies veranschaulicht unsere Behauptung, dass Ungenauigkeiten von Finanzmodellen Merkmale und keine Fehler sind. Schließlich haben wir es mit Menschen zu tun, nicht mit Teilchen oder Pendeln.

Finanzen sind keine genaue Wissenschaft wie die Physik, die sich mit präzisen Schätzungen und Vorhersagen befasst, wie uns die Wissenschaft glauben machen will. Es ist eine ungenaue Sozialstudie, die sich mit einer Reihe von Werten mit unterschiedlichen Plausibilitäten auseinandersetzt, die sich ständig und oft abrupt ändern.

Zum Abschluss des Kapitels erläutern wir, warum KI im Allgemeinen und probabilistisches maschinelles Lernen (ML) im Besonderen den nützlichsten und vielversprechendsten theoretischen Rahmen und Technologien für die Entwicklung der nächsten Generation von Systemen für Finanzen und Investitionen bietet.

Was ist ein Modell?

KI-Systeme basieren auf Modellen. Ein Modell bildet funktionale Beziehungen zwischen seinen Eingangs- und Ausgangsvariablen auf der Grundlage von Annahmen und Einschränkungen ab. Im Allgemeinen werden die Eingangsvariablen als unabhängige Variablen und die Ausgangsvariablen als abhängige Variablen bezeichnet.

In der Schule hast du gelernt, dass die Gleichung einer beliebigen Geraden in der XY-Ebene als y = mx + b ausgedrückt werden kann, wobei m die Steigung und b der y-Achsenabschnitt der Geraden ist. Wenn du zum Beispiel annimmst, dass die Konsumausgaben - die outputabhängige Variable y - in einem linearen Verhältnis zum persönlichen Einkommen - der inputunabhängigen Variable x - stehen, nennt man die Gleichung für die Linie ein Modell für die Konsumausgaben. Außerdem werden die Steigung m und der Achsenabschnitt b als Parameter des Modells bezeichnet. Sie werden als Konstanten behandelt, und ihre spezifischen Werte definieren eindeutige funktionale Beziehungen oder Modelle.

Abhängig von der Art der funktionalen Beziehungen, den Parametern und der Art der Input- und Outputvariablen, können Modelle als deterministisch oder probabilistisch klassifiziert werden. Bei einem deterministischen Modell gibt es keine Ungewissheiten über die Art der funktionalen Beziehungen, die Parameter oder die Ein- und Ausgänge des Modells. Für die in diesem Buch behandelten probabilistischen Modelle gilt genau das Gegenteil.

Finanzen sind keine Physik

Adam Smith, der allgemein als Begründer der modernen Ökonomie anerkannt wird , bewunderte Newtons Gesetze der Mechanik und der Gravitation.¹ Seitdem sind Wirtschaftswissenschaftler/innen bestrebt, ihre Disziplin zu einer mathematischen Wissenschaft wie die Physik zu machen. Sie streben danach, Theorien zu formulieren, die die wirtschaftlichen Aktivitäten der Menschen auf der Mikro- und Makroebene genau erklären und vorhersagen. Dieser Wunsch nahm Anfang des 20. Jahrhunderts mit Ökonomen wie Irving Fisher an Fahrt auf und gipfelte in der Ökonophysikbewegung des späten 20.

Trotz all der komplizierten Mathematik der modernen Finanzwelt sind ihre Theorien jämmerlich unzureichend, fast schon erbärmlich, vor allem im Vergleich zu denen der Physik. Die Physik kann zum Beispiel die Bewegung des Mondes und der Elektronen in deinem Computer mit atemberaubender Präzision vorhersagen. Diese Vorhersagen können von jedem Physiker zu jeder Zeit und überall auf der Welt berechnet werden. Im Gegensatz dazu haben Marktteilnehmer - Händler, Investoren, Analysten, Finanzmanager - Schwierigkeiten, die Ursachen der täglichen Marktbewegungen zu erklären oder den Preis eines Vermögenswerts jederzeit und überall auf der Welt vorherzusagen.

Die politische Ökonomie der falschen Darstellung eines Nobelpreises

In seinem Testament hat Alfred Nobel nicht einen Preis für Wirtschaftswissenschaften oder Mathematik oder eine andere Disziplin neben Physik, Chemie, Medizin, Literatur und Frieden gestiftet. Der Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel, der heute fälschlicherweise als Nobelpreis für Wirtschaftswissenschaften bezeichnet wird, wurde 1968 von der schwedischen Zentralbank ins Leben gerufen. Die Zentralbank finanziert den Preis auf Dauer und bezahlt die Nobel-Stiftung für die Verwaltung des Preises, genau wie bei den Nobelpreisen, die von ihrem Stifter gestiftet wurden.

Indem sie die Wirtschaftswissenschaften in den Rang der Naturwissenschaften erhob und sich die anhaltende Unterstützung der angesehenen Nobel-Stiftung erkaufte, konnte die schwedische Zentralbank in ihrer Entscheidungsfindung von den Politikern des Landes unabhängig werden und ihre marktfreundliche Politik verfolgen. Wirtschaftspolitische Entscheidungen sollten den Wirtschafts "wissenschaftlern" überlassen werden, so wie gesundheitspolitische Entscheidungen den Medizinern überlassen wurden.² Damit missachtet die Stiftung jedoch den Willen Alfred Nobels und stellt das grundlegende Wesen der Wirtschaftswissenschaft als Sozialwissenschaft falsch dar.

In seiner Dankesrede 1974 erkannte Friedrich Hayek ( ), ein Pionier der libertären Ökonomie und Verfechter der freien Marktwirtschaft, deutlich, wie der neu geschaffene Wirtschaftspreis missbraucht werden könnte, als er sagte: "Der Nobelpreis verleiht einem Einzelnen eine Autorität, die in der Ökonomie kein Mensch besitzen sollte... In den Naturwissenschaften spielt das keine Rolle. Hier ist der Einfluss, den ein Einzelner ausübt, vor allem ein Einfluss auf seine Fachkollegen; und die werden ihn schnell zurechtstutzen, wenn er seine Kompetenzen überschreitet. Aber der Einfluss eines Ökonomen, auf den es hauptsächlich ankommt, ist der Einfluss auf Laien: Politiker, Journalisten, Beamte und die Öffentlichkeit im Allgemeinen."³

Vielleicht ist das Finanzwesen schwieriger als die Physik. Anders als Teilchen und Pendel sind Menschen komplexe, emotionale, kreative Wesen mit freiem Willen und latenten kognitiven Verzerrungen. Sie neigen dazu, sich widersprüchlich zu verhalten und auf die Handlungen anderer auf unvorhersehbare Weise zu reagieren. Außerdem profitieren die Marktteilnehmer, indem sie die Systeme, in denen sie agieren, überlisten oder austricksen.

Nachdem er mit seiner Investition in die South Sea Company ein Vermögen verloren hatte, bemerkte Newton: "Ich kann die Bewegung der Sterne berechnen, aber nicht den Wahnsinn der Menschen."⁴ Newton war übrigens kein unerfahrener Investor. Er war fast 31 Jahre lang Münzmeister in England und half dabei, das britische Pfund auf den Goldstandard zu bringen, wo es über zwei Jahrhunderte lang bleiben sollte.

Alle Finanzmodelle sind falsch, die meisten sind nutzlos

Einige Wissenschaftler/innen haben sogar behauptet , dass theoretische Finanzmodelle nicht nur falsch, sondern auch gefährlich sind. Unter dem Deckmantel der Wissenschaftlichkeit wird den Anhängern von Wirtschaftsmodellen eine falsche Gewissheit über die Genauigkeit ihrer Vorhersagekraft vorgegaukelt.⁵ Dieser blinde Glaube hat zu vielen katastrophalen Folgen für ihre Anhänger und für die Gesellschaft insgesamt geführt.⁶ Nichts veranschaulicht die gefährlichen Folgen der akademischen Arroganz und des blinden Glaubens an analytische Finanzmodelle besser als das spektakuläre Desaster von LTCM, das in der Seitenleiste beschrieben wird.

Das Desaster von Long-Term Capital Management (LTCM)

LTCM war ein Hedgefonds, der 1994 von den Wall Street-Veteranen und Akademikern Myron Scholes und Robert Merton, den Erfindern der berühmten Black-Scholes-Merton-Optionspreisformel, gegründet wurde. Das LTCM-Team war so überzeugt von seinen Anlagemodellen, die von zwei zukünftigen "Nobelpreisträgern" überwacht wurden, dass es seine Portfolios auf ein gefährlich hohes Niveau hebelte. Das Team beabsichtigte, die winzigen Gewinne, die LTCM mit seinen verschiedenen Anlagen erzielte, zu vergrößern. In den ersten vier Jahren erzielte LTCM sehr beeindruckende jährliche Renditen und musste Anlegergelder abweisen.

Die unvorhersehbare Komplexität sozialer Systeme zeigte jedoch 1998 ihr hässliches Gesicht, als die russische Regierung ihre inländischen Lokalwährungsanleihen nicht mehr bedienen konnte. Ein solches Ereignis wurde von den Modellen von LTCM nicht vorhergesehen, da eine Regierung immer mehr Geld drucken kann, anstatt ihre Schulden zu begleichen. Dies schockierte die Weltmärkte und führte zum raschen Zusammenbruch von LTCM - und zeigte, dass die Hebelwirkung die Verluste ebenso vergrößert wie die Gewinne. Um zu verhindern, dass sich die Krise von LTCM ausbreitet und die globalen Finanzmärkte zusammenbrechen, retteten die Federal Reserve und ein Konsortium großer Banken LTCM. In Abbildung 1-1 wird der Wert von 1.000 US-Dollar verglichen, die separat in LTCM, den Dow Jones (DJIA) und US-Staatsanleihen investiert wurden.

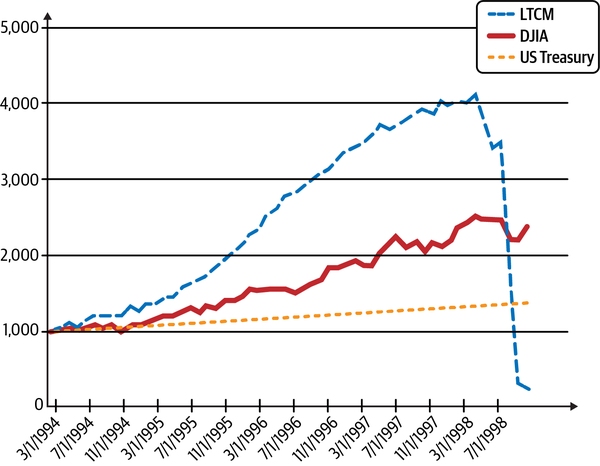
Abbildung 1-1. Das epische Desaster von Long Term Capital Management (LTCM)⁷

Mit einem diametral anderen Ansatz als Hedgefonds wie LTCM hat Renaissance Technologies, der erfolgreichste Hedgefonds der Geschichte, seine kritischen Ansichten zu Finanztheorien in die Praxis umgesetzt. Anstatt Mitarbeiter mit Finanz- oder Wall Street-Hintergrund einzustellen, zieht es das Unternehmen vor, Physiker, Mathematiker, Statistiker und Informatiker zu engagieren. Es handelt an den Märkten mit quantitativen Modellen, die auf nicht-finanziellen Theorien wie der Informationstheorie, der Datenwissenschaft und dem maschinellen Lernen basieren.

Die Trifecta der Modellierungsfehler

Unabhängig davon, ob Finanzmodelle auf akademischen Theorien oder empirischen Data-Mining-Strategien beruhen, unterliegen sie alle der Dreifaltigkeit von Modellierungsfehlern. Fehler bei der Analyse und Prognose können aus einem der folgenden Modellierungsprobleme resultieren: Verwendung einer ungeeigneten Funktionsform, Eingabe ungenauer Parameter oder fehlgeschlagene Anpassung an strukturelle Veränderungen auf dem Markt.⁸

Fehler in der Modellspezifikation

Fast alle Finanztheorien verwenden die Gaußsche oder normale Verteilung in ihren Modellen. Die Normalverteilung ist zum Beispiel die Grundlage für die moderne Portfoliotheorie von Markowitz und die Optionspreistheorie von Black-Scholes-Merton.⁹ In der akademischen Forschung ist es jedoch eine gut dokumentierte Tatsache, dass Aktien, Anleihen, Währungen und Rohstoffe eine Fat-Tailed-Verteilung aufweisen, die eindeutig nicht gaußförmig ist.¹⁰ Mit anderen Worten: Extremereignisse treten viel häufiger auf, als die Normalverteilung vorhersagt. In den Kapiteln 3 und 4 werden wir eine Finanzdatenanalyse in Python durchführen, um die nicht-gaußsche Struktur der Aktienrenditeverteilungen zu demonstrieren.

Wenn die Renditen von Vermögenswerten normalverteilt wären, würde keine der folgenden Finanzkatastrophen innerhalb des Zeitalters des Universums auftreten: Schwarzer Montag, die mexikanische Peso-Krise, die asiatische Währungskrise, der Konkurs von LTCM oder der Flash Crash. "Mini-Flash-Crashs" einzelner Aktien treten mit noch größerer Häufigkeit auf als diese Makroereignisse.

Dennoch verwenden Lehrbücher, Programme und Fachleute im Finanzwesen weiterhin die Normalverteilung in ihren Modellen zur Bewertung von Vermögenswerten und Risiken, weil sie so einfach und analytisch nachvollziehbar ist. Angesichts der fortschrittlichen Algorithmen und Rechenressourcen von heute sind diese Gründe nicht mehr zu rechtfertigen. Dieses Zögern, die Normalverteilung aufzugeben, ist ein klares Beispiel für die "Suche des Betrunkenen": ein Prinzip, das von einem Witz über einen Betrunkenen abgeleitet ist, der seinen Schlüssel in der Dunkelheit eines Parks verliert und ihn verzweifelt unter einem Laternenpfahl sucht, weil dort das Licht ist.

Fehler bei der Schätzung der Modellparameter

Fehler dieser Art können entstehen weil die Marktteilnehmer/innen Zugang zu unterschiedlichen Informationen haben, die unterschiedlich schnell zur Verfügung stehen. Außerdem haben sie unterschiedlich ausgeprägte Verarbeitungsfähigkeiten und unterschiedliche kognitive Verzerrungen. Außerdem werden diese Parameter in der Regel anhand von Daten aus der Vergangenheit geschätzt, die die aktuellen Marktbedingungen möglicherweise nicht genau wiedergeben. Diese Faktoren führen zu einer tiefgreifenden epistemischen Unsicherheit über die Modellparameter.

Betrachten wir ein konkretes Beispiel: die Zinssätze. Bei der Bewertung eines finanziellen Vermögenswerts werden die Zinssätze verwendet, um die ungewissen zukünftigen Cashflows des Vermögenswerts abzuzinsen und seinen Wert in der Gegenwart zu schätzen. Auf der Verbraucherebene haben Kreditkarten zum Beispiel variable Zinssätze, die an eine Benchmark, den Leitzins, gekoppelt sind. Dieser Zinssatz ändert sich in der Regel im Gleichschritt mit der Federal Funds Rate, einem Zinssatz, der für die US- und die Weltwirtschaft von großer Bedeutung ist.

Stellen wir uns vor, du möchtest den Zinssatz für deine Kreditkarte in einem Jahr schätzen. Nehmen wir an, der aktuelle Leitzins beträgt 2% und dein Kreditkartenunternehmen berechnet dir 10% plus Leitzins. In Anbetracht der derzeitigen Wirtschaftslage glaubst du, dass die Federal Reserve die Zinsen eher anheben wird als nicht. Nach unseren derzeitigen Informationen wissen wir, dass die Fed in den nächsten 12 Monaten acht Mal tagen und den Leitzins entweder um 0,25 % anheben oder auf dem bisherigen Niveau belassen wird.

Im folgenden Python-Codebeispiel verwenden wir die Binomialverteilung, um den Zinssatz deiner Kreditkarte am Ende des 12-Monats-Zeitraums zu modellieren. Konkret verwenden wir die folgenden Parameter für unseren Schätzbereich für die Wahrscheinlichkeit, dass die Fed den Leitzins bei jeder Sitzung um 0,25 % anhebt: fed_meetings = 8 (Anzahl der Versuche oder Sitzungen); probability_raises = [0,6, 0,7,0,8, 0,9]:

# Import binomial distribution from sciPy library
from scipy.stats import binom
# Import matplotlib library for drawing graphs
import matplotlib.pyplot as plt

# Total number of meetings of the Federal Open Market Committee (FOMC) in any 
# year
fed_meetings = 8
# Range of total interest rate increases at the end of the year
total_increases = list(range(0, fed_meetings + 1))
# Probability that the FOMC will raise rates at any given meeting
probability_raises = [0.6, 0.7, 0.8, 0.9]

fig, axs = plt.subplots(2, 2, figsize=(10, 8))

for i, ax in enumerate(axs.flatten()):
    # Use the probability mass function to calculate probabilities of total 
    # raises in eight meetings
    # Based on FOMC bias for raising rates at each meeting
    prob_dist = binom.pmf(k=total_increases, n=fed_meetings, 
    p=probability_raises[i])
    # How each 25 basis point increase in the federal funds rate affects your 
    # credit card interest rate
    cc_rate = [j * 0.25 + 12 for j in total_increases]

    # Plot the results for different FOMC probability
    ax.hist(cc_rate, weights=prob_dist, bins=fed_meetings, alpha=0.5, 
    label=probability_raises[i])
    ax.legend()
    ax.set_ylabel('Probability of credit card rate')
    ax.set_xlabel('Predicted range of credit card rates after 12 months')
    ax.set_title(f'Probability of raising rates at each meeting: 
    {probability_raises[i]}')

# Adjust spacing between subplots
plt.tight_layout()

# Show the plot
plt.show()

In Abbildung 1-2 siehst du, wie die Wahrscheinlichkeitsverteilung für deinen Kreditkartenzins in 12 Monaten entscheidend von deiner Einschätzung der Wahrscheinlichkeit abhängt, dass die Fed die Zinsen bei jeder der acht Sitzungen anhebt. Du siehst, dass sich der erwartete Zinssatz für deine Kreditkarte in 12 Monaten um etwa 0,2 % erhöht, wenn deine Schätzung für eine Zinserhöhung der Fed bei jeder Sitzung um 0,1 steigt.

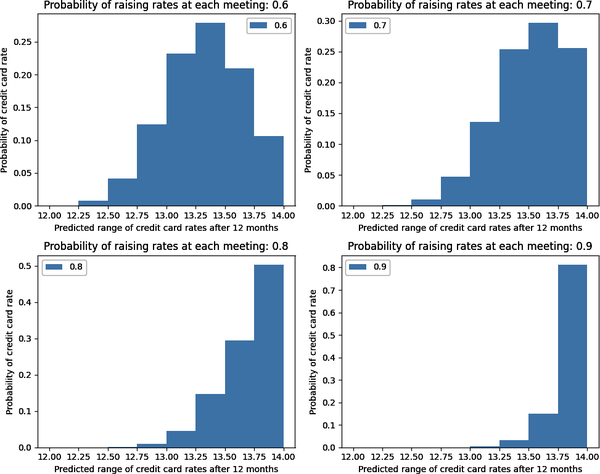
Abbildung 1-2. Wahrscheinlichkeitsverteilung der Kreditkartenraten hängt von deinen Parameterschätzungen ab

Selbst wenn alle Marktteilnehmer die Binomialverteilung in ihren Modellen verwenden würden, ist es leicht nachvollziehbar, dass sie sich über den zukünftigen Leitzins nicht einig sind, weil ihre Schätzungen über die Zinserhöhungen der Fed bei jeder Sitzung voneinander abweichen. In der Tat ist dieser Parameter schwer zu schätzen. Viele Institutionen haben eigene Analysten, darunter auch ehemalige Fed-Mitarbeiter, die alle Dokumente, Reden und Veranstaltungen der Fed analysieren, um diesen Parameter zu schätzen. Das liegt daran, dass sich der Leitzins direkt auf die Preise aller Finanzanlagen und indirekt auf die Beschäftigungs- und Inflationsraten in der Realwirtschaft auswirkt.

Erinnere dich daran, dass wir angenommen haben, dass dieser Parameter, probability_raises, in unserem Modell für jede der nächsten acht Fed-Sitzungen konstant ist. Wie realistisch ist das? Die Mitglieder des Federal Open Market Committee (FOMC), des Gremiums, das die Zinssätze festlegt, sind nicht nur eine Gruppe von voreingenommenen Münzen. Sie können ihre individuellen Vorlieben ändern, je nachdem, wie sich die Wirtschaft im Laufe der Zeit verändert, und das tun sie auch. Die Annahme, dass der Parameter probabil⁠ity_​raises in den nächsten 12 Monaten konstant sein wird, ist nicht nur unrealistisch, sondern auch riskant.

Fehler, die dadurch entstehen, dass sich ein Modell nicht an strukturelle Veränderungen anpassen kann

Der zugrundeliegende stochastische Prozess, der die Daten erzeugt, kann sich im Laufe der Zeit verändern, d.h. der Prozess ist nicht stationär ergodisch. Das bedeutet, dass die statistischen Momente der Verteilung, wie Mittelwert und Varianz, die aus Finanzstichproben zu einem bestimmten Zeitpunkt oder über einen ausreichend langen Zeitraum berechnet werden, die zukünftigen statistischen Momente der zugrunde liegenden Verteilung nicht genau vorhersagen. Die Konzepte der Stationarität und Ergodizität sind in der Finanzwelt sehr wichtig und werden im weiteren Verlauf des Buches näher erläutert.

Wir leben in einer dynamischen kapitalistischen Wirtschaft, die durch technologische Innovationen und eine sich verändernde Geld- und Finanzpolitik gekennzeichnet ist. Zeitvariable Verteilungen von Vermögenswerten und Risiken sind die Regel, nicht die Ausnahme. Bei solchen Verteilungen führen Parameterwerte, die auf historischen Daten basieren, zwangsläufig zu Fehlern in den Prognosen.

In unserem vorherigen Beispiel könnte die US-Notenbank bei ihrer vierten Sitzung eine neutralere Haltung einnehmen, wenn die Wirtschaft Anzeichen einer Verlangsamung zeigt, so dass du deinen Parameter probability_raises von 70% auf 50% ändern musst. Diese Änderung deines Parameters wird wiederum die Prognose für deinen Kreditkartenzinssatz verändern.

Manchmal ändern sich die zeitvariablen Verteilungen und ihre Parameter kontinuierlich oder abrupt, wie bei der mexikanischen Peso-Krise. Sowohl bei kontinuierlichen als auch bei abrupten Veränderungen müssen die verwendeten Modelle an die sich verändernden Marktbedingungen angepasst werden. Eine neue Funktionsform mit anderen Parametern könnte erforderlich sein, um die Werte und Risiken von Vermögenswerten unter den neuen Marktbedingungen zu erklären und vorherzusagen.

Angenommen, nach der fünften Sitzung in unserem Beispiel wird die US-Wirtschaft von einem externen Schock getroffen - zum Beispiel beschließt eine neue populistische Regierung in Griechenland, ihre Schulden nicht zu bedienen. Jetzt wird die Fed die Zinsen wahrscheinlich eher senken als erhöhen. Angesichts dieser strukturellen Veränderung in den Aussichten der Fed müssen wir die binomiale Wahrscheinlichkeitsverteilung in unserem Modell in eine trinomiale Verteilung mit entsprechenden Parametern umwandeln.

Probabilistische Finanzmodelle

Ungenauigkeiten von Finanzmodellen sind Merkmale, keine Fehler. Es ist intellektuell unehrlich und töricht riskant, Finanzschätzungen als wissenschaftlich präzise Werte darzustellen. Alle Modelle sollten die Unsicherheiten quantifizieren, die mit finanziellen Schlussfolgerungen und Vorhersagen verbunden sind, damit sie für eine solide Entscheidungsfindung und das Risikomanagement in der Geschäftswelt nützlich sind. Finanzdaten sind verrauscht und weisen Messfehler auf. Die geeignete Funktionsform eines Modells kann unbekannt oder eine Annäherung sein. Modellparameter und -ergebnisse können eine Reihe von Werten mit entsprechenden Plausibilitäten haben. Mit anderen Worten: Wir brauchen mathematisch fundierte probabilistische Modelle, weil sie Ungenauigkeiten ausgleichen und Unsicherheiten mit logischer Konsistenz quantifizieren.

Derzeit gibt es zwei Möglichkeiten, die Modellunsicherheit zu quantifizieren: Vorwärtspropagation für die Output-Unsicherheit und inverse Propagation für die Input-Unsicherheit. Abbildung 1-3 zeigt die gebräuchlichen Arten von probabilistischen Modellen, die heute in der Finanzwelt zur Quantifizierung beider Arten von Unsicherheiten verwendet werden.

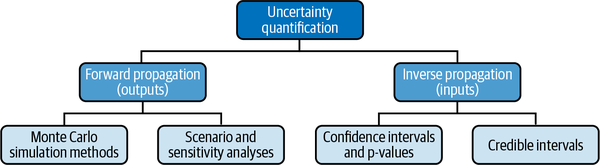
Abbildung 1-3. Quantifizierung der Input- und Output-Unsicherheit mit probabilistischen Modellen

Bei der Vorwärtsunsicherheitsfortpflanzung werden die Unsicherheiten, die sich aus den ungenauen Parametern und Eingaben eines Modells ergeben, auf das gesamte Modell übertragen, um die Unsicherheit der Ergebnisse des Modells zu erzeugen. Die meisten Finanzanalysten verwenden Szenario- und Sensitivitätsanalysen, um die Unsicherheit in den Vorhersagen ihrer Modelle zu quantifizieren. Dabei handelt es sich jedoch um grundlegende Instrumente, die nur einige wenige Möglichkeiten berücksichtigen.

Bei der Szenarioanalyse werden nur drei Fälle betrachtet: Best-Case-, Base-Case- und Worst-Case-Szenarien. Jeder Fall hat einen festen Wert für alle Eingaben und Parameter eines Modells. Bei der Sensitivitätsanalyse werden nur einige wenige Eingaben oder Parameter geändert, um ihre Auswirkungen auf die Gesamtleistung des Modells zu bewerten. Eine Sensitivitätsanalyse kann zum Beispiel untersuchen, wie sich der Wert eines Unternehmens in Abhängigkeit von den Zinssätzen oder den zukünftigen Gewinnen verändert. In Kapitel 3 lernen wir, wie man mit Python Monte-Carlo-Simulationen (MCS) durchführt und sie auf gängige Finanzprobleme anwendet. MCS ist eines der leistungsstärksten probabilistischen numerischen Werkzeuge in allen Wissenschaften und wird sowohl für die Analyse deterministischer als auch probabilistischer Systeme verwendet. Es handelt sich dabei um eine Reihe von numerischen Methoden, die unabhängige Stichproben aus bestimmten Verteilungen von Eingangsparametern verwenden, um neue Daten zu erzeugen, die wir in der Zukunft beobachten könnten. Auf diese Weise können wir die erwartete Unsicherheit eines Modells berechnen, insbesondere wenn die funktionalen Beziehungen nicht analytisch nachvollziehbar sind.

Bei der inversen Unsicherheitsfortpflanzung wird die Unsicherheit der Eingangsparameter des Modells aus den beobachteten Daten abgeleitet. Dies ist ein schwierigeres Rechenproblem als die Vorwärtspropagation, da die Parameter mithilfe von abhängigen Zufallsstichproben aus den Daten gelernt werden müssen. Um Konfidenzintervalle oder glaubwürdige Intervalle für die Eingangsparameter eines Modells zu berechnen, werden fortgeschrittene statistische Schlussfolgerungstechniken oder komplexe numerische Berechnungen eingesetzt. In Kapitel 4 erläutern wir die tiefgreifenden Fehler und Einschränkungen bei der Verwendung von p-Werten und Konfidenzintervallen, statistischen Techniken, die heute in der Finanzdatenanalyse häufig verwendet werden. In Kapitel 6 erläutern wir Markov Chain Monte Carlo, eine fortschrittliche, abhängige Zufallsstichprobenmethode, die zur Berechnung von Konfidenzintervallen verwendet werden kann, um die Unsicherheit der Eingangsparameter eines Modells zu quantifizieren .

Wir brauchen ein umfassendes probabilistisches Rahmenwerk, das sowohl die vorwärtsgerichtete als auch die inverse Unsicherheitsausbreitung nahtlos kombiniert. Wir wollen keinen stückweisen Ansatz, wie er heute in der Praxis üblich ist. Das heißt, wir wollen, dass unsere probabilistischen Modelle die Unsicherheit in den Ergebnissen von zeitvariablen stochastischen Prozessen quantifizieren, deren ungenaue Eingangsparameter aus Beispieldaten gelernt wurden.

Unser probabilistisches System muss die Ergebnisse des Modells oder seine Eingabeparameter - oder beides - ständig auf der Grundlage neuer Datensätze aktualisieren. Solche Modelle müssen mit kleinen Datensätzen entwickelt werden, da sich das zugrundeliegende Umfeld möglicherweise zu schnell verändert hat, um eine große Menge an relevanten Daten zu sammeln. Am wichtigsten ist, dass unsere probabilistischen Modelle wissen müssen, was sie nicht wissen. Wenn sie aus Datensätzen extrapolieren, mit denen sie noch nie in Berührung gekommen sind, müssen sie Antworten mit niedrigem Konfidenzniveau oder größeren Unsicherheitsspannen liefern.

Finanzielle KI und ML

Probabilistisches maschinelles Lernen (ML) erfüllt alle oben genannten Anforderungen für den Aufbau moderner Finanzsysteme der nächsten Generation.¹¹ Aber was ist probabilistisches ML? Bevor wir diese Frage beantworten, müssen wir zunächst klären, was wir unter ML im Besonderen und KI im Allgemeinen verstehen. Häufig werden diese Begriffe als Synonyme verwendet, obwohl sie es nicht sind. ML ist ein Teilbereich der KI. Siehe Abbildung 1-4.

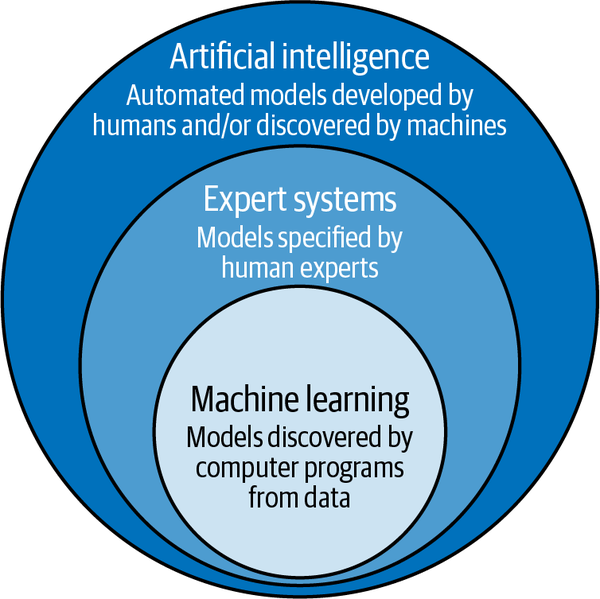
Abbildung 1-4. ML ist ein Teilbereich der KI

KI ist der allgemeine Bereich, der versucht, die kognitiven Fähigkeiten des Menschen zu automatisieren, wie z. B. analytisches Denken, Entscheidungsfindung und Sinneswahrnehmung. Im 20. Jahrhundert entwickelten Informatikerinnen und Informatiker einen Teilbereich der KI, die symbolische KI (SAI), die Methoden und Werkzeuge umfasst, um symbolische Darstellungen menschlichen Wissens in Form von wohldefinierten Regeln oder Algorithmen in Computersysteme einzubetten.

SAI-Systeme automatisieren die von Fachleuten spezifizierten Modelle und werden daher auch als Expertensysteme bezeichnet. Zum Beispiel arbeiten Händler, Finanzmanager und Systementwickler zusammen, um alle Regeln und Parameter des Modells zu formulieren, die von ihren Finanz- und Investitionsmanagementsystemen automatisiert werden sollen. In einem meiner früheren Unternehmen habe ich mehrere solcher Projekte für namhafte Finanzinstitute geleitet.

Die SAI schlug jedoch bei der Automatisierung komplexer Aufgaben wie der Bilderkennung und der Verarbeitung natürlicher Sprache fehl - Technologien, die heute in der Finanzwirtschaft und bei Investitionen weit verbreitet sind. Die Regeln für diese Arten von Expertensystemen sind zu komplex und müssen ständig für verschiedene Situationen aktualisiert werden. In der zweiten Hälfte des 20. Jahrhunderts entstand durch das Zusammentreffen von verbesserten Algorithmen, reichlich Daten und billigen Rechenressourcen ein neuer KI-Teilbereich, die ML.

ML stellt das Paradigma der SAI auf den Kopf. Anstelle von Experten, die Modelle für die Datenverarbeitung vorgeben, stellen Menschen mit wenig oder gar keinem Fachwissen Allzweckalgorithmen bereit, die ein Modell aus Datenproben lernen. Noch wichtiger ist, dass ML-Programme kontinuierlich aus neuen Datensätzen lernen und ihre Modelle aktualisieren, ohne dass der Mensch bei der Codepflege eingreifen muss. In der nächsten Seitenleiste findest du eine einfache Erklärung, wie Parameter aus Daten gelernt werden.

Training eines linearen ML-Systems zum Lernen

Erinnere dich an das deterministische lineare Modell , das wir bereits besprochen haben und das durch die Gleichung y = mx + b ausgedrückt wird. Eine eindeutige Linie kreuzt mindestens zwei verschiedene Punkte in der XY-Ebene. Anhand dieser beiden Punkte können wir die genauen Werte der Parameter m und b mit einfacher Algebra analytisch ermitteln. Sobald du die Parameter berechnet hast, kannst du dein Modell nutzen, um genaue Vorhersagen zu treffen: Für jeden beliebigen Punkt x kannst du genau vorhersagen, wie y sein wird.

Finanzmodelle sind jedoch nicht deterministisch, sondern probabilistisch. Wenn du zum Beispiel die Aktienkursrenditen eines Unternehmens auf der y-Achse und die Wachstumsrate der Quartalsgewinne auf der x-Achse aufträgst, wirst du sehen, dass die Aktienrenditen im Allgemeinen mit dem Gewinnwachstum eines Unternehmens steigen. Wenn du annimmst, dass die Beziehung zwischen Aktienkursrenditen und vierteljährlichem Gewinnwachstum annähernd linear ist, kannst du ein analytisches statistisches Verfahren anwenden, um die Parameter m und b des Modells zu bestimmen, das dir die Linie liefert, die am besten zu den Stichprobendaten des Unternehmens passt. Wenn die lineare Annäherung auch in Zukunft bestehen bleibt, sind die Vorhersagen deines Modells zwar nicht präzise, aber besser als zufällige Vermutungen oder Glück.

Alternativ kannst du auch ML-Software verwenden, die ähnliche Berechnungen für dich durchführt. In ML-Systemen wird die unabhängige Variable x als Merkmal oder Prädiktor und die abhängige Variable y als Ziel- oder Antwortvariable bezeichnet. Das Einspeisen von Beispieldaten in das ML-System wird als Training des Systems bezeichnet. Wenn unser lineares ML-System die Werte der Parameter m und b berechnet, sagen wir, dass das ML-System das Modell aus den Beispieldaten gelernt hat. Das Ziel von ML ist es, die Zielwerte für Daten außerhalb der Stichprobe vorherzusagen, für die das System nicht trainiert wurde. Hier werden die Vorhersagen zur Herausforderung.

In der zweiten Hälfte des Buches werden wir uns mit der Modellierung, dem Training und dem Testen probabilistischer ML-Systeme befassen. Hier ist eine nützliche Definition von ML von Tom Mitchell, einem ML-Pionier: "Ein Computerprogramm lernt aus Erfahrung E in Bezug auf eine Klasse von Aufgaben T und ein Leistungsmaß P, wenn sich seine Leistung bei Aufgaben in T, gemessen an P, mit der Erfahrung E verbessert."¹² Siehe Abbildung 1-5.

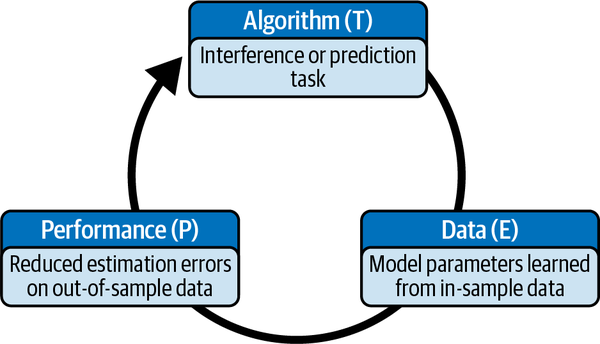
Abbildung 1-5. Ein ML-Modell lernt seine Parameter anhand von In-Sample-Daten, aber seine Leistung wird anhand von Out-of-Sample-Daten bewertet

Die Leistung wird anhand einer vorgegebenen Zielfunktion gemessen, z. B. der Maximierung der jährlichen Aktienkursrendite oder der Senkung des mittleren absoluten Fehlers der Parameterschätzungen.

ML-Systeme werden in der Regel in drei Typen eingeteilt, je nachdem, wie viel Unterstützung sie von ihren menschlichen Lehrern oder Betreuern benötigen.

Überwachtes Lernen

ML-Algorithmen lernen funktionale Beziehungen aus Daten, die als Paare von Eingaben und gewünschten Ausgaben vorliegen. Dies ist die häufigste Form von ML, die in Forschung und Industrie eingesetzt wird. Einige Beispiele für ML-Systeme sind lineare Regression, logistische Regression, Random Forests, Gradient-Boosted-Maschinen und Deep Learning.

Unüberwachtes Lernen

ML-Algorithmen erhalten nur Eingabedaten und lernen die strukturellen Beziehungen in den Daten selbständig. Der K-Means-Clustering-Algorithmus ist ein gängiger Algorithmus zur Datenexploration, der von Investmentanalysten verwendet wird. Die Hauptkomponentenanalyse ist ein beliebter Algorithmus zur Dimensionalitätsreduktion.

Verstärkungslernen

Ein ML-Algorithmus aktualisiert kontinuierlich eine Strategie oder eine Reihe von Aktionen auf der Grundlage von Rückmeldungen aus der Umgebung mit dem Ziel, den aktuellen Wert der kumulierten Belohnungen zu maximieren. Der Unterschied zum überwachten Lernen besteht darin, dass das Feedbacksignal nicht eine gewünschte Ausgabe oder Klasse ist, sondern eine Belohnung oder Strafe. Beispiele für Algorithmen sind Q-Learning, Deep Q-Learning und Policy-Gradient-Methoden. Reinforcement-Learning-Algorithmen werden in fortschrittlichen Handelsanwendungen eingesetzt.

Im 21. Jahrhundert trainieren Finanzdatenwissenschaftler/innen ML-Algorithmen, um komplexe funktionale Beziehungen anhand von Daten aus verschiedenen finanziellen und nicht-finanziellen Quellen zu entdecken. Die neu entdeckten Zusammenhänge können die Erkenntnisse von Finanz- und Investmentmanagern ergänzen oder ersetzen. ML-Programme sind in der Lage, Muster in sehr hochdimensionalen Datensätzen zu erkennen, was für Menschen schwierig oder sogar unmöglich ist. Sie sind auch in der Lage, die Dimensionen zu reduzieren, um eine Visualisierung für Menschen zu ermöglichen.

KI wird in allen Bereichen des Finanz- und Investitionsprozesses eingesetzt - von der Ideenfindung über die Analyse und Ausführung bis hin zum Portfolio- und Risikomanagement. Die führenden KI-gestützten Systeme im Finanz- und Investitionsbereich nutzen heute eine Kombination aus Expertensystemen und ML-basierten Systemen, indem sie die Vorteile beider Arten von Ansätzen und Fachwissen nutzen. Darüber hinaus nutzen KI-gestützte Finanzsysteme weiterhin die menschliche Intelligenz (HI) für Forschung, Entwicklung und Wartung. Der Mensch kann auch in extremen Marktsituationen eingreifen, in denen es für KI-Systeme schwierig ist, aus abrupten Veränderungen zu lernen. Du kannst dir moderne Finanzsysteme also als eine komplexe Kombination aus SAI + ML + HI vorstellen.

Probabilistische ML

Probabilistic ML ist die nächste Generation von ML Framework und Technologie für KI-gestützte Finanz- und Anlagesysteme. Führende Technologieunternehmen haben die Grenzen herkömmlicher KI-Technologien erkannt und entwickeln ihre probabilistischen Versionen, um ihre Anwendbarkeit auf komplexere Probleme auszuweiten.

Google hat kürzlich TensorFlow Probability eingeführt, um seine etablierte TensorFlow-Plattform zu erweitern. Ähnlich haben Facebook und Uber Pyro eingeführt, um ihre PyTorch-Plattform zu erweitern. Die derzeit beliebtesten Open-Source-Technologien für probabilistisches ML sind PyMC und Stan. PyMC ist in Python geschrieben, Stan in C++. In Kapitel 7 verwenden wir die PyMC-Bibliothek, weil sie Teil des Python-Ökosystems ist.

Die probabilistische ML, wie sie in diesem Buch behandelt wird , basiert auf einem generativen Modell. Sie unterscheidet sich grundlegend von der herkömmlichen ML, die heute verwendet wird, wie lineare, nichtlineare und Deep-Learning-Systeme, auch wenn diese anderen Systeme probabilistische Ergebnisse berechnen. Abbildung 1-6 zeigt die wichtigsten Unterschiede zwischen den beiden Arten von Systemen.

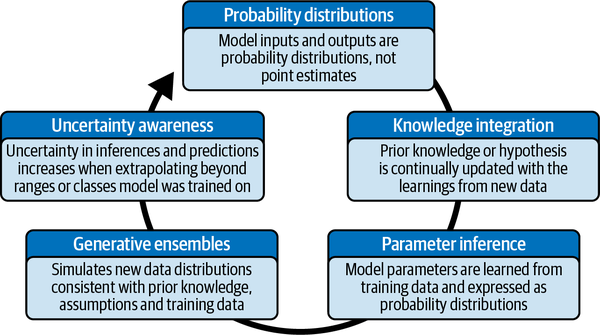
Abbildung 1-6. Zusammenfassung der wichtigsten Merkmale von probabilistischen ML-Systemen

Wahrscheinlichkeitsverteilungen

Auch wenn herkömmliche ML-Systeme kalibrierte Wahrscheinlichkeiten verwenden, berechnen sie nur die wahrscheinlichsten Schätzungen und die damit verbundenen Wahrscheinlichkeiten als Ein-Punkt-Werte für Eingaben und Ausgaben. Das funktioniert gut in Bereichen wie der Bilderkennung, in denen es viele Daten gibt und das Signal-Rausch-Verhältnis hoch ist. Wie in den vorangegangenen Abschnitten erläutert und gezeigt wurde, ist eine Punktschätzung eine ungenaue und irreführende Darstellung der finanziellen Realität, in der die Unsicherheit sehr hoch ist. Außerdem sind die kalibrierten Wahrscheinlichkeiten möglicherweise keine gültigen Wahrscheinlichkeiten, da die unbedingte Wahrscheinlichkeitsverteilung der Daten fast nie von MLE-Modellen berechnet wird. Dies kann zu einer schlechten Quantifizierung der Unsicherheit führen, wie in Kapitel 6 erläutert wird.

Probabilistische ML-Systeme arbeiten bei der Berechnung von Eingangsparametern und Modellergebnissen ausschließlich mit Wahrscheinlichkeitsverteilungen. Dies ist eine realistische und ehrliche Darstellung der Unsicherheit der Variablen eines Finanzmodells. Darüber hinaus lassen Wahrscheinlichkeitsverteilungen dem Nutzer eine große Flexibilität bei der Auswahl des geeigneten Punktschätzers, falls erforderlich, basierend auf seinen Geschäftszielen.

Wissensintegration

Herkömmliche ML-Systeme verfügen nicht über einen theoretisch fundierten Rahmen für die Einbeziehung von Vorwissen, egal ob es sich um etabliertes wissenschaftliches Wissen, institutionelles Wissen oder persönliche Erkenntnisse handelt. Im weiteren Verlauf des Buches werden wir sehen, dass konventionelle Statistiker Vorwissen mit statistischen Ad-hoc-Methoden wie Nullhypothesen, statistischen Signifikanzniveaus und L1- und L2-Regularisierungen einfließen lassen, während sie darauf pochen, dass nur "die Daten für sich selbst sprechen".

Es ist töricht, Vorwissen nicht in unser persönliches und berufliches Leben zu integrieren. Das ist das Gegenteil von Lernen und widerspricht dem Wesen der wissenschaftlichen Methode. Dies ist jedoch die Grundlage der Nullhypothesen-Signifikanztests (NHST), der vorherrschenden statistischen Methode in Wissenschaft, Forschung und Industrie seit den 1960er Jahren. NHST verbietet die Berücksichtigung von Vorwissen in Experimenten mit der fadenscheinigen Begründung, dass die Objektivität verlangt, dass wir nur die Daten für sich selbst sprechen lassen. Mit dieser fadenscheinigen Behauptung begeht die NHST den Trugschluss des Staatsanwalts, wie wir in Kapitel 4 zeigen werden.

Nach NHSTs Definition von Objektivität müssten wir überall und jedes Mal, wenn wir Feuer finden, Feuer anfassen, weil wir unser Vorwissen darüber, wie es sich in ähnlichen Situationen in der Vergangenheit angefühlt hat, nicht einbeziehen können. Das ist die Definition von Dummheit, nicht von Objektivität. In Kapitel 4 werden wir erörtern, wie und warum mehrere Metastudien gezeigt haben, dass die Mehrheit der veröffentlichten medizinischen Forschungsergebnisse, die auf NHST basieren, falsch sind. Ja, du hast richtig gelesen, und das ist seit einem bahnbrechenden Artikel aus dem Jahr 2005 ein offenes Geheimnis.¹³

Glücklicherweise müssen wir in diesem Buch nicht viel Tinte oder Pixel auf dieses fadenscheinige Argument über Objektivität oder die Verbreitung der von der NHST produzierten Junk Science verschwenden. Probabilistische ML-Systeme bieten einen mathematisch strengen Rahmen für die Einbeziehung von Vorwissen und dessen angemessene Aktualisierung durch neue Informationen. Die Darstellung des Vorwissens erfolgt explizit, so dass jeder es in Frage stellen oder ändern kann. Das ist die Essenz des Lernens und die Grundlage der wissenschaftlichen Methode.

Eine der wichtigsten Implikationen des No-Free-Lunch-Theorems (NFL-Theorem) ist, dass das Wissen über einen bestimmten Bereich notwendig ist, um die Leistung eines Algorithmus für einen bestimmten Problembereich zu optimieren. Wenn wir unser Vorwissen nicht anwenden, ist die Leistung unseres unvoreingenommenen Algorithmus im Durchschnitt aller Problemdomänen nicht besser als das zufällige Raten. Es gibt kein kostenloses Mittagessen, vor allem nicht im Finanz- und Investitionsbereich. Im nächsten Kapitel werden wir die NFL-Theoreme im Detail besprechen.

Es ist allgemein bekannt, dass die Integration von angesammeltem institutionellem Wissen in die Organisation, Prozesse und Systeme eines Unternehmens zu einem nachhaltigen Wettbewerbsvorteil in der Wirtschaft führt. Darüber hinaus können persönliche Einsichten und Erfahrungen mit den Märkten zu "Alpha" oder zur Erzielung außergewöhnlicher Renditen im Handel und beim Investieren für den Fondsmanager führen, der zu einer subjektiv anderen Sichtweise als der Rest der Masse gelangt. Auf diese Weise hat Warren Buffet, einer der größten Investoren aller Zeiten, sein riesiges Vermögen gemacht. Die Märkte verhöhnen dogmatische und unrealistische Definitionen von Objektivität mit entgangenen Gewinnen und schließlich mit dem finanziellen Ruin.

Parameter Inferenz

Fast alle konventionellen ML-Systeme verwenden ebenso konventionelle statistische Methoden wie p-Werte und Konfidenzintervalle, um die Unsicherheit der Parameter eines Modells zu schätzen. Wie in Kapitel 4 erläutert wird, handelt es sich dabei um zutiefst fehlerhafte - fast schon skandalöse - statistische Methoden, die die Sozialwissenschaften, einschließlich der Finanz- und Wirtschaftswissenschaften, plagen. Diese Methoden beruhen auf einem frommen Anspruch auf Objektivität und auf impliziten und unrealistischen Annahmen, die durch einen undurchschaubaren Statistikjargon verschleiert werden, um Lösungen zu finden, die für eine kleine Anzahl von Szenarien analytisch nachvollziehbar sind.

Die probabilistische ML basiert auf einer einfachen und intuitiven Definition von Wahrscheinlichkeit als Logik und dem strengen Kalkül der Wahrscheinlichkeitstheorie im Allgemeinen und der inversen Wahrscheinlichkeitsregel im Besonderen. Im nächsten Kapitel zeigen wir, wie die inverse Wahrscheinlichkeitsregel - fälschlicherweise und beschämend als Satz von Bayes bekannt - eine triviale Umformulierung der Produktregel ist. Es ist eine logische Tautologie, die peinlich einfach zu beweisen ist. Sie verdient die Bezeichnung Theorem nicht, wenn man bedenkt, wie schwierig es ist, die meisten mathematischen Theoreme abzuleiten.

Aufgrund der Normalisierungskonstante in der Inversionsformel war es bisher jedoch unmöglich, Wahrscheinlichkeiten analytisch zu invertieren, außer bei einfachen Problemen. Mit den jüngsten Fortschritten bei modernen numerischen Algorithmen wie Hamiltonian Monte Carlo und automatischer Differenzierungs-Variationsinferenz sind probabilistische ML-Systeme jetzt in der Lage, Wahrscheinlichkeiten zu invertieren, um Modellparameterschätzungen aus In-Sample-Daten für fast jedes reale Problem zu berechnen. Noch wichtiger ist, dass sie in der Lage sind, die Parameterunsicherheiten mit mathematisch fundierten Glaubwürdigkeitsintervallen für jedes Vertrauensniveau zu quantifizieren. Dies ermöglicht die inverse Unsicherheitsfortpflanzung.

Generative Ensembles

Fast alle herkömmlichen ML-Systeme basieren auf diskriminativen Modellen. Diese Art von statistischen Modellen lernt nur eine Entscheidungsgrenze aus den Daten in der Stichprobe, aber nicht, wie die Daten statistisch verteilt sind. Daher können herkömmliche diskriminative ML-Systeme keine neuen Daten simulieren und die Gesamtunsicherheit der Ergebnisse nicht quantifizieren.

Probabilistische ML-Systeme basieren auf generativen Modellen. Diese Art von statistischem Modell lernt die statistische Struktur der Datenverteilung und kann so einfach und nahtlos neue Daten simulieren, einschließlich der Generierung von Daten, die fehlen oder verfälscht sein könnten. Außerdem erzeugt die Verteilung der Parameter ein Ensemble von Modellen. Am wichtigsten ist, dass diese Systeme in der Lage sind, zweidimensionale Ausgangsunsicherheiten zu simulieren, die auf der Variabilität der Daten und der Unsicherheit der Eingangsparameter beruhen, deren Wahrscheinlichkeitsverteilungen sie zuvor aus den In-Sample-Daten gelernt haben. Dies ermöglicht eine nahtlose Weitergabe der Unsicherheit.

Bewusstsein für Unsicherheit

Bei der Berechnung von Wahrscheinlichkeiten verwendet ein herkömmliches ML-System die Methode der Maximum-Likelihood-Schätzung (MLE). Diese Technik optimiert die Parameter einer angenommenen Wahrscheinlichkeitsverteilung so, dass die Daten in der Stichprobe am wahrscheinlichsten beobachtet werden, wenn die Punktschätzungen für die Parameter des Modells vorliegen. Wie wir später im Buch sehen werden, führt die MLE-Methode zu falschen Schlussfolgerungen und Vorhersagen, wenn die Daten spärlich sind, was im Finanz- und Investitionsbereich häufig vorkommt, vor allem wenn sich ein Marktregime abrupt ändert.

Was es noch schlimmer macht, ist, dass diese MLE-basierten ML-Systeme diesen falschen Schätzungen erschreckend hohe Wahrscheinlichkeiten zuordnen. Wir automatisieren die Selbstüberschätzung mächtiger Systeme, denen es an gesundem Menschenverstand mangelt. Das macht herkömmliche ML-Systeme potenziell riskant und gefährlich, vor allem, wenn sie bei missionskritischen Einsätzen von Personal eingesetzt werden, das entweder die Grundlagen dieser ML-Systeme nicht versteht oder blindes Vertrauen in sie hat.

Probabilistische ML-Systeme verlassen sich nicht auf eine einzelne Schätzung, egal wie wahrscheinlich oder optimal sie ist, sondern auf einen gewichteten Durchschnitt aller möglichen Schätzungen der gesamten Wahrscheinlichkeitsverteilung eines Parameters. Außerdem erhöht sich die Unsicherheit dieser Schätzungen entsprechend, wenn die Systeme mit Datenklassen arbeiten, die sie beim Training noch nie gesehen haben, oder wenn sie über bekannte Datenbereiche hinaus extrapolieren. Im Gegensatz zu MLE-basierten Systemen wissen probabilistische ML-Systeme, was sie nicht wissen. Dadurch bleibt die Quantifizierung der Unsicherheit ehrlich und verhindert übermäßiges Vertrauen in die Schätzungen und Vorhersagen.

Zusammenfassung

Die Wirtschaftswissenschaft ist keine präzise Vorhersagewissenschaft wie die Physik. Nicht einmal annähernd. Also lass uns nicht so tun, als ob es anders wäre, und die akademischen Theorien und Modelle der Wirtschaftswissenschaften so behandeln, als wären sie Modelle der Quantenphysik, ungeachtet der verwirrenden Mathematik.

Alle Finanzmodelle, egal ob sie auf akademischen Theorien oder ML-Strategien basieren, sind der Trias der Modellierungsfehler ausgeliefert. Dieses Trio von Fehlern kann zwar mit geeigneten Instrumenten wie probabilistischen ML-Systemen gemildert, aber nicht ausgeschlossen werden. Es wird immer Informationsasymmetrien und kognitive Verzerrungen geben. Die Modelle für Vermögenswerte und Risiken werden sich im Laufe der Zeit aufgrund der Dynamik des Kapitalismus, des menschlichen Verhaltens und der technologischen Innovation ändern.

Probabilistische ML-Technologien basieren auf einer einfachen und intuitiven Definition von Wahrscheinlichkeit als Logik und dem strengen Kalkül der Wahrscheinlichkeitstheorie. Sie ermöglichen die explizite und systematische Integration von Vorwissen, das kontinuierlich mit neuen Erkenntnissen aktualisiert wird.

Diese Systeme behandeln Unsicherheiten und Fehler in Finanz- und Anlagesystemen als Eigenschaften, nicht als Fehler. Sie quantifizieren die Unsicherheiten, die durch ungenaue Eingaben, Parameter und Ergebnisse von Finanz- und Investitionssystemen entstehen, als Wahrscheinlichkeitsverteilungen und nicht als Punktschätzungen. Dies ermöglicht realistische finanzielle Schlussfolgerungen und Vorhersagen, die für die Entscheidungsfindung und das Risikomanagement nützlich sind. Vor allem aber sind diese Systeme in der Lage, uns zu warnen, wenn ihre Schlussfolgerungen und Vorhersagen im aktuellen Marktumfeld nicht mehr sinnvoll sind.

Es gibt mehrere Gründe, warum probabilistische ML das ML-Framework und die Technologie der nächsten Generation für KI-gestützte Finanz- und Anlagesysteme ist. Der probabilistische Rahmen entfernt sich von fehlerhaften statistischen Methoden (NHST, p-Werte, Konfidenzintervalle) und der restriktiven konventionellen Auffassung von Wahrscheinlichkeit als Grenzfrequenz. Er führt uns zu einer intuitiven Sichtweise der Wahrscheinlichkeit als Logik und einem mathematisch strengen statistischen Rahmen, der Unsicherheit ganzheitlich und erfolgreich quantifiziert. So können wir uns von den falschen, idealistischen, analytischen Modellen der Vergangenheit zu weniger falschen, realistischeren, numerischen Modellen für die Zukunft bewegen.

Die Algorithmen der probabilistischen Programmierung gehören zu den ausgeklügeltsten Algorithmen in der KI-Welt, die wir in der zweiten Hälfte des Buches näher beleuchten werden. In den nächsten drei Kapiteln werden wir näher darauf eingehen, warum es sehr riskant ist, dein Kapital mit herkömmlichen ML-Systemen einzusetzen, weil sie auf orthodoxen probabilistischen und statistischen Methoden basieren, die skandalöse Fehler aufweisen.

Referenzen

Géron, Aurélien. "The Machine Learning Landscape". In Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 1-34. 3rd ed. O'Reilly Media, 2022.

Hayek, Friedrich von. "Bankett-Rede". Rede auf dem Nobel-Bankett, Stockholm, Schweden, 10. Dezember 1974. Nobel Prize Outreach AB, 2023, https://www.nobelprize.org/prizes/economic-sciences/1974/hayek/speech/.

Ioannidis, John P. A. "Warum die meisten veröffentlichten Forschungsergebnisse falsch sind". PLOS Medicine 2, no. 8 (2005): e124. https://doi.org/10.1371/journal.pmed.0020124.

Offer, Avner, und Gabriel Söderberg. Der Nobel-Faktor: The Prize in Economics, Social Democracy, and the Market Turn. Princeton, NJ: Princeton University Press, 2016.

Orrell, David, und Paul Wilmott. Die Geldformel: Fragwürdige Finanzen, Pseudowissenschaft und wie Mathematiker die Märkte eroberten. West Sussex, Großbritannien: Wiley, 2017.

Sekerke, Matt. Bayesianisches Risikomanagement. Wiley, 2015.

Simons, Katerina. "Modellfehler". New England Economic Review (November 1997): 17-28.

Thompson, J. R., L. S. Baggett, W. C. Wojciechowski, und E. E. Williams. "Nobels für Unsinn". Journal of Post Keynesian Economics 29, Nr. 1 (Herbst 2006): 3-18.

Weitere Lektüre

Jaynes, E. T. Wahrscheinlichkeitsrechnung: Die Logik der Wissenschaft. New York: Cambridge University Press, 2003.

Lopez de Prado, Marcos. Advances in Financial Machine Learning. Hoboken, New Jersey: Wiley, 2018.

Taleb, Nassim Nicholas. Vom Zufall getäuscht: Die verborgene Rolle des Zufalls im Leben und auf den Märkten. New York: Random House Trade, 2005.

¹ David Orrell und Paul Wilmott, "Going Random", in The Money Formula: Dodgy Finance, Pseudo Science, and How Mathematicians Took Over the Markets (West Sussex, UK: Wiley, 2017).

² Avner Offer und G. Söderberg, The Nobel Factor: The Prize in Economics, Social Democracy, and the Market Turn (Princeton, NJ: Princeton University Press, 2016).

³ Friedrich von Hayek, "Banquet Speech", Nobel Prize Outreach AB, 2023, https://www.nobelprize.org/prizes/economic-sciences/1974/hayek/speech.

⁴ David Orrell und Paul Wilmott, "Early Models", in The Money Formula: Dodgy Finance, Pseudo Science, and How Mathematicians Took Over the Markets (West Sussex, UK: Wiley, 2017).

⁵ J. R. Thompson, L. S. Baggett, W. C. Wojciechowski und E. E. Williams, "Nobels For Nonsense", Journal of Post Keynesian Economics 29, Nr. 1 (Herbst 2006): 3-18.

⁶ Orrell und Wilmott, Die Geldformel.

⁷ Angepasst an ein Bild von Wikimedia Commons.

⁸ Orrell und Wilmott, The Money Formula; M. Sekerke, Bayesian Risk Management (Hoboken, NJ: Wiley, 2015); J. R. Thompson, L. S. Baggett, W. C. Wojciechowski, und E. E. Williams, "Nobels for Nonsense," Journal of Post Keynesian Economics 29, Nr. 1 (Herbst 2006): 3-18; und Katerina Simons, "Model Error", New England Economic Review (November 1997): 17-28.

⁹ Orrell und Wilmott, The Money Formula; Sekerke, Bayesian Risk Management; und Thompson, Baggett, Wojciechowski, und Williams, "Nobels for Nonsense".

¹⁰ Orrell und Wilmott, The Money Formula; Sekerke, Bayesian Risk Management; und Thompson, Baggett, Wojciechowski, und Williams, "Nobels for Nonsense".

¹¹ Sekerke, Bayesianisches Risikomanagement.

¹² Aurélien Géron, "The Machine Learning Landscape," in Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 3rd edition (O'Reilly Media, 2022), 1-34.

¹³ Es handelt sich um John P. A. Ioannidis, "Why Most Published Research Findings Are False," PLOS Medicine 2, no. 8 (2005): e124, https://doi.org/10.1371/journal.pmed.0020124. Siehe auch Julia Belluz, "This Is Why You Shouldn't Believe That Exciting New Medical Study," Vox, February 27, 2017, https://www.vox.com/2015/3/23/8264355/research-study-hype.