Principles of Superconducting Quantum Computers

5 Resonators: Classical Treatment

Resonators play an important role in superconducting quantum computers. The qubits themselves are nonlinear resonators, and in many architectures, the qubits are coupled to other qubits and to external circuits through transmission line segments functioning as resonators. In quantum computers these resonators are excited with small numbers of photons, and so must ultimately be analyzed quantum mechanically. However, it is helpful to gain intuition about the behavior of both lumped circuits and transmission line resonators using classical analysis. Consequently we will focus on a classical treatment in this chapter, and then consider a quantum mechanical treatment in Chapter 6.

5.1 Parallel Lumped Element Resonator

Consider the lumped-element circuit shown in Figure 5.1(a) consisting of a capacitor, inductor, and resistor in parallel.

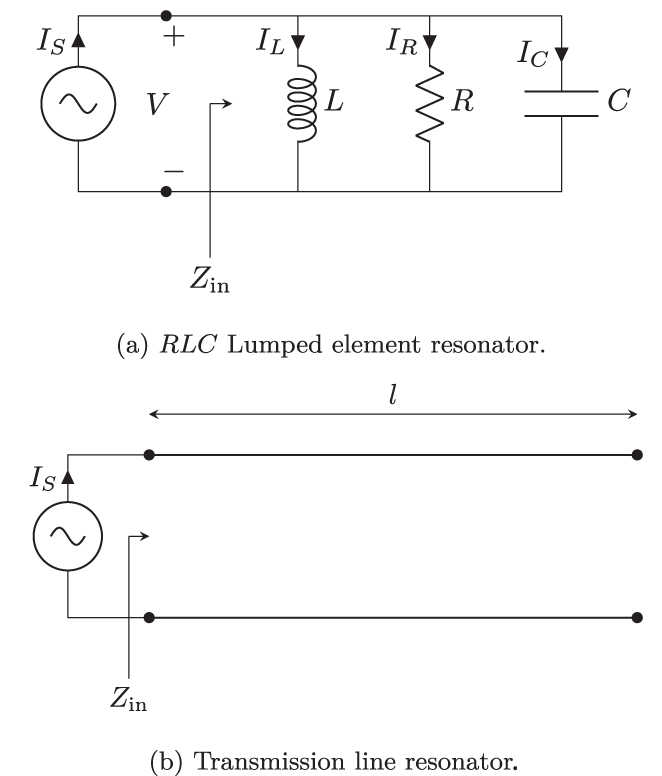
The impedance Z_in of the circuit is given by:

(5.1)

For large R, the impedance will be sharply peaked around ${\omega }_0=1/\sqrt{LC}$. Consequently, let us expand the impedance about ω₀, i.e., $\omega ={\omega }_0+\mathrm{\Delta }\omega$:

  (5.2)

The first term can be re-written using the series expansion for small x

(5.3)

where $x=\mathrm{\Delta }\omega /{\omega }_0$:

(5.4)

This expression can be ...