Mathematica Cookbook

Chapter 4. Patterns and Rule-Based Programming

You are an obsession I cannot sleep I am your possession Unopened at your feet There’s no balance No equality Be still I will not accept defeat
I will have you Yes, I will have you I will find a way and I will have you Like a butterfly A wild butterly I will collect you and capture you
—Animation, “Obsession”

4.0 Introduction

In Chapter 2, I argue that the functional style of programming is the preferred way to solve problems in Mathematica. Although functions form much of the brawn, pattern matching provides the brains. In fact, functions and patterns should be thought of as partners rather than competitors. By mastering both functional programming and pattern-based programming, you will be able to use Mathematica to its fullest potential. In fact, once you get the hang of pattern-based solutions they may become a bit of an obsession.

If you have done any programming that involves text manipulation, you have no doubt been exposed to regular expressions, a concise syntax for describing patterns in text and manipulating text. Mathematica’s pattern syntax generalizes regular expressions to the domain of symbolic processing, which allows you to manipulate arbitrary symbolic structures. Patterns and rules are at the foundation of Mathematica’s symbolic processing capabilities. Symbolic integration, differentiation, equation solving, and simplification are all driven by the pattern primitives explained in this chapter.

In the context of Mathematica, a pattern is an expression that acts as a template against which other expressions can be matched. Some of the most useful patterns contain variables that are bound to values as a result of the matching process. However, many times just knowing that a pattern matched is sufficient. Patterns are central to specifying constraints in function arguments (e.g., Integer). They also play roles in parsing, replacing, and counting, as we show in the recipes here. I defer the role of patterns in string manipulation to Chapter 5.

Rules build on patterns by specifying a mapping from a pattern to another expression that uses all or parts of the matched results. Rules pervade Mathematica, as you will see in this chapter’s recipes and throughout this book. It’s safe to say that Mathematica would be almost as crippled by the removal of rules as it would be by the removal of the definition for Plus.

The rest of this introduction gives a brief overview of the most important primitives associated with pattern matching. This will make the recipes a bit easier to follow if you are new to these concepts. The recipes will explore the primitives more deeply, and as usual, you should refer to the Mathematica documentation for subtle details or clarification.

Blanks

The most basic pattern constructs are Blank[] (__), BlankSequence[] (_), and BlankNullSequence[] (__). Blank[] matches any expression (_), whereas Blank[h] (_h) matches any expression with head h. BlankSequence (__) means one or more; BlankNullSequence means zero or more. Thus, ___h means zero or more expressions with head h. Here MatchQ tests if a pattern matches an expression.

In[1]:=  MatchQ[a,_]
Out[1]=  True

In[2]:=  MatchQ[a[l], _a]
Out[2]=  True

In[3]:=  (*By itself a has head Symbol.*)
         MatchQ[a,_a]
Out[3]=  False

In[4]:=  MatchQ[{1, 2}, _List]
Out[4]=  True

Blanks are more powerful when you can determine what they are matched against so you can use the matched value for further processing. This is most often done using a prefix symbol (e.g., x_, x__, x___). This syntax should be familiar since it is most commonly used for function arguments. However, as shown in this recipe, there are other contexts where binding symbols to matches comes into play.

 In[5]:=  (*f1 will match when called with a single integer argument.*)
          f1[n_Integer] := {n}
          (*f2 will match when called with one or more integers.*)
          f2[n__Integer] := {n}
          (*f3 will match when called with zero or more integers.*)
          f3[n___Integer] := {n}

 In[8]:=  f1[10] (*Match*)
 Out[8]=  {10}

 In[9]:=  f1[10, 20] (*No match*)
 Out[9]=  f1[10, 20]

In[10]:=  f2[10, 20] (*Match*)
Out[10]=  {10, 20}

In[11]:=  f2[] (*No match*)
Out[11]=  f2[]

In[12]:=  f3[] (*Match*)
Out[12]=  {}

In[13]:=  f3[1, 2, "3"] (*No match*)
Out[13]=  f3[1, 2, 3]

Alternatives

Sometimes you need to construct patterns that match two or more forms. This can be done using Alternatives[p1,p2, ...,pn] or, more commonly, using vertical bar p1|p2|...|pn.

In[14]:=  Cases[{a, r, t, i, c, h, o, k, e}, a|e|i|o|u]
Out[14]=  {a, i, o, e}

This form can also appear in functions.

In[15]:=  Clear[f]
          f[x_Complex |x_Real|x_Integer]  := x

Repeats

You use Repeated[p] or p.. to match one or more instances of some pattern p; you use RepeatedNull[p] or p... to match zero or more instances of p.

In[18]:=  Cases[{{0, 0, 0}, {0, 0, 1}, {0, 1, 0}, {0, 1, 1},
            {1, 0, 0}, {1, 0, 1}, {1, 1, 0}, {1, 1, 1}}, {1 .., 0 ..}]
Out[18]=  {{1, 0, 0}, {1, 1, 0}}

In[19]:=  Cases[{{0, 0, 0}, {0, 0, 1}, {0, 1, 0}, {0, 1, 1},
            {1, 0, 0}, {1, 0, 1}, {1, 1, 0}, {1, 1, 1}}, {1 ..., 0 ...}]
Out[19]=  {{0, 0, 0}, {1, 0, 0}, {1, 1, 0}, {1, 1, 1}}

PatternSequence

Repeated (p..) matches a very specific sequence, whereas BlankSequence (x__) is very general. Sometimes you need to match a sequence of intermediate specificity. PatternSequence was introduced in Mathematica 6 to help achieve this. The following means f is a function that takes exactly two expressions.

In[20]:=  Clear [f];
          f[x : PatternSequence[_, _]] := Power[x]

In[22]:=  f[1]  (*No match, too few*)
Out[22]=  f[1]

In[23]:=  f[2, 3] (*Match*)
Out[23]=  8

In[24]:=  f[2, 3, 4] (*No match, too many*)
Out[24]=  f[2, 3, 4]

Above, Pattern Sequence is not strictly necessary because f[x_,y_] := Power[x,y] is the more conventional notation, but consider these more interesting use cases.

f[0 | PatternSequence[]] := 0 (*Matches either f[0] or f[]*)
f[p : PatternSequence[_,_],___] := {p} (*Names the first two elements of a
sequence and discards the rest*)
f[p : Longest@PatternSequence[a,b]..,rest___] (*The longest repeated
sequence of a,b*)

Except

Often, it is easier to describe what you don’t want to match than what you do. In these cases, you can use Except[p] to indicate matching for everything except what matches p.

In[25]:=  Cases[{a, r, t, i, c, h, o, k, e}, Except[a|e|i|o|u]]
Out[25]=  {r, t, c, h, k}

Conditions and Pattern Tests

Conditions allow you to qualify a pattern with an additional test that the matching element must pass for the match to succeed. This is a powerful construct because it extends the degree of control over the matching process to any criteria Mathematica can compute.

In[26]:=  Cases[{{0, 0, 0}, {0, 0, 1}, {0, 1, 0}, {0, 1, 1},
            {1, 0, 0}, {1, 0, 1}, {1, 1, 0}, {1, 1, 1}}, b__/; Total[b] >1]
Out[26]=  {{0, 1, 1}, {1, 0, 1}, {1, 1, 0}, {1, 1, 1}}

Pattern tests also qualify the match, but they apply to the entire pattern and, therefore, don’t require pattern variables. The following lists all primes less than 2⁵⁰ + 2 of the form 2ⁿ± 1.

In[27]:=  Cases[Union[Flatten[Table[{2^n - 1, 2^n + 1}, {n, 0, 50}]]], _?PrimeQ]
Out[27]=  {2, 3, 5, 7, 17, 31, 127, 257, 8191, 65 537, 131071, 524287, 2147483647}

In[28]:=  Cases[Union[Flatten[Table[{2^n - 1, 2^n + 1}, {n, 0, 50}]]],
           _?(#1 < 127 &)]
Out[28]=  {0, 1, 2, 3, 5, 7, 9, 15, 17, 31, 33, 63, 65}

Note

A common mistake is to write the last example in one of two ways that will not work:

In[29]:=  Cases[Union[Flatten[Table[{2^n - 1, 2^n + 1},
          {n, 0, 50}]]], _?(#1 < 127)&] (*wrong!*)
Out[29]=  {}
In[30]:=  Cases[Union[Flatten[Table[{2^n - 1, 2^n + 1},
          {n, 0, 50}]]], _?#1 < 127&]  (*wrong!*)
Out[30]=  {}

I still make this mistake from time to time, and it’s frustrating; pay attention to those parentheses!

Rules

Rules take pattern matching to a new level of expressiveness, allowing you to perform transformations on matched expressions. Rules are an integral part of Mathematica internal operations and are used in expressing solutions to equations (see 11.6 Solving Differential Equations), Options (see 2.17 Creating Functions That Accept Options), and SparseArrays (see 3.8 Using Sparse Arrays to Conserve Memory). Rules are also the foundation of Mathematica’s symbolic abilities. With all these applications, no serious user of Mathematica can afford to ignore them.

A good way to gain insight into the difference between -¿ and :-i is to consider replacements of a randomly generated number.

4.1 Collecting Items That Match (or Don’t Match) a Pattern

Problem

You have a list or other expression and want to find values that match a pattern. You may also want to transform the matching values as they are found.

Solution

Use Cases with a pattern to produce a list of expressions that match the pattern.

In[36]:=  list = {1, 1.2, "test", 3, {2}, x + 1};
          Cases[list, _Integer]
Out[37]=  {1, 3}

Use a rule to transform matches to other forms. Here the matched integers are squared to produce the result. This added capability of Cases is extremely powerful.

In[38]:=  Cases[list, x_Integer :> x^2]
Out[38]=  {1, 9}

Wrapping the pattern in Except gives the nonmatching values.

In[39]:=  Cases[{1, 1.2, "test", 3, {2}, x + 1}, Except[_Integer]]
Out[39]=  {1.2, test, {2}, 1 + x}

Note the use of colon syntax when capturing the value matched using Except with a rule-based transformation. Here I use a rule that demonstrates that the type of object produced does not need to be the same as the type that matched (i.e., all results here are symbols).

Discussion

Cases will work with any expression, not just lists. However, you need to keep in mind that Mathematica will rearrange the expression before the pattern is applied.

In[41]:=  Cases[x + y - z^2 + z^3 + x^5, _^_]
Out[41]=  {x⁵, z³}

You may have expected z^2 or -z^2 to be selected; examining the FullForm of the expression will reveal why it was not. FullForm is your friend when it comes to debugging pattern matching because that is the form that Mathematica sees.

   In[42]:=  x + y - z^2 + z^3 + x^5 // FullForm
Out[42]//FullForm=
             Plus[x, Power[x, 5], y, Times[-1, Power[z, 2]], Power[z, 3]]

Providing a level specification will allow you to reach down deeper. Level specifications are discussed in 3.9 Manipulating Deeply Nested Lists Using Functions with Level Specifications.

In[43]:=  Cases[x + y - z^2 + z^3 + x^5, _^_, 2]
Out[43]=  {x⁵, z², z³}

You can also limit the number of matches using an optional fourth argument.

In[44]:= Cases [x + y - z^2 + z^3 + x^5, _^_, 2, 1]
Out[44]= {x⁵}

Take into account the attributes Flat and Orderless when pattern matching. Flat means nested expressions like Plus[a,Plus[b,c]] will be flattened; Orderless means the operation is communicative, and Mathematica will account for this when pattern matching.

In[45]:= Attributes[Plus]
Out[45]= {Flat, Listable, NumericFunction, OneIdentity, Orderless, Protected}

Here we select every expression that contains b +, no matter its level or order in the input expression.

In[46]:= Cases[{a + b, a + c, b + a, a^2 + b, Plus[a, Plus[b, c]]}, b + _]
Out[46]= {a + b, a + b, a² + b, a + b + c}

Hold will suppress transformations due to Flat and Orderless, but the pattern itself is still reordered from b + a to a + b. In 4.8 Preventing Evaluation Until Replace Is Complete we show how to prevent this using HoldPattern.

In[47]:= Cases[Hold[a + b, a + c, b + a, a^2 + b, Plus[a, Plus[b, c]]], b + a]
Out[47]= {a + b}

An alternative to Cases is the combination of Position and Extract. Here Position locates the items, and Extract returns them. This variation would be more helpful than Cases, for example, if you needed to know the positions as well as the items, since Cases does not provide positional information. By default, Position will search every level, but you can restrict it with a levelspec as I do here.

In[48]:=  list = {1, 1.2, "test", 3, {2}, x +1};
          positions = Position[list, _Integer, {1}];
          Extract[list, positions]
Out[50]=  {1, 3}

One useful application of this idiom is matching on one list and extracting from a parallel list.

In[51]:=  names = {"Jane", "Jim", "Jeff", "Jessie", "Jezebel"};
          ages = {30, 20, 42, 16, 69} ;
          Extract[names, Position[ages, x_ /; x >30]]
Out[53]=  {Jeff, Jezebel}

4.2 Excluding Items That Match (or Don’t Match) a Pattern

Problem

You have a list or other expression and want to exclude elements that do not match a pattern.

Solution

DeleteCases has features similar to Cases but excludes elements that match.

In[54]:=  DeleteCases[{1, 1.2, "test", 3, {2}, x + 1}, _Integer]
Out[54]=  {1.2, test,{2}, 1 + x}

Wrapping the pattern in Except makes DeleteCases work like Cases for the noninverted pattern.

In[55]:=  DeleteCases[{1, 1.2, "test", 3, {2}, x + 1}, Except[_Integer]]
Out[55]=  {1, 3}

Cases and DeleteCases can be made to return the same result by using Except, but Cases should be used when you want to transform the items that remain (see 4.1 Collecting Items That Match (or Don’t Match) a Pattern).

In[56]:=  DeleteCases[{1, 1.2, "test", 3, {2}, x + 1}, Except[_Integer]]  =
            Cases[{1, 1.2, "test", 3, {2}, x + 1}, _Integer]
Out[56]=  True

Discussion

Most of the variations supported by Cases discussed in 4.1 Collecting Items That Match (or Don’t Match) a Pattern apply to DeleteCases as well. In fact, given the existence of Except, one could argue that DeleteCases is redundant. However, given the context of the problem, usually either Cases or DeleteCases will be easier to understand compared to using pattern inversions. Also, Except has some limitations since pattern variables like x_ can’t appear inside of an Except.

Use levelspecs to constrain deletions to particular portions of an expression tree. Here is an expression that is nine levels deep.

You can delete roots at level four.

You can also delete roots at levels up to four.

Or, you delete roots at every level.

Just as Extract plus Position is the equivalent of Cases (discussed in 4.1 Collecting Items That Match (or Don’t Match) a Pattern), Delete plus Position is the equivalent for DeleteCases. Again, remember that Position looks at all levels unless you restrict it.

This leads to a way to get the results of Cases and DeleteCases without executing the pattern match twice.

4.3 Counting Items That Match a Pattern

Problem

You need to know the number of expressions that match a pattern by matching the expressions themselves or their position.

Solution

Use Count to count matching elements in an expression or at particular levels in an expression. Counting literal matches is perhaps the simplest application of Count.

In[67]:= Count[{a, 1, a, 2, a, 3}, a]
Out[67]= 3

By default, Count works only on level one (levelspec {1}), but you can provide alternate levelspecs as a third argument.

In[68]:=  expr = 1 + 3 I + 4 + I x + x ^ 2 + y^{x^x};
          { Count[expr, x],
           Count[expr, x, Infinity]}
Out[69]=  {0, 4}

Count can be derived from Position or Cases, so these are handy if you need the matching items (or positions) in addition to the count.

In[70]:= Length[Cases[{a, 1, a, 2, a, 3}, a]]
Out[70]= 3

In[71]:= Length[Position[{a, 1, a, 2, a, 3}, a, {1}]]
Out[71]= 3

Discussion

Other counting functions include LeafCount and Tally. It is difficult to emulate LeafCount using Count because LeafCount treats complex numbers in their FullForm (e.g., Complex[1,1] has LeafCount == 3) but using FullForm on an expression does not provide the right answer.

You need to eliminate the complex numbers using ReplaceAll before performing the count, so LeafCount is rather unique.

Tally counts equivalent elements in a list using SameQ or a user-supplied equality test. It works only on lists, so you’ll need to convert expressions with other heads to List before using Tally. The output is a list of pairs showing the element and its count.

In[74]:= Tally[{a, x, a, x, a, a, b, y}]
Out[74]= {{a, 4}, {x , 2}, {b, 1}, {y, 1}}

In[75]:= Tally[Flatten@Apply[List, expr, {0, Infinity}]]
Out[75]= {{5 + 3 i, 1}, {i, 1}, {x , 4}, {2, 1}, {y, 1}}

Here is an example using a different equivalence relation (congruence module 7).

In[76]:=  Tally[Prime[Range[100]], Mod[#1, 7] == Mod[#2, 7] &]
Out[76]=  {{2, 18}, {3, 18}, {5, 18}, {7, 1}, {11, 14}, {13, 16}, {29, 15}}

4.4 Replacing Parts of an Expression

Problem

You want to transform the parts of an expression designated by an index.

Solution

Use ReplacePart, which can use indices or index patterns to limit the scope of a replacement.

Place an x at prime-numbered positions. Note that the position is being tested for primality, not for value.

In[79]:= ReplacePart[{a, b, c, d, e, f, g, h, i}, {i_?PrimeQ :> x}]
Out[79]= {a, x, x, d, x, f, x, h, i}

If you want access to the value as well, you can use the position to index into the list.

Discussion

On first encounter, you might think ReplacePart and part assignment are redundant.

In[81]:=  list1 = {1, 2, 3, 4, 5, 6};
          list1[[{1, 3}]]  = 99;
          list1
Out[83}=  {99, 2, 99, 4, 5, 6}

This seems similar to what is achieved using ReplacePart.

However, there are a multitude of differences. First, ReplacePart does not modify the list but creates a new list with modified values.

In[86]:= {list1, list2}
Out[86]= {{1, 2, 3, 4, 5, 6}, {99, 2, 99, 4, 5, 6}}

A related difference is that assignment is meaningful only to symbols, not expressions. In contrast, ReplacePart can use either as input.

Another important difference is that it is harmless to specify an index that does not match. ReplacePart simply returns a new list with the same content. Contrast this to part assignment, where you get an error.

Part assignment gains flexibility by supporting ranges and lists of position, whereas ReplacePart uses index patterns.

ReplacePart works on arbitrarily nested expressions, including matrices. Also note that the index patterns can be referenced on the right side of rules.

The following use case performs a transpose.

4.5 Finding the Longest (or Shortest) Match for a Pattern

Problem

A replacement rule is not working the way you think it should. In particular, it seems to work on only part of the expression. Often this is an indication that you need greedy matching provided by Longest.

Solution

By default, sequence patterns like a__ and a___ act as if they are surrounded by Shortest. This means they match as little as possible to still be consistent with the entire pattern. The following repeated replacement seems like it should shuffle items in the list until all equal values are adjacent. It almost works, but a 3 and a 1 stubbornly remain in place. This happens because on the final pass a__ matches nothing (which is shortest), b_ matches 1, c__ matches 1, b_ matches the third 1, and d___ matches the remainder. This results in a null transformation, so Replace-Repeated stops.

In[98]:=  {1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 8} //.
           {{a___, b_, c__, b_, d___}  -> {b , b, a, c, d}}
Out[98]=  {1, 1, 1, 3, 4, 3, 4, 2, 7, 1, 8}

Contrast this to the same transformation using Longest. Here we force a___ to greedily gobble up as many elements as it can and still keep the rest of the pattern matching.

In[99]:=  {1, 3, 1, 4, 1, 3, 4, 2, 7, 1, 8} //.
           {{Longest[a___], b_, c__, b_, d___}  -> {b , b, a, c, d}}
Out[99]=  {1, 1, 1, 1, 3, 3, 4, 4, 2, 7, 8}

Forcing a___ to match as much as it can and yet still satisfy the rest of the pattern results in all sequences of identical elements separated by one or more other elements (b_, c__ ,b_) to be found.

Discussion

Readers familiar with regular expression will recognize the solution example as illustrating the difference between greedy and nongreedy matching. This difference is the source of infinite frustration to pattern writers because, depending on your test case, nongreedy patterns can appear to work most of the time. Always consider what will happen if patterns like a__ match only one item and a__ matches nothing. Often this is what you want, but almost as often it is not!

A reasonable question to ask is why there is a Shortest if it is the default. For string patterns (see Chapter 5), the default is reversed. You may also use Shortest to document that it is your intent, but you should probably limit this to portions of the pattern that are up front.

Also keep in mind that if multiple Shortest or Longest directives are used, the ones that appear earlier are given higher priority to match the shortest or longest number of elements, respectively.

4.6 Implementing Algorithms in Terms of Rules

Problem

You need to implement an algorithm that can be viewed as a transformation from a start state to a goal state.

Solution

Many problems are elegantly stated in a few simple transformation rules. Here I show some simple examples; the discussion will try a few more ambitious tasks.

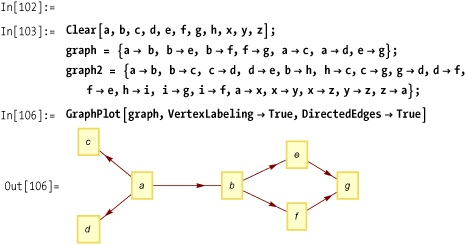
Imagine you have a graph of vertex-to-vertex connection rules. This is the notation used by GraphPlot and the functions in the GraphUtilities' package.

The idea in this solution is to find a path from the from node to some intermediate node x, and from x to some node y, and then add the path from→y if it does not already exist. Continue this until the graph no longer changes (hence FixedPoint). Then check if from→to is present using MemberQ.

You can test hasPath on the graph in Out[106] on See Also.

In[109]:= hasPath[graph, a, g]
Out[109]= True

In[110]:= hasPath[graph, b, d]
Out[110]= False

Here is an exhaustive test of the vertex c in the graph in Out[113].

Here is a related function to compute the transitive closure of a graph.

Here you compute the transitive closure of Out[113].

Out[115] is the plot of the transitive closure of the simpler graph from Out[106] on See Also.

Discussion

The hasPath and transitiveClosure functions share a common property. They are implemented by repeated transformation of the input until some goal state is achieved. The search terminates when there are no more available transformations, as determined by FixedPoint. TransitiveClosure uses the final state as the result, whereas hasPath makes one more match using MemberQ to see if the goal was reached.

Although rule-driven algorithms tend to be small, they are not always the most efficient. HasPath finds all paths from the start node before making a determination.

The hasPath2 implementation here uses Catch-Throw to exit as soon as the solution is found.

The main components of this solution are:

Localization: Module[ {rules, start, next, final}, .. ]
Rules: Enumeration of the rules with tests against next (graph2 plays the role of next in the examples). An optional Throw rule detects success for early termination.
Repetition: next = ReplaceAll[next, rules]
Stopping criteria: final = FixedPoint[ .. , start]. Assignment to final allows the result to undergo some post processing. In the examples, final was implicit. If a Throw rule is used, FixedPoint should be wrapped in a Catch.
Postprocessing: Extract results from final. Here MemberQ is used to test if the path was found.

If you have trouble following one of these solutions, Mathematica will show its work if you use FixedPointList. For example, here is the expansion of the steps in hasPath.

This shows each step in the transition from the original graph to the one with all intermediate steps filled in. Try to work out how the rule took each line to the next line. Only by working through examples like this will you begin to master the concepts.

4.7 Debugging Infinite Loops When Using ReplaceRepeated

Problem

Mathematica went into an infinite loop when you used //. (ReplaceRepeated), and the reason is not immediately obvious.

Solution

ReplaceRepeated is often very handy but also dangerous because it only terminates when the result stops changing. The simplest thing to do is to test ReplaceRepeated with the option MaxIterations set to a reasonably small value (the default is 65,536).

It should be clear that this will never terminate. Any transformation that adds structure is doomed. However, sometimes the end result obtained when clamping iterations does not immediately reveal the problem. In such cases, it helps to see the whole sequence of transformations. You can do that using NestList and ReplaceAll to emulate a ReplaceRepeated with a small number of iterations that return the result after each iteration.

Here the problem is an oscillating transformation that will never settle down. You could probably see that by inspection, but seeing each step makes it obvious.

Discussion

Sometimes applying the debugging techniques in the solution can still leave you stumped. Here is an example that one would expect to terminate based on the fact that NumberQ[Infinity] is false.

In situations like this, you should try applying FullForm to the output to see what Mathematica sees rather than what it shows you.

  In[126]:=  FullForm[%]
Out[126]//FullForm=
             List[F[DirectedInfinity[
                F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                      F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[F[
                              DirectedInfinity[F[DirectedInfinity[
                                 F[DirectedInfinity[1]]]]]]]]]]]]]]]]]]]],
             a, F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                    F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                           F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                                  F[DirectedInfinity[1]]]]]]]]]]]]]]]]]]]],
             b, F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                    F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                           F[DirectedInfinity[F[DirectedInfinity[F[DirectedInfinity[
                                  F[DirectedInfinity[1]]]]]]]]]]]]]]]]]]]], c]

Do you see the problem? It is near the end of the output. If you can’t see it, consider this.

  In[127]:=  FullForm[Infinity]
Out[127]//FullForm=
             DirectedInfinity[1]

The full form of Infinity contains the integer 1, which is being matched and replaced with F[DirectedInfinity[l]] and so on, ad infinitum. In this simple case, ReplaceRepeated was not needed because ReplaceAll would do the trick. If ReplaceRepeated is necessary, break the process into two steps, first using a proxy for the construct that has the hidden representation that is messing you up. Here I use Inf instead of Infinity.

4.8 Preventing Evaluation Until Replace Is Complete

Problem

You are trying to transform an expression, but the structure you want to transform is disappearing due to evaluation before you can transform it.

Solution

Use Hold and ReleaseHold with the replacement.

This does not work the way you probably intended.

This preserves the structure until the transformation is complete, then allows it to evaluate.

A related problem is wanting the left side of a replacement rule to remain unevaluated. In this case, you need to use HoldPattern.

This is equivalent to ReleaseHold[Hold[1 + 1 + 1 + 1 + 1] /. 4 :> 2 + 2 + 2 + 2].

In[131]:=  ReleaseHold[Hold[1 + 1 + 1 + 1 + 1] /. 1 + 1 + 1 + 1 :>  2 + 2 + 2 + 2 ]
Out[131]=  5

In[132]:=  (*This works as intended by preserving the structure of the pattern.*)
           ReleaseHold[
            Hold[1 + 1 + 1 + 1 + 1 ] /. HoldPattern[1 + 1 + 1 + 1]  : > 2 + 2 + 2 +2]
Out[132]=  9

Discussion

Keep in mind that HoldPattern[expr] differs from Hold[expr]. From a pattern-matching point of view, HoldPattern[expr] is equivalent to expr alone except it prevents evaluation. Hold[expr] includes the Hold as part of the pattern.

In[133]:=  GO = "gone";

In[134]:=  Hold[1 + 2 + 3] /. HoldPattern[1 + 2 + 3] :> GO
Out[134]=  Hold[GO]

In[135]:=  Hold[1 + 2 + 3] /. Hold[1 + 2 + 3] :> GO
Out[135]=  gone

4.9 Manipulating Patterns with Patterns

Problem

You need to transform a pattern expression using patterns.

Solution

Use Verbatim to allow a pattern to match another pattern. Here Verbatim tells Mathematica to treat the expression literally.

Here we want to split up a pattern variable into the name and the head it matches.

Discussion

The key to understanding the solution is to consider the FullForm of pattern variables.

In[138]:=  {FullForm[x_], FullForm[x__], FullForm[x___], FullForm[x_Integer]}
Out[138]=  {Pattern[x, Blank[]], Pattern[x, BlankSequence[]],
            Pattern[x, BlankNullSequence[]], Pattern[x, Blank[Integer]]}

Without Verbatim, the first example in the first part of the solution would go wrong.

The second part of the solution would fail because a pattern can’t have another pattern as its name.

Verbatim[expr] says “match expr exactly as it appears.” You will not use Verbatim often unless you find yourself writing Mathematica code to transform Mathematica code, as you might if you were writing a special interpreter or code to rewrite Mathematica code containing patterns in some other form.

4.10 Optimizing Rules

Problem

You have a large list of frequently used rules and want to speed up processing.

Solution

Use Dispatch to create a dispatch table and use that in place of the rules.

Discussion

If you do a lot of multiple-rule transformations, it is convenient to store all the rules in a single variable. This common practice makes maintenance of your code simpler since there is only a single definition to maintain for all rules. However, the penalty for doing this is that the performance of a replace decreases as the number of rules increases. This is because each rule must be scanned in turn, even if it ends up being inapplicable to a given transformation. Rule dispatch tables optimize rule dispatch so it is mostly independent of the number of rules.

To test this claim, I generate a list of 5,000 rules, called monsterRuleSet, and then optimize it to create monsterDispatch. The timing on the monsterRuleSet is very poor, whereas the dispatched version is lickety-split.

Peering into the implementation, you can see that the secret to Dispatch’s success is a hash table.

  In[148]:=  monsterDispatch[[2]] // Short
Out[148]//Short=
             {HashTable[1, 5000, 1, {{10, 2856}, {}, {3110, 3440}, {}, {1245}, <<4989>>,
              {3060}, {1008}, {912}, {879, 3696, 4165, 4971}, {545, 676, 4204}}]}

4.11 Using Patterns As a Query Language

Problem

You want to perform SQL-like queries on data stored in Mathematica.

Solution

Consider data of the sort one might encounter in a relational database but encoded in Mathematica form. This example is taken from the classic introduction to databases by C. J. Date.

In[149]:=  S = {
              supplier["S1" , "Smith", 20, "London"],
              supplier["S2", "Jones" , 10 , "Paris"],
              supplier["S3", "Blake" , 30 , "Paris"],
              supplier["S4", "Clark" , 20 , "London"],
              supplier["S5", "Adams" , 30 , "Athens"]
             };

           P = {
               part["P1", "Nut" , "Red", 12, "London"] ,
              part["P2" , "Bolt" , "Green", 17, "Paris"],
              part["P3" , "Screw", "Blue", 17, "Rome"],
              part["P4" , "Screw", "Red", 14, "London"],
              part["P5" , "Cam", "Blue", 12, "Paris"],
              part["P6" , "Cog", "Red" , 19, "London"]
             };
           INV = {
               inventory["S1" , "P1" , 300],
              inventory["S1" , "P2" , 200],
              inventory["S1" , "P3" , 400],
              inventory["S1" , "P4" , 200],
              inventory["S1" , "P5" , 100],
              inventory["S1" , "P6" , 100],
              inventory["S2" , "P1" , 300],
              inventory["S2" , "P2" , 400],
              inventory["S3" , "P2" , 200],
              inventory["S4" , "P2" , 200],
              inventory["S4" , "P4" , 300],
              inventory["S4" , "P5" , 400]
             };

Simple queries can be done using Cases alone.

In[152]:=  (*Find suppliers in Paris.*)
           Cases[S, supplier[_, _, _, "Paris"] ]
Out[152]=  {supplier[S2, Jones, 10, Paris], supplier[S3, Blake, 30, Paris]}

In[153]:=  (*Find suppliers in Paris with status greater than 10.*)
           Cases[S, supplier[_, _, status_/; status > 10, "Paris"]]
Out[153]=  {supplier[S3, Blake, 30, Paris]}

Queries involving joins can be implemented with the help of Outer.

Discussion

If the data you need to query resides in a database, it makes more sense to let that database do the query work before the data is imported into Mathematica. If this is not the case, Mathematica can easily do the job, even for rather sophisticated queries. Here are some simple examples with SQL equivalents.

Find all pairs of cities where a supplier in the first city has inventory on a part in the second city.

In this case, ReplaceRepeated can be used to implement GROUP BY. The idea is to continually search for pairs of items that match on the grouping criteria and combine them according to some aggregation method, in this case the sum of qty. Since each replacement removes an inventory item, we are guaranteed to terminate when all items are unique. A final ReplaceAll is used to extract the relevant information. The use of Null in the replacement rule is just for aesthetics, conveying that when you aggregate two inventory records you no longer have a valid record for a particular supplier.

Suppose you want the names of suppliers who have inventory in the part P1. This involves integrating information from S and INV. This can be done as a join, but in SQL it can also be done via a subquery. You can emulate that using rules. Here MemberQ implements the semantics of the SQL IN.

In the examples given, I have demonstrated queries for which the data is in relational form. One feature of relational form is that it is normalized so that each column can hold only atomic data. However, Mathematica is not a relational database, so data can appear in just about any form with any level of nesting. This is no problem because patterns are much more flexible than SQL. Still, I find it easier to put data in a tabular form before trying to extract information and relationships with other collections of data. Let’s consider an example that is more in the Mathematica domain.

GraphData and PolyhedronData are two extensive data sources that are bundled with Mathematica 6 and later versions. The relationship between these data sources is that each polyhedron has an associated graph. In PolyhedronData, the property that ties the two sources together is called SkeletonGraph. In database jargon, SkeletonGraph is a foreign key to GraphData, and thus, allows us to investigate relationships between polyhedra and their associated graphs. For this example, I want to consider all graphs that are both Eulerian and Hamiltonian with their associated polyhedron being Archimedean. (An Archimedean solid is a highly symmetric, semiregular, convex polyhedron composed of two or more types of regular polygons meeting in identical vertices.)

It’s often a good idea to see how many results you received.

There are exactly 4 cases out of 13 Archimedean polyhedra that meet the criteria of having both Eulerian and Hamiltonian graphs.

You might find more intuitive ways to solve this problem, but the solution given emphasizes pattern matching. You could also use Intersection with an appropriate SameTest, as shown here. The r @@@ serves only to put the result in the same form as we used previously and is not strictly needed.

In[165]:=  results = r @@@
              Intersection[Archimedean, Graphs, SameTest ->(#1[[3]] == #2[[1]] &)];

4.12 Semantic Pattern Matching

Problem

You want to work with patterns that reach beyond syntactic (structural) relationships to consider semantic relationships.

Solution

This solution is a simplified adaptation of concepts from “Sernantica: Semantic Pattern Matching in Mathematica” by Jason Harris, published in the Mathematica Journal, Volume 7, Issue 3, 1999.

Pattern matching in Mathematica is strictly structural. Consider the following function f.

In[166]:=  Clear[f]
           SetAttributes[f, HoldFirst];
           f[x_Integer^2]  := 1

Clearly, 3^2 matches the first version of the function. However, neither f[9] nor f[10] are in the correct form, so they fail to match, even though in the second case 9 == 3^2.

In[169]:=  {f[3^2], f[9], f[10]}]
Out[169]=  {1,f[9], f[10]}

All hope is not lost. By exploiting patterns, you can create a semantic match that uses Condition, which is commonly abbreviated as /;.

In[170]:=  Clear[f];
           SetAttributes[f, HoldFirst];
           f[x_ /; IntegerQ[x] && (Reduce[z^2 == x,{z}, Integers]  =!= False)] := 1

Now both the first and second cases match but not the last.

In[173]:= {f[3^2], f[9], f[10]}
Out[173]= {1, 1, f[10]}

Discussion

Mathematica deals with structural patterns simply because, in general, it is impossible to determine if two expressions are semantically equivalent. In the 1930s, Gödel, Turing, Church, and others performed the theoretical work that underlies this unfortunate truth. Still, there are many restricted cases for which semantic matching can succeed, as demonstrated in the solution.

4.13 Unification Pattern Matching

Problem

You want to emulate unification-based matching, à la Prolog.

Solution

Unification is more powerful than Mathematica pattern matching in that it allows pattern variables on both sides of the match. We can’t use normal pattern variables for this purpose, so we use the syntax $[var] to denote unification variable.

Test unify on various expressions:

Here you pass in a preexisting binding so the unification fails.

Chapter 4. Patterns and Rule-Based Programming

4.0 Introduction

Blanks

Alternatives

Repeats

PatternSequence

Except

Conditions and Pattern Tests

Note

Rules

See Also

4.1 Collecting Items That Match (or Don’t Match) a Pattern

Problem

Solution

Discussion

See Also

4.2 Excluding Items That Match (or Don’t Match) a Pattern

Problem

Solution

Discussion

4.3 Counting Items That Match a Pattern

Problem

Solution

Discussion

See Also

4.4 Replacing Parts of an Expression

Problem

Solution

Discussion

See Also

4.5 Finding the Longest (or Shortest) Match for a Pattern

Problem

Solution

Discussion

See Also

4.6 Implementing Algorithms in Terms of Rules

Problem

Solution

Discussion

See Also

4.7 Debugging Infinite Loops When Using ReplaceRepeated

Problem

Solution

Discussion

See Also

4.8 Preventing Evaluation Until Replace Is Complete

Problem

Solution

Discussion

See Also

4.9 Manipulating Patterns with Patterns

Problem

Solution

Discussion

See Also

4.10 Optimizing Rules

Problem

Solution

Discussion

4.11 Using Patterns As a Query Language

Problem

Solution

Discussion

See Also

4.12 Semantic Pattern Matching

Problem

Solution

Discussion

4.13 Unification Pattern Matching

Problem

Solution

Discussion

See Also

Don’t leave empty-handed

It’s yours, free.

Check it out now on O’Reilly