Linear Algebra with Applications, 10th Edition

1.6 Partitioned Matrices

Often it is useful to think of a matrix as being composed of a number of submatrices. A matrix C can be partitioned into smaller matrices by drawing horizontal lines between the rows and vertical lines between the columns. The smaller matrices are often referred to as blocks. For example, let

$$C=\left[\begin{array}{ccccc}1& \hfill -2& 4& \hfill 1& \hfill 3\\ 2& \hfill 1& 1& \hfill 1& \hfill 1\\ 3& \hfill 3& 2& \hfill -1& \hfill 2\\ 4& \hfill 6& 2& \hfill 2& \hfill 4\end{array}\right]$$

If lines are drawn between the second and third rows and between the third and fourth columns, then C will be divided into four submatrices, $C_{11}$, $C_{12}$, $C_{21}$, and $C_{22}$.

1.11-31 Full Alternative Text

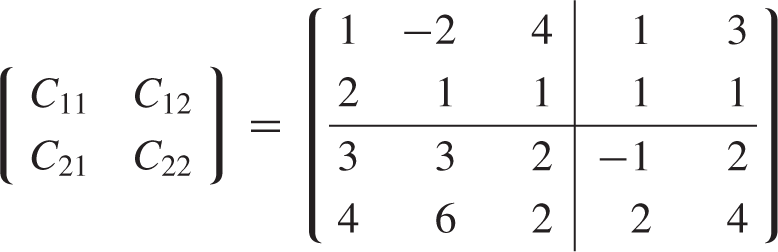
One useful way of partitioning a matrix is to partition it into columns. For example, if

$$B=\left[\begin{array}{ccc}\hfill -1& 2& 1\\ \hfill 2& 3& 1\\ \hfill 1& 4& 1\end{array}\right]$$