Chapter 1. Problem Solving

What Is an Algorithm?

Explaining how an algorithm works is like telling a story. Each algorithm introduces a novel concept or innovation that improves upon ordinary solutions. In this chapter I explore several solutions to a simple problem to explain the factors that affect an algorithm’s performance. Along the way I introduce techniques used to analyze an algorithm’s performance independent of its implementation, though I will always provide empirical evidence from actual implementations.

Note

An algorithm is a step-by-step problem-solving method implemented as a computer program that returns a correct result in a predictable amount of time. The study of algorithms is concerned with both correctness (will this algorithm work for all input?) and performance (is this the most efficient way to solve this problem?).

Let’s walk through an example of a problem-solving method to see what this looks like in practice. What if you wanted to find the largest value in an unordered list? Each Python list in Figure 1-1 is a problem instance, that is, the input processed by an algorithm (shown as a cylinder); the correct answer appears on the right. How is this algorithm implemented? How would it perform on different problem instances? Can you predict the time needed to find the largest value in a list of one million values?

Algorithm Processing
Figure 1-1. Three different problem instances processed by an algorithm

An algorithm is more than just a problem-solving method; the program also needs to complete in a predictable amount of time. The built-in Python function max() already solves this problem. Now, it can be hard to predict an algorithm’s performance on problem instances containing random data, so it’s worth identifying problem instances that are carefully constructed.

Table 1-1 shows the results of timing max() on two kinds of problem instances of size N: one where the list contains ascending integers and one where the list contains descending integers. While your execution may yield different results in the table, based on the configuration of your computing system, you can verify the following two statements:

  • The timing for max() on ascending values is always slower than on descending values once N is large enough.

  • As N increases ten-fold in subsequent rows, the corresponding time for max() also appears to increase ten-fold, with some deviation, as is to be expected from live performance trials.

For this problem, the maximum value is returned, and the input is unchanged. In some cases, the algorithm updates the problem instance directly instead of computing a new value—for example, sorting a list of values, as you will see in Chapter 5. In this book, N represents the size of a problem instance.

Table 1-1. Executing max() on two kinds of problem instances of size N (time in ms)
N Ascending values Descending values

100

0.001

0.001

1,000

0.013

0.013

10,000

0.135

0.125

100,000

1.367

1.276

1,000,000

14.278

13.419

When it comes to timing:

  • You can’t predict in advance the value of T(100,000)—that is, the time required by the algorithm to solve a problem instance of size 100,000—because computing platforms vary, and different programming languages may be used.

  • However, once you empirically determine T(10,000), you can predict T(100,000)—that is, the time to solve a problem instance ten times larger—though the prediction will inevitably be inaccurate to an extent.

When designing an algorithm, the primary challenge is to ensure it is correct and works for all input. I will spend more time in Chapter 2 explaining how to analyze and compare the behavior of different algorithms that solve the exact same problem. The field of algorithm analysis is tied to the study of interesting, relevant problems that arise in real life. While the mathematics of algorithms can be challenging to understand, I will provide specific examples to always connect the abstract concepts with real-world problems.

The standard way to judge the efficiency of an algorithm is to count how many computing operations it requires. But this is exceptionally hard to do! Computers have a central processing unit (CPU) that executes machine instructions that perform mathematical computations (like add and multiply), assign values to CPU registers, and compare two values with each other. Modern programming languages (like C or C++) are compiled into machine instructions. Other languages (like Python or Java) are compiled into an intermediate byte code representation. The Python interpreter (which is itself a C program) executes the byte code, while built-in functions, such as min() and max(), are implemented in C and ultimately compiled into machine instructions for execution.

It is nearly impossible to count the total number of executed machine instructions for an algorithm, not to mention that modern day CPUs can execute billions of instructions per second! Instead, I will count the number of times a key operation is invoked for each algorithm, which could be “the number of times two values in an array are compared with each other” or “how many times a function is called.” In this discussion of max(), the key operation is “how many times the less-than (<) operator is invoked.” I will expand on this counting principle in Chapter 2.

Now is a good time to lift up the hood on the max() algorithm to see why it behaves the way it does.

Finding the Largest Value in an Arbitrary List

Consider the flawed Python implementation in Listing 1-1 that attempts to find the largest value in an arbitrary list containing at least one value by comparing each value in A against my_max, updating my_max as needed when larger values are found.

Listing 1-1. Flawed implementation to locate largest value in list
def flawed(A):
  my_max = 0        1
  for v in A:       2
    if my_max < v:
      my_max = v    3
  return my_max
1

my_max is a variable that holds the maximum value; here my_max is initialized to 0.

2

The for loop defines a variable v that iterates over each element in A. The if statement executes once for each value, v.

3

Update my_max if v is larger.

Central to this solution is the less-than operator (<) that compares two numbers to determine whether a value is smaller than another. In Figure 1-2, as v takes on successive values from A, you can see that my_max is updated three times to determine the largest value in A. flawed() determines the largest value in A, invoking less-than six times, once for each of its values. On a problem instance of size N, flawed() invokes less-than N times.

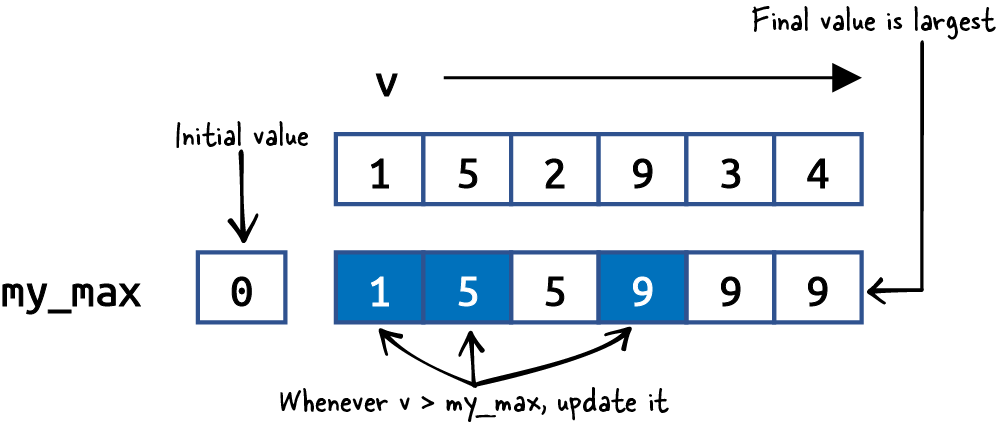
LargestVisualization
Figure 1-2. Visualizing the execution of flawed()

This implementation is flawed because it assumes that at least one value in A is greater than 0. Computing flawed([–5,–3,–11]) returns 0, which is incorrect. One common fix is to initialize my_max to the smallest possible value, such as my_max = float('-inf'). This approach is still flawed since it would return this value if A is the empty list []. Let’s fix this defect now.

Tip

The Python statement range(x,y) produces the integers from x up to, but not including, y. You can also request range(x,y,–1), which produces the integers from x counting down to, but not including, y. Thus list(range(1,7)) produces [1,2,3,4,5,6], and list(range(5,0,–1)) produces [5,4,3,2,1]. You can count by arbitrary increments, thus list(range(1,10,2)) produces [1,3,5,7,9] using a difference of 2 between values.

Counting Key Operations

Since the largest value must actually be contained in A, the correct largest() function in Listing 1-2 selects the first value of A as my_max, checking other values to see if any value is larger.

Listing 1-2. Correct function to find largest value in list
def largest(A):
  my_max = A[0]                 1
  for idx in range(1, len(A)):  2
    if my_max < A[idx]:
      my_max = A[idx]           3
  return my_max
1

Set my_max to the first value in A, found at index position 0.

2

idx takes on integer values from 1 up to, but not including, len(A).

3

Update my_max if the value in A at position idx is larger.

Warning

If you invoke largest() or max() with an empty list, it will raise a ValueError: list index out of range exception. These runtime exceptions are programmer errors, reflecting a failure to understand that largest() requires a list with at least one value.

Now that we have a correct Python implementation of our algorithm, can you determine how many times less-than is invoked in this new algorithm? Right! N – 1 times. We have fixed the flaw in the algorithm and improved its performance (admittedly, by just a tiny bit).

Why is it important to count the uses of less-than? This is the key operation used when comparing two values. All other program statements (such as for or while loops) are arbitrary choices during implementation, based on the program language used. We will expand on this idea in the next chapter, but for now counting key operations is sufficient.

Models Can Predict Algorithm Performance

What if someone shows you a different algorithm for this same problem? How would you determine which one to use? Consider the alternate() algorithm in Listing 1-3 that repeatedly checks each value in A to see if it is larger than or equal to all other values in the same list. Will this algorithm return the correct result? How many times does it invoke less-than on a problem of size N?

Listing 1-3. A different approach to locating largest value in A
def alternate(A):
  for v in A:
    v_is_largest = True        1
    for x in A:
      if v < x:
        v_is_largest = False   2
        break
    if v_is_largest:
      return v	               3
  return None                  4
1

When iterating over A, assume each value, v, could be the largest.

2

If v is smaller than another value, x, stop and record that v is not greatest.

3

If v_is_largest is true, return v since it is the maximum value in A.

4

If A is an empty list, return None.

alternate() attempts to find a value, v, in A such that no other value, x, in A is greater. The implementation uses two nested for loops. This time it’s not so simple to compute how many times less-than is invoked, because the inner for loop over x stops as soon as an x is found that is greater than v. Also, the outer for loop over v stops once the maximum value is found. Figure 1-3 visualizes executing alternate() on our list example.

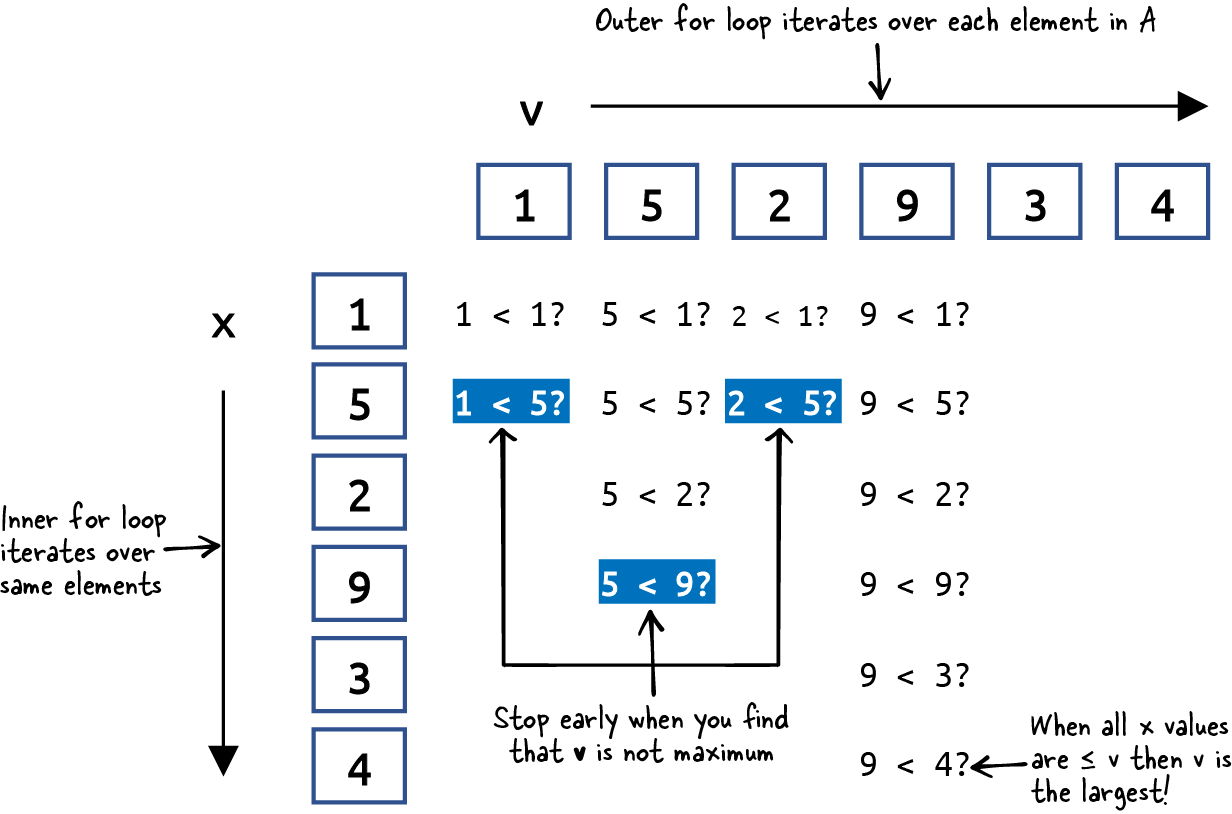
Alternate Visualization
Figure 1-3. Visualizing the execution of alternate()

For this problem instance, less-than is invoked 14 times. But you can see that this total count depends on the specific values in the list A. What if the values were in a different order? Can you think of an arrangement of values that requires the least number of less-than invocations? Such a problem instance would be considered a best case for alternate(). For example, if the first value in A is the largest of all N values, then the total number of calls to less-than is always N. To summarize:

Best case

A problem instance of size N that requires the least amount of work performed by an algorithm

Worst case

A problem instance of size N that demands the most amount of work

Let’s try to identify a worst case problem instance for alternate() that requires the most number of calls to less-than. More than just ensuring that the largest value is the last value in A, in a worst case problem instance for alternate(), the values in A must appear in ascending order.

Figure 1-4 visualizes a best case on the top where p = [9,5,2,1,3,4] and a worst case on the bottom where p = [1,2,3,4,5,9].

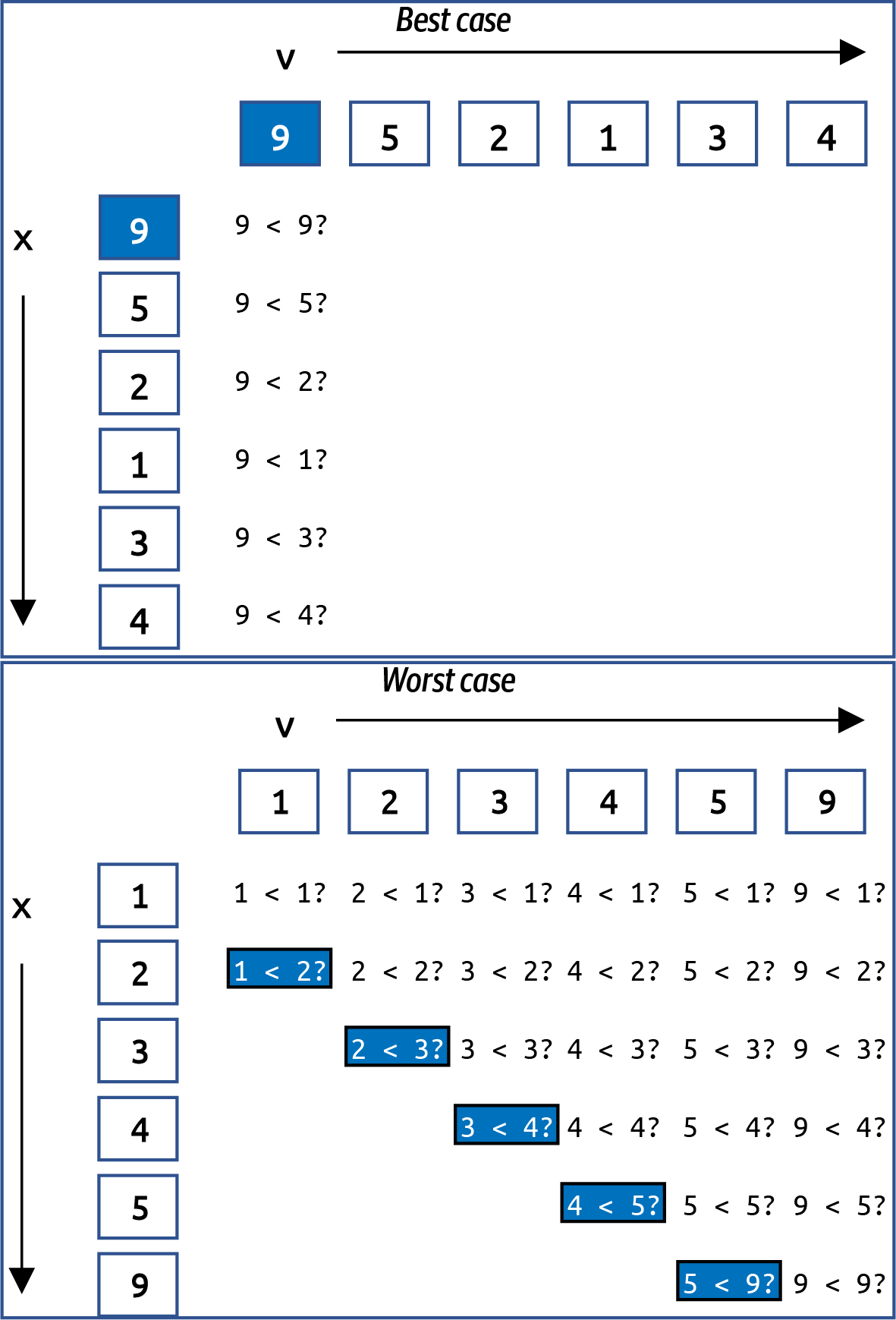
Best and Worst Case
Figure 1-4. Visualizing the execution of alternate() on best and worst cases

In the best case, there are six calls to less-than; if there were N values in a best case, then the total number of invocations to less-than would be N. It’s a bit more complicated for the worst case. In Figure 1-4 you can see there are a total of 26 calls to less-than when the list of N values is in ascending sorted order. With a little bit of mathematics, I can show that for N values, this count will always be (N2 + 3N – 2)/2.

Table 1-2 presents empirical evidence on largest() and alternate() on worst case problem instances of size N.

Table 1-2. Comparing largest() with alternate() on worst case problem instances
N Largest Alternate Largest Alternate
(# less-than) (# less-than) (time in ms) (time in ms)

8

7

43

0.001

0.001

16

15

151

0.001

0.003

32

31

559

0.002

0.011

64

63

2,143

0.003

0.040

128

127

8,383

0.006

0.153

256

255

33,151

0.012

0.599

512

511

131,839

0.026

2.381

1,024

1,023

525,823

0.053

9.512

2,048

2,047

2,100,223

0.108

38.161

For small problem instances, it doesn’t seem bad, but as the problem instances double in size, the number of less-than invocations for alternate() essentially quadruples, far surpassing the count for largest(). The next two columns in Table 1-2 show the performance of these two implementations on 100 random trials of problem instances of size N. The completion time for alternate() quadruples as well.

Note

I measure the time required by an algorithm to process random problem instances of size N. From this set of runs, I select the quickest completion time (i.e., the smallest). This is preferable to simply averaging the total running time over all runs, which might skew the results.

Throughout this book, I am going to present tables, like Table 1-2, containing the total number of executions of a key operation (here, the less-than operator) as well as the runtime performance. Each row will represent a different problem instance size, N. Read the table from top to bottom to see how the values in each column change as the problem instance size doubles.

Counting the number of less-than invocations explains the behaviors of largest() and alternate(). As N doubles, the number of calls to less-than doubles for largest() but quadruples for alternate(). This behavior is consistent and you can use this information to predict the runtime performance of these two algorithms on larger-sized problems. Figure 1-5 plots the count of less-than invocations by alternate() (using the y-axis on the left) against its runtime performance (using the y-axis on the right), showing how directly they correlate with each other.

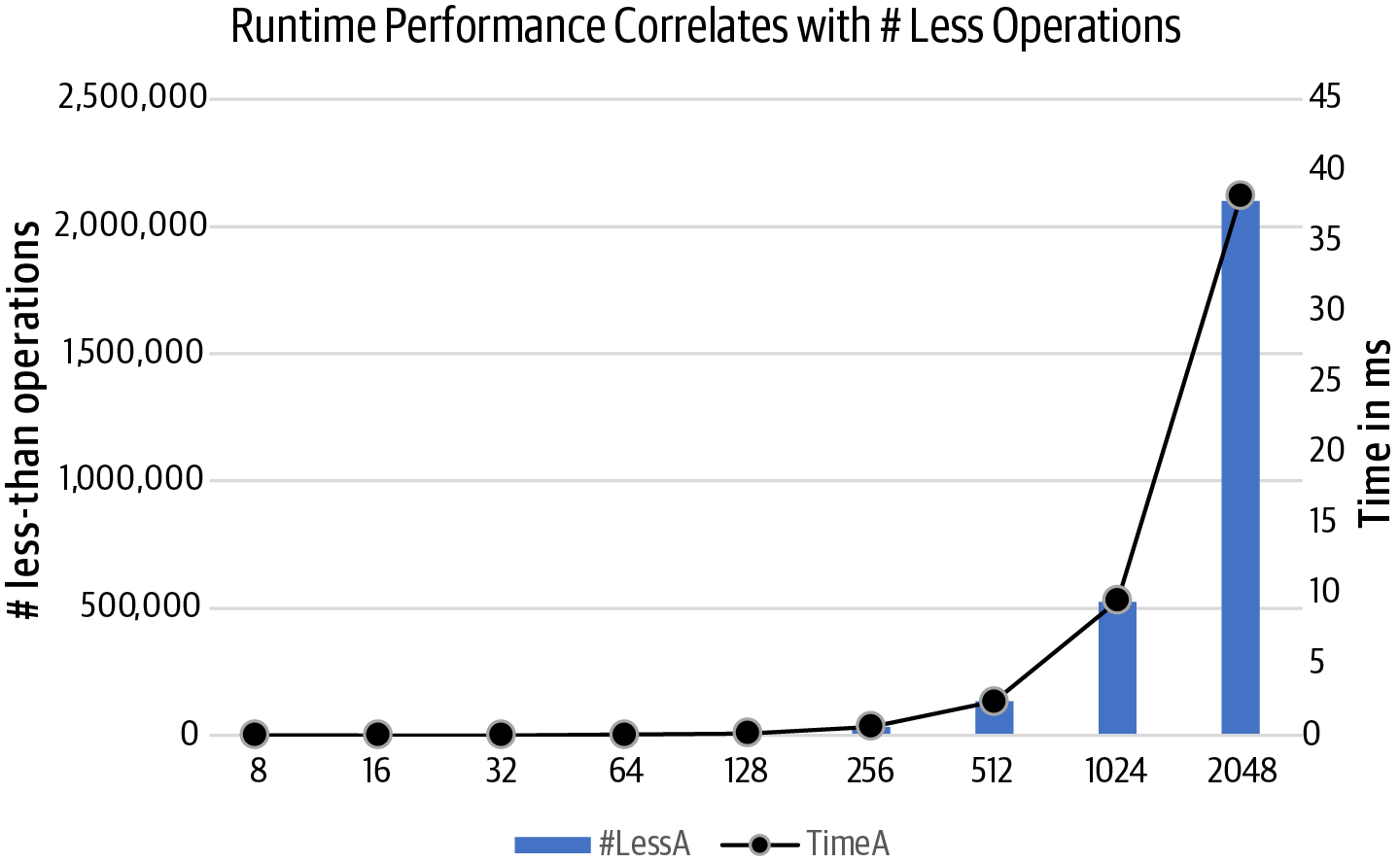
Tournament
Figure 1-5. Relationship between the number of less-than operations and runtime performance

Congratulations! You’ve just performed a key step in algorithmic analysis: judging the relative performance of two algorithms by counting the number of times a key operation is performed. You can certainly go and implement both variations (as I did) and measure their respective runtime performance on problem instances that double in size; but it actually isn’t necessary since the model predicts this behavior and confirms that largest() is the more efficient algorithm of the two.

largest() and max() are implementations of the same algorithm, but as Table 1-3 shows, largest() is always significantly slower than max(), typically four times slower. The reason is that Python is an interpreted language, which means it is compiled to an intermediate byte code that is executed by a Python interpreter. Built-in functions, such as max(), will always outperform Python code written for the same purpose because the built-in function is implemented within the interpreter. What you should observe is that in all cases, as N doubles, the corresponding performance of largest() and max()—for both best case and worst case—also doubles.

Table 1-3 shows it is possible to predict the time required to solve problem instances of increasing size. Once you know the runtime performance of largest() or max() on a best or worst case problem instance of size N, you can predict that the runtime performance will double as N doubles. Now let’s change the problem slightly to make it more interesting.

Table 1-3. Performance of largest() and max() on best and worst cases
N largest() worst case max() worst case largest() best case max() best case

4,096

0.20

0.05

0.14

0.05

8,192

0.40

0.11

0.29

0.10

16,384

0.80

0.21

0.57

0.19

32,768

1.60

0.41

1.14

0.39

65,536

3.21

0.85

2.28

0.78

131,072

6.46

1.73

4.59

1.59

262,144

13.06

3.50

9.32

3.24

524,288

26.17

7.00

18.74

6.50

Find Two Largest Values in an Arbitrary List

Devise an algorithm that finds the two largest values in an arbitrary list. Perhaps you can modify the existing largest() algorithm with just a few tweaks. Why don’t you take a stab at solving this modified problem and come back here with your solution? Listing 1-4 contains my solution.

Listing 1-4. Find two largest values by tweaking largest() approach
def largest_two(A):
  my_max,second = A[:2]                1
  if my_max < second:
    my_max,second = second,my_max

  for idx in range(2, len(A)):
    if my_max < A[idx]:                2
      my_max,second = A[idx],my_max
    elif second < A[idx]:              3
      second = A[idx]
  return (my_max, second)
1

Ensure my_max and second are the first two values from A in descending order.

2

If A[idx] is a newly found maximum value, then set my_max to A[idx], and second becomes the old my_max.

3

If A[idx] is larger than second (but smaller than my_max), only update second.

largest_two() feels similar to largest(): compute my_max and second to be the first two values in A, properly ordered. Then for each of the remaining values in A (how many? N – 2, right!), if you find an A[idx] larger than my_max, adjust both my_max and second, otherwise check to see whether only second needs updating.

Counting the number of times less-than is invoked is more complicated because, once again, it depends on the values in the problem instance.

largest_two() performs the fewest less-than invocations when the condition of the if statement inside the for loop is true. When A contains values in ascending order, this less-than is always true, so it is invoked N – 2 times; don’t forget to add 1 because of the use of less-than at the beginning of the function. In the best case, therefore, you only need N – 1 invocations of less-than to determine the top two values. The less-than in the elif condition is never used in the best case.

For largest_two(), can you construct a worst case problem instance? Try it yourself: it happens whenever the less-than in the if condition within the for loop is False.

I bet you can see that whenever A contains values in descending order, largest_two() requires the most invocations of less-than. In particular, for the worst case, less-than is used twice each time through the for loop, or 1 + 2 × (N – 2) = 2N – 3 times. Somehow this feels right, doesn’t it? If you need to use less-than N – 1 times to find the largest value in A, perhaps you truly do need an additional N – 2 less-than invocations (leaving out the largest value, of course) to also find the second-largest value.

To summarize the behavior of largest_two():

  • For best case, it finds both values with N – 1 less-than invocations.

  • For worst case, it finds both values with 2N – 3 less-than invocations.

Are we done? Is this the “best” algorithm to solve the problem of finding the two largest values in an arbitrary list? We can choose to prefer one algorithm over another based on a number of factors:

Required extra storage

Does an algorithm need to make a copy of the original problem instance?

Programming effort

How few lines of code must the programmer write?

Mutable input

Does the algorithm modify the input provided by the problem instance in place, or does it leave it alone?

Speed

Does an algorithm outperform the competition, independent of the provided input?

Let’s investigate three different algorithms to solve this exact same problem, shown in Listing 1-5. sorting_two() creates a new list containing the values in A in descending order, grabs the first two values, and returns them as a tuple. double_two() uses max() to find the maximum value in A, removes it from a copy of A, and then uses max() of that reduced list to find the second largest. mutable_two() finds the location of the largest value in A and removes it from A; then it sets second to the largest value remaining in A before reinserting the my_max value into its original location. The first two algorithms require extra storage, while the third modifies its input: all three only work on problem instances containing more than one value.

Listing 1-5. Three different approaches using Python utilities
def sorting_two(A):
  return tuple(sorted(A, reverse=True)[:2])    1

def double_two(A):
  my_max = max(A)                              2
  copy = list(A)
  copy.remove(my_max)                          3
  return (my_max, max(copy))                   4

def mutable_two(A):
  idx = max(range(len(A)), key=A.__getitem__)  5
  my_max = A[idx]                              6
  del A[idx]
  second = max(A)                              7
  A.insert(idx, my_max)                        8
  return (my_max, second)
1

Create a new list by sorting A in descending order and return its top two values.

2

Use built-in max() function to find largest.

3

Create a copy of the original A, and remove my_max.

4

Return a tuple containing my_max and the largest value in copy.

5

This Python trick finds the index location of the maximum value in A, rather than the value itself.

6

Record my_max value and delete it from A.

7

Now find max() of remaining values.

8

Restore A by inserting my_max to its original location.

These different approaches do not directly use less-than because they rely on existing Python libraries. Both sorting_two() and double_two() make a copy of the array, A, which seems unnecessary, since largest_two() doesn’t do this. In addition, it seems excessive to sort the entire list just to find the top two largest values. In the same way that I count operations when analyzing runtime performance, I will evaluate the extra storage used by an algorithm—for both of these approaches, the amount of storage is directly proportional to N. The third approach, mutable_two(), briefly updates A by deleting its maximum value, only to add it back later. The caller might be surprised to see that the original list was modified.

With a bit of Python expertise, I can compute exactly how many times less-than is invoked using a special RecordedItem class.1 Table 1-4 shows that double_two() invokes the most less-than operations when the values are in ascending order, while largest_two() (and others) perform the most less-than operations when the values are in descending order. In the last column, labeled “Alternating,” the 524,288 values are arranged with even numbers in ascending order, alternating with odd numbers in descending order: for N = 8, the input would be [0,7,2,5,4,3,6,1].

Table 1-4. Performance of different approaches on 524,288 ascending and descending values
Algorithm Ascending Descending Alternating

largest_two

524,287

1,048,573

1,048,573

sorting_two

524,287

524,287

2,948,953

double_two

1,572,860

1,048,573

1,048,573

mutable_two

1,048,573

1,048,573

1,048,573

tournament_two

524,305

524,305

524,305

The tournament_two() algorithm I describe next has the fewest number of less-than invocations regardless of input. Basketball fans will find its logic familiar.

Warning

If you determine the worst case problem instance for an algorithm that solves a given problem, perhaps a different algorithm solving the same problem would not be so negatively affected by that problem instance. Different algorithms can have different weaknesses that you can uncover with diligent analysis.

Tournament Algorithm

A single-elimination tournament consists of a number of teams competing to be the champion. Ideally, the number of teams is a power of 2, like 16 or 64. The tournament is built from a sequence of rounds where all remaining teams in the tournament are paired up to play a match; match losers are eliminated, while winners advance to the next round. The final team remaining is the tournament champion.

Consider the problem instance p = [3,1,4,1,5,9,2,6] with N = 8 values. Figure 1-6 shows the single-elimination tournament whose initial round compares eight neighboring values using less-than; larger values advance in the tournament.2 In the Elite Eight round, four values are eliminated, leaving values [3,4,9,6]. In the Final Four round, values [4,9] advance, and eventually 9 is declared the champion.

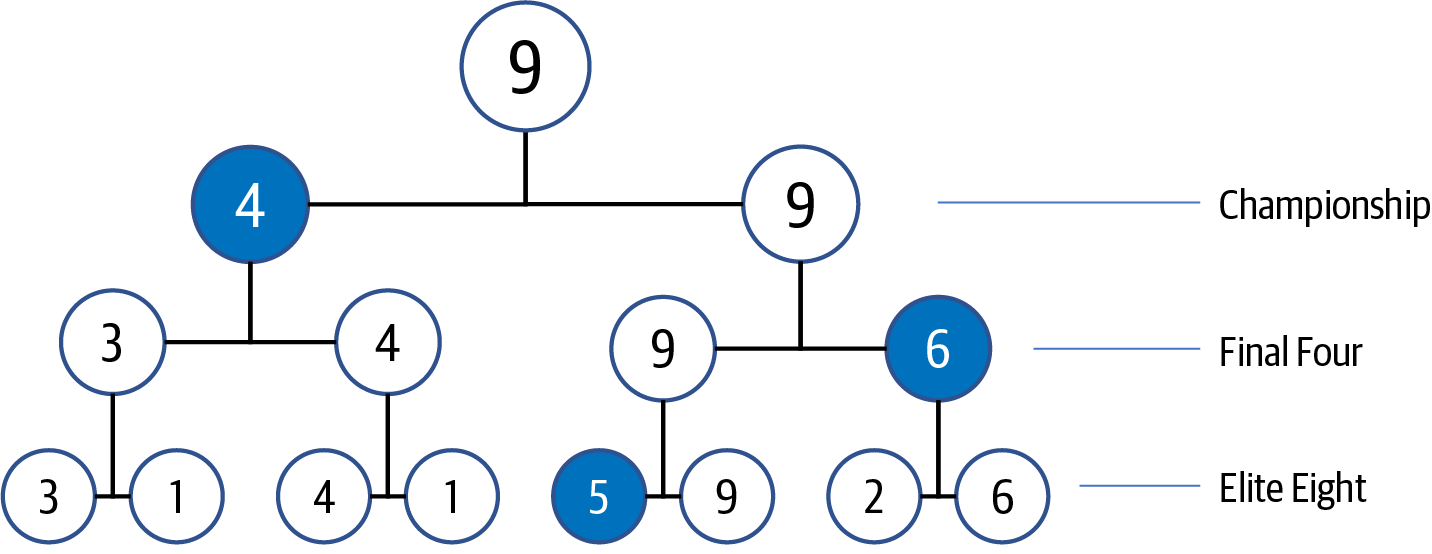
Tournament
Figure 1-6. A tournament with eight initial values

In this tournament, there are seven less-than invocations (i.e., one for each match), which should be reassuring, since this means the largest value is found with N – 1 uses of less-than, as we had discussed earlier. If you store each of these N – 1 matches, then you can quickly locate the second-largest value, as I now show.

Where can the second-largest value be “hiding” once 9 is declared the champion? Start with 4 as the candidate second-largest value, since this was the value that lost in the Championship round. But the largest value, 9, had two earlier matches, so you must check the other two losing values—value 6 in the Final Four round and value 5 in the Elite Eight round. Thus the second-largest value is 6.

For eight initial values, you need just 2 additional less-than invocations—(is 4 < 6?) and (is 6 < 5?)—to determine that 6 is the second-largest value. It’s no coincidence that 8 = 23 and you need 3 – 1 = 2 comparisons. It turns out that for N = 2K, you need an additional K – 1 comparisons, where K is the number of rounds.

When there are 8 = 23 initial values, the algorithm constructs a tournament with 3 rounds. Figure 1-7 visualizes a five-round tournament consisting of 32 values. To double the number of values in the tournament, you only need one additional round of matches; in other words, with each new round K, you can add 2K more values. Want to find the largest of 64 values? You only need 6 rounds since 26 = 64.

Hierarchy
Figure 1-7. A tournament with 32 initial values

To determine the number of rounds for any N, turn to the logarithm function, log(), which is the opposite of the exponent function. With N = 8 initial values, there are 3 rounds required for the tournament, since 23 = 8 and log2(8) = 3. In this book—and traditionally in computer science—the log() operator is in base 2.

Tip

Most handheld calculators compute log() in base 10. The function ln() represents the natural logarithm in base e (which is approximately 2.718). To quickly compute log(N) in base 2 using a calculator (or in Microsoft Excel), compute log(N)/log(2).

When N is a power of 2—like 64 or 65,536—the number of rounds in a tournament is log(N), which means the number of additional less-than invocations is log(N) – 1. The algorithm implemented in Listing 1-6 minimizes the invocations of less-than by using extra storage to record the results of all matches.

Listing 1-6. Algorithm to find two largest values in A using tournament
def tournament_two(A):
  N = len(A)
  winner = [None] * (N-1)          1
  loser = [None] * (N-1)
  prior = [-1] * (N-1)             2

  idx = 0
  for i in range(0, N, 2):         3
    if A[i] < A[i+1]:
      winner[idx] = A[i+1]
      loser[idx] = A[i]
    else:
      winner[idx] = A[i]
      loser[idx] = A[i+1]
    idx += 1

  m = 0                            4
  while idx < N-1:
    if winner[m] < winner[m+1]:    5
      winner[idx] = winner[m+1]
      loser[idx]  = winner[m]
      prior[idx]  = m+1
    else:
      winner[idx] = winner[m]
      loser[idx]  = winner[m+1]
      prior[idx]  = m
    m += 2                         6
    idx += 1

  largest = winner[m]
  second = loser[m]                7
  m = prior[m]
  while m >= 0:
    if second < loser[m]:          8
      second = loser[m]
    m = prior[m]

  return (largest, second)
1

These arrays store the winners and losers of match idx; there will be N – 1 of them in the tournament.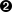

2

When a value advances in match m, prior[m] records earlier match, or –1 when it was initial match.

3

Initialize the first N/2 winner/loser pairs using N/2 invocations of less-than. These represent the matches in the lowest round.

4

Pair up winners to find a new winner, and record prior match index.

5

An additional N/2 – 1 invocations of less-than are needed.

6

Advance m by 2 to find next pair of winners. When idx reaches N – 1, winner[m] is largest.

7

Initial candidate for second largest, but must check all others that lost to largest to find actual second largest.

8

No more than log(N) – 1 additional invocations of less-than.

Figure 1-8 shows the execution of this algorithm. After the initialization step, the N values from the original array, A, are separated into N/2 winners and losers; in the example from Figure 1-6, there are four pairs. During each advance step in the while loop, the winner/loser of two consecutive matches, m and m+1, are placed in winner[idx] and loser[idx] respectively; prior[idx] records the prior match from which the winner came (as drawn by an arrow from right to left). After three steps, all match information is stored, and then the algorithm inspects the losers of all prior matches for the winner. You can visualize this by following the arrows backward until they stop. You can see that the candidate second-largest value is found in loser[6]: with just two less-than invocations with loser[5] and loser[2], it determines which one is largest.

I have just sketched an algorithm to compute the largest and second-largest value in A using just N – 1 + log(N) – 1 = N + log(N) – 2 less-than invocations for any N that is a power of 2. Is tournament_two() practical? Will it outperform largest_two()? If you only count the number of times less-than is invoked, tournament_two() should be faster. largest_two() requires 131,069 less-than operations on problems of size N = 65,536, while tournament_two() only requires 65,536 + 16 – 2 = 65,550, just about half. But there is more to this story.

Step by step execution
Figure 1-8. Step-by-step execution of tournament algorithm

Table 1-5 reveals that tournament_two() is significantly slower than any of its competitors! Let’s record the total time it takes to solve 100 random problem instances (of size N growing from 1,024 to 2,097,152). While I’m at it, I will include the performance results of the different algorithms from Listing 1-5. Note that if you run the sample code on your computer, your individual results will be different, but the overall trend in each column will remain the same.

Table 1-5. Comparing runtime performance (in ms) of all four algorithms
N double_two mutable_two largest_two sorting_two tournament_two

1,024

0.00

0.01

0.01

0.01

0.03

2,048

0.01

0.01

0.01

0.02

0.05

4,096

0.01

0.02

0.03

0.03

0.10

8,192

0.03

0.05

0.05

0.08

0.21

16,384

0.06

0.09

0.11

0.18

0.43

32,768

0.12

0.20

0.22

0.40

0.90

65,536

0.30

0.39

0.44

0.89

1.79

131,072

0.55

0.81

0.91

1.94

3.59

262,144

1.42

1.76

1.93

4.36

7.51

524,288

6.79

6.29

5.82

11.44

18.49

1,048,576

16.82

16.69

14.43

29.45

42.55

2,097,152

35.96

38.10

31.71

66.14

…

Table 1-5 can be overwhelming to look at, since it just looks like a wall of numbers. If you run these functions on a different computer—perhaps with less memory or a slower CPU—your results might be quite different; however, there are some trends that should reveal themselves no matter on what computer you execute. For the most part, as you read down any column, the time to execute more or less doubles as the problem size doubles.

There are some unexpected situations in this table: note that double_two() starts out being the fastest of the five solutions, but eventually (once N > 262,144), largest_two() becomes the fastest to complete. The clever tournament_two() approach is by far the slowest, simply because it needs to allocate ever-larger storage arrays to be processed. It is so slow, I do not even run it on the largest problem instance because it will take so long.

To make sense of these numbers, Figure 1-9 visualizes the runtime trends as the problem size instance grows ever larger.

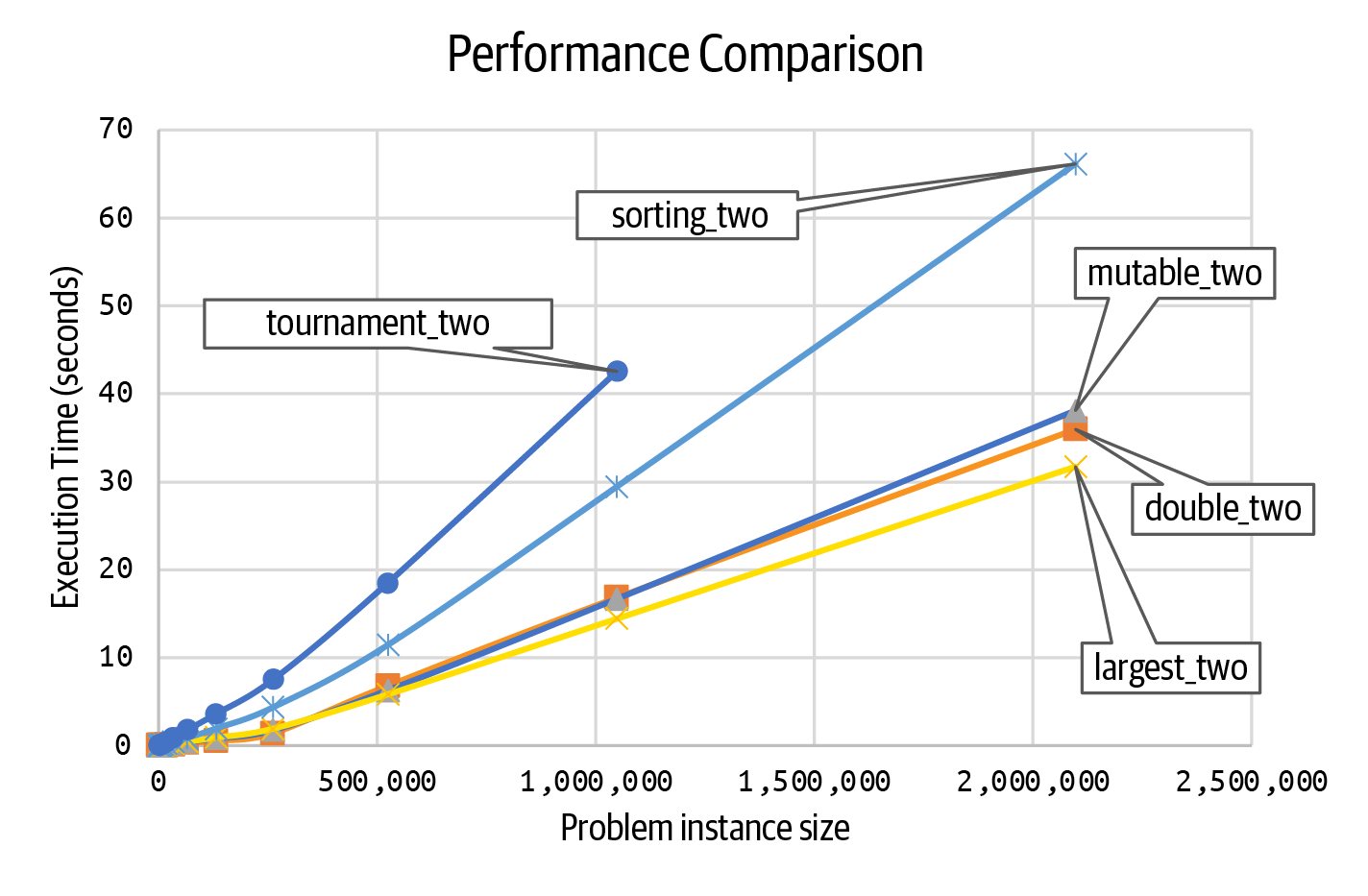
Hierarchy
Figure 1-9. Runtime performance comparison

This image reveals more details about the runtime performance of these five approaches:

  • You can see that the performances of mutable_two(), double_two(), and largest_two() are all more similar to each other than the other two approaches. It’s almost like they are all in the same “family,” all on a straight-line trajectory that appears quite predictable.

  • tournament_two() is the least efficient, and it noticeably behaves differently from the other approaches. Given that there are so few data points, it is not clear whether it is “curving upward” to greater inefficiencies or whether it also will follow a straight line.

  • sorting_two() appears to do better than tournament_two() but is slower than the other three approaches. Will it curve further upward, or eventually straighten out?

To understand why these lines are shaped the way they are, you need to learn the two fundamental concepts that explain the inherent complexity of an algorithm.

Time Complexity and Space Complexity

It can be hard to count the number of elementary operations (such as addition, variable assignment, or control logic), because of the difference in programming languages, plus the fact that some languages, such as Java and Python, are executed by an interpreter. But if you could count the total number of elementary operations executed by an algorithm, then you would see that the total number of operations varies based on the size of the problem instance. The goal of time complexity is to come up with a function C(N) that counts the number of elementary operations performed by an algorithm as a function of N, the size of a problem instance.

Assuming that each elementary operation takes a fixed amount of time, t, based on the CPU executing the operation, I can model the time to perform the algorithm as T(N) = t × C(N). Listing 1-7 confirms the insight that the structure of a program is critical. For functions f0, f1, f2, and f3, you can exactly compute how many times each one executes the operation ct = ct + 1 based on the input size, N. Table 1-6 contains the counts for a few values of N.

Listing 1-7. Four different functions with different performance profiles
def f0(N):      def f1(N):            def f2(N):             def f3(N):
  ct = 0          ct = 0                ct = 0                 ct = 0
  ct = ct + 1     for i in range(N):    for i in range(N):     for i in range(N):
  ct = ct + 1       ct = ct + 1           ct = ct + 1            for j in range(N):
  return ct       return ct               ct = ct + 1              ct = ct + 1
                                          ct = ct + 1          return ct
                                          ct = ct + 1
                                          ct = ct + 1
                                          ct = ct + 1
                                          ct = ct + 1
                                        return ct

The count for f0 is always the same, independent of N. The count for f2 is always seven times greater than f1, and both of them double in size as N doubles. In contrast, the count for f3 increases far more rapidly; as you have seen before, as N doubles, the count for f3(N) quadruples. Here, f1 and f2 are more similar to each other than they are to f3. In the next chapter, we will explain the importance of for loops and nested for loops when evaluating an algorithm’s performance.

Table 1-6. Counting operations in four different functions
N f0 f1 f2 f3

512

2

512

3,584

262,144

1,024

2

1,024

7,168

1,048,576

2,048

2

2,048

14,336

4,194,304

When evaluating an algorithm, we also have to consider space complexity, which accounts for extra memory required by an algorithm based on the size, N, of a problem instance. Memory is a generic term for data stored in the file system or the RAM of a computer. largest_two() has minimal space requirements: it uses two variables, my_max and second, and an iterator variable, idx. No matter the size of the problem instance, its extra space never changes. This means the space complexity is independent of the size of the problem instance, or constant; mutable_two() has similar behavior. In contrast, tournament_two() allocated three arrays—winner, loser, and prior—all of size N – 1. As N increases, the total extra storage increases in a manner that is directly proportional to the size of the problem instance.3 Building the tournament structure is going to slow tournament_two() down, when compared against largest_two(). Both double_two() and sorting_two() make a copy of the input, A, which means their storage usage is much more like tournament_two() than largest_two(). Throughout this book, I will evaluate both the time complexity and space complexity of each algorithm.

If you review Table 1-5, you can see that the timing results for the column largest_two more or less double in subsequent rows; columns double_two and mutable_two behave similarly, as I have already observed. This means that the total time appears to be directly proportional to the size of the problem instance, which is doubling in subsequent rows. This is an important observation, since these functions are more efficient than sorting_two(), which appears to follow a different, less-efficient trajectory. tournament_two() is still the least efficient, with a runtime performance that more than doubles, growing so rapidly that I don’t bother executing it for large problem instances.

As a computer scientist, I cannot just proclaim that the performance curves of largest_two() and mutable_two() “look the same.” I need to rely on a formal theory and notation to capture this idea. In the next chapter, I will present the mathematical tools necessary to analyze algorithm behavior properly.

Summary

This chapter provided an introduction to the rich and diverse field of algorithms. I showed how to model the performance of an algorithm on a problem instance of size N by counting the number of key operations it performs. You can also empirically evaluate the runtime performance of the implementation of an algorithm. In both cases, you can determine the order of growth of the algorithm as the problem instance size N doubles.

I introduced several key concepts, including:

  • Time complexity as estimated by counting the number of key operations executed by an algorithm on a problem instance of size N.

  • Space complexity as estimated by the amount of memory required when an algorithm executes on a problem instance of size N.

In the next chapter, I will introduce the mathematical tools of asymptotic analysis that will complete my explanation of the techniques needed to properly analyze algorithms.

Challenge Exercises

  1. Palindrome word detector: A palindrome word reads the same backward as forward, such as madam. Devise an algorithm that validates whether a word of N characters is a palindrome. Confirm empirically that it outperforms the two alternatives in Listing 1-8:

    Listing 1-8. Four different functions with different performance profiles
    def is_palindrome1(w):
  """Create slice with negative step and confirm equality with w."""
  return w[::-1] == w

def is_palindrome2(w):
  """Strip outermost characters if same, return false when mismatch."""
  while len(w) > 1:
    if w[0] != w[-1]:     # if mismatch, return False
      return False
    w = w[1:-1]           # strip characters on either end; repeat

  return True             # must have been palindrome

    Once you have this problem working, modify it to detect palindrome strings with spaces, punctuation, and mixed capitalization. For example, the following string should classify as a palindrome: "A man, a plan, a canal. Panama!"

  2. Linear time median: A wonderful algorithm exists that efficiently locates the median value in an arbitrary list (for simplicity, assume size of list is odd). Review the code in Listing 1-9 and count the number of times less-than is invoked, using RecordedItem values as shown in the chapter. This implementation rearranges the arbitrary list as it processes.

    Listing 1-9. A linear-time algorithm to compute the median value in an unordered list
    def partition(A, lo, hi, idx):
  """Partition using A[idx] as value."""
  if lo == hi: return lo

  A[idx],A[lo] = A[lo],A[idx]    # swap into position
  i = lo
  j = hi + 1
  while True:
    while True:
      i += 1
      if i == hi: break
      if A[lo] < A[i]: break

    while True:
      j -= 1
      if j == lo: break
      if A[j] < A[lo]: break

    if i >= j: break
    A[i],A[j] = A[j],A[i]

  A[lo],A[j] = A[j],A[lo]
  return j

def linear_median(A):
  """
  Efficient implementation that returns median value in arbitrary list,
  assuming A has an odd number of values. Note this algorithm will
  rearrange values in A.
  """
  lo = 0
  hi = len(A) - 1
  mid = hi // 2
  while lo < hi:
    idx = random.randint(lo, hi)     # select valid index randomly
    j = partition(A, lo, hi, idx)

    if j == mid:
      return A[j]
    if j < mid:
      lo = j+1
    else:
      hi = j-1
  return A[lo]

    Implement a different approach (which requires extra storage) that creates a sorted list from the input and selects the middle value. Compare its runtime performance with linear_median() by generating a table of runtime performance.

  3. Counting Sort: If you know that an arbitrary list, A, only contains nonnegative integers from 0 to M, then the following algorithm will properly sort A using just an extra storage of size M.

    Listing 1-10 has nested loops—a for loop within a while loop. However, you can demonstrate that A[pos+idx] = v only executes N times.

    Listing 1-10. A linear-time Counting Sort algorithm
    def counting_sort(A, M):
  counts = [0] * M
  for v in A:
    counts[v] += 1

  pos = 0
  v = 0
  while pos < len(A):
    for idx in range(counts[v]):
      A[pos+idx] = v
    pos += counts[v]
    v += 1

    Conduct a performance analysis to demonstrate that the time to sort N integers in the range from 0 to M doubles as the size of N doubles.

    You can eliminate the inner for loop, and improve the performance of this operation, using the ability in Python to replace a sublist using sublist[left:right] = [2,3,4]. Make the change and empirically validate that it, too, doubles as N doubles, while yielding a 30% improvement in speed.

  4. Modify tournament algorithm to work with an odd number of values.

  5. Will the code in Listing 1-11 correctly locate the two largest values in A?

    Listing 1-11. Another attempt to try to compute two largest values in unordered list
    def two_largest_attempt(A):
  m1 = max(A[:len(A)//2])
  m2 = max(A[len(A)//2:])
  if m1 < m2:
    return (m2, m1)
  return (m1, m2)

    Explain the circumstances when this code works correctly and when it fails.

1 The RecordedItem wrapper class overrides the __lt__() less-than operator to count whenever it (or the __gt__() greater-than operator) is invoked.

2 If a match contains two equal values, then only one of these values advances.

3 That is, storage in addition to the data encoding the problem instance, which is not counted as part of the space complexity of any algorithm.

Get Learning Algorithms now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial