Capítulo 4. Representación de datos y características de ingeniería
Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: translation-feedback@oreilly.com
Hasta ahora, hemos supuesto que nuestros datos llegan como una matriz bidimensional de números en coma flotante, donde cada columna es una característica continua que describe los puntos de datos. En muchas aplicaciones, no es así como se recogen los datos. Un tipo de característica especialmente común son las características categóricas. También conocidas como características discretas, no suelen ser numéricas. La distinción entre características categóricas y características continuas es análoga a la distinción entre clasificación y regresión, sólo que en el lado de la entrada y no en el de la salida. Ejemplos de características continuas que hemos visto son el brillo de los píxeles y las medidas del tamaño de las flores de las plantas. Ejemplos de características categóricas son la marca de un producto, el color de un producto o el departamento (libros, ropa, ferretería) en el que se vende. Todas ellas son propiedades que pueden describir un producto, pero no varían de forma continua. Un producto pertenece al departamento de ropa o al de libros. No hay un término medio entre los libros y la ropa, ni un orden natural para las distintas categorías (los libros no son mayores ni menores que la ropa, la ferretería no está entre los libros y la ropa, etc.).
Independientemente de los tipos de características de que consten tus datos, la forma de representarlos puede tener un efecto enorme en el rendimiento de los modelos de aprendizaje automático. En los Capítulos 2 y 3 vimos que el escalado de los datos es importante. En otras palabras, si no reescalas tus datos (digamos, a la varianza unitaria), entonces es diferente si representas una medida en centímetros o en pulgadas. También vimos en el Capítulo 2 que puede ser útil aumentar tus datos con características adicionales, como añadir interacciones (productos) de características o polinomios más generales.
La cuestión de cómo representar mejor tus datos para una aplicación concreta se conoce como ingeniería de características, y es una de las principales tareas de los científicos de datos y los profesionales del aprendizaje automático que intentan resolver problemas del mundo real. Representar tus datos de la forma adecuada puede influir más en el rendimiento de un modelo supervisado que los parámetros exactos que elijas.
En este capítulo, primero repasaremos el importante y muy común caso de los rasgos categóricos, y luego daremos algunos ejemplos de transformaciones útiles para combinaciones específicas de rasgos y modelos.
4.1 Variables categóricas
Como ejemplo, utilizaremos el conjunto de datos de los ingresos de los adultos en Estados Unidos, derivados de la base de datos del censo de 1994. La tarea del conjunto de datos adultes predecir si un trabajador tiene unos ingresos superiores a 50.000 $ o inferiores a 50.000 $. Las características de este conjunto de datos incluyen la edad de los trabajadores, su forma de empleo (autónomo, empleado de la industria privada, empleado del gobierno, etc.), su educación, su sexo, sus horas de trabajo a la semana, su ocupación, etc. La Tabla 4-1 muestra las primeras entradas del conjunto de datos.
| edad | clase obrera | educación | género | horas a la semana | ocupación | ingresos | |
|---|---|---|---|---|---|---|---|
0 |
39 |
Gobierno estatal |
Licenciados |
Hombre |
40 |
Adm-clerical |
<=50K |
1 |
50 |
Self-emp-not-inc |
Licenciados |
Hombre |
13 |
Dirección ejecutiva |
<=50K |
2 |
38 |
Privado |
HS-grad |
Hombre |
40 |
Manipuladores-limpiadores |
<=50K |
3 |
53 |
Privado |
Undécimo |
Hombre |
40 |
Manipuladores-limpiadores |
<=50K |
4 |
28 |
Privado |
Licenciados |
Mujer |
40 |
Prof-especialidad |
<=50K |
5 |
37 |
Privado |
Maestros |
Mujer |
40 |
Dirección ejecutiva |
<=50K |
6 |
49 |
Privado |
Noveno |
Mujer |
16 |
Otros servicios |
<=50K |
7 |
52 |
Self-emp-not-inc |
HS-grad |
Hombre |
45 |
Dirección ejecutiva |
>50K |
8 |
31 |
Privado |
Maestros |
Mujer |
50 |
Prof-especialidad |
>50K |
9 |
42 |
Privado |
Licenciados |
Hombre |
40 |
Dirección ejecutiva |
>50K |
10 |
37 |
Privado |
Alguna universidad |
Hombre |
80 |
Dirección ejecutiva |
>50K |
La tarea se plantea como una tarea de clasificación con las dos clases de ingresos <=50k y >50k. También sería posible predecir los ingresos exactos, y hacer de esto una tarea de regresión. Sin embargo, eso sería mucho más difícil, y la división 50K es interesante de entender por sí misma.
En este conjunto de datos, age y hours-per-week son características continuas, que sabemos cómo tratar. Sin embargo, las características workclass, education, sex yoccupation son categóricas. Todas ellas proceden de una lista fija de valores posibles, en lugar de un intervalo, y denotan una propiedad cualitativa, en lugar de una cantidad.
Como punto de partida, digamos que queremos aprender un clasificador de regresión logística sobre estos datos. Sabemos por el Capítulo 2 que una regresión logística hace predicciones, ŷ, utilizando la siguiente fórmula:
- ŷ = w[0] * x[0] + w[1] * x[1] + ... + w[p] * x[p] + b > 0
donde w[i] y b son coeficientes aprendidos del conjunto de entrenamiento yx[i] son las características de entrada. Esta fórmula tiene sentido cuando x[i] son números, pero no cuando x[2] es "Masters" o "Bachelors". Está claro que tenemos que representar nuestros datos de alguna forma diferente al aplicar la regresión logística. En la siguiente sección explicaremos cómo podemos superar este problema.
4.1.1 Codificación en caliente (variables ficticias)
Con mucho, la forma más habitual de representar variables categóricas es utilizar la codificación de un punto o de uno fuera de N, también conocidas como variables ficticias. La idea que subyace a las variables ficticias es sustituir una variable categórica por una o más características nuevas que pueden tener los valores 0 y 1. Los valores 0 y 1 tienen sentido en la fórmula de la clasificación binaria lineal (y para todos los demás modelos en scikit-learn), y podemos representar cualquier número de categorías introduciendo una característica nueva por categoría, como se describe aquí.
Digamos que para la característica workclass tenemos los valores posibles "Government Employee", "Private Employee","Self Employed", y "Self Employed Incorporated". Para codificar estos cuatro valores posibles, creamos cuatro características nuevas, llamadas"Government Employee", "Private Employee", "Self Employed", y"Self Employed Incorporated". Una característica es 1 si workclass para esta persona tiene el valor correspondiente y 0 en caso contrario, por lo que exactamente una de las cuatro nuevas características será 1 para cada punto de datos. Por eso se denomina codificación de un punto o de uno fuera de N.
El principio se ilustra en la Tabla 4-2. Una única característica se codifica utilizando cuatro características nuevas. Al utilizar estos datos en un algoritmo de aprendizaje automático, eliminaríamos la característica original workclass y sólo conservaríamos las características 0-1.
| clase obrera | Empleado público | Empleado privado | Autónomo | Autónomo Incorporado |
|---|---|---|---|---|
Empleado público |
1 |
0 |
0 |
0 |
Empleado privado |
0 |
1 |
0 |
0 |
Autónomo |
0 |
0 |
1 |
0 |
Autónomo Incorporado |
0 |
0 |
0 |
1 |
Nota
La codificación binaria que utilizamos es bastante similar, aunque no idéntica, a la codificación binaria utilizada en estadística. Para simplificar, codificamos cada categoría con una característica binaria diferente. En estadística, es habitual codificar un rasgo categórico con k valores posibles diferentes en k-1rasgos (el último se representa como todos ceros). Esto se hace para simplificar el análisis (más técnicamente, así se evita que la matriz de datos sea deficiente en cuanto al rango).
Hay dos formas de convertir tus datos en una codificación de variables categóricas, utilizando pandas o scikit-learn. Veamos cómo podemos hacerlo utilizando pandas. Empezaremos cargando los datos utilizando pandas desde un archivo de valores separados por comas (CSV):
In[1]:
importos# The file has no headers naming the columns, so we pass header=None# and provide the column names explicitly in "names"adult_path=os.path.join(mglearn.datasets.DATA_PATH,"adult.data")data=pd.read_csv(adult_path,header=None,index_col=False,names=['age','workclass','fnlwgt','education','education-num','marital-status','occupation','relationship','race','gender','capital-gain','capital-loss','hours-per-week','native-country','income'])# For illustration purposes, we only select some of the columnsdata=data[['age','workclass','education','gender','hours-per-week','occupation','income']]# IPython.display allows nice output formatting within the Jupyter notebookdisplay(data.head())
La Tabla 4-3 muestra el resultado.
| edad | clase obrera | educación | género | horas a la semana | ocupación | ingresos | |
|---|---|---|---|---|---|---|---|
0 |
39 |
Gobierno estatal |
Licenciados |
Hombre |
40 |
Adm-clerical |
<=50K |
1 |
50 |
Self-emp-not-inc |
Licenciados |
Hombre |
13 |
Dirección ejecutiva |
<=50K |
2 |
38 |
Privado |
HS-grad |
Hombre |
40 |
Manipuladores-limpiadores |
<=50K |
3 |
53 |
Privado |
Undécimo |
Hombre |
40 |
Manipuladores-limpiadores |
<=50K |
4 |
28 |
Privado |
Licenciados |
Mujer |
40 |
Prof-especialidad |
<=50K |
Comprobación de datos categóricos codificados en cadena
Después de leer un conjunto de datos como éste, a menudo es bueno comprobar primero si una columna contiene realmente datos categóricos significativos. Cuando se trabaja con datos introducidos por humanos (por ejemplo, usuarios de un sitio web), puede que no haya un conjunto fijo de categorías, y las diferencias de ortografía y mayúsculas pueden requerir un preprocesamiento. Por ejemplo, puede ocurrir que algunas personas hayan especificado el género como "hombre" y otras como "hombre", y queramos representar estas dos entradas utilizando la misma categoría. Una buena forma de comprobar el contenido de una columna es utilizar el método value_countsde un pandas Series (el tipo de una sola columna en unDataFrame), para que nos muestre cuáles son los valores únicos y con qué frecuencia aparecen:
In[2]:
(data.gender.value_counts())
Out[2]:
Male 21790 Female 10771 Name: gender, dtype: int64
Podemos ver que hay exactamente dos valores para el género en este conjunto de datos, Male y Female, lo que significa que los datos ya tienen un buen formato para ser representados utilizando la codificación de un solo golpe. En una aplicación real, deberías mirar todas las columnas y comprobar sus valores. Nos saltaremos esto aquí en aras de la brevedad.
Hay una forma muy sencilla de codificar los datos en pandas, utilizando la funciónget_dummies. La función get_dummies transforma automáticamente todas las columnas que tienen tipo objeto (como las cadenas) o son categóricas (que es un concepto especial de pandas del que aún no hemos hablado):
In[3]:
("Original features:\n",list(data.columns),"\n")data_dummies=pd.get_dummies(data)("Features after get_dummies:\n",list(data_dummies.columns))
Out[3]:
Original features: ['age', 'workclass', 'education', 'gender', 'hours-per-week', 'occupation', 'income'] Features after get_dummies: ['age', 'hours-per-week', 'workclass_ ?', 'workclass_ Federal-gov', 'workclass_ Local-gov', 'workclass_ Never-worked', 'workclass_ Private', 'workclass_ Self-emp-inc', 'workclass_ Self-emp-not-inc', 'workclass_ State-gov', 'workclass_ Without-pay', 'education_ 10th', 'education_ 11th', 'education_ 12th', 'education_ 1st-4th', ... 'education_ Preschool', 'education_ Prof-school', 'education_ Some-college', 'gender_ Female', 'gender_ Male', 'occupation_ ?', 'occupation_ Adm-clerical', 'occupation_ Armed-Forces', 'occupation_ Craft-repair', 'occupation_ Exec-managerial', 'occupation_ Farming-fishing', 'occupation_ Handlers-cleaners', ... 'occupation_ Tech-support', 'occupation_ Transport-moving', 'income_ <=50K', 'income_ >50K']
Puedes ver que las características continuas age y hours-per-week no se tocaron, mientras que las características categóricas se ampliaron en una nueva característica para cada valor posible:
In[4]:
data_dummies.head()
Out[4]:
| edad | horas a la semana | ¿clase de trabajo_ ? | clase trabajadora_gobierno_federal | clase_de_trabajo_gobierno_local | ... | ocupación_ Soporte técnico | ocupación_ Transporte-mudanzas | ingresos_ <=50K | ingresos_ >50K | |
|---|---|---|---|---|---|---|---|---|---|---|
0 |
39 |
40 |
0.0 |
0.0 |
0.0 |
... |
0.0 |
0.0 |
1.0 |
0.0 |
1 |
50 |
13 |
0.0 |
0.0 |
0.0 |
... |
0.0 |
0.0 |
1.0 |
0.0 |
2 |
38 |
40 |
0.0 |
0.0 |
0.0 |
... |
0.0 |
0.0 |
1.0 |
0.0 |
3 |
53 |
40 |
0.0 |
0.0 |
0.0 |
... |
0.0 |
0.0 |
1.0 |
0.0 |
4 |
28 |
40 |
0.0 |
0.0 |
0.0 |
... |
0.0 |
0.0 |
1.0 |
0.0 |
5 rows × 46 columns
Ahora podemos utilizar el atributo values para convertir la data_dummiesDataFrame en una matriz NumPy, y luego entrenar un modelo de aprendizaje automático con ella. Ten cuidado de separar la variable de salida (que ahora está codificada en dos columnas income ) de los datos antes de entrenar un modelo. Incluir la variable de salida, o alguna propiedad derivada de la variable de salida, en la representación de características es un error muy común en la construcción de modelos supervisados de aprendizaje automático.
Advertencia
Ten cuidado: la indexación de columnas en pandas incluye el final del rango, por lo que 'age':'occupation_ Transport-moving' incluyeoccupation_ Transport-moving. Esto es diferente del corte de una matriz NumPy, donde no se incluye el final de un rango: por ejemplo,np.arange(11)[0:10] no incluye la entrada con índice 10.
En este caso, extraemos sólo las columnas que contienen rasgos, es decir, todas las columnas de age a occupation_ Transport-moving. Este rango contiene todos los rasgos, pero no el objetivo:
In[5]:
features=data_dummies.loc[:,'age':'occupation_ Transport-moving']# Extract NumPy arraysX=features.valuesy=data_dummies['income_ >50K'].values("X.shape: {} y.shape: {}".format(X.shape,y.shape))
Out[5]:
X.shape: (32561, 44) y.shape: (32561,)
Ahora los datos están representados de forma que scikit-learn pueda trabajar con ellos, y podemos proceder como de costumbre:
In[6]:
fromsklearn.linear_modelimportLogisticRegressionfromsklearn.model_selectionimporttrain_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)logreg=LogisticRegression()logreg.fit(X_train,y_train)("Test score: {:.2f}".format(logreg.score(X_test,y_test)))
Out[6]:
Test score: 0.81
Advertencia
En este ejemplo, hemos llamado a get_dummies en un DataFrameque contiene tanto los datos de entrenamiento como los de prueba. Esto es importante para garantizar que los valores categóricos se representan de la misma manera en el conjunto de entrenamiento y en el conjunto de prueba.
Imagina que tenemos los conjuntos de entrenamiento y de prueba en dosDataFrames diferentes. Si el valor "Private Employee" para la característica workclass no aparece en el conjunto de prueba, pandas asumirá que sólo hay tres valores posibles para esta característica y creará sólo tres nuevas características ficticias. Ahora nuestros conjuntos de entrenamiento y de prueba tienen números diferentes de características, y ya no podemos aplicar el modelo que aprendimos en el conjunto de entrenamiento al conjunto de prueba. Peor aún, imagina que la característica workclass tiene los valores "Government Employee" y "Private Employee" en el conjunto de entrenamiento, y "Self Employed" y "Self Employed Incorporated" en el conjunto de prueba. En ambos casos pandas creará dos nuevas características ficticias, de modo que el DataFrames codificado tendrá el mismo número de características. Sin embargo, las dos características ficticias tienen significados totalmente distintos en los conjuntos de entrenamiento y de prueba. La columna que significa "Government Employee" para el conjunto de entrenamiento codificaría "Self Employed" para el conjunto de prueba.
Si construyéramos un modelo de aprendizaje automático con estos datos, funcionaría muy mal, porque supondría que las columnas significan lo mismo (porque están en la misma posición), cuando en realidad significan cosas muy distintas. Para solucionarlo, llama a get_dummies en un DataFrame que contenga los puntos de datos de entrenamiento y de prueba, o asegúrate de que los nombres de las columnas son los mismos para los conjuntos de entrenamiento y de prueba después de llamar a get_dummies, para garantizar que tienen la misma semántica.
4.1.2 Los números pueden codificar categóricos
En el ejemplo del conjunto de datos adult, las variables categóricas se codificaron como cadenas. Por un lado, eso abre la posibilidad de errores ortográficos, pero por otro, marca claramente una variable como categórica. A menudo, ya sea por facilidad de almacenamiento o por la forma en que se recogen los datos, las variables categóricas se codifican como números enteros. Por ejemplo, imagina que los datos del censo del conjunto de datos adult se recogieron mediante un cuestionario, y las respuestas de workclass se registraron como 0 (primera casilla marcada), 1 (segunda casilla marcada), 2 (tercera casilla marcada), etcétera. Ahora la columna contendrá números del 0 al 8, en lugar de cadenas como "Private", y no será inmediatamente obvio para alguien que mire la tabla que representa el conjunto de datos si debe tratar esta variable como continua o categórica. Sin embargo, sabiendo que los números indican la situación laboral, está claro que se trata de estados muy distintos y que no deben modelizarse mediante una única variable continua.
Advertencia
Los rasgos categóricos suelen codificarse utilizando números enteros. Que sean números no significa que deban tratarse necesariamente como rasgos continuos. No siempre está claro si un rasgo entero debe tratarse como continuo o discreto (y codificarse con un solo número). Si no hay orden entre las semánticas que se codifican (como en el ejemplo deworkclass ), la característica debe tratarse como discreta. Para otros casos, como las valoraciones de cinco estrellas, la mejor codificación depende de la tarea y los datos concretos y del algoritmo de aprendizaje automático que se utilice.
La función get_dummies de pandas trata todos los números como continuos y no creará variables ficticias para ellos. Para ilustrarlo, vamos a crear un objeto DataFrame con dos columnas correspondientes a dos características categóricas diferentes, una representada como una cadena y otra como un número entero.
In[7]:
# create a DataFrame with an integer feature and a categorical string featuredemo_df=pd.DataFrame({'Integer Feature':[0,1,2,1],'Categorical Feature':['socks','fox','socks','box']})display(demo_df)
La Tabla 4-4 muestra el resultado.
| Característica categórica | Función de número entero | |
|---|---|---|
0 |
calcetines |
0 |
1 |
zorro |
1 |
2 |
calcetines |
2 |
3 |
caja |
1 |
Si utilizas get_dummies, sólo codificarás la característica cadena y no cambiarás la característica número entero, como puedes ver en la Tabla 4-5:
In[8]:
display(pd.get_dummies(demo_df))
| Característica de número entero | Característica categórica_box | Característica categórica_fox | Característica_categórica | |
|---|---|---|---|---|
0 |
0 |
0.0 |
0.0 |
1.0 |
1 |
1 |
0.0 |
1.0 |
0.0 |
2 |
2 |
0.0 |
0.0 |
1.0 |
3 |
1 |
1.0 |
0.0 |
0.0 |
Si quieres que se creen variables ficticias para la columna "Característica entera", puedes enumerar explícitamente las columnas que quieres codificar utilizando el parámetrocolumns. Entonces, ambas características se tratarán como categóricas (ver Tabla 4-6):
In[9]:
demo_df['Integer Feature']=demo_df['Integer Feature'].astype(str)display(pd.get_dummies(demo_df,columns=['Integer Feature','Categorical Feature']))
| Entero Característica_0 | Entero Característica_1 | Entero Característica_2 | Característica categórica_box | Característica categórica_fox | Característica_categórica | |
|---|---|---|---|---|---|---|
0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
1.0 |
1 |
0.0 |
1.0 |
0.0 |
0.0 |
1.0 |
0.0 |
2 |
0.0 |
0.0 |
1.0 |
0.0 |
0.0 |
1.0 |
3 |
0.0 |
1.0 |
0.0 |
1.0 |
0.0 |
0.0 |
4.2 OneHotEncoder y ColumnTransformer: Variables categóricas con scikit-learn
Como ya se ha mencionado, scikit-learn también puede realizar la codificación en un solo paso. Utilizar scikit-learn tiene la ventaja de facilitar el tratamiento de los conjuntos de entrenamiento y prueba de forma coherente. La codificación en caliente se aplica en la clase OneHotEncoder 1 En particular, OneHotEncoder aplica la codificación a todas las columnas de entrada:
In[10]:
fromsklearn.preprocessingimportOneHotEncoder# Setting sparse=False means OneHotEncode will return a numpy array,# not a sparse matrixohe=OneHotEncoder(sparse=False)(ohe.fit_transform(demo_df))
Out[10]:
[[1. 0. 0. 0. 0. 1.] [0. 1. 0. 0. 1. 0.] [0. 0. 1. 0. 0. 1.] [0. 1. 0. 1. 0. 0.]]
Puedes ver que tanto la característica de cadena como la de número entero se transformaron. Como es habitual en scikit-learn, la salida no es un DataFrame, por lo que no hay nombres de columnas. Para obtener la correspondencia de las características transformadas con las variables categóricas originales, podemos utilizar el métodoget_feature_names:
In[11]:
(ohe.get_feature_names())
Out[11]:
['x0_0' 'x0_1' 'x0_2' 'x1_box' 'x1_fox' 'x1_socks']
En ella, las tres primeras columnas corresponden a los valores 0, 1 y 2 de la primera característica original (denominada aquí x0 ), mientras que las tres últimas columnas corresponden a los valores box, fox y socks de la segunda característica original (denominada aquí x1 ).
En la mayoría de las aplicaciones, algunas características son categóricas y otras continuas, por lo que OneHotEncoder no es directamente aplicable, ya que asume que todas las características son categóricas. Aquí es donde la clase ColumnTransformerresulta útil: te permite aplicar diferentes transformaciones a distintas columnas de los datos de entrada. Esto es increíblemente útil, ya que las características continuas y categóricas necesitan tipos de preprocesamiento muy diferentes.
Volvamos al ejemplo de los datos del censo de adultos que hemos considerado antes:
In[12]:
display(data.head())
Out[12]:
[cols=",,,,,,,",options="header",] |======================================================================= | |age |workclass |education |gender |hours-per-week |occupation |income |0 |39 |State-gov |Bachelors |Male |40 |Adm-clerical |<=50K |1 |50 |Self-emp-not-inc |Bachelors |Male |13 |Exec-managerial |<=50K |2 |38 |Private |HS-grad |Male |40 |Handlers-cleaners |<=50K |3 |53 |Private |11th |Male |40 |Handlers-cleaners |<=50K |4 |28 |Private |Bachelors |Female |40 |Prof-specialty |<=50K |=======================================================================
Para aplicar, digamos, un modelo lineal a este conjunto de datos para predecir los ingresos, además de aplicar la codificación de un solo paso a las variables categóricas, es posible que también queramos escalar las variables continuas age yhours-per-week. Esto es exactamente lo que ColumnTransformer puede hacer por nosotros. Cada transformación del transformador de columna se especifica mediante un nombre (más adelante veremos por qué es útil), un objeto transformador y las columnas a las que debe aplicarse este transformador. Las columnas pueden especificarse mediante nombres de columna, índices enteros o máscaras booleanas. Cada transformador se aplica a las columnas correspondientes, y el resultado de las transformaciones se concatena (horizontalmente). Para el ejemplo anterior, utilizando nombres de columnas la especificación tiene este aspecto:
In[13]:
fromsklearn.composeimportColumnTransformerfromsklearn.preprocessingimportStandardScalerct=ColumnTransformer([("scaling",StandardScaler(),['age','hours-per-week']),("onehot",OneHotEncoder(sparse=False),['workclass','education','gender','occupation'])])
Ahora podemos utilizar el objeto ColumnTransformer como lo haríamos con cualquier otra transformaciónscikit-learn, utilizando fit y transform. Así que vamos a construir un modelo lineal como antes, pero esta vez incluyendo el escalado de las variables continuas. Ten en cuenta que estamos llamando a train_test_split en elDataFrame que contiene las características, no en una matriz NumPy. Necesitamos conservar los nombres de las columnas para poder utilizarlos enColumnTransformer.
In[14]:
fromsklearn.linear_modelimportLogisticRegressionfromsklearn.model_selectionimporttrain_test_split# get all columns apart from income for the featuresdata_features=data.drop("income",axis=1)# split dataframe and incomeX_train,X_test,y_train,y_test=train_test_split(data_features,data.income,random_state=0)ct.fit(X_train)X_train_trans=ct.transform(X_train)(X_train_trans.shape)
Out[14]:
(24420, 44)
Puedes ver que hemos obtenido 44 rasgos, lo mismo que cuando utilizamos antespd.get_dummies, salvo que también hemos escalado los rasgos continuos. Ahora podemos construir un modelo LogisticRegression:
In[15]:
logreg=LogisticRegression()logreg.fit(X_train_trans,y_train)X_test_trans=ct.transform(X_test)("Test score: {:.2f}".format(logreg.score(X_test_trans,y_test)))
Out[15]:
Test score: 0.81
En este caso, escalar los datos no supuso ninguna diferencia, pero encapsular todo el preprocesamiento dentro de un transformador tiene ventajas adicionales que discutiremos más adelante. Puedes acceder a los pasos dentro del ColumnTransformer mediante el atributo named_transformers_:
In[16]:
ct.named_transformers_.onehot
Out[16]:
OneHotEncoder(categorical_features=None, categories=None,
dtype=<class 'numpy.float64'>, handle_unknown='error',
n_values=None, sparse=False)
4.3 Cómoda creación de ColumnTransformer con make_columntransformer
Crear un ColumnTransformer utilizando la sintaxis descrita anteriormente es a veces un poco engorroso, y a menudo no necesitamos nombres especificados por el usuario para cada paso. Existe una función de conveniencia (make_columntransformer) que creará un ColumnTranformer por nosotros y nombrará automáticamente cada paso basándose en su clase. La sintaxis de make_columntransformer es la siguiente:
In[17]:
fromsklearn.composeimportmake_column_transformerct=make_column_transformer((['age','hours-per-week'],StandardScaler()),(['workclass','education','gender','occupation'],OneHotEncoder(sparse=False)))
Una desventaja de utilizar el ColumnTransformer es que en la versión 0.20 todavía no es posible encontrar fácilmente qué columnas de entrada corresponden a qué columnas de salida del transformador de columna en todos los casos.
4.4 Binning, Discretización, Modelos Lineales y Árboles
La mejor forma de representar los datos depende no sólo de la semántica de los datos, sino también del tipo de modelo que estés utilizando. Los modelos lineales y los modelos basados en árboles (como los árboles de decisión, los árboles potenciados por gradiente y los bosques aleatorios), dos familias grandes y muy utilizadas, tienen propiedades muy diferentes en cuanto a cómo funcionan con distintas representaciones de características. Volvamos al conjunto de datos de regresión wave que utilizamos en el Capítulo 2. Sólo tiene una característica de entrada. He aquí una comparación de un modelo de regresión lineal y un regresor de árbol de decisión en este conjunto de datos (ver Figura 4-1):
In[18]:
fromsklearn.linear_modelimportLinearRegressionfromsklearn.treeimportDecisionTreeRegressorX,y=mglearn.datasets.make_wave(n_samples=120)line=np.linspace(-3,3,1000,endpoint=False).reshape(-1,1)reg=DecisionTreeRegressor(min_samples_leaf=3).fit(X,y)plt.plot(line,reg.predict(line),label="decision tree")reg=LinearRegression().fit(X,y)plt.plot(line,reg.predict(line),label="linear regression")plt.plot(X[:,0],y,'o',c='k')plt.ylabel("Regression output")plt.xlabel("Input feature")plt.legend(loc="best")
Como sabes, los modelos lineales sólo pueden modelizar relaciones lineales, que son líneas en el caso de una única característica. El árbol de decisión puede construir un modelo mucho más complejo de los datos. Sin embargo, esto depende en gran medida de la representación de los datos. Una forma de hacer que los modelos lineales sean más potentes en datos continuos es utilizar el binning (también conocido comodiscretización) de la característica para dividirla en múltiples características, como se describe aquí.

Figura 4-1. Comparación de la regresión lineal y un árbol de decisión en el conjunto de datos de olas
Imaginamos una partición del intervalo de entrada de la característica (en este caso, los números de -3 a 3) en un número fijo de intervalos, digamos10. Un punto de datos se representará entonces por el intervalo en el que se encuentra. Un punto de datos se representará por el intervalo en el que se encuentra. Hay varias formas de definir los perímetros de las casillas; por ejemplo, dándoles una anchura uniforme (haciendo que los perímetros de las casillas sean equidistantes) o utilizando los cuantiles de los datos (es decir, teniendo casillas más pequeñas donde hay más datos). Ambas estrategias se aplican en KBinsDiscretizer:
In[19]:
fromsklearn.preprocessingimportKBinsDiscretizer
In[20]:
kb=KBinsDiscretizer(n_bins=10,strategy='uniform')kb.fit(X)("bin edges:\n",kb.bin_edges_)
Out[20]:
bin edges:
[array([-2.967, -2.378, -1.789, -1.2 , -0.612, -0.023, 0.566, 1.155,
1.744, 2.333, 2.921])]
Aquí, la primera bandeja contiene todos los puntos de datos con valores de característica de -2,967 (el valor más pequeño de los datos) a -2,378, la segunda contiene todos los puntos con valores de característica de -2,378 a -1,789, y así sucesivamente.KBinsDiscretizer puede aplicarse a varias características a la vez, y las bin_edges_ contienen los perímetros por característica. Por eso en este caso son una lista de longitud uno.
Utilizando transform, podemos codificar cada punto de datos según la casilla en la que se encuentre. Por defecto, KBinDiscretizer aplica una codificación de un solo punto a los contenedores, de modo que hay una nueva característica por contenedor, y produce una matriz dispersa. Como hemos especificado 10 contenedores, los datos transformados tienen diez dimensiones.
In[21]:
X_binned=kb.transform(X)X_binned
Out[21]:
<120x10 sparse matrix of type '<class 'numpy.float64'>' with 120 stored elements in Compressed Sparse Row format>
Podemos convertir la matriz dispersa en una matriz densa y comparar los puntos de datos con su codificación:
In[22]:
(X[:10])X_binned.toarray()[:10]
Out[22]:
[[-0.753]
[ 2.704]
[ 1.392]
[ 0.592]
[-2.064]
[-2.064]
[-2.651]
[ 2.197]
[ 0.607]
[ 1.248]]
array([[0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0.]])
Podemos ver que el primer punto de datos con valor -0.753 se colocó en la 4ª casilla, el segundo punto de datos con valor 2.704 se colocó en la 10ª casilla, y así sucesivamente.
Lo que hemos hecho aquí es transformar la única característica de entrada continua del conjunto de datoswave en una característica categórica codificada en un solo paso, que codifica en qué casilla se encuentra un punto de datos. Puedes renunciar a la codificación de un punto especificando encode='ordinal', aunque suele ser menos útil. Para facilitar la demostración, utilizaremosencode='onehot-dense', que utiliza una codificación densa de un punto, de modo que podamos imprimir directamente todas las características.
In[23]:
kb=KBinsDiscretizer(n_bins=10,strategy='uniform',encode='onehot-dense')kb.fit(X)X_binned=kb.transform(X)
Ahora construimos un nuevo modelo de regresión lineal y un nuevo modelo de árbol de decisión sobre los datos codificados con un solo disparo. El resultado se visualiza en la Figura 4-2, junto con los límites de los contenedores, mostrados como líneas negras discontinuas:
In[24]:
line_binned=kb.transform(line)reg=LinearRegression().fit(X_binned,y)plt.plot(line,reg.predict(line_binned),label='linear regression binned')reg=DecisionTreeRegressor(min_samples_split=3).fit(X_binned,y)plt.plot(line,reg.predict(line_binned),label='decision tree binned')plt.plot(X[:,0],y,'o',c='k')plt.vlines(kb.bin_edges_[0],-3,3,linewidth=1,alpha=.2)plt.legend(loc="best")plt.ylabel("Regression output")plt.xlabel("Input feature")
La línea discontinua y la línea continua están exactamente una encima de la otra, lo que significa que el modelo de regresión lineal y el árbol de decisión hacen exactamente las mismas predicciones. Para cada casilla, predicen un valor constante. Como las características son constantes dentro de cada casilla, cualquier modelo debe predecir el mismo valor para todos los puntos de una casilla. Si comparamos lo que aprendieron los modelos antes de agrupar las características y después, vemos que el modelo lineal se hizo mucho más flexible, porque ahora tiene un valor diferente para cada casilla, mientras que el modelo del árbol de decisión se hizo mucho menos flexible. En general, la clasificación de las características no tiene ningún efecto beneficioso para los modelos basados en árboles, ya que estos modelos pueden aprender a dividir los datos en cualquier lugar. En cierto sentido, eso significa que los árboles de decisión pueden aprender cualquier binning que sea más útil para predecir sobre estos datos. Además, los árboles de decisión analizan varias características a la vez, mientras que el agrupamiento suele hacerse por característica. Sin embargo, el modelo lineal se benefició mucho en expresividad de la transformación de los datos.
Si hay buenas razones para utilizar un modelo lineal para un conjunto de datos concreto -por ejemplo, porque es muy grande y de alta dimensión, pero algunas características tienen relaciones no lineales con el resultado-, el reagrupamiento puede ser una forma estupenda de aumentar la potencia de modelado.

Figura 4-2. Comparación de la regresión lineal y la regresión del árbol de decisión en características binned
4.5 Interacciones y polinomios
Otra forma de enriquecer una representación de características, sobre todo para los modelos lineales, es añadir características de interacción y características polinómicas de los datos originales. Este tipo de ingeniería de características se utiliza a menudo en el modelado estadístico, pero también es habitual en muchas aplicaciones prácticas de aprendizaje automático.
Como primer ejemplo, observa de nuevo la Figura 4-2. El modelo lineal aprendió un valor constante para cada recipiente del conjunto de datos wave. Sin embargo, sabemos que los modelos lineales pueden aprender no sólo desplazamientos, sino también pendientes. Una forma de añadir una pendiente al modelo lineal en los datos divididos en cubos es volver a añadir la característica original (el eje x en el gráfico). Esto da lugar a un conjunto de datos de 11 dimensiones, como se ve en la Figura 4-3:
In[25]:
X_combined=np.hstack([X,X_binned])(X_combined.shape)
Out[25]:
(120, 11)
In[26]:
reg=LinearRegression().fit(X_combined,y)line_combined=np.hstack([line,line_binned])plt.plot(line,reg.predict(line_combined),label='linear regression combined')plt.vlines(kb.bin_edges_[0],-3,3,linewidth=1,alpha=.2)plt.legend(loc="best")plt.ylabel("Regression output")plt.xlabel("Input feature")plt.plot(X[:,0],y,'o',c='k')

Figura 4-3. Regresión lineal utilizando características binadas y una única pendiente global
En este ejemplo, el modelo aprendió un desplazamiento para cada casilla, junto con una pendiente. La pendiente aprendida es descendente y se comparte en todos los intervalos: hay una única característica del eje x, que tiene una única pendiente. Como la pendiente se comparte en todas las casillas, no parece ser muy útil. Preferiríamos tener una pendiente distinta para cada casilla. Podemos conseguirlo añadiendo una característica de interacción o producto que indique en qué casilla se encuentra un punto de datos y dónde se sitúa en el eje x. Esta característica es un producto del indicador de ubicación y la característica original. Vamos a crear este conjunto de datos:
In[27]:
X_product=np.hstack([X_binned,X*X_binned])(X_product.shape)
Out[27]:
(120, 20)
El conjunto de datos tiene ahora 20 características: los indicadores de la ubicación en la que se encuentra un punto de datos, y un producto de la característica original y el indicador de ubicación. Puedes considerar la característica producto como una copia independiente de la característica del eje x para cada ubicación. Es la característica original dentro del contenedor, y cero en el resto. La Figura 4-4 muestra el resultado del modelo lineal en esta nueva representación:
In[28]:
reg=LinearRegression().fit(X_product,y)line_product=np.hstack([line_binned,line*line_binned])plt.plot(line,reg.predict(line_product),label='linear regression product')plt.vlines(kb.bin_edges_[0],-3,3,linewidth=1,alpha=.2)plt.plot(X[:,0],y,'o',c='k')plt.ylabel("Regression output")plt.xlabel("Input feature")plt.legend(loc="best")
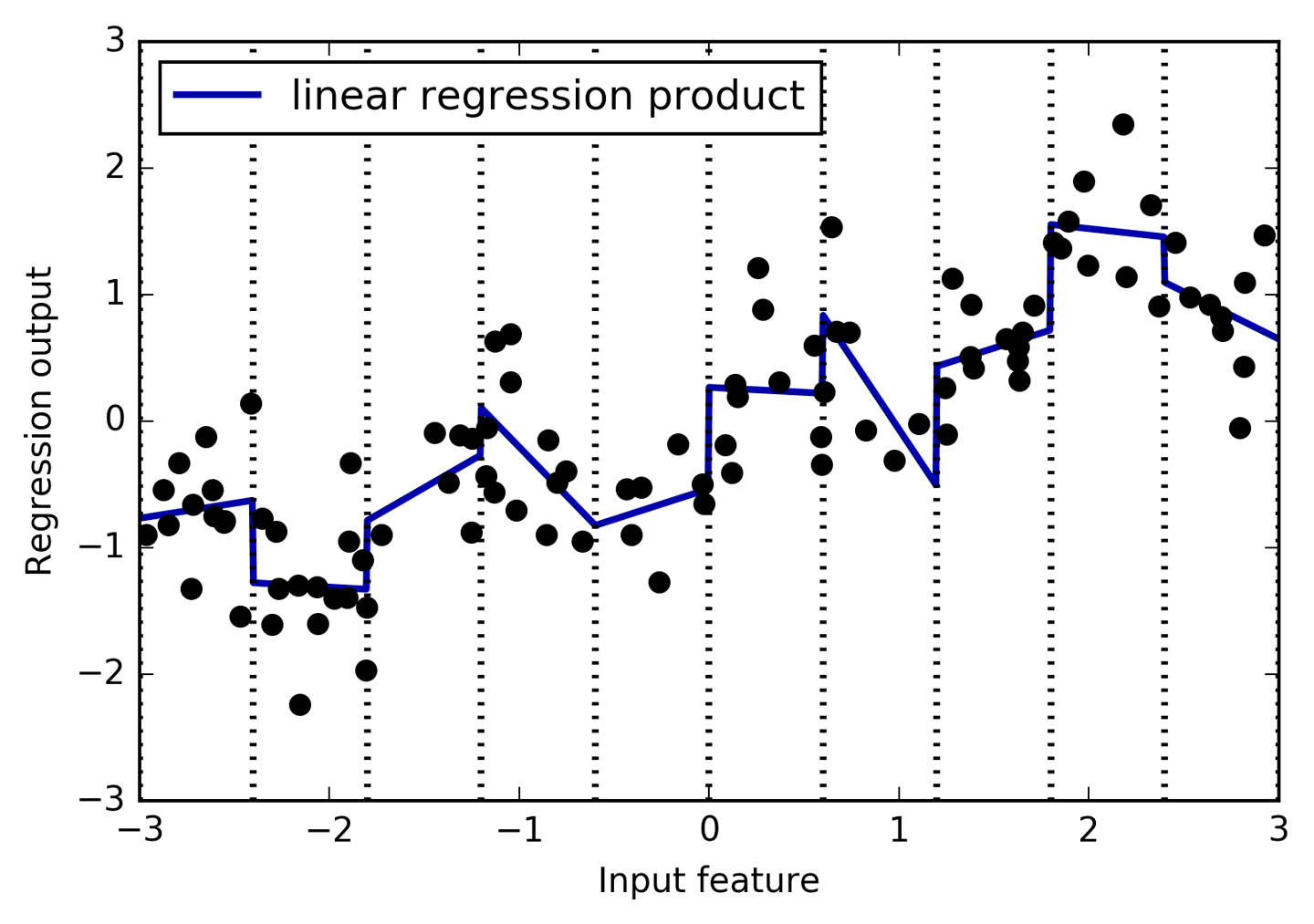
Figura 4-4. Regresión lineal con una pendiente distinta por recipiente
Como puedes ver, ahora cada recipiente tiene su propio desplazamiento y pendiente en este modelo.
Utilizar el binning es una forma de ampliar una característica continua. Otra es utilizar polinomios de las características originales. Para una característica dada x, podríamos considerar x ** 2x ** 3, x ** 4, etc. Esto se implementa en PolynomialFeatures en el módulo preprocessing:
In[29]:
fromsklearn.preprocessingimportPolynomialFeatures# include polynomials up to x ** 10:# the default "include_bias=True" adds a feature that's constantly 1poly=PolynomialFeatures(degree=10,include_bias=False)poly.fit(X)X_poly=poly.transform(X)
Utilizando un grado de 10 se obtienen 10 características:
In[30]:
("X_poly.shape: {}".format(X_poly.shape))
Out[30]:
X_poly.shape: (120, 10)
Comparemos las entradas de X_poly con las de X:
In[31]:
("Entries of X:\n{}".format(X[:5]))("Entries of X_poly:\n{}".format(X_poly[:5]))
Out[31]:
Entries of X:
[[-0.753]
[ 2.704]
[ 1.392]
[ 0.592]
[-2.064]]
Entries of X_poly:
[[ -0.753 0.567 -0.427 0.321 -0.242 0.182 -0.137
0.103 -0.078 0.058]
[ 2.704 7.313 19.777 53.482 144.632 391.125 1057.714
2860.36 7735.232 20918.278]
[ 1.392 1.938 2.697 3.754 5.226 7.274 10.125
14.094 19.618 27.307]
[ 0.592 0.35 0.207 0.123 0.073 0.043 0.025
0.015 0.009 0.005]
[ -2.064 4.26 -8.791 18.144 -37.448 77.289 -159.516
329.222 -679.478 1402.367]]
Puedes obtener la semántica de las características llamando al métodoget_feature_names, que proporciona el exponente de cada característica:
In[32]:
("Polynomial feature names:\n{}".format(poly.get_feature_names()))
Out[32]:
Polynomial feature names: ['x0', 'x0^2', 'x0^3', 'x0^4', 'x0^5', 'x0^6', 'x0^7', 'x0^8', 'x0^9', 'x0^10']
Puedes ver que la primera columna de X_poly corresponde exactamente a X, mientras que las demás columnas son las potencias de la primera entrada. Es interesante ver lo grandes que pueden llegar a ser algunos de los valores. La segunda fila tiene entradas por encima de 20.000, órdenes de magnitud diferentes del resto.
Utilizando características polinómicas junto con un modelo de regresión lineal se obtiene el modelo clásico de regresión polinómica (ver Figura 4-5):
In[33]:
reg=LinearRegression().fit(X_poly,y)line_poly=poly.transform(line)plt.plot(line,reg.predict(line_poly),label='polynomial linear regression')plt.plot(X[:,0],y,'o',c='k')plt.ylabel("Regression output")plt.xlabel("Input feature")plt.legend(loc="best")
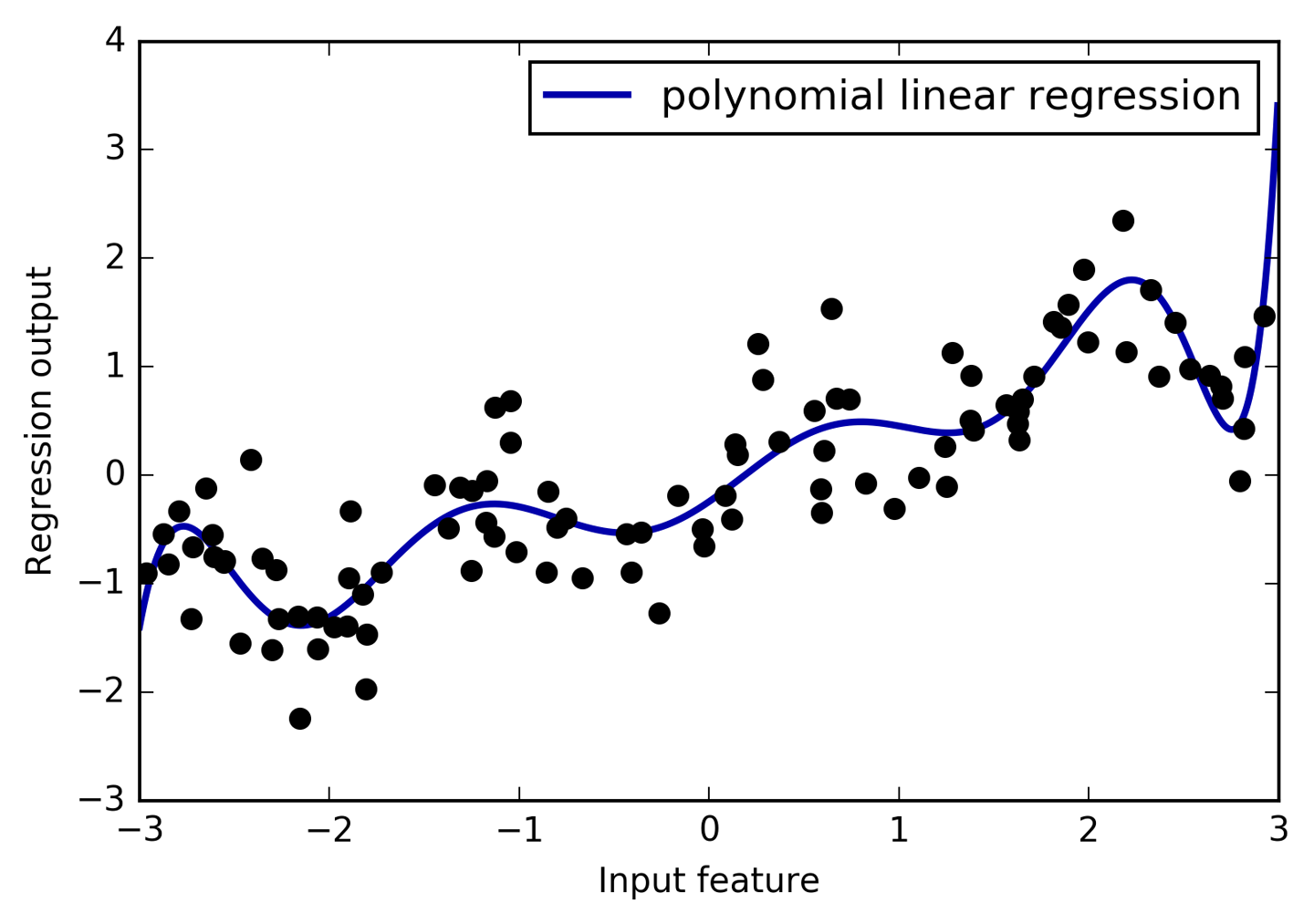
Figura 4-5. Regresión lineal con características polinómicas de décimo grado
Como puedes ver, las características polinómicas producen un ajuste muy suave en estos datos unidimensionales. Sin embargo, los polinomios de alto grado tienden a comportarse de forma extrema en los límites o en regiones con pocos datos.
A modo de comparación, aquí tienes un modelo SVM de núcleo aprendido sobre los datos originales, sin ninguna transformación (ver Figura 4-6):
In[34]:
fromsklearn.svmimportSVRforgammain[1,10]:svr=SVR(gamma=gamma).fit(X,y)plt.plot(line,svr.predict(line),label='SVR gamma={}'.format(gamma))plt.plot(X[:,0],y,'o',c='k')plt.ylabel("Regression output")plt.xlabel("Input feature")plt.legend(loc="best")

Figura 4-6. Comparación de distintos parámetros gamma para una SVM con núcleo RBF
Utilizando un modelo más complejo, una SVM de núcleo, podemos aprender una predicción de complejidad similar a la de la regresión polinómica sin una transformación explícita de las características.
Como aplicación más realista de las interacciones y los polinomios, veamos de nuevo el conjunto de datos de Viviendas de Boston. Ya utilizamos características polinómicas en este conjunto de datos en el Capítulo 2. Veamos ahora cómo se construyeron estas características y en qué medida ayudan las características polinómicas. Primero cargamos los datos y los reescalamos para que estén entre 0 y 1 utilizandoMinMaxScaler:
In[35]:
fromsklearn.datasetsimportload_bostonfromsklearn.model_selectionimporttrain_test_splitfromsklearn.preprocessingimportMinMaxScalerboston=load_boston()X_train,X_test,y_train,y_test=train_test_split(boston.data,boston.target,random_state=0)# rescale datascaler=MinMaxScaler()X_train_scaled=scaler.fit_transform(X_train)X_test_scaled=scaler.transform(X_test)
Ahora, extraemos características polinómicas e interacciones hasta un grado de 2:
In[36]:
poly=PolynomialFeatures(degree=2).fit(X_train_scaled)X_train_poly=poly.transform(X_train_scaled)X_test_poly=poly.transform(X_test_scaled)("X_train.shape: {}".format(X_train.shape))("X_train_poly.shape: {}".format(X_train_poly.shape))
Out[36]:
X_train.shape: (379, 13) X_train_poly.shape: (379, 105)
Los datos tenían originalmente 13 rasgos, que se ampliaron a 105 rasgos de interacción. Estos nuevos rasgos representan todas las interacciones posibles entre dos rasgos originales diferentes, así como el cuadrado de cada rasgo original. degree=2 significa aquí que consideramos todos los rasgos que son el producto de hasta dos rasgos originales. La correspondencia exacta entre las características de entrada y de salida se puede encontrar utilizando el método get_feature_names:
In[37]:
("Polynomial feature names:\n{}".format(poly.get_feature_names()))
Out[37]:
Polynomial feature names: ['1', 'x0', 'x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x11', 'x12', 'x0^2', 'x0 x1', 'x0 x2', 'x0 x3', 'x0 x4', 'x0 x5', 'x0 x6', 'x0 x7', 'x0 x8', 'x0 x9', 'x0 x10', 'x0 x11', 'x0 x12', 'x1^2', 'x1 x2', 'x1 x3', 'x1 x4', 'x1 x5', 'x1 x6', 'x1 x7', 'x1 x8', 'x1 x9', 'x1 x10', 'x1 x11', 'x1 x12', 'x2^2', 'x2 x3', 'x2 x4', 'x2 x5', 'x2 x6', 'x2 x7', 'x2 x8', 'x2 x9', 'x2 x10', 'x2 x11', 'x2 x12', 'x3^2', 'x3 x4', 'x3 x5', 'x3 x6', 'x3 x7', 'x3 x8', 'x3 x9', 'x3 x10', 'x3 x11', 'x3 x12', 'x4^2', 'x4 x5', 'x4 x6', 'x4 x7', 'x4 x8', 'x4 x9', 'x4 x10', 'x4 x11', 'x4 x12', 'x5^2', 'x5 x6', 'x5 x7', 'x5 x8', 'x5 x9', 'x5 x10', 'x5 x11', 'x5 x12', 'x6^2', 'x6 x7', 'x6 x8', 'x6 x9', 'x6 x10', 'x6 x11', 'x6 x12', 'x7^2', 'x7 x8', 'x7 x9', 'x7 x10', 'x7 x11', 'x7 x12', 'x8^2', 'x8 x9', 'x8 x10', 'x8 x11', 'x8 x12', 'x9^2', 'x9 x10', 'x9 x11', 'x9 x12', 'x10^2', 'x10 x11', 'x10 x12', 'x11^2', 'x11 x12', 'x12^2']
El primer rasgo nuevo es un rasgo constante, denominado aquí "1". Las 13 características siguientes son las características originales (denominadas "x0" a "x12"). A continuación viene la primera característica al cuadrado ("x0^2") y combinaciones de la primera y las demás características.
Comparemos el rendimiento utilizando Ridge en los datos con y sin interacciones:
In[38]:
fromsklearn.linear_modelimportRidgeridge=Ridge().fit(X_train_scaled,y_train)("Score without interactions: {:.3f}".format(ridge.score(X_test_scaled,y_test)))ridge=Ridge().fit(X_train_poly,y_train)("Score with interactions: {:.3f}".format(ridge.score(X_test_poly,y_test)))
Out[38]:
Score without interactions: 0.621 Score with interactions: 0.753
Está claro que las interacciones y las características polinómicas nos proporcionaron un buen aumento del rendimiento cuando utilizamos Ridge. Sin embargo, cuando se utiliza un modelo más complejo, como un bosque aleatorio, la historia es un poco diferente:
In[39]:
fromsklearn.ensembleimportRandomForestRegressorrf=RandomForestRegressor(n_estimators=100).fit(X_train_scaled,y_train)("Score without interactions: {:.3f}".format(rf.score(X_test_scaled,y_test)))rf=RandomForestRegressor(n_estimators=100).fit(X_train_poly,y_train)("Score with interactions: {:.3f}".format(rf.score(X_test_poly,y_test)))
Out[39]:
Score without interactions: 0.798 Score with interactions: 0.765
Puedes ver que, incluso sin características adicionales, el bosque aleatorio supera el rendimiento de Ridge. En realidad, añadir interacciones y polinomios disminuye ligeramente el rendimiento.
4.6 Transformaciones no lineales univariantes
Acabamos de ver que añadir características al cuadrado o al cubo puede ayudar a los modelos lineales para la regresión. Hay otras transformaciones que a menudo resultan útiles para transformar ciertos rasgos: en concreto, aplicar funciones matemáticas como log, exp o sin. Mientras que a los modelos basados en árboles sólo les importa el orden de los rasgos, los modelos lineales y las redes neuronales están muy ligados a la escala y la distribución de cada rasgo, y si hay una relación no lineal entre el rasgo y el objetivo, eso se vuelve difícil de modelar, sobre todo en la regresión. Las funciones logy exp pueden ayudar ajustando las escalas relativas de los datos para que puedan ser captadas mejor por un modelo lineal o una red neuronal. Vimos una aplicación de esto en el Capítulo 2 con los datos del precio de la memoria. Las funcionessin y cos pueden resultar útiles cuando se trata de datos que codifican patrones periódicos.
La mayoría de los modelos funcionan mejor cuando cada característica (y en la regresión también el objetivo) tiene una distribución ligeramente gaussiana, es decir, un histograma de cada característica debe tener una forma parecida a la conocida "curva de campana". Utilizar transformaciones como log y exp es una forma poco práctica pero sencilla y eficaz de conseguirlo. Un caso especialmente común en el que una transformación de este tipo puede ser útil es cuando se trata de datos de recuento de números enteros. Por datos de recuento, nos referimos a características como "¿con qué frecuencia se conectó el usuario A?" Los recuentos nunca son negativos, y a menudo siguen patrones estadísticos particulares. Aquí estamos utilizando un conjunto de datos sintéticos de recuentos que tiene propiedades similares a las que puedes encontrar en la naturaleza. Todas las características tienen valores enteros, mientras que la respuesta es continua:
In[40]:
rnd=np.random.RandomState(0)X_org=rnd.normal(size=(1000,3))w=rnd.normal(size=3)X=rnd.poisson(10*np.exp(X_org))y=np.dot(X_org,w)
Veamos las 10 primeras entradas de la primera característica. Todas son valores enteros y positivos, pero aparte de eso es difícil distinguir un patrón concreto.
Si contamos la aparición de cada valor, la distribución de valores se hace más clara:
In[41]:
("Number of feature appearances:\n{}".format(np.bincount(X[:,0])))
Out[41]:
Number of feature appearances: [28 38 68 48 61 59 45 56 37 40 35 34 36 26 23 26 27 21 23 23 18 21 10 9 17 9 7 14 12 7 3 8 4 5 5 3 4 2 4 1 1 3 2 5 3 8 2 5 2 1 2 3 3 2 2 3 3 0 1 2 1 0 0 3 1 0 0 0 1 3 0 1 0 2 0 1 1 0 0 0 0 1 0 0 2 2 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
El valor 2 parece ser el más común, con 68 apariciones (bincountsiempre empieza en 0), y los recuentos de valores superiores caen rápidamente. Sin embargo, hay algunos valores muy altos, como 84 y 85, que aparecen dos veces. Visualizamos los recuentos en la Figura 4-7:
In[42]:
bins=np.bincount(X[:,0])plt.bar(range(len(bins)),bins,color='grey')plt.ylabel("Number of appearances")plt.xlabel("Value")
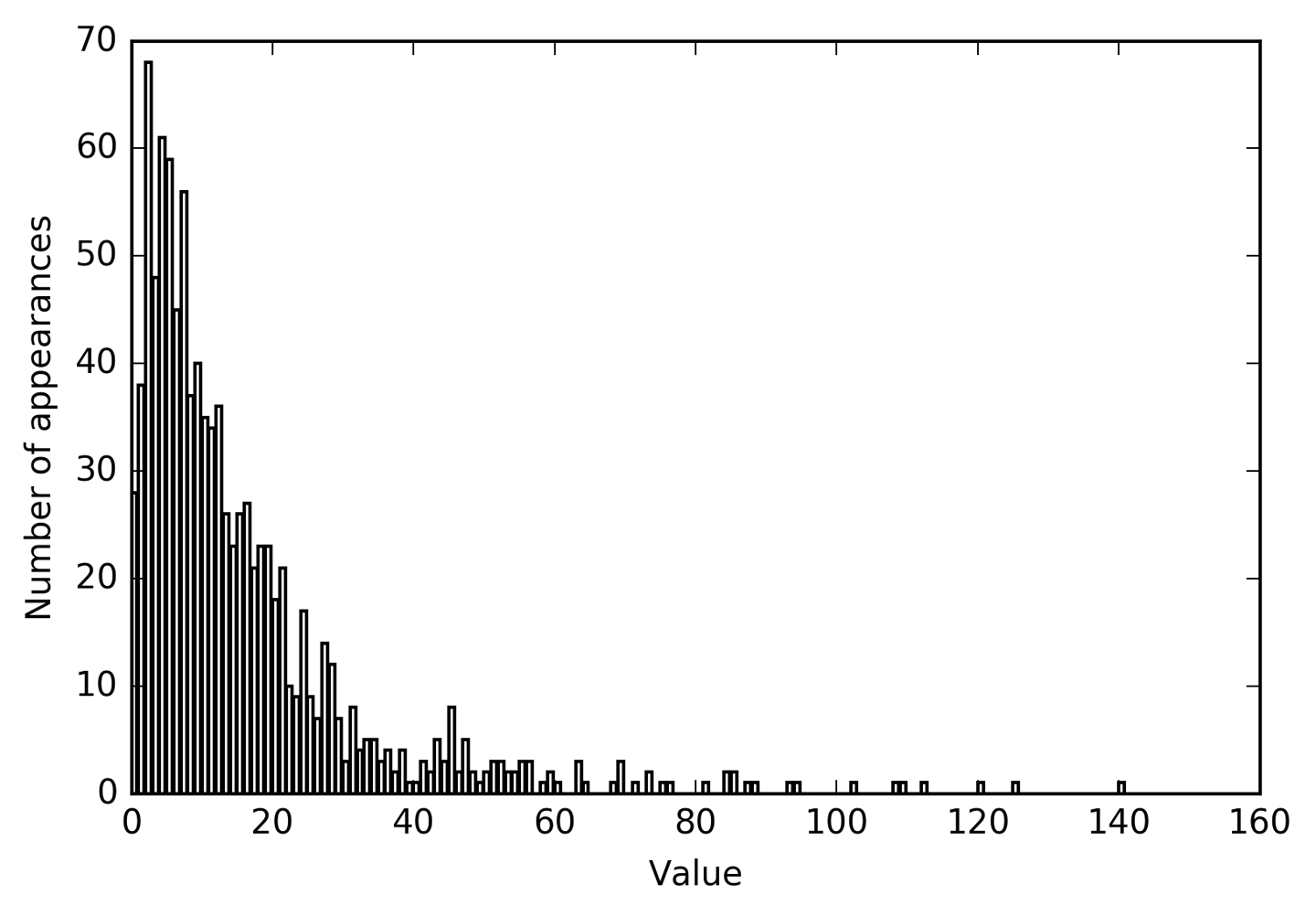
Figura 4-7. Histograma de los valores de las características para X[0]
Los rasgos X[:, 1] y X[:, 2] tienen propiedades similares. Este tipo de distribución de valores (muchos pequeños y unos pocos muy grandes) es muy común en la práctica.2 Sin embargo, es algo que la mayoría de los modelos lineales no pueden manejar muy bien. Intentemos ajustar una regresión ridge a este modelo:
In[43]:
fromsklearn.linear_modelimportRidgeX_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)score=Ridge().fit(X_train,y_train).score(X_test,y_test)("Test score: {:.3f}".format(score))
Out[43]:
Test score: 0.622
Como puedes ver por la puntuaciónR2 relativamente baja, Ridge no fue capaz de captar realmente la relación entre X y y. Sin embargo, aplicar una transformación logarítmica puede ayudar. Como el valor 0 aparece en los datos (y el logaritmo no está definido en 0), en realidad no podemos aplicar simplemente log, sino que tenemos que calcular log(X + 1):
In[44]:
X_train_log=np.log(X_train+1)X_test_log=np.log(X_test+1)
Tras la transformación, la distribución de los datos es menos asimétrica y ya no tiene valores atípicos muy grandes (ver Figura 4-8):
In[45]:
plt.hist(X_train_log[:,0],bins=25,color='gray')plt.ylabel("Number of appearances")plt.xlabel("Value")
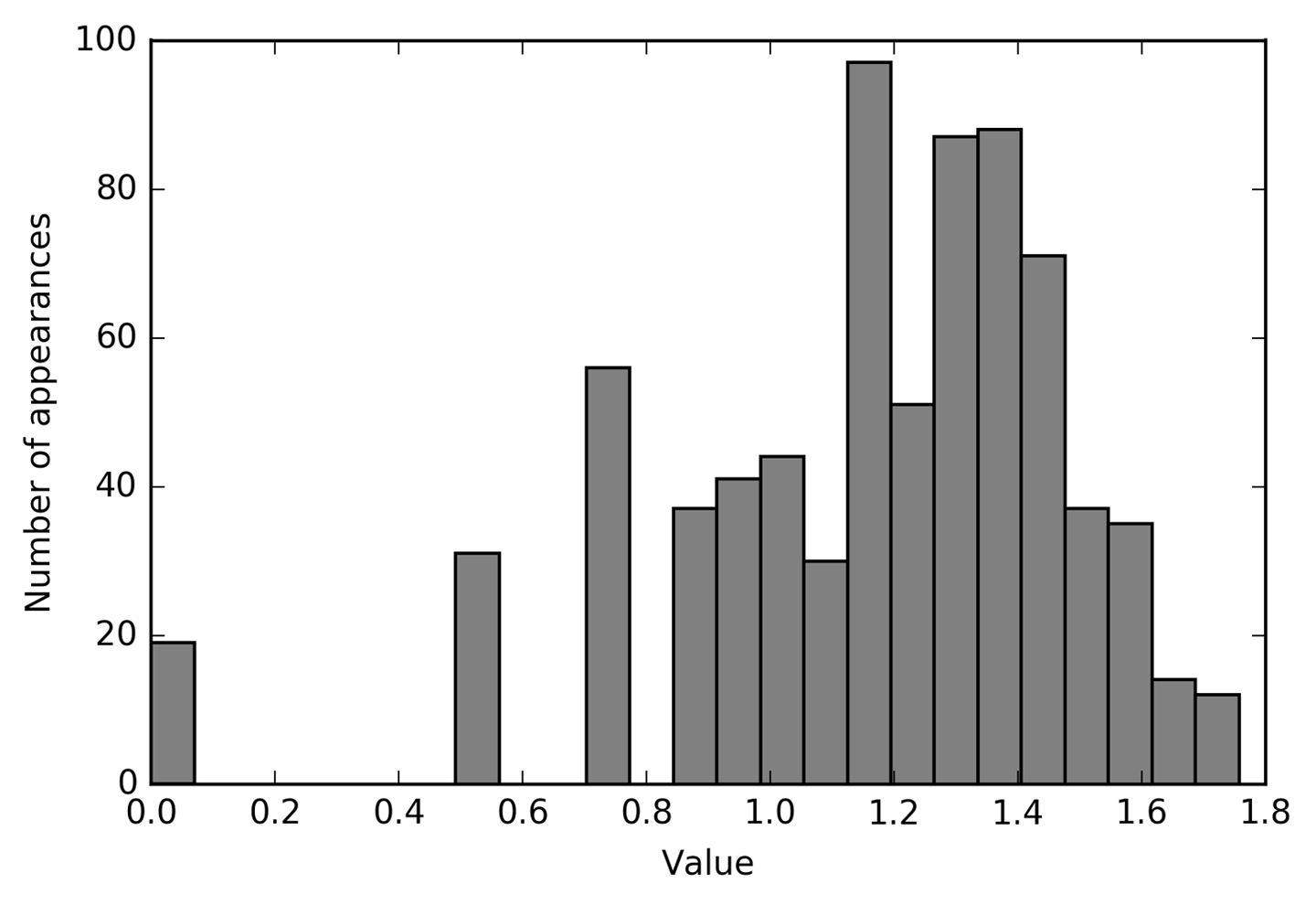
Figura 4-8. Histograma de los valores de las características de X[0] tras la transformación logarítmica
Construir un modelo de cresta sobre los nuevos datos proporciona un ajuste mucho mejor:
In[46]:
score=Ridge().fit(X_train_log,y_train).score(X_test_log,y_test)("Test score: {:.3f}".format(score))
Out[46]:
Test score: 0.875
Encontrar la transformación que mejor funcione para cada combinación de conjunto de datos y modelo es en cierto modo un arte. En este ejemplo, todas las características tenían las mismas propiedades. Rara vez ocurre así en la práctica, y normalmente sólo debe transformarse un subconjunto de las características, o a veces cada característica debe transformarse de un modo distinto. Como hemos dicho antes, este tipo de transformaciones son irrelevantes para los modelos basados en árboles, pero pueden ser esenciales para los modelos lineales. A veces también es buena idea transformar la variable objetivo y en regresión. Intentar predecir recuentos (digamos, el número de pedidos) es una tarea bastante habitual, y utilizar la transformación log(y + 1) suele ser de ayuda.3
Como has visto en los ejemplos anteriores, el binning, los polinomios y las interacciones pueden influir enormemente en el rendimiento de los modelos en un conjunto de datos determinado. Esto es especialmente cierto en el caso de los modelos menos complejos, como los modelos lineales y los modelos Bayes ingenuos. Los modelos basados en árboles, por otra parte, a menudo son capaces de descubrir interacciones importantes por sí mismos, y no requieren transformar los datos explícitamente la mayoría de las veces. Otros modelos, como los SVM, los vecinos más próximos y las redes neuronales, pueden beneficiarse a veces del uso de binning, interacciones o polinomios, pero las implicaciones en estos casos suelen ser mucho menos claras que en el caso de los modelos lineales.
4.7 Selección automática de rasgos
Con tantas formas de crear nuevas características, puedes caer en la tentación de aumentar la dimensionalidad de los datos mucho más allá del número de características originales. Sin embargo, añadir más características hace que todos los modelos sean más complejos y, por tanto, aumenta la probabilidad de sobreajuste. Al añadir nuevas características, o con conjuntos de datos de alta dimensionalidad en general, puede ser una buena idea reducir el número de características a sólo las más útiles, y descartar el resto. Esto puede dar lugar a modelos más sencillos que generalicen mejor. Pero, ¿cómo puedes saber lo buena que es cada característica? Hay tres estrategias básicas: la estadística univariante, la selección basada en modelos y laselección iterativa. Discutiremos las tres en detalle. Todos estos métodos son supervisados, lo que significa que necesitan el objetivo para ajustar el modelo. Esto significa que tenemos que dividir los datos en conjuntos de entrenamiento y de prueba, y ajustar la selección de características sólo a la parte de entrenamiento de los datos.
4.7.1 Estadísticas univariantes
En la estadística univariante, calculamos si existe una relación estadísticamente significativa entre cada característica y el objetivo. A continuación, se seleccionan las características que están relacionadas con la mayor confianza. En el caso de la clasificación, esto también se conoce como análisis de la varianza(ANOVA). Una propiedad clave de estas pruebas es que son univariantes, lo que significa que sólo consideran cada característica individualmente. En consecuencia, una característica se descartará si sólo es informativa cuando se combina con otra. Las pruebas univariantes suelen ser muy rápidas de calcular y no requieren la construcción de un modelo. Por otra parte, son completamente independientes del modelo que quieras aplicar tras la selección de características.
Para utilizar la selección univariante de características en scikit-learn, tienes que elegir una prueba, normalmente f_classif (la predeterminada) para la clasificación of_regression para la regresión, y un método para descartar características basado en los valores p determinados en la prueba. Todos los métodos para descartar parámetros utilizan un umbral para descartar todas las características con unvalor p demasiado alto (lo que significa que es poco probable que estén relacionadas con el objetivo). Los métodos difieren en cómo calculan este umbral, siendo los más sencillos SelectKBest, que selecciona un número fijo k de características, y SelectPercentile, que selecciona un porcentaje fijo de características. Apliquemos la selección de características para la clasificación en el conjunto de datos cancer. Para dificultar un poco la tarea, añadiremos algunas características de ruido no informativo a los datos. Esperamos que la selección de rasgos sea capaz de identificar los rasgos no informativos y eliminarlos:
In[47]:
fromsklearn.datasetsimportload_breast_cancerfromsklearn.feature_selectionimportSelectPercentilefromsklearn.model_selectionimporttrain_test_splitcancer=load_breast_cancer()# get deterministic random numbersrng=np.random.RandomState(42)noise=rng.normal(size=(len(cancer.data),50))# add noise features to the data# the first 30 features are from the dataset, the next 50 are noiseX_w_noise=np.hstack([cancer.data,noise])X_train,X_test,y_train,y_test=train_test_split(X_w_noise,cancer.target,random_state=0,test_size=.5)# use f_classif (the default) and SelectPercentile to select 50% of featuresselect=SelectPercentile(percentile=50)select.fit(X_train,y_train)# transform training setX_train_selected=select.transform(X_train)("X_train.shape: {}".format(X_train.shape))("X_train_selected.shape: {}".format(X_train_selected.shape))
Out[47]:
X_train.shape: (284, 80) X_train_selected.shape: (284, 40)
Como puedes ver, el número de características se redujo de 80 a 40 (el 50% del número original de características). Podemos averiguar qué características se han seleccionado utilizando el método get_support, que devuelve una máscara booleana de las características seleccionadas (visualizada en la Figura 4-9):
In[48]:
mask=select.get_support()(mask)# visualize the mask -- black is True, white is Falseplt.matshow(mask.reshape(1,-1),cmap='gray_r')plt.xlabel("Sample index")plt.yticks(())
Out[48]:
[ True True True True True True True True True False True False True True True True True True False False True True True True True True True True True True False False False True False True False False True False False False False True False False True False False True False True False False False False False False True False True False False False False True False True False False False False True True False True False False False False]

Figura 4-9. Características seleccionadas por SelectPercentile
Como puedes ver en la visualización de la máscara, la mayoría de los rasgos seleccionados son los rasgos originales, y se eliminaron la mayoría de los rasgos con ruido. Sin embargo, la recuperación de las características originales no es perfecta. Comparemos el rendimiento de la regresión logística en todas las características con el rendimiento utilizando sólo las características seleccionadas:
In[49]:
fromsklearn.linear_modelimportLogisticRegression# transform test dataX_test_selected=select.transform(X_test)lr=LogisticRegression()lr.fit(X_train,y_train)("Score with all features: {:.3f}".format(lr.score(X_test,y_test)))lr.fit(X_train_selected,y_train)("Score with only selected features: {:.3f}".format(lr.score(X_test_selected,y_test)))
Out[49]:
Score with all features: 0.930 Score with only selected features: 0.940
En este caso, eliminar las características de ruido mejoró el rendimiento, aunque se perdieron algunas de las características originales. Se trataba de un ejemplo sintético muy sencillo, y los resultados con datos reales suelen ser desiguales. No obstante, la selección univariante de rasgos puede ser muy útil si el número de rasgos es tan grande que no resulta factible construir un modelo con ellos, o si sospechas que muchos rasgos carecen totalmente de información.
4.7.2 Selección de rasgos basada en modelos
La selección de rasgos basada en modelos utiliza un modelo supervisado de aprendizaje automático para juzgar la importancia de cada rasgo, y conserva sólo los más importantes. El modelo supervisado que se utiliza para la selección de características no tiene por qué ser el mismo modelo que se utiliza para el modelado final supervisado. El modelo de selección de rasgos tiene que proporcionar alguna medida de importancia para cada rasgo, de modo que puedan clasificarse según esta medida. Los árboles de decisión y los modelos basados en árboles de decisión proporcionan un atributo feature_importances_, que codifica directamente la importancia de cada característica. Los modelos lineales tienen coeficientes, que también pueden utilizarse para captar la importancia de las características considerando los valores absolutos. Como vimos en elCapítulo 2, los modelos lineales con penalización L1 aprenden coeficientes dispersos, que sólo utilizan un pequeño subconjunto de características. Esto puede considerarse una forma de selección de rasgos para el propio modelo, pero también puede utilizarse como paso previo al procesamiento para seleccionar rasgos para otro modelo. A diferencia de la selección univariante, la selección basada en el modelo tiene en cuenta todas las características a la vez, por lo que puede captar interacciones (si el modelo puede captarlas). Para utilizar la selección de características basada en el modelo, tenemos que utilizar el transformadorSelectFromModel transformador:
In[50]:
fromsklearn.feature_selectionimportSelectFromModelfromsklearn.ensembleimportRandomForestClassifierselect=SelectFromModel(RandomForestClassifier(n_estimators=100,random_state=42),threshold="median")
La clase SelectFromModel selecciona todas las características que tienen una medida de importancia de la característica (proporcionada por el modelo supervisado) mayor que el umbral proporcionado. Para obtener un resultado comparable al que obtuvimos con la selección univariante de características, utilizamos la mediana como umbral, de modo que se seleccionen la mitad de las características. Utilizamos un clasificador de bosque aleatorio con 100 árboles para calcular las importancias de las características. Se trata de un modelo bastante complejo y mucho más potente que el uso de pruebas univariantes. Ahora vamos a ajustar realmente el modelo:
In[51]:
select.fit(X_train,y_train)X_train_l1=select.transform(X_train)("X_train.shape: {}".format(X_train.shape))("X_train_l1.shape: {}".format(X_train_l1.shape))
Out[51]:
X_train.shape: (284, 80) X_train_l1.shape: (284, 40)
De nuevo, podemos echar un vistazo a las características seleccionadas(Figura 4-10):
In[52]:
mask=select.get_support()# visualize the mask -- black is True, white is Falseplt.matshow(mask.reshape(1,-1),cmap='gray_r')plt.xlabel("Sample index")plt.yticks(())

Figura 4-10. Características seleccionadas por SelectFromModel utilizando el RandomForestClassifier
Esta vez, se seleccionaron todas las características originales menos dos. Como especificamos que se seleccionaran 40 características, también se seleccionaron algunas de las características de ruido. Veamos el rendimiento:
In[53]:
X_test_l1=select.transform(X_test)score=LogisticRegression().fit(X_train_l1,y_train).score(X_test_l1,y_test)("Test score: {:.3f}".format(score))
Out[53]:
Test score: 0.951
Con la mejor selección de funciones, también hemos conseguido algunas mejoras aquí.
4.7.3 Selección iterativa de rasgos
En la prueba univariante no utilizamos ningún modelo, mientras que en la selección basada en modelos utilizamos un único modelo para seleccionar características. En la selección iterativa de rasgos, se construye una serie de modelos, con un número variable de rasgos. Hay dos métodos básicos: empezar sin rasgos y añadir rasgos uno a uno hasta alcanzar algún criterio de parada, o empezar con todos los rasgos y eliminar rasgos uno a uno hasta alcanzar algún criterio de parada. Como se construyen una serie de modelos, estos métodos son mucho más costosos computacionalmente que los métodos que hemos discutido anteriormente. Un método concreto de este tipo es la eliminación recursiva de rasgos (RFE), que comienza con todos los rasgos, construye un modelo y descarta el rasgo menos importante según el modelo. A continuación, se construye un nuevo modelo utilizando todos los rasgos menos el descartado, y así sucesivamente hasta que sólo quede un número predeterminado de rasgos. Para que esto funcione, el modelo utilizado para la selección debe proporcionar alguna forma de determinar la importancia de las características, como ocurría con la selección basada en el modelo. Aquí, utilizamos el mismo modelo de bosque aleatorio que antes, y obtenemos los resultados que se muestran en la Figura 4-11:
In[54]:
fromsklearn.feature_selectionimportRFEselect=RFE(RandomForestClassifier(n_estimators=100,random_state=42),n_features_to_select=40)select.fit(X_train,y_train)# visualize the selected features:mask=select.get_support()plt.matshow(mask.reshape(1,-1),cmap='gray_r')plt.xlabel("Sample index")plt.yticks(())

Figura 4-11. Características seleccionadas mediante la eliminación recursiva de características con el modelo clasificador de bosque aleatorio
La selección de características mejoró en comparación con la selección univariante y la basada en modelos, pero aún se omitió una característica. Ejecutar este código también lleva bastante más tiempo que el de la selección basada en modelos, porque el modelo de bosque aleatorio se entrena 40 veces, una por cada característica que se omite. Comprobemos la precisión del modelo de regresión logística cuando se utiliza RFE para la selección de características:
In[55]:
X_train_rfe=select.transform(X_train)X_test_rfe=select.transform(X_test)score=LogisticRegression().fit(X_train_rfe,y_train).score(X_test_rfe,y_test)("Test score: {:.3f}".format(score))
Out[55]:
Test score: 0.951
También podemos utilizar el modelo utilizado dentro del RFE para hacer predicciones. Esto utiliza sólo el conjunto de características que se seleccionó:
In[56]:
("Test score: {:.3f}".format(select.score(X_test,y_test)))
Out[56]:
Test score: 0.951
Aquí, el rendimiento del bosque aleatorio utilizado dentro del RFE es el mismo que el que se consigue entrenando un modelo de regresión logística sobre las características seleccionadas. En otras palabras, una vez que hemos seleccionado las características adecuadas, el modelo lineal funciona tan bien como el bosque aleatorio.
Si no estás seguro a la hora de seleccionar qué utilizar como entrada para tus algoritmos de aprendizaje automático, la selección automática de características puede ser bastante útil. También es estupenda para reducir la cantidad de características necesarias, por ejemplo, para acelerar la predicción o para permitir modelos más interpretables. En la mayoría de los casos del mundo real, es poco probable que la aplicación de la selección de características proporcione grandes ganancias de rendimiento. Sin embargo, sigue siendo una herramienta valiosa en la caja de herramientas del ingeniero de características.
4.8 Utilizar el conocimiento experto
La ingeniería de características suele ser un lugar importante para utilizar el conocimiento experto para una aplicación concreta. Aunque el propósito del aprendizaje automático en muchos casos es evitar tener que crear un conjunto de reglas diseñadas por expertos, eso no significa que deba descartarse el conocimiento previo de la aplicación o el dominio. A menudo, los expertos del dominio pueden ayudar a identificar características útiles que son mucho más informativas que la representación inicial de los datos. Imagina que trabajas para una agencia de viajes y quieres predecir los precios de los vuelos. Digamos que tienes un registro de precios junto con fechas, aerolíneas, lugares de salida y destinos. Un modelo de aprendizaje automático podría construir un modelo decente a partir de eso. Sin embargo, algunos factores importantes de los precios de los vuelos no pueden aprenderse. Por ejemplo, los vuelos suelen ser más caros durante los meses de vacaciones y los días festivos. Mientras que las fechas de algunas fiestas (como Navidad) son fijas, y por tanto su efecto puede aprenderse a partir de la fecha, otras pueden depender de las fases de la luna (como Hanukkah y Pascua) o ser establecidas por las autoridades (como las vacaciones escolares). Estos acontecimientos no pueden aprenderse de los datos si cada vuelo sólo se registra utilizando la fecha (gregoriana). Sin embargo, es fácil añadir una característica que codifique si un vuelo coincidió, precedió o siguió a una fiesta pública o escolar. De este modo, el conocimiento previo sobre la naturaleza de la tarea puede codificarse en las características para ayudar a un algoritmo de aprendizaje automático. Añadir una característica no obliga a un algoritmo de aprendizaje automático a utilizarla, e incluso si la información sobre los días festivos resulta no ser informativa para los precios de los vuelos, aumentar los datos con esta información no hace daño.
A continuación veremos un caso concreto de utilización del conocimiento experto, aunque en este caso podría llamarse más bien "sentido común": la tarea consiste en predecir el alquiler de bicicletas delante de la casa de Andreas.
En Nueva York, Citi Bike gestiona una red de estaciones de alquiler de bicicletas con un sistema de suscripción. Las estaciones están por toda la ciudad y proporcionan una forma cómoda de desplazarse. Los datos de alquiler de bicicletas se hacen públicos de forma anónimay se han analizado de varias maneras. La tarea que queremos resolver es predecir, para una hora y un día determinados, cuántas personas alquilarán una bicicleta delante de la casa de Andreas, para que sepa si le dejarán alguna.
Primero cargamos los datos de agosto de 2015 de esta estación concreta comopandas DataFrame . Remuestreamos los datos en intervalos de tres horas para obtener las tendencias principales de cada día:
In[57]:
citibike=mglearn.datasets.load_citibike()
In[58]:
("Citi Bike data:\n{}".format(citibike.head()))
Out[58]:
Citi Bike data: starttime 2015-08-01 00:00:00 3 2015-08-01 03:00:00 0 2015-08-01 06:00:00 9 2015-08-01 09:00:00 41 2015-08-01 12:00:00 39 Freq: 3H, Name: one, dtype: int64
El siguiente ejemplo muestra una visualización de las frecuencias de alquiler para todo el mes(Figura 4-12):
In[59]:
plt.figure(figsize=(10,3))xticks=pd.date_range(start=citibike.index.min(),end=citibike.index.max(),freq='D')plt.xticks(xticks.astype("int"),xticks.strftime("%a%m-%d"),rotation=90,ha="left")plt.plot(citibike,linewidth=1)plt.xlabel("Date")plt.ylabel("Rentals")
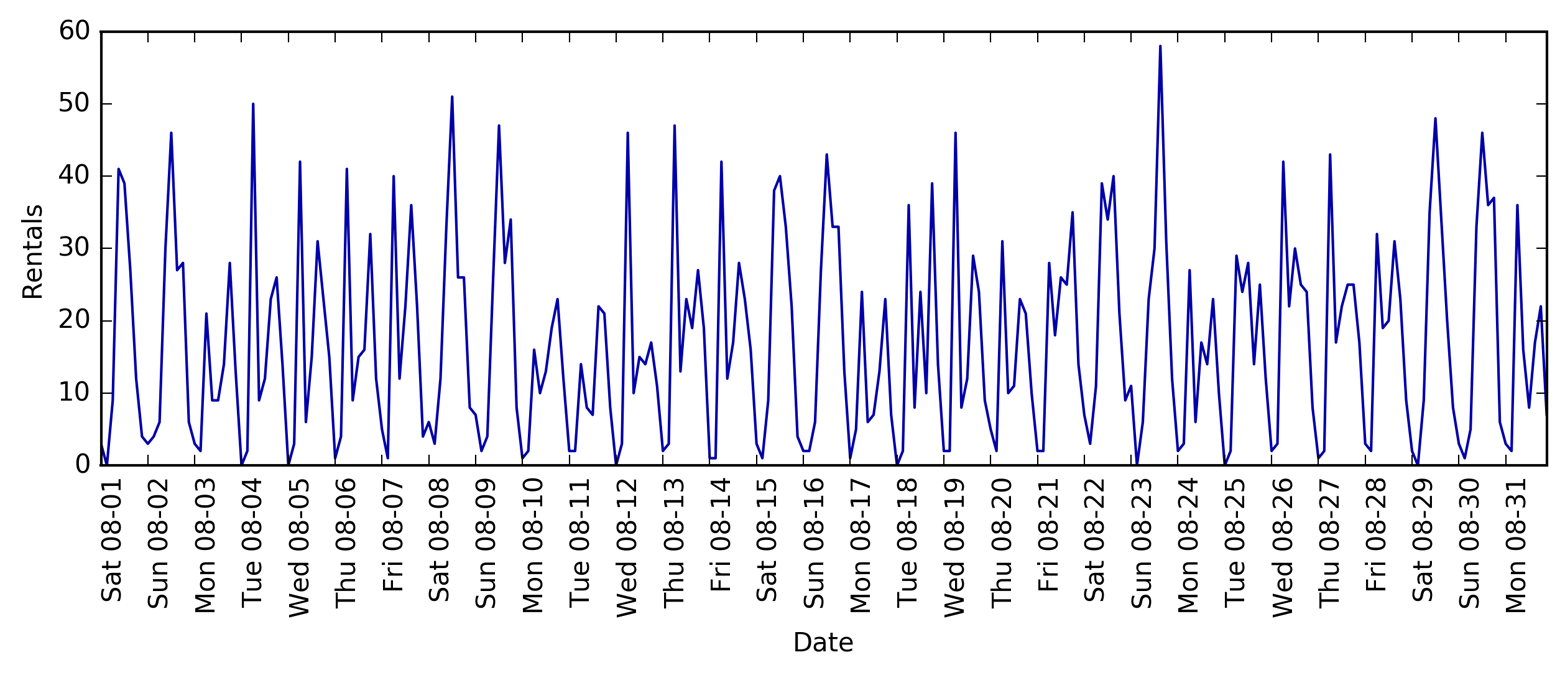
Figura 4-12. Número de bicicletas alquiladas a lo largo del tiempo en una estación de Citi Bike seleccionada
Observando los datos, podemos distinguir claramente el día y la noche para cada intervalo de 24 horas. Los patrones para los días laborables y los fines de semana también parecen ser bastante diferentes. Al evaluar una tarea de predicción sobre una serie temporal como ésta, normalmente queremos aprender del pasado y predecir para el futuro, lo que significa que al hacer una división en un conjunto de entrenamiento y otro de prueba, queremos utilizar todos los datos hasta una fecha determinada como conjunto de entrenamiento y todos los datos posteriores a esa fecha como conjunto de prueba. Así es como utilizaríamos normalmente la predicción de series temporales: dado todo lo que sabemos sobre los alquileres en el pasado, ¿qué creemos que ocurrirá mañana? Utilizaremos los 184 primeros puntos de datos, correspondientes a los 23 primeros días, como conjunto de entrenamiento, y los 64 puntos de datos restantes, correspondientes a los 8 días restantes, como conjunto de prueba.
La única característica que utilizamos en nuestra tarea de predicción es la fecha y la hora en que se produjo un determinado número de alquileres. Así pues, la característica de entrada es la fecha y la hora -digamos, 2015-08-01 00:00:00- y la de salida es el número de alquileres en las tres horas siguientes (tres en este caso, según nuestro DataFrame).
Una forma (sorprendentemente) habitual de almacenar fechas en los ordenadores es utilizando la hora POSIX, que es el número de segundos transcurridos desde enero de 1970 00:00:00 (también conocido como el inicio de la hora Unix). Como primer intento, podemos utilizar esta característica de número entero único como representación de nuestros datos:
In[60]:
# extract the target values (number of rentals)y=citibike.values# convert to POSIX time by dividing by 10**9X=citibike.index.astype("int64").values.reshape(-1,1)//10**9
Primero definimos una función para dividir los datos en conjuntos de entrenamiento y de prueba, construir el modelo y visualizar el resultado:
In[61]:
# use the first 184 data points for training, and the rest for testingn_train=184# function to evaluate and plot a regressor on a given feature setdefeval_on_features(features,target,regressor):# split the given features into a training and a test setX_train,X_test=features[:n_train],features[n_train:]# also split the target arrayy_train,y_test=target[:n_train],target[n_train:]regressor.fit(X_train,y_train)("Test-set R^2: {:.2f}".format(regressor.score(X_test,y_test)))y_pred=regressor.predict(X_test)y_pred_train=regressor.predict(X_train)plt.figure(figsize=(10,3))plt.xticks(range(0,len(X),8),xticks.strftime("%a%m-%d"),rotation=90,ha="left")plt.plot(range(n_train),y_train,label="train")plt.plot(range(n_train,len(y_test)+n_train),y_test,'-',label="test")plt.plot(range(n_train),y_pred_train,'--',label="prediction train")plt.plot(range(n_train,len(y_test)+n_train),y_pred,'--',label="prediction test")plt.legend(loc=(1.01,0))plt.xlabel("Date")plt.ylabel("Rentals")
Hemos visto antes que los bosques aleatorios requieren muy poco preprocesamiento de los datos, por lo que parece un buen modelo para empezar. Utilizamos la característica de tiempo POSIX X y pasamos un regresor de bosque aleatorio a nuestra funcióneval_on_features. La Figura 4-13 muestra el resultado:
In[62]:
fromsklearn.ensembleimportRandomForestRegressorregressor=RandomForestRegressor(n_estimators=100,random_state=0)eval_on_features(X,y,regressor)
Out[62]:
Test-set R^2: -0.04
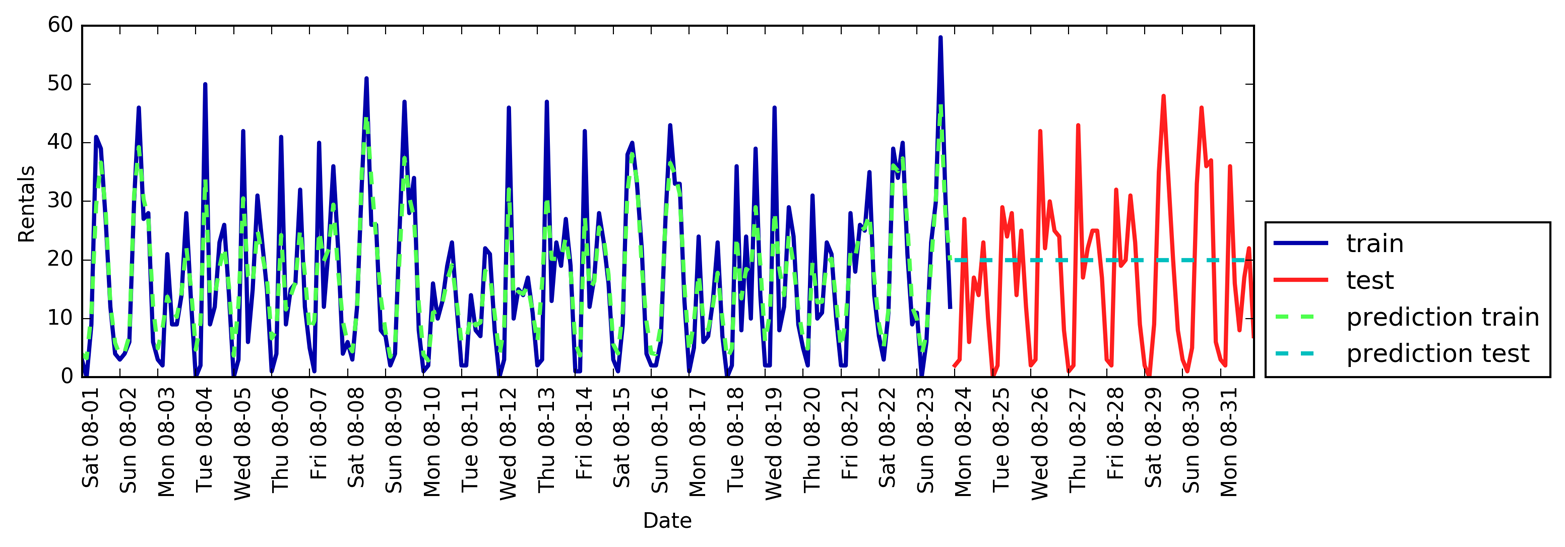
Figura 4-13. Predicciones realizadas por un bosque aleatorio utilizando sólo el tiempo POSIX
Las predicciones en el conjunto de entrenamiento son bastante buenas, como es habitual en los bosques aleatorios. Sin embargo, para el conjunto de pruebas, se predice una línea constante. ElR2 es -0,04, lo que significa que no hemos aprendido nada. ¿Qué ha ocurrido?
El problema reside en la combinación de nuestra característica y el bosque aleatorio. El valor de la característica de tiempo POSIX para el conjunto de pruebas está fuera del rango de valores de la característica en el conjunto de entrenamiento: los puntos del conjunto de pruebas tienen marcas de tiempo que son posteriores a todos los puntos del conjunto de entrenamiento. Los árboles, y por tanto los bosques aleatorios, no pueden extrapolarrangos de características fuera del conjunto de entrenamiento. El resultado es que el modelo simplemente predice el valor objetivo del punto más cercano del conjunto de entrenamiento, que es la última vez que observó algún dato.
Está claro que podemos hacerlo mejor. Aquí es donde entra en juego nuestro "conocimiento experto". Observando las cifras de alquiler de los datos de entrenamiento, hay dos factores que parecen muy importantes: la hora del día y el día de la semana. Así que añadamos estas dos características. En realidad no podemos aprender nada de la hora POSIX, así que eliminamos esa característica. En primer lugar, utilicemos sólo la hora del día. Como muestra la Figura 4-14, ahora las predicciones tienen el mismo patrón para cada día de la semana:
In[63]:
X_hour=citibike.index.hour.values.reshape(-1,1)eval_on_features(X_hour,y,regressor)
Out[63]:
Test-set R^2: 0.60
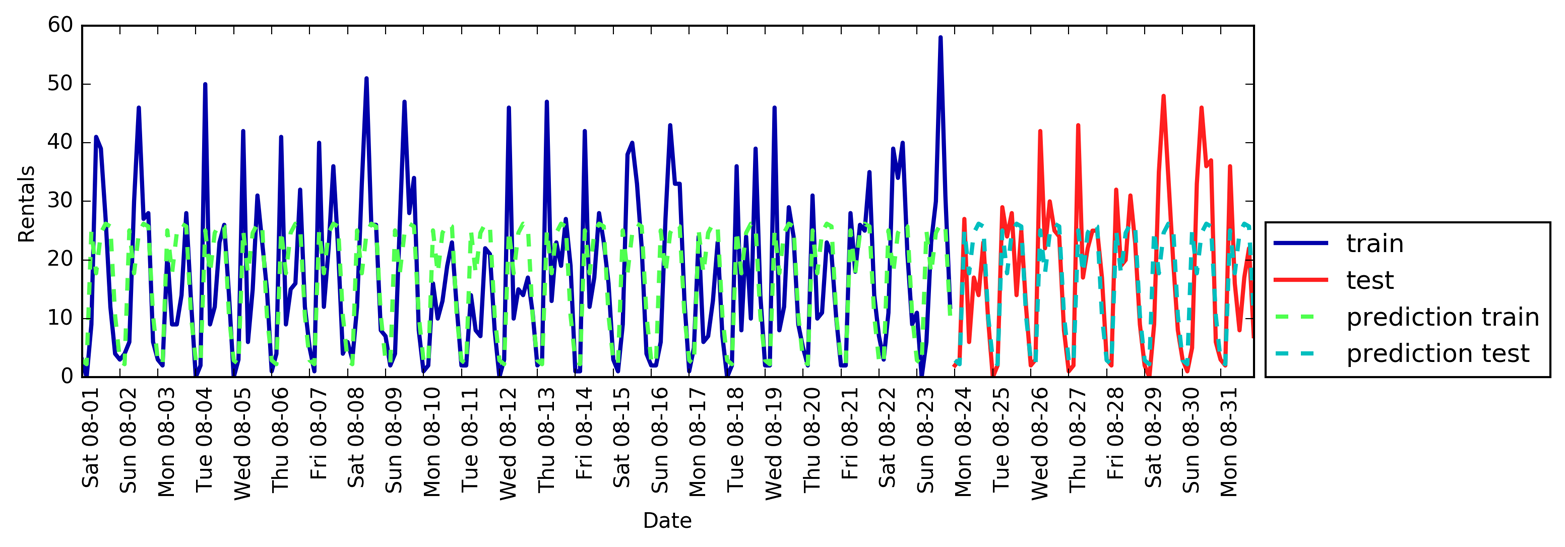
Figura 4-14. Predicciones realizadas por un bosque aleatorio utilizando sólo la hora del día
ElR2 ya es mucho mejor, pero las predicciones fallan claramente en el patrón semanal. Ahora añadamos también el día de la semana (ver Figura 4-15):
In[64]:
X_hour_week=np.hstack([citibike.index.dayofweek.values.reshape(-1,1),citibike.index.hour.values.reshape(-1,1)])eval_on_features(X_hour_week,y,regressor)
Out[64]:
Test-set R^2: 0.84

Figura 4-15. Predicciones con un bosque aleatorio utilizando características de día de la semana y hora del día
Ahora tenemos un modelo que capta el comportamiento periódico teniendo en cuenta el día de la semana y la hora del día. Tiene unR2 de 0,84, y muestra un rendimiento predictivo bastante bueno. Lo que probablemente está aprendiendo este modelo es el número medio de alquileres para cada combinación de día de la semana y hora del día de los 23 primeros días de agosto. En realidad, esto no requiere un modelo complejo como un bosque aleatorio, así que probemos con un modelo más sencillo, LinearRegression (ver Figura 4-16):
In[65]:
fromsklearn.linear_modelimportLinearRegressioneval_on_features(X_hour_week,y,LinearRegression())
Out[65]:
Test-set R^2: 0.13

Figura 4-16. Predicciones realizadas mediante regresión lineal utilizando el día de la semana y la hora del día como características
LinearRegression
funciona mucho peor, y el patrón periódico tiene un aspecto extraño. El motivo es que codificamos el día de la semana y la hora del día mediante números enteros, que se interpretan como variables continuas. Por tanto, el modelo lineal sólo puede aprender una función lineal de la hora del día, y aprendió que a última hora del día hay más alquileres. Sin embargo, los patrones son mucho más complejos que eso. Podemos captarlo interpretando los números enteros como variables categóricas, transformándolos mediante OneHotEncoder (véase la Figura 4-17):
In[66]:
enc=OneHotEncoder()X_hour_week_onehot=enc.fit_transform(X_hour_week).toarray()
In[67]:
eval_on_features(X_hour_week_onehot,y,Ridge())
Out[67]:
Test-set R^2: 0.62

Figura 4-17. Predicciones realizadas por regresión lineal utilizando una codificación de un solo disparo de la hora del día y el día de la semana
Ahora el modelo lineal aprende un coeficiente para cada día de la semana, y un coeficiente para cada hora del día. Eso significa que el patrón "hora del día" se comparte en todos los días de la semana.
Utilizando características de interacción, podemos permitir que el modelo aprenda un coeficiente para cada combinación de día y hora del día (véase la Figura 4-18):
In[68]:
poly_transformer=PolynomialFeatures(degree=2,interaction_only=True,include_bias=False)X_hour_week_onehot_poly=poly_transformer.fit_transform(X_hour_week_onehot)lr=Ridge()eval_on_features(X_hour_week_onehot_poly,y,lr)
Out[68]:
Test-set R^2: 0.85
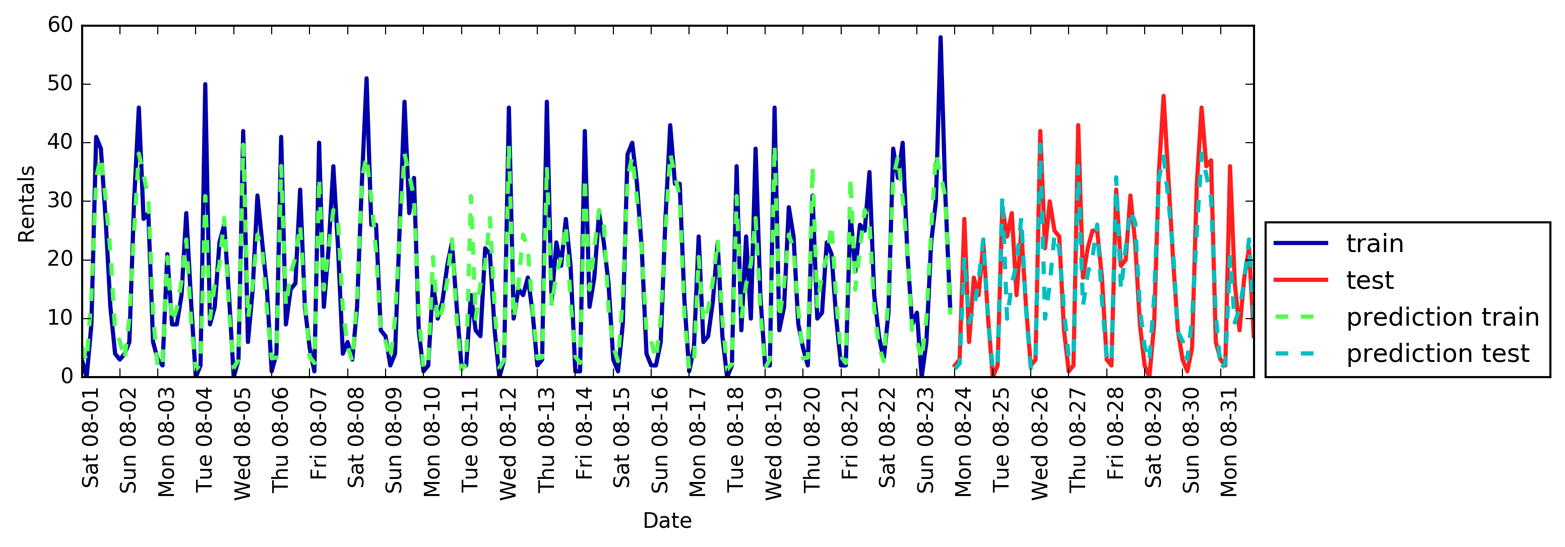
Figura 4-18. Predicciones realizadas por regresión lineal utilizando un producto de las características día de la semana y hora del día
Esta transformación produce finalmente un modelo con un rendimiento similar al del bosque aleatorio. Una gran ventaja de este modelo es que está muy claro lo que se aprende: un coeficiente para cada día y hora. Podemos trazar simplemente los coeficientes aprendidos por el modelo, algo que no sería posible para el bosque aleatorio.
En primer lugar, creamos nombres de rasgos para los rasgos de hora y día:
In[69]:
hour=["%02d:00"%iforiinrange(0,24,3)]day=["Mon","Tue","Wed","Thu","Fri","Sat","Sun"]features=day+hour
A continuación, nombramos todas las características de interacción extraídas porPolynomialFeatures, utilizando el método get_feature_names, y conservamos sólo las características con coeficientes distintos de cero:
In[70]:
features_poly=poly_transformer.get_feature_names(features)features_nonzero=np.array(features_poly)[lr.coef_!=0]coef_nonzero=lr.coef_[lr.coef_!=0]
Ahora podemos visualizar los coeficientes aprendidos por el modelo lineal, como se ve en la Figura 4-19:
In[71]:
plt.figure(figsize=(15,2))plt.plot(coef_nonzero,'o')plt.xticks(np.arange(len(coef_nonzero)),features_nonzero,rotation=90)plt.xlabel("Feature name")plt.ylabel("Feature magnitude")

Figura 4-19. Coeficientes del modelo de regresión lineal utilizando un producto de hora y día
4.9 Resumen y perspectivas
En este capítulo hemos hablado de cómo tratar con distintos tipos de datos (en particular, con variables categóricas). Hemos destacado la importancia de representar los datos de forma adecuada para el algoritmo de aprendizaje automático, por ejemplo, codificando las variables categóricas de una sola vez. También hablamos de la importancia de diseñar nuevas características, y de la posibilidad de utilizar conocimientos de expertos para crear características derivadas de tus datos. En concreto, los modelos lineales podrían beneficiarse enormemente de la generación de nuevas características mediante el agrupamiento y la adición de polinomios e interacciones, mientras que los modelos no lineales más complejos, como los bosques aleatorios y las SVM, podrían aprender tareas más complejas sin ampliar explícitamente el espacio de características. En la práctica, las características que se utilizan (y la correspondencia entre las características y el método) suele ser la pieza más importante para que un enfoque de aprendizaje automático funcione bien.
Ahora que tienes una buena idea de cómo representar tus datos de forma adecuada y qué algoritmo utilizar para cada tarea, el siguiente capítulo se centrará en evaluar el rendimiento de los modelos de aprendizaje automático y en seleccionar la configuración de parámetros adecuada.
1 Esta clase sufrió cambios significativos en la versión 0.20.0, así que asegúrate de que tienes la versión actual de scikit-learn.
2 Se trata de una distribución de Poisson, fundamental para los datos de recuento.
3 Se trata de una aproximación muy burda al uso de la regresión de Poisson, que sería la solución adecuada desde un punto de vista probabilístico.
Get Introducción al Aprendizaje Automático con Python now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

