Hands-On Differential Privacy

Chapter 4. Private Mechanisms

A mechanism is a randomized function that takes a data set as input and returns a sample from a known probability distribution. The mechanism is considered private if it can be proven to satisfy differential privacy. Differentially private mechanisms are designed to convey useful information about the input data set.

This chapter formalizes and generalizes differentially private mechanisms. Private mechanisms build on concepts discussed in Chapter 3, like metric spaces, distance bounds, and stability. These concepts form the foundation of a mathematically rigorous, yet approachable, introduction to a variety of differentially private mechanisms.

Informally, differentially private mechanisms are similar in nature to transformations, in that they transform data in a way that keeps outputs “close.” However, the kind of closeness for mechanism output is different: it is defined over the probabilities of the possible outputs. The unifying perspective is that differential privacy is a system for relating distances.

Each query decomposes into a series of functions: stable transformations followed by one private mechanism and then zero or more postprocessors. If you chain a transformation and mechanism, or a mechanism and postprocessor, you get a new mechanism (see Figure 4-1).

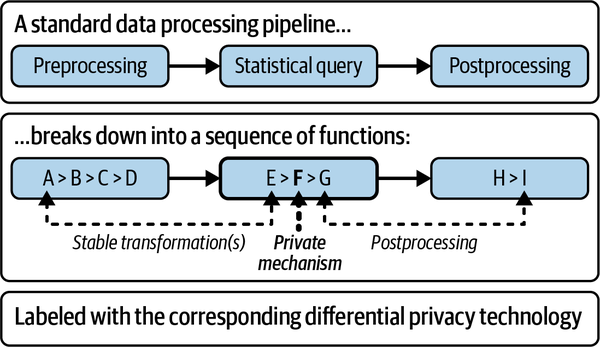
Figure 4-1. A data processing pipeline from both the non-DP perspective and DP perspective

This chapter will also walk through a series of examples to help familiarize you with mechanisms. Each example will demonstrate how to use the mechanism and how it satisfies differential privacy.

Warning

Please be aware that code examples given in this chapter do not satisfy privacy or stability guarantees, because they do not account for finite-precision arithmetic.

Before diving into examples, you will need to become acquainted with two concepts: a privacy measure and the definition of privacy. A privacy measure is the key distinction between mechanisms and transformations, and the definition of privacy presented here is a more general definition of differential privacy that complements the definition of stability from Chapter 3.

Privacy Measure

Differentially private mechanisms return samples from a known probability distribution. Differential privacy limits how dissimilar, or distinguishable, these probability distributions can be when run on any two neighboring data sets.

The dissimilarity or distinguishability between distributions is precisely quantified by their divergence. Just as there are a variety of metrics to compute the distance between data sets, there are also a variety of divergences that can be used to measure the distance between distributions.

This chapter will only introduce one privacy measure: the max-divergence. The next chapter focuses on introducing other privacy measures.

Privacy Measure: Max-Divergence

Privacy loss parameters (like $ϵ$) represent an upper bound on the divergence between the output distributions on any two neighboring data sets.

There is a measure that corresponds to the kind of divergence used in pure $ϵ$-DP. To find this measure, first recall the definition of pure differential privacy from Chapter 2:

Pure differential privacy

A mechanism $M(·)$ is $ϵ$-differentially private if for all possible neighboring data sets $x$ and $x^{\text{'}}$, and every possible output $y$:

$$Pr[M\left(x\right)=y]\le Pr[M\left(x^{\text{'}}\right)=y]·e^{ϵ}$$

Recall how this definition was reworded to isolate $ϵ$:¹

$$\underset{x\sim x^{\text{'}}}{max}\underset{z\in supp\left(M\right(·\left)\right)}{max}ln\left(\frac{Pr\left[M\right(x)=z]}{Pr[M\left(x^{\text{'}}\right)=z]}\right)\le ϵ$$

You can rewrite this definition by substituting the max-divergence.

Max-divergence

The max-divergence between two probability distributions $Y$ and $Y^{\text{'}}$ is:²

$$D_{\infty }(Y,Y^{\text{'}})=\underset{y\in supp\left(Y\right)}{max}ln\left(\frac{Pr[Y=y]}{Pr[Y’=y]}\right)$$

With the max-divergence, the definition of pure differential privacy simplifies:

Pure differential privacy

A mechanism $M$ is $ϵ$-differentially private if:

$$\underset{x\sim x^{\text{'}}}{max}{D}_{\infty }(M\left(x\right),M\left(x^{\text{'}}\right))\le ϵ$$

This representation of pure-differential privacy is appealing because it is directly interpretable: the privacy loss can be no greater than $ϵ$.

In this notation, $M\left(x\right)$ doesn’t refer to the output of the mechanism but rather to a random variable. That is, the divergence is computing the distance between the distributions of the releases, not of the releases themselves.

Metric Versus Divergence Versus Privacy Measure

While metrics and divergences may feel very similar, they differ primarily in that divergences compute the distance between distributions, whereas metrics compute the distance between data sets.

Note

The function that computes a divergence customarily uses a capital D instead of a lowercase d, as is used in metrics.

Divergences also don’t satisfy two of the three requirements of metrics:

• Divergences are not symmetric; for any two distributions $A$ and $B$, $D(A,B)$ is not necessarily equal to $D(B,A)$.

• Divergences do not satisfy the triangle inequality; for any three distributions $A$, $B$ and $C$, $D(A,B)+D(B,C)$ may be less than $D(B,C)$.

Therefore, measures are categorically not metrics. You may even wonder how measures could be useful, given that they are not symmetric. It turns out that this is not particularly impactful in differential privacy, because you only care about the bigger of the two divergences (the case of the greatest distinguishability).

The key requirement for a divergence to qualify as a privacy measure is that it must be closed under postprocessing. That is, the divergence must have the property that you cannot postprocess a random variable in a way that will increase the divergence. Many types of divergence in probability theory do not satisfy this requirement, but this is an essential requirement for privacy: an adversary should never be able to process the outputs of a mechanism in a way that reveals more information about the sensitive data.

Now that you have some familiarity with privacy measures, you are ready for the definition of privacy.

Private Mechanisms

Private mechanisms share the same intuition and general structure as stable transformations but differ in that the output metric has been replaced with a privacy measure.

The definition of privacy here is more general than has been previously discussed, and is abstracted in the same way as transformations in Chapter 3.

Private mechanism

A mechanism $M(·)$ is $(b_{in},b_{out})$-private with respect to an input metric $IM$ and a privacy measure $PM$ if, for any choice of data sets $x$ and $x^{\text{'}}$ such that $d_{IM}(x,x^{\text{'}})\le b_{in}$, then $D_{PM}(M\left(x\right),M\left(x^{\text{'}}\right))\le b_{out}$.³

The input distance is a bound on how much an individual can influence a data set, and the output distance is a bound on how much an individual can influence the output distribution—in other words, how private the data release is.

Compared to the previous definition of privacy in Chapter 2, this definition of privacy better shows how the privacy loss parameter $b_{out}$ complements $b_{in}$. This definition also clearly defines how two data sets may differ. Together, the input and output distance fully characterize the privacy guarantee of a differentially private algorithm.

Notice how similar this definition is to the definition of stability. The key change is the replacement of the output metric with a privacy measure.

Metric spaces are another concept that carries over from stable transformations. Transformations are a way to map data from one metric space to another metric space. Mechanisms are a way to map data from a metric space to a differentially private release. Metric spaces are essential for the input and output of transformations, and the input of mechanisms, but are not a good fit to model the output of mechanisms. There is no need to keep track of the output domain or find a suitable metric, as the output is already private and will remain that way due to closure under postprocessing.

You now have the framework in place to learn a vast collection of algorithms used in differential privacy. Just as was done in Chapter 3, this chapter will cover many examples of private mechanisms using the same proof technique: first, ask how much outputs can change (but this time under the privacy measure), and then simplify the resulting expression.

Now, let’s revisit randomized response and the Laplace mechanism. While both were discussed in previous chapters, now you will study them in the context of this generalized definition.

Randomized Response

Randomized response was chosen for an introduction to differential privacy in Chapter 2 precisely because the input metric space is so simple as to be somewhat implicit. The input domain just consists of all booleans ($\{\top ,\perp \}$), and the input metric is the discrete distance.

Discrete distance

The discrete distance between two values $x$ and $x^{\text{'}}$ is 0 if $x=x^{\text{'}}$, otherwise 1.

Justified by the prior proof, you can claim that the randomized response mechanism is $(1,ln(p/(1-p)\left)\right)$-private under the discrete distance and pure-DP, because when $d_{\mathrm{Discrete}}(u,v)\le 1$, then $D_{\infty }(M\left(u\right),M\left(v\right))\le ln(p/(1-p))$.

A common way to generalize the randomized response mechanism is to replace the input domain with some known discrete set, as exemplified in the following code:

import opendp.prelude as dp
from random import random, choice
import math

def make_randomized_response_multi(p: float, support: list):
    """
    :param p: probability of returning true answer
    :param support: all possible outcomes"""
    dp.assert_features("contrib", "floating-point")
    t = len(support)
    
    # CONDITIONS (see exercise 2)
    if t != len(set(support)):
        raise ValueError("elements in support must be distinct")
    if p < 1 / t or p > 1:
        raise ValueError(f"prob must be within [{1 / t}, 1.0]")
    
    def f_randomize_response(arg):
        lie = choice([x for x in support if arg != x])
        return arg if arg in support and random() < p else lie

    c = math.log(p / (1 - p) * (t - 1))

    return dp.m.make_user_measurement(
        input_domain=dp.atom_domain(T=type(support[0])),
        input_metric=dp.discrete_distance(),
        output_measure=dp.max_divergence(T=float),
        function=f_randomize_response,
        privacy_map=lambda b_in: min(max(b_in, 0), 1) * c,
        TO=type(support[0])
    )

You could use this measurement to privately release someone’s multiple-choice answer:

rr_multi = make_randomized_response_multi(p=.4, support=["A", "B", "C", "D"])

print('privately release a response of "B":', rr_multi("B"))
print('privacy expenditure ε:',               rr_multi.map(1))  # ~0.288

The OpenDP Library contains a secure implementation of this mechanism.

It is left as an exercise to demonstrate that this generalization of randomized response is private under the discrete distance and pure DP.

The Vector Laplace Mechanism

Instead of just adapting the scalar-valued Laplace mechanism, as defined in Chapter 2, to the updated definition, this section also generalizes the Laplace to operate over vector aggregates with bounded $L^1$ sensitivity. In this case, the Laplace mechanism is applied to a $k$-dimensional vector $a=[a_1,a_2,...,a_k]$, where $a$ is a data set of aggregates that is typically output by a stable transformation, like a vector-valued sum transformation.

The vector-valued Laplace mechanism can be written in several equivalent ways. Each of these ways returns a sample from the Laplace distribution centered at $a$ with scale $r$:

$$\begin{array}{cccccccccc}\hfill M\left(a\right)& =[a_1+\mathrm{Lap}(\mu =0,r),\hfill & & a_2+\mathrm{Lap}(\mu =0,r),\hfill & & ...,\hfill & & a_k+\mathrm{Lap}(\mu =0,r)\hfill & & ]\hfill \\ & =[\mathrm{Lap}(\mu =a_1,r),\hfill & & \mathrm{Lap}(\mu =a_2,r),\hfill & & ...,\hfill & & \mathrm{Lap}(\mu =a_k,r)\hfill & & ]\hfill \\ & =\mathrm{VLap}(\mu =a,r)\hfill & & \text{equivalent}\text{representations}\hfill \end{array}$$

This mechanism satisfies pure differential privacy, where $b_{out}$ corresponds to $ϵ$, and the privacy measure is the max-divergence:

$$\begin{array}{cc}& \underset{a\sim a^{\text{'}}}{max}{D}_{\infty }(M\left(a\right),M\left(a^{\text{'}}\right))\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in supp\left(M\right(·\left)\right)}{max}ln\left(\frac{Pr\left[M\left(a\right)=y\right]}{Pr\left[M\left(a^{\text{'}}\right)=y\right]}\right)\hfill & & \text{substitute}{D}_{\infty }\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in ℝ}{max}ln\left(\frac{Pr\left[\mathrm{VLap}(a,r)=y\right]}{Pr\left[\mathrm{VLap}(a^{\text{'}},r)=y\right]}\right)\hfill & & \text{substitute}M(·)\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in ℝ}{max}ln\left(\frac{{\prod }_{i=1}^k\frac{1}{2r}exp\left(-\frac{|a_i-y_i|}{r}\right)}{{\prod }_{i=1}^k\frac{1}{2r}exp\left(-\frac{|a_i^{\text{'}}-y_i|}{r}\right)}\right)\hfill & & \text{use}\text{pdf}\text{of}\text{multivariate}\text{Laplace}\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in ℝ}{max}\sum _{i=1}^{k}ln\left(\frac{exp\left(-\frac{|a_i-y_i|}{r}\right)}{exp\left(-\frac{|a_i^{\text{'}}-y_i|}{r}\right)}\right)\hfill & & \text{extract}\text{the}\text{sum}\text{by}\text{log}\text{rules}\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in ℝ}{max}\sum _{i=1}^k\frac{|a_i^{\text{'}}-y_i|-|a_i-y_i|}{r}\hfill & & \text{exp}\text{and}\text{ln}\text{cancel}\hfill \\ & \le \underset{a\sim a^{\text{'}}}{max}\frac{{\sum }_{i=1}^k|a_i-a_i^{\text{'}}|}{r}\hfill & & \text{by}\text{reverse}\text{triangle}\text{inequality}\hfill \\ & =\frac{{max}_{a\sim a^{\text{'}}}{\parallel a-a^{\text{'}}\parallel }_1}{r}\hfill & & \text{by}\text{definition}\text{of}{L}^1\text{distance}\hfill \end{array}$$

Observe how the Laplace mechanism complements queries with known $L^1$ sensitivity: the $L^1$ sensitivity even appears directly in the formula. Substituting ${max}_{x\sim x^{\text{'}}}{\parallel y-y^{\text{'}}\parallel }_1=b_{in}$ gives the final bound, which holds for any possible pair of adjacent data sets:

$$ma{x}_{x\sim x^{\text{'}}}{D}_{\infty }(M\left(x\right),M\left(x^{\text{'}}\right))\le \frac{b_{in}}{r}$$

Thus we can say the divergence between output distributions will never be greater than $\frac{b_{in}}{r}$, so the smallest upper bound on divergences $ϵ$ is $\frac{b_{in}}{r}$.

In the overall scheme of relating distances, this function that samples Laplace noise is $(b_{in},b_{out})$-private, where $b_{out}$ is $\frac{b_{in}}{r}$, $b_{in}$ is with respect to the $L^1$ distance, and $b_{out}$ is in terms of $ϵ$ pure-DP.

Many very common queries (like counts, sums, and means) are well-suited for the Laplace mechanism.

Discrete Laplace mechanism (geometric mechanism)

Some statistics are more naturally represented as integers, like the count. The Laplace mechanism has a variation supported on the integers: the discrete Laplace mechanism. The discrete Laplace mechanism has similar arguments as the Laplace mechanism, but its noise is sampled from the discrete Laplace distribution, which is supported on the integers $\mathbb{Z}$:

$$Pr[\mathrm{DLap}(\mu ,r)=y]=\frac{{exp}^{1/r}-1}{{exp}^{1/r}+1}·exp\left(-\frac{|x-\mu |}{r}\right),$$

where $\mu$ is the integer-valued shift, and $r$ is the real-valued positive scale.

Another common name for the mechanism is the geometric mechanism, because the tails follow the geometric distribution, as shown in Figure 4-2.

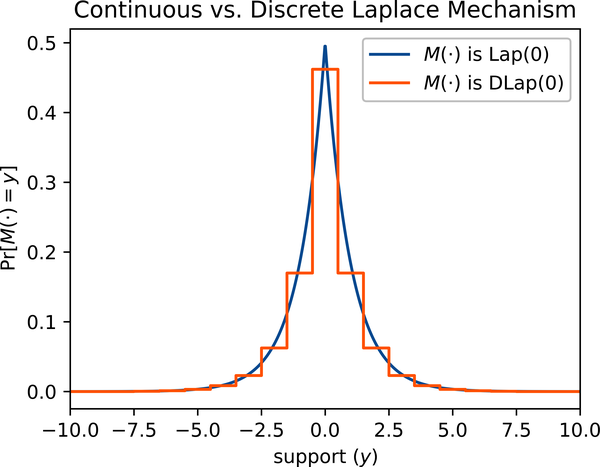
Figure 4-2. Laplace (Lap) versus geometric (DLap) distributions

An abridged proof is given for the privacy map on the scalar-valued discrete Laplace mechanism:

$$\begin{array}{cc}& \underset{a\sim a^{\text{'}}}{max}{D}_{\infty }(M\left(a\right),M\left(a^{\text{'}}\right))\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in \mathbb{Z}}{max}ln\left(\frac{Pr\left[\mathrm{DLap}(a,r)=y\right]}{Pr\left[\mathrm{DLap}(a^{\text{'}},r)=y\right]}\right)\hfill & & \text{substitute}{M}_{\infty }\text{and}M(·)\hfill \\ & =\underset{a\sim a^{\text{'}}}{max}\underset{y\in \mathbb{Z}}{max}\frac{|a’-y|-|a-y|}{r}\hfill & & \text{substitute}\text{pdf}\text{and}\text{simplify}\hfill \\ & \le \frac{{max}_{a\sim a^{\text{'}}}|a-a^{\text{'}}|}{r}\hfill & & \text{by}\text{reverse}\text{triangle}\text{inequality}\hfill \\ & =\frac{b_{in}}{r}\hfill & & \text{by}\text{definition}\text{of}\text{absolute}\text{distance}\hfill \end{array}$$

The same can be shown for a vector-valued version of the mechanism (this is left as an exercise).

While the Laplace mechanism is an incredibly useful primitive, it is not always the best-suited algorithm to privatize your query. The Laplace mechanism can only privatize numbers, whereas some queries may involve private selection from a set or detection of the first anomaly in a sequence of events. Some numeric queries may also lose significant utility when the addition of noise perturbs the release beyond some unknown threshold.

Exponential Mechanism

As defined in Chapter 2, the exponential mechanism is used for private selection from a set of candidates.⁴ In this setting, you know what the set of possible outputs can be (your candidate set), and you want to choose one (or more) candidates from that set that best answers a query on the private data set. The best candidate is defined according to a scoring function that assigns the score $s_c=\mathrm{score}(x,c)$ to a candidate $c$ for a data set $x$.

A motivating example (similar to the seminal paper) involves pricing: imagine that you have decided to sell off each of your baseball cards and want to choose the best price point to maximize profit. If you set the price too high, you will fail to find buyers, whereas setting the price too low will also mean losing money. This problem is not suitable for the Laplace mechanism, because a small perturbation to the chosen price may result in an extreme loss in realized profit, as there may be many buyers right at the edge. In this setting, assume that prospective buyers will tell you what they are willing to spend, so long as this information isn’t leaked to other buyers.

To use the exponential mechanism, you must define a set of potential price points before conferring with the buyers. This set of potential price points forms the candidate set. The exponential mechanism selects one of those candidates based on the private information from the buyers.

Just like many other DP mechanisms, you can break the algorithm into a stable transformation and a private mechanism. The stable transformation is the scoring function, which maps the private data set to a vector of scores. The private mechanism is the exponential mechanism, which selects one of the candidates based on the scores. A small postprocessor is then employed to index into the candidate set to retrieve the final selection.

You can think of the scoring as a data set aggregation, just like you might think of a data set sum as an aggregation. You can define a scoring transformation $T(·)$ that aggregates a data set down to a vector of scores, where each score corresponds to a different candidate price point.

You can then use the infinity norm $L^{\infty }$ to define a metric that computes the distance between adjacent score vectors. The sensitivity of this score vector is based on the greatest amount any one score may change.

$L^{\infty }$ distance

The $L^{\infty }$ distance between two vectors of scores and $s=[s_1,s_2,...,s_k]$ and $s^{\text{'}}=[s_1^{\text{'}},s_2^{\text{'}},...,s_k^{\text{'}}]$ is $d_{L\infty }(s,s^{\text{'}})={\parallel s-s’\parallel }_{\infty }={max}_i|s_i-s_i^{\text{'}}|$.

The $L^{\infty }$ metric is used on the output of the scorer and input to the exponential mechanism.

Quantile Score Transformation

An example of a useful scoring function is the quantile score transformation. This transformation assigns a score to each candidate in a vector $c_i$ in a set of candidates $C$.⁵

The score function gives higher scores to candidates nearer the $\alpha$-quantile in the data set $x$:

$$\mathrm{score}(x,c)=-\left|\right(1-\alpha )·\#(x<c)-\alpha ·\#(x>c\left)\right|$$

The score function is based on the number of records in the data set that are less than $c$ (denoted $\#(x<c)$) or greater than $c$ (denoted $\#(x>c)$) for each candidate quantile $c$.

If you’d like to find the median, let $\alpha$ = 0.5. Candidates that evenly divide the data set will have the greatest possible score of zero, because the two terms will cancel each other out. The more unevenly that a candidate divides the data set, the more negative the score will become. It may help to think through how the scoring function will behave for other choices of $\alpha$, like zero or one.

As written in Python, the score transformation executes this score function for each candidate, returning a vector of scores (one score for each candidate):

def make_score_quantile_finite(candidates, alpha):
    dp.assert_features("contrib")
    assert 0 <= alpha <= 1, "alpha must be in [0, 1]"
    assert len(set(candidates)) == len(candidates), "candidates must be unique"
    def f_score_candidates(x):
        """Assuming `x` is sorted, scores every element in `candidates`
        according to rank distance from the `alpha`-quantile."""
        num_leq = (np.array(x)[None] <= candidates[:, None]).sum(axis=1)
        return -abs(num_leq - alpha * len(x))
    
    return dp.t.make_user_transformation(
        input_domain=dp.vector_domain(dp.atom_domain(T=type(candidates[0]))),
        input_metric=dp.symmetric_distance(),
        output_domain=dp.vector_domain(dp.atom_domain(T=float)),
        output_metric=dp.linf_distance(T=float),
        function=f_score_candidates,
        stability_map=lambda b_in: b_in * max(alpha, 1 - alpha))

The scoring transformation is stable because, when the distance between the input data sets is bounded, the distance between the output vectors is also bounded under the $L^{\infty }$ distance:

$$\underset{x\sim x^{\text{'}}}{max}{d}_{L\infty }(x,x^{\text{'}})=\underset{x\sim x^{\text{'}}}{max}{\parallel \mathrm{score}(x,c_i)-\mathrm{score}(x^{\text{'}},c_i)\parallel }_{\infty }\le b_{in}·max(\alpha ,1-\alpha )$$

This bound skips over many steps for brevity, but it would be good practice to fill in the gaps yourself. Start by substituting the definition of $S$, and then consider the cases of adding or removing a single record from the data set.

Finite support exponential mechanism

We are now ready to define the exponential mechanism when the input is a score vector $x$, containing one score for each candidate. The likelihood of selecting the $i^{th}$ candidate is proportional to the exponentiated score:

$$L\left(i\right)\sim exp\left(\frac{x_i}{\tau }\right)$$

The $\tau$ parameter is the temperature. The temperature behaves in the same way as the scale parameter for additive noise distributions: higher temperatures result in more entropic sampling, which better masks the influence of individuals on the scores.

Note

Because of the exponential, better scores become exponentially more likely to be selected, which leads to nice utility guarantees.

You include a normalization term for the likelihoods to become probabilities:

$$Pr[Y=i]=\frac{exp\left(\frac{x_i}{\tau }\right)}{{\sum }_{j}exp\left(\frac{x_j}{\tau }\right)}$$

To show the exponential mechanism is private, start by measuring the divergence between the two distributions:

$$\begin{array}{cc}& \underset{s\sim s^{\text{'}}}{max}{D}_{\infty }(M\left(s\right),M\left(s^{\text{'}}\right))\hfill \\ & =\underset{s\sim s^{\text{'}}}{max}ln\left(\frac{exp\frac{s_i}{\tau }}{{\sum }_{k}exp\frac{s_k}{\tau }}/\frac{exp\frac{s_i^{\text{'}}}{\tau }}{{\sum }_{k}exp\frac{s_k^{\text{'}}}{\tau }}\right)\hfill & & \text{substitute}\text{into}{D}_{\infty }\text{definition}\hfill \\ & =\underset{s\sim s^{\text{'}}}{max}ln\left(\frac{exp\frac{s_i}{\tau }}{exp\frac{s_i^{\text{'}}}{\tau }}\right)+ln\left(\frac{{\sum }_{k}exp\frac{s_k^{\text{'}}}{\tau }}{{\sum }_{k}exp\frac{s_k}{\tau }}\right)\hfill & & \text{break}\text{the}\text{ln}\hfill \\ & =\underset{s\sim s^{\text{'}}}{max}\frac{s_i-s_i^{\text{'}}}{\tau }+ln\left(\frac{{\sum }_{k}exp\frac{s_k^{\text{'}}-s_k}{\tau }exp\frac{s_k}{\tau }}{{\sum }_{k}exp\frac{s_k}{\tau }}\right)\hfill & & \text{factor}{s}_i^{\text{'}}=s_i^{\text{'}}-s_i+s_i\hfill \\ & \le \underset{s\sim s^{\text{'}}}{max}\frac{{max}_j(s_j-s_j^{\text{'}})}{\tau }+\frac{{max}_j(s_j^{\text{'}}-s_j)}{\tau }\hfill & & \text{take}\text{max}\text{of}\text{differences}\hfill \\ & =\frac{2b_{in}}{\tau }\hfill & & \text{since}{b}_{in}=\underset{s\sim s^{\text{'}}}{max}\underset{j}{max}(s_j-s_j^{\text{'}})\hfill \end{array}$$

From this, we can say that for any possible choice of score data sets $s$ and $s^{\text{'}}$, the divergence can never be greater than $\frac{2b_{in}}{\tau }$. Since $ϵ$ is the maximum divergence over any pair of neighboring data sets, then $ϵ=\frac{2b_{in}}{\tau }$.

Notice how this is the same as the relationship between $ϵ$, $b_{in}$ and the scale (temperature) in the Laplace mechanism. The reason is that the exponential mechanism is a generalization of the Laplace mechanism. In fact, you can choose a scoring function that recovers the Laplace mechanism:

$$\mathrm{score}(x,c)=-|x-c|$$

The sampling distribution of an exponential mechanism parameterized by this scoring function is a Laplace distribution:

$$exp\left(\frac{-|x-c|}{\tau }\right)$$

A key difference between the two mechanisms is that the exponential is looser by a factor of 2. This is the price to pay for using a more general mechanism: the exponential mechanism can be used with scoring functions where a change in the underlying data set causes one score to increase and another score to decrease. You can avoid this penalty if the scoring function is monotonic (all scores will differ in the same direction on an adjacent data set). This can be captured mathematically with a metric extracted directly from the proof of the exponential:

Range distance

The range distance is $d_{\text{Range}}(x,x^{\text{'}})={max}_i(x_i-x_i^{\text{'}})-{min}_i(x_i-x_i^{\text{'}})$, where $x$ and $x^{\text{'}}$ are numeric vectors.⁶

Continuing the previous derivation from right before this metric is used:

$$\begin{array}{cccc}& =\underset{s\sim s^{\text{'}}}{max}\frac{s_i-s_i^{\text{'}}}{\tau }+ln\left(\frac{{\sum }_{k}exp\frac{s_k^{\text{'}}-s_k}{\tau }exp\frac{s_k}{\tau }}{{\sum }_{k}exp\frac{s_k}{\tau }}\right)\hfill & & \text{continuing}\text{from}\text{above}\hfill \\ & \le \frac{{max}_j(s_j-s_j^{\text{'}})}{\tau }-\frac{{min}_j(s_j-s_j^{\text{'}})}{\tau }\hfill & & \text{take}\text{max}\text{of}\text{differences,}\text{flip}\text{sign}\hfill \\ & =\frac{b_{in}}{\tau }\hfill \end{array}$$

Where $b_{in}={max}_{s\sim s^{\text{'}}}{max}_j(s_j-s_j^{\text{'}})-{min}_j(s_j-s_j^{\text{'}})$.

With this new metric, the exponential mechanism is no longer looser by a factor of two, but the sensitivity of the quantile score transformation gains a factor of two because it is not monotonic. Going forward, all mechanisms introduced for private selection will use the range metric.

The derived bound ($\tau =\frac{b_{in}}{ϵ}$) is referred to as temperature in the following implementation. The intuition behind the naming is that particles have greater disorder, and more entropy, as the temperature rises. Similarly, the following implementation tends toward a maximally entropic, perfectly private, uniformly distributed output as the temperature parameter increases:

def make_finite_exponential_mechanism(temperature, monotonic=False):
    """Privately select the index of the best score from a vector of scores"""
    dp.assert_features("contrib", "floating-point")
    def f_select_index(scores):
        scores = np.array(scores)
        scores -= scores.max() # for numerical stability; doesn't affect probs

        likelihoods = np.exp(scores * temperature) # each candidate's likelihood
        probabilities = likelihoods / likelihoods.sum() # normalize
        # use inverse transform sampling from the cdf to select a candidate
        return np.argmax(probabilities.cumsum() >= np.random.uniform())
    
    return dp.m.make_user_measurement(
        input_domain=dp.vector_domain(dp.atom_domain(T=float)),
        input_metric=dp.linf_distance(T=float, monotonic=monotonic),
        output_measure=dp.max_divergence(T=float),
        function=f_select_index,
        privacy_map=lambda b_in: b_in / temperature * (1 if monotonic else 2))

As shown, this mechanism privately selects the single candidate with approximately the highest score. Together with the scorer transformation, since each function is stable, the entire function is stable. Starting from a bound on the distance between the input data sets, you can bound the distance between score vectors (sensitivity). Then, you can use this sensitivity to bound the distance between the probabilities of selecting each candidate. This gives the final bound on privacy.

To make use of this mechanism in practice, chain the scorer, mechanism, and finally postprocessor:

def make_private_quantile_in_candidates(candidates, alpha, scale):
    return make_score_quantile_finite(candidates, alpha=alpha) >> \
        make_finite_exponential_mechanism(scale) >> \
        (lambda idx: candidates[idx]) # postprocess: retrieve the candidate

Note

The noisy score itself cannot be released. If you would like to release it, then prepare a separate query and use composition to release both. Since the score vector has bounded $L^{\infty }$ sensitivity, then an index into the score vector can itself be seen as a data set transformation from a score vector to a score scalar with sensitivity measured via the absolute distance. You are already familiar with a mechanism on this metric space (Laplace)!

The previous example samples from a distribution with a finite number of possible outcomes. In general, the exponential mechanism samples from some scoring distribution, where values of the support with more utility are given higher scores, and are thus more likely to be selected. The exponential mechanism requires sampling from some distribution of scores, and in theory this scoring distribution could be just about anything. In practice, the exponential mechanism is only implemented for distributions from which finite computers can sample. Sometimes you can employ a clever trick to accomplish this sampling. The following variation of the exponential mechanism samples from a score distribution supported on an interval of real numbers.

Piecewise-Constant Support Exponential Mechanism

It can also be possible to efficiently implement the exponential mechanism when the support is a continuous interval. If the score distribution’s density function is piecewise constant, then the sampling can be done in stages:⁷

1. Partition the interval by the data points

2. Privately select an interval using the finite-support exponential

3. Sample uniformly from the discretized interval

The following algorithm is a modification of the finite-support mechanism, where some key changes are marked “NEW” in comments:

def make_interval_exponential_mechanism(bounds, scorer, entropy):
    L, U = bounds; assert L < U, "bounds must be increasing"
    def f_select_from_interval(x):
        # NEW: sort, clip and bookend x with bounds
        x = np.concatenate(([L], np.clip(np.sort(x), *bounds), [U]))

        scores = np.array(scorer(x)) # score all intervals in x
        scores -= scores.max() # for numerical stability; doesn't affect probs

        # NEW: area = width      * height; gives each interval's likelihood
        likelihoods = np.diff(x) * np.exp(scores * entropy)
        probabilities = likelihoods / likelihoods.sum() # normalize

        # use inverse transform sampling from the cdf to select an interval
        index = np.argmax(probabilities.cumsum() >= np.random.uniform())
        # NEW: sample uniformly from the selected interval
        return np.random.uniform(low=x[index], high=x[index + 1])
    
    mono = 1 if "monotonic" in str(scorer.output_metric) else 2
    return dp.m.make_user_measurement(
        input_domain=scorer.input_domain,
        input_metric=scorer.input_metric,
        output_measure=dp.max_divergence(T=float),
        function=f_select_from_interval,
        privacy_map=lambda b_in: scorer.map(b_in) / entropy * mono)

The quantile score transformation is similarly modified:

def make_score_quantile_interval(alpha, T=float):
    assert 0 <= alpha <= 1, "alpha must be in [0, 1]"
    def f_score_quantile_interval(x):
        """Assuming `x` is sorted, scores each gap in `x`
        according to rank distance from the `alpha`-quantile."""
        ranks = np.arange(len(x) - 1)
        left, right = abs(ranks - alpha * len(x)), abs(ranks + 1 - alpha * len(x))
        return -np.minimum(left, right)
    
    return dp.t.make_user_transformation(
        input_domain=dp.vector_domain(dp.atom_domain(T=T)),
        input_metric=dp.symmetric_distance(),
        output_domain=dp.vector_domain(dp.atom_domain(T=float)),
        output_metric=dp.linf_distance(T=float),
        function=f_score_quantile_interval,
        stability_map=lambda b_in: b_in * max(alpha, 1 - alpha))

This time, the scoring function assumes the input data is sorted and returns a vector of ranks staggered around the expected alpha-quantile.

The exponential mechanism on an interval support uses the finite-support sampler to choose one interval (out of N + 1, since two boundary points were added):

def make_private_quantile_in_bounds(bounds, alpha, scale):
    scorer = make_score_quantile_interval(alpha)
    return make_interval_exponential_mechanism(bounds, scorer, scale)

meas = make_private_quantile_in_bounds(bounds=(0, 100.), alpha=.5, scale=1.)
print(meas(np.random.normal(22., scale=12, size=1000))) # ~> 21.37
print(meas.map(1)) # -> 1 = ε

Sampling from the distribution of the exponential mechanism is often computationally intractable, but sampling is possible for some well-behaved distributions, like finite and piecewise constant. Many more algorithms have been developed for sampling from other distributions, such as an infinite discrete support,⁸ convex sets,⁹ and spheres.¹⁰

Top-K

Both examples shown thus far are examples of selecting the top-1 candidate. However, in many common use cases, you instead want to select the top-$k$ candidates.

The top-$k$ can be released by peeling.¹¹ Repeatedly run the exponential mechanism on the data to select one candidate, and each time remove the selected candidate from the candidate set. The resulting output gives you a ranked ordering of the top-$k$ candidates. The final privacy loss parameter is derived via the sequential composition of each of the mechanism invocations.

Unfortunately, this approach is computationally inefficient. You must run the mechanism $k$ times, each time with one fewer candidate. There is an equivalent approach that resolves this while also bringing other convenient benefits: Report Noisy Max.

Report Noisy Max Mechanisms

Report Noisy Max (RNM) is a family of algorithms for private selection from a finite set of candidates.

To privately select the index of the best score from a vector of scores $S=[s_1,s_2,...,s_k]$ in a way that satisfies $ϵ$-differential privacy, return $\underset{i}{\text{argmax}}{s}_i+z_i$, where $z_i$ denotes the $i^{th}$ independent and identically distributed sample from an appropriate distribution. There are several possible distributions where this mechanism satisfies $ϵ$-differentially privacy.

For example, noisy max with noise sampled from a carefully calibrated Gumbel distribution is equivalent to the finite-support exponential mechanism. Since both approaches effectively sample an index from the same distribution, they can be used interchangeably.

The Gumbel distribution for a scale parameter $\beta$ is defined by the following probability density function:

$$Pr[Z=z]=\frac{1}{\beta }·exp\left(\frac{z}{\beta }-exp\left(\frac{z}{\beta }\right)\right)$$

By sampling $z_i$ from the Gumbel distribution with scale parameter $\beta =\frac{2{\dot{b}}_{in}}{ϵ}$, the resulting noisy max mechanism is $ϵ$-differentially private.

This algorithm is much simpler than make_finite_exponential_mechanism: the scores are left as log-likelihoods, which avoids the numerical instability of exponentiating scores:

def make_report_noisy_max_gumbel(scale, monotonic=False, T=float):
    dp.assert_features("contrib")
    assert scale >= 0, "scale must not be negative"
    return dp.m.make_user_measurement(
        input_domain=dp.vector_domain(dp.atom_domain(T=T)),
        input_metric=dp.linf_distance(T=T),
        output_measure=dp.max_divergence(T=float),
        # the value with the largest noisy score is the selected bin index
        function=lambda scores: np.argmax(np.random.gumbel(scores, scale=scale)),
        privacy_map=lambda b_in: b_in / scale * (1 if monotonic else 2))

Another nice computational benefit is that the algorithm can be adjusted to run on a data stream. In addition, the distribution of the top $k$ indexes by noisy scores is equivalent to peeling the top $k$ scores. Therefore, it is easy to adjust the algorithm to efficiently release the top $k$ scores together in one shot.

Note

A more careful analysis of the privacy proof also allows you to release the size of the gap between the score of the released index and the next smaller score, without any additional privacy cost.¹² This can help you get a sense of how confident the mechanism is in its selection.

Keep in mind that this noisy max approach is only useful when the support is finite, as it is clearly impossible to add noise to an infinite number of candidates.

Alternative distributions

The noise from several distributions can be added to scores to satisfy differential privacy in the noisy max mechanism. Noise from the Laplace and exponential distributions have seen common use in the noisy max as well. Laplace Noisy Max (LNM) also satisfies differential privacy and has been popularized in the literature, but it results in slightly less utility than Exponential Noisy Max (ENM).¹³ For this reason, this section will just focus on the exponential distribution.

When the exponential report noisy max satisfies the same level of privacy as the Gumbel report noisy max, the utility of ENM can be better by up to a factor of 2 because it adds less noise overall. However, as of the time of this writing, there is no one-shot variation of ENM for releasing the top $k$ noisy samples, nor has ENM been shown to satisfy a tighter zero-concentrated differential privacy guarantee like Gumbel report noisy max has (zCDP will be discussed in Chapter 5).

While the mechanisms discussed thus far in the book have been quite diverse, you can argue that all of them were in some way an instance of the exponential mechanism. The next mechanism is decidedly not representable via the exponential mechanism.

One way you can generalize the definition of privacy is to also allow for interactivity.

Interactivity

Private mechanisms can either be interactive or non-interactive. This distinction is based on how communication is modeled between the algorithm and the analyst. The Laplace and exponential mechanisms are both non-interactive, because communication is one-way from the algorithm to the analyst.

Realistically, analysts often expect more; it is more natural for analysts to want to ask questions interactively. This involves a strengthening of the definition of privacy. The privacy is measured not just over all choices of data sets $x$ and $x^{\text{'}}$ but also all possible strategies an adversary may have. That is, the insights that an analyst/adversary gains into adjacent data sets will remain similar.¹⁴

Note

More definitions of privacy will be discussed in Chapter 5. This distinction also generalizes the definition of privacy across all measures of privacy.

Some keywords to introduce in this context are queries and queryables: a query is a piece of communication from an analyst to a state machine, or queryable. One round of communication consists of the query sent to a queryable and the answer it returns.

There are many more interactive mechanisms in differential privacy, the first example of which will be the above threshold mechanism. The above threshold mechanism is an example of an interactive mechanism, and it satisfies this more general definition of privacy.

Above Threshold

The above threshold mechanism is used to find the identity of the first value in a stream above a threshold. The mechanism then terminates, refusing to answer any more queries.^15,16

Before diving into the details of the mechanism, you should become familiar with the stream data type.

Streams

A stream is a sequence of values that are produced consecutively. The terminology is common in signal processing (where data is produced by a sensor) and in functional languages (where data is produced by a function).

Just as you can measure the distance between vectors, scalars, dataframes, and other forms of data, you can also measure the distance between streams. The same is true for the divergence between the distributions of randomized streams.

And similarly, just as you have many metrics to choose from when measuring the distance between vectors, you have many metrics to choose from when measuring the distance between streams. Instead of exploring the set of possible metrics, we’ll just focus on the metric needed for the above threshold mechanism and introduce more as necessary.

The $L^{\infty }$ distance between streams is very similar to the $L^{\infty }$ distance for vectors. If a stream has bounded $L^{\infty }$ sensitivity of $d$, then each element in a neighboring stream may differ by up to $d$. A similar extension can be made to the max-divergence.

In stream processing terminology, a filter processes a stream, producing another stream. A filter can even be proven to be a stable transformation or private mechanism and can be implemented via a queryable. Above threshold is an example of a stream filter: it is a private mechanism that returns a queryable.

Online Private Selection

You can think of “above threshold” as online private selection from a stream of candidates. The closest analogue to existing mechanisms is the Laplace Noisy Max (LNM) mechanism, but LNM still requires all candidates to be known up front.

The mechanism privatizes a stream with bounded $L^{\infty }$ sensitivity:

def make_above_threshold(threshold, scale, monotonic=False):
    """Privately find the first item above `threshold` in a stream."""
    dp.assert_features("contrib", "floating-point")

    def f_above_threshold(stream):
        found, threshold_p = False, laplace(loc=threshold, scale=scale)
        def transition(query):
            nonlocal found # the state of the queryable
            assert not found, "queryable is exhausted"

            value = laplace(loc=stream(query), scale=2 * scale)
            if value >= threshold_p:
                found = True
            return found
        return dp.new_queryable(transition, Q=query_type(stream), A=bool)
        
    return dp.m.make_user_measurement(
        input_domain=queryable_domain(dp.atom_domain(T=type(threshold))),
        input_metric=dp.linf_distance(T=type(threshold), monotonic=monotonic),
        output_measure=dp.max_divergence(T=float),
        function=f_above_threshold,
        privacy_map=lambda b_in: b_in / scale * (1 if monotonic else 2),
    )

In the case of above_threshold, the state of the queryable simply consists of the found boolean.

When you invoke above_threshold, you get a queryable. The queryable implements a private filter on the input stream, emitting a private output stream:

meas = make_above_threshold(threshold=4, scale=1.)
# since the measurement privatizes a stream, initialize with a dummy stream
qbl = meas(lambda x: x)

qbl(2) # very likely to emit False
qbl(3) # likely to emit False
qbl(6) # likely to emit True for the first time
qbl(4) # expected to throw an assertion error

There are more connections between the above threshold mechanism and noisy max:

• The gap between the noisy threshold and noisy query can also be released without additional privacy consumption.

• You can apply another private mechanism to release an estimate of the score with additional privacy consumption.

• You can tighten the analysis with the range distance.

Differentially private stream processing algorithms share the modularity of other DP algorithms.

Stable Transformations on Streams

You may now be wondering what you can do with the above threshold mechanism: under what conditions are your analyses best served by privatizing a stream?

Consider a situation where you want to know the first query on a data set that returns a value above a threshold. To accomplish this, first construct a stable transformation from a sensitive data set to a stable filter, and then chain this transformation and the above threshold mechanism together:

def make_query_stream(input_domain, input_metric, b_in, b_out):
    """Return a stream for asking queries about a data set"""
    dp.assert_features("contrib")
    T = type(b_out)
    input_space = input_domain, input_metric
    output_space = dp.atom_domain(T=T), dp.absolute_distance(T=T)
    stream_space = queryable_domain(output_space[0]), dp.linf_distance(T=T)

    def f_query_stream(data):
        def transition(trans):
            assert trans.input_space == input_space
            assert trans.output_space == output_space
            assert trans.map(b_in) <= b_out, "query is too sensitive"
            return trans(data)
        return dp.new_queryable(transition, A=T)

    return dp.t.make_user_transformation(
        *input_space, *stream_space, f_query_stream,
        stability_map=lambda b_in_p: b_in_p / b_in * b_out
    )

The query_stream function takes a data set $x$ and returns a queryable, upon which you may submit a stream of transformations. Since each transformation has bounded sensitivity, the resulting stream has bounded $L^{\infty }$ sensitivity and can be privatized by the preceding threshold mechanism:

space = dp.vector_domain(dp.atom_domain(T=int)), dp.symmetric_distance()
meas = make_query_stream(*space, b_in=1, b_out=1) >> \
       make_above_threshold(threshold=4, scale=1.)

The algorithm now searches for the first query above a threshold in a stream of queries. This example submits a sensitivity-1 unique count first (which is likely below the threshold) and then a sensitivity-1 count (which is likely above the threshold):

qbl = meas([1, 2, 2, 2, 3])
print(qbl(dp.t.make_count_distinct(*space))) # likely to emit False
print(qbl(dp.t.make_count(*space))) # likely to emit True

There are many stable transformations on streams that can be used with the above threshold mechanism. It is your responsibility to ensure that the stream processing transformations you use satisfy the necessary stability properties of the mechanism you want to use them with. Luckily, stable or differentially private primitives are completely encapsulated to be easily composable and provably correct in isolation.

Summary

You are now familiar with the core primitives of pure-differential privacy. At this point, you should be comfortable reasoning about privacy measures and understanding how privacy can be defined relative to the max-divergence. Given a mechanism like randomized response, you should be able to demonstrate the mechanism is private. Further, you should understand the difference between the interactive and non-interactive models of privacy.

Pure differential privacy enables a wide variety of useful algorithms, but it is not the only way to satisfy differential privacy. There are relaxations of differential privacy that enable another suite of useful differentially private algorithms. You can think of these as different kinds of divergence—different ways to measure the distance between distributions.

The next chapter will focus on these relaxations to the definition of privacy, and the mechanisms that become possible when you use them.

Exercises

1. Use the randomized response mechanism to construct a local-DP mechanism for estimating the mean. Hint: use lower and upper extreme values as the mechanism’s support.

2. Imagine you are an adversary who is trying to violate privacy. How would you attack make_randomized_response_multi if it were missing either of its two CONDITIONS?

3. Create a central-DP mechanism for releasing the precision metric: the number of true positives divided by the total number of positive examples. Assume all data is boolean, expected values are not private, and predicted values are private.

4. A list of sales arrives once a day. Assume you know customers make at most one purchase per day and that the most expensive sale is 10.

   1. Write an $ϵ=1$ reporting tool that alerts you the first day sales are above 100. A starter script is provided:

      from ch04_stream import make_above_threshold, queryable_domain
      import opendp.prelude as dp
      TODO = "fix usages of this variable"
      
      def make_sum_stream(bounds):
          dp.assert_features("contrib")
          T, L, U = type(bounds[0]), *bounds
          def f_sum_stream(stream):
              transition = lambda b_in: TODO # implement the new stream
              return dp.new_queryable(transition, Q=dp.Vec[T], A=T)
          
          stream_output_domain = dp.vector_domain(dp.atom_domain(bounds=bounds))
          return dp.t.make_user_transformation(
              input_domain=queryable_domain(stream_output_domain),
              # technically l-infty of sym dists
              input_metric=dp.symmetric_distance(), 
              output_domain=queryable_domain(dp.atom_domain(T=float)),
              output_metric=dp.linf_distance(T=T, monotonic=True),
              function=f_sum_stream,
              stability_map=TODO # what is the stability of the new stream?
          )
      
      meas = TODO # construct the complete measurement
      assert meas.map(1) <= 1, "ε should be at most 1"
      qbl = meas(lambda x: x) # `meas` will privatize the identity stream
      
      #        Day 1,        Day 2,      DAY 3 (BIG), Day 4 (likely never seen)
      sales = [[9.27, 9.32], [1.34] * 3, [8.92] * 30, [12.73, 8.34, 7.32], ...]
      # scan the sales data stream until the mechanism detects high sales
      print("high sales on day:", 
            next(i + 1 for i, s in enumerate(sales) if qbl(s)))

   2. How would you modify the reporting tool to detect low sales?

¹ This representation is useful when analyzing the randomized response mechanism.

² Salil Vadhan, “Notes on the Definition of Differential Privacy,” course notes from MIT 6.889, February 2013, https://people.seas.harvard.edu/~salil/diffprivcourse/spring13/definition-notes.pdf.

³ Hay, Gaboardi, and Vadhan, “A Programming Framework for OpenDP.”

⁴ Frank McSherry and Kunal Talwar, “Mechanism Design via Differential Privacy,” in Proceedings of the Annual IEEE Symposium on Foundations of Computer Science (Piscataway, NJ: IEEE, 2007), 94-103.

⁵ Adapted from Adam Smith, “Privacy-Preserving Statistical Estimation with Optimal Convergence Rates,” in Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing (New York: ACM, 2011), 813–22. https://doi.org/10.1145/1993636.1993743.

⁶ Section 2.1 of Jinshuo Dong et al., “Optimal Differential Privacy Composition for Exponential Mechanisms,” in Proceedings of the 37th International Conference on Machine Learning (PMLR, 2020), 2597–606.

⁷ Adam Smith, “Privacy-Preserving Statistical Estimation with Optimal Convergence Rates,” in Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing (New York: ACM, 2011), 813–22. https://doi.org/10.1145/1993636.1993743.

⁸ Jeremiah Blocki, Anupam Datta, and Joseph Bonneau, “Differentially Private Password Frequency Lists.” IACR Cryptology. ePrint Arch., 2016. https://eprint.iacr.org/2016/153.

⁹ Raef Bassily, Adam Smith, and Abhradeep Thakurta, “Private Empirical Risk Minimization: Efficient Algorithms and Tight Error Bounds,” IEEE 55th Annual Symposium on Foundations of Computer Science (Piscataway, NJ: IEEE, 2014), 464–73.

¹⁰ Kareem Amin et al., “Differentially Private Covariance Estimation,” in Advances in Neural Information Processing Systems, vol. 32 (Red Hook, NY: Curran Associates, 2019).

¹¹ David Durfee and Ryan Rogers, “Practical Differentially Private Top-k Selection with Pay-What-You-Get Composition,” in Proceedings of the 33rd International Conference on Neural Information Processing Systems (Red Hook, NY: Curran Associates, 2019), 3532–42.

¹² Zeyu Ding et al., “Free Gap Information from the Differentially Private Sparse Vector and Noisy Max Mechanisms,” in Proceedings of the VLDB Endowment 13, no. 3 (September 2019): 293–306.

¹³ The Exponential Noisy Max has also shown to be equivalent to the Permute-and-Flip mechanism; see Zeyu Ding et al., “The Permute-and-Flip Mechanism Is Identical to Report-Noisy-Max with Exponential Noise,” arXiv, June 5, 2021. https://arxiv.org/abs/2105.07260.

¹⁴ Salil Vadhan and Tianhao Wang. “Concurrent Composition of Differential Privacy,” in Theory of Cryptography (Berlin: Springer, 2021): 582–604.

¹⁵ From section 3.6 of Cynthia Dwork and Aaron Roth, The Algorithmic Foundations of Differential Privacy (Norwell, MA: Now Publishers, 2014).

¹⁶ Overview paper: Min Lyu, Dong Su, and Ninghui Li, “Understanding the Sparse Vector Technique for Differential Privacy,” in Proceedings of the VLDB Endowment 10, no. 6 (February 1, 2017): 637–48.