Essential Math for AI

Preface

Why I Wrote This Book

AI is built on mathematical models. We need to know how.

I wrote this book in purely colloquial language, leaving most of the technical details out. It is a math book about AI with very few mathematical formulas and equations, no theorems, no proofs, and no coding. My goal is to not keep this important knowledge in the hands of the very few elite, and to attract more people to technical fields. I believe that many people get turned off by math before they ever get a chance to know that they might love it and be naturally good at it. This also happens in college or in graduate school, where many students switch their majors from math, or start a Ph.D. and never finish it. The reason is not that they do not have the ability, but that they saw no motivation or an end goal for learning torturous methods and techniques that did not seem to transfer to anything useful in their lives. It is like going to a strenuous mental gym every day only for the sake of going there. No one even wants to go to a real gym every day (this is a biased statement, but you get the point). In math, formalizing objects into functions, spaces, measure spaces, and entire mathematical fields comes after motivation, not before. Unfortunately, it gets taught in reverse, with formality first and then, if we are lucky, some motivation.

The most beautiful thing about math is that it has the expressive ability to connect seemingly disparate things together. A field as big and as consequential as AI not only builds on math, as that is a given; it also needs the binding ability that only math can provide in order to tell its big story concisely. In this book I will extract the math required for AI in a way that does not deviate at all from the real-life AI application in mind. It is infeasible to go through existing tools in detail and not fall into an encyclopedic and overwhelming treatment. What I do instead is try to teach you how to think about these tools and view them from above, as a means to an end that we can tweak and adjust when we need to. I hope that you will get out of this book a way of seeing how things relate to each other and why we develop or use certain methods among others. In a way, this book provides a platform that launches you to whatever area you find interesting or want to specialize in.

Another goal of this book is to democratize mathematics, and to build more confidence to ask about how things work. Common answers such as “It’s complicated mathematics,” “It’s complicated technology,” or “It’s complex models,” are no longer satisfying, especially since the technologies that build on mathematical models currently affect every aspect of our lives. We do not need to be experts in every field in mathematics (no one is) in order to understand how things are built and why they operate the way they do. There is one thing about mathematical models that everyone needs to know: they always give an answer. They always spit out a number. A model that is vetted, validated, and backed with sound theory gives an answer. Also, a model that is complete trash gives an answer. Both compute mathematical functions. Saying that our decisions are based on mathematical models and algorithms does not make them sacred. What are the models built on? What are their assumptions? Limitations? Data they were trained on? Tested on? What variables did they take into account? And what did they leave out? Do they have a feedback loop for improvement, ground truths to compare to and improve on? Is there any theory backing them up? We need to be transparent with this information when the models are ours, and ask for it when the models are deciding our livelihoods for us.

The unorthodox organization of the topics in this book is intentional. I wanted to avoid getting stuck in math details before getting to the applicable stuff. My stand on this is that we do not ever need to dive into background material unless we happen to be personally practicing something, and that background material becomes an unfulfilled gap in our knowledge that is stopping us from making progress. Only then it is worth investing serious time to learn the intricate details of things. It is much more important to see how it all ties together and where everything fits. In other words, this book provides a map for how everything between math and AI interacts nicely together.

I also want to make a note to newcomers about the era of large data sets. Before working with large data, real or simulated, structured or unstructured, we might have taken computers and the internet for granted. If we came up with a model or needed to run analytics on small and curated data sets, we might have assumed that our machine’s hardware would handle the computations, or that the internet would just give more curated data when we needed it, or more information about similar models. The reality and limitations to access data, errors in the data, errors in the outputs of queries, hardware limitations, storage, data flow between devices, and vectorizing unstructured data such as natural language or images and movies hits us really hard. That is when we start getting into parallel computing, cloud computing, data management, databases, data structures, data architectures, and data engineering in order to understand the compute infrastructure that allows us to run our models. What kind of infrastructure do we have? How is it structured? How did it evolve? Where is it headed? What is the architecture like, including the involved solid materials? How do these materials work? And what is all the fuss about quantum computing? We should not view the software as separate from the hardware, or our models separate from the infrastructure that allows us to simulate them. This book focuses only on the math, the AI models, and some data. There are neither exercises nor coding. In other words, we focus on the soft, the intellectual, and the I do not need to touch anything side of things. But we need to keep learning until we are able to comprehend the technology that powers many aspects of our lives as the one interconnected body that it actually is: hardware, software, sensors and measuring devices, data warehouses, connecting cables, wireless hubs, satellites, communication centers, physical and software security measures, and mathematical models.

Who Is This Book For?

I wrote this book for:

• A person who knows math but wants to get into AI, machine learning, and data science.

• A person who practices AI, data science, and machine learning but wants to brush up on their mathematical thinking and get up-to-date with the mathematical ideas behind the state-of-the-art models.

• Undergraduate or early graduate students in math, data science, computer science, operations research, science, engineering, or other domains who have an interest in AI.

• People in management positions who want to integrate AI and data analytics into their operations but want a deeper understanding of how the models that they might end up basing their decisions on actually work.

• Data analysts who are primarily doing business intelligence, and are now, like the rest of the world, driven into AI-powered business intelligence. They want to know what that actually means before adopting it into business decisions.

• People who care about the ethical challenges that AI might pose to the world and want to understand the inner workings of the models so that they can argue for or against certain issues such as autonomous weapons, targeted advertising, data management, etc.

• Educators who want to put together courses on math and AI.

• Any person who is curious about AI.

Who Is This Book Not For?

This book is not for a person who likes to sit down and do many exercises to master a particular mathematical technique or method, a person who likes to write and prove theorems, or a person who wants to learn coding and development. This is not a math textbook. There are many excellent textbooks that teach calculus, linear algebra, and probability (but few books relate this math to AI). That said, this book has many in-text pointers to the relevant books and scientific publications for readers who want to dive into technicalities, rigorous statements, and proofs. This is also not a coding book. The emphasis is on concepts, intuition, and general understanding, rather than on implementing and developing the technology.

How Will the Math Be Presented in This Book?

Writing a book is ultimately a decision-making process: how to organize the material of the subject matter in a way that is most insightful into the field, and how to choose what and what not to elaborate on. I will detail some math in a few places, and I will omit details in others. This is on purpose, as my goal is to not get distracted from telling the story of:

Which math do we use, why do we need it, and where exactly do we use it in AI?

I always define the AI context, with many applications. Then I talk about the related mathematics, sometimes with details and other times only with the general way of thinking. Whenever I skip details, I point out the relevant questions that we should be asking and how to go about finding answers. I showcase the math, the AI, and the models as one connected entity. I dive deeper into math only if it must be part of the foundation. Even then, I favor intuition over formality. The price I pay here is that on very few occasions, I might use some technical terms before defining them, secretly hoping that you might have encountered these terms before. In this sense, I adopt AI’s transformer philosophy (see Google Brain’s 2017 article: “Attention Is All You Need”) for natural language understanding: the model learns word meanings from their context. So when you encounter a technical term that I have not defined before, focus on the term’s surrounding environment. Over the course of the section within which it appears, you will have a very good intuition about its meaning. The other option, of course, is to google it. Overall, I avoid jargon and I use zero acronyms.

Since this book lies at the intersection of math, data science, AI, machine learning, and philosophy, I wrote it expecting a diverse audience with drastically different skill sets and backgrounds. For this reason, depending on the topic, the same material might feel trivial to some but complicated to others. I hope I do not insult anyone’s mind in the process. That said, this is a risk that I am willing to take, so that all readers will find useful things to learn from this book. For example, mathematicians will learn the AI application, and data scientists and AI practitioners will learn deeper math.

The sections go in and out of technical difficulty, so if a section gets too confusing, make a mental note of its existence and skip to the next section. You can come back to what you skipped later.

Most of the chapters are independent, so readers can jump straight to their topics of interest. When chapters are related to other chapters, I point that out. Since I try to make each chapter as self-contained as possible, I may repeat a few explanations across different chapters. I push the probability chapter to all the way near the end (Chapter 11), but I use and talk about probability distributions all the time (especially the joint probability distribution of the features of a data set). The idea is to get used to the language of probability and how it relates to AI models before learning its grammar, so when we get to learning the grammar, we have a good idea of the context that it fits in.

I believe that there are two types of learners: those who learn the specifics and the details, then slowly start formulating a bigger picture and a map for how things fit together; and those who first need to understand the big picture and how things relate to each other, then dive into the details only when needed. Both are equally important, and the difference is only in someone’s type of brain and natural inclination. I tend to fit more into the second category, and this book is a reflection of that: how does it all look from above, and how do math and AI interact with each other? The result might feel like a whirlwind of topics, but you’ll come out on the other side with a great knowledge base for both math and AI, plus a healthy dose of confidence.

When my dad taught me to drive, he sat in the passenger’s seat and asked me to drive. Ten minutes in, the road became a cliffside road. He asked me to stop, got out of the car, then said: “Now drive, just try not to fall off the cliff, don’t be afraid, I am watching” (like that was going to help). I did not fall off the cliff, and in fact I love cliffside roads the most. Now tie this to training self-driving cars by reinforcement learning, with the distinction that the cost of falling off the cliff would’ve been minus infinity for me. I could not afford that; I am a real person in a real car, not a simulation.

This is how you’ll do math and AI in this book. There are no introductions, conclusions, definitions, theorems, exercises, or anything of the like. There is immersion.

You are already in it. You know it. Now drive.

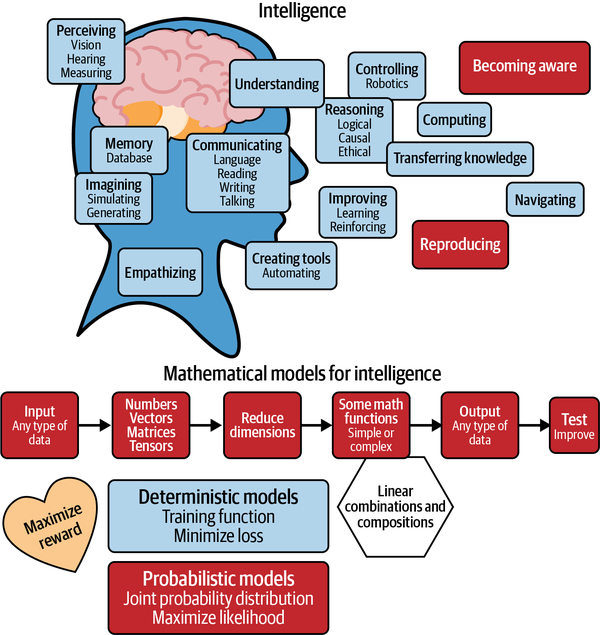
Infographic

I accompany this book with an infographic, visually tying all the topics together. You can also find this on the book’s GitHub page.

What Math Background Is Expected from You to Be Able to Read This Book?

This book is self-contained in the sense that we motivate everything that we need to use. I do hope that you have been exposed to calculus and some linear algebra, including vector and matrix operations, such as addition, multiplication, and some matrix decompositions. I also hope that you know what a function is and how it maps an input to an output. Most of what we do mathematically in AI involves constructing a function, evaluating a function, optimizing a function, or composing a bunch of functions. You need to know about derivatives (these measure how fast things change) and the chain rule for derivatives. You do not necessarily need to know how to compute them for each function, as computers, Python, Desmos, and/or Wolfram|Alpha mathematics do a lot for us nowadays, but you need to know their meaning. Some exposure to probabilistic and statistical thinking are helpful as well. If you do not know any of the above, that is totally fine. You might have to sit down and do some examples (from some other books) on your own to familiarize yourself with certain concepts. The trick here is to know when to look up the things that you do not know…​only when you need them, meaning only when you encounter a term that you do not understand, and you have a good idea of the context within which it appeared. If you are truly starting from scratch, you are not too far behind. This book tries to avoid technicalities at all costs.

Overview of the Chapters

We have a total of 14 chapters.

If you are a person who cares for math and the AI technology as they relate to ethics, policy, societal impact, and the various implications, opportunities, and challenges, then read Chapters 1 and 14 first. If you do not care for those, then we make the case that you should. In this book, we treat math as the binding agent of seemingly disparate topics, rather than the usual presentation of math as an oasis of complicated formulas, theorems, and Greek letters.

Chapter 13 might feel separate from the book if you’ve never encountered differential equations (ODEs and PDEs), but you will appreciate it if you are into mathematical modeling, the physical and natural sciences, simulation, or mathematical analysis, and you would like to know how AI can benefit your field, and in turn how differential equations can benefit AI. Countless scientific feats build on differential equations, so we cannot leave them out when we are at a dawn of a computational technology that has the potential to address many of the field’s long-standing problems. This chapter is not essential for AI per se, but it is essential for our general understanding of mathematics as a whole, and for building theoretical foundations for AI and neural operators.

The rest of the chapters are essential for AI, machine learning, and data science. There is no optimal location for Chapter 6 on the singular value decomposition (the essential math for principal component analysis and latent semantic analysis, and a great method for dimension reduction). Let your natural curiosity dictate when you read this chapter: before or after whichever chapter you feel would be the most fitting. It all depends on your background and which industry or academic discipline you happen to come from.

Let’s briefly overview Chapters 1 through 14:

Chapter 1, “Why Learn the Mathematics of AI?”

Artificial intelligence is here. It has already penetrated many areas of our lives, is involved in making important decisions, and soon will be employed in every sector of our society and operations. The technology is advancing very fast and its investments are skyrocketing. What is artificial intelligence? What is it able to do? What are its limitations? Where is it headed? And most importantly, how does it work, and why should we really care about knowing how it works? In this introductory chapter we briefly survey important AI applications, the problems usually encountered by companies trying to integrate AI into their systems, incidents that happen when systems are not well implemented, and the math typically used in AI solutions.

Chapter 2, “Data, Data, Data”

This chapter highlights the fact that data is central to AI. It explains the differences between concepts that are usually a source of confusion: structured and unstructured data, linear and nonlinear models, real and simulated data, deterministic functions and random variables, discrete and continuous distributions, prior probabilities, posterior probabilities, and likelihood functions. It also provides a map for the probability and statistics needed for AI without diving into any details, and introduces the most popular probability distributions.

Chapter 3, “Fitting Functions to Data”

At the core of many popular machine learning models, including the highly successful neural networks that brought artificial intelligence back into the popular spotlight since 2012, lies a very simple mathematical problem: fit a given set of data points into an appropriate function, then make sure this function performs well on new data. This chapter highlights this widely useful fact with a real data set and other simple examples. We discuss regression, logistic regression, support vector machines, and other popular machine learning techniques, with one unifying theme: training function, loss function, and optimization.

Chapter 4, “Optimization for Neural Networks”

Neural networks are modeled after the brain cortex, which involves millions of neurons arranged in a layered structure. The brain learns by reinforcing neuron connections when faced with a concept it has seen before, and weakening connections if it learns new information that undoes or contradicts previously learned concepts. Machines only understand numbers. Mathematically, stronger connections correspond to larger numbers (weights), and weaker connections correspond to smaller numbers. This chapter explains the optimization and backpropagation steps used when training neural networks, similar to how learning happens in our brain (not that humans fully understand this). It also walks through various regularization techniques, explaining their advantages, disadvantages, and use cases. Furthermore, we explain the intuition behind approximation theory and the universal approximation theorem for neural networks.

Chapter 5, “Convolutional Neural Networks and Computer Vision”

Convolutional neural networks are widely popular for computer vision and natural language processing. In this chapter we start with the convolution and cross-correlation operations, then survey their uses in systems design and filtering signals and images. Then we integrate convolution with neural networks to extract higher-order features from images.

Chapter 6, “Singular Value Decomposition: Image Processing, Natural Language Processing, and Social Media”

Diagonal matrices behave like scalar numbers and hence are highly desirable. Singular value decomposition is a crucially important method from linear algebra that transforms a dense matrix into a diagonal matrix. In the process, it reveals the action of a matrix on space itself: rotating and/or reflecting, stretching and/or squeezing. We can apply this simple process to any matrix of numbers. This wide applicability, along with the ability to dramatically reduce the dimensions while retaining essential information, make singular value decomposition popular in the fields of data science, AI, and machine learning. It is the essential mathematics behind principal component analysis and latent semantic analysis. This chapter walks through singular value decomposition along with its most relevant and up-to-date applications.

Chapter 7, “Natural Language and Finance AI: Vectorization and Time Series”

We present the mathematics in this chapter in the context of natural language models, such as identifying topics, machine translation, and attention models. The main barrier to overcome is moving from words and sentences that carry meaning to low-dimensional vectors of numbers that a machine can process. We discuss state-of-the-art models such as Google Brain’s transformer (starting in 2017), among others, while we keep our attention only the relevant math. Time series data and models (such as recurrent neural networks) appear naturally here. We briefly introduce finance AI, as it overlaps with natural language both in terms of modeling and how the two fields feed into each other.

Chapter 8, “Probabilistic Generative Models”

Machine-generated images, including those of humans, are becoming increasingly realistic. It is very hard nowadays to tell whether an image of a model in the fashion industry is that of a real person or a computer-generated image. We have generative adversarial networks (GANs) and other generative models to thank for this progress, where it is harder to draw a line between the virtual and the real. Generative adversarial networks are designed to repeat a simple mathematical process using two neural networks until the machine itself cannot tell the difference between a real image and a computer-generated one, hence the “very close to reality” success. Game theory and zero-sum games occur naturally here, as the two neural networks “compete” against each other. This chapter surveys generative models, which mimic imagination in the human mind. These models have a wide range of applications, from augmenting data sets to completing masked human faces to high energy physics, such as simulating data sets similar to those produced at the CERN Large Hadron Collider.

Chapter 9, “Graph Models”

Graphs and networks are everywhere: cities and roadmaps, airports and connecting flights, the World Wide Web, the cloud (in computing), molecular networks, our nervous system, social networks, terrorist organization networks, even various machine learning models and artificial neural networks. Data that has a natural graph structure can be better understood by a mechanism that exploits and preserves that structure, building functions that operate directly on graphs, as opposed to embedding graph data into existing machine learning models that attempt to artificially reshape the data before analyzing it. This is the same reason convolutional neural networks are successful with image data, recurrent neural networks are successful with sequential data, and so on. The mathematics behind graph neural networks is a marriage among graph theory, computing, and neural networks. This chapter surveys this mathematics in the context of many applications.

Chapter 10, “Operations Research”

Another suitable name for operations research would be optimization for logistics. This chapter introduces the reader to problems at the intersection of AI and operations research, such as supply chain, traveling salesman, scheduling and staffing, queuing, and other problems whose defining features are high dimensionality, complexity, and the need to balance competing interests and limited resources. The math required to address these problems draws from optimization, game theory, duality, graph theory, dynamic programming, and algorithms.

Chapter 11, “Probability”

Probability theory provides a systematic way to quantify randomness and uncertainty. It generalizes logic to situations that are of paramount importance in artificial intelligence: when information and knowledge are uncertain. This chapter highlights the essential probability used in AI applications: Bayesian networks and causal modeling, paradoxes, large random matrices, stochastic processes, Markov chains, and reinforcement learning. It ends with rigorous probability theory, which demystifies measure theory and introduces interested readers to the universal approximation theorem for neural networks.

Chapter 12, “Mathematical Logic”

This important topic is positioned near the end to not interrupt the book’s natural flow. Designing agents that are able to gather knowledge, reason logically about the environment within which they exist, and make inferences and good decisions based on this logical reasoning is at the heart of artificial intelligence. This chapter briefly surveys propositional logic, first-order logic, probabilistic logic, fuzzy logic, and temporal logic, within an intelligent knowledge-based agent.

Chapter 13, “Artificial Intelligence and Partial Differential Equations”

Differential equations model countless phenomena in the real world, from air turbulence to galaxies to the stock market to the behavior of materials and population growth. Realistic models are usually very hard to solve and require a tremendous amount of computational power when relying on traditional numerical techniques. AI has recently stepped in to accelerate solving differential equations. The first part of this chapter acts as a crash course on differential equations, highlighting the most important topics and arming the reader with a bird’s-eye view of the subject. The second part explores new AI-based methods that simplify the whole process of solving differential equations. These have the potential to unlock long-standing problems in the natural sciences, finance, and other fields.

Chapter 14, “Artificial Intelligence, Ethics, Mathematics, Law, and Policy”

I believe this chapter should be the first chapter in any book on artificial intelligence; however, this topic is so wide and deep that it needs multiple books to cover it completely. This chapter only scratches the surface and summarizes various ethical issues associated with artificial intelligence, including: equity, fairness, bias, inclusivity, transparency, policy, regulation, privacy, weaponization, and security. It presents each problem along with possible solutions (mathematical or with policy and regulation).

My Favorite Books on AI

There are many excellent and incredibly insightful books on AI and on topics intimately related to the field. The following is not even close to being an exhaustive list. Some are technical books heavy on mathematics, and others are either introductory or completely nontechnical. Some are code-oriented (Python 3) and others are not. I have learned a lot from all of them:

• Brunton, Steven L. and J. Nathan Kutz, Data-Driven Science and Engineering: Machine Learning, Dynamical Systems and Control (Cambridge University Press, 2022)

• Crawford, Kate, Atlas of AI (Yale University Press, 2021)

• Ford, Martin, Architects of Intelligence (Packt Publishing, 2018)

• Géron, Aurélien, Hands-On Machine Learning with Scikit-Learn, Keras and TensorFlow (O’Reilly, 2022)

• Goodfellow, Ian, Yoshua Bengio, and Aaron Courville, Deep Learning (MIT Press, 2016)

• Grus, Joel, Data Science from Scratch (O’Reilly, 2019)

• Hawkins, Jeff, A Thousand Brains (Basic Books, 2021)

• Izenman, Alan J., Modern Multivariate Statistical Techniques (Springer, 2013)

• Jones, Herbert, Data Science: The Ultimate Guide to Data Analytics, Data Mining, Data Warehousing, Data Visualization, Regression Analysis, Database Querying, Big Data for Business and Machine Learning for Beginners (Bravex Publications, 2020)

• Kleppmann, Martin, Designing Data-Intensive Applications (O’Reilly, 2017)

• Lakshmanan, Valliappa, Sara Robinson, and Michael Munn, Machine Learning Design Patterns (O’Reilly, 2020)

• Lane, Hobson, Hannes Hapke, and Cole Howard, Natural Language Processing in Action (Manning, 2019)

• Lee, Kai-Fu, AI Superpowers (Houghton Mifflin Harcourt, 2018)

• Macey, Tobias, ed., 97 Things Every Data Engineer Should Know (O’Reilly, 2021)

• Marr, Bernard and Matt Ward, Artificial Intelligence in Practice (Wiley, 2019)

• Moroney, Laurence, AI and Machine Learning for Coders (O’Reilly, 2021)

• Mount, George, Advancing into Analytics: From Excel to Python and R (O’Reilly, 2021)

• Norvig, Peter and Stuart Russell, Artificial Intelligence: A Modern Approach (Pearson, 2021)

• Pearl, Judea, The Book of Why (Basic Books, 2020)

• Planche, Benjamin and Eliot Andres, Hands-On Computer Vision with TensorFlow2 (Packt Publishing, 2019)

• Potters, Marc, and Jean-Philippe Bouchaud, A First Course in Random Matrix Theory for Physicists, Engineers, and Data Scientists (Cambridge University Press, 2020)

• Rosenthal, Jeffrey S., A First Look at Rigorous Probability Theory (World Scientific Publishing, 2016)

• Roshak, Michael, Artificial Intelligence for IoT Cookbook (Packt Publishing, 2021)

• Strang, Gilbert, Linear Algebra and Learning from Data (Wellesley Cambridge Press, 2019)

• Stone, James V., Artificial Intelligence Engines (Sebtel Press, 2020)

• Stone, James V., Bayes’ Rule, A Tutorial Introduction to Bayesian Analysis (Sebtel Press, 2013)

• Stone, James V., Information Theory: A Tutorial Introduction (Sebtel Press, 2015)

• Vajjala, Sowmya et al., Practical Natural Language Processing (O’Reilly, 2020)

• Van der Hofstad, Remco, Random Graphs and Complex Networks (Cambridge, 2017)

• Vershynin, Roman, High-Dimensional Probability: An Introduction with Applications in Data Science (Cambridge University Press, 2018)

Conventions Used in This Book

The following typographical conventions are used in this book:

Italic

Indicates new terms, URLs, email addresses, filenames, and file extensions.

Constant width

Used for program listings, as well as within paragraphs to refer to program elements such as variable or function names, databases, data types, environment variables, statements, and keywords.

Constant width bold

Shows commands or other text that should be typed literally by the user.

Constant width italic

Shows text that should be replaced with user-supplied values or by values determined by context.

This element signifies a tip or suggestion.

This element signifies a general note.

This element indicates a warning or caution.

Using Code Examples

The very few code examples that we have in this book are available for download at https://github.com/halanelson/Essential-Math-For-AI.

If you have a technical question or a problem using the code examples, please send an email to [e-mail].

This book is here to help you get your job done. In general, if example code is offered with this book, you may use it in your programs and documentation. You do not need to contact us for permission unless you’re reproducing a significant portion of the code. For example, writing a program that uses several chunks of code from this book does not require permission. Selling or distributing examples from O’Reilly books does require permission. Answering a question by citing this book and quoting example code does not require permission. Incorporating a significant amount of example code from this book into your product’s documentation does require permission.

We appreciate, but generally do not require, attribution. An attribution usually includes the title, author, publisher, and ISBN. For example: “Essential Math for AI by Hala Nelson (O’Reilly). Copyright 2023 Hala Nelson, 978-1-098-10763-5.”

If you feel your use of code examples falls outside fair use or the permission given above, feel free to contact us at [e-mail].

O’Reilly Online Learning

For more than 40 years, O’Reilly Media has provided technology and business training, knowledge, and insight to help companies succeed.

Our unique network of experts and innovators share their knowledge and expertise through books, articles, and our online learning platform. O’Reilly’s online learning platform gives you on-demand access to live training courses, in-depth learning paths, interactive coding environments, and a vast collection of text and video from O’Reilly and 200+ other publishers. For more information, visit https://oreilly.com.

How to Contact Us

Please address comments and questions concerning this book to the publisher:

• O’Reilly Media, Inc.
• 1005 Gravenstein Highway North
• Sebastopol, CA 95472
• 800-998-9938 (in the United States or Canada)
• 707-829-0515 (international or local)
• 707-829-0104 (fax)

We have a web page for this book, where we list errata, examples, and any additional information. You can access this page at https://oreil.ly/essentialMathAI.

Email [e-mail] to comment or ask technical questions about this book.

For news and information about our books and courses, visit https://oreilly.com.

Find us on LinkedIn: https://linkedin.com/company/oreilly-media

Follow us on Twitter: https://twitter.com/oreillymedia

Watch us on YouTube: https://www.youtube.com/oreillymedia

Acknowledgments

My dad, Yousef Zein, who taught me math, and made sure to always remind me: Don’t think that the best thing we gave you in this life is land, or money. These come and go. Humans create money, buy assets, and create more money. What we did give you is a brain, a really good brain. That’s your real asset, so go out and use it. I love your brain, this book is for you, dad.

My mom, Samira Hamdan, who taught me both English and philosophy, and who gave up everything to make sure we were happy and successful. I wrote this book in English, not my native language, thanks to you, mom.

My daughter, Sary, who kept me alive during the most vulnerable times, and who is the joy of my life.

My husband, Keith, who gives me the love, passion, and stability that allow me to be myself, and to do so many things, some of them unwise, like writing a five-hundred-or-so-page book on math and AI. I love you.

My sister, Rasha, who is my soulmate. This says it all.

My brother, Haitham, who went against all our cultural norms and traditions to support me.

The memory of my uncle Omar Zein, who also taught me philosophy, and who made me fall in love with the mysteries of the human mind.

My friends Sharon and Jamie, who let me write massive portions of this book at their house, and were great editors any time I asked.

My lifetime friend Oren, who on top of being one of the best friends anyone can wish for, agreed to read and review this book.

My friend Huan Nguyen, whose story should be its own book, and who also took the time to read and review this book. Thank you, admiral.

My friend and colleague John Webb, who read every chapter word by word, and provided his invaluable pure math perspective.

My wonderful friends Deb, Pankaj, Jamie, Tamar, Sajida, Jamila, Jen, Mattias, and Karen, who are part of my family. I love life with you.

My mentors Robert Kohn (New York University) and John Schotland (Yale University), to whom I owe reaching many milestones in my career. I learned a great deal from you.

The memory of Peter, whose impact was monumental, and who will forever inspire me.

The reviewers of this book, who took time and care despite their busy schedules to make it much better. Thank you for your great expertise and for generously giving me your unique perspectives from all your different domains.

All the waiters and waitresses in many cities in the world, who tolerated me sitting at my laptop at their restaurants for hours and hours and hours, writing this book. I got so much energy and happiness from you.

My incredible, patient, cheerful, and always supportive editors, Angela Rufino and Kristen Brown.