Essential Math for AI

Chapter 4. Optimization for Neural Networks

I have lived each and every day of my life optimizing…​.My first aha moment was when I learned that our brain, too, learns a model of the world.

H.

Various artificial neural networks have fully connected layers in their architecture. In this chapter, we explain how the mathematics of a fully connected neural network works. We design and experiment with various training and loss functions. We also explain that the optimization and backpropagation steps used when training neural networks are similar to how learning happens in our brains. The brain learns by reinforcing neuron connections when faced with a concept it has seen before, and weakening connections if it learns new information that contradicts previously learned concepts. Machines only understand numbers. Mathematically, stronger connections correspond to larger numbers, and weaker connections correspond to smaller numbers.

Finally, we walk through various regularization techniques, explaining their advantages, disadvantages, and use cases.

The Brain Cortex and Artificial Neural Networks

Neural networks are modeled after the brain cortex, which involves billions of neurons arranged in a layered structure. Figure 4-1 shows an image of three vertical cross-sections of the brain neocortex, and Figure 4-2 shows a diagram of a fully connected artificial neural network.

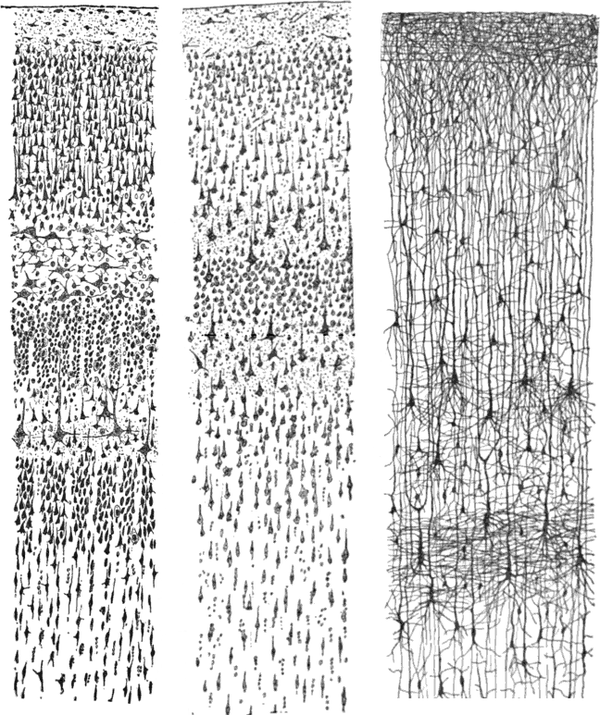
Figure 4-1. Three drawings of cortical lamination by Santiago Ramón y Cajal, taken from the book Comparative Study of the Sensory Areas of the Human Cortex (Andesite Press) (image source: Wikipedia)

In Figure 4-1, each drawing shows a vertical cross-section of the cortex, with the surface (outermost side closest to the skull) of the cortex at the top. On the left is a Nissl-stained visual cortex of a human adult. In the middle is a Nissl-stained motor cortex of a human adult. On the right is a Golgi-stained cortex of a month-and-a half-old infant. The Nissl stain shows the cell bodies of neurons. The Golgi stain shows the dendrites and axons of a random subset of neurons. The layered structure of the neurons in the cortex is evident in all three cross-sections.

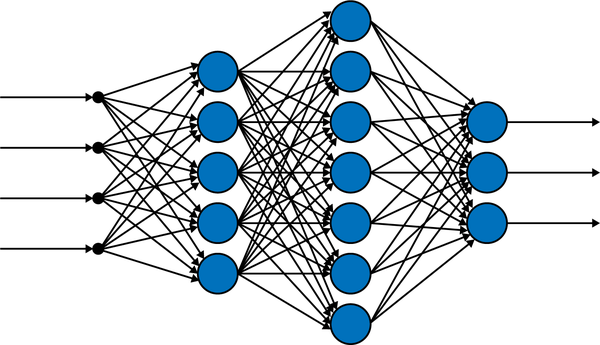
Figure 4-2. A fully connected or dense artificial neural network with four layers

Even though different regions of the cortex are responsible for different functions, such as vision, auditory perception, logical thinking, language, speech, etc., what actually determines the function of a specific region are its connections: which sensory and motor skills input and output regions it connects to. This means that if a cortical region is connected to a different sensory input/output region—for example, a vision locality instead of an auditory one—then it will perform vision tasks (computations), not auditory tasks. In a very simplified sense, the cortex performs one basic function at the neuron level. In an artificial neural network, the basic computation unit is the perceptron, and it functions in the same way across the whole network. The various connections, layers, and architecture of the neural network (both the brain cortex and artificial neural networks) are what allow these computational structures to do very impressive things.

Training Function: Fully Connected, or Dense, Feed Forward Neural Networks

In a fully connected or dense artificial neural network (see Figure 4-2), every neuron, represented by a node (the circles), in every layer is connected to all the neurons in the next layer. The first layer is the input layer, the last layer is the output layer, and the intermediate layers are called hidden layers. The neural network itself, whether fully connected or not (the networks that we will encounter in the new few chapters are convolutional and are not fully connected), is a computational graph representing the formula of the training function. Recall that we use this function to make predictions after training.

Training in the neural networks context means finding the parameter values, or weights, that enter into the formula of the training function via minimizing a loss function. This is similar to training linear regression, logistic regression, softmax regression, and support vector machine models, which we discussed in Chapter 3. The mathematical structure here remains the same:

1. Training function

2. Loss function

3. Optimization

The only difference is that for the simple models of Chapter 3, the formulas of the training functions are very uncomplicated. They linearly combine the data features, add a bias term (${\omega }_0$), and pass the result into at most one nonlinear function (for example, the logistic function in logistic regression). As a consequence, the results of these models are also simple: a linear (flat) function for linear regression, and a linear division boundary between different classes in logistic regression, softmax regression, and support vector machines. Even when we use these simple models to represent nonlinear data, such as in the cases of polynomial regression (fitting the data into polynomial functions of the features) or support vector machines with the kernel trick, we still end up with linear functions or division boundaries, but these will either be in higher dimensions (for polynomial regression, the dimensions are the feature and its powers) or in transformed dimensions (such as when we use the kernel trick with support vector machines).

For neural network models, on the other hand, the process of linearly combining the features, adding a bias term, then passing the result through a nonlinear function (now called activation function) is the computation that happens only in one neuron. This simple process happens over and over again in dozens, hundreds, thousands, or sometimes millions of neurons, arranged in layers, where the output of one layer acts as the input of the next layer. Similar to the brain cortex, the aggregation of simple and similar processes over many neurons and layers produces, or allows for the representation of, much more complex functionalities. This is sort of miraculous. Thankfully, we are able to understand much more about artificial neural networks than our brain’s neural networks, mainly because we design them, and after all, an artificial neural network is just one mathematical function. No black box remains dark once we dissect it under the lens of mathematics. That said, the mathematical analysis of artificial neural networks is a relatively new field. There are still many questions to be answered and a lot to be discovered.

A Neural Network Is a Computational Graph Representation of the Training Function

Even for a network with only five neurons, such as the one in Figure 4-3, it is pretty messy to write the formula of the training function. This justifies the use of computational graphs to represent neural networks in an organized and easy way. Graphs are characterized by two things: nodes and edges (congratulations, this was lesson one in graph theory). In a neural network, an edge connecting node i in layer m to node j in layer n is assigned a weight ${\omega }_{mn,ij}$. That is four indices for only one edge! At the risk of drowning in a deep ocean of indices, we must organize a neural network’s weights in matrices.

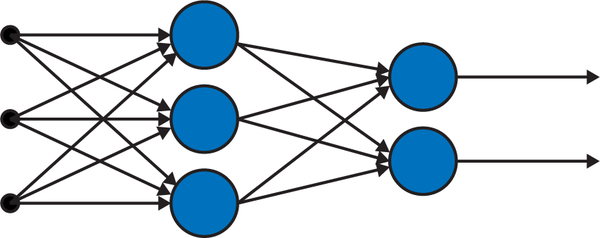
Figure 4-3. A fully connected (or dense) feed forward neural network with only five neurons arranged in three layers. The first layer (the three black dots on the very left) is the input layer, the second layer is the only hidden layer with three neurons, and the last layer is the output layer with two neurons.

Let’s model the training function of a feed forward fully connected neural network. Feed forward means that the information flows forward through the computational graph representing the network’s training function.

Linearly Combine, Add Bias, Then Activate

What kind of computations happen within a neuron when it receives input from other neurons? Linearly combine the input information using different weights, add a bias term, then use a nonlinear function to activate the neuron. We will go through this process one step at a time.

The weights

Let the matrix $W^1$ contain the weights of the edges incident to hidden layer 1, $W^2$ contain the weights of the edges incident to hidden layer 2, and so on, until we reach the output layer.

So for the small neural network represented in Figure 4-3, we only have h = 1 hidden layer, obtaining two matrices of weights:

$W^1=\left(\begin{array}{ccc}{\omega }_{11}^1& {\omega }_{12}^1& {\omega }_{13}^1\\ {\omega }_{21}^1& {\omega }_{22}^1& {\omega }_{23}^1\\ {\omega }_{31}^1& {\omega }_{32}^1& {\omega }_{33}^1\end{array}\right)\text{and}{W}^{h+1}=W^2=W^{output}=\left(\begin{array}{ccc}{\omega }_{11}^2& {\omega }_{12}^2& {\omega }_{13}^2\\ {\omega }_{21}^2& {\omega }_{22}^2& {\omega }_{23}^2\end{array}\right),$

where the superscripts indicate the layer to which the edges point. Note that if we only had one node at the output layer instead of two, then the last matrix of weights $W^{h+1}=W^{output}$ would only be a row vector:

$W^{h+1}=W^2=W^{output}=\left(\begin{array}{ccc}{\omega }_{11}^2& {\omega }_{12}^2& {\omega }_{13}^2\end{array}\right)$

Now at one node of this neural network, two computations take place:

1. A linear combination plus bias

2. Passing the result through a nonlinear activation function (the composition operation from calculus)

We elaborate on these two, then ultimately construct the training function of the fully connected feed forward neural network represented in Figure 4-3.

A linear combination plus bias

At the first node in the first hidden layer (the only hidden layer for this small network), we linearly combine the inputs:

$z_1^1={\omega }_{11}^1{x}_1+{\omega }_{12}^1{x}_2+{\omega }_{13}^1{x}_3+{\omega }_{01}^1$

At the second node in the first hidden layer, we linearly combine the inputs using different weights than the previous linear combination:

$z_2^1={\omega }_{21}^1{x}_1+{\omega }_{22}^1{x}_2+{\omega }_{23}^1{x}_3+{\omega }_{02}^1$

At the third node in the first hidden layer, we linearly combine the inputs using different weights than the previous two linear combinations:

$z_3^1={\omega }_{31}^1{x}_1+{\omega }_{32}^1{x}_2+{\omega }_{33}^1{x}_3+{\omega }_{03}^1$

Let’s express the three equations above using vector and matrix notation. This will be extremely convenient for our optimization task later, and of course it will preserve our sanity:

$\left(\begin{array}{c}{z}_1^1\\ z_2^1\\ z_3^1\end{array}\right)=\left(\begin{array}{c}{\omega }_{11}^1\\ {\omega }_{21}^1\\ {\omega }_{31}^1\end{array}\right)x_1+\left(\begin{array}{c}{\omega }_{12}^1\\ {\omega }_{22}^1\\ {\omega }_{32}^1\end{array}\right)x_2+\left(\begin{array}{c}{\omega }_{13}^1\\ {\omega }_{23}^1\\ {\omega }_{33}^1\end{array}\right)x_3+\left(\begin{array}{c}{\omega }_{01}^1\\ {\omega }_{02}^1\\ {\omega }_{03}^1\end{array}\right)=\left(\begin{array}{ccc}{\omega }_{11}^1& {\omega }_{12}^1& {\omega }_{13}^1\\ {\omega }_{21}^1& {\omega }_{22}^1& {\omega }_{23}^1\\ {\omega }_{31}^1& {\omega }_{32}^1& {\omega }_{33}^1\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)+\left(\begin{array}{c}{\omega }_{01}^1\\ {\omega }_{02}^1\\ {\omega }_{03}^1\end{array}\right)$

We can now summarize the above expression compactly as:

${\overrightarrow{z}}^1=W^1\overrightarrow{x}+{\overrightarrow{\omega }}_0^1$

Pass the result through a nonlinear activation function

Linearly combining the features and adding bias are not enough to pick up on more complex information in the data, and neural networks would have never been successful without this crucial but very simple step: compose with a nonlinear function at each node of the hidden layers.

Linear Combination of a Linear Combination Is Still a Linear Combination

If we skip the step of composing with a nonlinear function, and pass the information from the first layer to the next layer using only linear combinations, then our network will not learn anything new in the next layer. It will not be able to pick up on more complex features from one layer to the next. The math of why this is the case is straightforward. Suppose for simplicity that we only have two input features, the first hidden layer has only two nodes, and the second one has two nodes as well. Then the outputs of the first hidden layer without a nonlinear activation function would be:

$\begin{array}{cc}\hfill z_1^1& ={\omega }_{11}^1{x}_1+{\omega }_{12}^1{x}_2+{\omega }_{01}^1\hfill \\ \hfill z_2^1& ={\omega }_{21}^1{x}_1+{\omega }_{22}^1{x}_2+{\omega }_{02}^1\hfill \end{array}$

At the second hidden layer, these will be linearly combined again, so the output of the first node of this layer would be:

$\begin{array}{cc}\hfill z_1^2& ={\omega }_{11}^2{z}_1^1+{\omega }_{12}^2{z}_2^1+{\omega }_{01}^2\hfill \\ & ={\omega }_{11}^2({\omega }_{11}^1{x}_1+{\omega }_{12}^1{x}_2+{\omega }_{01}^1)+{\omega }_{21}^2({\omega }_{21}^1{x}_1+{\omega }_{22}^1{x}_2+{\omega }_{02}^1)+{\omega }_{01}^2\hfill \\ & =({\omega }_{11}^2{\omega }_{11}^1+{\omega }_{21}^2{\omega }_{21}^1)x_1+({\omega }_{11}^2{\omega }_{12}^1+{\omega }_{21}^2{\omega }_{22}^1)x_2+({\omega }_{11}^2{\omega }_{01}^1+{\omega }_{21}^2{\omega }_{02}^1+{\omega }_{01}^2)\hfill \\ & ={\omega }_1{x}_1+{\omega }_2{x}_2+{\omega }_3\hfill \end{array}$

This output is nothing but a simple linear combination of the original features plus bias. Hence, adding a layer without any nonlinear activation contributes nothing new. In other words, the training function would remain linear and would lack the ability to pick up on any nonlinear relationships in the data.

We are the ones who decide on the formula for the nonlinear activation function, and different nodes can have different activation functions, even though it is rare to do this in practice. Let f be this activation function, then the output of the first hidden layer will be:

${\overrightarrow{s}}^1=\overrightarrow{f}\left({\overrightarrow{z}}^1\right)=\overrightarrow{f}(W^1\overrightarrow{x}+{\overrightarrow{\omega }}_0^1)$

It is now straightforward to see that if we had more hidden layers, their outputs will be chained with those of previous layers, making writing the training function a bit tedious:

$\begin{array}{cc}\hfill {\overrightarrow{s}}^2& =\overrightarrow{f}\left({\overrightarrow{z}}^2\right)=\overrightarrow{f}(W^2{\overrightarrow{s}}^1+{\overrightarrow{\omega }}_0^2)=\overrightarrow{f}(W^2\left(\overrightarrow{f}(W^1\overrightarrow{x}+{\overrightarrow{\omega }}_0^1)\right)+{\overrightarrow{\omega }}_0^2)\hfill \\ \hfill {\overrightarrow{s}}^3& =\overrightarrow{f}\left({\overrightarrow{z}}^3\right)=\overrightarrow{f}(W^3{\overrightarrow{s}}^2+{\overrightarrow{\omega }}_0^3)=\overrightarrow{f}(W^3\left(\overrightarrow{f}(W^2\left(\overrightarrow{f}(W^1\overrightarrow{x}+{\overrightarrow{\omega }}_0^1)\right)+{\overrightarrow{\omega }}_0^2)\right)+{\overrightarrow{\omega }}_0^3)\hfill \end{array}$

This chaining goes on until we reach the output layer. What happens at this very last layer depends on the task of the network. If the goal is regression (predict one numerical value) or binary classification (classify into two classes), then we only have one output node (see Figure 4-4).

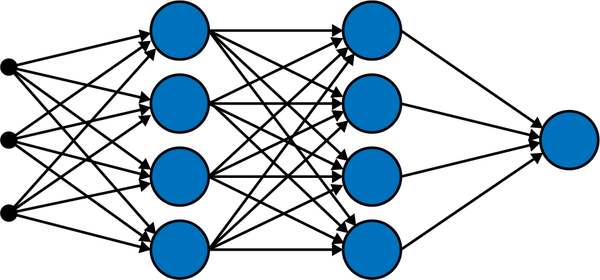
Figure 4-4. A fully connected (or dense) feed forward neural network with only nine neurons arranged in four layers. The first layer on the very left is the input layer, the second and third layers are the two hidden layers with four neurons each, and the last layer is the output layer with only one neuron (this network performs either a regression task or a binary classification task).

• If the task is regression, we linearly combine the outputs of the previous layer at the final output node, add bias, and go home (we do not pass the result through a nonlinear function in this case). Since the output layer only has one node, the output matrix is just a row vector $W^{output}=W^{h+1}$, and one bias ${\omega }_0^{h+1}$. The prediction of the network will now be:

  $y_{predict}=W^{h+1}{\overrightarrow{s}}^h+{\omega }_0^{h+1}$

  where h is the total number of hidden layers in the network (this does not include the input and output layers).

• If, on the other hand, the task is binary classification, then again we have only one output node, where we linearly combine the outputs of the previous layer, add bias, then pass the result through the logistic function $\sigma \left(s\right)=\frac{1}{1+e^{-s}}$, resulting in the network’s prediction:

  $y_{predict}=\sigma (W^{h+1}{\overrightarrow{s}}^h+{\omega }_0^{h+1})$

• If the task is to classify into multiple classes, say, five classes, then the output layer would include five nodes. At each of these nodes, we linearly combine the outputs of the previous layer, add bias, then pass the result through the softmax function:

  $\begin{array}{cc}\hfill \sigma \left(z^1\right)& =\frac{e^{z^1}}{e^{z^1}+e^{z^2}+e^{z^3}+e^{z^4}+e^{z^5}}\hfill \\ \hfill \sigma \left(z^2\right)& =\frac{e^{z^2}}{e^{z^1}+e^{z^2}+e^{z^3}+e^{z^4}+e^{z^5}}\hfill \\ \hfill \sigma \left(z^3\right)& =\frac{e^{z^3}}{e^{z^1}+e^{z^2}+e^{z^3}+e^{z^4}+e^{z^5}}\hfill \\ \hfill \sigma \left(z^4\right)& =\frac{e^{z^4}}{e^{z^1}+e^{z^2}+e^{z^3}+e^{z^4}+e^{z^5}}\hfill \\ \hfill \sigma \left(z^5\right)& =\frac{e^{z^5}}{e^{z^1}+e^{z^2}+e^{z^3}+e^{z^4}+e^{z^5}}\hfill \end{array}$

Group those into a vector function $\overrightarrow{\sigma }$ that also takes vectors as input: $\overrightarrow{\sigma }\left(\overrightarrow{z}\right)$, then the final prediction of the neural network is a vector of five probability scores where a data instance belongs to each of the five classes:

$\begin{array}{cc}\hfill {\overrightarrow{y}}_{predict}& =\overrightarrow{\sigma }\left(\overrightarrow{z}\right)\hfill \\ & =\overrightarrow{\sigma }(W^{output}{\overrightarrow{s}}^h+{\overrightarrow{{\omega }_0}}^{h+1})\hfill \end{array}$

Notation overview

We will try to remain consistent with notation throughout our discussion of neural networks. The x’s are the input features, the W’s are the matrices or column vectors containing the weights that we use for linear combinations, the ${\omega }_0$’s are the biases that are sometimes grouped into a vector, the z’s are the results of linear combinations plus biases, and the s’s are the results of passing the z’s into the nonlinear activation functions.

Common Activation Functions

In theory, we can use any nonlinear function to activate our nodes (think of all the calculus functions we’ve ever encountered). In practice, there are some popular ones, listed next and graphed in Figure 4-5.

By far the Rectified Linear Unit function (ReLU) is the most commonly used in today’s networks, and the success of AlexNet in 2012 is partially attributed to the use of this activation function, as opposed to the hyperbolic tangent and logistic functions (sigmoid) that were commonly used in neural networks at the time (and are still in use).

The first four functions in the following list and in Figure 4-5 are all inspired by computational neuroscience, where they attempt to model a threshold for the activation (firing) of one neuron cell. Their graphs look similar to each other: some are smoother variants of others, some output only positive numbers, others output more balanced numbers between –1 and 1, or between $-\frac{\pi }{2}$ and $\frac{\pi }{2}$. They all saturate for small or large inputs, meaning their graphs become flat for inputs large in magnitude. This creates a problem for learning, since if these functions output the same numbers over and over again, there will not be much learning happening.

Mathematically, this phenomenon manifests itself as the vanishing gradient problem. The second set of activation functions attempts to rectify this saturation problem, which it does, as we see in the graphs of the second row in Figure 4-5. This, however, introduces another problem, called the exploding gradient problem, since these activation functions are unbounded and can now output big numbers, and if these numbers grow over multiple layers, we have a problem.

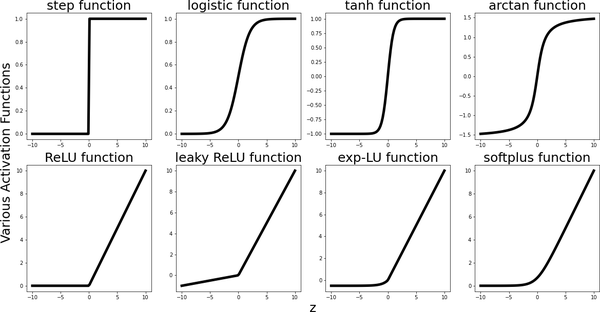
Figure 4-5. Various activation functions for neural networks. The first row consists of sigmoidal-type activation functions, shaped like the letter S. These saturate (become flat and output the same values) for inputs large in magnitude. The second row consists of ReLU-type activation functions, which do not saturate. An engineer pointed out the analogy of these activation functions to the physical function of a transistor.

Every new set of problems that gets introduced comes with its own set of techniques attempting to fix it, such as gradient clipping, normalizing the outputs after each layer, etc. The take-home lesson is that none of this is magic. A lot of it is trial and error, and new methods emerge to fix problems that other new methods introduced. We only need to understand the principles, the why and the how, and get a decent exposure to what is popular in the field, while keeping an open mind for improving things, or doing things entirely differently.

Let’s state the formulas of common activation functions, as well as their derivatives. We need to calculate one derivative of the training function when we optimize the loss function in our search for the best weights of the neural network:

• Step function: $f\left(z\right)=\left\{\begin{array}{cc}& 0\text{if}z<0\hfill \\ & 1\text{if}z\ge 0\hfill \end{array}\right.$

  Its derivative: $f^{\text{'}}\left(z\right)=\left\{\begin{array}{cc}& 0\text{if}z\ne 0\hfill \\ & undefined\text{if}z=0\hfill \end{array}\right.$

• Logistic function: $\sigma \left(z\right)=\frac{1}{1+e^{-z}}$.

  Its derivative: ${\sigma }^{\text{'}}\left(z\right)=\frac{e^{-z}}{{(1+e^{-z})}^2}=\sigma \left(z\right)(1-\sigma \left(z\right))$.

• Hyperbolic tangent function: $tanh\left(z\right)=\frac{e^z-e^{-z}}{e^z+e^{-z}}=\frac{2}{1+e^{-2z}}-1$

  Its derivative: ${tanh}^{\text{'}}\left(z\right)=\frac{4}{{(e^z+e^{-z})}^2}=1-f{\left(z\right)}^2$

• Inverse tangent function: $f\left(z\right)=arctan\left(z\right)$.

  Its derivative: $f^{\text{'}}\left(z\right)=\frac{1}{1+z^2}$.

• Rectified Linear Unit function or ReLU(z): $f\left(z\right)=\left\{\begin{array}{cc}& 0\text{if}z<0\hfill \\ & z\text{if}z\ge 0\hfill \end{array}\right.$

  Its derivative: $f^{\text{'}}\left(z\right)=\left\{\begin{array}{cc}& 0\text{if}z<0\hfill \\ & undefined\text{if}z=0\hfill \\ & 1\text{if}z>0\hfill \end{array}\right.$

• Leaky Rectified Linear Unit function (or parametric linear unit): $f\left(z\right)=\left\{\begin{array}{cc}& \alpha z\text{if}z<0\hfill \\ & z\text{if}z\ge 0\hfill \end{array}\right.$

  Its derivative: $f^{\text{'}}\left(z\right)=\left\{\begin{array}{cc}& \alpha \text{if}z<0\hfill \\ & undefined\text{if}z=0\hfill \\ & 1\text{if}z>0\hfill \end{array}\right.$

• Exponential Linear Unit function: $f\left(z\right)=\left\{\begin{array}{cc}& \alpha (e^z-1)\text{if}z<0\hfill \\ & z\text{if}z\ge 0\hfill \end{array}\right.$

  Its derivative: $f^{\text{'}}\left(z\right)=\left\{\begin{array}{cc}& f\left(z\right)+\alpha \text{if}z<0\hfill \\ & 1\text{if}z\ge 0\hfill \end{array}\right.$

• Softplus function: $f\left(z\right)=ln(1+e^z)$

  Its derivative: $f^{\text{'}}\left(z\right)=\frac{1}{1+e^{-z}}=\sigma \left(z\right)$

Note that all of these activations are rather elementary functions. This is a good thing, since both they and their derivatives are usually involved in massive computations with thousands of parameters (weights) and data instances during training, testing, and deployment of neural networks, so better keep them elementary. The other reason is that in theory, it doesn’t really matter what activation function we end up choosing because of the universal function approximation theorems, discussed next. Careful here: operationally, it definitely matters what activation function we choose for our neural network nodes. As we mentioned earlier in this section, AlexNet’s success in image classification tasks is partly due to its use of the Rectified Linear Unit function, ReLU(z). Theory and practice do not contradict each other in this case, even though it seems so on the surface. We explain this in the next subsection.

Universal Function Approximation

Approximation theorems, when available, are awesome because they tell us, with mathematical confidence and authority, that if we have a function that we do not know, or that we know but that is difficult to include in our computations, then we do not have to deal with this unknown or difficult function altogether. We can, instead, approximate it using known functions that are much easier to compute, to a great degree of precision. This means that under certain conditions on both the unknown or complicated function, and the known and simple (sometimes elementary) functions, we can use the simple functions and be confident that our computations are doing the right thing. These types of approximation theorems quantify how far off the true function is from its approximation, so we know exactly how much error we are committing when substituting the true function with this approximation.

The fact that neural networks, even sometimes nondeep neural networks with only one hidden layer, have proved so successful for accomplishing various tasks in vision, speech recognition, classification, regression, and others means that they have some universal approximation property going on for them. The training function that a neural network represents (built from elementary linear combinations, biases, and very simple activation functions) approximates the underlying unknown function that truly represents or generates the data rather well.

The natural questions that mathematicians must now answer with a theorem, or a bunch of theorems, are:

Given some function that we don’t know but we really care about (because we think it is the true function underlying or generating our data), is there a neural network that can approximate it to a good degree of precision (without ever having to know this true function)?

Practice using neural networks successfully suggests that the answer is yes, and universal approximation theorems for neural networks prove that the answer is yes for a certain class of functions and networks.

If there is a neural network that approximates this true and elusive data generating function, how do we construct it? How many layers should it have? How many nodes in each layer? What type of activation function should it include?

In other words, what is the architecture of this network? Sadly, as of now, little is known on how to construct these networks, and experimentation with various architectures and activations is the only way forward until more mathematicians get on this.

Are there multiple neural network architecture that work well? Are there some that are better than others?

Experiments suggest that the answer is yes, given the comparable performance of various architectures on the same tasks and data sets.

Note that having definite answers for these questions is very useful. An affirmative answer to the first question tells us: hey, there is no magic here, neural networks do approximate a wide class of functions rather well! This wide coverage, or universality, is crucial, because recall that we do not know the underlying generating function of the data, but if the approximation theorem covers a wide class of functions, our unknown and elusive function might as well be included, hence the success of the neural network. Answering the second and third sets of questions is even more useful for practical applications, because if we know which architecture works best for each task type and data set, then we would be saved from so much experimentation, and we’d immediately choose an architecture that performs well.

Before stating the universal approximation theorems for neural networks and discussing their proofs, let’s go over two examples where we already encountered approximation type theorems, even when we were in middle school. The same principle applies for all examples: we have an unruly quantity that for whatever reason is difficult to deal with or is unknown, and we want to approximate it using another quantity that is easier to deal with. If we want universal results, we need to specify three things:

1. What class or what kind of space does the unruly quantity or function belong to? Is it the set of real numbers $ℝ$? The set of irrational numbers? The space of continuous functions on an interval? The space of compactly supported functions on $ℝ$? The space of Lebesgue measurable functions (I did slide in some measure theory stuff in here, hoping that no one notices or runs away)? Etc.

2. What kind of easier quantities or functions are we using to approximate the unruly entities, and how does using these quantities instead of the true function benefit us? How do these approximations fare against other approximations, if there are already some other popular approximations?

3. In what sense is the approximation happening, meaning that when we say we can approximate $f_{true}$ using $f_{approximate}$, how exactly are we measuring the distance between $f_{true}$ and $f_{approximate}$? Recall that in math we can measure sizes of objects, including distances, in many ways. So exactly which way are we using for our particular approximations? This is where we hear about the Euclidean norm, uniform norm, supremum norm, L² norm, etc. What do norms (sizes) have to do with distances? A norm induces a distance. This is intuitive: if our space allows us to talk about sizes of objects, then it better allow us talk about distances as well.

Example 1: Approximating irrational numbers with rational numbers

Any irrational number can be approximated by a rational number, up to any precision that we desire. Rational numbers are so well-behaved and useful, since they are just pairs of whole numbers. Our minds can easily intuit about whole numbers and fractions. Irrational numbers are quite the opposite. Have you ever been asked, maybe in grade 6, to calculate $\sqrt{47}=6.8556546...$ without a calculator, and stay at it until you had a definite answer? I have. Pretty mean! Even calculators and computers approximate irrational numbers with rationals. But I had to sit there thinking I could keep writing digits until I either found a pattern or the computation terminated. Of course neither happened, and around 30 digits later, I learned that some numbers are just irrational.

There is more than one way to write a mathematical statement quantifying this approximation. They are all equivalent and useful:

The approximating entity can be made arbitrarily close to the true quantity

This is the most intuitive way.

Given an irrational number s and any precision $ϵ$, no matter how small, we can find a rational number q within a distance $ϵ$ from s:

$|s-q|<ϵ$

This means that rational and irrational numbers live arbitrarily close to each other on the real line $ℝ$. This introduces the idea of denseness.

Denseness and closure

Approximating entities are dense in the space where the true quantities live.

This means that if we focus only on the space of approximating members, then add in all the limits of all their sequences, we get the whole space of the true members. Adding in all the limiting points of a certain space S is called closing the space, or taking its closure, $\overline{S}$. For example, when we add to the open interval $(a,b)$ its limit points a and b, we get the closed interval [a,b]. Thus the closure of $(a,b)$ is [a,b]. We write $\overline{(a,b)}=$[a,b].

The set of rational numbers $\mathbb{Q}$ is dense in the real line $ℝ$. In other words, the closure of $\mathbb{Q}$ is $ℝ$. We write $\overline{\mathbb{Q}}=ℝ$.

Limits of sequences

The true quantity is the limit of a sequence of the approximating entities.

The idea of adding in the limit points in the previous bullet introduces approximation using the terminology of sequences and their limits.

In the context of rational numbers approximating irrational numbers, we can therefore write: for any irrational number s, there is a sequence $q_n$ of rational numbers such that ${lim}_{n\to \infty }{q}_n=s$. This gives us the chance to write as an example one of the favorite definitions of the most famous irrational number: e = 2.71828182…​

${lim}_{n\to \infty }{(1+\frac{1}{n})}^n=e$

That is, the irrational number e is the limit of the sequence of rational numbers ${(1+\frac{1}{1})}^1,{(1+\frac{1}{2})}^2,{(1+\frac{1}{3})}^3,\cdots$ which is equivalent to $2,2.25,2.370370...,\cdots$.

Whether we approximate an irrational number with a rational number using the arbitrarily close concept, the denseness and closure concepts, or the limits of sequences concept, any distance involved in the mathematical statements is measured using the usual Euclidean norm: $d(s,q)=|s-q|$, which is the normal distance between two numbers.

Closeness Statements Need to Be Accompanied by a Specific Norm

We might wonder: what if we change the norm? Would the approximation property still hold? Can we still approximate irrationals using rationals if we measure the distance between them using some other definition of distance than the usual Euclidean norm? Welcome to mathematical analysis. In general, the answer is no. Quantities can be close to each other using some norm and very far using another norm. So in mathematics, when we say that quantities are close to each other, approximate others, or converge somewhere, we need to mention the accompanying norm in order to pinpoint in what sense these closeness statements are happening.

Example 2: Approximating continuous functions with polynomials

Continuous functions can be anything. A child can draw a wiggly line on a piece of paper and that would be a continuous function that no one knows the formula of. Polynomials, on the other hand, are a special type of continuous function that are extremely easy to evaluate, differentiate, integrate, explain, and do computations with. The only operations involved in polynomial functions are powers, scalar multiplication, addition, and subtraction. A polynomial of degree n has a simple formula:

$p_n\left(x\right)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_n{x}^n$

where the $a_i$’s are scalar numbers. Naturally, it is extremely desirable to be able to approximate nonpolynomial continuous functions using polynomial functions. The wonderful news is that we can, up to any precision $ϵ$. This is a classical result in mathematical analysis, called the Weierstrass Approximation Theorem:

Suppose f is a continuous real-valued function defined on a real interval [a,b]. For any precision $ϵ>0$, there exists a polynomial $p_n$ such that for all x in [a,b], we have $|f\left(x\right)-p_n\left(x\right)|<ϵ$, or equivalently, the supremum norm $\parallel f-p_n\parallel <ϵ$.

Note that the same principle as the one that we discussed for using rational numbers to approximate irrationals applies here. The theorem asserts that we can always find polynomials that are arbitrarily close to a continuous function, which means that the set of polynomials is dense in the space of continuous functions over the interval [a,b]; or equivalently, for any continuous function f, we can find a sequence of polynomial functions that converge to f (so f is the limit of a sequence of polynomials). In all of these variations of the same fact, the distances are measured with respect to the supremum norm. In Figure 4-6, we verify that the continuous function $sinx$ is the limit of the sequence of the polynomial functions $\{x,x-\frac{x^3}{3!},x-\frac{x^3}{3!}+\frac{x^5}{5!},\cdots \}$.

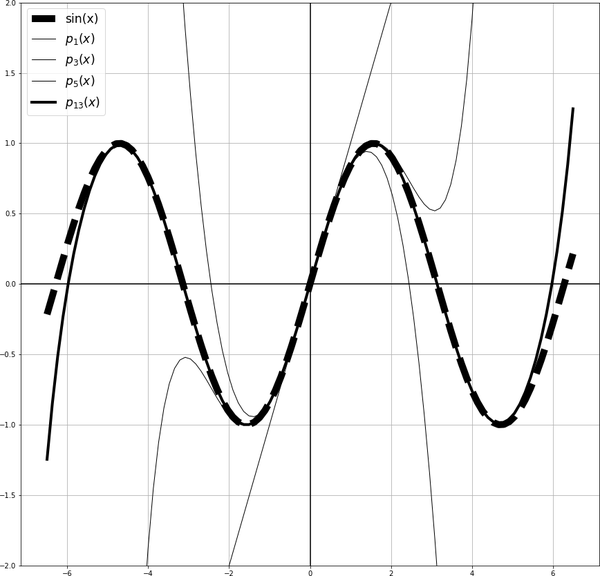
Figure 4-6. Approximation of the continuous function $sinx$ by a sequence of polynomials

Statement of the universal approximation theorem for neural networks

Now that we understand the principles of approximation, let’s state the most recent approximation theorems for neural networks.

Recall that a neural network is the representation of the training function as a computational graph. We want this training function to approximate the unknown function that generates the data well. This allows us to use the training function instead of the underlying true function, which we do not know and probably will never know, to make predictions. The following approximation theorems assert that neural networks can approximate the underlying functions up to any precision. When we compare the statements of these theorems to the two previous examples on irrational numbers and continuous functions, we notice that they are the same kind of mathematical statements.

The following result is from Hornik, Stinchombe, and White (1989): let f be a continuous function on a compact set K (this is the true but unknown function underlying the data) whose outputs are in ${ℝ}^d$. Then:

Arbitrarily close

There exists a feed forward neural network, having only a single hidden layer, which uniformly approximates f to within an arbitrary $ϵ>0$ on K.

Denseness

The set of neural networks, with prescribed nonlinear activations and bounds on the number of neurons and layers depending on d, is dense in the uniform topology of $C(K,{ℝ}^d)$.

In both variations of the same fact, the distances are measured with respect to the supremum norm on continuous functions.

The proof needs mathematical concepts from measure theory and functional analysis. We will introduce measure theory in Chapter 11 on probability. For now we only list what is needed for the proof without any details: Borel and Radon measures, Hahn-Banach theorem, and Riesz representation theorem.

Approximation Theory for Deep Learning

We only motivated approximation theory and stated one of its main results for deep learning. For more information and a deeper discussion, we point to the state-of-the-art results such as the ability of neural networks to learn probability distributions, Barron’s theorem, the neural tangent kernel, and others.

Loss Functions

Even though in this chapter we transitioned from Chapter 3’s traditional machine learning to the era of deep learning, the structure of the training function, loss function, and optimization is still exactly the same. The loss functions used for neural networks are not different from those discussed in Chapter 3, since the goal of a loss function has not changed: to capture the error between the ground truth and prediction made by the training function. In deep learning, the neural network represents the training function, and for feed forward neural networks, we saw that this is nothing more than a sequence of linear combinations followed by compositions with nonlinear activation functions.

The most popular loss functions used in deep learning are still the mean squared error for regression tasks and the cross-entropy function for classification tasks. Go back to Chapter 3 for a thorough explanation of these functions.

There are other loss functions that we sometimes come across in the field. When we encounter a new loss function, usually the designers of the model have a certain reason to prefer it over the other more popular ones, so make sure you go through their rationale for using that specific loss function for their particular setup. Ideally, a good loss function penalizes bad predictions, is not expensive to compute, and has one derivative that is easy to compute. We need this derivative so that our optimization method behaves well. As we discussed in Chapter 3, functions with one good derivative have smoother terrains than functions with discontinuous derivatives, and hence are easier to navigate during the optimization process\when searching for minimizers of the loss function.

Cross-Entropy Function, log-likelihood Function, and KL Divergence

Minimizing the cross-entropy loss function is the same as maximizing the log-likelihood function; KL divergence for probability distributions is closely related. Recall that the cross-entropy function is borrowed from information theory and statistical mechanics, and it quantifies the cross entropy between the true (empirical) distribution of the data and the distribution (of predictions) produced by the neural network’s training function. The cross-entropy function has a negative sign and a $log$ function in its formula. Minimizing the minus of a function is the same as maximizing the same function without the minus sign, so sometimes you encounter the following statement in the field: maximizing the log likelihood function, which for us is equivalent to minimizing the cross-entropy loss function. A closely related concept is the Kullback-Leibler divergence, also called KL divergence. Sometimes, as in the cases where we generate images or machine audio, we need to learn a probability distribution, not a deterministic function. Our loss function in this case should capture the difference (I will not say distance since its mathematical formula is not a distance metric) between the true probability distribution of the data and the learned probability distribution. KL divergence is an example of such a loss function that quantifies the amount of information lost when the learned distribution is used to approximate the true distribution, or the relative entropy of the true distribution with respect to the learned distribution.

Optimization

Faithful to our training function, loss function, and optimization mathematical structure, we now discuss the optimization step. Our goal is to perform an efficient search of the landscape of the loss function $L\left(\overrightarrow{\omega }\right)$ to find the minimizing $\omega$’s. Note that when we previously explicitly wrote formulas for the training functions of the neural network, we bundled up the $\omega$ weights in matrices W, and the biases in vectors ${\overrightarrow{\omega }}_0$. In this section, for the sake of simplifying notation and to keep the focus on the mathematics, we put all the weights and biases in one very long vector $\overrightarrow{\omega }$. That is, we write the loss function as $L\left(\overrightarrow{\omega }\right)$, while in reality, for a fully connected neural network with h hidden layers, it is:

$\text{Loss}\text{function}=L(W^1,{\overrightarrow{\omega }}_0^1,W^2,{\overrightarrow{\omega }}_0^2,\cdots ,W^{h+1},{\overrightarrow{\omega }}_0^{h+1})$

We only need that representation when we explicitly compute the derivative of the loss function using backpropagation, which we will cover later in this chapter.

For deep learning, the number of $\omega$’s in the vector $\overrightarrow{\omega }$ can be extremely high, as in tens of thousands, millions, or even billions. OpenAI’s GPT-2 for natural language has 1.5 billion parameters, and was trained on a data set of eight million web pages. We need to solve for these many unknowns! Think parallel computing, or mathematical and algorithmic pipelining.

Using optimization methods, such as Newton-type methods that require computing matrices of second derivatives of the loss function in that many unknowns, is simply unfeasible even with our current powerful computational abilities. This is a great example where the mathematical theory of a numerical method works perfectly fine but is impractical for computational and real-life implementation. The sad part here is that numerical optimization methods that use the second derivative usually converge faster than those that use only the first derivative, because they take advantage of the extra knowledge about the concavity of the function (the shape of its bowl), as opposed to only using the information on whether the function is increasing or decreasing that the first derivative provides. Until we invent even more powerful computers, we have to satisfy ourselves with first-order methods that use only one derivative of the loss function with respect to the unknown $\omega$’s. These are the gradient-descent-type methods, and luckily, they perform extremely well for many real-life AI systems that are currently deployed for use in our everyday life, such as Amazon’s Alexa.

Mathematics and the Mysterious Success of Neural Networks

It is worth pausing here to reflect on the success of neural networks, which in the context of this section translates to: our ability to locate a minimizer for the loss function $L\left(\overrightarrow{\omega }\right)$ that makes the training function generalize to new and unseen data really well. I do not have a North American accent, and Amazon’s Alexa understands me perfectly fine. Mathematically, this success of neural networks is still puzzling for various reasons:

• The loss function’s $\overrightarrow{\omega }$-domain $L\left(\overrightarrow{\omega }\right)$, where the search for the minimum is happening, is very high-dimensional (can reach billions of dimensions). We have billions or even trillions of options. How are we finding the right one?

• The landscape of the loss function itself is nonconvex, so it has a bunch of local minima and saddle points where optimization methods can get stuck or converge to the wrong local minimum. Again, how are we finding the right one?

• In some AI applications, such as computer vision, there are much more $\omega$’s than data points (images). Recall that for images, each pixel is a feature, so that is already a lot of $\omega$’s only at the input level. For such applications, there are much more unknowns (the $\omega$’s) than information required to determine them (the data points). Mathematically, this is an under-determined system, and such systems have infinitely many possible solutions! So exactly how is the optimization method for our network picking up on the good solutions? The ones that generalize well?

Some of this mysterious success is attributed to techniques that have become a staple during the training process, such as regularization (discussed later in this chapter), validation, testing, etc. However, deep learning still lacks a solid theoretical foundation. This is why a lot of mathematicians have recently converged to answer such questions. The efforts of the National Science Foundation (NSF) in this direction, and the quotes that we copy next from its announcements are quite informative and give great insight on how mathematics is intertwined with advancing AI:

The NSF has recently established 11 new artificial intelligence research institutes to advance AI in various fields, such as human-AI interaction and collaboration, AI for advances in optimization, AI and advanced cyberinfrastructure, AI in computer and network systems, AI in dynamic systems, AI-augmented learning, and AI-driven innovation in agriculture and the food system. The NSF’s ability to bring together numerous fields of scientific inquiry, including computer and information science and engineering, along with cognitive science and psychology, economics and game theory, engineering and control theory, ethics, linguistics, mathematics, and philosophy, uniquely positions the agency to lead the nation in expanding the frontiers of AI. NSF funding will help the U.S. capitalize on the full potential of AI to strengthen the economy, advance job growth, and bring benefits to society for decades to come.

The following is quoted from the NSF’s Mathematical and Scientific Foundations of Deep Learning (SCALE MoDL) webcast.

Deep learning has met with impressive empirical success that has fueled fundamental scientific discoveries and transformed numerous application domains of artificial intelligence. Our incomplete theoretical understanding of the field, however, impedes accessibility to deep learning technology by a wider range of participants. Confronting our incomplete understanding of the mechanisms underlying the success of deep learning should serve to overcome its limitations and expand its applicability. The SCALE MoDL program will sponsor new research collaborations consisting of mathematicians, statisticians, electrical engineers, and computer scientists. Research activities should be focused on explicit topics involving some of the most challenging theoretical questions in the general area of Mathematical and Scientific Foundations of Deep Learning. Each collaboration should conduct training through research involvement of recent doctoral degree recipients, graduate students, and/or undergraduate students from across this multidisciplinary spectrum. A wide range of scientific themes on theoretical foundations of deep learning may be addressed in these proposals. Likely topics include but are not limited to geometric, topological, Bayesian, or game-theoretic formulations, to analysis approaches exploiting optimal transport theory, optimization theory, approximation theory, information theory, dynamical systems, partial differential equations, or mean field theory, to application-inspired viewpoints exploring efficient training with small data sets, adversarial learning, and closing the decision-action loop, not to mention foundational work on understanding success metrics, privacy safeguards, causal inference, and algorithmic fairness.

Gradient Descent ${\overrightarrow{\omega }}^{i+1}={\overrightarrow{\omega }}^i-\eta \nabla L\left({\overrightarrow{\omega }}^i\right)$

The widely used gradient descent method for optimization in deep learning is so simple that we could fit its formula in this subsection’s title. This is how gradient descent searches the landscape of the loss function $L\left(\overrightarrow{\omega }\right)$ for a local minimum:

Initialize somewhere at ${\overrightarrow{\omega }}^0$

Randomly pick starting numerical values for ${\overrightarrow{\omega }}^0=({\omega }_0,{\omega }_1,\cdots ,{\omega }_n)$. This choice places us somewhere in the search space and at the landscape of $L\left(\overrightarrow{\omega }\right)$. One big warning here: where we start matters! Do not initialize with all zeros or all equal numbers. This will diminish the network’s ability to learn different features, since different nodes will output exactly the same numbers. We will discuss initialization shortly.

Move to a new point ${\overrightarrow{\omega }}^1$

The gradient descent moves in the direction opposite to the gradient vector of the loss function $-\nabla L\left({\overrightarrow{\omega }}^0\right)$. This is guaranteed to decrease the gradient if the step size $\eta$, also called the learning rate, is not too large:

${\overrightarrow{\omega }}^1={\overrightarrow{\omega }}^0-\eta \nabla L\left({\overrightarrow{\omega }}^0\right)$

Move to a new point ${\overrightarrow{\omega }}^2$

Again, the gradient descent moves in the direction opposite to the gradient vector of the loss function $-\nabla L\left({\overrightarrow{\omega }}^1\right)$. This is guaranteed to decrease the gradient if the learning $\eta$ is not too large:

${\overrightarrow{\omega }}^2={\overrightarrow{\omega }}^1-\eta \nabla L\left({\overrightarrow{\omega }}^1\right)$

Keep going until the sequence of points $\{{\overrightarrow{\omega }}^0,{\overrightarrow{\omega }}^1,{\overrightarrow{\omega }}^2,\cdots \}$ converges

Note that in practice, we sometimes have to stop before it is clear that this sequence has converged—for example, when it becomes painfully slow due to a flattening landscape.

Figure 4-7 shows minimizing a certain loss function $L({\omega }_1,{\omega }_2)$ using gradient descent. We as humans are limited to the three-dimensional space that we exist in, so we cannot visualize beyond three dimensions. This is a severe limitation for us in terms of visualization since our loss functions usually act on very high-dimensional spaces. They are functions of many $\omega$’s, but we can only visualize them accurately if they depend on at most two $\omega$’s. That is, we can visualize a loss function $L({\omega }_1,{\omega }_2)$ depending on two $\omega$’s, but not a loss function $L({\omega }_1,{\omega }_2,{\omega }_3)$ depending on three (or more) $\omega$’s. Even with this severe limitation on our capacity to visualize loss functions acting on high-dimensional spaces, Figure 4-7 gives an accurate picture of how the gradient descent method operates in general. In Figure 4-7, the search happens in the two-dimensional $({\omega }_1,{\omega }_2)$ plane (the flat ground in Figure 4-7), and we track the progress on the landscape of the function $L({\omega }_1,{\omega }_2)$ that is embedded in ${ℝ}^3$. The search space always has one dimension less than the dimension of the space in which the landscape of the loss function is embedded. This makes the optimization process harder, since we are looking for a minimizer of a busy landscape in a flattened or squished version of its terrain (the ground level in Figure 4-7).

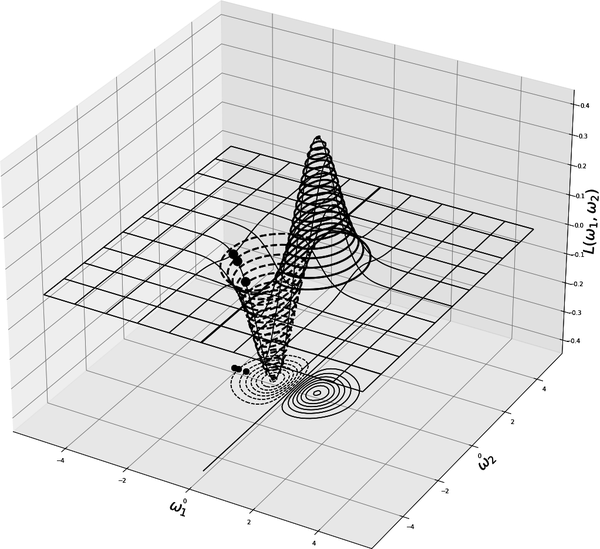
Figure 4-7. Two gradient descent steps. Note that if we start on the other side of the mountain, we wouldn’t converge to the minimum. So when we are searching for the minimum of a nonconvex function, where we start or how we initiate the $\omega$’s matters a lot.

Explaining the Role of the Learning Rate Hyperparameter $\eta$

At each iteration, the gradient descent method ${\overrightarrow{\omega }}^{i+1}={\overrightarrow{\omega }}^i-\eta \nabla L\left({\overrightarrow{\omega }}^i\right)$ moves us from the point ${\overrightarrow{\omega }}^i$ in the search space to another point ${\overrightarrow{\omega }}^{i+1}$. The gradient descent adds $-\eta \nabla L\left({\overrightarrow{\omega }}^i\right)$ to the current ${\overrightarrow{\omega }}^i$ to obtain ${\overrightarrow{\omega }}^{i+1}$. The quantity $-\eta \nabla L\left({\overrightarrow{\omega }}^i\right)$ is made up of a scalar number $\eta$ multiplied by the negative of the gradient vector $-\nabla L\left({\overrightarrow{\omega }}^i\right)$, which points in the direction of the steepest decrease of the loss function from the point ${\overrightarrow{\omega }}^i$. Thus, the scaled $-\eta \nabla L\left({\overrightarrow{\omega }}^i\right)$ tells us how far in the search space we are going to go along the steepest descent direction in order to choose the next point ${\overrightarrow{\omega }}^{i+1}$. In other words, the vector $-\nabla L\left({\overrightarrow{\omega }}^i\right)$ specifies in which direction we will move away from our current point, and the scalar number $\eta$, called the learning rate, controls how far we are going to step along that direction. Figure 4-8 shows one step of gradient descent with two different learning rates $\eta$. Too large of a learning rate might overshoot the minimum and cross to the other side of the valley. On the other hand, too small of a learning rate takes a while to get to the minimum. So the trade-off is between choosing a large learning rate and risking overshooting the minimum, and choosing a small learning rate and increasing computational cost and time for convergence.

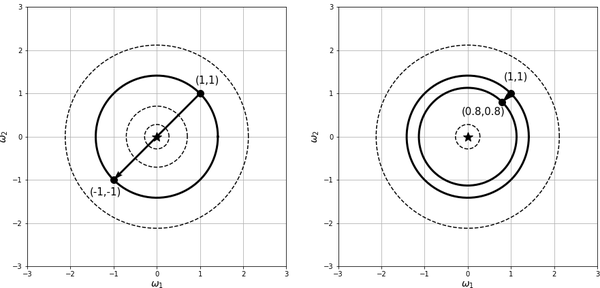
Figure 4-8. One-step gradient descent with two different learning rates. On the left, the learning rate is too large, so the gradient descent overshoots the minimum (the star point) and lands on the other side of the valley. On the right, the learning rate is small, however, it will take a while to get to the minimum (the star point). Note how the gradient vector at a point is perpendicular to the level set at that point.

The learning rate $\eta$ is another example of a hyperparameter of a machine learning model. It is not one of the weights that goes into the formula of the training function. It is a parameter that is intrinsic to the algorithm that we employ to estimate the weights of the training function.

The scale of the features affects the performance of the gradient descent

This is one of the reasons to standardize the features ahead of time. Standardizing a feature means subtracting from each data instance the mean and dividing by the standard deviation. This forces all the data values to have the same scale, with mean zero and standard deviation one, as opposed to having vastly different scales, such as a feature measured in the millions and another measured in 0.001. But why does this affect the performance of the gradient descent method? Read on.

Recall that the values of the input features get multiplied by the weights in the training function, and the training function in turn enters into the formula of the loss function. Very different scales of the input features change the shape of the bowl of the loss function, making the minimization process harder. Figure 4-9 shows the level sets of the function $L({\omega }_1,{\omega }_2)={\omega }_1^2+a{\omega }_2^2$ with different values of a, mimicking different scales of input features. Note how the level sets of loss function become much more narrow and elongated as the value of a increases. This means that the shape of the bowl of the loss function is a long, narrow valley.

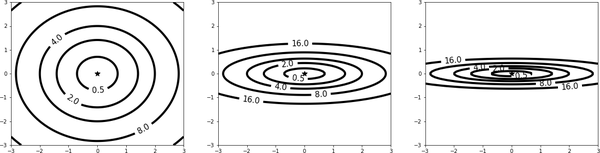
Figure 4-9. The level sets of the loss function $L({\omega }_1,{\omega }_2)={\omega }_1^2+a{\omega }_2^2$ become much more narrow and elongated as the value of a increases from 1 to 20 to 40

When the gradient descent method tries to operate in such a narrow valley, its points hop from one side of the valley to the other, zigzagging as it tries to locate the minimum, and slowing down the convergence considerably. Imagine zigzagging along all the streets of Rome before arriving at the Vatican, as opposed to taking a helicopter straight to the Vatican.

But why does this zigzagging behavior happen? One hallmark of the gradient vector of a function is that it is perpendicular to the level sets of that function. So if the valley of the loss function is so long and narrow, its level sets almost look like lines that are parallel to each other, and with a large enough step size (learning rate), we can literally cross from one side of the valley to the other since it is so narrow. Google gradient descent zigzag and you will see many images illustrating this behavior.

One fix for zigzagging, even with a narrow, long valley (assuming we did not scale the input feature values ahead of time), is to choose a very small learning rate, preventing the gradient descent method from stepping from one side of the valley to the other. However, that slows down the arrival to the minimum in its own way, since the method will step only incrementally at each iteration. We will eventually arrive at the Vatican from Rome, but at a turtle’s pace.

Near the minima (local and/or global), flat regions, or saddle points of the loss function’s landscape, the gradient descent method crawls

The gradient descent method updates the current point ${\overrightarrow{\omega }}^i$ by adding the vector $-\eta \nabla L\left({\overrightarrow{\omega }}^i\right)$. Therefore, the exact length of the step from the point ${\overrightarrow{\omega }}^i$ in the direction of the negative gradient vector is $\eta$ multiplied by the length of the gradient vector $\nabla L\left({\overrightarrow{\omega }}^i\right)$. At a minimum, maximum, saddle point, or any flat region of the landscape of the loss function, the gradient vector is zero, hence its length is zero as well. This means that near a minimum, maximum, saddle point, or any flat region, the step size of the gradient descent method becomes very small, and the method slows down significantly. If this happens near a minimum, then there is not much worry since this can be used as a stopping criterion, unless this minimum is a local minimum very far from the global minimum. If, on the other hand, it happens in a flat region or near a saddle point, then the method will get stuck there for a while, and that is undesirable. Some practitioners put the learning rate $\eta$ on a schedule, changing its value during the optimization process. When we look into these, we notice that the goals are to avoid crawling, save computational time, and speed up convergence.

We will discuss stochastic (random) gradient descent later in this chapter. Due to the random nature of this method, the points hop around a lot, as opposed to following a more consistent route toward the minimum. This works to our advantage in situations where we are stuck, such as saddle points or local minima, since we might get randomly propelled out of the local minimum or away from the saddle point into a part of the landscape with a better route toward the minimum.

Convex Versus Nonconvex Landscapes

We cannot have an optimization chapter without discussing convexity. In fact, entire mathematical fields are dedicated solely to convex optimization. It is equally important to immediately note that optimization for neural networks is in general, nonconvex.

When we use nonconvex activation functions, such as the sigmoid-type functions in the first row of Figure 4-5, the landscapes of the loss functions involved in the resulting neural networks are not convex. This is why we spend a good amount of time talking about getting stuck at local minima, flat regions, and saddle points, which we wouldn’t worry about for convex landscapes. The contrast between convex and nonconvex landscapes is obvious in Figure 4-10, which shows a convex loss function and its level sets, and Figures 4-11 and 4-12, which show nonconvex functions and their level sets.

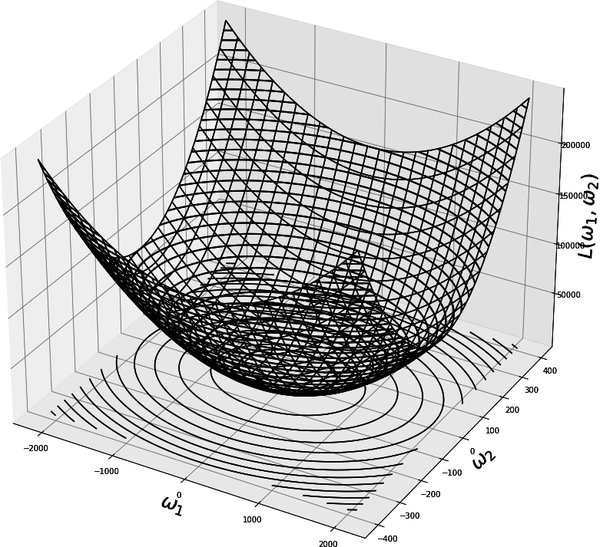
Figure 4-10. Plot of three-dimensional convex function and its level sets. Gradient vectors live in the same space (${ℝ}^2$) as the level sets, not in ${ℝ}^3$.

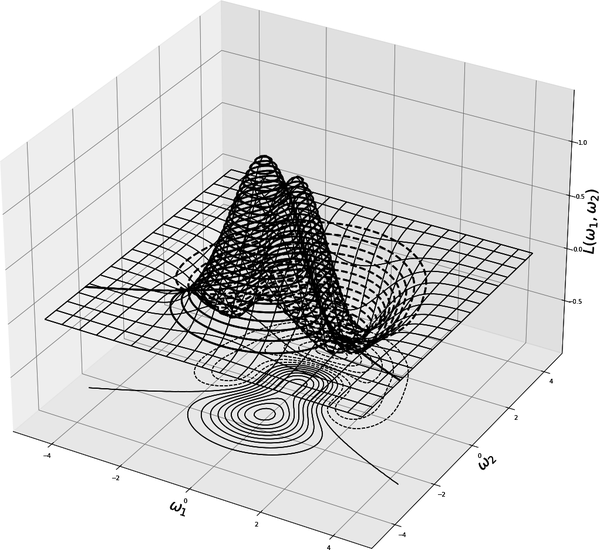
Figure 4-11. Plots of three-dimensional nonconvex functions and their level sets. Gradient vectors live in the same space (${ℝ}^2$) as the level sets, not in ${ℝ}^3$.

Figure 4-12. Plots of three-dimensional nonconvex functions and their level sets. Gradient vectors live in the same space (${ℝ}^2$) as the level sets, not in ${ℝ}^3$.

When we use convex activation functions throughout the network, such as the ReLU-type functions in the second row of Figure 4-5, and convex loss functions, we can still end up with a nonconvex optimization problem, because the composition of two convex functions is not necessarily convex. If the loss function happens to be nondecreasing and convex, then its composition with a convex function is convex. The loss functions that are popular for neural networks, such as mean squared error, cross-entropy, and hinge loss, are all convex but not nondecreasing.

It is important to become familiar with central concepts from convex optimization. If you do not know where to start, keep in mind that convexity replaces linearity when linearity is too simplistic or unavailable, then learn everything about the following (which will be tied to AI, deep learning, and reinforcement learning when we discuss operations research in Chapter 10):

• Max of linear functions is convex

• Max-min and min-max

• Saddle points

• Two-player zero-sum games

• Duality

Since convex optimization is such a well-developed and understood field (at least more than the mathematical foundations for neural networks), and neural networks still have a long way to go mathematically, it would be nice if we could exploit our knowledge about convexity in order to gain a deeper understanding of neural networks. Research in this area is ongoing. For example, in a 2020 paper titled “Convex Geometry of Two-Layer ReLU Networks: Implicit Autoencoding and Interpretable Models,” Tolga Ergen and Mert Pilanci frame the problem of training two layered ReLU networks as a convex analytic optimization problem. The following is the abstract of the paper:

We develop a convex analytic framework for ReLU neural networks which elucidates the inner workings of hidden neurons and their function space characteristics. We show that rectified linear units in neural networks act as convex regularizers, where simple solutions are encouraged via extreme points of a certain convex set. For one dimensional regression and classification, we prove that finite two-layer ReLU networks with norm regularization yield linear spline interpolation. In the more general higher dimensional case, we show that the training problem for two-layer networks can be cast as a convex optimization problem with infinitely many constraints. We then provide a family of convex relaxations to approximate the solution, and a cutting-plane algorithm to improve the relaxations. We derive conditions for the exactness of the relaxations and provide simple closed form formulas for the optimal neural network weights in certain cases. Our results show that the hidden neurons of a ReLU network can be interpreted as convex autoencoders of the input layer. We also establish a connection to $l_0-l_1$ equivalence for neural networks analogous to the minimal cardinality solutions in compressed sensing. Extensive experimental results show that the proposed approach yields interpretable and accurate models.

Stochastic Gradient Descent

So far, training a feed forward neural network has progressed as follows:

1. Fix an initial set of weights ${\overrightarrow{\omega }}^0$ for the training function.

2. Evaluate this training function at all the data points in the training subset.

3. Calculate the individual losses at all the data points in the training subset by comparing their true labels to the predictions made by the training function.

4. Do this for all the data in the training subset.

5. Average all these individual losses. This average is the loss function.

6. Evaluate the gradient of this loss function at this initial set of weights.

7. Choose the next set of weights according to the steepest descent rule.

8. Repeat until you converge somewhere, or stop after a certain number of iterations determined by the performance of the training function on the validation set.

The problem with this process is that when we have a large training subset with thousands of points, and a neural network with thousands of weights, it gets too expensive to evaluate the training function, the loss function, and the gradient of the loss function on all the data points in the training subset. The remedy is to randomize the process: randomly choose a very small portion of the training subset to evaluate the training function, loss function, and gradient of this loss function at each step. This slashes the computational cost dramatically.

Keep repeating this random selection (in principle with replacement but in practice without replacement) of small portions of the training subset until you converge somewhere, or stop after a certain number of iterations determined by the performance of the training function on the validation set. One pass through the whole training subset is called one epoch.

Stochastic gradient descent performs remarkably well, and it has become a staple in training neural networks.

Initializing the Weights ${\overrightarrow{\omega }}^0$ for the Optimization Process

We have already established that initializing with all zero weights or all the same weights is a really bad idea. The next logical step, and what was the traditional practice (before 2010), would be to choose the weights in the initial ${\overrightarrow{\omega }}^0$ randomly, sampled either from the uniform distribution over small intervals, such as [-1,1], [0,1], or [-0.3,0.3], or from the Gaussian distribution with a preselected mean and variance. Even though this has not been studied in depth, it seems from empirical evidence that it doesn’t matter whether the initial weights are sampled from the uniform distribution or Gaussian distribution, but it does seem that the scale of the initial weights matters when it comes to both the progress of the optimization process and the ability of the network to generalize well to unseen data. It turns out that some choices are better than others in this respect. Currently, the two state-of-the-art choices depend on the choice of the activation function: whether it is sigmoid-type or ReLU-type.

Xavier Glorot initialization

Here, initial weights are sampled from uniform distribution over the interval [$-\frac{\sqrt{6}}{\sqrt{n+m}},\frac{\sqrt{6}}{\sqrt{n+m}}$], where n is the number of inputs to the node (e.g., the number of nodes in the previous layer), and m is the number of outputs from the layer (e.g., the number of nodes in the current layer).

Kaiming He initialization

Here, the initial weights are sampled from the Gaussian distribution with zero mean and variance 2/n, where n is the number of inputs to the node.

Regularization Techniques

Regularization helps us arrive at a good choice for the weights of the training function while at the same time avoiding overfitting the data. We want our trained function to follow the signal in the data rather than the noise, so it can generalize well to unseen data. Here we include four simple yet popular regularization techniques that are used while training a neural network: dropout, early stopping, batch normalization, and weight decay (ridge, lasso, and elastic net) regularizations.

Dropout

Drop some randomly selected neurons from each layer during training. Usually, about 20% of the input layer’s nodes and about half of each of the hidden layers’ nodes are randomly dropped. No nodes from the output layer are dropped. Dropout is partially inspired by genetic reproduction, where half a parent’s genes are dropped and there is a small random mutation. This has the effect of training different networks at once (with a different number of nodes at each layer) and averaging their results, which typically produces more reliable results.

One way to implement dropout is by introducing a hyperparameter p for each layer that specifies the probability at which each node in that layer will be dropped. Recall the basic operations that take place at each node: linearly combine the outputs of the nodes of the previous layer, then activate. With dropout, each output of the nodes of the previous layer (starting with the input layer), is multiplied by a random number r, which can be either 0 or 1 with probability p. Thus when a node’s r takes the value 0, that node is essentially dropped from the network, which now forces the other retained nodes to pick up the slack when adjusting the weights in one gradient descent step. We will explain this further in “Backpropagation in Detail”, and this link provides a step-by-step route to implementing dropout.

For a deeper mathematical exploration, a 2015 paper connects dropout to Bayesian approximations of model uncertainty.

Early Stopping

As we update the weights during training, in particular during gradient descent, after each epoch, we evaluate the error made by the training function at the current weights on the validation subset of the data.

This error should be decreasing as the model learns the training data; however, after a certain number of epochs, this error will start increasing, indicating that the training function has now started overfitting the training data and is failing to generalize well to the validation data. Once we observe this increase in the model’s prediction over the validation subset, we stop training and go back to the set of weights where that error was lowest, right before we started observing the increase.

Batch Normalization of Each Layer

The main idea here is to normalize the inputs to each layer of the network. This means that the inputs to each layer will have mean 0 and variance 1. This is usually accomplished by subtracting the mean and dividing by the variance for each of the layer’s inputs. We will detail this in a moment. The reason this is good to do at each hidden layer is similar to why it is good at the original input layer.

Applying batch normalization often eliminates the need for dropout, and allows us to be less particular about initialization. It makes the training faster and safer from vanishing and exploding gradients. It also has the added advantage of regularization. The cost for all of these gains is not too high, as it usually involves training only two additional parameters, one for scaling and one for shifting, at each layer.

The 2015 paper by Ioffe and Szegedy introduced the method. The abstract of their paper describes the batch normalization process and the problems it addresses (the brackets are my own comments):

Training Deep Neural Networks is complicated by the fact that the distribution of each layer’s inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities [such as the sigmoid type activation functions, in Figure 4-5, which become almost constant, outputting the same value when the input is large in magnitude. This renders the nonlinearity useless in the training process, and the network stops learning at subsequent layers]. We refer to this phenomenon [the change in the distribution of the inputs to each layer] as internal covariate shift, and address the problem by normalizing layer inputs. Our method draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini-batch. Batch Normalization allows us to use much higher learning rates and be less careful about initialization, and in some cases eliminates the need for Dropout. Applied to a state-of-the-art image classification model, Batch Normalization achieves the same accuracy with 14 times fewer training steps, and beats the original model by a significant margin. Using an ensemble of batch-normalized networks, we improve upon the best published result on ImageNet classification: reaching 4.82% top-5 test error, exceeding the accuracy of human raters.

Batch normalization is often implemented in the architecture of a network either in its own layer before the activation step, or after activation. The process, during training, usually follows these steps:

1. Choose a batch from the training data of size b. Each data point in this has feature vector $\overrightarrow{x_i}$, so the whole batch has feature vectors $\overrightarrow{x_1},\overrightarrow{x_2},\cdots ,\overrightarrow{x_b}$.

2. Calculate the vector whose entries are the means of each feature in this particular batch: $\overrightarrow{\mu }=\frac{\overrightarrow{x_1}+\overrightarrow{x_2}+\cdots +\overrightarrow{x_b}}{b}$.

3. Calculate the variance across the batch: subtract $\overrightarrow{\mu }$ from each $\overrightarrow{x_1},\overrightarrow{x_2},\cdots ,\overrightarrow{x_b}$, calculate the result’s $l^2$ norm, add, and divide by b.

4. Normalize each of $\overrightarrow{x_1},\overrightarrow{x_2},\cdots ,\overrightarrow{x_b}$ by subtracting the mean and dividing by the square root of the variance:

5. Scale and shift by trainable parameters that can be initialized and learned by gradient descent, the same way the weights of the training function are learned. This becomes the input to the first hidden layer.

6. Do the same for the input of each of the subsequent layers.

7. Repeat for the next batch.

During testing and prediction, there is no batch of data to train on, and the parameters at each layer are already learned. The batch normalization step, however, is already incorporated into the formula of the training function. During training, we were changing these per batch of training data. This in turn was changing the formula of the loss function slightly per batch. However, the point of normalization was partly not to change the formula of the loss function too much, because that in turn would change the locations of its minima, and that would cause us to forever chase a moving target. Alright, we fixed that with batch normalization during training, and now we want to validate, test, and predict. Which mean vector and variance do we use for a particular data point that we are testing/predicting at? Do we use the means and variances of the features of the original data set? We have to make such decisions.

Control the Size of the Weights by Penalizing Their Norm

Another way to regularize the training function to avoid overfitting the data is to introduce a competing term into the minimization problem. Instead of solving for the set of weights $\overrightarrow{\omega }$ that minimizes only the loss function:

${min}_{\overrightarrow{\omega }}L\left(\overrightarrow{\omega }\right)$

we introduce a new term $\alpha \parallel \overrightarrow{\omega }\parallel$ and solve for the set of weights $\overrightarrow{\omega }$ that minimizes:

${min}_{\overrightarrow{\omega }}L\left(\overrightarrow{\omega }\right)+\alpha \parallel \overrightarrow{\omega }\parallel$

For example, for the mean squared error loss function usually used for regression problems, the minimization problem looks like:

${min}_{\overrightarrow{\omega }}\frac{1}{m}{\sum }_{i=1}^m|y_{predict}\left(\overrightarrow{\omega }\right)-y_{true}{|}^2+\alpha \parallel \overrightarrow{\omega }\parallel$

Recall that so far we have established two ways to solve that minimization problem:

The minimum happens at points where the derivative (gradient) is equal to zero

So the minimizing $\overrightarrow{\omega }$ must satisfy $\nabla L\left(\overrightarrow{\omega }\right)+\alpha \nabla (\parallel \overrightarrow{\omega }\parallel )=0$. Then we solve this equation for $\overrightarrow{\omega }$ if we have the luxury to get a closed form for the solution. In the case of linear regression (which we can think about as an extremely simplified neural network, with only one layer and zero nonlinear activation function), we do have this luxury, and for this regularized case, the formula for the minimizing $\overrightarrow{\omega }$ is:

$\overrightarrow{\omega }={(X^{t}X+\alpha B)}^{-1}{X}^t{\overrightarrow{y}}_{true}$

where the columns of X are the feature columns of the data augmented with a vector of ones, and B is the identity matrix (if we use ridge regression, discussed later). The closed form solution for the extremely simple linear regression problem with regularization helps us appreciate weight decay type regularization and see the important role it plays. Instead of inverting the matrix $\left(X^{t}X\right)$ in the unregularized solution and worrying about its ill-conditioning (for example, from highly correlated input features) and the resulting instabilities, we invert $(X^{t}X+\alpha B)$ in the regularized solution. Adding this $\alpha B$ term is equivalent to adding a small positive term to the denominator of a scalar number that helps us avoid division by zero. Instead of using $1/x$ where x runs the risk of being zero, we use $1/(x+\alpha )$ where $\alpha$ is a positive constant. Recall that matrix inversion is the analog of scalar number division.

Gradient descent

We use gradient descent or any of its variations, such as stochastic gradient descent, when we do not have the luxury of obtaining closed form solutions for the derivative equals zero equation, and when our problem is very large, that computing second-order derivatives is extremely expensive.

Commonly used weight decay regularizations

There are three popular regularizations that control the size of the weights that we are forever searching for in this book:

Ridge regression

Penalize the $l^2$ norm of $\overrightarrow{\omega }$. In this case, we add the term $\alpha {\sum }_{i=1}^n{\left|{\omega }_i\right|}^2$ to the loss function, then we minimize.

Lasso regression

Penalize the $l^1$ norm of the $\omega$’s. In this case, we add the term $\alpha {\sum }_{i=1}^n\left|{\omega }_i\right|$ to the loss function, then we minimize.

Elastic net

This is a middle-ground case between ridge and lasso regressions. We introduce one additional hyperparameter $\gamma$, which can take any value between zero and one, and add a term to the loss function that combines both ridge and lasso regressions through $\gamma$: $\gamma \alpha {\sum }_{i=1}^n|{\omega }_i{|}^2+(1-\gamma )\alpha {\sum }_{i=1}^n\left|{\omega }_i\right|$. When $\gamma =0$, this becomes lasso regression; when it is equal to one, it is ridge regression; and when it is between zero and one, it is some sort of a middle ground.

When do we use plain linear regression, ridge, lasso, or elastic net?

If you are already confused and slightly overwhelmed by the multitude of choices that are available for building machine learning models, join the club, but do not get frustrated. Until the mathematical analysis that tells us exactly which choices are better than others and under what circumstances becomes available (or catches us with mathematical computation and experimentation), think about the enormity of available choices the same way you think about a home renovation: we have to choose from many available materials, designs, and architectures to produce a final product. This is a home renovation, not a home decoration, so our decisions are fateful and more consequential than a mere home decoration. They do affect the quality and the function of our final product, but they are choices nevertheless. Rest easy, there is more than one way to skin AI:

• Some regularization is always good. Adding a term that controls the sizes of the weights and competes with minimizing the loss function is good in general.

• Ridge regression is usually a good choice because the $l^2$ norm is differentiable. Minimizing this is more stable than minimizing the $l^1$ norm.

• If we decide to go with the $l^1$ norm, even though it is not differentiable at 0, we can still define its subdifferential or subgradient at 0. For example, we can set that to be zero. Note that $f\left(x\right)=\left|x\right|$ is differentiable when $x\ne 0$: it has derivative 1 when x > 0 and -1 when x < 0; the only problematic point is x=0.

• If we suspect only a few features are useful, then it is good to use either lasso or elastic net as a data preprocessing step to kill off the less important features.

• Elastic net is usually preferred over lasso because lasso might behave badly when the number of features is greater than the number of training instances or when several features are strongly correlated.

Penalizing the $l^2$ Norm Versus Penalizing the $l^1$ Norm

Our goal is to find $\overrightarrow{\omega }$ that solves the minimization:

${min}_{\overrightarrow{\omega }}L(\overrightarrow{\omega },\overrightarrow{{\omega }_0})+\alpha \parallel \overrightarrow{\omega }\parallel$

The first term wants to decrease the loss $L(\overrightarrow{\omega },\overrightarrow{{\omega }_0})$. The other term wants to decrease the values of the coordinates of $\overrightarrow{\omega }$ all the way to zeros. The type of the norm that we choose for $\parallel \overrightarrow{\omega }\parallel$ determines the path $\overrightarrow{\omega }$ follows on its way to $\overrightarrow{0}$.

If we use the $l^1$ norm, the coordinates of $\overrightarrow{\omega }$ will decrease; however, a lot of them might encounter premature death, hitting zero before others. That is, the $l^1$ norm encourages sparsity: when a weight dies, it kills the contribution of the associated feature to the training function.

The plot on the right in Figure 4-13 shows the diamond-shaped level sets of $\parallel \overrightarrow{\omega }{\parallel }_{l^1}=|{\omega }_1|+|{\omega }_2|$ in two dimensions (if we only had two features), namely, $|{\omega }_1|+|{\omega }_2|=c$ for various values of c. If a minimization algorithm follows the path of steepest descent, such as the gradient descent, then we must travel in the direction perpendicular to the level sets, and as the arrow shows in the plot, ${\omega }_2$ becomes zero pretty fast since going perpendicular to the diamond-shaped level sets is bound to hit one of the coordinate axes, effectively killing the respective feature. ${\omega }_1$ then travels to zero along the horizontal axis.

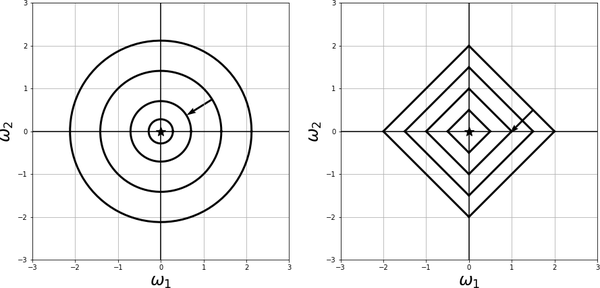
Figure 4-13. The plot on the left shows the circular level sets of the $l^2$ norm of $\overrightarrow{\omega }$, along with the direction the gradient descent follows toward the minimum at $(0,0)$. The plot on the right shows the diamond-shaped level sets of the $l^1$ norm of $\overrightarrow{\omega }$, along with the direction the gradient descent follows toward the minimum at $(0,0)$.

• If we use the $l^2$ norm, the weight sizes get smaller without necessarily killing them. The plot on the left in Figure 4-13 shows the circular-shaped level sets of $\parallel \overrightarrow{\omega }{\parallel }_{l^2}={\omega }_1^2+{\omega }_2^2$ in two dimensions, namely, ${\omega }_1^2+{\omega }_2^2=c$ for various values of c. We see that following the path perpendicular to the circular level sets toward the minimum at $(0,0)$ decreases the values of both ${\omega }_1$ and ${\omega }_2$ without either of them becoming zero before the other.

Which norm to choose depends on our use cases. Note that in all cases, we do not regularize the bias weights $\overrightarrow{{\omega }_0}$. This is why in this section we wrote them separately in the loss function $L(\overrightarrow{\omega },\overrightarrow{{\omega }_0})$.

Explaining the Role of the Regularization Hyperparameter $\alpha$

The minimization problem with weight decay regularization looks like:

${min}_{\overrightarrow{\omega }}L\left(\overrightarrow{\omega }\right)+\alpha \parallel \overrightarrow{\omega }\parallel$

To understand the role of the regularization hyperparameter $\alpha$, we observe the following:

• There is a competition between the first term, where the loss function $L\left(\overrightarrow{\omega }\right)$ chooses $\omega$’s that fit the training function to the training data, and the second term that just cares about making the $\omega$ values small. These two objectives are not necessarily in sync. The values of $\omega$’s that make the first term smaller might make the second term bigger and vice versa.

• If $\alpha$ is big, then the minimization process will compensate by making values of $\omega$’s very small, regardless of whether these small values of $\omega$’s will make the first term small as well. So the more we increase $\alpha$, the more important minimizing the second term becomes than the first term, so our ultimate model might end up not fitting the data perfectly (high bias), but this is sometimes desired (low variance) so that it generalizes well to unseen data.

• If, on the other hand, $\alpha$ is small (say, close to zero), then we can choose larger $\omega$ values, and minimizing the first term becomes more important. Here, the minimization process will result in $\omega$ values that make the first term happy, so the data will fit into the model nicely (low bias) but the variance might be high. In this case, our model would work well on seen data (it is designed to fit it nicely through minimizing $L\left(\overrightarrow{\omega }\right)$), but might not generalize well to unseen data.

• As $\alpha \to 0$, we can prove mathematically that the solution of the regularized problem converges to the solution of the unregularized problem.

Hyperparameter Examples That Appear in Machine Learning

We have now encountered many hyperparameters that enter machine learning models. It is good practice to list the ones that enter our particular model along with their values. Let’s list the ones we have come across and recall that tuning these enhances the performance of our models. Most of the time, there are recommended values for us to use. These are usually implemented as default values in machine learning libraries and software packages. However, it is always good to experiment with different values during the validation stage of our modeling process, given that we have the available time and resources. The hyperparameters include:

• The learning rate in gradient descent.

• Weight decay coefficients, such as the ones that appear in ridge, lasso, and elastic net regularizations.

• The number of epochs before we stop training.

• The sizes of data split into training, validation, and testing subsets.

• The sizes of mini-batches during stochastic gradient descent and its variants.

• The acceleration coefficients in momentum methods.

• The architecture of a neural network: number of layers, number of neurons in each layer, what happens at each layer (batch normalization, type of activation function), type of regularization (dropout, ridge, lasso), type of network (feed forward, dense, convolutional, adversarial, recurrent), type of loss functions, etc.

Chain Rule and Backpropagation: Calculating $\nabla L\left({\overrightarrow{\omega }}^i\right)$

It is time to get our hands dirty and compute something important: the gradient of the loss function, namely, $\nabla L\left({\overrightarrow{\omega }}^i\right)$. Whether we decide to find our optimal weights using gradient descent, stochastic gradient descent, mini-batch gradient descent, or any other variant of gradient descent, there is no escape from calculating this quantity. Recall that the loss function includes in its formula the neural network’s training function, which in turn is made up of subsequent linear combinations and compositions with activation functions. This means that we have to cleverly use the chain rule. Back in calculus, we only used the single variable chain rule for derivatives, but now we somehow have to transition to a chain rule of several variables: several, as in, sometimes billions.

It is the layered architecture of a neural network that forces us to pause and think: how exactly are we going to compute this one derivative of the loss function? The workhorse here is the backpropagation algorithm (also called backward mode automatic differentiation), and it is a powerful one.

Before writing formulas, let’s summarize the steps that we follow as we train a neural network:

• The training function is a function of $\overrightarrow{\omega }$, so the outcome of the neural network after a data point passes through it, which is the same as evaluating the training function at the data point, is: $outcome=function\left(\overrightarrow{\omega }\right)$. This is made up of linear combinations of node outputs, followed by compositions with activation functions, repeated over all of the network’s layers. The output layer might or might not have an activation function and could have one node or multiple nodes, depending on the ultimate task of the network.

• The loss function provides a measure of how badly the outcome of the training function diverged from what is true.

• We initialize our learning function with a random set of weights ${\overrightarrow{\omega }}^0$, according to preferred initialization rules prescribed in the previous sections. Then we compute the loss, or error, that we committed because of using these particular weight values. This is the forward pass of the data point through the net.

• We want to move to the next set of weights ${\overrightarrow{\omega }}^1$ that gives a lower error. We move in the direction opposite to the gradient vector of the loss function.

• But: the training function is built into the loss function, and given the layered structure of this function, which comes from the architecture of the neural network, along with its high dimensionality, how do we efficiently perform the multivariable chain rule to find the gradient and evaluate it at the current set of weights?

The answer is that we send the data point back through the network, computing the gradient backward from the output layer all the way to the input layer, evaluating along the way how each node contributed to the error. In essence, we compute $\frac{\partial L}{\partial \text{node}\text{functions}}$, then we tweak the weights accordingly, updating them from ${\overrightarrow{\omega }}^0$ to ${\overrightarrow{\omega }}^1$. The process continues as we pass more data points into the network, usually in batches. One epoch is then counted each time the network has seen the full training set.

Backpropagation Is Not Too Different from How Our Brain Learns

When we encounter a new math concept, the neurons in our brain make certain connections. The next time we see the same concept, the same neurons connect better. The analogy for our neural network is that the value $\omega$ of the edge connecting the neurons increases. When we see the same concept again and again, it becomes part of our brain’s model. This model will not change, unless we learn new information that undoes the previous information. In that case, the connection between the neurons weakens. For our neural network, the $\omega$ value connecting the neurons decreases. Tweaking the $\omega$’s via minimizing the loss function accomplishes exactly that: establishing the correct connections between the neurons.

The neuroscientist Donald Hebb mentions in his 1949 book The Organization of Behavior: A Neuropsychological Theory (paraphrased): When a biological neuron triggers another neuron often, the connection between these two neurons grows stronger. In other words, cells that fire together, wire together.

Similarly, a neural network’s computational model takes into account the error made by the network when it produces an outcome. Since computers only understand numbers, the $\omega$ of an edge increases if the node contributes to lowering the error, and decreases if the node contributes to increasing the error function. So a neural network’s learning rule reinforces the connections that reduce the error by increasing the corresponding $\omega$’s, and weakens the connections that increase the error by decreasing the corresponding $\omega$’s.

Why Is It Better to Backpropagate?

Backpropagation computes the derivative of the training function with respect to each node, moving backward through the network. This measures the contribution of each node to both the training function and the loss function $L\left(\overrightarrow{\omega }\right)$.

The most important formula to recall here is: the chain rule from calculus. This calculates the derivatives of chained functions (or function compositions). The calculus chain rule mostly deals with functions depending only on one variable $\omega$; for example, for three chained functions, the derivative with respect to $\omega$ is:

$\frac{d}{d\omega }{f}_3\left(f_2\left(f_1\left(\omega \right)\right)\right)=\left\{\frac{d}{d\omega }{f}_1\left(\omega \right)\right\}\left\{\frac{d}{d{f}_1}{f}_2\left(f_1\left(\omega \right)\right)\right\}\left\{\frac{d}{f_2}{f}_3\left(f_2\left(f_1\left(\omega \right)\right)\right)\right\}$

For neural networks, we must apply the chain rule to the loss function that depends on the matrices and vectors of variables W and $\overrightarrow{{\omega }_0}$. So we have to generalize the above rule to a many variables chain rule. The easiest way to do this is to follow the structure of the network computing the derivatives backward, from the outcome layer all the way back to the input layer.

If instead we decide to compute the derivatives forward through the network, we would not know whether these derivatives with respect to each variable will ultimately contribute to our final outcome, because we do not know if they will connect through the graph of the network. Even when the graph is fully connected, the weights for deeper layers are not present in earlier layers, so it is a big waste to compute for their derivatives in the early layers.

When we compute the derivatives backward through the network, we start with the output and follow the edges of the graph of the network back, computing the derivatives at each node. Each node’s contribution is calculated only from the edges leading to it and edges going out of it. This is computationally much cheaper because now we are sure of how and when these nodes contribute to the network’s outcome.

In linear algebra, it is much cheaper to compute the multiplication of a matrix with a vector than to compute the multiplication of two matrices together. We must always avoid multiplying two matrices with each other: computing $A\left(B𝐯\right)$ is cheaper than computing $\left(AB\right)𝐯$, even though in theory, these two are exactly the same. Over large matrices and vectors, this simple observation provides enormous cost savings.

Backpropagation in Detail

Let’s pause and be thankful that software packages exist so that we never have to implement the following computation ourselves. Let’s also not forget to be grateful to the creators of these software packages. Now we compute.

For a neural network with h hidden layers, we can write the loss function as a function of the training function, which in turn is a function of all the weights that appear in the network:

$L=L\left(g(W^1,{\overrightarrow{{\omega }_0}}^1,W^2,{\overrightarrow{{\omega }_0}}^2,\cdots ,W^h,{\overrightarrow{{\omega }_0}}^h,W^{h+1},{\overrightarrow{{\omega }_0}}^{h+1})\right)$

We will compute the partial derivatives of L backward, starting with $\frac{\partial L}{\partial W^{h+1}}$ and $\frac{\partial L}{\partial {\overrightarrow{{\omega }_0}}^{h+1}}$, and working our way back to $\frac{\partial L}{\partial W^1}$ and $\frac{\partial L}{\partial {\overrightarrow{{\omega }_0}}^1}$. Their derivatives are taken with respect to each entry in the corresponding matrix or vector.

Suppose for simplicity, but without loss of generality, that the network is a regression network predicting a single numerical value, so that the training function g is scalar (not a vector). Suppose also that we use the same activation function f for each neuron throughout the network. The output neuron has no activation since this is a regression.

Let’s find the derivatives with respect to the weights pointing to the output layer. The loss function is:

$L=L(W^{h+1}{\overrightarrow{s}}^h+{\omega }_0^{h+1})$

so that

$\frac{\partial L}{\partial {\omega }_0^{h+1}}=1\times L^{\text{'}}(W^{h+1}{\overrightarrow{s}}^h+{\omega }_0^{h+1})$

and

$\frac{\partial L}{\partial W^{h+1}}={\left({\overrightarrow{s}}^h\right)}^t{L}^{\text{'}}(W^{h+1}{\overrightarrow{s}}^h+{\omega }_0^{h+1})$

Recall that ${\overrightarrow{s}}^h$ is the output of the last layer, so it depends on all the weights of the previous layers, namely, $(W^1,{\overrightarrow{{\omega }_0}}^1,W^2,{\overrightarrow{{\omega }_0}}^2,\cdots ,W^h,{\overrightarrow{{\omega }_0}}^h)$.

To compute derivatives with respect to the weights pointing to the last hidden layer, we show them explicitly in the formula of the loss function:

$L=L(W^{h+1}\left(f(W^h{\overrightarrow{s}}^{h-1}+{\overrightarrow{{\omega }_0}}^h)\right)+{\omega }_0^{h+1})$

so that

$\frac{\partial L}{\partial {\overrightarrow{{\omega }_0}}^h}=\overrightarrow{1}\left(W^{h+1}{f}^{\text{'}}(W^h{\overrightarrow{s}}^{h-1}+{\overrightarrow{{\omega }_0}}^h)\right)L^{\text{'}}(W^{h+1}\left(f(W^h{\overrightarrow{s}}^{h-1}+{\overrightarrow{{\omega }_0}}^h)\right)+{\omega }_0^{h+1})$

and

$\frac{\partial L}{\partial W^h}={\overrightarrow{s}}^{h-1}\left(W^{h+1}{f}^{\text{'}}(W^h{\overrightarrow{s}}^{h-1}+{\overrightarrow{{\omega }_0}}^h)\right)L^{\text{'}}(W^{h+1}\left(f(W^h{\overrightarrow{s}}^{h-1}+{\overrightarrow{{\omega }_0}}^h)\right)+{\omega }_0^{h+1})$

Recall that ${\overrightarrow{s}}^{h-1}$ is the output of the hidden layer before the last hidden layer, so it depends on all the weights of the previous layers, namely, $(W^1,{\overrightarrow{{\omega }_0}}^1,W^2,{\overrightarrow{{\omega }_0}}^2,\cdots ,W^{h-1},{\overrightarrow{{\omega }_0}}^{h-1})$.

We continue the process systematically until we reach the input layer.

Assessing the Significance of the Input Data Features

One goal of data analysts is to assess the significance of the input variables (data features) with respect to the output or target variable.

The main question to answer here is: if we tweak the value of a certain input variable, what is the relative change of the output?

For example, if we add one more bus on a given bus route, would that affect the overall bus ridership?

The math question that we are asking is a derivative question: find the partial derivative of the output with respect to the input variable in question.

We have plenty of literature in statistics on variable significance when the models are linear (sensitivity analysis). When the models are nonlinear, such as our neural network models, there isn’t as much literature. We cannot make our predictions based on nonlinear models, then employ variable significance analysis that is built for linear models. Many data analysts who use built-in software packages for their analysis fall into this trap. This is another reason to seek to understand deeply the assumptions of the models on which we base our business decisions.

Summary and Looking Ahead

This chapter represents our official transition to the deep learning era in the AI field. While Chapter 3 presented traditional yet still very useful machine learning models, Chapter 4 adds neural networks to our arsenal of machine learning models. Both chapters built the models with the general mathematical structure of: training function, loss function, and optimization, where each was tailored to the particular task and model at hand.

By employing nonlinear activation functions at each neuron of a neural network, over multiple layers, our training function is able to pick up on complex features in the data that are otherwise hard to describe using an explicit formula of a nonlinear function. Mathematical analysis—in particular, universal approximation theorems for neural networks—back up this intuition and provide a theoretical background that justifies the wild success of neural networks. These theorems, however, still lack the ability to provide us with a map to construct special networks tailored to specific tasks and data sets, so we must experiment with various architectures, regularizations, and hyperparameters until we obtain a neural network model that performs well on new and unseen data.

Neural networks are well tailored to large problems with large data sets. The optimization task for such large problems requires efficient and computationally inexpensive methods, though all computations at that scale can be considered expensive. Stochastic gradient descent is the popular optimization method of choice, and the backpropagation algorithm is the workhorse of this method. More specifically, the backpropagation algorithm computes the gradient of the loss function (or the objective function when we add weight decay regularization) at the current weight choice. Understanding the landscape of the objective function remains central for any optimization task, and as a rule of thumb, convex problems are easier to optimize than nonconvex ones. Loss functions involved in neural network models are generally nonconvex.

Chapter 4 is the last foundational (and long) chapter in this book. We can finally discuss more specialized AI models, as well as deeper mathematics, when needed. The next chapters are independent from each other, so read them in the order that feels most relevant to your immediate application area.

Finally, let’s summarize the mathematics that appeared in this chapter, which we must elaborate more on as we progress in the field:

Probability and measure

This is needed to prove universal approximation-type theorems, and will be discussed in Chapter 11. It is also related to uncertainty analysis for dropout.

Statistics

Input standardizing steps during batch normalization at each layer of the neural network, and the resulting reshaping of the related distributions.

Optimization

Gradient descent, stochastic gradient descent, convex, and nonconvex landscapes.

Calculus on linear algebra

Backpropagation algorithm: this is the chain rule from calculus applied on functions of matrices of variables.