Chapter 1. Elegant NumPy: The Foundation of Scientific Python
[NumPy] is everywhere. It is all around us. Even now, in this very room. You can see it when you look out your window or when you turn on your television. You can feel it when you go to work…when you go to church…when you pay your taxes.
Morpheus, The Matrix
This chapter touches on some statistical functions in SciPy, but more than that, it focuses on exploring the NumPy array, a data structure that underlies almost all numerical scientific computation in Python. We will see how NumPy array operations enable concise and efficient code for manipulating numerical data.
Our use case is using gene expression data from The Cancer Genome Atlas (TCGA) project to predict mortality in skin cancer patients. We will be working toward this goal throughout this chapter and Chapter 2, learning about some key SciPy concepts along the way. Before we can predict mortality, we will need to normalize the expression data using a method called RPKM normalization. This allows the comparison of measurements between different samples and genes. (We will unpack what “gene expression” means in just a moment.)
Let’s start with a code snippet to tantalize you and introduce the ideas in this chapter. As we will do in each chapter, we open with a code sample that we believe epitomizes the elegance and power of a particular function from the SciPy ecosystem. In this case, we want to highlight NumPy’s vectorization and broadcasting rules, which allow us to manipulate and reason about data arrays very efficiently.
defrpkm(counts,lengths):"""Calculate reads per kilobase transcript per million reads.RPKM = (10^9 * C) / (N * L)Where:C = Number of reads mapped to a geneN = Total mapped reads in the experimentL = Exon length in base pairs for a geneParameters----------counts: array, shape (N_genes, N_samples)RNAseq (or similar) count data where columns are individual samplesand rows are genes.lengths: array, shape (N_genes,)Gene lengths in base pairs in the same orderas the rows in counts.Returns-------normed : array, shape (N_genes, N_samples)The RPKM normalized counts matrix."""N=np.sum(counts,axis=0)# sum each column to get total reads per sampleL=lengthsC=countsnormed=1e9*C/(N[np.newaxis,:]*L[:,np.newaxis])return(normed)
This example illustrates some of the ways that NumPy arrays can make your code more elegant:
-
Arrays can be 1D, like lists, but they can also be 2D, like matrices, and higher-dimensional still. This allows them to represent many different kinds of numerical data. In our case, we are manipulating a 2D matrix.
-
Arrays can be operated on along axes. In the first line, we calculate the sum down each column by specifying
axis=0. -
Arrays allow the expression of many numerical operations at once. For example, toward the end of the function we divide the 2D array of counts (C) by the 1D array of column sums (N). This is broadcasting. More on how this works in just a moment!
Before we delve into the power of NumPy, let’s spend some time looking at the biological data that we will be working with.
Introduction to the Data: What Is Gene Expression?
We will work our way through a gene expression analysis to demonstrate the power of NumPy and SciPy to solve a real-world biological problem. We will use the pandas library, which builds on NumPy, to read and munge our data files, and then we will manipulate our data efficiently in NumPy arrays.
The so-called central dogma of molecular biology states that all the information needed to run a cell (or an organism, for that matter) is stored in a molecule called deoxyribonucleic acid, or DNA. This molecule has a repetitive backbone on which lie chemical groups called bases, in sequence (Figure 1-1). There are four kinds of bases, abbreviated as A, C, G, and T, comprising an alphabet with which information is stored.

Figure 1-1. The chemical structure of DNA (image by Madeleine Price Ball, used under the terms of the CC0 public domain license)
To access this information, the DNA is transcribed into a sister molecule called messenger ribonucleic acid, or mRNA. Finally, this mRNA is translated into proteins, the workhorses of the cell (Figure 1-2). A section of DNA that encodes the information to make a protein (via mRNA) is called a gene.
The amount of mRNA produced from a given gene is called the expression of that gene. Although we would ideally like to measure protein levels, this is a much harder task than measuring mRNA. Fortunately, expression levels of an mRNA and levels of its corresponding protein are usually correlated.1 Therefore, we usually measure mRNA levels and base our analyses on that. As you will see below, it often doesn’t matter, because we are using mRNA levels for their power to predict biological outcomes, rather than to make specific statements about proteins.

Figure 1-2. Central dogma of molecular biology
It’s important to note that the DNA in every cell of your body is identical. Thus, the differences between cells arise from differential expression of that DNA into RNA: in different cells, different parts of the DNA are processed into downstream molecules (Figure 1-3). Similarly, as we will see in this chapter and the next, differential expression can distinguish different kinds of cancer.
The state-of-the-art technology to measure mRNA is RNA sequencing (RNAseq). RNA is extracted from a tissue sample (e.g., from a biopsy from a patient), reverse transcribed back into DNA (which is more stable), and then read out using chemically modified bases that glow when they are incorporated into the DNA sequence. Currently, high-throughput sequencing machines can only read short fragments (approximately 100 bases is common). These short sequences are called “reads.” We measure millions of reads and then based on their sequence we count how many reads came from each gene (Figure 1-4). We’ll be starting our analysis directly from this count data.

Figure 1-3. Gene expression

Figure 1-4. RNA sequencing (RNAseq)
Table 1-1 shows a minimal example of a gene expression count data.
| Cell type A | Cell type B | |
|---|---|---|
| Gene 0 | 100 | 200 |
| Gene 1 | 50 | 0 |
| Gene 2 | 350 | 100 |
The data is a table of counts, integers representing how many reads were observed for each gene in each cell type. See how the counts for each gene differ between the cell types? We can use this information to learn about the differences between these two types of cells.
One way to represent this data in Python would be as a list of lists:
gene0=[100,200]gene1=[50,0]gene2=[350,100]expression_data=[gene0,gene1,gene2]
Above, each gene’s expression across different cell types is stored in a list of Python integers. Then, we store all of these lists in a list (a meta-list, if you will). We can retrieve individual data points using two levels of list indexing:
expression_data[2][0]
350
Because of the way the Python interpreter works, this is a very inefficient way to store these data points. First, Python lists are always lists of objects, so that the above list gene2 is not a list of integers, but a list of pointers to integers, which is unnecessary overhead. Additionally, this means that each of these lists and each of these integers ends up in a completely different, random part of your computer’s RAM. However, modern processors actually like to retrieve things from memory in chunks, so this spreading of the data throughout the RAM is inefficient.
This is precisely the problem solved by the NumPy array.
NumPy N-Dimensional Arrays
One of the key NumPy data types is the N-dimensional array (ndarray, or just array). Ndarrays underpin lots of awesome data manipulation techniques in SciPy. In particular, we’re going to explore vectorization and broadcasting, techniques that allow us to write powerful, elegant code to manipulate our data.
First, let’s get our heads around the ndarray. These arrays must be homogeneous: all items in an array must be the same type. In our case we will need to store integers. Ndarrays are called N-dimensional because they can have any number of dimensions. A one-dimensional array is roughly equivalent to a Python list:
importnumpyasnparray1d=np.array([1,2,3,4])(array1d)(type(array1d))
[1 2 3 4] <class 'numpy.ndarray'>
Arrays have particular attributes and methods you can access by placing a dot after the array name. For example, you can get the array’s shape with the following:
(array1d.shape)(4,)
Here, it’s just a tuple with a single number. You might wonder why you wouldn’t just use len, as you would for a list. That will work, but it doesn’t extend to 2D arrays.
This is what we use to represent the data in Table 1-1:
array2d=np.array(expression_data)(array2d)(array2d.shape)(type(array2d))
[[100 200] [ 50 0] [350 100]] (3, 2) <class 'numpy.ndarray'>
Now you can see that the shape attribute generalizes len to account for the size of multiple dimensions of an array of data.

Figure 1-5. Visualizing NumPy’s ndarrays in one, two, and three dimensions
Arrays have other attributes, such as ndim, the number of dimensions:
(array2d.ndim)
2
You’ll become familiar with all of these as you start to use NumPy more for your own data analysis.
NumPy arrays can represent data that has even more dimensions, such as magnetic resonance imaging (MRI) data, which includes measurements within a 3D volume. If we store MRI values over time, we might need a 4D NumPy array.
For now, we’ll stick to 2D data. Later chapters will introduce higher-dimensional data and will teach you to write code that works for data of any number of dimensions.
Why Use ndarrays Instead of Python Lists?
Arrays are fast because they enable vectorized operations, written in the low-level language C, that act on the whole array. Say you have a list and you want to multiply every element in the list by five. A standard Python approach would be to write a loop that iterates over the elements of the list and multiply each one by five. However, if your data is instead represented as an array, you can multiply every element in the array by five in a single bound. Behind the scenes, the highly optimized NumPy library is doing the iteration as fast as possible.
importnumpyasnp# Create an ndarray of integers in the range# 0 up to (but not including) 1,000,000array=np.arange(1e6)# Convert it to a listlist_array=array.tolist()
Let’s compare how long it takes to multiply all the values in the array by five, using the IPython timeit magic function. First, when the data is in a list:
%timeit-n10y=[val*5forvalinlist_array]
10 loops, average of 7: 102 ms +- 8.77 ms per loop (using standard deviation)
Now, using NumPy’s built-in vectorized operations:
%timeit-n10x=array*5
10 loops, average of 7: 1.28 ms +- 206 µs per loop (using standard deviation)
Over 50 times faster, and more concise, too!
Arrays are also size efficient. In Python, each element in a list is an object and is given a healthy memory allocation (or is that unhealthy?). In contrast, in arrays, each element takes up just the necessary amount of memory. For example, an array of 64-bit integers takes up exactly 64 bits per element, plus some very small overhead for array metadata, such as the shape attribute we discussed above. This is generally much less than would be given to objects in a Python list. (If you’re interested in digging into how Python memory allocation works, check out Jake VanderPlas’s blog post, “Why Python Is Slow: Looking Under the Hood”.)
Plus, when computing with arrays, you can also use slices that subset the array without copying the underlying data.
# Create an ndarray xx=np.array([1,2,3],np.int32)(x)
[1 2 3]
# Create a "slice" of xy=x[:2](y)
[1 2]
# Set the first element of y to be 6y[0]=6(y)
[6 2]
Notice that although we edited y, x has also changed, because y was referencing the same data!
# Now the first element in x has changed to 6!(x)
[6 2 3]
This means you have to be careful with array references. If you want to manipulate the data without touching the original, it’s easy to make a copy:
y=np.copy(x[:2])
Vectorization
Earlier we talked about the speed of operations on arrays. One of the tricks NumPy uses to speed things up is vectorization. Vectorization is where you apply a calculation to each element in an array, without having to use a for loop. In addition to speeding things up, this can result in more natural, readable code. Let’s look at some examples.
x=np.array([1,2,3,4])(x*2)
[2 4 6 8]
Here, we have x, an array of 4 values, and we have implicitly multiplied every element in x by 2, a single value.
y=np.array([0,1,2,1])(x+y)
[1 3 5 5]
Now, we have added together each element in x to its corresponding element in y, an array of the same shape.
Both of these operations are simple and, we hope, intuitive examples of vectorization. NumPy also makes them very fast, much faster than iterating over the arrays manually. (Feel free to play with this yourself using the %timeit IPython magic we saw earlier.)
Broadcasting
One of the most powerful and often misunderstood features of ndarrays is broadcasting. Broadcasting is a way of performing implicit operations between two arrays. It allows you to perform operations on arrays of compatible shapes, to create arrays bigger than either of the starting ones. For example, we can compute the outer product of two vectors by reshaping them appropriately:
x=np.array([1,2,3,4])x=np.reshape(x,(len(x),1))(x)
[[1] [2] [3] [4]]
y=np.array([0,1,2,1])y=np.reshape(y,(1,len(y)))(y)
[[0 1 2 1]]
Two shapes are compatible when, for each dimension, either is equal to 1 (one) or they match one another.2
Let’s check the shapes of these two arrays.
(x.shape)(y.shape)
(4, 1) (1, 4)
Both arrays have two dimensions and the inner dimensions of both arrays are 1, so the dimensions are compatible!
outer=x*y(outer)
[[0 1 2 1] [0 2 4 2] [0 3 6 3] [0 4 8 4]]
The outer dimensions tell you the size of the resulting array. In our case we expect a (4, 4) array:
(outer.shape)
(4, 4)
You can see for yourself that outer[i, j] = x[i] * y[j] for all (i, j).
This was accomplished by NumPy’s broadcasting rules, which implicitly expand dimensions of size 1 in one array to match the corresponding dimension of the other array. Don’t worry, we will talk about these rules in more detail later in this chapter.
As we will see in the rest of the chapter, as we explore real data, broadcasting is extremely valuable for real-world calculations on arrays of data. It allows us to express complex operations concisely and efficiently.
Exploring a Gene Expression Dataset
The dataset that we’ll be using is an RNAseq experiment of skin cancer samples from The Cancer Genome Atlas (TCGA) project. We’ve already cleaned and sorted the data for you, so you can just use data/counts.txt in the book repository.
In Chapter 2 we will be using this gene expression data to predict mortality in skin cancer patients, reproducing a simplified version of Figures 5A and 5B of a paper from the TCGA consortium. But first we need to get our heads around the biases in our data, and think about how we could improve it.
Reading in the Data with pandas
We’re first going to use pandas to read in the table of counts. pandas is a Python library for data manipulation and analysis, with particular emphasis on tabular and time series data. Here, we will use it to read in tabular data of mixed type. It uses the DataFrame type, which is a flexible tabular format based on the data frame object in R. For example, the data we will read has a column of gene names (strings) and multiple columns of counts (integers), so reading it into a homogeneous array of numbers would be the wrong approach. Although NumPy has some support for mixed data types (called “structured arrays”), it is not primarily designed for this use case, which makes subsequent operations harder than they need to be.
By reading in the data as a pandas data frame we can let pandas do all the parsing, then extract the relevant information and store it in a more efficient data type. Here we are just using pandas briefly to import data. In later chapters we will see a bit more of pandas, but for details, read Python for Data Analysis (O’Reilly) by the creator of pandas, Wes McKinney.
importnumpyasnpimportpandasaspd# Import TCGA melanoma datafilename='data/counts.txt'withopen(filename,'rt')asf:data_table=pd.read_csv(f,index_col=0)# Parse file with pandas(data_table.iloc[:5,:5])
00624286-41dd-476f-a63b-d2a5f484bb45 TCGA-FS-A1Z0 TCGA-D9-A3Z1 \
A1BG 1272.36 452.96 288.06
A1CF 0.00 0.00 0.00
A2BP1 0.00 0.00 0.00
A2LD1 164.38 552.43 201.83
A2ML1 27.00 0.00 0.00
02c76d24-f1d2-4029-95b4-8be3bda8fdbe TCGA-EB-A51B
A1BG 400.11 420.46
A1CF 1.00 0.00
A2BP1 0.00 1.00
A2LD1 165.12 95.75
A2ML1 0.00 8.00
We can see that pandas has kindly pulled out the header row and used it to name the columns. The first column gives the name of each gene, and the remaining columns represent individual samples.
We will also need some corresponding metadata, including the sample information and the gene lengths.
# Sample namessamples=list(data_table.columns)
We will need some information about the lengths of the genes for our normalization. So that we can take advantage of some fancy pandas indexing, we’re going to set the index of the pandas table to be the gene names in the first column.
# Import gene lengthsfilename='data/genes.csv'withopen(filename,'rt')asf:# Parse file with pandas, index by GeneSymbolgene_info=pd.read_csv(f,index_col=0)(gene_info.iloc[:5,:])
GeneID GeneLength
GeneSymbol
CPA1 1357 1724
GUCY2D 3000 3623
UBC 7316 2687
C11orf95 65998 5581
ANKMY2 57037 2611
Let’s check how well our gene length data matches up with our count data.
("Genes in data_table: ",data_table.shape[0])("Genes in gene_info: ",gene_info.shape[0])
Genes in data_table: 20500 Genes in gene_info: 20503
There are more genes in our gene length data than were actually measured in the experiment. Let’s filter so we only get the relevant genes, and we want to make sure they are in the same order as in our count data. This is where pandas indexing comes in handy! We can get the intersection of the gene names from our two sources of data and use these to index both datasets, ensuring they have the same genes in the same order.
# Subset gene info to match the count datamatched_index=pd.Index.intersection(data_table.index,gene_info.index)
Now let’s use the intersection of the gene names to index our count data.
# 2D ndarray containing expression counts for each gene in each individualcounts=np.asarray(data_table.loc[matched_index],dtype=int)gene_names=np.array(matched_index)# Check how many genes and individuals were measured(f'{counts.shape[0]} genes measured in {counts.shape[1]} individuals.')
20500 genes measured in 375 individuals.
And our gene lengths:
# 1D ndarray containing the lengths of each genegene_lengths=np.asarray(gene_info.loc[matched_index]['GeneLength'],dtype=int)
And let’s check the dimensions of our objects:
(counts.shape)(gene_lengths.shape)
(20500, 375) (20500,)
As expected, they now match up nicely!
Normalization
Real-world data contains all kinds of measurement artifacts. Before doing any kind of analysis with it, it is important to take a look at it to determine whether some normalization is warranted. For example, measurements with digital thermometers may systematically vary from those taken with mercury thermometers and read by a human. Thus, comparing samples often requires some kind of data wrangling to bring every measurement to a common scale.
In our case, we want to make sure that any differences we uncover correspond to real biological differences, and not to technical artifact. We will consider two levels of normalization often applied jointly to a gene expression dataset: normalization between samples (columns) and normalization between genes (rows).
Between Samples
For example, the number of counts for each individual can vary substantially in RNAseq experiments. Let’s take a look at the distribution of expression counts over all the genes. First, we will sum the columns to get the total counts of expression of all genes for each individual, so we can just look at the variation between individuals. To visualize the distribution of total counts, we will use kernel density estimation (KDE), a technique commonly used to smooth out histograms because it gives a clearer picture of the underlying distribution.
Before we start, we have to do some plotting setup (which we will do in every chapter). See “A Quick Note on Plotting” for details about each line of the following code.
# Make all plots appear inline in the Jupyter notebook from now onwards%matplotlibinline# Use our own style file for the plotsimportmatplotlib.pyplotaspltplt.style.use('style/elegant.mplstyle')
Now back to plotting our counts distribution!
total_counts=np.sum(counts,axis=0)# sum columns together# (axis=1 would sum rows)fromscipyimportstats# Use Gaussian smoothing to estimate the densitydensity=stats.kde.gaussian_kde(total_counts)# Make values for which to estimate the density, for plottingx=np.arange(min(total_counts),max(total_counts),10000)# Make the density plotfig,ax=plt.subplots()ax.plot(x,density(x))ax.set_xlabel("Total counts per individual")ax.set_ylabel("Density")plt.show()(f'Count statistics:\nmin: {np.min(total_counts)}'f'\nmean: {np.mean(total_counts)}'f'\nmax: {np.max(total_counts)}')
Count statistics: min: 6231205 mean: 52995255.33866667 max: 103219262
We can see that there is an order-of-magnitude difference in the total number of counts between the lowest and the highest individual (Figure 1-6). This means that a different number of RNAseq reads were generated for each individual. We say that these individuals have different library sizes.

Figure 1-6. Density plot of gene expression counts per individual using KDE smoothing
Normalizing library size between samples
Let’s take a closer look at ranges of gene expression for each individual, so when we apply our normalization we can see it in action. We’ll subset a random sample of just 70 columns to keep the plotting from getting too messy.
# Subset data for plottingnp.random.seed(seed=7)# Set seed so we will get consistent results# Randomly select 70 samplessamples_index=np.random.choice(range(counts.shape[1]),size=70,replace=False)counts_subset=counts[:,samples_index]
# Some custom x-axis labelling to make our plots easier to readdefreduce_xaxis_labels(ax,factor):"""Show only every ith label to prevent crowding on x-axise.g. factor = 2 would plot every second x-axis label,starting at the first.Parameters----------ax : matplotlib plot axis to be adjustedfactor : int, factor to reduce the number of x-axis labels by"""plt.setp(ax.xaxis.get_ticklabels(),visible=False)forlabelinax.xaxis.get_ticklabels()[factor-1::factor]:label.set_visible(True)
# Bar plot of expression counts by individualfig,ax=plt.subplots(figsize=(4.8,2.4))withplt.style.context('style/thinner.mplstyle'):ax.boxplot(counts_subset)ax.set_xlabel("Individuals")ax.set_ylabel("Gene expression counts")reduce_xaxis_labels(ax,5)
There are obviously a lot of outliers at the high expression end of the scale and a lot of variation between individuals, but these are hard to see because everything is clustered around zero (Figure 1-7). So let’s do log(n + 1) of our data so it’s a bit easier to look at (Figure 1-8). Both the log function and the n + 1 step can be done using broadcasting to simplify our code and speed things up.

Figure 1-7. Boxplot of gene expression counts per individual
# Bar plot of expression counts by individualfig,ax=plt.subplots(figsize=(4.8,2.4))withplt.style.context('style/thinner.mplstyle'):ax.boxplot(np.log(counts_subset+1))ax.set_xlabel("Individuals")ax.set_ylabel("log gene expression counts")reduce_xaxis_labels(ax,5)

Figure 1-8. Boxplot of gene expression counts per individual (log scale)
Now let’s see what happens when we normalize by library size (Figure 1-9).
# Normalize by library size# Divide the expression counts by the total counts for that individual# Multiply by 1 million to get things back in a similar scalecounts_lib_norm=counts/total_counts*1000000# Notice how we just used broadcasting twice there!counts_subset_lib_norm=counts_lib_norm[:,samples_index]# Bar plot of expression counts by individualfig,ax=plt.subplots(figsize=(4.8,2.4))withplt.style.context('style/thinner.mplstyle'):ax.boxplot(np.log(counts_subset_lib_norm+1))ax.set_xlabel("Individuals")ax.set_ylabel("log gene expression counts")reduce_xaxis_labels(ax,5)

Figure 1-9. Boxplot of library-normalized gene expression counts per individual (log scale)
Much better! Also notice how we used broadcasting twice there. Once to divide all the gene expression counts by the total for that column, and then again to multiply all the values by 1 million.
Finally, let’s compare our normalized data to the raw data.
importitertoolsasitfromcollectionsimportdefaultdictdefclass_boxplot(data,classes,colors=None,**kwargs):"""Make a boxplot with boxes colored according to the class they belong to.Parameters----------data : list of array-like of floatThe input data. One boxplot will be generated for each elementin `data`.classes : list of string, same length as `data`The class each distribution in `data` belongs to.Other parameters----------------kwargs : dictKeyword arguments to pass on to `plt.boxplot`."""all_classes=sorted(set(classes))colors=plt.rcParams['axes.prop_cycle'].by_key()['color']class2color=dict(zip(all_classes,it.cycle(colors)))# map classes to data vectors# other classes get an empty list at that position for offsetclass2data=defaultdict(list)fordistrib,clsinzip(data,classes):forcinall_classes:class2data[c].append([])class2data[cls][-1]=distrib# then, do each boxplot in turn with the appropriate colorfig,ax=plt.subplots()lines=[]forclsinall_classes:# set color for all elements of the boxplotforkeyin['boxprops','whiskerprops','flierprops']:kwargs.setdefault(key,{}).update(color=class2color[cls])# draw the boxplotbox=ax.boxplot(class2data[cls],**kwargs)lines.append(box['whiskers'][0])ax.legend(lines,all_classes)returnax
Now we can plot a colored boxplot according to normalized versus unnormalized samples. We show only three samples from each class for illustration:
log_counts_3=list(np.log(counts.T[:3]+1))log_ncounts_3=list(np.log(counts_lib_norm.T[:3]+1))ax=class_boxplot(log_counts_3+log_ncounts_3,['raw counts']*3+['normalized by library size']*3,labels=[1,2,3,1,2,3])ax.set_xlabel('sample number')ax.set_ylabel('log gene expression counts');
You can see that the normalized distributions are a little more similar when we take library size (the sum of those distributions) into account (Figure 1-10). Now we are comparing like with like between the samples! But what about differences between the genes?

Figure 1-10. Comparing raw and library-normalized gene expression counts in three samples (log scale)
Between Genes
We can also get into some trouble when trying to compare different genes. The number of counts for a gene is related to the gene length. Suppose gene B is twice as long as gene A. Both are expressed at similar levels in the sample (i.e., both produce a similar number of mRNA molecules). Remember that in an RNAseq experiment, we fragment the transcripts and sample reads from that pool of fragments. So if a gene is twice as long, it’ll produce twice as many fragments, and we are twice as likely to sample it. Therefore, we would expect gene B to have about twice as many counts as gene A (Figure 1-11). If we want to compare the expression levels of different genes, we will have to do some more normalization.

Figure 1-11. Relationship between counts and gene length
Let’s see if the relationship between gene length and counts plays out in our dataset. First, we define a utility function for plotting:
defbinned_boxplot(x,y,*,# check out this Python 3 exclusive! (*see tip box)xlabel='gene length (log scale)',ylabel='average log counts'):"""Plot the distribution of `y` dependent on `x` using many boxplots.Note: all inputs are expected to be log-scaled.Parameters----------x: 1D array of floatIndependent variable values.y: 1D array of floatDependent variable values."""# Define bins of `x` depending on density of observationsx_hist,x_bins=np.histogram(x,bins='auto')# Use `np.digitize` to number the bins# Discard the last bin edge because it breaks the right-open assumption# of `digitize`. The max observation correctly goes into the last bin.x_bin_idxs=np.digitize(x,x_bins[:-1])# Use those indices to create a list of arrays, each containing the `y`# values corresponding to `x`s in that bin. This is the input format# expected by `plt.boxplot`binned_y=[y[x_bin_idxs==i]foriinrange(np.max(x_bin_idxs))]fig,ax=plt.subplots(figsize=(4.8,1))# Make the x-axis labels using the bin centersx_bin_centers=(x_bins[1:]+x_bins[:-1])/2x_ticklabels=np.round(np.exp(x_bin_centers)).astype(int)# make the boxplotax.boxplot(binned_y,labels=x_ticklabels)# show only every 10th label to prevent crowding on x-axisreduce_xaxis_labels(ax,10)# Adjust the axis namesax.set_xlabel(xlabel)ax.set_ylabel(ylabel);
We now compute the gene lengths and counts:
log_counts=np.log(counts_lib_norm+1)mean_log_counts=np.mean(log_counts,axis=1)# across sampleslog_gene_lengths=np.log(gene_lengths)
withplt.style.context('style/thinner.mplstyle'):binned_boxplot(x=log_gene_lengths,y=mean_log_counts)
We can see in the following image that the longer a gene is, the higher its measured counts! As previously explained, this is an artifact of the technique, not a biological signal! How do we account for this?

Normalizing Over Samples and Genes: RPKM
One of the simplest normalization methods for RNAseq data is RPKM: reads per kilobase transcript per million reads. RPKM puts together the ideas of normalizing by sample and by gene. When we calculate RPKM, we are normalizing for both the library size (the sum of each column) and the gene length.
To work through how RPKM is derived, let’s define the following values:
- C = Number of reads mapped to a gene
- L = Exon length in base-pairs for a gene
- N = Total mapped reads in the experiment
First, let’s calculate reads per kilobase.
Reads per base would be:
The formula asks for reads per kilobase instead of reads per base. One kilobase = 1,000 bases, so we’ll need to divide length (L) by 1,000.
Reads per kilobase would be:

Next, we need to normalize by library size. If we just divide by the number of mapped reads we get:
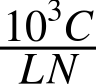
But biologists like thinking in millions of reads so that the numbers don’t get too big. Counting per million reads we get:

In summary, to calculate reads per kilobase transcript per million reads:

Now let’s implement RPKM over the entire counts array.
# Make our variable names the same as the RPKM formula so we can compare easilyC=countsN=counts.sum(axis=0)# sum each column to get total reads per sampleL=gene_lengths# lengths for each gene, matching rows in `C`
First, we multiply by 10^9. Because counts (C) is an ndarray, we can use broadcasting. If we multiple an ndarray by a single value, that value is broadcast over the entire array.
# Multiply all counts by 10^9C_tmp=10^9*C
Next, we need to divide by the gene length. Broadcasting a single value over a 2D array was pretty clear. We were just multiplying every element in the array by the value. But what happens when we need to divide a 2D array by a 1D array?
Broadcasting rules
Broadcasting allows calculations between ndarrays that have different shapes. Numpy uses broadcasting rules to make these manipulations a little easier. When two arrays have the same number of dimensions, broadcasting can occur if the sizes of each dimension match, or one of them is equal to 1. If arrays have different numbers of dimensions, then (1,) is prepended to the shorter array until the numbers match, and then the standard broadcasting rules apply.
For example, suppose we have two ndarrays, A and B, with shapes (5,2) and (2,). We define the product A * B using broadcasting. B has fewer dimensions than A, so during the calculation, a new dimension is prepended to B with value 1, so B’s new shape is (1,2). Finally, where B’s shape doesn’t match A’s, it is multiplied by stacking enough versions of B, giving the shape (5,2). This is done “virtually,” without using up any additional memory. At this point, the product is just an element-wise multiplication, giving an output array of the same shape as A.
Now let’s say we have another array, C, of shape (2.5). To multiply (or add) C to B, we might try to prepend (1,) to the shape of B, but in that case, we still end up with incompatible shapes: (2,5) and (1,2). If we want the arrays to broadcast, we have to append a dimension to B, manually. Then, we end up with (2,5) and (2,1), and broadcasting can proceed.
In NumPy, we can explicitly add a new dimension to B using np.newaxis. Let’s see this in our normalization by RPKM.
Let’s look at the dimensions of our arrays.
('C_tmp.shape',C_tmp.shape)('L.shape',L.shape)
C_tmp.shape (20500, 375) L.shape (20500,)
We can see that C_tmp has two dimensions, while L has one. So during broadcasting, an additional dimension will be prepended to L. Then we will have:
C_tmp.shape (20500, 375) L.shape (1, 20500)
The dimensions won’t match! We want to broadcast L over the first dimension of C_tmp, so we need to adjust the dimensions of L ourselves.
L=L[:,np.newaxis]# append a dimension to L, with value 1('C_tmp.shape',C_tmp.shape)('L.shape',L.shape)
C_tmp.shape (20500, 375) L.shape (20500, 1)
Now that our dimensions match or are equal to one, we can broadcast.
# Divide each row by the gene length for that gene (L)C_tmp=C_tmp/L
Finally, we need to normalize by the library size, the total number of counts for that column. Remember that we have already calculated N with:
N = counts.sum(axis=0) # sum each column to get total reads per sample
# Check the shapes of C_tmp and N('C_tmp.shape',C_tmp.shape)('N.shape',N.shape)
C_tmp.shape (20500, 375) N.shape (375,)
Once we trigger broadcasting, an additional dimension will be prepended to N:
N.shape (1, 375)
The dimensions will match so we don’t have to do anything. However, for readability, it can be useful to add the extra dimension to N anyway.
# Divide each column by the total counts for that column (N)N=N[np.newaxis,:]('C_tmp.shape',C_tmp.shape)('N.shape',N.shape)
C_tmp.shape (20500, 375) N.shape (1, 375)
# Divide each column by the total counts for that column (N)rpkm_counts=C_tmp/N
Let’s put this in a function so we can reuse it.
defrpkm(counts,lengths):"""Calculate reads per kilobase transcript per million reads.RPKM = (10^9 * C) / (N * L)Where:C = Number of reads mapped to a geneN = Total mapped reads in the experimentL = Exon length in base pairs for a geneParameters----------counts: array, shape (N_genes, N_samples)RNAseq (or similar) count data where columns are individual samplesand rows are genes.lengths: array, shape (N_genes,)Gene lengths in base pairs in the same orderas the rows in counts.Returns-------normed : array, shape (N_genes, N_samples)The RPKM normalized counts matrix."""N=np.sum(counts,axis=0)# sum each column to get total reads per sampleL=lengthsC=countsnormed=1e9*C/(N[np.newaxis,:]*L[:,np.newaxis])return(normed)
counts_rpkm=rpkm(counts,gene_lengths)
RPKM between gene normalization
Let’s see the RPKM normalization’s effect in action. First, as a reminder, here’s the distribution of mean log counts as a function of gene length (see Figure 1-12):
log_counts=np.log(counts+1)mean_log_counts=np.mean(log_counts,axis=1)log_gene_lengths=np.log(gene_lengths)withplt.style.context('style/thinner.mplstyle'):binned_boxplot(x=log_gene_lengths,y=mean_log_counts)

Figure 1-12. The relationship between gene length and average expression before RPKM normalization (log scale)
Now, the same plot with the RPKM-normalized values:
log_counts=np.log(counts_rpkm+1)mean_log_counts=np.mean(log_counts,axis=1)log_gene_lengths=np.log(gene_lengths)withplt.style.context('style/thinner.mplstyle'):binned_boxplot(x=log_gene_lengths,y=mean_log_counts)

You can see that the mean expression counts have flattened quite a bit, especially for genes larger than about 3,000 base pairs. (Smaller genes still appear to have low expression—these may be too small for the statistical power of the RPKM method.)
RPKM normalization can be useful to compare the expression profile of different genes. We’ve already seen that longer genes have higher counts, but this doesn’t mean their expression level is actually higher. Let’s choose a short gene and a long gene and compare their counts before and after RPKM normalization to see what we mean.
gene_idxs=np.array([80,186])gene1,gene2=gene_names[gene_idxs]len1,len2=gene_lengths[gene_idxs]gene_labels=[f'{gene1}, {len1}bp',f'{gene2}, {len2}bp']log_counts=list(np.log(counts[gene_idxs]+1))log_ncounts=list(np.log(counts_rpkm[gene_idxs]+1))ax=class_boxplot(log_counts,['raw counts']*3,labels=gene_labels)ax.set_xlabel('Genes')ax.set_ylabel('log gene expression counts over all samples');
If we look at just the raw counts, it looks like the longer gene, TXNDC5, is expressed slightly more than the shorter one, RPL24 (Figure 1-13). But, after RPKM normalization, a different picture emerges:
ax=class_boxplot(log_ncounts,['RPKM normalized']*3,labels=gene_labels)ax.set_xlabel('Genes')ax.set_ylabel('log RPKM gene expression counts over all samples');

Figure 1-13. Comparing expression of two genes before RPKM normalization
Now it looks like RPL24 is actually expressed at a much higher level than TXNDC5 (see Figure 1-14). This is because RPKM includes normalization for gene length, so we can now directly compare between genes of different lengths.

Figure 1-14. Comparing expression of two genes after RPKM normalization
Taking Stock
So far we have done the following:
- Imported data using pandas
- Become familiar with the key NumPy object class—the ndarray
- Used the power of broadcasting to make our calculations more elegant
In Chapter 2 we will continue working with the same dataset, implementing a more sophisticated normalization technique, then use clustering to make some predictions about mortality in skin cancer patients.
1 Tobias Maier, Marc Güell, and Luis Serrano, “Correlation of mRNA and protein in complex biological samples”, FEBS Letters 583, no. 24 (2009).
2 We always start by comparing the last dimensions, and work our way forward, ignoring excess dimensions in the case of one array having more than the other (e.g., (3, 5, 1) and (5, 8) would match).
Get Elegant SciPy now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

