Diseñar IA autónoma

Capítulo 1. A veces las máquinas toman malas decisiones

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

¿Por qué con tanta frecuencia los seres humanos dirigen, supervisan, intervienen para ayudar o anulan los sistemas automatizados? ¿Cuáles son las cualidades de la toma de decisiones humana que los sistemas automatizados no pueden reproducir? Comparar estos puntos fuertes y débiles nos ayuda a diseñar una IA útil y a evitar pensar que la IA es una panacea mágica o una completa exageración.

Hice un viaje a Australia y, mientras estaba allí, una empresa de recursos me pidió ayuda con su proceso de producción de aluminio. La empresa utiliza un sistema experto para tomar decisiones automatizadas durante el proceso.

El aluminio se fabrica en grandes cubas llamadas celdas (ver Figura 1-1). El aluminio se funde mediante un proceso llamado electrólisis. En la electrólisis del aluminio, se inyecta polvo de alúmina en una celda llena de criolita. La electricidad pasa a través de la criolita, y la reacción resultante produce aluminio. He aquí el problema: es casi imposible saber exactamente lo que ocurre en la célula porque la temperatura es lo bastante alta y la criolita es lo bastante corrosiva como para destruir los sensores. Así que los expertos y los sistemas automatizados se basan en los cambios de las propiedades eléctricas de la célula para obtener información. La tensión es la fuerza con que la electricidad empuja a través del sistema. La corriente (medida en amperios) es la cantidad de electricidad que fluye por el sistema, y la resistencia es la cantidad de oposición que el sistema ofrece al flujo de electricidad.

Así pues, la práctica habitual para controlar las células de alúmina (en toda la industria, no sólo en esta empresa concreta) consiste en emplear las dos estrategias siguientes:

• Sobrealimenta la célula (inyecta más alúmina de la necesaria para alimentar la reacción) hasta que baje la resistencia de la célula. Esto es señal de que ha llegado el momento de cambiar de estrategia.

• Subalimenta la célula (inyecta menos alúmina de la necesaria para alimentar la reacción) hasta que aumente la resistencia de la célula.

Una buena producción de aluminio oscila entre estas dos estrategias. El truco está en saber cuándo cambiar a la estrategia contraria. Esta decisión sobre cómo navegar entre estrategias es matizada y requiere prestar atención a cómo cambia la resistencia de la célula, así como a otras variables. Esta empresa utiliza un sistema experto automatizado para tomar esta decisión para cada célula. Los sistemas expertos almacenan reglas expertas (y a veces ecuaciones que describen relaciones entre variables) para tomar decisiones. Discuto en detalle los pros y los contras de los sistemas expertos en "Los sistemas expertos recuerdan la experiencia almacenada".

En la mayoría de las situaciones, el sistema experto toma decisiones acertadas sobre cuándo realizar la transición entre estrategias, pero el límite entre las estrategias es difuso. En algunas situaciones, el sistema experto realiza transiciones demasiado pronto o demasiado tarde. Tanto las transiciones tempranas como las tardías provocan efectos que degradan la producción de aluminio. Cuando se producen estos efectos, se recurre a expertos humanos para que anulen al sistema experto y tomen las decisiones matizadas sobre cuándo y cómo ejecutar las estrategias.

Figura 1-1. Células de alúmina para fabricar aluminio. El ejemplo de los sistemas expertos en la fabricación de aluminio ilustra cómo los procesos automatizados requieren que los humanos intervengan y tomen decisiones cuando los sistemas automatizados toman malas decisiones.

Se requiere curiosidad previa

¡Hay muchos ejemplos en este libro! ¿Por qué hay tantos ejemplos de casos de uso en este libro? O dicho de otro modo: "¿Por qué sigues mencionando tantos procesos de ingeniería diferentes de los que nunca he oído hablar? Es mucho que asimilar". He aquí mi respuesta: la práctica de la enseñanza de máquinas requiere sobre todo curiosidad e interés por aprender cosas nuevas. Me han pedido que formule diseños autónomos de IA para todo tipo de máquinas, sistemas y procesos, de la mayoría de los cuales no había oído hablar en mi vida (incluida la fundición de aluminio). A veces, me pidieron que ideara estos diseños muy rápidamente, en horas o incluso minutos. Esto fue posible gracias a mi intensa curiosidad por los procesos de ingeniería y al marco que enseño en este libro. A medida que leas los ejemplos de este libro, espero que te des cuenta de que, para diseñar una IA autónoma eficaz, tienes que tener ganas de aprender.

Matemáticas, Menús y Manuales: Cómo las máquinas toman decisiones automatizadas

Si quieres diseñar bien los cerebros, primero tienes que entender cómo toman decisiones los sistemas automatizados. Utilizarás este conocimiento para comparar técnicas y decidir cuándo la IA autónoma superará a los métodos existentes. También combinarás la toma de decisiones automatizada con la IA para diseñar cerebros más explicables, fiables e implementables. Aunque hay muchas subcategorías y matices, los sistemas automatizados se basan en tres métodos principales para tomar decisiones: matemáticas, menús y manuales.

La Teoría del Control utiliza las matemáticas para calcular las decisiones

La teoría de control utiliza ecuaciones matemáticas para calcular la siguiente acción de control, normalmente basada en la realimentación, utilizando relaciones matemáticas bien entendidas. Cuando haces esto, debes confiar en que las matemáticas describen la dinámica del sistema lo suficientemente bien como para utilizarlas para calcular qué hacer a continuación. Te pondré un ejemplo. Hay una ecuación que describe cuánto espacio ocupará un gas en función de su temperatura y presión. Se llama ley de los gases ideales. Así que si quisiéramos diseñar un cerebro que controlara una válvula que inflara globos de fiesta, podríamos utilizar esta ecuación para calcular cuánto ajustar la válvula abierta y cerrada para inflar los globos hasta un tamaño determinado.

En el ejemplo anterior, nos basamos en las matemáticas para describir lo que ocurrirá de forma tan completa y precisa que ni siquiera necesitamos retroalimentación. El control basado en ecuaciones como ésta se denomina control de bucle abierto porque no hay un bucle cerrado de realimentación que nos diga si nuestras acciones han conseguido los resultados deseados. Confiamos tanto en la ecuación que ni siquiera necesitamos retroalimentación. Pero, ¿y si la ecuación no describe completamente todos los factores que afectan a si tenemos éxito o no? Por ejemplo, la ley de los gases ideales no modela bien los gases a alta presión y baja temperatura, los gases densos o los gases pesados. Incluso cuando controlamos la respuesta a la retroalimentación, las limitaciones del modelo matemático pueden llevarnos a tomar malas decisiones.

Veo la historia de la teoría del control como una evolución de la capacidad en la que cada tecnología de control puede hacer cosas que las tecnologías de control anteriores no podían. La Marina estadounidense inventó el controlador Proporcional Integral Derivativo (PID ) para dirigir automáticamente los timones de los barcos y controlar el rumbo (la dirección a la que apunta el barco). Imagina que un barco apunta en una dirección y el capitán quiere cambiar el rumbo para que el barco apunte en otra dirección, como se muestra en la Figura 1-2.

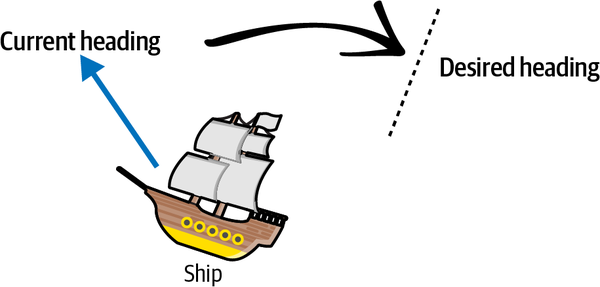
Figura 1-2. Buque cambiando de rumbo.

El controlador utiliza las matemáticas para calcular cuánto debe mover el timón basándose en la información que obtiene de su última acción. Hay tres números que determinan cómo se comportará el controlador: la constante P, la I y la D. La constante P te mueve hacia el objetivo, así que para el barco, la constante P se asegura de que la acción del timón haga que el barco se mueva hacia su nuevo rumbo. Pero, ¿qué ocurre si el controlador sigue girando el timón y la nave se desplaza más allá del rumbo objetivo? Para eso está la constante I. La constante I controla cuánto error total tienes en el sistema y evita que te pases o te quedes corto respecto al objetivo. La constante D garantiza que llegues al destino objetivo suavemente en lugar de bruscamente. Así que una D en el controlador de la nave haría más probable que ésta desacelerara y llegara con más precisión a su rumbo de destino.

Un barco con un controlador P (sin I ni D) podría sobrepasar el objetivo, barriendo el barco más allá del nuevo rumbo. Después de que el barco sobrepase el objetivo, tendrás que volver atrás. El diagrama de la izquierda de la Figura 1-3 muestra cómo podría ser esto. La línea horizontal representa el rumbo de destino. Un controlador PI convergerá más rápidamente en el objetivo porque el término I se asegura de que sobrepases el objetivo lo menos posible. El controlador PD se aproxima al objetivo más suavemente, pero tarda más en alcanzarlo.

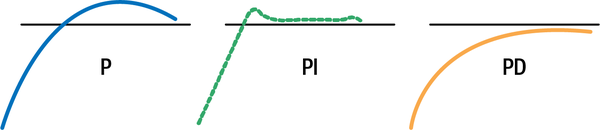
Figura 1-3. Ejemplos de comportamiento de varios controladores.

El controlador PID puede ser muy eficaz y lo encontrarás en casi todas las fábricas y máquinas modernas, pero puede confundir las perturbaciones y el ruido con acontecimientos a los que debe responder. Por ejemplo, si un controlador PID controlara el acelerador de tu coche, podría confundir un badén (que es una perturbación menor y temporal) con una cuesta que requiere una aceleración importante. En este caso, el controlador podría acelerar en exceso y superar la velocidad ordenada, para luego tener que frenar.

El controlador feedforward mide y responde por separado a las perturbaciones, no sólo a la variable que estás controlando. En contraste con el control de realimentación PID, Jacques Smuts escribe:

El control feedforward actúa en el momento en que se produce una perturbación, sin tener que esperar a que se produzca una desviación en la variable del proceso. Esto permite a un controlador feedforward anular rápida y directamente el efecto de una perturbación. Para ello, un controlador feedforward produce su acción de control basándose en una medición de la perturbación.

Cuando se utiliza, el control de avance casi siempre se implementa como complemento del control de realimentación. El controlador de avance se encarga de la perturbación principal, y el controlador de realimentación se encarga de todo lo demás que pueda hacer que la variable del proceso se desvíe de su punto de consigna.¹

En nuestro ejemplo del control de crucero, esto significa que el controlador puede diferenciar mejor entre un badén y una cuesta midiendo y respondiendo a la perturbación (el cambio en la elevación de la carretera) en lugar de medir y responder sólo al cambio en la velocidad del vehículo. Mira la Figura 1-4 para ver un ejemplo que muestra cómo responde mucho mejor a una perturbación la realimentación con control de realimentación que el control de realimentación solo.

El controlador feedforward, más sofisticado, también tiene limitaciones. Tanto los controladores PID como los feedforward sólo pueden controlar una variable a la vez para un objetivo por bucle de realimentación. Así que necesitarías dos bucles de realimentación/realimentación, por ejemplo, si necesitaras controlar tanto el pedal del acelerador como el volante del coche. Y ninguno de esos bucles puede maximizar el consumo de gasolina y mantener la velocidad constante almismo tiempo.

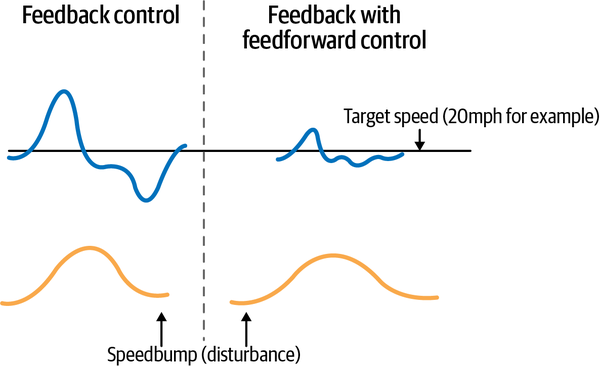
Figura 1-4. Comparación de cómo responde a un badén un coche controlado por control de realimentación PID frente a otro controlado por feedforward; la fluctuación de la velocidad es mucho menor con el control feedforward.

Entonces, ¿qué ocurre si necesitas controlar más de una variable o perseguir más de un objetivo? Hay formas de solucionarlo, pero en la vida real a menudo vemos que la gente crea bucles de retroalimentación separados que no pueden hablar entre sí ni coordinar acciones. Así, del mismo modo que los humanos duplicamos el trabajo y calculamos mal lo que hay que hacer cuando no nos coordinamos entre nosotros, los bucles de control separados no gestionan bien los objetivos múltiples y a menudo malgastan energía.

Entra lo último en la evolución de los sistemas de control ampliamente adoptados: el control predictivo de modelos (MPC). El MPC amplía la capacidad del PID y del feedforward para controlar múltiples entradas y salidas. Ahora, el mismo controlador puede utilizarse para controlar múltiples variables y perseguir múltiples objetivos. El controlador MPC utiliza un modelo de sistema muy preciso para probar varias acciones de control por adelantado y luego elegir la mejor acción. En realidad, esta técnica de control toma prestado del segundo tipo de toma de decisiones automatizada (menús). Tiene muchas características atractivas, pero vive o muere por la precisión del modelo del sistema, o las ecuaciones que predicen cómo responderá el sistema a tus acciones. Pero los sistemas reales cambian: las máquinas se desgastan, o los equipos se sustituyen, el clima cambia, y esto puede hacer que el modelo del sistema sea inexacto con el tiempo. Muchos de nosotros lo hemos experimentado en nuestros vehículos. A medida que se desgastan los frenos, tenemos que aplicarlos antes para detenernos. A medida que se desgastan los neumáticos, no podemos conducir tan rápido ni girar tan bruscamente sin perder el control. Como el MPC utiliza el modelo del sistema para anticiparse y probar posibles acciones, un modelo inexacto le inducirá a decidir acciones que no funcionarán bien en el sistema real. Por eso, muchos sistemas MPC que se instalaron, sobre todo en plantas químicas en los años 90, se desmantelaron más tarde cuando las plantas se desviaron de los modelos del sistema. Los controladores MPC que dependían en gran medida de estos modelos del sistema para ser precisos ya no controlaban bien.

En 2020, McKinsey QuantumBlack construyó una IA autónoma para ayudar a dirigir al equipo de vela Emirates Team New Zealand hacia la victoria, controlando el timón de su barco. Este cerebro de IA puede introducir muchísimas variables, incluidas algunas que los controladores basados en matemáticas no pueden, como señales de vídeo de cámaras y categorías (como adelante, atrás, izquierda, derecha). Aprende practicando en simulación y adquiere estrategias creativas para perseguir múltiples objetivos simultáneamente. Por ejemplo, en su experimentación y autodescubrimiento, intentó navegar con el barco al revés porque durante un tiempo, durante la práctica en simulación, le pareció un enfoque prometedor para lograr los objetivos de navegación.

La teoría del control utiliza las matemáticas para calcular qué hacer a continuación, las técnicas para hacerlo evolucionan continuamente, y la IA autónoma es simplemente una extensión de estas técnicas que ofrece algunas características de control realmente atractivas, como la capacidad de controlar múltiples variables y seguir hacia múltiples objetivos.

¿Cuándo debes utilizar la Teoría del Control para tomar decisiones?

• Utiliza la teoría de control cuando necesites un control fiable y predecible de procesos que puedas medir bien.

• Utiliza la teoría de control cuando entiendas bien la dinámica del sistema y puedas expresarla en términos matemáticos.

Limitaciones de la Teoría del Control

• Los controladores que utilizan las matemáticas para tomar decisiones dependen en gran medida del modelo matemático. Si no puedes modelar bien el sistema con las matemáticas, no podrás controlarlo bien con la teoría de control.

• Los ajustes de los controladores hacen que funcionen bien para sistemas lineales, pero no tan bien cuando hay relaciones no lineales entre las variables.

• El regulador no cambiará su comportamiento a menos que expertos humanos reajusten las constantes.

Los algoritmos de optimización utilizan menús de opciones para evaluar las decisiones

Los algoritmos de optimización buscan en una lista de opciones y seleccionan una acción de control utilizando criterios objetivos. Piensa en la forma en que funciona la optimización, como si se tratara de seleccionar opciones de un menú. Por ejemplo, un sistema de optimización podría enumerar todas las rutas posibles para entregar un paquete desde el punto de fabricación A hasta el punto de entrega B, y luego seleccionar decisiones de ruta secuenciales ordenando la ruta más corta al principio de la lista de opciones. Podrías llegar a diferentes acciones de control si ordenas por la duración más corta del trayecto. En este ejemplo, la distancia de la ruta y la duración del viaje son los criterios objetivos (las metas de la optimización). Imagina que juegas al tres en raya de esta forma. El tres en raya es un juego sencillo para dos jugadores que se juega en una cuadrícula en la que colocas tu símbolo, una X o una O, en casillas de la cuadrícula y ganas cuando eres el primer jugador que ocupa tres casillas seguidas con tu símbolo. Si quieres jugar al juego como un algoritmo de optimización, puedes utilizar el siguiente procedimiento:

1. Haz una lista de todas las casillas (hay 9, mira un ejemplo en la Figura 1-5 ).

2. Tacha (de la lista) las casillas que ya tengan una X o una O.

3. Elige un objetivo para optimizar. Por ejemplo, puedes decidir hacer movimientos basándote en cuántas casillas en blanco hay adyacentes a cada casilla. Este objetivo te da la mayor flexibilidad para futuros movimientos. Por eso muchos jugadores eligen la casilla central para su primer movimiento (hay 8 casillas adyacentes a la casilla central).

4. Ordena tus opciones en función de los criterios objetivos.

5. La opción superior es tu siguiente movimiento. Si hay varias jugadas con exactamente la misma puntuación de criterios objetivos, elige una al azar.

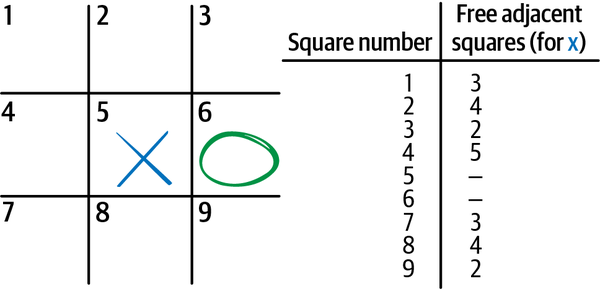
Figura 1-5. Diagrama de un tablero de tres en raya que muestra a X haciendo el primer movimiento, a O haciendo el segundo movimiento, el número de casillas adyacentes que están abiertas o bajo el control de X para cada opción disponible para el siguiente movimiento de X, y una lista que registra los atributos de cada casilla.

Este ejercicio muestra la primera limitación de los algoritmos de optimización. No saben nada sobre la tarea. Por eso tienen que elegir una casilla al azar si hay varias casillas con la misma puntuación objetivo en la parte superior de la búsqueda. Claude Shannon, uno de los primeros pioneros de la IA, habló de esto en su famoso artículo de 1950 sobre la IA que juega al ajedrez.² Observó que había dos formas de programar una IA de ajedrez. Las denominó Sistema A y Sistema B. El Sistema A, que en realidad es el tercer método de toma de decisiones automatizadas (manuales), programa estrategias de ajedrez. Estas reglas y excepciones son difíciles de gestionar y actualizar, pero expresan la comprensión del juego. El Sistema B, que es la optimización, busca posibles jugadas legales de ajedrez con un único algoritmo fácil de mantener, pero no tiene una comprensión real de los conceptos o estrategias del ajedrez.

Estrategia frente a búsqueda

Creo que la estrategia es uno de los ingredientes clave que faltan en la investigación de la IA. Creo que Claude Shannon (uno de los primeros pioneros de la IA) estaría de acuerdo conmigo. La estrategia es una forma clave de dar sentido al mundo, y Shannon predijo hace mucho tiempo que habría fricción sobre si utilizar la estrategia o las opciones de búsqueda, como se muestra en la Figura 1-6.

Figura 1-6. Dos enfoques para tomar decisiones secuenciales complejas.

Las soluciones son como puntos en un mapa

Los algoritmos de optimización son como exploradores que buscan en la superficie de la tierra la montaña más alta o el punto más bajo. Las soluciones a los problemas son puntos del mapa a los que, si llegas, consigues algún buen resultado. Si tu objetivo es la altitud, estás buscando la cima del monte Everest, a 8.848 metros sobre el nivel del mar (véase en la Figura 1-7 un mapa del relieve de la Tierra por altitud en relación con el nivel del mar). Si tu objetivo es encontrar el lugar más repleto de gente (densidad de población), buscas la isla china de Macao, que tiene una densidad de población de 21.081 personas/km² (consulta la Figura 1-8 para ver un mapa del relieve de la Tierra por densidad de población). Si buscas el lugar más frío de la Tierra en promedio, entonces buscas la Estación Vostok, en la Antártida.

Ahora, imagina que eres un algoritmo de optimización que busca en la tierra el pico más alto. Una forma de asegurarte de que encuentras el pico más alto es poner el pie en cada metro cuadrado de tierra, tomar medidas en cada punto y luego, cuando hayas terminado, ordenar tus medidas por altitud. El punto más alto de la tierra estará ahora al principio de tu lista.

Como hay 510 millones de kilómetros cuadrados de masa terrestre en la Tierra, tardarías muchísimas vidas en obtener tu respuesta.³ Este método se llama búsqueda por fuerza bruta y sólo es factible cuando el área geográfica de búsqueda de posibles decisiones es muy pequeña (como en el juego tres en raya). Para problemas geográficos más complejos, necesitamos otro método.

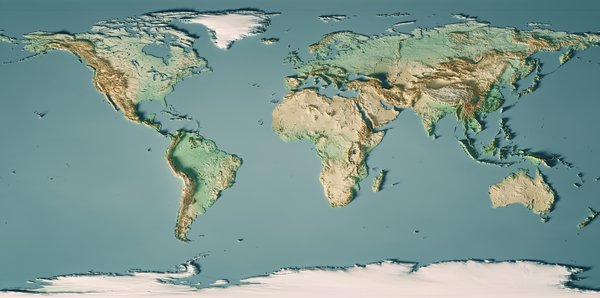
Figura 1-7. Relieve del mapa del mundo por altitud.

Figura 1-8. Relieve del mapa del mundo por densidad de población.

Una forma más eficaz de buscar en la Tierra el pico más alto consiste en recorrerla a pie y sólo dar pasos en la dirección que más se incline hacia arriba. Utilizando este método, puedes evitar explorar gran parte de la geografía viajando sólo cuesta arriba. En optimización, esta clase de métodos se denomina métodos basados en el gradiente, porque la pendiente de una colina se denomina grado o gradiente. Este método plantea dos problemas. El primero es que, dependiendo de dónde empieces tu exploración de búsqueda, podrías acabar en una montaña alta que no sea el punto más alto de la Tierra. Si empiezas tu búsqueda en África, podrías acabar en el monte Kilimanjaro (que no es el pico más alto del mundo). Si empiezas en Norteamérica, podrías acabar en la cima de una de las montañas de la cordillera de las Montañas Rocosas. Incluso podrías acabar en un pico mucho menor, porque una vez que asciendes a cualquier pico utilizando este método de búsqueda, no puedes volver a descender por ninguna colina. La Figura 1-9 demuestra cómo funciona esto.

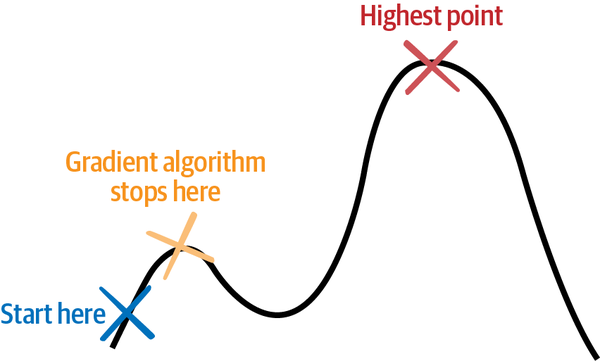
Figura 1-9. Un algoritmo basado en el gradiente dejará de buscar en relación con el punto más alto de una curva.

La segunda limitación de este método es que sólo puede utilizarse en situaciones en las que puedas calcular la pendiente del terreno por el que caminas. Si hay huecos en el terreno (piensa en desniveles verticales o fosos sin fondo), no es posible calcular la pendiente (técnicamente es infinita) en los desniveles verticales, por lo que no puedes utilizar métodos de optimización basados en el gradiente para buscar soluciones en ese espacio. Consulta la Figura 1-10 para ver ejemplos de terrenos de soluciones que los algoritmos de gradiente no pueden buscar.

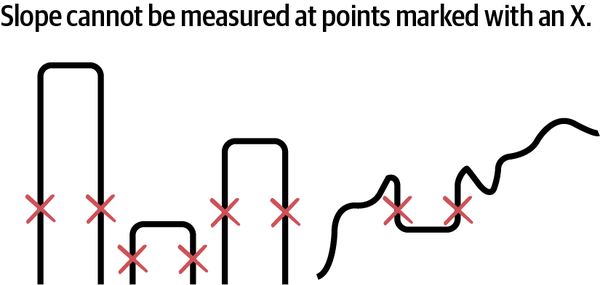
Figura 1-10. Estos ejemplos de curvas de función no pueden buscarse con métodos basados en el gradiente.

Ahora, imagina que empleas a varios exploradores para que empiecen en distintos lugares del paisaje y busquen el punto más alto. Después de cada paso, los exploradores comparan notas sobre su altitud y elevación actuales y utilizan sus conocimientos combinados para cartografiar mejor la Tierra. Esto podría conducir a una búsqueda más rápida y evitar que todos los exploradores se queden atascados en un punto alto que no es la cima del monte Everest. Estas y otras innovaciones permiten a los algoritmos de optimización explorar de forma más eficiente y eficaz más tipos de paisajes, incluso los que se muestran en la Figura 1-10. Muchos de estos algoritmos se inspiran en procesos de la naturaleza. La naturaleza tiene muchas formas eficaces de explorar a fondo, como el agua que fluye sobre un trozo de tierra. He aquíalgunos ejemplos:

Algoritmos evolutivos

Inspirados en la teoría de la selección natural de Darwin, los algoritmos evolutivos generan una población de decisiones de soluciones potenciales, comprueban lo bien que cada una de las soluciones de la población alcanza los objetivos del proceso, eliminan las soluciones ineficaces y luego mutan la población para seguir explorando.

Métodos de enjambre

Inspirados en cómo las hormigas, las abejas y las partículas forman enjambres, se mueven e interactúan, estos métodos de optimización exploran el espacio de soluciones con muchos exploradores que se mueven por el paisaje y se comunican entre sí sobre lo que encuentran. La Figura 1-11 ilustra cómo funcionan estos exploradores.

Métodos para árboles

Estos métodos tratan las soluciones potenciales como ramas de árboles. Imagina una novela de "elige tu propia aventura" (y otras ficciones interactivas) que te pide que decidas qué dirección tomar en un momento determinado de la historia. Las decisiones proliferan con el número de opciones en cada punto de decisión. Los métodos basados en árboles utilizan diversas técnicas para buscar soluciones en el árbol de forma eficiente (sin tener que visitar cada rama). Algunos de los métodos arbóreos más conocidos son la rama y el límite y la búsqueda arbórea Monte Carlo (MCTS).

Recocido simulado

Inspirado en la forma en que se enfría el metal, el recocido simulado busca en el espacio utilizando diferentes comportamientos de búsqueda a lo largo del tiempo. Todos los metales tienen una estructura cristalina que se enfría de una forma común. Esa estructura cambia más cuando el metal está más caliente y menos cuando se enfría. El recocido es un proceso por el que un material como el metal se calienta por encima de su temperatura de recristalización y luego se enfría lentamente para hacerlo más maleable para los siguientes pasos de diversos procesos industriales. Este algoritmo imita ese proceso. Al principio, el recocido simulado lanza una amplia red de búsqueda (explora más) y, con el tiempo, se vuelve más seguro de que se centra en el área correcta (explora menos).

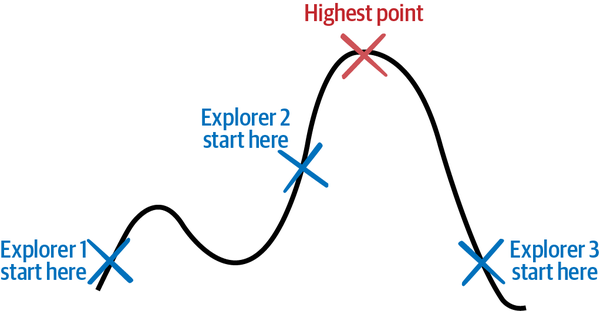
Figura 1-11. Algunos algoritmos de optimización utilizan varios exploradores coordinados.

Resolver el juego de las damas

Hay una escena en la película Matrix en la que el protagonista Neo encuentra a un niño, vestido de monje Shaolin, doblando una cuchara con la mente. Al ver que Neo se queda perplejo, el niño le explica que no hay ninguna cuchara. Neo y el niño están en un mundo digital virtual manipulador que una IA máquina malvada conjuró para atrapar a los humanos en sus mentes. El niño está manipulando el mundo imaginario basado en códigos que ocupan sus mentes humanas.

Lo mismo ocurre cuando se trata de tomar la decisión secuencial perfecta al realizar una tarea compleja. Los expertos en optimización llaman a estas "mejores decisiones posibles" (como el Monte Everest o los puntos topográficos más altos de las Figuras 1-9 y 1-11) óptimos globales. Los algoritmos de optimización prometen la posibilidad de alcanzar óptimos globales para cada decisión, pero no es así como funciona en los sistemas reales y complejos. Por ejemplo, en una partida de ajedrez no hay una "jugada perfecta". Hay jugadas fuertes, jugadas creativas, jugadas débiles, jugadas sorprendentes, pero no jugadas perfectas para ganar una partida concreta. Es decir, a menos que juegues a las damas.

En 2007, tras casi 20 años de búsqueda continua en el espacio con algoritmos de optimización en potentes ordenadores, los investigadores declararon resueltas las damas. Las damas son aproximadamente 1 millón de veces más complejas que Conecta Cuatro, con 500 billones de billones de posiciones posibles (5 × ¹⁰²⁰). Hablé con el Dr. Jonathan Schaeffer, uno de los investigadores principales del proyecto, y esto es lo que me dijo:

Hemos demostrado que el juego perfecto conduce al empate. Eso no es lo mismo que conocer el valor de cada posición. La prueba elimina gran parte de la búsqueda. Por ejemplo, si encontramos una victoria, el programa no se molesta en buscar las jugadas inferiores que producen un empate o una derrota. Así, si estableces una posición que se produce en una de esas líneas de empate/pérdida, el programa podría no conocer su valor resuelto.

Entonces, ¿por qué no resolvemos nuestros problemas industriales como las damas? Además del hecho de que los algoritmos de optimización tardaron 20 años en resolver las damas, la mayoría de los problemas reales son más complejos que eso, y el espacio de las damas no está completamente explorado, incluso después de todo ese cálculo. ¿Recuerdas los métodos de optimización basados en árboles? Pues bien, una forma que idearon los informáticos para medir la complejidad de las tareas es contar el número de opciones posibles en la rama media del árbol. Esto se denomina factor de ramificación. El factor de ramificación de las damas es de 2,8, lo que significa que, por término medio, hay unas 3 jugadas posibles en cualquier turno de una partida de damas. Esto se debe principalmente a la regla de captura forzada de las damas. En una posición de captura, el factor de bifurcación es ligeramente superior a 1. En una posición de no captura, el factor de bifurcación es aproximadamente 8. En la Tabla 1-1 se resumen los factores de bifurcación de algunos de los juegos de mesa más populares.

Tabla 1-1. Factores de ramificación para juegos comunes

Juego	Factor de ramificación
Damas	2.8
Tres en raya	4
Conecta Cuatro	4
Ajedrez	35
Ve a	250

Luego está la incertidumbre. Un aspecto muy conveniente de juegos como las damas y el ajedrez es que las cosas siempre suceden exactamente como tú quieres. Por ejemplo, si quiero mover mi alfil por todo el tablero (el término ajedrecístico para colocar el alfil en esta carretera transversal de la diagonal más larga, como se ilustra en la Figura 1-12, es fiancetto), puedo estar seguro de que el alfil llegará hasta G7 como yo pretendía. Pero en las campañas bélicas de la vida real que sirvieron de modelo al ajedrez, no está garantizado el éxito de una ofensiva para tomar una determinada colina, por lo que nuestro alfil podría llegar a F6 o E5 en lugar de a G7, como pretendíamos. Este tipo de incertidumbre sobre el éxito de cada jugada probablemente cambiará nuestra estrategia. Hablaré más sobre la incertidumbre dentro de un momento.

Así que para los problemas reales (como doblar cucharas en Matrix), cuando se trata de encontrar soluciones óptimas para cada movimiento que tengas que hacer, efectivamente no hay cuchara.

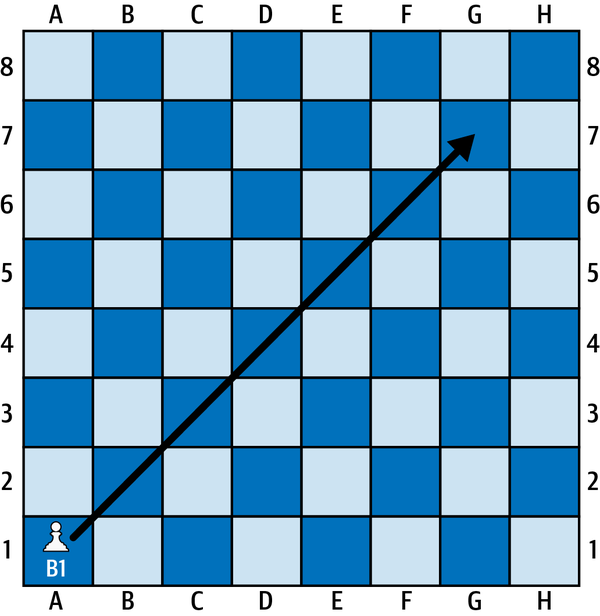
Figura 1-12. Alfil moviéndose de A1 a G7 en un tablero de ajedrez.

Reconocimiento

El reconocimiento sólo significa explorar por adelantado. No puedes explorar todo el espacio con antelación, pero en algunas situaciones puedes explorar las áreas locales circundantes con algunos movimientos de antelación. Por ejemplo, el control predictivo por modelos (CPM) mira al menos un movimiento por adelantado cuando toma decisiones. Para ello, necesitas un modelo que prediga con exactitud lo que ocurrirá después de tomar una decisión.

La mayoría de las IA que realizan este tipo de reconocimiento lo hacen en situaciones con resultados discretos en cada paso. Esto es cierto para juegos como el ajedrez y el Go, pero también lo es para las decisiones en la planificación de la fabricación y la logística. Imagina determinar en qué máquinas fabricar productos o qué transportista utilizar para una entrega.

Las IA autónomas como AlphaChess, AlphaGo y AlphaZero no pueden tomar buenas decisiones sin explorar muchas jugadas por delante. Estas IA utilizan la búsqueda en árbol de Montecarlo (MCTS) para navegar por grandes espacios como el ajedrez, el shogi y el Go, como se muestra en la Figura 1-13.

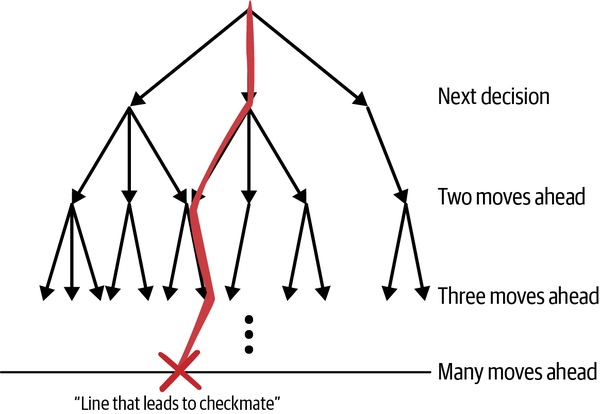
Figura 1-13. Línea de jugadas que conducen a un resultado ganador expresado en un árbol de opciones lookahead.

Puedes utilizar árboles para buscar muchas jugadas futuras. El primer conjunto de ramas del árbol representa opciones para tu próximo movimiento y cada rama posterior del árbol representa más movimientos futuros. La idea es seguir buscando más movimientos futuros hasta que llegues al final de la partida. Cuando lo hagas, habrá caminos a través de las ramas (llamados líneas en ajedrez) que lleven a resultados ganadores y otros que lleven a resultados perdedores. Si consigues llegar tan lejos en la búsqueda, tendrás muchas líneas ganadoras que podrás seguir. La partida de ajedrez media dura de 20 a 40 movimientos y el árbol que representa cualquiera de esas partidas tiene más ramas que el número de átomos del universo. Sin embargo, eso no significa que no debas utilizar jugadas de anticipación. Hay muchas formas de reducir el número de ramas que necesitas examinar para llegar a resultados ganadores.

MCTS busca aleatoriamente ramas en el árbol durante todo el tiempo que dispongas de tiempo y potencia de cálculo. La Federación Mundial de Ajedrez (comúnmente conocida por su nombre en francés, Fédération Internationale des Échecs [FIDE]) ordena 90 minutos para los primeros 40 movimientos de cada jugador, y luego 30 minutos en total para que ambos jugadores terminen la partida. AlphaZero utiliza 44 núcleos de CPU para buscar aleatoriamente unas 72.000 ramas de árbol para cada jugada. Dependiendo del azar, el algoritmo puede o no encontrar una línea ganadora durante la búsqueda entre cada uno de sus movimientos.

Tanto los jugadores profesionales de ajedrez como los de Go dicen que la IA tiene un "estilo de juego alienígena" y yo digo que eso se debe a la aleatoriedad del MCTS. Verás, cuando el algoritmo de búsqueda encuentra una línea, la persigue y hará absolutamente cualquier cosa (por poco ortodoxa o sacrificada que sea) para seguirla. Luego, dependiendo del juego del adversario, el algoritmo puede elegir una nueva línea con movimientos y sacrificios poco ortodoxos aparentemente inconexos. Algunas de estas líneas son brillantes, creativas y emocionantes de ver, pero también son a veces erráticas. Antes de seguir adelante, reconozcamos el mérito: AlphaZero venció a la IA estándar de facto en el ajedrez automático (Stockfish) por 1.000 partidas a cero en 2019.

Los humanos miran hacia delante, pero no de esta forma. La investigación de los psicólogos sobre los jugadores de ajedrez muestra que los ajedrecistas expertos sólo se centran en un pequeño subconjunto de piezas totales y revisan un subconjunto aún más pequeño de ramas del árbol cuando exploran por delante en busca de opciones.⁴ ¿Cómo son capaces de mirar muchas jugadas por delante sin explorar al azar tantas opciones? Son parciales. Muchas opciones no tienen sentido como jugadas fuertes de ajedrez, otras no tienen sentido según la estrategia que esté utilizando el jugador, otras aún no tienen sentido según la estrategia que esté utilizando el adversario. Sugiero que un área de investigación prometedora es utilizar la experiencia y la estrategia humanas para sesgar la búsqueda en el árbol (explorar sólo las opciones que coincidan con la estrategia actual).

¿Qué pasa con la incertidumbre?

Utilizar algoritmos de optimización para mirar hacia delante depende de acciones discretas y de la certeza sobre lo que ocurrirá cuando realices una acción. Muchos de los problemas en los que trabajes tendrán que lidiar con la incertidumbre y las acciones continuas. Casi todos los problemas de logística y fabricación para los que he diseñado un cerebro muestran estacionalidad. Del mismo modo que las mareas fluyen y refluyen y la luna crece y mengua en el cielo, las variaciones estacionales siguen un patrón periódico. He aquí algunos ejemplos de patrones estacionales de incertidumbre:

• Tráfico

• Demanda estacional

• Patrones meteorológicos

• Ciclo de desgaste y sustitución de piezas

La buena noticia es que esta incertidumbre no es aleatoria. La incertidumbre difumina los escenarios según patrones predefinidos, del mismo modo que los límites difusos difuminan los perímetros de las formas de la Figura 1-14.

Figura 1-14. Círculos borrosos.

Cada una de las formas es como un escenario para uno de los problemas que resuelves. Para el tráfico, hay escenarios de tráfico intenso (como durante las horas de trabajo y después de un accidente) y hay escenarios con tráfico más ligero. Pero los límites de estos escenarios son difusos. A veces el tráfico de la mañana empieza antes, a veces más tarde. Pero estos escenarios y la incertidumbre que los difumina obedecen a patrones. Necesitaremos algo más que algoritmos de optimización para reconocer y responder a estos patrones y tomar decisiones a través de la incertidumbre que se asienta sobre estos patrones.

Puedes pasarte toda una carrera profesional o académica en aprendiendo sobre métodos de optimización, pero esta visión general debería proporcionarte el contexto que necesitas para diseñar cerebros que incorporen métodos de optimización y superen a los métodos de optimización en la toma de decisiones sobre tareas y procesos concretos. Si quieres aprender más sobre métodos de optimización, te recomiendo Numerical Optimization de Nocedal yWright (Springer).

¿Cuándo debes utilizar algoritmos de optimización para tomar decisiones?

• Cuando no tienes experiencia ni fórmulas matemáticas que te digan lo que tienes que hacer

• Cuando el paisaje de búsqueda es muy grande o cuando parte del espacio de búsqueda está sin explorar

• Cuando hay muchas reglas para la toma de decisiones (restricciones) que hay que seguir

• Cuando el valor para ti de tener una respuesta mejor (por mínima que sea) es significativo

Limitaciones de la optimización

• Los algoritmos de optimización no encierran ninguna comprensión del sistema ni de las habilidades y estrategias necesarias para optimizarlo.

• Los algoritmos de optimización necesitan mucho tiempo y recursos informáticos para buscar entre las opciones las decisiones que eligen.

Los sistemas expertos recuperan la experiencia almacenada

Los sistemas expertos buscan acciones de control en una base de datos de reglas expertas, es decir, en un manual complejo. Esto proporciona un acceso computacionalmente eficiente a las acciones de control eficaces, pero la creación de esa base de datos requiere la experiencia humana existente: al fin y al cabo, tienes que saber cómo hacer un pastel para escribir la receta. Los sistemas expertos aprovechan la comprensión de la dinámica del sistema y las estrategias eficaces para controlarlo, pero requieren tantas reglas para captar todas las excepciones matizadas que pueden ser engorrosos de programar y gestionar.

Utilicemos un ejemplo de un sistema de climatización como el que podría controlar la temperatura en un edificio de oficinas. El sistema utiliza una válvula de compuerta que puede abrirse para dejar entrar aire fresco o cerrarse para reciclar el aire. El sistema puede ahorrar energía reciclando el aire en momentos del día en que el precio de la energía es alto o cuando el aire está muy frío y hay que calentarlo. Sin embargo, reciclar demasiado aire, sobre todo cuando hay muchas personas en el edificio, disminuye la calidad del aire al acumularse dióxido de carbono.

Supongamos que implementamos un sistema experto con dos reglas sencillas que establecen la estructura básica:

• Cierra la compuerta para reciclar el aire cuando la energía sea cara o cuando el aire esté muy frío (o muy caliente).

• Abre la compuerta para que entre aire fresco cuando la calidad del aire se aproxime a los límites legales.

Estas reglas representan las dos estrategias fundamentales para controlar el sistema. Consulta la Figura 1-15 para ver un diagrama del funcionamiento de la compuerta.

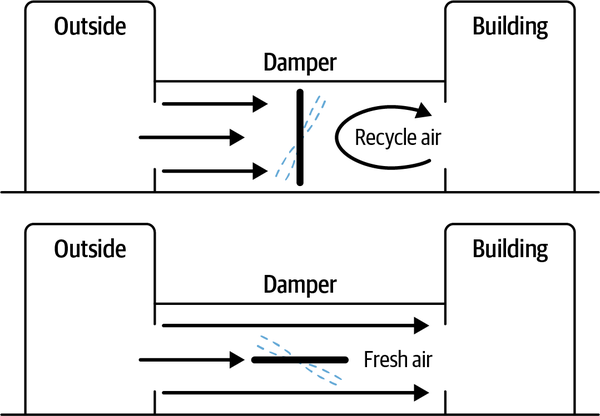
Figura 1-15. Cómo recicla y refresca el aire una válvula de compuerta en un sistema comercial de climatización.

La primera estrategia de control es perfecta para ahorrar dinero cuando la energía es cara y cuando las temperaturas son extremas. Funciona mejor cuando la ocupación del edificio es baja. La segunda estrategia funciona bien cuando la energía es menos cara y la ocupación del edificio esalta.

Pero aún no hemos terminado. Aunque las dos primeras reglas de nuestro sistema experto son sencillas de entender y manejar, necesitamos añadir muchas más reglas para ejecutar estas estrategias en todas las condiciones posibles. El mundo real es difuso, y cada regla tiene cientos de excepciones que habría que codificar en un sistema experto. Por ejemplo, la primera regla nos dice que debemos reciclar el aire cuando la energía sea cara y cuando la temperatura del aire sea extrema (muy caliente o muy fría). ¿Cómo de cara debe ser la energía para justificar el reciclaje del aire? ¿Y cuánto debes cerrar la válvula de compuerta para reciclar el aire? Bueno, eso depende de los niveles de dióxido de carbono en las habitaciones y de la temperatura exterior. Es matizable, y la respuesta correcta depende de la superficie del paisaje definido por las relaciones entre los precios de la energía, las temperaturas del aire exterior y el número de personas del edificio.

if (temp > 90 or temp < 20) and price > 0.15: # Recycle Air
	if temp < 00 and price > 0.17:
		valve = 0.1
	elif temp < 10 and price > 0.17:
		valve = 0.2
	elif temp < 20 and price > 0.17:
		valve = 0.3

El código anterior muestra algunas de las reglas adicionales necesarias para aplicar eficazmente dos estrategias de control de climatización en condiciones muy diferentes.

Los sistemas expertos son como mapas del terreno geográfico: exploraciones grabadas y trazadas a partir de expediciones anteriores. Ocupan un lugar especial en la historia de la IA: de hecho, constituyeron la mayor parte de su segunda oleada. El término inteligencia artificial se acuñó en 1956 en una conferencia de informáticos en el Dartmouth College. La primera oleada de IA utilizaba representaciones simbólicas (legibles por humanos) de los problemas, la lógica y la búsqueda para razonar y tomar decisiones. Este enfoque suele denominarse IA simbólica.

La segunda oleada de IA comprendía principalmente sistemas expertos. Durante algún tiempo, se tuvo la esperanza de que el sistema experto sirviera como sistema inteligente completo, hasta el punto de alcanzar una inteligencia comparable a la mente humana. Gente tan famosa como Marvin Minsky, considerado el "Padrino de la IA", así lo afirmaba. Desde el punto de vista de la investigación, gran parte de la exploración de lo que era y podía ser un sistema experto se consideró completa. Incluso, se registró una decepción tan generalizada sobre la capacidad de estos sistemas.

Una gran razón por la que murieron los sistemas expertos es el cuello de botella de la adquisición de conocimientos. Esta es otra idea de mi entrevista con Jonathan Schaeffer. Los sistemas expertos utilizan conocimientos obtenidos de los humanos, pero ¿cómo se obtienen los conocimientos de los humanos en términos que puedan trasladarse fácilmente al código? En general, no es tan fácil. Por eso murieron los primeros sistemas expertos. Eran demasiado frágiles. Obtener el conocimiento era difícil. Identificar y manejar todas las excepciones es más difícil. El gran maestro de ajedrez Kevin Spraggett lo dice muy bien: "Pasé la primera mitad de mi carrera aprendiendo los principios para jugar un ajedrez fuerte y la segunda mitad aprendiendo cuándo violarlos".

Descendió un largo "invierno" de la IA en medio de la decepción por el hecho de que el sistema experto no fuera suficiente para reproducir la inteligencia de la mente humana (el campo de la investigación de la IA denomina inteligencia general artificial, o AGI, a la hipotética capacidad de una IA para comprender y aprender intelectualmente, como podría hacerlo un humano). Faltaba la percepción, por ejemplo. Los sistemas expertos no pueden percibir relaciones y patrones complejos en el mundo de la forma en que vemos (identificamos objetos basándonos en patrones de formas y colores), oímos (detectamos y nos comunicamos basándonos en patrones de sonidos) y predecimos (pronosticamos resultados y probabilidades basándonos en correlaciones entre variables). También necesitamos un mecanismo para manejar las excepciones difusas que ponen en aprietos a los sistemas expertos. Así que los sistemas expertos descendieron silenciosamente bajo tierra para ser utilizados en finanzas e ingeniería, donde brillan en la toma de decisiones de alto valor hasta el día de hoy.

El "verano" actual de la IA hizo oscilar el péndulo en sentido contrario, como se ilustra en la Figura 1-16. Se rechazó el sistema experto en favor de la percepción, y luego en favor de los algoritmos de aprendizaje que toman decisiones secuenciales.

Nota

¡Ahora tenemos la oportunidad de combinar lo mejor de los sistemas expertos con la percepción y los agentes de aprendizaje en la IA autónoma de próxima generación! Los sistemas expertos pueden codificar los principios de los que hablaba Spraggett y las partes de aprendizaje de la IA autónoma pueden identificar las excepciones por ensayo y error.

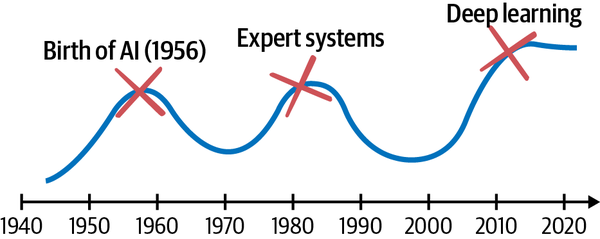
Figura 1-16. Cronología de la historia de la IA.

Si quieres saber más sobre cómo encajan los sistemas expertos en la historia de la IA, te recomiendo encarecidamente el libro de Luke Dormehl Thinking Machines: The Quest for Artificial Intelligence and Where It's Taking Us Next (TarcherPerigee), un estudio accesible y relevante de la historia de la IA. Si quieres leer detalles sobre un sistema experto real, te recomiendo este artículo sobre DENDRAL, ampliamente reconocido como el primer sistema experto "real".

Si avanzamos rápidamente hasta hoy, encontramos sistemas expertos integrados incluso en la IA autónoma más avanzada. Un experto me describió una vez una IA autónoma que se construyó para controlar coches autoconducidos. En lo más profundo de la lógica que orquesta la IA de aprendizaje para percibir y actuar mientras conduce, hay reglas expertas que toman el control en situaciones críticas para la seguridad. La IA de aprendizaje percibe y toma decisiones difusas y matizadas, pero los componentes del sistema experto también hacen lo que saben hacer realmente bien: tomar medidas predecibles para mantener a salvo el vehículo (y a las personas). Así es exactamente como utilizaremos las matemáticas, los menús y los manuales cuando diseñemos cerebros. Asignaremos la tecnología de toma de decisiones para ejecutar mejor cada habilidad de toma de decisiones.

¿Cuándo debes utilizar sistemas expertos para tomar decisiones?

• Cuando tienes mucha experiencia explorando el espacio, sabes qué hacer en muchos escenarios diferentes y puedes expresar las acciones deseadas y en términos de reglas y/o estrategias

• Cuando tienes muchas restricciones que deben cumplirse (como en los algoritmos de optimización)

• Cuando necesitas explicar tus decisiones pero no tienes un modelo matemático en el que confíes lo suficiente como para utilizar sus cálculos para determinar acciones

Limitaciones de los sistemas expertos

• Los sistemas expertos están limitados por el conocimiento de la exploración previa.

• Mantener las reglas -y todas las excepciones- en la base de conocimientos es tedioso y propenso a errores.

Ahora que he hablado de cada método que utilizan las máquinas para tomar decisiones automatizadas, puedes ver que cada método tiene puntos fuertes y débiles. En algunas situaciones, un método puede ser una elección clara y obvia para las decisiones automatizadas. En otras aplicaciones, otro método podría funcionar mucho mejor. Ahora, incluso podemos considerar la posibilidad de mezclar métodos para conseguir mejores resultados, como hace el MPC. Toma mejores decisiones de control mezclando matemáticas con manuales en forma de algoritmo de optimización de restricciones. Pero antes, echemos un vistazo a las capacidades de la IA autónoma.

¹ Jacques Smuts, "A Tutorial on Feedback Control", Control Notes: Reflexiones de un Profesional del Control de Procesos, 17 de enero de 2011, https://blog.opticontrols.com/archives/297.

² Claude E. Shannon, "Programar un ordenador para jugar al ajedrez", Revista Filosófica, 7ª serie, 41, nº. 314 (marzo de 1950): 256-75.

³ El libro de George Heineman Learning Algorithms (O'Reilly) proporciona detalles sobre cómo evaluar estos algoritmos.

⁴ W. G. Chase y H. A. Simon, "Percepción en el ajedrez", Psicología cognitiva 4, nº 1 (1973): 55-81. https://dx.doi.org/10.1016/0010-0285(73)90004-2