Avanzar en la Analítica

Capítulo 4. Correlación y regresión

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

¿Has oído que el consumo de helado está relacionado con los ataques de tiburón? Al parecer, Tiburón tiene un apetito letal por el chocolate con menta. La Figura 4-1 visualiza esta relación propuesta.

Figura 4-1. La relación propuesta entre el consumo de helado y los ataques de tiburón

"No es así", puedes replicar. "Esto no significa necesariamente que los ataques de tiburón se desencadenen por el consumo de helado".

"Podría ser", razonas, "que al aumentar la temperatura exterior se consuma más helado. La gente también pasa más tiempo cerca del océano cuando hace calor, y esa coincidencia provoca más ataques de tiburones."

"La correlación no implica causalidad"

Seguro que has oído repetidamente en que "correlación no implica causalidad".

En el Capítulo 3, aprendiste que la causalidad es una expresión tensa en estadística. En realidad, sólo rechazamos la hipótesis nula porque, sencillamente, no tenemos todos los datos para afirmar con seguridad la causalidad. Dejando a un lado esa diferencia semántica, ¿tiene algo que ver la correlación con la causalidad? La expresión estándar simplifica en cierto modo su relación; verás por qué en este capítulo utilizando las herramientas de la estadística inferencial que has aprendido antes.

Este será nuestro último capítulo, realizado principalmente en Excel. Después, habrás comprendido suficientemente el marco de la analítica para estar preparado para pasar a R y Python.

Introducción a la correlación

Hasta ahora, la mayoría de las veces hemos analizado estadísticas de una variable cada vez: hemos hallado la puntuación media en lectura o la varianza de los precios de la vivienda, por ejemplo. Esto se conoce en como análisis univariante.

También hemos hecho un poco de análisis bivariante en . Por ejemplo, comparamos las frecuencias de dos variables categóricas utilizando una tabla de frecuencias bidireccional. También analizamos una variable continua agrupada por múltiples niveles de una variable categórica, hallando estadísticas descriptivas para cada grupo.

Ahora calcularemos una medida bivariada de dos variables continuas utilizando la correlación. Más concretamente, utilizaremos el coeficiente de correlación de Pearson para medir la fuerza de la relación lineal entre dos variables. Sin una relación lineal, la correlación de Pearson no es adecuada.

Entonces, ¿cómo sabemos que nuestros datos son lineales? Hay formas más rigurosas de comprobarlo, pero, como siempre, una visualización es un buen comienzo. En concreto, utilizaremos un diagrama de dispersión para representar todas las observaciones en función de sus coordenadas x e y.

Si parece que puede trazarse una línea a través del diagrama de dispersión que resuma el patrón general, entonces se trata de una relación lineal y puede utilizarse la correlación de Pearson. Si se necesitara una curva u otra forma para resumir el patrón, entonces ocurre lo contrario. La figura 4-2 muestra una relación lineal y dos no lineales.

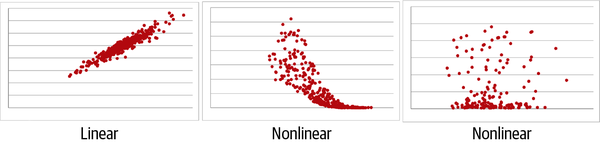
Figura 4-2. Relaciones lineales frente a no lineales

En concreto, la Figura 4-2 ofrece un ejemplo de relación lineal positiva en : a medida que aumentan los valores en el eje x, también lo hacen los valores en el eje y (a un ritmo lineal).

También es posible tener una correlación negativa, en la que una línea negativa resume la relación, o ninguna correlación, en la que una línea plana la resume. Estos distintos tipos de relaciones lineales se muestran en en la Figura 4-3. Recuerda que todas ellas deben ser relaciones lineales para que se aplique la correlación.

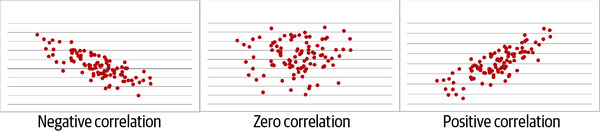
Figura 4-3. Correlaciones negativas, nulas y positivas

Una vez que hemos establecido que los datos son lineales, podemos hallar el coeficiente de correlación . Siempre toma un valor entre -1 y 1, donde -1 indica una relación lineal negativa perfecta, 1 una relación lineal positiva perfecta y 0 ninguna relación lineal. La Tabla 4-1 muestra algunas reglas empíricas de para evaluar la fuerza de un coeficiente de correlación. No se trata en absoluto de normas oficiales, sino de un punto de partida útil para la interpretación.

Tabla 4-1. Interpretación de los coeficientes de correlación

Coeficiente de correlación	Interpretación
-1.0	Relación lineal negativa perfecta
-0.7	Fuerte relación negativa
-0.5	Relación negativa moderada
-0.3	Relación negativa débil
0	No hay relación lineal
+0.3	Relación positiva débil
+0.5	Relación positiva moderada
+0.7	Fuerte relación positiva
+1.0	Relación lineal positiva perfecta

Con el marco conceptual básico de las correlaciones en mente, vamos a hacer algunos análisis en Excel. Utilizaremos un conjunto de datos de kilometraje de vehículos; puedes encontrar mpg.xlsx en la subcarpeta mpg de la carpeta de conjuntos de datos del repositorio del libro. Se trata de un nuevo conjunto de datos, así que tómate un tiempo para conocerlo: ¿con qué tipos de variables estamos trabajando? Resúmelas y visualízalas utilizando las herramientas tratadas en el Capítulo 1. Para facilitar el análisis posterior, no olvides añadir una columna de índice y convertir el conjunto de datos en una tabla, que llamaré mpg.

Excel incluye la función CORREL() para calcular el coeficiente de correlación entre dos matrices:

CORREL(array1, array2)

Utilicemos esta función para encontrar la correlación entre weight ympg en nuestro conjunto de datos:

=CORREL(mpg[weight], mpg[mpg])

Efectivamente, devuelve un valor entre -1 y 1: -0,832. (¿Recuerdas cómo interpretarlo?)

Una matriz de correlaciones presenta las correlaciones entre todos los pares de variables. Construyamos una utilizando el Paquete de Herramientas de Análisis de Datos. En la cinta, ve a Datos → Análisis de Datos → Correlación.

Recuerda que se trata de una medida de relación lineal entre dos variablescontinuas, por lo que deberíamos excluir variables categóricas como origen y ser juiciosos a la hora de incluir variables discretas como cilindros o modelo.año. El ToolPak insiste en que todas las variables estén en un intervalo contiguo, así que incluiré cautelosamente cilindros. La Figura 4-4 muestra el aspecto que debería tener el menú fuente del ToolPak.

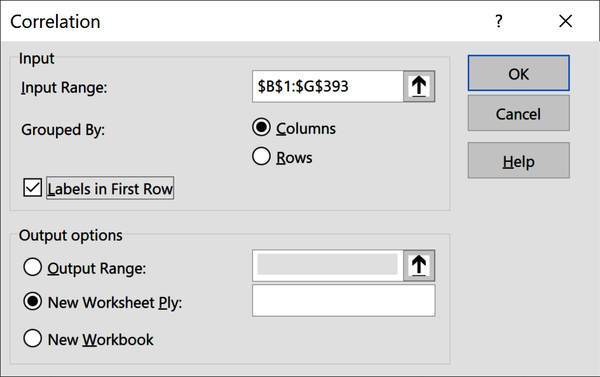
Figura 4-4. Insertar una matriz de correlaciones en Excel

El resultado es una matriz de correlaciones como la de la Figura 4-5.

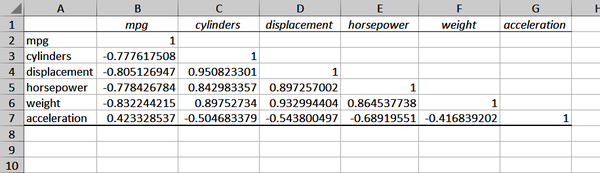
Figura 4-5. Matriz de correlación en Excel

Podemos ver el -0,83 en la celda B6: es la intersección de peso ympg. También veríamos el mismo valor en la celda F2, pero Excel dejó en blanco esta mitad de la matriz, ya que es información redundante. Todos los valores a lo largo de la diagonal son 1, ya que cualquier variable está perfectamente correlacionada con la propia .

Advertencia

El coeficiente de correlación de Pearson sólo es una medida adecuada cuando la relación entre las dos variables es lineal.

Hemos dado un gran salto en nuestras suposiciones sobre nuestras variables al analizar sus correlaciones. ¿Se te ocurre qué es eso? Hemos supuesto que su relación es lineal. Comprobemos esa suposición con gráficos de dispersión . Por desgracia, en Excel básico no hay forma de generar gráficos de dispersión de cada par de variables a la vez. Para practicar, considera la posibilidad de trazarlos todos, pero vamos a intentarlo con las variables peso y mpg. Resalta estos datos, ve a la cinta de opciones y haz clic en Insertar → Dispersión.

Añadiré un título personalizado al gráfico y reetiquetaré los ejes para facilitar la interpretación. Para cambiar el título del gráfico, haz doble clic sobre él. Para reetiquetar los ejes, haz clic en el perímetro del gráfico y luego selecciona el signo más que aparece para desplegar el menú Elementos del Gráfico . (En Mac, haz clic dentro del gráfico y luego Diseño de Gráfico → Añadir Elemento de Gráfico). Selecciona Títulos de Eje en el menú. La Figura 4-6 muestra el gráfico de dispersión resultante. No es mala idea incluir unidades de medida en los ejes para ayudar a los ajenos a entender los datos.

La Figura 4-6 se parece básicamente a una relación lineal negativa , con una mayor dispersión dado un menor peso y un mayor kilometraje. Por defecto, Excel traza la primera variable de nuestra selección de datos a lo largo del eje x y la segunda a lo largo del eje y. Pero, ¿por qué no al revés? Prueba a cambiar el orden de estas columnas en tu hoja de cálculo para que el peso esté en la columna E y el mpg en la columna F, y luego inserta un nuevo gráfico de dispersión.

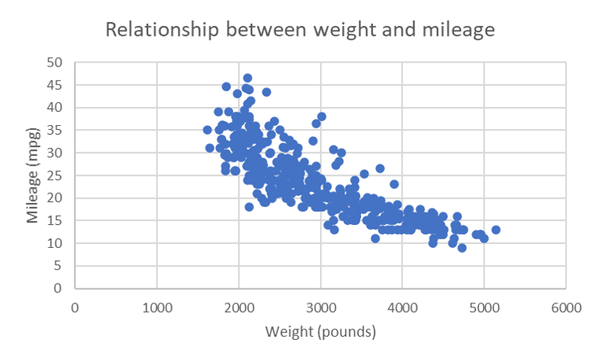
Figura 4-6. Diagrama de dispersión del peso y el kilometraje

La Figura 4-7 muestra una imagen especular de la relación. Excel es una gran herramienta, pero como con cualquier herramienta, tienes que decirle lo que tiene que hacer. Excel calculará correlaciones independientemente de si la relación es lineal. También te hará un diagrama de dispersión sin preocuparse de qué variable debe ir en cada eje.

Entonces, ¿qué diagrama de dispersión es "correcto"? ¿Importa? Por convención de , la variable independiente va en el eje x, y la dependiente en el eje y. Tómate un momento para considerar cuál es cuál. Si no estás seguro, recuerda que la variable independiente suele ser la que se mide primero.

Nuestra variable independiente es el peso porque viene determinado por el diseño y la construcción del coche. El mpg es la variable dependiente porque suponemos que se ve afectado por el peso del coche. Esto coloca el pesoen el eje x y los mpg en el eje y.

En business analytics, no es habitual haber recopilado datos sólo para realizar análisis estadísticos; por ejemplo, los coches de nuestro conjunto de datos dempg se fabricaron para generar ingresos, no para un estudio de investigación sobre el impacto del peso en el kilometraje. Como no siempre hay variables independientes y dependientes claras, tenemos que ser tanto más conscientes de lo que miden esas variables y de cómo se miden. Por eso es tan valioso tener algún conocimiento del ámbito que estás estudiando, o al menos descripciones de tus variables y de cómo se recogieron tus observaciones .

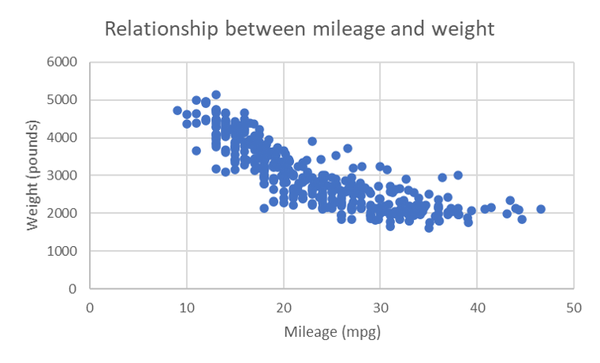
Figura 4-7. Diagrama de dispersión del kilometraje y el peso

De la correlación a la regresión

Aunque es convencional colocar la variable independiente en el eje x, no hay diferencia en el coeficiente de correlación relacionado. Sin embargo, aquí hay una gran advertencia, y se refiere a la idea anterior de utilizar una línea para resumir la relación hallada por el diagrama de dispersión. Esta práctica empieza a divergir de la correlación , y es una de las que quizá hayas oído hablar: la regresión lineal.

La correlación es agnóstica respecto a qué variable llamas independiente y cuál dependiente; eso no influye en su definición como "el grado en que dos variables se mueven juntas linealmente".

Por otra parte, la regresión lineal se ve afectada intrínsecamente por esta relación como "el impacto estimado de un cambio unitario de la variable independiente X sobre la variable dependiente Y".

Vas a ver que la recta que ajustamos a través de nuestro diagrama de dispersión puede expresarse como una ecuación; a diferencia del coeficiente de correlación, esta ecuación depende de cómo definamos nuestras variables independiente y dependiente.

Regresión lineal y modelos lineales

A menudo oirás referirte a la regresión lineal como modelo lineal, que no es más que uno de los muchos modelos estadísticos. Al igual que un modelo de tren que podrías construir, un modelo estadístico sirve como aproximación factible a un tema de la vida real. En concreto, utilizamos modelos estadísticos para comprender la relación entre variables dependientes e independientes. Los modelos no podrán explicarlo todo sobre lo que representan, pero eso no significa que no puedan ayudar. Pero como dijo el famoso matemático británico George Box: "Todos los modelos son erróneos, pero algunos son útiles".

Al igual que la correlación, la regresión lineal supone que existe una relación lineal entre las dos variables. Existen otros supuestos que es importante tener en cuenta al modelizar los datos. Por ejemplo, no queremos tener observaciones extremas que puedan afectar desproporcionadamente a la tendencia general de la relación lineal.

A efectos de nuestra demostración, por ahora pasaremos por alto éste y otros supuestos. Estas suposiciones suelen ser difíciles de comprobar utilizando Excel; tus conocimientos de programación estadística te serán útiles cuando profundices en los puntos más profundos de la regresión lineal.

Respira hondo; es hora de otra ecuación :

Ecuación 4-1. La ecuación de la regresión lineal

$$Y={\beta }_0+{\beta }_1\times X+ϵ$$

El objetivo de la Ecuación 4-1 es predecir nuestra variable dependiente Y. Ése es el lado izquierdo. Quizá recuerdes de la escuela que una recta puede descomponerse en suintercepto y su pendiente. Ahí es donde ${\beta }_0$ y${\beta }_1\times X_i$respectivamente. En el segundo término, multiplicamos nuestra variable independiente por un coeficiente de pendiente.

Por último, habrá una parte de la relación entre nuestra variable independiente y la dependiente que no pueda explicarse por el modelo en sí, sino por alguna influencia externa. Esto se conoce en como error del modelo y viene indicado por ${\epsilon }_i$.

Antes hemos utilizado la prueba t de muestras independientes para examinar una diferencia significativa de medias entre dos grupos. Aquí estamos midiendo la influencia lineal de una variable continua sobre otra. Lo haremos examinando si la pendiente de la línea de regresión ajustada es estadísticamente distinta de cero. Eso significa que nuestra prueba de hipótesis funcionará más o menos así:

H0: No hay influencia lineal de nuestra variable independiente sobre nuestra variable dependiente. (La pendiente de la recta de regresión es igual a cero).

Ha: Existe una influencia lineal de nuestra variable independiente sobre nuestra variable dependiente. (La pendiente de la recta de regresión no es igual a cero).

La Figura 4-8 muestra algunos ejemplos de de cómo podrían ser las pendientes significativas e insignificantes.

Recuerda que no tenemos todos los datos, por lo que no sabemos cuál sería la pendiente "verdadera" para la población de . En su lugar, estamos deduciendo si, dada nuestra muestra, esta pendiente sería estadísticamente diferente de cero. Podemos utilizar la misma metodología del valor p de para estimar la significación de la pendiente que utilizamos para hallar la diferencia de medias de dos grupos de . Seguiremos realizando pruebas de dos colas en el intervalo de confianza del 95%. Pasemos a buscar los resultados utilizando Excel.

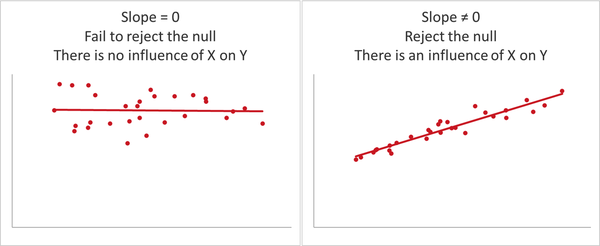
Figura 4-8. Modelos de regresión con pendientes significativas y no significativas

Regresión lineal en Excel

En esta demostración de regresión lineal sobre el conjunto de datos mpg en Excel, comprobamos si el peso de un coche(weight) tiene una influencia significativa sobre su kilometraje(mpg). Eso significa que nuestras hipótesis serán:

H0: No hay influencia lineal del peso sobre el kilometraje.

Ha: Hay una influencia lineal del peso sobre el kilometraje.

Antes de empezar, es una buena idea escribir la ecuación de regresión utilizando las variables específicas de interés, lo que he hecho en la Ecuación 4-2:

Ecuación 4-2. Nuestra ecuación de regresión para estimar el kilometraje

$$mpg={\beta }_0+{\beta }_1\times weight+ϵ$$

Empecemos por visualizar los resultados de la regresión: ya tenemos el gráfico de dispersión de la Figura 4-6, ahora sólo es cuestión de superponer o "ajustar" la recta de regresión sobre él. Haz clic en el perímetro del gráfico para abrir el menú "Elementos del gráfico". Haz clic en "Línea de tendencia" y, a continuación, en "Más opciones" a un lado. Haz clic en el botón de opción de la parte inferior de la pantalla "Formato de la línea de tendencia" que dice "Mostrar ecuación en el gráfico".

Ahora vamos a hacer clic en la ecuación resultante en el gráfico para añadirle formato de negrita y aumentar su tamaño de fuente a 14. Haremos que la línea de tendencia sea de color negro sólido y le daremos una anchura de 2,5 puntos haciendo clic sobre ella en el gráfico, y luego yendo al icono del cubo de pintura en la parte superior del menú Formato de línea de tendencia. Ya tenemos la realización de la regresión lineal. Nuestro gráfico de dispersión con la línea de tendencia tiene el aspecto de la Figura 4-9. Excel también incluye la ecuación de regresión que buscamos en la Ecuación 4-2 para estimar el kilometraje de un coche en función de su peso.

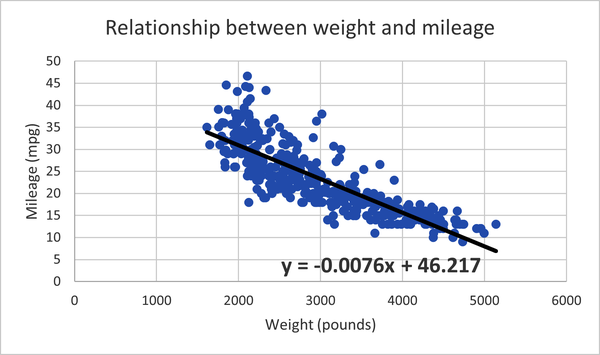
Figura 4-9. Diagrama de dispersión con línea de tendencia y ecuación de regresión para el efecto del peso sobre el kilometraje

Podemos colocar la intercepción antes de la pendiente en nuestra ecuación para obtener la Ecuación 4-3.

Ecuación 4-3. Ecuación 4-3. Nuestra ecuación de regresión ajustada para estimar el kilometraje

$$mpg=46.217-0.0076\times weight$$

Observa que Excel no incluye el término de error como parte de la ecuación de regresión. Ahora que hemos ajustado la recta de regresión, hemos cuantificado la diferencia entre los valores que esperamos de la ecuación y los valores que se encuentran en los datos. Esta diferencia se conoce como residuo, y volveremos a él más adelante en este capítulo. En primer lugar, volveremos a lo que nos habíamos propuesto: establecer la significación estadística.

Está muy bien que Excel haya ajustado la recta por nosotros y nos haya dado la ecuación resultante . Pero esto no nos da suficiente información para realizar la prueba de hipótesis: seguimos sin saber si la pendiente de la recta es estadísticamente distinta de cero. Para obtener esta información, volveremos a utilizar el paquete de herramientas de análisis. En la cinta, ve a Datos → Análisis de Datos → Regresión. Se te pedirá que selecciones tus rangos Y y X; éstas son tus variables dependiente e independiente, respectivamente. Asegúrate de indicar que tus variables de entrada incluyen etiquetas, como se muestra en la Figura 4-10.

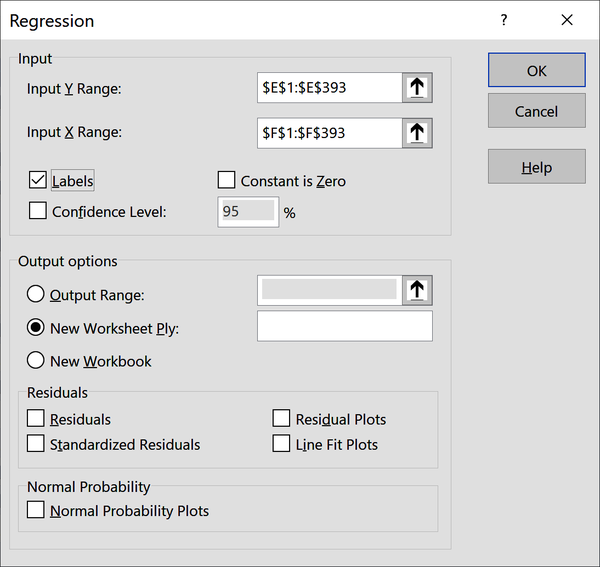
Figura 4-10. Ajustes del menú para derivar una regresión con el ToolPak

Esto da como resultado bastante información, que se muestra en la Figura 4-11. Vamos arecorrerla.

Ignora por ahora la primera sección en las celdas A3:B8; volveremos a ella más adelante. Nuestra segunda sección en A10:F14 se denomina ANOVA (abreviatura de análisis de la varianza). Nos dice si nuestra regresión funciona significativamente mejor con el coeficiente de la pendiente incluido frente a una con sólo el intercepto .

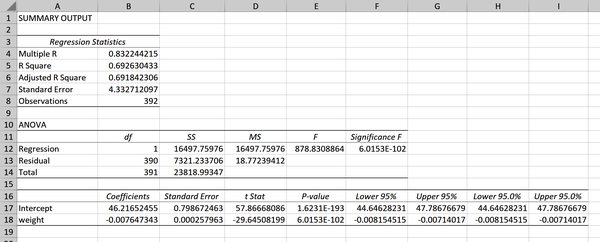
Figura 4-11. Resultado de la regresión

La Tabla 4-2 detalla cuáles son aquí las ecuaciones que compiten.

Tabla 4-2. Modelo de sólo intercepción frente a modelo de regresión completa

Modelo sólo Incercept	Modelo con coeficientes
mpg = 46,217	mpg = 46,217 - 0,0076 × peso

Un resultado estadísticamente significativo indica que nuestros coeficientes sí mejoran el modelo. Podemos determinar los resultados de la prueba a partir del valor p que aparece en la celda F12de la Figura 4-11. Recuerda que se trata de notación científica, así que lee el valor p como 6,01 veces 10 a la potencia de -102: mucho menor que 0,05. Podemos concluir que vale la pena mantener el peso como coeficiente en el modelo de regresión.

Esto nos lleva a la tercera sección en las celdas A16:I18; aquí es donde encontramos lo que buscábamos en un principio. Este rango contiene mucha información, así que vayamos columna por columna empezando por los coeficientes en las celdas B17:B18. Deberían parecernos familiares como la intersección y la pendiente de la recta que se dieron en la Ecuación 4-3.

A continuación, el error típico en C17:C18. Ya hablamos de él en el Capítulo 3: es una medida de la variabilidad en muestras repetidas y, en este caso, puede considerarse como una medida de la precisión de nuestros coeficientes.

Entonces tenemos lo que Excel denomina "estadístico t", también conocido como estadístico t o estadístico de prueba, en D17:D18; se obtiene dividiendo el coeficiente por el error típico. Podemos compararlo con nuestro valor crítico de 1,96 para establecer la significación estadística con un 95% de confianza.

Sin embargo, es más habitual interpretar y informar sobre el valor p, que da la misma información. Tenemos dos valores p que interpretar. En primer lugar, el coeficiente del intercepto en E17. Esto nos dice si el intercepto es significativamente distinto de cero. Lasignificación del intercepto no forma parte de nuestra prueba de hipótesis, por lo que esta información es irrelevante. (Este es otro buen ejemplo de por qué no siempre podemos tomar al pie de la letra los resultados de Excel).

Advertencia

Aunque la mayoría de los paquetes estadísticos (incluido Excel) informan del valor p del intercepto, no suele ser información relevante.

En cambio, queremos el valor p del peso en la celda E18: está relacionado con la pendiente de la recta. El valor p es muy inferior a 0,05, por lo que rechazamos el nulo y concluimos que es probable que el peso influya en el kilometraje. En otras palabras, la pendiente de la recta es significativamente distinta de cero. Al igual que con nuestras pruebas de hipótesis anteriores, evitaremos concluir que hemos "demostrado" una relación, o que más peso causa menos kilometraje. De nuevo, estamos haciendo inferencias sobre una población basada en una muestra, por lo que la incertidumbre es inherente.

La salida también nos da el intervalo de confianza del 95% para nuestra intercepción y pendiente en las celdas F17:I18. Por defecto, esto se indica dos veces: si hubiéramos pedido un intervalo de confianza diferente en el menú de entrada, habríamos recibido ambos aquí.

Ahora que ya sabes cómo interpretar el resultado de la regresión, vamos a intentar hacer una estimación puntual basada en la línea de la ecuación: ¿cuál esperaríamos que fuera el kilometraje de un coche que pesa 3.021 libras? Introduzcámoslo en nuestra ecuación de regresión en la Ecuación 4-4:

Ecuación 4-4. Ecuación 4-4. Hacer una estimación puntual basada en nuestra ecuación

$$mpg=46.217-0.0076\times 3021$$

Basándonos en la ecuación 4-4, esperamos que un coche que pese 3.021 libras obtenga 23,26 millas por galón. Echa un vistazo al conjunto de datos de origen: hay una observación que pesa 3.021 libras (Ford Maverick, fila 101 en el conjunto de datos) y obtiene 18 millas por galón, no 23,26. ¿Qué ocurre?

Esta discrepancia de es el residuo que se mencionó antes: es la diferencia entre los valores que estimamos en la ecuación de regresión y los que se encuentran en los datos reales. He incluido ésta y otras observaciones en la Figura 4-12. Los puntos de dispersión representan los valores que se encuentran realmente en el conjunto de datos, y la línea representa los valores que predijimos con la regresión.

Es lógico que nos motive minimizar la diferencia entre estos valores. Para ello, Excel y la mayoría de las aplicaciones de regresión utilizan mínimos cuadrados ordinarios (MCO ). Nuestro objetivo en MCO es minimizar los residuos, en concreto, la suma de los residuos al cuadrado, de modo que tanto los residuos negativos como los positivos se midan por igual. Cuanto menor sea la suma de los residuos al cuadrado, menor será la diferencia entre nuestros valores reales y los esperados, y mejor será nuestra ecuación de regresión para hacer estimaciones.

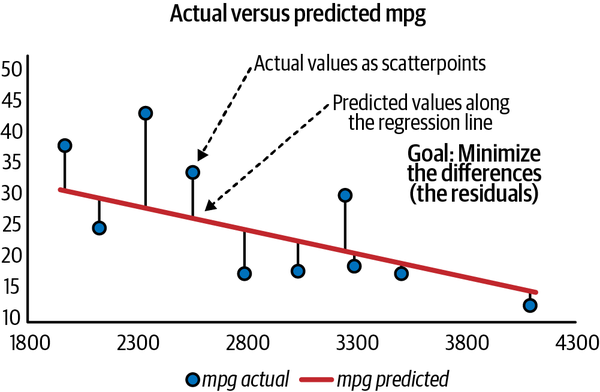
Figura 4-12. Los residuos son las diferencias entre los valores reales y los previstos

Del valor p de nuestra pendiente hemos aprendido que existe una relación significativa entre las variables independiente y dependiente . Pero esto no nos dice qué parte de la variabilidad de nuestra variable dependiente se explica por nuestra variable independiente.

Recuerda que la variabilidad es el núcleo de lo que estudiamos como analistas; las variables varían, y queremos estudiar por qué varían. Los experimentos nos permiten hacerlo, al comprender la relación entre una variable independiente y una dependiente. Pero no podremos explicar todo sobre nuestra variable dependiente con nuestra variable independiente. En siempre habrá algún error sin explicar.

R-cuadrado, o el coeficiente de determinación (que Excel denomina R-cuadrado), expresa en porcentaje cuánta variabilidad de la variable dependiente explica nuestro modelo de regresión. Por ejemplo, un R-cuadrado de 0,4 indica que el 40% de la variabilidad de Y puede ser explicada por el modelo. Esto significa que 1 menos R-cuadrado es la variabilidad que no puede explicar el modelo. Si R-cuadrado es 0,4, entonces el 60% de la variabilidad de Y no se explica.

Excel calcula R-cuadrado para nosotros en el primer cuadro de la salida de regresión; echa un vistazo a la celda B5 de la Figura 4-11. La raíz cuadrada de R-cuadrado es R múltiple, que también se ve en la celda B4 de la salida. La R-cuadrado ajustada (celda B6) se utiliza como una estimación más conservadora de la R-cuadrado para un modelo con múltiples variables independientes. Esta medida es de interés cuando se realiza una regresión lineal múltiple, que está fuera del alcance de este libro.

Regresión lineal múltiple

Este capítulo se ha centrado en la regresión lineal univariante, o la influencia de una independiente sobre una variable dependiente. También es posible construir modelos de regresión múltiple, o multivariante, para estimar la influencia de varias variables independientes sobre una variable dependiente. Estas variables independientes pueden incluir variables categóricas, no sólo continuas, interacciones entre variables y más. Para una mirada detallada a la realización de una regresión lineal más compleja en Excel, consulta Regression Analysis Microsoft Excel (Que) de Conrad Carlberg.

Hay otras formas, además de la R-cuadrado, de medir el rendimiento de la regresión: Excel incluye una de ellas, el error típico de la regresión , en su salida (celda B7 de la Figura 4-11). Esta medida nos indica la distancia media a la que los valores observados se desvían de la recta de regresión. Algunos analistas de prefieren ésta u otras medidas a la R-cuadrado para evaluar los modelos de regresión, aunque la R-cuadrado sigue siendo una opción dominante. Independientemente de las preferencias, la mejor evaluación suele provenir de la evaluación de múltiples cifras en su contexto adecuado, por lo que no hay necesidad de jurar o renegar de una sola medida.

Enhorabuena: has realizado e interpretado un análisis de regresión completo .

Repensar nuestros resultados: Relaciones espurias

Basándonos en su orden temporal y en nuestra propia lógica, en nuestro ejemplo del kilometraje es casi absoluto que el peso debe ser la variable independiente y las mpg la dependiente. Pero, ¿qué ocurre si ajustamos la recta de regresión con estas variables invertidas? Inténtalo con el ToolPak. La ecuación de regresión resultante se muestra en la Ecuación 4-5.

Ecuación 4-5. Ecuación 4-5. Ecuación de regresión para estimar el peso en función del kilometraje

$$weight=5101.1-90.571\times mpg$$

Podemos dar la vuelta a nuestras variables independiente y dependiente y obtener el mismo coeficiente de correlación. Pero cuando las cambiamos para la regresión, nuestros coeficientes cambian.

Si descubriéramos que el mpg y el peso están influidos simultáneamente por alguna variable externa, entonces ninguno de estos modelos sería correcto. Y éste es el mismo escenario al que nos enfrentamos en el consumo de helado y los ataques de tiburón. Es una tontería decir que el consumo de helado influye en los ataques de tiburón, porque ambos están influidos por la temperatura, como muestra la Figura 4-13.

Figura 4-13. Consumo de helado y ataques de tiburón: una relación espuria

Esto se denomina relación espuria. Se encuentra con frecuencia en los datos, y puede que no sea tan obvia como en este ejemplo. Tener cierto conocimiento del dominio de los datos que estás estudiando puede ser muy valioso para detectar relaciones espurias .

Advertencia

Las variables pueden estar correlacionadas; incluso podría haber indicios de una relación causal. Pero la relación podría estar impulsada por alguna variable que ni siquiera has tenido en cuenta.

Conclusión

¿Recuerdas esta vieja frase?

La correlación no implica causalidad.

La analítica es altamente incremental: solemos superponer un concepto sobre otro para construir análisis cada vez más complejos. Por ejemplo, siempre empezaremos con estadísticas descriptivas de la muestra antes de intentar inferir parámetros de la población. Aunque correlación no implique causalidad, la causalidad se construye sobre los cimientos de la correlación. Eso significa que una forma mejor de resumir la relación podría ser

La correlación es una condición necesaria pero no suficiente para la causalidad.

En este capítulo y en los anteriores sólo hemos arañado la superficie de la estadística inferencial. Existe todo un mundo de pruebas, pero todas ellas utilizan el mismo marco de pruebas de hipótesis que hemos utilizado aquí. Domina este proceso y podrás comprobar todo tipo de relaciones entre los datos.

Avanzar en la programación

Espero que hayas visto y estés de acuerdo en que Excel es una herramienta fantástica para aprender estadística y analítica. Tuviste una visión práctica de los principios estadísticos que impulsan gran parte de este trabajo, y aprendiste a explorar y comprobar las relaciones en conjuntos de datos reales.

Dicho esto, Excel puede tener rendimientos decrecientes cuando se trata de análisis más avanzados. Por ejemplo, hemos estado comprobando propiedades como la normalidad y la linealidad mediante visualizaciones; es un buen comienzo, pero hay formas más sólidas de comprobarlas (a menudo, de hecho, mediante inferencia estadística). Estas técnicas a menudo se basan en el álgebra matricial y otras operaciones computacionalmente intensivas que pueden ser tediosas de derivar en Excel. Aunque existen complementos para compensar estas deficiencias, pueden ser caros y carecer de determinadas funciones. Por otro lado, como herramientas de código abierto, R y Python son gratuitas e incluyen muchas funciones similares a las de las aplicaciones, llamadas paquetes, que sirven para casi cualquier caso de uso. Este entorno te permitirá centrarte en el análisis conceptual de tus datos más que en el cálculo en bruto, pero tendrás que aprender a programar. Estas herramientas, y el conjunto de herramientas analíticas en general, serán el tema central del Capítulo 5.

Ejercicios

Practica tus habilidades de correlación y regresión en analizando en el conjunto de datos ais que se encuentra en la carpeta de conjuntos de datos del repositorio del libro. Este conjunto de datos incluye la altura, el peso y las lecturas de sangre de atletas australianos masculinos y femeninos de diferentes deportes.

Con el conjunto de datos, prueba lo siguiente:

1. Elabora una matriz de correlaciones de las variables relevantes de este conjunto de datos.

2. Visualiza la relación entre la altura y el peso. ¿Es una relación lineal? Si es así, ¿es negativa o positiva?

3. De la altura y la masa, ¿cuál supones que es la variable independiente y cuál la dependiente?

   • ¿Existe una influencia significativa de la variable independiente sobre la variable dependiente?

   • ¿Cuál es la pendiente de tu línea de regresión ajustada?

   • ¿Qué porcentaje de la varianza de la variable dependiente explica la variable independiente?

4. Este conjunto de datos contiene una variable para el índice de masa corporal, bmi. Si no estás familiarizado con esta métrica, dedica un momento a investigar cómo se calcula. Sabiendo esto, ¿te gustaría analizar la relación entre la altura y el IMC? No dudes en apoyarte aquí en en el sentido común más que en el mero razonamiento estadístico.