Capítulo 4. Redes Generativas Adversariales
Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: translation-feedback@oreilly.com
En 2014, Ian Goodfellow et al. presentaron una ponencia titulada "Generative Adversarial Nets" (Redes Generativas Adversariales)1 en la conferencia Neural Information Processing Systems (NeurIPS) de Montreal. La introducción de las redes generativas adversariales (o GAN, como se conocen más comúnmente) se considera ahora un punto de inflexión clave en la historia del modelado generativo, ya que las ideas centrales presentadas en este artículo han dado lugar a algunos de los modelos generativos más exitosos e impresionantes jamás creados.
En este capítulo se expondrán primero los fundamentos teóricos de los GAN, y después veremos cómo construir nuestro propio GAN utilizando Keras.
Introducción
Empecemos con una breve historia para ilustrar algunos de los conceptos fundamentales utilizados en el proceso de entrenamiento del GAN.
La historia de los ladrillos Brickki y los falsificadores describe el proceso de entrenamiento de una red generativa adversarial.
Una GAN es una batalla entre dos adversarios, el generador y el discriminador. El generador intenta convertir el ruido aleatorio en observaciones que parezcan haber sido muestreadas del conjunto de datos original, y el discriminador intenta predecir si una observación procede del conjunto de datos original o es una de las falsificaciones del generador. En la Figura 4-2 se muestran ejemplos de las entradas y salidas de las dos redes.
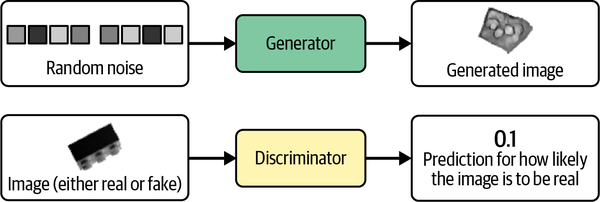
Figura 4-2. Entradas y salidas de las dos redes de una GAN
Al principio del proceso, el generador emite imágenes ruidosas y el discriminador predice aleatoriamente. La clave de las GAN reside en cómo alternamos el entrenamiento de las dos redes, de modo que a medida que el generador se vuelve más experto en engañar al discriminador, éste debe adaptarse para mantener su capacidad de identificar correctamente qué observaciones son falsas. Esto lleva al generador a encontrar nuevas formas de engañar al discriminador, y así continúa el ciclo.
GAN Convolucional Profundo (DCGAN)
Para ver esto en acción, empecemos a construir nuestro primer GAN en Keras, para generar imágenes de ladrillos.
Nosotros seguiremos de cerca uno de los primeros artículos importantes sobre las GAN, "Unsupervised Representation Learning with Deep Convolutional Generative AdversarialNetworks".2 En este artículo de 2015, los autores muestran cómo construir una GAN convolucional profunda para generar imágenes realistas a partir de diversos conjuntos de datos. También introducen varios cambios que mejoran significativamente la calidad de las imágenes generadas.
Ejecutar el código de este ejemplo
El código de este ejemplo se encuentra en el cuaderno Jupyter situado en notebooks/04_gan/01_dcgan/dcgan.ipynb en el repositorio del libro.
El conjunto de datos Bricks
En primer lugar, necesitarás para descargar los datos de entrenamiento. Utilizaremos el conjunto de datos Images of LEGO Bricks que está disponible en Kaggle. Se trata de una colección renderizada por ordenador de 40.000 imágenes fotográficas de 50 ladrillos de juguete diferentes, tomadas desde múltiples ángulos. En la Figura 4-3 se muestran algunas imágenes de ejemplo de productos Brickki.
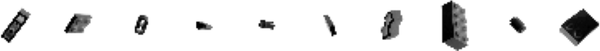
Figura 4-3. Ejemplos de imágenes del conjunto de datos Ladrillos
Puedes descargar el conjunto de datos ejecutando el script Kaggle dataset downloader en el repositorio del libro, como se muestra en el Ejemplo 4-1. Esto guardará las imágenes y los metadatos que las acompañan localmente en la carpeta /data.
Ejemplo 4-1. Descargar el conjunto de datos Ladrillos
bashscripts/download_kaggle_data.shjoosthazelzetlego-brick-images
Utilizamos la función Keras image_dataset_from_directory para crear un Conjunto de Datos TensorFlow apuntando al directorio donde se almacenan las imágenes, como se muestra en el Ejemplo 4-2. Esto nos permite leer lotes de imágenes en la memoria sólo cuando sea necesario (por ejemplo, durante el entrenamiento), de modo que podemos trabajar con grandes conjuntos de datos y no preocuparnos por tener que meter todo el conjunto de datos en la memoria. También redimensiona las imágenes a 64 × 64, interpolando entre los valores de los píxeles.
Ejemplo 4-2. Creación de un conjunto de datos TensorFlow a partir de archivos de imagen en un directorio
train_data=utils.image_dataset_from_directory("/app/data/lego-brick-images/dataset/",labels=None,color_mode="grayscale",image_size=(64,64),batch_size=128,shuffle=True,seed=42,interpolation="bilinear",)
Los datos originales se escalan en el intervalo [0, 255] para denotar la intensidad de los píxeles. Al entrenar las GAN, reescalamos los datos al intervalo [-1, 1] para poder utilizar la función de activación tanh en la capa final del generador, que tiende a proporcionar gradientes más fuertes que la función sigmoidea(Ejemplo 4-3).
Ejemplo 4-3. Preprocesamiento del conjunto de datos Ladrillos
defpreprocess(img):img=(tf.cast(img,"float32")-127.5)/127.5returnimgtrain=train_data.map(lambdax:preprocess(x))
Veamos ahora cómo construimos el discriminador.
El Discriminador
El objetivo del discriminador es predecir si una imagen es real o falsa. Se trata de un problema de clasificación supervisada de imágenes, por lo que podemos utilizar una arquitectura similar a las que trabajamos en el Capítulo 2: capas convolucionales apiladas, con un único nodo de salida.
La arquitectura completa del discriminador que vamos a construir se muestra en la Tabla 4-1.
| Capa (tipo) | Forma de salida | Param # |
|---|---|---|
Capa de entrada |
(Ninguno, 64, 64, 1) |
0 |
Conv2D |
(Ninguno, 32, 32, 64) |
1,024 |
LeakyReLU |
(Ninguno, 32, 32, 64) |
0 |
Abandono |
(Ninguno, 32, 32, 64) |
0 |
Conv2D |
(Ninguno, 16, 16, 128) |
131,072 |
BatchNormalization |
(Ninguno, 16, 16, 128) |
512 |
LeakyReLU |
(Ninguno, 16, 16, 128) |
0 |
Abandono |
(Ninguno, 16, 16, 128) |
0 |
Conv2D |
(Ninguno, 8, 8, 256) |
524,288 |
BatchNormalization |
(Ninguno, 8, 8, 256) |
1,024 |
LeakyReLU |
(Ninguno, 8, 8, 256) |
0 |
Abandono |
(Ninguno, 8, 8, 256) |
0 |
Conv2D |
(Ninguno, 4, 4, 512) |
2,097,152 |
BatchNormalization |
(Ninguno, 4, 4, 512) |
2,048 |
LeakyReLU |
(Ninguno, 4, 4, 512) |
0 |
Abandono |
(Ninguno, 4, 4, 512) |
0 |
Conv2D |
(Ninguno, 1, 1, 1) |
8,192 |
Aplanar |
(Ninguno, 1) |
0 |
Parámetros totales |
2,765,312 |
Parámetros entrenables |
2,763,520 |
Parámetros no entrenables |
1,792 |
El código Keras para construir el discriminador se proporciona en el Ejemplo 4-4.
Ejemplo 4-4. El discriminador
discriminator_input=layers.Input(shape=(64,64,1))x=layers.Conv2D(64,kernel_size=4,strides=2,padding="same",use_bias=False)(discriminator_input)x=layers.LeakyReLU(0.2)(x)x=layers.Dropout(0.3)(x)x=layers.Conv2D(128,kernel_size=4,strides=2,padding="same",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)x=layers.Dropout(0.3)(x)x=layers.Conv2D(256,kernel_size=4,strides=2,padding="same",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)x=layers.Dropout(0.3)(x)x=layers.Conv2D(512,kernel_size=4,strides=2,padding="same",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)x=layers.Dropout(0.3)(x)x=layers.Conv2D(1,kernel_size=4,strides=1,padding="valid",use_bias=False,activation='sigmoid')(x)discriminator_output=layers.Flatten()(x)discriminator=models.Model(discriminator_input,discriminator_output)
Define la capa
Inputdel discriminador (la imagen).
Apila las capas
Conv2Duna encima de otra, con las capasBatchNormalization,LeakyReLUde activación yDropoutintercaladas.
Aplana la última capa convolucional: en este punto, la forma del tensor es 1 × 1 × 1, por lo que no es necesaria una capa final
Dense.
El modelo Keras que define el discriminador: un modelo que toma una imagen de entrada y emite un único número entre 0 y 1.
Observa cómo utilizamos una zancada de 2 en algunas de las capas Conv2D para reducir la forma espacial del tensor a medida que pasa por la red (64 en la imagen original, luego 32, 16, 8, 4 y, finalmente, 1), al tiempo que aumentamos el número de canales (1 en la imagen de entrada en escala de grises, luego 64, 128, 256 y, finalmente, 512), antes de colapsar en una únicapredicción.
Utilizamos una activación sigmoidea en la capa final Conv2D para obtener un número entre 0 y 1.
El generador
Ahora vamos a construir el generador. La entrada del generador será un vector extraído de una distribución normal estándar multivariante. La salida es una imagen del mismo tamaño que una imagen de los datos de entrenamiento originales.
Esta descripción puede recordarte al descodificador de un autoencodificador variacional. De hecho, el generador de una GAN cumple exactamente la misma función que el descodificador de un VAE: convertir un vector del espacio latente en una imagen. El concepto de mapeo desde un espacio latente de vuelta al dominio original es muy común en el modelado generativo, ya que nos da la capacidad de manipular vectores en el espacio latente para cambiar características de alto nivel de las imágenes en el dominio original.
La arquitectura del generador que vamos a construir se muestra en la Tabla 4-2.
| Capa (tipo) | Forma de salida | Param # |
|---|---|---|
Capa de entrada |
(Ninguno, 100) |
0 |
Remodela |
(Ninguno, 1, 1, 100) |
0 |
Conv2DTransponer |
(Ninguno, 4, 4, 512) |
819,200 |
BatchNormalization |
(Ninguno, 4, 4, 512) |
2,048 |
ReLU |
(Ninguno, 4, 4, 512) |
0 |
Conv2DTransponer |
(Ninguno, 8, 8, 256) |
2,097,152 |
BatchNormalization |
(Ninguno, 8, 8, 256) |
1,024 |
ReLU |
(Ninguno, 8, 8, 256) |
0 |
Conv2DTransponer |
(Ninguno, 16, 16, 128) |
524,288 |
BatchNormalization |
(Ninguno, 16, 16, 128) |
512 |
ReLU |
(Ninguno, 16, 16, 128) |
0 |
Conv2DTransponer |
(Ninguno, 32, 32, 64) |
131,072 |
BatchNormalization |
(Ninguno, 32, 32, 64) |
256 |
ReLU |
(Ninguno, 32, 32, 64) |
0 |
Conv2DTransponer |
(Ninguno, 64, 64, 1) |
1,024 |
Parámetros totales |
3,576,576 |
Parámetros entrenables |
3,574,656 |
Parámetros no entrenables |
1,920 |
El código para construir el generador se muestra en el Ejemplo 4-5.
Ejemplo 4-5. El generador
generator_input=layers.Input(shape=(100,))x=layers.Reshape((1,1,100))(generator_input)x=layers.Conv2DTranspose(512,kernel_size=4,strides=1,padding="valid",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)x=layers.Conv2DTranspose(256,kernel_size=4,strides=2,padding="same",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)x=layers.Conv2DTranspose(128,kernel_size=4,strides=2,padding="same",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)x=layers.Conv2DTranspose(64,kernel_size=4,strides=2,padding="same",use_bias=False)(x)x=layers.BatchNormalization(momentum=0.9)(x)x=layers.LeakyReLU(0.2)(x)generator_output=layers.Conv2DTranspose(1,kernel_size=4,strides=2,padding="same",use_bias=False,activation='tanh')(x)generator=models.Model(generator_input,generator_output)
Define la capa
Inputdel generador: un vector de longitud 100.
Utilizamos una capa
Reshapepara obtener un tensor de 1 × 1 × 100, de modo que podamos empezar a aplicar operaciones de transposición convolucional.
Pasamos esto a través de cuatro capas
Conv2DTranspose, con las capasBatchNormalizationyLeakyReLUintercaladas.
La capa final
Conv2DTransposeutiliza una función de activación tanh para transformar la salida al intervalo [-1, 1], para que coincida con el dominio de la imagen original.
El modelo Keras que define el generador: un modelo que acepta un vector de longitud 100 y produce un tensor de forma
[64, 64, 1].
Observa cómo utilizamos una zancada de 2 en algunas de las capas de Conv2DTranspose para aumentar la forma espacial del tensor a medida que pasa por la red (1 en el vector original, luego 4, 8, 16, 32 y, finalmente, 64), al tiempo que disminuimos el número de canales (512, luego 256, 128, 64 y, finalmente, 1 para que coincida con la salida en escala de grises).
Formación del DCGAN
Como hemos visto en, las arquitecturas del generador y el discriminador en un DCGAN son muy sencillas y no difieren tanto de los modelos VAE que vimos en el Capítulo 3. La clave para entender los GAN reside en comprender el proceso de entrenamiento del generador y el discriminador.
Podemos entrenar el discriminador creando un conjunto de entrenamiento en el que algunas de las imágenes sean observaciones reales del conjunto de entrenamiento y otras sean salidas falsas del generador. Entonces lo tratamos como un problema de aprendizaje supervisado, en el que las etiquetas son 1 para las imágenes reales y 0 para las imágenes falsas, con la entropía cruzada binaria comofunción de pérdida.
¿Cómo debemos entrenar al generador? Tenemos que encontrar una forma de puntuar cada imagen generada para que pueda optimizar hacia las imágenes de alta puntuación. Por suerte, ¡tenemos un discriminador que hace exactamente eso! Podemos generar un lote de imágenes y pasarlas por el discriminador para obtener una puntuación para cada imagen. La función de pérdida del generador es simplemente la entropía cruzada binaria entre estas probabilidades y un vector de unos, porque queremos entrenar al generador para que produzca imágenes que el discriminador considere reales.
Fundamentalmente, debemos alternar el entrenamiento de estas dos redes, asegurándonos de que sólo actualizamos los pesos de una red cada vez. Por ejemplo, durante el proceso de entrenamiento del generador, sólo se actualizan los pesos del generador. Si permitimos que cambien también los pesos del discriminador, éste sólo se ajustaría para tener más probabilidades de predecir que las imágenes generadas son reales, lo que no es el resultado deseado. Queremos que las imágenes generadas se predigan cercanas a 1 (reales) porque el generador es fuerte, no porque el discriminador sea débil.
En la Figura 4-5 se muestra un diagrama del proceso de entrenamiento del discriminador y el generador.
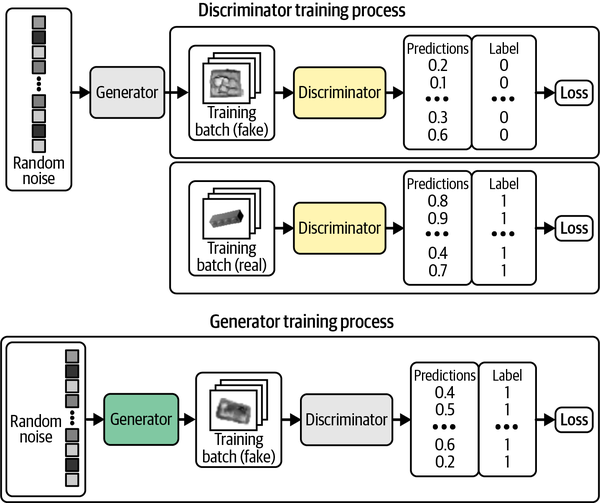
Figura 4-5. Entrenando el DCGAN -los recuadros grises indican que los pesos están congelados durante el entrenamiento
Keras nos proporciona la posibilidad de crear una función train_step personalizada para implementar esta lógica. El Ejemplo 4-7 muestra la clase modelo DCGAN completa.
Ejemplo 4-7. Compilar el DCGAN
classDCGAN(models.Model):def__init__(self,discriminator,generator,latent_dim):super(DCGAN,self).__init__()self.discriminator=discriminatorself.generator=generatorself.latent_dim=latent_dimdefcompile(self,d_optimizer,g_optimizer):super(DCGAN,self).compile()self.loss_fn=losses.BinaryCrossentropy()self.d_optimizer=d_optimizerself.g_optimizer=g_optimizerself.d_loss_metric=metrics.Mean(name="d_loss")self.g_loss_metric=metrics.Mean(name="g_loss")@propertydefmetrics(self):return[self.d_loss_metric,self.g_loss_metric]deftrain_step(self,real_images):batch_size=tf.shape(real_images)[0]random_latent_vectors=tf.random.normal(shape=(batch_size,self.latent_dim))withtf.GradientTape()asgen_tape,tf.GradientTape()asdisc_tape:generated_images=self.generator(random_latent_vectors,training=True)real_predictions=self.discriminator(real_images,training=True)fake_predictions=self.discriminator(generated_images,training=True)real_labels=tf.ones_like(real_predictions)real_noisy_labels=real_labels+0.1*tf.random.uniform(tf.shape(real_predictions))fake_labels=tf.zeros_like(fake_predictions)fake_noisy_labels=fake_labels-0.1*tf.random.uniform(tf.shape(fake_predictions))d_real_loss=self.loss_fn(real_noisy_labels,real_predictions)d_fake_loss=self.loss_fn(fake_noisy_labels,fake_predictions)d_loss=(d_real_loss+d_fake_loss)/2.0g_loss=self.loss_fn(real_labels,fake_predictions)gradients_of_discriminator=disc_tape.gradient(d_loss,self.discriminator.trainable_variables)gradients_of_generator=gen_tape.gradient(g_loss,self.generator.trainable_variables)self.d_optimizer.apply_gradients(zip(gradients_of_discriminator,discriminator.trainable_variables))self.g_optimizer.apply_gradients(zip(gradients_of_generator,generator.trainable_variables))self.d_loss_metric.update_state(d_loss)self.g_loss_metric.update_state(g_loss)return{m.name:m.result()forminself.metrics}dcgan=DCGAN(discriminator=discriminator,generator=generator,latent_dim=100)dcgan.compile(d_optimizer=optimizers.Adam(learning_rate=0.0002,beta_1=0.5,beta_2=0.999),g_optimizer=optimizers.Adam(learning_rate=0.0002,beta_1=0.5,beta_2=0.999),)dcgan.fit(train,epochs=300)
La función de pérdida para el generador y el discriminador es
BinaryCrossentropy.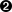
Para entrenar la red, primero muestrea un lote de vectores de una distribución normal estándar multivariante.

A continuación, pásalas por el generador para producir un lote de imágenes generadas.

Ahora pide al discriminador que prediga la veracidad del lote de imágenes reales...

...y el lote de imágenes generadas.

La pérdida del discriminador es la entropía cruzada binaria media de las imágenes reales (con etiqueta 1) y las imágenes falsas (con etiqueta 0).

La pérdida del generador es la entropía cruzada binaria entre las predicciones del discriminador para las imágenes generadas y una etiqueta de 1.

Actualiza los pesos del discriminador y del generador por separado.
El discriminador y el generador luchan constantemente por el dominio, lo que puede hacer que el proceso de entrenamiento del DCGAN sea inestable. Idealmente, el proceso de entrenamiento encontrará un equilibrio que permita al generador aprender información significativa del discriminador y la calidad de las imágenes empezará a mejorar. Después de suficientes épocas, el discriminador tiende a acabar dominando, como se muestra en la Figura 4-6, pero esto puede no ser un problema, ya que el generador puede haber aprendido ya a producir imágenes de calidad suficiente en este punto.
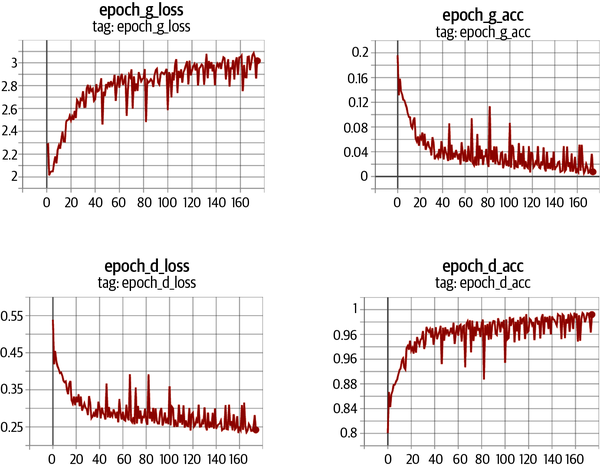
Figura 4-6. Pérdida y precisión del discriminador y el generador durante el entrenamiento
Añadir ruido a las etiquetas
Un truco útil de cuando se entrenan GANs es añadir una pequeña cantidad de ruido aleatorio a las etiquetas de entrenamiento. Esto ayuda a mejorar la estabilidad del proceso de entrenamiento y a suavizar las imágenes generadas. Este suavizado de etiquetas actúa como una forma de domesticar al discriminador, de modo que se le presente una tarea más desafiante y no domine al generador.
Análisis del DCGAN
Observando en las imágenes producidas por el generador en determinadas épocas del entrenamiento(Figura 4-7), queda claro que el generador es cada vez más experto en producir imágenes que podrían haberse extraído del conjunto de entrenamiento.

Figura 4-7. Salida del generador en determinadas épocas del entrenamiento
Resulta un tanto milagroso que una red neuronal sea capaz de convertir ruido aleatorio en algo con sentido. Conviene recordar que no hemos proporcionado al modelo ninguna característica adicional más allá de los píxeles en bruto, por lo que tiene que resolver por sí mismo conceptos de alto nivel, como dibujar sombras, cubos y círculos.
Otro requisito para que un modelo generativo tenga éxito es que no sólo reproduzca imágenes del conjunto de entrenamiento. Para comprobarlo, podemos encontrar la imagen del conjunto de entrenamiento que más se aproxime a un ejemplo generado concreto. Una buena medida para la distancia es la distancia L1, definida como
def compare_images(img1, img2):
return np.mean(np.abs(img1 - img2))
La Figura 4-8 muestra las observaciones más cercanas del conjunto de entrenamiento para una selección de imágenes generadas. Podemos ver que, aunque hay cierto grado de similitud entre las imágenes generadas y el conjunto de entrenamiento, no son idénticas. Esto demuestra que el generador ha comprendido estas características de alto nivel y puede generar ejemplos distintos de los que ya ha visto.

Figura 4-8. Coincidencias más cercanas de las imágenes generadas a partir del conjunto de entrenamiento
Formación en GAN: Trucos y consejos
Aunque las GAN de son un gran avance para el modelado generativo, también son notoriamente difíciles de entrenar. En esta sección exploraremos algunos de los problemas y retos más comunes que se plantean al entrenar las GAN, junto con posibles soluciones. En la siguiente sección, veremos algunos ajustes más fundamentales del marco GAN que podemos hacer para remediar muchos de estos problemas.
El discriminador supera al generador
Si el discriminador se vuelve demasiado fuerte, la señal de la función de pérdida se vuelve demasiado débil para impulsar ninguna mejora significativa en el generador. En el peor de los casos, el discriminador aprende perfectamente a separar las imágenes reales de las falsas y los gradientes desaparecen por completo, con lo que no hay entrenamiento alguno, como puede verse en la Figura 4-9.

Figura 4-9. Ejemplo de salida cuando el discriminador supera al generador
Si ves que la función de pérdida de tu discriminador se colapsa, tienes que encontrar formas de debilitar el discriminador. Prueba las siguientes sugerencias:
-
Aumenta el parámetro
ratede las capasDropoutdel discriminador para amortiguar la cantidad de información que fluye por la red. -
Reduce la velocidad de aprendizaje del discriminador.
-
Reduce el número de filtros convolucionales en el discriminador.
-
Añade ruido a las etiquetas al entrenar el discriminador.
-
Voltea las etiquetas de algunas imágenes al azar cuando entrenes el discriminador.
El generador supera al discriminador
Si el discriminador no es lo suficientemente potente, el generador encontrará la forma de engañarlo fácilmente con una pequeña muestra de imágenes casi idénticas. Esto se conoce como colapso del modo.
Por ejemplo, supongamos que entrenáramos al generador a lo largo de varios lotes sin actualizar el discriminador entre ellos. El generador se inclinaría a encontrar una única observación (también conocida como modo) que siempre engaña al discriminador y empezaría a mapear cada punto del espacio de entrada latente a esta imagen. Además, los gradientes de la función de pérdida se colapsarían hasta cerca de 0, por lo que no podría recuperarse de este estado.
Aunque intentáramos volver a entrenar al discriminador para que dejara de engañarse por este único punto, el generador simplemente encontraría otro modo que engañara al discriminador, puesto que ya se ha insensibilizado a su entrada y, por tanto, no tiene ningún incentivo para diversificar su salida.
El efecto del colapso modal puede verse en la Figura 4-10.

Figura 4-10. Ejemplo de colapso del modo cuando el generador supera al discriminador
Si ves que tu generador sufre un colapso de modo, puedes intentar reforzar el discriminador utilizando las sugerencias opuestas a las enumeradas en el apartado anterior. También puedes probar a reducir la tasa de aprendizaje de ambas redes y aumentar el tamaño del lote.
Pérdida no informativa
Puesto que el modelo de aprendizaje profundo se compila para minimizar la función de pérdida, sería natural pensar que cuanto menor sea la función de pérdida del generador, mejor será la calidad de las imágenes producidas. Sin embargo, como el generador sólo se evalúa con respecto al discriminador actual y éste mejora constantemente, no podemos comparar la función de pérdida evaluada en distintos puntos del proceso de entrenamiento. De hecho, en la Figura 4-6, la función de pérdida del generador aumenta con el tiempo, a pesar de que la calidad de las imágenes mejora claramente. Esta falta de correlación entre la pérdida del generador y la calidad de las imágenes dificulta a veces el monitoreo del entrenamiento GAN.
Hiperparámetros
Como hemos visto en, incluso con las GAN sencillas, hay que ajustar un gran número de hiperparámetros. Además de la arquitectura general del discriminador y del generador, hay que tener en cuenta los parámetros que rigen la normalización del lote, el abandono, la tasa de aprendizaje, las capas de activación, los filtros convolucionales, el tamaño del núcleo, el desplazamiento, el tamaño del lote y el tamaño del espacio latente. Las GAN son muy sensibles a cambios muy ligeros en todos estos parámetros, y encontrar un conjunto de parámetros que funcione suele ser un caso de ensayo y error educado, en lugar de seguir un conjunto establecido de directrices.
Por eso es importante comprender el funcionamiento interno de la GAN y saber interpretar la función de pérdida, para poder identificar los ajustes razonables de los hiperparámetros que podrían mejorar la estabilidad del modelo.
Afrontar los retos de la GAN
En los últimos años, varios avances clave han mejorado drásticamente la estabilidad general de los modelos GAN y han disminuido la probabilidad de algunos de los problemas enumerados anteriormente, como el colapso de modos.
En el resto de este capítulo examinaremos la GAN de Wasserstein con Penalización de Gradiente (WGAN-GP), que realiza varios ajustes clave en el marco de la GAN que hemos explorado hasta ahora para mejorar la estabilidad y la calidad del proceso de generación de imágenes.
GAN de Wasserstein con Penalización de Gradiente (WGAN-GP)
En esta sección construiremos un WGAN-GP para generar caras a partir del conjunto de datos CelebA que utilizamos en el Capítulo 3.
Ejecutar el código de este ejemplo
El código de este ejemplo se encuentra en el cuaderno Jupyter situado en notebooks/04_gan/02_wgan_gp/wgan_gp.ipynb en el repositorio del libro.
El código se ha adaptado del excelente tutorial WGAN-GP creado por Aakash Kumar Nain, disponible en el sitio web de Keras.
El Wasserstein GAN (WGAN), introducido en un artículo de 2017 por Arjovsky et al.,4 fue uno de los primeros grandes pasos hacia la estabilización del entrenamiento de GAN. Con unos pocos cambios, los autores pudieron demostrar cómo entrenar GAN que tienen las dos propiedades siguientes (citadas del artículo):
-
Una métrica de pérdida significativa que se correlacione con la convergencia del generador y la calidad de la muestra
-
Mejora de la estabilidad del proceso de optimización
En concreto, el artículo introduce la función de pérdida de Wasserstein tanto para el discriminador como para el generador. Utilizando esta función de pérdida en lugar de la entropía cruzada binaria se consigue una convergencia más estable de la GAN.
En esta sección definiremos la función de pérdida de Wasserstein y luego veremos qué otros cambios tenemos que hacer en la arquitectura del modelo y en el proceso de entrenamiento para incorporar nuestra nueva función de pérdida.
Puedes encontrar la clase modelo completa en el cuaderno Jupyter situado en chapter05/wgan-gp/faces/train.ipynb en el repositorio del libro.
Pérdida Wasserstein
En primer lugar, recordemos en la definición de pérdida de entropía cruzada binaria, la función que utilizamos actualmente para entrenar el discriminador y el generador del GAN(ecuación 4-1).
Ecuación 4-1. Pérdida de entropía cruzada binaria
Para entrenar el discriminador GAN calculamos la pérdida al comparar las predicciones de las imágenes reales a la respuesta y las predicciones para las imágenes generadas a la respuesta . Por tanto, para el discriminador GAN, la minimización de la función de pérdida puede escribirse como se muestra en la ecuación 4-2.
Ecuación 4-2. Minimización de la pérdida del discriminador GAN
Para entrenar al generador GAN calculamos la pérdida al comparar las predicciones de las imágenes generadas a la respuesta . Por tanto, para el generador GAN, la minimización de la función de pérdida puede escribirse como se muestra en la Ecuación 4-3.
Ecuación 4-3. Minimización de las pérdidas del generador GAN
Ahora comparemos esto con la función de pérdida de Wasserstein.
En primer lugar, la pérdida de Wasserstein requiere que utilicemos y = -1 como etiquetas, en lugar de 1 y 0. También eliminamos la activación sigmoidea de la capa final del discriminador, de modo que las predicciones ya no están limitadas a caer en el intervalo [0, 1], sino que ahora pueden ser cualquier número del intervalo (, ). Por esta razón, eldiscriminador de un WGAN se suele denominar crítico, que emite una puntuación en lugar de unaprobabilidad.
La función de pérdida de Wasserstein se define como sigue:
Formar al crítico del WGAN calculamos la pérdida al comparar predicciones de imágenes reales a la respuesta y las predicciones para las imágenes generadas a la respuesta = -1. Por tanto, para el crítico WGAN, la minimización de la función de pérdida puede escribirse como sigue
En otras palabras, el crítico WGAN intenta maximizar la diferencia entre sus predicciones para las imágenes reales y las imágenes generadas.
Para entrenar al generador de WGAN, calculamos la pérdida al comparar las predicciones de las imágenes generadas a la respuesta . Por lo tanto, para el generador WGAN, la minimización de la función de pérdida puede escribirse como sigue:
En otras palabras, el generador de WGAN intenta producir imágenes que el crítico puntúe lo más alto posible (es decir, se engaña al crítico haciéndole creer que son reales).
La Restricción Lipschitz
Puede que te sorprenda que ahora permitamos que el crítico muestre cualquier número del rango (, ), en lugar de aplicar una función sigmoidea para restringir la salida al intervalo habitual [0, 1]. Por lo tanto, la pérdida de Wasserstein puede ser muy grande, lo que resulta inquietante, ya que, normalmente, en las redes neuronales hay que evitar los números grandes.
De hecho, los autores del artículo del WGAN demuestran que, para que la función de pérdida de Wasserstein funcione, también tenemos que imponer una restricción adicional al crítico. En concreto, se requiere que el crítico sea una función continua 1-Lipschitz. Desmenucemos esto para entender lo que significa con más detalle.
El crítico es una función que convierte una imagen en una predicción. Decimos que esta función es 1-Lipschitz si satisface la siguiente desigualdad para dos imágenes de entrada cualesquiera, y :
Toma, es la diferencia absoluta media por píxel entre dos imágenes y es la diferencia absoluta entre las predicciones del crítico. Esencialmente, exigimos un límite a la velocidad a la que pueden cambiar las predicciones del crítico entre dos imágenes (es decir, el valor absoluto del gradiente debe ser como máximo 1 en todas partes). Podemos ver esto aplicado a una función Lipschitz continua 1D en la Figura 4-11: enningún punto la recta entra en el cono, independientemente de dónde coloques el cono sobre la recta. En otras palabras, existe un límite en la velocidad a la que la recta puede subir o bajar en cualquier punto.
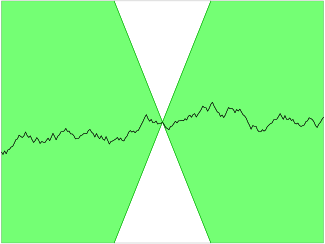
Figura 4-11. Una función continua Lipschitz (fuente: Wikipedia)
Consejo
Para los que quieran profundizar en los fundamentos matemáticos de por qué la pérdida de Wasserstein sólo funciona cuando se aplica esta restricción, Jonathan Hui ofrece una explicación excelente.
Aplicación de la restricción Lipschitz
En el documento original del WGAN, los autores muestran cómo es posible hacer cumplir la restricción de Lipschitz recortando los pesos del crítico para que se encuentren dentro de un pequeño intervalo,[-0,01, 0,01], después de cada tanda de entrenamiento.
Una de las críticas a este planteamiento es que la capacidad de aprendizaje del crítico disminuye mucho, ya que estamos recortando sus pesos. De hecho, incluso en el documento original del WGAN los autores escriben: "El recorte de pesos es una forma claramente terrible de hacer cumplir una restricción de Lipschitz". Un crítico fuerte es fundamental para el éxito de un WGAN, ya que sin gradientes precisos, el generador no puede aprender a adaptar sus pesos para producir mejores muestras.
Por eso, otros investigadores han buscado formas alternativas de hacer cumplir la restricción de Lipschitz y mejorar la capacidad del GAN para aprender características complejas. Uno de estos métodos es el GAN de Wasserstein con Penalización de Gradiente.
En el artículo que presenta esta variante5 los autores muestran cómo puede aplicarse directamente la restricción de Lipschitz incluyendo un término de penalización de gradiente en la función de pérdida para el crítico que penaliza al modelo si la norma de gradiente se desvía de 1. Esto da como resultado un proceso de entrenamiento mucho más estable.
En la siguiente sección, veremos cómo incorporar este término adicional a la función de pérdida de nuestro crítico.
La pérdida por penalización del gradiente
La Figura 4-12 es un diagrama del proceso de entrenamiento para el crítico de un WGAN-GP. Si lo comparamos con el proceso de entrenamiento del discriminador original de la Figura 4-5, podemos ver que la adición clave es la pérdida por penalización de gradiente incluida como parte de la función de pérdida global, junto con la pérdida de Wasserstein de las imágenes real y falsa.
Figura 4-12. El proceso de formación de críticos del WGAN-GP
La pérdida por penalización de gradiente mide la diferencia al cuadrado entre la norma del gradiente de las predicciones respecto a las imágenes de entrada y 1. El modelo se inclinará naturalmente por encontrar pesos que garanticen que el término de penalización de gradiente se minimiza, animando así al modelo a ajustarse a la restricción de Lipschitz.
Es intratable calcular este gradiente en todas partes durante el proceso de entrenamiento, así que en su lugar el WGAN-GP evalúa el gradiente sólo en un puñado de puntos. Para garantizar una mezcla equilibrada, utilizamos un conjunto de imágenes interpoladas que se encuentran en puntos elegidos al azar a lo largo de líneas que conectan el lote de imágenes reales con el lote de imágenes falsas por pares, como se muestra en la Figura 4-13.
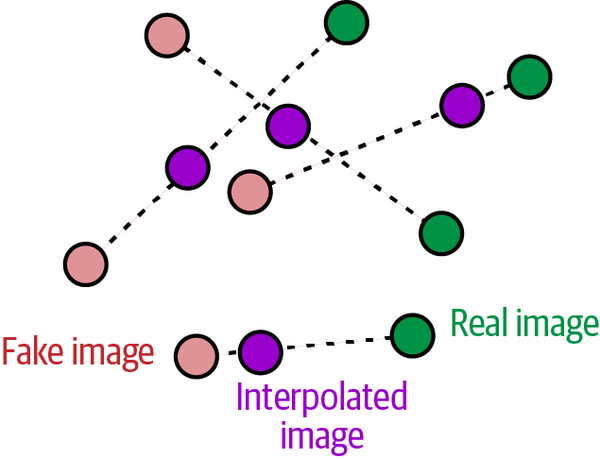
Figura 4-13. Interpolar entre imágenes
En el Ejemplo 4-8, mostramos cómo se calcula la penalización del gradiente en código.
Ejemplo 4-8. La función de pérdida por penalización de gradiente
defgradient_penalty(self,batch_size,real_images,fake_images):alpha=tf.random.normal([batch_size,1,1,1],0.0,1.0)diff=fake_images-real_imagesinterpolated=real_images+alpha*diffwithtf.GradientTape()asgp_tape:gp_tape.watch(interpolated)pred=self.critic(interpolated,training=True)grads=gp_tape.gradient(pred,[interpolated])[0]norm=tf.sqrt(tf.reduce_sum(tf.square(grads),axis=[1,2,3]))gp=tf.reduce_mean((norm-1.0)**2)returngp
Cada imagen del lote recibe un número aleatorio, entre 0 y 1, almacenado como vector
alpha.
Se calcula un conjunto de imágenes interpoladas.

Se pide al crítico que puntúe cada una de estas imágenes interpoladas.

El gradiente de las predicciones se calcula con respecto a las imágenes de entrada.

Se calcula la norma L2 de este vector.

La función devuelve la distancia media al cuadrado entre la norma L2 y 1.
Formación del WGAN-GP
Una ventaja clave de utilizar la función de pérdida de Wasserstein es que ya no tenemos que preocuparnos de equilibrar el entrenamiento del crítico y del generador; de hecho, cuando se utiliza la pérdida de Wasserstein, el crítico debe entrenarse hasta la convergencia antes de actualizar el generador, para garantizar que los gradientes de la actualización del generador sean precisos. Esto contrasta con una GAN estándar, en la que es importante no dejar que el discriminador sea demasiado fuerte.
Por lo tanto, con las GAN de Wasserstein, podemos simplemente entrenar al crítico varias veces entre las actualizaciones del generador, para asegurarnos de que está cerca de la convergencia. Una proporción típica utilizada es de tres a cinco actualizaciones del crítico por cada actualización del generador.
Ya hemos introducido los dos conceptos clave del WGAN-GP: la pérdida de Wasserstein y el término de penalización del gradiente que se incluye en la función de pérdida crítica. El paso de entrenamiento del modelo WGAN que incorpora todas estas ideas se muestra en el Ejemplo 4-9.
Ejemplo 4-9. Entrenamiento del WGAN-GP
deftrain_step(self,real_images):batch_size=tf.shape(real_images)[0]foriinrange(3):random_latent_vectors=tf.random.normal(shape=(batch_size,self.latent_dim))withtf.GradientTape()astape:fake_images=self.generator(random_latent_vectors,training=True)fake_predictions=self.critic(fake_images,training=True)real_predictions=self.critic(real_images,training=True)c_wass_loss=tf.reduce_mean(fake_predictions)-tf.reduce_mean(real_predictions)c_gp=self.gradient_penalty(batch_size,real_images,fake_images)c_loss=c_wass_loss+c_gp*self.gp_weightc_gradient=tape.gradient(c_loss,self.critic.trainable_variables)self.c_optimizer.apply_gradients(zip(c_gradient,self.critic.trainable_variables))random_latent_vectors=tf.random.normal(shape=(batch_size,self.latent_dim))withtf.GradientTape()astape:fake_images=self.generator(random_latent_vectors,training=True)fake_predictions=self.critic(fake_images,training=True)g_loss=-tf.reduce_mean(fake_predictions)gen_gradient=tape.gradient(g_loss,self.generator.trainable_variables)self.g_optimizer.apply_gradients(zip(gen_gradient,self.generator.trainable_variables))self.c_loss_metric.update_state(c_loss)self.c_wass_loss_metric.update_state(c_wass_loss)self.c_gp_metric.update_state(c_gp)self.g_loss_metric.update_state(g_loss)return{m.name:m.result()forminself.metrics}
Realiza tres actualizaciones críticas.
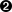
Calcula la pérdida de Wasserstein para el crítico: la diferencia entre la predicción media de las imágenes falsas y las imágenes reales.

Calcula el término de penalización del gradiente (ver Ejemplo 4-8).

La función de pérdida crítica es una suma ponderada de la pérdida de Wasserstein y la penalización del gradiente.

Actualiza los pesos del crítico.

Calcula la pérdida de Wasserstein del generador.

Actualiza los pesos del generador.
Normalización por lotes en un WGAN-GP
Una última consideración que debemos tener en cuenta antes de entrenar un WGAN-GP es que no se debe utilizar la normalización por lotes en el crítico. Esto se debe a que la normalización por lotes crea correlación entre las imágenes del mismo lote, lo que hace que la pérdida por penalización de gradiente sea menos eficaz. Los experimentos han demostrado que los WGAN-GP pueden producir excelentes resultados incluso sin la normalización por lotes en el crítico.
En ya hemos cubierto todas las diferencias clave entre una GAN estándar y una WGAN-GP. Recapitulando:
-
Un WGAN-GP utiliza la pérdida de Wasserstein.
-
El WGAN-GP se entrena utilizando etiquetas de 1 para lo real y -1 para lo falso.
-
No hay activación sigmoidea en la capa final del crítico.
-
Incluye un término de penalización por gradiente en la función de pérdida del crítico.
-
Entrena al crítico varias veces para cada actualización del generador.
-
No hay capas de normalización por lotes en el crítico.
Análisis del WGAN-GP
Veamos en algunas salidas de ejemplo del generador, tras 25 épocas de entrenamiento(Figura 4-14).

Figura 4-14. Ejemplos de caras WGAN-GP
El modelo ha aprendido los atributos significativos de alto nivel de un rostro, y no hay signos de colapso del modo.
También podemos ver cómo evolucionan las funciones de pérdida del modelo a lo largo del tiempo(Figura 4-15): las funciones de pérdida tanto del crítico como del generador son muy estables y convergentes.
Si comparamos el resultado del WGAN-GP con el resultado del VAE del capítulo anterior, podemos ver que las imágenes del GAN son, en general, más nítidas, especialmente la definición entre el pelo y el fondo. Esto es cierto en general; las VAE tienden a producir imágenes más suaves que difuminan los límites de color, mientras que las GAN son conocidas por producir imágenes más nítidas y bien definidas.
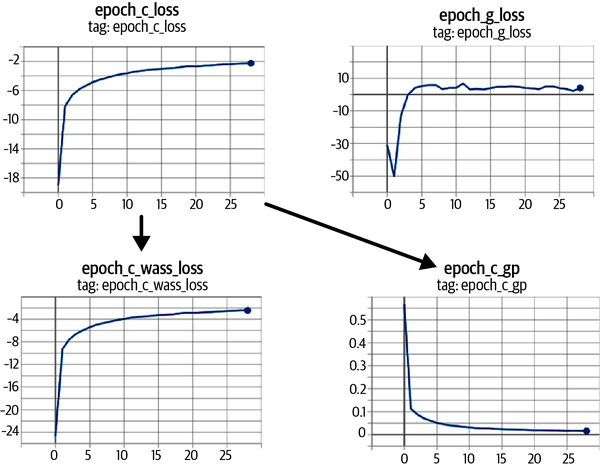
Figura 4-15. Curvas de pérdida WGAN-GP: la pérdida crítica (epoch_c_loss) se descompone en la pérdida Wasserstein (epoch_c_wass) y la pérdida por penalización de gradiente (epoch_c_gp)
También es cierto que las GAN suelen ser más difíciles de entrenar que las VAE y tardan más en alcanzar una calidad satisfactoria. Sin embargo, hoy en día muchos modelos generativos de última generación se basan en GAN, ya que las recompensas de entrenar GAN a gran escala en GPU durante un período de tiempo más largo son significativas.
GAN condicional (CGAN)
Así que hasta ahora en este capítulo, hemos construido GANs capaces de generar imágenes realistas a partir de un conjunto de entrenamiento dado. Sin embargo, no hemos podido controlar el tipo de imagen que queremos generar: por ejemplo, un rostro masculino o femenino, o un ladrillo grande o pequeño. Podemos muestrear un punto aleatorio del espacio latente, pero no tenemos la capacidad de comprender fácilmente qué tipo de imagen se producirá dada la elección de la variable latente.
En , la parte final de este capítulo, centraremos nuestra atención en la construcción de una GAN en la que podamos controlar la salida: la llamada GAN condicional. Esta idea, introducida por primera vez en "Conditional Generative Adversarial Nets" de Mirza y Osindero en 20146 es una extensión relativamente sencilla de la arquitectura GAN.
Ejecutar el código de este ejemplo
El código de este ejemplo se encuentra en el cuaderno Jupyter situado en notebooks/04_gan/03_cgan/cgan.ipynb enel repositorio del libro.
El código se ha adaptado del excelente tutorial CGAN creado por Sayak Paul, disponible en el sitio web de Keras.
Arquitectura del CGAN
En este ejemplo, condicionaremos nuestro CGAN al atributo de pelo rubio del conjunto de datos de caras. Es decir, podremos especificar explícitamente si queremos generar una imagen con pelo rubio o no. Esta etiqueta se proporciona como parte del conjunto de datos CelebA.
La arquitectura CGAN de alto nivel se muestra en la Figura 4-16.
Figura 4-16. Entradas y salidas del generador y del crítico en un CGAN
La diferencia clave entre un GAN estándar y un CGAN es que en un CGAN pasamos información extra al generador y al crítico relativa a la etiqueta. En el generador, simplemente se añade a la muestra del espacio latente como un vector codificado de un solo golpe. En el crítico, añadimos la información de la etiqueta como canales adicionales a la imagen RGB. Lo hacemos repitiendo el vector codificado de un solo golpe para que tenga la misma forma que las imágenes de entrada.
Los CGAN funcionan porque ahora el crítico tiene acceso a información adicional sobre el contenido de la imagen, por lo que el generador debe asegurarse de que su resultado coincide con la etiqueta proporcionada, para seguir engañando al crítico. Si el generador produjera imágenes perfectas que no coincidieran con la etiqueta de la imagen, el crítico podría darse cuenta de que son falsas simplemente porque las imágenes y las etiquetas no coinciden.
Consejo
En nuestro ejemplo, nuestra etiqueta codificada de un solo golpe tendrá una longitud de 2, porque hay dos clases (Rubia y No rubia). Sin embargo, puedes tener tantas etiquetas como quieras: por ejemplo, podrías entrenar un CGAN en el conjunto de datos Moda-MNIST para que diera como resultado uno de los 10 artículos de moda diferentes, incorporando un vector de etiquetas codificadas de un solo golpe de longitud 10 en la entrada del generador y 10 canales adicionales de etiquetas codificadas de un solo golpe en la entrada del crítico.
El único cambio que tenemos que hacer en la arquitectura es concatenar la información de la etiqueta a las entradas existentes del generador y el crítico, como se muestra en el Ejemplo 4-10.
Ejemplo 4-10. Capas de entrada en el CGAN
critic_input=layers.Input(shape=(64,64,3))label_input=layers.Input(shape=(64,64,2))x=layers.Concatenate(axis=-1)([critic_input,label_input])...generator_input=layers.Input(shape=(32,))label_input=layers.Input(shape=(2,))x=layers.Concatenate(axis=-1)([generator_input,label_input])x=layers.Reshape((1,1,34))(x)...
Formación del CGAN
En también debemos hacer algunos cambios en el train_step del CGAN para adaptarlo a los nuevos formatos de entrada del generador y del crítico, como se muestra en el Ejemplo 4-11.
Ejemplo 4-11. La página train_step del CGAN
deftrain_step(self,data):real_images,one_hot_labels=dataimage_one_hot_labels=one_hot_labels[:,None,None,:]image_one_hot_labels=tf.repeat(image_one_hot_labels,repeats=64,axis=1)image_one_hot_labels=tf.repeat(image_one_hot_labels,repeats=64,axis=2)batch_size=tf.shape(real_images)[0]foriinrange(self.critic_steps):random_latent_vectors=tf.random.normal(shape=(batch_size,self.latent_dim))withtf.GradientTape()astape:fake_images=self.generator([random_latent_vectors,one_hot_labels],training=True)fake_predictions=self.critic([fake_images,image_one_hot_labels],training=True)real_predictions=self.critic([real_images,image_one_hot_labels],training=True)c_wass_loss=tf.reduce_mean(fake_predictions)-tf.reduce_mean(real_predictions)c_gp=self.gradient_penalty(batch_size,real_images,fake_images,image_one_hot_labels)c_loss=c_wass_loss+c_gp*self.gp_weightc_gradient=tape.gradient(c_loss,self.critic.trainable_variables)self.c_optimizer.apply_gradients(zip(c_gradient,self.critic.trainable_variables))random_latent_vectors=tf.random.normal(shape=(batch_size,self.latent_dim))withtf.GradientTape()astape:fake_images=self.generator([random_latent_vectors,one_hot_labels],training=True)fake_predictions=self.critic([fake_images,image_one_hot_labels],training=True)g_loss=-tf.reduce_mean(fake_predictions)gen_gradient=tape.gradient(g_loss,self.generator.trainable_variables)self.g_optimizer.apply_gradients(zip(gen_gradient,self.generator.trainable_variables))
Las imágenes y las etiquetas se descomprimen a partir de los datos de entrada.
Los vectores codificados a un disparo se expanden a imágenes codificadas a un disparo que tienen el mismo tamaño espacial que las imágenes de entrada (64 × 64).

El generador se alimenta ahora con una lista de dos entradas: los vectores latentes aleatorios y los vectores de etiquetas codificados con un solo golpe.

El crítico se alimenta ahora con una lista de dos entradas: las imágenes falsas/reales y los canales de etiquetas codificados con un solo disparo.

La función de penalización del gradiente también requiere que pasen los canales de etiqueta codificados con un solo disparo, ya que utiliza el crítico.

Los cambios realizados en el paso de entrenamiento del crítico también se aplican al paso de entrenamiento del generador.
Análisis del CGAN
En podemos controlar la salida del CGAN pasando una determinada etiqueta codificada en un punto a la entrada del generador. Por ejemplo, para generar una cara con pelo no rubio, pasamos el vector [1, 0]. Para generar una cara con pelo rubio, pasamos el vector [0, 1].
El resultado del CGAN puede verse en la Figura 4-17. Aquí, mantenemos los vectores latentes aleatorios iguales en todos los ejemplos y cambiamos sólo el vector etiqueta condicional. Está claro que el CGAN ha aprendido a utilizar el vector etiqueta para controlar sólo el atributo color del pelo de las imágenes. Es impresionante que el resto de la imagen apenas cambie, lo que demuestra que las GAN son capaces de organizar los puntos en el espacio latente de forma que las características individuales puedan desacoplarse unas de otras.

Figura 4-17. Salida del CGAN cuando los vectores Rubio y No Rubio se añaden a la muestra latente
Consejo
Si hay etiquetas disponibles para tu conjunto de datos, suele ser una buena idea incluirlas como entrada a tu GAN, aunque no necesites necesariamente condicionar la salida generada a la etiqueta, ya que tienden a mejorar la calidad de las imágenes generadas. Puedes considerar las etiquetas como una extensión altamente informativa de la entrada de píxeles.
Resumen
En este capítulo hemos explorado tres modelos diferentes de redes generativas adversariales (GAN): la GAN convolucional profunda (DCGAN), la GAN de Wasserstein con Penalización de Gradiente (WGAN-GP), más sofisticada, y la GAN condicional (CGAN).
Todas las GAN se caracterizan por una arquitectura de generador frente a discriminador (o crítico), en la que el discriminador intenta "detectar la diferencia" entre imágenes reales y falsas y el generador pretende engañar al discriminador. Equilibrando el entrenamiento de estos dos adversarios, el generador GAN puede aprender gradualmente a producir observaciones similares a las del conjunto de entrenamiento.
Primero vimos cómo entrenar un DCGAN para generar imágenes de ladrillos de juguete. Fue capaz de aprender a representar de forma realista objetos 3D como imágenes, incluyendo representaciones precisas de sombra, forma y textura. También exploramos las distintas formas en que puede fallar el entrenamiento de GAN, incluyendo el colapso de modos y la desaparición de gradientes.
A continuación, exploramos cómo la función de pérdida de Wasserstein remedia muchos de estos problemas y hace que el entrenamiento de GAN sea más predecible y fiable. El WGAN-GP sitúa el requisito de 1-Lipschitz en el centro del proceso de entrenamiento, incluyendo un término en la función de pérdida para tirar de la norma de gradiente hacia 1.
Aplicamos el GAN-GP al problema de la generación de caras y vimos cómo, simplemente eligiendo puntos de una distribución normal estándar, podemos generar caras nuevas. Este proceso de muestreo es muy similar al de una VAE, aunque las caras producidas por una GAN son bastante diferentes: a menudo más nítidas, con mayor distinción entre las distintas partes de la imagen.
Por último, construimos un CGAN que nos permitía controlar el tipo de imagen que se genera. Esto funciona pasando la etiqueta como entrada al crítico y al generador, dando así a la red la información adicional que necesita para condicionar la salida generada a una etiqueta dada.
En general, hemos visto cómo el marco GAN es extremadamente flexible y capaz de adaptarse a muchos dominios de problemas interesantes. En particular, las GAN han impulsado avances significativos en el campo de la generación de imágenes, con muchas extensiones interesantes del marco subyacente, como veremos en el Capítulo 10.
En el próximo capítulo, exploraremos una familia diferente de modelos generativos que son ideales para modelar datos secuenciales: los modelos autorregresivos.
1 Ian J. Goodfellow y otros, "Generative Adversarial Nets", 10 de junio de 2014, https://arxiv.org/abs/1406.2661
2 Alec Radford y otros, "Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks", 7 de enero de 2016, https://arxiv.org/abs/1511.06434.
3 Augustus Odena et al., "Deconvolution and Checkerboard Artifacts", 17 de octubre de 2016, https://distill.pub/2016/deconv-checkerboard.
4 Martin Arjovsky et al., "Wasserstein GAN", 26 de enero de 2017, https://arxiv.org/abs/1701.07875.
5 Ishaan Gulrajani et al., "Improved Training of Wasserstein GANs", 31 de marzo de 2017, https://arxiv.org/abs/1704.00028.
6 Mehdi Mirza y Simon Osindero, "Redes Adversariales Generativas Condicionales", 6 de noviembre de 2014, https://arxiv.org/abs/1411.1784.
Get Aprendizaje profundo generativo, 2ª edición now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

