Análisis Práctico de Series Temporales

Capítulo 4. Simulación de datos de series temporales

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

Hasta ahora hemos hablado de dónde encontrar datos de series temporales y cómo procesarlos. Ahora veremos cómo crear datos de series temporales mediante simulación.

Nuestro debate se divide en tres partes. En primer lugar, comparamos las simulaciones de datos de series temporales con otros tipos de simulaciones de datos, señalando qué nuevas áreas de especial preocupación surgen cuando tenemos que tener en cuenta el paso del tiempo. En segundo lugar, examinamos algunas simulaciones basadas en códigos. En tercer lugar, analizamos algunas tendencias generales en la simulación de series temporales.

La mayor parte de este capítulo se centrará en ejemplos de código específicos para generar diversos tipos de datos de series temporales. Repasaremos los siguientes ejemplos:

• Simulamos el comportamiento de apertura y donación de correos electrónicos de los miembros de una organización sin ánimo de lucro a lo largo de varios años. Esto está relacionado con los datos que examinamos en "Adaptación de una colección de datos de series temporales a partir de una colección de tablas".

• Simulamos sucesos en una flota de taxis de 1.000 vehículos con varias horas de inicio de turno y frecuencias de recogida de pasajeros dependientes de la hora del día en el transcurso de un solo día.

• Simulamos paso a paso la evolución del estado de un sólido magnético para una temperatura y un tamaño dados, utilizando las leyes físicas pertinentes.

Estos tres ejemplos de código se corresponden con tres clases de simulaciones de series temporales:

Simulaciones heurísticas

Decidimos cómo debe funcionar el mundo, nos aseguramos de que tenga sentido y lo codificamos, regla a regla.

Simulaciones de eventos discretos

Construimos actores individuales con determinadas reglas en nuestro universo y luego ejecutamos esos actores para ver cómo evoluciona el universo con el tiempo.

Simulaciones basadas en la física

Aplicamos leyes físicas para ver cómo evoluciona un sistema a lo largo del tiempo.

La simulación de series temporales puede ser un valioso ejercicio analítico, que también demostraremos en capítulos posteriores en relación con modelos concretos.

¿Qué tiene de especial simular series temporales?

La simulación de datos es un área de la ciencia de datos que rara vez se enseña, pero que es una habilidad especialmente útil para los datos de series temporales. Esto se debe a uno de los inconvenientes de disponer de datos temporales: no hay dos puntos de datos de la misma serie temporal que sean exactamente comparables, ya que suceden en momentos distintos. Si queremos pensar en lo que podría haber ocurrido en un momento dado, nos adentramos en el mundo de la simulación.

Las simulaciones pueden ser simples o complejas. En el lado más simple, encontrarás datos sintéticos en cualquier libro de texto de estadística sobre series temporales, como en forma de paseo aleatorio. Suelen generarse como sumas acumulativas de un proceso aleatorio (como rnorm de R) o mediante una función periódica (como una curva senoidal). En el lado más complejo, muchos científicos e ingenieros hacen carrera simulando series temporales. Las simulaciones de series temporales siguen siendo un área activa de investigación -y muy exigente desde el punto de vista computacional- en muchos campos, entre ellos:

• Meteorología

• Finanzas

• Epidemiología

• Química cuántica

• Física del plasma

En algunos de estos casos, las reglas fundamentales del comportamiento se comprenden bien, pero aún así puede resultar difícil dar cuenta de todo lo que puede ocurrir debido a la complejidad de las ecuaciones (meteorología, química cuántica, física del plasma). En otros casos, nunca pueden conocerse todas las variables predictivas, y los expertos ni siquiera están seguros de que puedan hacerse predicciones perfectas debido a la naturaleza estocástica no lineal de los sistemas estudiados (finanzas, epidemiología).

Simulación frente a previsión

La simulación y la previsión son ejercicios similares. En ambos casos debes formular hipótesis sobre la dinámica y los parámetros subyacentes del sistema, y luego extrapolar a partir de esas hipótesis para generar puntos de datos.

No obstante, hay diferencias importantes que hay que tener en cuenta a la hora de aprender y desarrollar simulaciones en lugar de previsiones:

• Puede ser más fácil integrar observaciones cualitativas en una simulación que en una previsión.

• Las simulaciones se realizan a escala para que puedas ver muchos escenarios alternativos (miles o más), mientras que las previsiones deben elaborarse con más cuidado.

• En las simulaciones hay menos en juego que en las previsiones; no hay vidas ni recursos en juego, así que puedes ser más creativo y explorador en tus rondas iniciales de simulaciones. Por supuesto, al final querrás asegurarte de que puedes justificar cómo construyes tus simulaciones, igual que debes justificar tus previsiones.

Simulaciones en código

A continuación veremos tres ejemplos de codificación de simulaciones de series temporales. Mientras lees estos ejemplos, considera la amplia gama de datos que pueden simularse para producir una "serie temporal", y cómo el elemento temporal puede ser muy específico y dirigido por el ser humano, como los días de la semana y las horas del día de las donaciones, pero también puede ser muy inespecífico y esencialmente sin etiquetar, como el"enésimopaso" de una simulación física.

Los tres ejemplos de simulación que trataremos en esta sección son:

• Simular un conjunto de datos sintéticos para probar nuestras hipótesis sobre cómo los miembros de una organización pueden (o no) tener un comportamiento correlacionado entre la receptividad al correo electrónico de la organización y la disposición a hacer donativos. Éste es el ejemplo más DIY en el que codificamos relaciones y generamos datos tabulares con bucles for y similares.

• Simular el conjunto de datos sintéticos para explorar el comportamiento agregado en una flota de taxis, con horarios de turnos y frecuencia de pasajeros en función de la hora del día. En este conjunto de datos, hacemos uso de los atributos orientados a objetos de Python, así como de los generadores, que son bastante útiles cuando queremos poner en marcha un sistema y ver lo que hace.

• Simulando el proceso físico de un material magnético que orienta gradualmente sus elementos magnéticos individuales, que empiezan desordenados pero acaban uniéndose en un sistema bien ordenado. En este ejemplo, vemos cómo las leyes físicas pueden impulsar una simulación de series temporales e insertar un escalado temporal natural en un proceso.

Hacer el trabajo tú mismo

Cuando programes simulaciones, debes tener en cuenta las reglas lógicas que se aplican a tu sistema. Aquí veremos un ejemplo en el que el programador hace la mayor parte del trabajo de asegurarse de que los datos tienen sentido (por ejemplo, no especificando sucesos que ocurren en un orden ilógico).

Empezamos definiendo el universo de afiliados, es decir, cuántos afiliados tenemos y cuándo se afilió cada uno a la organización. También emparejamos a cada afiliado con un estado de afiliación:

## python
>>> ## membership status
>>> years        = ['2014', '2015', '2016', '2017', '2018']
>>> memberStatus = ['bronze', 'silver', 'gold', 'inactive']

>>> memberYears = np.random.choice(years, 1000, 
>>>               p = [0.1, 0.1, 0.15, 0.30, 0.35])
>>> memberStats = np.random.choice(memberStatus, 1000, 
>>>               p = [0.5, 0.3, 0.1, 0.1])

>>> yearJoined = pd.DataFrame({'yearJoined': memberYears,
>>>                          'memberStats': memberStats})

Observa que ya hay muchas reglas/suposiciones incorporadas a la simulación sólo con estas líneas de código. Imponemos probabilidades específicas de los años de afiliación de los miembros. También hacemos que el estatus del afiliado sea totalmente independiente del año en que se afilió. En el mundo real, es probable que ya podamos hacerlo mejor que esto, porque estas dos variables deberían tener alguna conexión, sobre todo si queremos incentivar a la gente para que siga siendo miembro.

Hacemos una tabla que indica cuándo los miembros abrieron los correos electrónicos cada semana. En este caso, definimos el comportamiento de nuestra organización: enviamos tres correos electrónicos a la semana. También definimos distintos patrones de comportamiento de los miembros con respecto al correo electrónico:

• No abrir nunca el correo electrónico

• Nivel constante de compromiso/tasa de apertura del correo

• Aumento o disminución del nivel de compromiso

Podemos imaginar formas de hacerlo más complejo y matizado en función de las observaciones anecdóticas de los veteranos o de las hipótesis novedosas que tengamos sobre los procesos inobservables que afectan a los datos:

## python
>>> NUM_EMAILS_SENT_WEEKLY = 3

>>> ## we define several functions for different patterns 
>>> def never_opens(period_rng):
>>>   return []

>>> def constant_open_rate(period_rng):
>>>   n, p = NUM_EMAILS_SENT_WEEKLY, np.random.uniform(0, 1)
>>>   num_opened = np.random.binomial(n, p, len(period_rng))
>>>   return num_opened

>>> def increasing_open_rate(period_rng):
>>>   return open_rate_with_factor_change(period_rng, 
>>>                                        np.random.uniform(1.01, 
>>>                                                          1.30))
 
>>> def decreasing_open_rate(period_rng):
>>>   return open_rate_with_factor_change(period_rng, 
>>>                                        np.random.uniform(0.5,  
>>>                                                          0.99))

>>> def open_rate_with_factor_change(period_rng, fac):
>>>     if len(period_rng) < 1 :
>>>         return [] 
>>>     times = np.random.randint(0, len(period_rng), 
>>>                                int(0.1 * len(period_rng)))    
>>>     num_opened = np.zeros(len(period_rng))
>>>     for prd in range(0, len(period_rng), 2):  
>>>         try:
>>>             n, p = NUM_EMAILS_SENT_WEEKLY, np.random.uniform(0, 
>>>                                                              1)
>>>             num_opened[prd:(prd + 2)] = np.random.binomial(n, p, 
>>>                                                            2)
>>>             p = max(min(1, p * fac), 0)
>>>         except:
>>>             num_opened[prd] = np.random.binomial(n, p, 1)
>>>     for t in range(len(times)):
>>>         num_opened[times[t]] = 0    
>>>     return num_opened

Hemos definido funciones para simular cuatro tipos distintos de comportamiento:

Miembros que nunca abren los correos electrónicos que les enviamos

(never_opens())

Miembros que abren aproximadamente el mismo número de correos electrónicos cada semana

(constant_open_rate())

Miembros que abren un número decreciente de correos electrónicos cada semana

(decreasing_open_rate())

Miembros que abren un número creciente de correos electrónicos cada semana

(increasing_open_rate())

Nos aseguramos de que los que se comprometen o se desvinculan cada vez más con el tiempo se simulan de la misma manera con la función open_rate_with_factor_change() a través de las funciones increasing_open_rate() y decreasing_open_rate().

También tenemos que idear un sistema para modelar el comportamiento de la donación. No queremos ser totalmente ingenuos, o nuestra simulación no nos dará una idea de lo que debemos esperar. Es decir, queremos incorporar al modelo nuestras hipótesis actuales sobre el comportamiento de los afiliados y luego comprobar si las simulaciones basadas en esas hipótesis coinciden con lo que vemos en nuestros datos reales. En este caso, hacemos que el comportamiento de las donaciones esté relacionado de forma vaga, pero no determinista, con el número de correos electrónicos que ha abierto un afiliado:

## python
>>> ## donation behavior
>>> def produce_donations(period_rng, member_behavior, num_emails, 
>>>                       use_id, member_join_year):
>>>     donation_amounts = np.array([0, 25, 50, 75, 100, 250, 500, 
>>>                                  1000, 1500, 2000])
>>>     member_has = np.random.choice(donation_amounts)    
>>>     email_fraction = num_emails  / 
>>>                        (NUM_EMAILS_SENT_WEEKLY * len(period_rng))  
>>>     member_gives = member_has * email_fraction
>>>     member_gives_idx = np.where(member_gives 
>>>                                  >= donation_amounts)[0][-1]
>>>     member_gives_idx = max(min(member_gives_idx, 
>>>                                len(donation_amounts) - 2), 
>>>                            1)
>>>     num_times_gave = np.random.poisson(2) * 
>>>                        (2018 - member_join_year)
>>>     times = np.random.randint(0, len(period_rng), num_times_gave)
>>>     dons = pd.DataFrame({'member'   : [], 
>>>                          'amount'   : [],  
>>>                          'timestamp': []})
                                   
>>>     for n in range(num_times_gave):    
>>>         donation = donation_amounts[member_gives_idx 
>>>                      + np.random.binomial(1, .3)]
>>>         ts = str(period_rng[times[n]].start_time 
>>>                   + random_weekly_time_delta())
>>>         dons = dons.append(pd.DataFrame(
>>>                   {'member'   : [use_id],
>>>                    'amount'   : [donation],
>>>                    'timestamp': [ts]}))
>>>     
>>>     if dons.shape[0] > 0:
>>>         dons = dons[dons.amount != 0]
>>>         ## we don't report zero donation events as this would not
>>>         ## be recorded in a real world database   
>>>                                    
>>>     return dons

Aquí hemos tomado algunas medidas para asegurarnos de que el código produce un comportamiento realista:

• Hacemos que el número total de donaciones dependa del tiempo que alguien lleva afiliado.

• Generamos un estado de riqueza por miembro, incorporando una hipótesis sobre el comportamiento según la cual la cantidad de donativos está relacionada con una cantidad estable que una persona habría destinado a hacer donativos.

Como los comportamientos de nuestros miembros están ligados a una marca de tiempo concreta, tenemos que elegir en qué semanas hizo donativos cada miembro y también en qué momento de esa semana hizo el donativo. Escribimos una función de utilidad para elegir una hora aleatoria durante la semana:

## python
>>> def random_weekly_time_delta():
>>>     days_of_week = [d for d in range(7)]
>>>     hours_of_day = [h for h in range(11, 23)]
>>>     minute_of_hour = [m for m in range(60)]
>>>     second_of_minute = [s for s in range(60)]
>>>     return pd.Timedelta(str(np.random.choice(days_of_week))   
>>>                             + " days" ) +
>>>          pd.Timedelta(str(np.random.choice(hours_of_day))     
>>>                             + " hours" )  +
>>>          pd.Timedelta(str(np.random.choice(minute_of_hour))   
>>>                             + " minutes") +
>>>          pd.Timedelta(str(np.random.choice(second_of_minute)) 
>>>                             + " seconds")

Habrás observado que sólo extraemos la hora de la marca de tiempo del intervalo de 11 a 23 (hours_of_day = [h for h in range(11, 23)]). Estamos postulando un universo con personas en un rango muy limitado de zonas horarias o incluso en una sola zona horaria, ya que no permitimos horas fuera del rango dado. Aquí estamos incorporando más de nuestro modelo subyacente sobre cómo se comportan los usuarios.

Por tanto, esperamos ver un comportamiento unificado de nuestros usuarios, como si todos estuvieran en una o varias zonas horarias contiguas, y además postulamos que un comportamiento razonable de donación es que la gente done desde última hora de la mañana hasta última hora de la tarde, pero no durante la noche ni a primera hora al despertarse.

Por último, juntamos todos los componentes que acabamos de desarrollar para simular un cierto número de miembros y eventos asociados, de forma que se garantice que los eventos sólo se producen una vez que un miembro se ha afiliado y que los eventos de correo electrónico de un miembro tienen alguna relación (pero no una relación irrealmente pequeña) con sus eventos de donación:

## python
>>> behaviors        = [never_opens, 
>>>                    constant_open_rate,
>>>                    increasing_open_rate, 
>>>                    decreasing_open_rate]
>>> member_behaviors = np.random.choice(behaviors, 1000, 
>>>                                    [0.2, 0.5, 0.1, 0.2])
                                    
>>> rng = pd.period_range('2015-02-14', '2018-06-01', freq = 'W')
>>> emails = pd.DataFrame({'member'      : [], 
>>>                        'week'        : [], 
>>>                        'emailsOpened': []})
>>> donations = pd.DataFrame({'member'   : [], 
>>>                           'amount'   : [], 
>>>                           'timestamp': []})

>>> for idx in range(yearJoined.shape[0]):
>>>     ## randomly generate the date when a member would have joined
>>>     join_date = pd.Timestamp(yearJoined.iloc[idx].yearJoined) + 
>>>                   pd.Timedelta(str(np.random.randint(0, 365)) + 
>>>                                   ' days')
>>>     join_date = min(join_date, pd.Timestamp('2018-06-01'))
>>>  
>>>     ## member should not have action timestamps before joining
>>>     member_rng = rng[rng > join_date]    
>>>   
>>>     if len(member_rng) < 1:
>>>         continue
>>> 
>>>     info = member_behaviors[idx](member_rng)
>>>     if len(info) == len(member_rng):
>>>         emails = emails.append(pd.DataFrame(
>>>            {'member': [idx] * len(info), 
>>>             'week': [str(r.start_time) for r in member_rng], 
>>>             'emailsOpened': info}))
>>>         donations = donations.append(
>>>            produce_donations(member_rng, member_behaviors[idx], 
>>>                                 sum(info), idx, join_date.year))

A continuación, observamos el comportamiento temporal de los donativos para hacernos una idea de cómo podríamos probarlo para posteriores análisis o previsiones. Trazamos la suma total de donaciones recibidas en cada mes del conjunto de datos (ver Figura 4-1):

## python
>>> df.set_index(pd.to_datetime(df.timestamp), inplace = True)
>>> df.sort_index(inplace = True)
>>> df.groupby(pd.Grouper(freq='M')).amount.sum().plot()

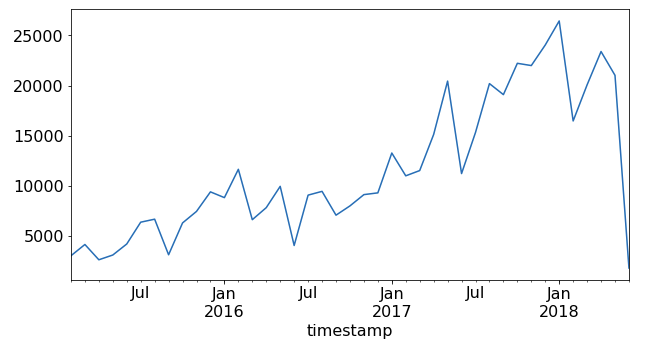
Figura 4-1. Suma total de donativos recibidos en cada mes del conjunto de datos.

Parece que el número de donaciones y de correos electrónicos abiertos aumentó con el tiempo desde 2015 hasta 2018. Esto no es sorprendente, ya que el número de miembros también aumentó con el tiempo, como indica la suma acumulada de miembros y el año en que se unieron. De hecho, un supuesto incorporado a nuestro modelo era que podíamos mantener a un miembro indefinidamente después de que se uniera. No hicimos ninguna provisión para la baja, salvo permitir que los miembros abrieran un número decreciente de correos electrónicos. Sin embargo, incluso en ese caso, dejamos abierta la posibilidad de que continuaran los donativos. Vemos este supuesto de afiliación indefinida (y el comportamiento correlativo de las donaciones) en la Figura 4-1. Probablemente deberíamos volver atrás y perfeccionar nuestro código, ya que la afiliación y la donación indefinidas no son un escenario realista.

No se trata de una simulación clásica de series temporales, por lo que puede parecer más bien un ejercicio de generación de datos tabulares. También lo es en absoluto, pero hemos tenido que ser conscientes de las series temporales:

• Tuvimos que tomar decisiones sobre en cuántas series temporales estaban nuestros usuarios.

• Tuvimos que tomar decisiones sobre qué tipo de tendencias modelaríamos a lo largo del tiempo:

  • En el caso del correo electrónico, decidimos tener tres tendencias: tasas de apertura del correo electrónico estables, en aumento y en descenso.

  • En el caso de los donativos, hicimos de los donativos un patrón de comportamiento estable relacionado con cuántos correos electrónicos había abierto el miembro a lo largo de su vida. Esto incluía una previsión, pero como estábamos generando datos, era una forma de decidir que la afinidad general de un miembro en la organización, que le llevaría a abrir más correos electrónicos, también aumentaría la frecuencia de los donativos.

• Tuvimos que tener cuidado para asegurarnos de que no había correos electrónicos abiertos o donaciones realizadas antes de que el miembro se uniera a la organización.

• Tuvimos que asegurarnos de que nuestros datos no fueran hacia el futuro, para que fuera más realista para los consumidores de los datos. Ten en cuenta que para una simulación no pasa nada si nuestros datos van al futuro.

Pero no es perfecto. El código presentado aquí es desgarbado y no produce un universo realista. Es más, como sólo el programador comprobó la lógica, podría haber pasado por alto casos de perímetro tales que los acontecimientos tuvieran lugar en un orden ilógico. Sería bueno establecer métricas y normas de validez externas antes de ejecutar la simulación, como protección contra tales errores.

Necesitamos un software que imponga un universo lógico y coherente. En la próxima sección veremos los generadores de Python como una opción mejor.

Construir un universo de simulación que funcione por sí mismo

A veces tienes un sistema concreto y quieres establecer las reglas de ese sistema y ver cómo se desenvuelve. Tal vez quieras prever qué utilizará un universo de miembros independientes que accedan a tu aplicación, o quieras intentar validar una teoría interna de toma de decisiones basada en un comportamiento externo supuesto. En estos casos, buscas ver cómo contribuyen los agentes individuales a tus métricas agregadas a lo largo del tiempo. Python es especialmente adecuado para este trabajo gracias a la disponibilidad de generadores. Cuando empiezas a construir software en lugar de quedarte puramente en el análisis, tiene sentido pasarse a Python aunque te sientas más cómodo en R.

Los generadores nos permiten crear una serie de actores independientes (¡o dependientes!) y darles cuerda para ver lo que hacen, sin demasiado código repetitivo para estar al tanto de todo.

En el siguiente ejemplo de código, exploramos una simulación de taxis.¹ Queremos imaginar cómo una flota de taxis, programados para comenzar sus turnos a horas diferentes, podría comportarse en conjunto. Para ello, queremos crear muchos taxis individuales, soltarlos en una ciberciudad y hacer que nos informen de sus actividades.

Una simulación de este tipo podría ser excepcionalmente complicada. A efectos de demostración, aceptamos que construiremos un mundo más sencillo de lo que imaginamos que es en realidad ("Todos los modelos son erróneos..."). Empezaremos intentando comprender qué es un generador Python.

Consideremos primero un método que escribí para recuperar un número de identificación de taxi:

## python
>>> import numpy as np

>>> def taxi_id_number(num_taxis):
>>>    arr = np.arange(num_taxis)
>>>    np.random.shuffle(arr)
>>>    for i in range(num_taxis):
>>>        yield arr[i]

Para quienes no estén familiarizados con los generadores, he aquí el código anterior en acción:

## python
>>> ids = taxi_id_number(10)
>>> print(next(ids))
>>> print(next(ids))
>>> print(next(ids))

que podría imprimirse:

7
2
5

Esto iterará hasta que haya emitido 10 números, momento en el que saldrá del bucle for que contiene el generador y emitirá una excepción StopIteration.

La página taxi_id_number() produce objetos de un solo uso, todos ellos independientes entre sí y que conservan su propio estado. Esto es una función generadora. Puedes pensar en los generadores como objetos diminutos que mantienen su propio pequeño conjunto de variables de estado, lo que resulta útil cuando quieres muchos objetos paralelos entre sí, cada uno cuidando sus propias variables.

En el caso de esta sencilla simulación de taxi, compartimentamos nuestros taxis en diferentes turnos, y también utilizamos un generador para indicar los turnos. Programamos más taxis en los turnos de mediodía que en los turnos de tarde o noche, estableciendo distintas probabilidades de empezar un turno a una hora determinada:

## python
>>> def shift_info():
>>>    start_times_and_freqs = [(0, 8), (8, 30), (16, 15)]
>>>    indices               = np.arange(len(start_times_and_freqs))
>>>    while True:
>>>        idx   = np.random.choice(indices, p = [0.25, 0.5, 0.25])
>>>        start = start_times_and_freqs[idx]
>>>        yield (start[0], start[0] + 7.5, start[1])

Presta atención a start_times_and_freqs. Éste es nuestro primer trozo de código que contribuirá a hacer de esto una simulación de series temporales. Estamos indicando que diferentes partes del día tienen diferentes probabilidades de tener un taxi asignado al turno. Además, las distintas horas del día tienen un número medio de viajes diferente.

Ahora crearemos un generador más complejo que utilizará los generadores anteriores para establecer parámetros de taxi individuales, así como para crear líneas temporales de taxi individuales:

## python
>>> def taxi_process(taxi_id_generator, shift_info_generator):
>>>    taxi_id = next(taxi_id_generator)
>>>    shift_start, shift_end, shift_mean_trips = 
>>>                                    next(shift_info_generator)
>>>    actual_trips = round(np.random.normal(loc   = shift_mean_trips, 
>>>                                          scale = 2))
>>>    average_trip_time = 6.5 / shift_mean_trips * 60 
>>>    # convert mean trip time to minutes
>>>    between_events_time = 1.0 / (shift_mean_trips - 1) * 60
>>>    # this is an efficient city where cabs are seldom unused
>>>    time = shift_start
>>>    yield TimePoint(taxi_id, 'start shift', time)    
>>>    deltaT = np.random.poisson(between_events_time) / 60
>>>    time += deltaT
>>>    for i in range(actual_trips):
>>>        yield TimePoint(taxi_id, 'pick up    ', time)
>>>        deltaT = np.random.poisson(average_trip_time) / 60
>>>        time += deltaT
>>>        yield TimePoint(taxi_id, 'drop off   ', time)
>>>        deltaT = np.random.poisson(between_events_time) / 60
>>>        time += deltaT        
>>>    deltaT = np.random.poisson(between_events_time) / 60
>>>    time += deltaT        
>>>    yield TimePoint(taxi_id, 'end shift  ', time)

Aquí el taxi accede a los generadores para determinar su número de identificación, las horas de inicio de turno y el número medio de viajes para su hora de inicio. A partir de ahí, emprende su propio viaje individual a medida que recorre un determinado número de viajes en su propia línea de tiempo y los emite al cliente que llama a next() en este generador. En efecto, este generador produce una serie temporal de puntos para un taxi individual.

El generador de taxis produce TimePoints, que se definen como sigue:

## python
>>> from dataclasses import dataclass

>>> @dataclass
>>> class TimePoint:
>>>    taxi_id:    int
>>>    name: str
>>>    time: float

>>>    def __lt__(self, other):
>>>        return self.time < other.time

Utilizamos el relativamente nuevo decorador dataclass para simplificar el código (esto requiere Python 3.7). Recomiendo a todos los científicos de datos que utilicen Python que se familiaricen con esta nueva adición a Python que facilita el uso de datos.

Métodos Dunder de Python

Los métodos dunder de Python, cuyos nombres empiezan y acaban con dos guiones bajos, son un conjunto de métodos incorporados a cada clase. Los métodos dunder se llaman automáticamente en el curso natural de utilización de un objeto dado. Existen implementaciones predefinidas que pueden ser anuladas cuando tú mismo las defines para tu clase. Hay muchas razones por las que puedes querer hacer esto, como en el caso del código anterior, en el que queremos que TimePoints se compare sólo en función de su tiempo y no en función de sus atributos taxi_id o name.

Dunder se originó como abreviatura de "doble bajo".

Además del inicializador generado automáticamente para TimePoint, sólo necesitamos otros dos métodos dunder, __lt__ (para comparar TimePoints) y __str__ (para imprimir TimePoints, no mostrados aquí). Necesitamos la comparación porque llevaremos todos los TimePoints producidos a una estructura de datos que los mantendrá en orden: una cola de prioridad. Una cola de prioridad es un tipo de datos abstracto en el que se pueden insertar objetos en cualquier orden, pero que emitirá objetos en un orden especificado en función de su prioridad.

Tipo de datos abstracto

Un tipo de datos abstracto es un modelo computacional definido por su comportamiento, que consiste en un conjunto enumerado de posibles acciones y datos de entrada y cuáles deben ser los resultados de dichas acciones para determinados conjuntos de datos.

Un tipo de datos abstracto comúnmente conocido es el tipo de datos FIFO (primero en entrar, primero en salir). Esto requiere que los objetos se emitan desde la estructura de datos en el mismo orden en que se introdujeron en ella. La forma en que el programador decida llevar esto a cabo es una cuestión de implementación y no una definición.

Tenemos una clase de simulación para ejecutar estos generadores de taxis y mantenerlos ensamblados. No se trata de un mero dataclass porque tiene bastante funcionalidad, incluso en el inicializador, para organizar las entradas en un conjunto sensato de información y procesamiento. Observa que la única funcionalidad de cara al público es la función run():

## python
>>> import queue

>>> class Simulator:
>>>    def __init__(self, num_taxis):
>>>        self._time_points = queue.PriorityQueue()
>>>        taxi_id_generator = taxi_id_number(num_taxis)
>>>        shift_info_generator = shift_info()
>>>        self._taxis = [taxi_process(taxi_id_generator, 
>>>                                    shift_info_generator) for 
>>>                                             i in range(num_taxis)]        
>>>        self._prepare_run()        

>>>    def _prepare_run(self):
>>>        for t in self._taxis:
>>>            while True:
>>>                try:
>>>                    e = next(t)
>>>                    self._time_points.put(e)
>>>                except:
>>>                    break        

>>>    def run(self):
>>>        sim_time = 0
>>>        while sim_time < 24:
>>>            if self._time_points.empty():
>>>                break
>>>            p = self._time_points.get()
>>>            sim_time = p.time
>>>            print(p)

Primero, creamos el número de generadores de taxis que necesitamos para representar el número correcto de taxis. A continuación, recorremos cada uno de estos taxis mientras aún tenga TimePoints y empujamos todos estos TimePoints a una cola de prioridad. La prioridad del objeto se determina para una clase personalizada como TimePoint mediante nuestra implementación de un TimePoint's __lt__, donde comparamos la hora de inicio. Así, a medida que los TimePoints son empujados a la cola de prioridad, ésta los preparará para ser emitidos en orden temporal.

Realizamos la simulación:

## python
>>> sim = Simulator(1000)
>>> sim.run()

Éste es el aspecto de la salida (tu salida será diferente, ya que no hemos establecido una semilla, y cada vez que ejecutes el código será diferente de la última iteración):

id: 0539 name: drop off    time: 23:58
id: 0318 name: pick up     time: 23:58
id: 0759 name: end shift   time: 23:58
id: 0977 name: pick up     time: 23:58
id: 0693 name: end shift   time: 23:59
id: 0085 name: end shift   time: 23:59
id: 0351 name: end shift   time: 23:59
id: 0036 name: end shift   time: 23:59
id: 0314 name: drop off    time: 23:59

Establecer una semilla al generar números aleatorios

Cuando escribes código que genera números aleatorios, puede que quieras asegurarte de que es reproducible (por ejemplo, si quisieras configurar pruebas unitarias para código que normalmente es aleatorio o si estuvieras intentando depurar y quisieras reducir las fuentes de variación para facilitar la depuración). Para asegurarte de que los números aleatorios salen en el mismo orden no aleatorio, estableces una semilla. Se trata de una operación habitual, por lo que existen guías sobre cómo establecer una semilla en cualquier lenguaje informático.

Hemos redondeado al minuto más próximo para simplificar la visualización, aunque disponemos de datos más precisos. La resolución temporal que utilicemos dependerá de nuestros objetivos:

• Si queremos hacer una exposición educativa para la gente de nuestra ciudad sobre cómo afecta la flota de taxis al tráfico, podríamos mostrar agregados horarios.

• Si somos una app de taxis y necesitamos entender la carga de nuestro servidor, probablemente querremos mirar los datos minuto a minuto o incluso datos de mayor resolución para pensar en el diseño y la capacidad de nuestra infraestructura.

Tomamos la decisión de informar sobre los taxis TimePoints tal y como "ocurren". Es decir, informamos del inicio de un trayecto en taxi ("recogida") sin la hora en que terminará el trayecto, aunque podríamos haberlo condensado fácilmente. Ésta es una forma de hacer que la serie temporal sea más realista, en el sentido de que probablemente habrías registrado los acontecimientos de esta forma en una retransmisión en directo.

Observa que, como en el caso anterior, nuestra simulación de series temporales aún no ha producido una serie temporal. Sin embargo, hemos producido un registro y podemos llegar a convertirlo en una serie temporal de varias maneras:

• Salida a un archivo CSV o a una base de datos de series temporales a medida que realizamos la simulación.

• Ejecuta algún tipo de modelo en línea conectado a nuestra simulación para aprender a desarrollar un canal de procesamiento de datos en tiempo real.

• Guarda el resultado en un archivo o en una base de datos y, a continuación, realiza más posprocesamientos para empaquetar los datos de una forma conveniente (pero posiblemente arriesgada con respecto al lookahead), como emparejar las horas de inicio y fin de un trayecto determinado para estudiar cómo se comporta la duración de un trayecto en taxi a distintas horas del día.

Simular estos datos tiene varias ventajas, además de poder probar hipótesis sobre la dinámica de un sistema de taxis. He aquí un par de situaciones en las que estos datos sintéticos de series temporales podrían ser útiles:.

• Probar los méritos de varios modelos de previsión en relación con la dinámica subyacente conocida de la simulación.

• Construye una canalización para los datos que esperas tener finalmente basándote en tus datos sintéticos mientras esperas los datos reales.

Serás un buen analista de series temporales si sabes utilizar los generadores y la programación orientada a objetos. Este ejemplo es sólo una muestra de cómo esos conocimientos pueden simplificarte la vida y mejorar la calidad de tu código.

Para simulaciones extensas, considera la modelización basada en agentes

La solución que codificamos aquí estaba bien, pero suponía una buena cantidad de boilerplate para garantizar que se respetaran las condiciones lógicas. Si una simulación de eventos discretos basada en las acciones de actores discretos fuera una fuente útil de datos de series temporales simuladas, deberías considerar un módulo orientado a la simulación. El módulo SimPy es una opción útil, con una API accesible y bastante flexibilidad para realizar el tipo de tareas de simulación que hemos tratado en esta sección.

Una simulación física

En otro tipo de escenario de simulación, puedes estar en plena posesión de las leyes de la física que definen un sistema. Sin embargo, no tiene por qué tratarse de la física en sí; también puede aplicarse a otras muchas áreas:

• Los investigadores cuantitativos en finanzas suelen formular hipótesis sobre las reglas "físicas" del mercado. También lo hacen los economistas, aunque a escalas de tiempo diferentes.

• Los psicólogos plantean las reglas "psicofísicas" de cómo toman decisiones los seres humanos. Éstas pueden utilizarse para generar reglas "físicas" sobre las respuestas humanas esperadas ante diversas opciones a lo largo del tiempo.

• Los biólogos investigan reglas sobre cómo se comporta un sistema a lo largo del tiempo en respuesta a diversos estímulos.

Un caso de conocer algunas reglas para un sistema físico simple es el de modelar un imán. Éste es el caso en el que vamos a trabajar, mediante un modelo de mecánica estadística muy enseñado, llamado modelo de Ising.² Veremos una versión simplificada de cómo simular su comportamiento a lo largo del tiempo. Inicializaremos un material magnético de modo que sus componentes magnéticos individuales apunten en direcciones aleatorias. Luego observaremos cómo este sistema evoluciona hacia un orden en el que todos los componentes magnéticos apuntan en la misma dirección, bajo la acción de leyes físicas conocidas y unas pocas líneas de código.

A continuación, analizamos cómo se lleva a cabo una simulación de este tipo mediante un método de Monte Carlo con Cadena de Markov (MCMC), discutiendo tanto el funcionamiento de ese método en general como su aplicación a este sistema concreto.

Simulaciones Monte Carlo y Cadenas de Markov

La idea de una simulación de Montecarlo es encontrar formas ingeniosas de aplicar números aleatorios a situaciones que en teoría deberían poder resolverse exactamente, pero que en la práctica son mucho más fáciles de resolver probabilísticamente.

La cadena de Markov es un complemento útil para una simulación general de Montecarlo y es especialmente aplicable a la simulación de series temporales. Una simulación de Montecarlo te ayudará a averiguar cómo es una determinada distribución o serie de términos, pero no cómo deben evolucionar esos términos a lo largo del tiempo. Aquí es donde entra en juego una cadena de Markov. Calcula una probabilidad de transición entre estados, y cuando la tenemos en cuenta, damos "pasos" en lugar de calcular simplemente una integral global. Ahora podemos tener una simulación de series temporales en lugar del mero cálculo de una integral.

En física, una simulación MCMC puede utilizarse, por ejemplo, para comprender cómo las transiciones cuánticas en moléculas individuales pueden afectar a las mediciones del conjunto agregado de ese sistema a lo largo del tiempo. En este caso, necesitamos aplicar algunas reglas específicas:

1. En un proceso de Markov, la probabilidad de una transición a un estado en el futuro sólo depende del estado actual (no de la información pasada).

2. Impondremos una condición específica de la física consistente en exigir una distribución de Boltzmann para la energía, es decir $T_{ij}/T_{ji}=e^{-b(E_j-E_i)}$. Para la mayoría de nosotros, esto es sólo un detalle de implementación y no algo de lo que deban preocuparse los no físicos.

Realizamos una simulación MCMC de la siguiente manera:

1. Selecciona aleatoriamente el estado inicial de cada uno de los sitios de la red.

2. Para cada paso de tiempo individual, elige un sitio individual de la red e invierte su dirección.

3. Calcula el cambio de energía que resultaría de este giro dadas las leyes físicas con las que trabajas. En este caso, esto significa

   • Si el cambio de energía es negativo, estás pasando a un estado de menor energía, que siempre se verá favorecido, por lo que mantienes el cambio y pasas al siguiente paso temporal.

   • Si el cambio de energía no es negativo, lo aceptas con la probabilidad de aceptación de $e^{(-\text{energía}\text{cambio})}$. Esto es coherente con la regla 2.

Continúa los pasos 2 y 3 indefinidamente hasta la convergencia para determinar el estado más probable para cualquier medición agregada que estés realizando.

Veamos los detalles concretos del modelo de Ising. Imagina que tenemos un material bidimensional compuesto por una rejilla de objetos, cada uno de los cuales tiene lo que se reduce a un miniimán que puede apuntar hacia arriba o hacia abajo. Colocamos esos miniimanes al azar en un giro hacia arriba o hacia abajo en el momento cero, y luego registramos el sistema a medida que evoluciona desde un estado aleatorio a un estado ordenado a baja temperatura.³

Primero configuramos nuestro sistema, como se indica a continuación:

## python
>>> ### CONFIGURATION
>>> ## physical layout
>>> N           = 5 # width of lattice
>>> M           = 5 # height of lattice
>>> ## temperature settings
>>> temperature = 0.5
>>> BETA        = 1 / temperature

Luego tenemos algunos métodos de utilidad, como la inicialización aleatoria de nuestro bloque inicial:

>>> def initRandState(N, M):
>>>     block = np.random.choice([-1, 1], size = (N, M))
>>>     return block

También calculamos la energía de una determinada alineación del estado central respecto a sus vecinos:

## python
>>> def costForCenterState(state, i, j, n, m):
>>>     centerS = state[i, j]
>>>     neighbors = [((i + 1) % n, j), ((i - 1) % n, j),
>>>                  (i, (j + 1) % m), (i, (j - 1) % m)]
>>>     ## notice the % n because we impose periodic boundary cond
>>>     ## ignore this if it doesn't make sense - it's merely a 
>>>     ## physical constraint on the system saying 2D system is like
>>>     ## the surface of a donut
>>>     interactionE = [state[x, y] * centerS for (x, y) in neighbors]
>>>     return np.sum(interactionE)

Y queremos determinar la magnetización de todo el bloque para un estado dado:

## python
>>> def magnetizationForState(state):
>>>    return np.sum(state)

Aquí es donde introducimos los pasos MCMC comentados anteriormente:

## python
>>> def mcmcAdjust(state):
>>>     n = state.shape[0]
>>>     m = state.shape[1]
>>>     x, y = np.random.randint(0, n), np.random.randint(0, m)
>>>     centerS = state[x, y]
>>>     cost = costForCenterState(state, x, y, n, m)
>>>     if cost < 0:
>>>         centerS *= -1
>>>     elif np.random.random() < np.exp(-cost * BETA):
>>>         centerS *= -1
>>>     state[x, y] = centerS
>>>     return state

Ahora, para realizar realmente una simulación, necesitamos algún registro, así como llamadas repetidas al ajuste MCMC:

## python
>>> def runState(state, n_steps, snapsteps = None):
>>>     if snapsteps is None:
>>>         snapsteps = np.linspace(0, n_steps, num = round(n_steps / (M * N * 100)),
>>>         						dtype = np.int32)
>>>     saved_states = []
>>>     sp = 0
>>>     magnet_hist = []
>>>     for i in range(n_steps):
>>>         state = mcmcAdjust(state)
>>>         magnet_hist.append(magnetizationForState(state))
>>>         if sp < len(snapsteps) and i == snapsteps[sp]:
>>>             saved_states.append(np.copy(state))
>>>             sp += 1
>>>     return state, saved_states, magnet_hist

Y ejecutamos la simulación:

## python
>>> ### RUN A SIMULATION
>>> init_state = initRandState(N, M)
>>> print(init_state)
>>> final_state = runState(np.copy(init_state), 1000)

Podemos sacar algunas conclusiones de esta simulación observando los estados inicial y final (ver Figura 4-2).

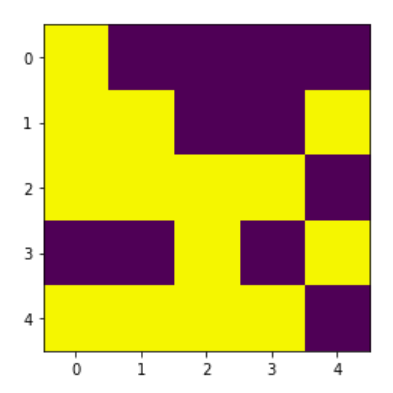
Figura 4-2. Estado inicial de un material ferromagnético simulado de 5 × 5, inicializado con cada estado seleccionado aleatoriamente para ser spin up o spin down con igual probabilidad.

En la Figura 4-2 examinamos un estado inicial generado aleatoriamente. Aunque podrías esperar ver los dos estados más mezclados, recuerda que probabilísticamente no es tan probable obtener un efecto de damero perfecto. Prueba a generar el estado inicial muchas veces, y verás que el estado aparentemente "aleatorio" o "50/50" del tablero de ajedrez no es en absoluto probable. Observa, sin embargo, que empezamos con aproximadamente la mitad de nuestros sitios en cada estado. Date cuenta también de que cualquier patrón que encuentres en los estados iniciales es probablemente tu cerebro siguiendo la tendencia muy humana de ver patrones incluso donde no los hay.

A continuación, pasamos el estado inicial a la función runState(), dejamos pasar 1.000 pasos de tiempo y examinamos el resultado en la Figura 4-3.

Esta es una instantánea del estado tomada en el paso 1.000. En este punto hay al menos dos observaciones interesantes. En primer lugar, el estado dominante se ha invertido en comparación con el paso 1.000. En segundo lugar, el estado dominante no es numéricamente más dominante de lo que era el otro estado dominante en el paso 1.000. Esto sugiere que la temperatura puede seguir volteando los sitios fuera del estado dominante incluso cuando, de otro modo, podría verse favorecida. Para comprender mejor esta dinámica, deberíamos considerar la posibilidad de trazar mediciones globales agregadas, como la magnetización, o hacer películas en las que podamos ver nuestros datos bidimensionales en un formato de serie temporal.

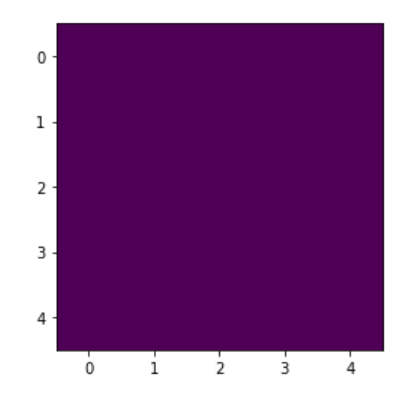
Figura 4-3. Estado final de baja temperatura en una ejecución de nuestra simulación, visto en 1.000 pasos de tiempo.

Lo hacemos con la magnetización en el tiempo de muchas ejecuciones independientes de la simulación anterior, como se muestra en la Figura 4-4:

## python
>>> we collect each time series as a separate element in results list
>>> results = []
>>> for i in range(100):
>>>     init_state = initRandState(N, M)
>>>     final_state, states, magnet_hist = runState(init_state, 1000)
>>>     results.append(magnet_hist)
>>> 
>>> ## we plot each curve with some transparency so we can see
>>> ## curves that overlap one another
>>> for mh in results:
>>>     plt.plot(mh,'r', alpha=0.2)

Las curvas de magnetización son sólo un ejemplo de cómo podríamos imaginar la evolución del sistema a lo largo del tiempo. También podríamos considerar el registro de series temporales 2D, como la instantánea del estado general en cada momento. O podría haber otras variables agregadas interesantes para medir en cada paso, como una medida de la entropía de disposición o una medida de la energía total. Cantidades como la magnetización o la entropía son magnitudes relacionadas, ya que son función de la disposición geométrica del estado en cada lugar de la red, pero cada cantidad es una medida ligeramente distinta.

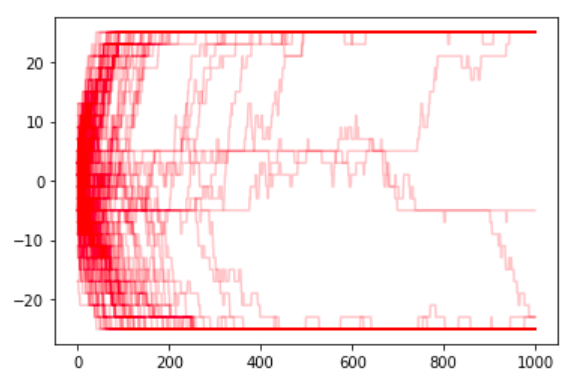
Figura 4-4. 100 simulaciones independientes de formas potenciales en que el sistema podría entrar en un estado magnetizado a baja temperatura, incluso cuando cada sitio original de la red se inicializara aleatoriamente.

Podemos utilizar estos datos de forma similar a lo que comentamos con los datos de los taxis, aunque el sistema subyacente sea bastante diferente. Por ejemplo, podríamos

• Utiliza los datos simulados como impulso para establecer una tubería.

• Probar los métodos de aprendizaje automático en estos datos sintéticos para ver si pueden ser útiles en los datos físicos antes de tomarnos la molestia de limpiar los datos del mundo real para ese modelado.

• Observa las imágenes cinematográficas de métricas importantes para desarrollar mejores intuiciones físicas sobre el sistema .

Notas finales sobre las simulaciones

Hemos examinado varios ejemplos muy diferentes de simulación de mediciones que describen el comportamiento a lo largo del tiempo. Hemos examinado la simulación de datos relacionados con el comportamiento del consumidor (afiliación y donación a ONG), la infraestructura de la ciudad (patrones de recogida de taxis) y las leyes de la física (el ordenamiento gradual de un material magnético aleatorio). Estos ejemplos deberían dejarte lo suficientemente cómodo como para empezar a leer ejemplos de código de datos simulados y también para que se te ocurran ideas sobre cómo tu propio trabajo podría beneficiarse de las simulaciones.

Lo más probable es que, en el pasado, hayas hecho suposiciones sobre tus datos sin saber cómo probarlas ni otras posibilidades alternativas. Las simulaciones te ofrecen una vía para hacerlo, lo que significa que tus conversaciones sobre los datos pueden ampliarse para incluir ejemplos hipotéticos emparejados con métricas cuantitativas procedentes de simulaciones. Esto fundamentará tus discusiones al tiempo que abre nuevas posibilidades, tanto en el ámbito de las series temporales como en otras ramas de la ciencia de datos.

Simulaciones estadísticas

Las simulaciones estadísticas son la vía más tradicional para simular datos de series temporales. Son especialmente útiles cuando conocemos la dinámica subyacente de un sistema estocástico y queremos estimar unos pocos parámetros desconocidos o ver cómo afectarían diferentes supuestos al proceso de estimación de parámetros (veremos un ejemplo de esto más adelante en el libro). Incluso para los sistemas físicos, a veces es mejor la simulación estadística.

Las simulaciones estadísticas de datos de series temporales también son muy valiosas cuando necesitamos disponer de una métrica cuantitativa definitiva para definir nuestra propia incertidumbre sobre la precisión de nuestras simulaciones. En las simulaciones estadísticas tradicionales, como un modelo ARIMA (que se analizará en el Capítulo 6), las fórmulas para el error están bien establecidas, lo que significa que para comprender un sistema con un modelo estadístico subyacente postulado, no necesitas realizar muchas simulaciones para hacer afirmaciones numéricas sobre el error y la varianza.

Simulaciones de Aprendizaje Profundo

Las simulaciones de aprendizaje profundo para series temporales son un campo incipiente pero prometedor. Las ventajas del aprendizaje profundo son que se puede captar una dinámica muy complicada y no lineal en los datos de series temporales, incluso sin que el profesional comprenda totalmente la dinámica. Sin embargo, esto también supone una desventaja, ya que el profesional no tiene una base de principios para comprender la dinámica del sistema.

Las simulaciones de aprendizaje profundo también son prometedoras cuando la privacidad es una preocupación. Por ejemplo, el aprendizaje profundo se ha utilizado para generar datos sintéticos de series temporales heterogéneas para aplicaciones médicas, basándose en datos de series temporales reales, pero sin la posibilidad de filtrar información privada. Un conjunto de datos de este tipo, si realmente puede producirse sin fugas de privacidad, tendría un valor incalculable porque los investigadores podrían tener acceso a una gran variedad de datos médicos (que de otro modo serían caros y violarían la privacidad).

Más recursos

Cristóbal Esteban, Stephanie L. Hyland y Gunnar Rätsch, "Real-Valued (Medical) Time Series Generation with Recurrent Conditional GANs", manuscrito inédito, revisado por última vez el 4 de diciembre de 2017, https://perma.cc/Q69W-L44Z.

Los autores demuestran cómo pueden utilizarse las redes generativas adversariales para producir datos de series temporales médicas heterogéneas de aspecto realista. Este es un ejemplo de cómo puede utilizarse la simulación del aprendizaje profundo para crear conjuntos de datos médicos éticos, legales y (esperemos) que preserven la privacidad, a fin de permitir un acceso más amplio a datos útiles para el aprendizaje automático y el aprendizaje profundo en el contexto sanitario.

Gordon Reikard y W. Erick Rogers, "Previsión de las olas oceánicas: Comparing a Physics-based Model with Statistical Models", Coastal Engineering 58 (2011): 409-16, https://perma.cc/89DJ-ZENZ.

Este artículo ofrece una comparación accesible y práctica de dos formas drásticamente distintas de modelizar un sistema, con la física o con la estadística. Los investigadores concluyen que, para el problema concreto que abordan, la escala temporal de interés para el pronosticador debe impulsar las decisiones sobre qué paradigma aplicar. Aunque este artículo trata de la previsión, la simulación está muy relacionada y se aplican las mismas ideas.

Wolfgang Härdle, Joel Horowitz y Jens-Peter Kreiss, "Bootstrap Methods for Time Series", International Statistical Review / Revue Internationale de Statistique 71, nº 2 (2003): 435-59, https://perma.cc/6CQA-EG2E.

Una revisión clásica de 2005 sobre las dificultades de la simulación estadística de datos de series temporales dadas las dependencias temporales. Los autores explican, en una revista de estadística muy técnica, por qué los métodos para aplicar bootstrap a los datos de series temporales van a la zaga de los métodos para otros tipos de datos, así como qué métodos prometedores había disponibles en el momento de escribir este artículo. El estado de la técnica no ha cambiado demasiado, por lo que se trata de una lectura útil, aunque desafiante.

¹ Este ejemplo está muy inspirado en el libro de Luciano Ramalho, Fluent Python (O'Reilly 2015). Te recomiendo encarecidamente que leas el capítulo completo sobre simulación de ese libro para mejorar tus conocimientos de programación en Python y ver oportunidades más elaboradas para la simulación basada en agentes.

² El modelo de Ising es un modelo mecánico estadístico clásico de imanes muy conocido y comúnmente enseñado. Puedes encontrar muchos ejemplos de código y más debates sobre este modelo en Internet, tanto en contextos de programación como de física, si te interesa saber más.

³ El modelo de Ising se utiliza más a menudo para comprender cuál es el estado de equilibrio de un ferromagneto que para considerar el aspecto temporal de cómo un ferromagneto puede llegar a un estado de equilibrio. Sin embargo, tratamos la evolución en el tiempo como una serie temporal.