Algorithmen in einer Kurzfassung, 2.

Kapitel 4. Sortier-Algorithmen

Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: [e-mail]

Zahlreiche Berechnungen und Aufgaben werden einfacher, wenn man Informationen im Voraus richtig sortiert. Die Suche nach effizienten Sortieralgorithmen dominierte die Anfänge der Computertechnik. Tatsächlich konzentrierte sich ein Großteil der frühen Forschung im Bereich der Algorithmen auf das Sortieren von Datensammlungen, die für die damaligen Computer zu groß waren, um sie im Speicher abzulegen. Da die heutigen Computer so viel leistungsfähiger sind als die von vor 50 Jahren, liegt die Größe der zu verarbeitenden Datensätze heute in der Größenordnung von Terabytes an Informationen. Auch wenn du vielleicht nicht dazu aufgefordert wirst, so große Datensätze zu sortieren, wirst du wahrscheinlich eine große Anzahl von Elementen sortieren müssen. In diesem Kapitel stellen wir dir die wichtigsten Sortieralgorithmen vor und präsentieren die Ergebnisse unserer Benchmarks, um dir bei der Auswahl des besten Sortieralgorithmus für die jeweilige Situation zu helfen.

Terminologie

Eine Sammlung von vergleichbaren Elementen A wird präsentiert, um an Ort und Stelle sortiert zu werden; wir verwenden die Bezeichnungen A[i] und _ai, um das ^i-te Element der Sammlung zu bezeichnen. Vereinbarungsgemäß ist das erste Element der Sammlung A[0]. Mit A[niedrig, niedrig + n) bezeichnen wir die Untersammlung A[niedrig] ... A[niedrig + n - 1] von n Elementen, während A[niedrig, niedrig + n] n + 1 Elemente enthält.

Um eine Sammlung zu sortieren, musst du die Elemente A so reorganisieren, dass i < j ist, wenn A[i] < A[j] ist. Wenn es doppelte Elemente gibt, müssen diese Elemente in der resultierenden geordneten Sammlung zusammenhängend sein, d.h. wenn A[i] = A[j] in einer sortierten Sammlung ist, kann es kein k geben, bei dem i < k < j ist undA[i] ≠ A[k]. Schließlich muss die sortierte Sammlung A eine Permutation der Elemente sein, aus denen A ursprünglich bestand.

Vertretung

Die Sammlung kann bereits im Arbeitsspeicher (RAM) des Computers gespeichert sein, aber auch nur in einer Datei im Dateisystem, der so genannten sekundären Speicherung. Die Sammlung kann teilweise auf einer tertiären Speicherung (z. B. auf Bandbibliotheken und optischen Jukeboxen) archiviert sein, was zusätzliche Verarbeitungszeit erfordert, nur um die Informationen zu finden; außerdem müssen die Informationen möglicherweise auf eine sekundäre Speicherung (z. B. auf Festplatten) kopiert werden, bevor sie verarbeitet werden können.

Informationen, die im Arbeitsspeicher gespeichert werden, haben normalerweise eine von zwei Formen: zeigerbasiert oder wertbasiert. Angenommen, wir wollen die Zeichenketten "Adler", "Katze", "Ameise", "Hund" und "Ball" sortieren. Bei der zeigerbasierten Speicherung, die in Abbildung 4-1 dargestellt ist, enthält ein Array mit Informationen (d. h. die zusammenhängenden Kästchen) Zeiger auf die eigentlichen Informationen (d. h. die Zeichenketten in den Ovalen), anstatt die Informationen selbst zu speichern. Mit diesem Ansatz können beliebig komplexe Datensätze gespeichert und sortiert werden.

Abbildung 4-1. Sortieren mit zeigerbasierter Speicherung

Im Gegensatz dazu wird bei der wertbasierten Speicherung eine Sammlung von n Elementen in Datensatzblöcke mit einer festen Größe s gepackt, die besser für die sekundäre oder tertiäre Speicherung geeignet sind. Abbildung 4-2zeigt, wie die inAbbildung 4-1 gezeigten Informationen in einem zusammenhängenden Speicherblock gespeichert werden können, der eine Reihe von Zeilen mit einer Größe von genau s = 5 Byte enthält. In diesem Beispiel werden die Informationen als Zeichenketten dargestellt, es kann sich aber auch um eine beliebige Sammlung von strukturierten, datensatzbasierten Informationen handeln. Das "¬"-Zeichen steht für ein Auffüllzeichen, das nicht Teil einer Zeichenkette sein kann; in dieser Kodierung benötigen Zeichenketten der Länge s kein Auffüllzeichen. Die Informationen sind zusammenhängend und können als ein eindimensionales Array B[0, n*s) betrachtet werden. Beachte, dass B[r*s + c] der ^c-te Buchstabe des ^r-ten Wortes ist (wobei c ≥ 0 und r≥ 0);außerdem ist das ^i-te Element der Sammlung (für i ≥ 0) das Unterarray B[i*s,(i + 1)*s).

Informationen werden in der Regel als wertbasierte, zusammenhängende Sammlung von Bytes in die sekundäre Speicherung geschrieben. Die Algorithmen in diesem Kapitel können auch so geschrieben werden, dass sie mit plattenbasierten Informationen arbeiten, indem sie einfach Swap-Funktionen implementieren, die Bytes innerhalb der Dateien auf der Platte austauschen; die daraus resultierende Leistung wird sich jedoch aufgrund der erhöhten Ein-/Ausgabekosten beim Zugriff auf die sekundäre Speicherung unterscheiden. Merge Sort eignet sich besonders gut für das Sortieren von Daten in der sekundären Speicherung.

Ob zeiger- oder wertbasiert, ein Sortieralgorithmus aktualisiert die Informationen (in beiden Fällen die Kästchen) so, dass A[0, n) geordnet ist. Der Einfachheit halber verwenden wir die Schreibweise A[i] für das ^i-teElement, auch wenn eine wertbasierte Speicherung verwendet wird.

Abbildung 4-2. Sortierung mit wertorientierter Speicherung

Vergleichbare Elemente

Die Elemente in der zu vergleichenden Sammlung müssen eine totale Ordnung zulassen. Das heißt, dass für zwei beliebige Elemente p und q in einer Sammlung genau eines der folgenden drei Prädikate wahr ist: p = q,p < q oder p > q. Zu den häufig sortierten primitiven Typen gehören Ganzzahlen, Fließkommazahlen und Zeichen. Wenn zusammengesetzte Elemente sortiert werden (z. B. Zeichenketten), wird die lexikografische Ordnung auf jedes einzelne Element des Verbunds angewandt, wodurch eine komplexe Sortierung in einzelne Sortierungen für primitive Typen reduziert wird. Zum Beispiel wird das Wort "Alphabet" als kleiner als "Alternative", aber größer als "Alligator" angesehen, indem jeder einzelne Buchstabe von links nach rechts verglichen wird, bis ein Wort keine Zeichen mehr hat oder ein einzelnes Zeichen in einem Wort sich von seinem Partner in einem anderen Wort unterscheidet (also ist "Ameise" kleiner als "Hymne").

Diese Frage der Reihenfolge ist alles andere als einfach, wenn man die Großschreibung (ist "A" größer als "a"?), diakritische Zeichen (ist "è" kleiner als "ê"?) und Diphthonge (ist "æ" kleiner als "a"?) berücksichtigt. Beachte, dass der mächtige Unicode-StandardKodierungen wie UTF-16 verwendet, um jedes einzelne Zeichen mit bis zu vier Bytes darzustellen. Das Unicode-Konsortium hat einen Sortierstandard (den so genannten "Collation Algorithm") entwickelt, der die vielen verschiedenen Ordnungsregeln der verschiedenen Sprachen und Kulturen berücksichtigt (Davis und Whistler, 2008).

Die in diesem Kapitel vorgestellten Algorithmen gehen davon aus, dass du eine Vergleichsfunktion cmp bereitstellen kannst, die das Element p mitq vergleicht und 0 zurückgibt, wenn p = q ist, eine negative Zahl, wenn p < q ist, und eine positive Zahl, wenn p > q ist. Wenn es sich bei den Elementen um komplexe Datensätze handelt, vergleicht die Funktion cmp möglicherweise nur einen "Schlüsselwert" der Elemente. Ein Flughafenterminal könnte zum Beispiel ausgehende Flüge in aufsteigender Reihenfolge nach Zielort oder Abflugzeit auflisten, während die Flugnummern ungeordnet erscheinen.

Stabiles Sortieren

Wenn die Vergleichsfunktion cmp feststellt, dass zwei Elemente _aiund _aj in der ursprünglichen ungeordneten Sammlung gleich sind, kann es wichtig sein, ihre relative Reihenfolge in der sortierten Menge beizubehalten - d.h. wenn i < j ist, muss die endgültige Position für _ai links von der endgültigen Position für _aj liegen. Sortieralgorithmen, die diese Eigenschaft garantieren, gelten als stabil. Die linken vier Spalten der Tabelle 4-1 zeigen zum Beispiel eine ursprüngliche Sammlung von Fluginformationen, die bereits nach der Flugzeit am Tag sortiert sind (unabhängig von der Fluggesellschaft oder der Zielstadt). Wenn eine stabile Sortierung diese Sammlung mit einer Vergleichsfunktion ordnet, die die Flüge nach der Zielstadt sortiert, ist das einzig mögliche Ergebnis in den rechten vier Spalten vonTabelle 4-1 zu sehen.

Tabelle 4-1. Stabile Sortierung der Flughafen-Terminal-Informationen

Ziel	Airline	Flug	Abfahrtszeit (aufsteigend)	→	Zielort (aufsteigend)	Airline	Flug	Abfahrtszeit
Büffel	Lufttransit	549	10:42 AM		Albany	Südwest	482	1:20 PM
Atlanta	Delta	1097	11:00 AM		Atlanta	Delta	1097	11:00 AM
Baltimore	Südwest	836	11:05 AM		Atlanta	Lufttransit	872	11:15 UHR
Atlanta	Lufttransit	872	11:15 UHR		Atlanta	Delta	28	12:00 UHR
Atlanta	Delta	28	12:00 UHR		Atlanta	Al Italia	3429	1:50 PM
Boston	Delta	1056	12:05 UHR		Austin	Südwest	1045	1:05 PM
Baltimore	Südwest	216	12:20 UHR		Baltimore	Südwest	836	11:05 AM
Austin	Südwest	1045	1:05 PM		Baltimore	Südwest	216	12:20 UHR
Albany	Südwest	482	1:20 PM		Baltimore	Südwest	272	1:40 PM
Boston	Lufttransit	515	1:21 PM		Boston	Delta	1056	12:05 UHR
Baltimore	Südwest	272	1:40 PM		Boston	Lufttransit	515	1:21 PM
Atlanta	Al Italia	3429	1:50 PM		Büffel	Lufttransit	549	10:42 AM

Du wirst feststellen, dass alle Flüge, die denselben Zielort haben, auch nach ihrer geplanten Abflugzeit sortiert sind; der Sortieralgorithmus war also in dieser Sammlung stabil. Ein instabiler Algorithmus achtet nicht auf die Beziehungen zwischen den Positionen der Elemente in der ursprünglichen Sammlung (er kann die relative Reihenfolge beibehalten, aber auch nicht).

Kriterien für die Auswahl eines Sortieralgorithmus

Um den zu verwendenden oder zu implementierenden Sortieralgorithmus auszuwählen, berücksichtige die qualitativen Kriterien in Tabelle 4-2.

Tabelle 4-2. Kriterien für die Auswahl eines Sortieralgorithmus

Kriterien	Sortieralgorithmus
Nur ein paar Artikel	Einfügen Sortieren
Die Artikel sind größtenteils schon sortiert	Einfügen Sortieren
Besorgt über Worst-Case-Szenarien	Heap Sort
Interessiert an einem guten Durchschnittsverhalten	Quicksort
Gegenstände werden aus einem einheitlichen, dichten Universum gezogen	Eimer sortieren
Den Wunsch, so wenig Code wie möglich zu schreiben	Einfügen Sortieren
Erforderlich ist eine stabile Sorte	Zusammenführen Sortieren

Transposition Sortierung

Frühe Sortieralgorithmen fanden Elemente in der Sammlung A, die fehl am Platz waren, und brachten sie an die richtige Stelle, indem sie die Elemente in A vertauschten. Selection Sort und (die berüchtigte) Bubble Sort gehören zu dieser Sortierfamilie. Diese Algorithmen werden jedoch von Insertion Sort übertroffen, das wir jetzt vorstellen.

Einfügen Sortieren

Insertion Sort ruft wiederholt eine insert Hilfsfunktion auf, um sicherzustellen, dass A[0, i] richtig sortiert ist; schließlich erreicht i das ganz rechte Element und sortiert A vollständig.

Einfügung Sortierung Zusammenfassung

Beste: O(n) Durchschnitt, Schlechteste: O(ⁿ²)

sort (A)
  for pos = 1 to n-1 do
    insert (A, pos, A[pos])
end

insert (A, pos, value)
  i = pos - 1
  while i >= 0 and A[i] > value do 
    A[i+1] = A[i]
    i = i-1
  A[i+1] = value 
end

Verschiebt Elemente, die größer als value sind, nach rechts.

Setze value an der richtigen Stelle ein.

Abbildung 4-3 zeigt, wie Insertion Sort mit einer ungeordneten Sammlung A der Größe n = 16 arbeitet. Die folgenden 15 Zeilen zeigen den Zustand von A nach jedem Aufruf von Insertion.

A wird an Ort und Stelle sortiert, indem pos = 1 bis n - 1 erhöht wird und das Element A[pos] an die richtige Stelle in der wachsenden sortierten Region A[0, pos] eingefügt wird, die rechts durch eine fette vertikale Linie abgegrenzt ist. Die grau schattierten Elemente wurden nach rechts verschoben, um Platz für das eingefügte Element zu schaffen. Insgesamt führte Insertion Sort60 benachbarte Transpositionen durch (eine Verschiebung um nur einen Platz um ein Element).

Kontext

Verwende Insertion Sort, wenn du nur eine kleine Anzahl von Elementen zu sortieren hast oder die Elemente in der ursprünglichen Sammlung bereits "fast sortiert" sind. Die Bestimmung, wann das Array "klein genug" ist, variiert von Maschine zu Maschine und von Programmiersprache zu Programmiersprache. Sogar die Art des zu vergleichenden Elements kann von Bedeutung sein.

Abbildung 4-3. Der Ablauf von Insertion Sort bei einem kleinen Array

Lösung

Wenn die Informationen mit Zeigern gespeichert werden, sortiert das C-Programm inBeispiel 4-1 ein Array ar von Elementen, die mit einer Vergleichsfunktion cmp verglichen werden können.

Beispiel 4-1. Einfügen Sortieren mit zeigerbasierten Werten

void sortPointers (void **ar, int n,
                   int (*cmp)(const void *, const void *)) {
  int j;
  for (j = 1; j < n; j++) {
    int i = j-1;
    void *value = ar[j];
    while (i >= 0 && cmp (ar[i], value) > 0) {
      ar[i+1] = ar[i];
      i--;
    }

   ar[i+1] = value;
  }
}

Wenn A mit einer wertbasierten Speicherung dargestellt wird, wird es inn Zeilen mit einer festen Elementgröße von s Byte gepackt. Um die Werte zu manipulieren, braucht man eine Vergleichsfunktion und die Möglichkeit, Werte von einem Ort zum anderen zu kopieren. Beispiel 4-2 zeigt ein geeignetes C-Programm, das memmove verwendet, um die zugrundeliegenden Bytes effizient für eine Menge zusammenhängender Einträge in A zu übertragen.

Beispiel 4-2. Einfügen Sortieren mit wertbasierten Informationen

void sortValues (void *base, int n, int s,
                 int (*cmp)(const void *, const void *)) {
  int j;
  void *saved = malloc (s);
  for (j = 1; j < n; j++) {
    int i = j-1;
    void *value = base + j*s;
    while (i >= 0 && cmp (base + i*s, value) > 0) { i--; }

    /* If already in place, no movement needed. Otherwise save value
     * to be inserted and move intervening values as a LARGE block.
     * Then insert into proper position. */
    if (++i == j) continue;

    memmove (saved, value, s);
    memmove (base+(i+1)*s, base+i*s, s*(j-i));
    memmove (base+i*s, saved, s);
  }
  free (saved);
}

Die optimale Leistung wird erreicht, wenn das Array bereits sortiert ist. Arrays, die in umgekehrter Reihenfolge sortiert sind, bringen die schlechteste Leistung für Insertion Sort. Wenn das Array bereits größtenteils sortiert ist, schneidetInsertion Sort gut ab, weil weniger Elemente transponiert werden müssen.

Insertion Sort benötigt nur sehr wenig zusätzlichen Platz, um zu funktionieren; es muss nur Platz für ein einzelnes Element reserviert werden. Für wertbasierte Darstellungen bieten die meisten Sprachbibliotheken eine Funktion zum Verschieben des Blockspeichers, um Transpositionen effizienter zu machen.

Analyse

Im besten Fall befindet sich jedes der n Elemente an seinem richtigen Platz und daher benötigt Insertion Sort lineare Zeit, also O(n). Dieser Punkt mag trivial erscheinen (wie oft willst du eine Menge bereits sortierter Elemente sortieren?), ist aber wichtig, weil Insertion Sortder einzige vergleichsbasierte Sortieralgorithmus ist, der dieses Best-Case-Verhalten aufweist.

Viele reale Daten sind bereits teilweise sortiert, sodass Optimismus und Realismus zusammenkommen können, um Insertion Sort zu einem effektiven Algorithmus zu machen. Die Effizienz von Insertion Sort steigt, wenn doppelte Elemente vorhanden sind, da weniger Vertauschungen vorgenommen werden müssen.

Leider ist Insertion Sort zu konservativ, wenn alle n Elemente unterschiedlich sind und das Array zufällig organisiert ist (d.h. alle Permutationen der Daten sind gleich wahrscheinlich), weil jedes Element im Durchschnitt n/3 Positionen im Array von seiner Endposition aus beginnt. Das Programm numTranspositions.c im Code Repository bestätigt diese Behauptung empirisch für kleine nbis zu 12 (siehe auch Trivedi, 2001). Im durchschnittlichen und schlimmsten Fall muss jedes der n Elemente eine lineare Anzahl von Positionen transponiert werden, sodass Insertion Sort O(ⁿ²) quadratische Zeit benötigt.

Insertion Sort arbeitet bei wertbasierten Daten ineffizient, weil viel Speicherplatz verschoben werden muss, um Platz für einen neuen Wert zu schaffen. Tabelle 4-3enthält direkte Vergleiche zwischen einer naiven Implementierung von wertbasiertem Insertion Sort und der Implementierung ausBeispiel 4-2. Es wurden zehn zufällige Sortierversuche mit n Elementen durchgeführt und die besten und schlechtesten Ergebnisse wurden verworfen. Diese Tabelle zeigt den Durchschnitt der verbleibenden acht Versuche. Beachte, wie sich die Implementierung durch die Verwendung eines Blockspeicherzuges anstelle eines individuellen Speicherswaps verbessert. Wenn sich die Array-Größe verdoppelt, vervierfacht sich die Leistungszeit ungefähr, was das O(ⁿ²)-Verhalten von Insertion Sort bestätigt. Selbst mit der Verbesserung der Blockverschiebung bleibt Insertion Sort immer noch quadratisch.

Tabelle 4-3. Einfügesortierung Bulk Move gegenüber Einfügesortierung (in Sekunden)

n	Einfügen Sortieren Bulk Move(Bn)	Naive Einfügung Sortieren(Sn)
1,024	0.0039	0.0130
2,048	0.0153	0.0516
4,096	0.0612	0.2047
8,192	0.2473	0.8160
16,384	0.9913	3.2575
32,768	3.9549	13.0650
65,536	15.8722	52.2913
131,072	68.4009	209.2943

Wenn Insertion Sort mit zeigerbasierten Eingaben arbeitet, ist das Auslagern von Elementen effizienter; der Compiler kann sogar optimierten Code erzeugen, um kostspielige Speicherzugriffe zu minimieren.

Auswahl Sortieren

Eine gängige Sortierstrategie besteht darin, den größten Wert aus dem Bereich A[0, n) auszuwählen und seine Position mit dem Element ganz rechts A[n - 1] zu vertauschen. Dieser Vorgang wird anschließend für jeden weiteren kleineren Bereich A[0, n - 1) wiederholt, bis A sortiert ist. Wir haben Selection Sort in Kapitel 3 als Beispiel für einen Greedy-Ansatz besprochen. Beispiel 4-3 enthält eine C-Implementierung.

Beispiel 4-3. Selection Sort Implementierung in C

static int selectMax (void **ar, int left, int right,
                      int (*cmp)(const void *, const void *)) {
  int  maxPos = left;
  int  i = left;
  while (++i <= right) {
    if (cmp(ar[i], ar[maxPos]) > 0) {
      maxPos = i;
    }
  }

  return maxPos;
}

void sortPointers (void **ar, int n,
                   int (*cmp)(const void *, const void *)) {
  /* repeatedly select max in ar[0,i] and swap with proper position */
  int i;
  for (i = n-1; i >= 1; i--) {
    int maxPos = selectMax (ar, 0, i, cmp);
    if (maxPos != i) {
      void *tmp = ar[i];
      ar[i] = ar[maxPos];
      ar[maxPos] = tmp;
    }
  }
}

Selection Sort ist der langsamste aller in diesem Kapitel beschriebenen Sortieralgorithmen; er benötigt selbst im besten Fall (d. h. wenn das Array bereits sortiert ist) quadratische Zeit. Er führt immer wieder fast die gleiche Aufgabe aus, ohne von einer Iteration zur nächsten etwas zu lernen. Die Auswahl des größten Elements, max, in A erfordert n - 1 Vergleiche, und die Auswahl des zweitgrößten Elements, second, erfordert n - 2 Vergleiche - kein großer Fortschritt! Viele dieser Vergleiche sind verschwendet, denn wenn ein Element kleiner als das zweite ist, kann es unmöglich das größte Element sein und hat daher keinen Einfluss auf die Berechnung von max. Anstatt weitere Details zu diesem schlecht funktionierenden Algorithmus vorzustellen, betrachten wir jetzt Heap Sort, das zeigt, wie man das Prinzip von Selection Sort effektiver anwenden kann.

Heap Sort

Wir brauchen immer mindestens n - 1 Vergleiche, um das größte Element in einem ungeordneten Feld A mit n Elementen zu finden, aber können wir die Anzahl der Elemente, die direkt verglichen werden, minimieren? Bei Sportturnieren wird zum Beispiel die "beste" Mannschaft aus einem Feld von n Mannschaften ermittelt, ohne dass der endgültige Sieger gegen alle anderen n - 1 Mannschaften spielen muss. Eines der beliebtesten Basketballturniere in den USA ist das NCAA-Meisterschaftsturnier, bei dem im Wesentlichen 64 College-Mannschaften um den nationalen Titel kämpfen. Die Mannschaft, die am Ende den Titel holt, spielt gegen fünf Mannschaften, bevor sie das entscheidende Spiel erreicht, und muss daher sechs Spiele gewinnen. Es ist kein Zufall, dass 6 = log (64) ist. Heap Sort zeigt, wie man dieses Verhalten zum Sortieren einer Gruppe von Elementen anwendet.

Heap Sort Zusammenfassung

Bester, Durchschnitt, Schlechtester: O(n log n)

sort (A)
  buildHeap (A)
  for i = n-1 downto 1 do
    swap A[0] with A[i]
    heapify (A, 0, i)
end

buildHeap (A)
  for i = n/2-1 downto 0 do
    heapify (A, i, n)
end

# Recursively enforce that A[idx,max) is valid heap
heapify (A, idx, max)
  largest = idx 
  left = 2*idx + 1
  right = 2*idx + 2

  if left < max and A[left] > A[idx] then
    largest = left 
  if right < max and A[right] > A[largest] then
    largest = right 
  if largest ≠ idx then
    swap A[idx] and A[largest]
    heapify (A, largest, max)
end

Angenommen, das Elternteil A[idx] ist größer oder gleich einem seiner Kinder.

Das linke Kind ist größer als sein Elternteil.

Das rechte Kind ist größer als sein Elternteil oder sein linkes Geschwisterkind.

Abbildung 4-4 zeigt die Ausführung von buildHeap für ein Array mit sechs Werten.

Abbildung 4-4. Beispiel für Heap Sort

Ein Heap ist ein binärer Baum, dessen Struktur zwei Eigenschaften gewährleistet:

Eigenschaft Form

Ein Blattknoten in der Tiefe k > 0 kann nur existieren, wenn alle ^2k-1 Knoten in der Tiefe k - 1 existieren. Außerdem müssen die Knoten auf einer teilweise gefüllten Ebene "von links nach rechts" hinzugefügt werden. Der Wurzelknoten hat eine Tiefe von 0.

Heap-Eigenschaft

Jeder Knoten im Baum enthält einen Wert, der größer oder gleich einem seiner beiden Kinder ist, sofern er welche hat.

Der Beispielhaufen in Abbildung 4-5(a) erfüllt diese Eigenschaften. Die Wurzel des Binärbaums enthält das größte Element des Baums; das kleinste Element kann jedoch in jedem Blattknoten gefunden werden. Obwohl ein Heap nur sicherstellt, dass ein Knoten größer als eines seiner Kinder ist, zeigt Heap Sort, wie man die Eigenschaft der Form ausnutzen kann, um ein Array von Elementen effizient zu sortieren.

Abbildung 4-5. (a) Beispielheap mit 16 eindeutigen Elementen; (b) Beschriftungen dieser Elemente; (c) Heap in einem Array gespeichert

Aufgrund der starren Struktur, die durch die Shape-Eigenschaft vorgegeben ist, kann ein Heap in einem Array A gespeichert werden, ohne dass seine Strukturinformationen verloren gehen. Abbildung 4-5(b) zeigt, dass jedem Knoten im Heap eine ganzzahlige Bezeichnung zugewiesen ist. Die Wurzel hat die Kennzeichnung 0. Ein Knoten mit der Kennzeichnung i erhält als linkes Kind (falls vorhanden) die Kennzeichnung 2*i + 1; sein rechtes Kind (falls vorhanden) erhält die Kennzeichnung 2*i + 2. Ebenso erhält ein Nicht-Wurzelknoten mit der Bezeichnung i die Bezeichnung⌊(i - 1)/2⌋ für seinen Elternknoten. Mit diesem Bezeichnungsschema können wir den Heap in einem Array speichern, indem wir den Elementwert eines Knotens an der Position im Array ablegen, die durch die Bezeichnung des Knotens gekennzeichnet ist. Das in Abbildung 4-5(c) dargestellte Array repräsentiert den in Abbildung 4-5(a) dargestellten Heap. Die Reihenfolge der Elemente innerhalb von A kann einfach von links nach rechts gelesen werden, wenn tiefere Ebenen des Baums erkundet werden.

Heap Sort sortiert ein Array A, indem es dieses Array zunächst mit buildHeap in einen Heap umwandelt, der wiederholt heapify aufruft. heapify(A, i, n) aktualisiert das Array A, um sicherzustellen, dass die Baumstruktur mit der Wurzel A[i] ein gültiger Heap ist. Abbildung 4-6 zeigt Details zu den Aufrufen von heapify, die ein ungeordnetes Array in einen Heap umwandeln. Der Fortschritt von buildHeap bei einem bereits sortierten Array ist in Abbildung 4-6 dargestellt. Jede nummerierte Zeile in dieser Abbildung zeigt das Ergebnis der Ausführung von heapify auf dem ursprünglichen Array vom mittleren Punkt⌊(n/2)⌋ - 1 bis zum ganz linken Index 0.

Wie du siehst, werden große Zahlen im resultierenden Heap schließlich "angehoben" (d.h. sie werden in A mit kleineren Elementen auf der linken Seite vertauscht). Die grauen Quadrate in Abbildung 4-6 zeigen die Elementpaare, die in heapifyvertauscht wurden - insgesamt 13 -, was weit weniger ist als die Gesamtzahl der Elemente, die in Abbildung 4-3 in Insertion Sort vertauscht wurden.

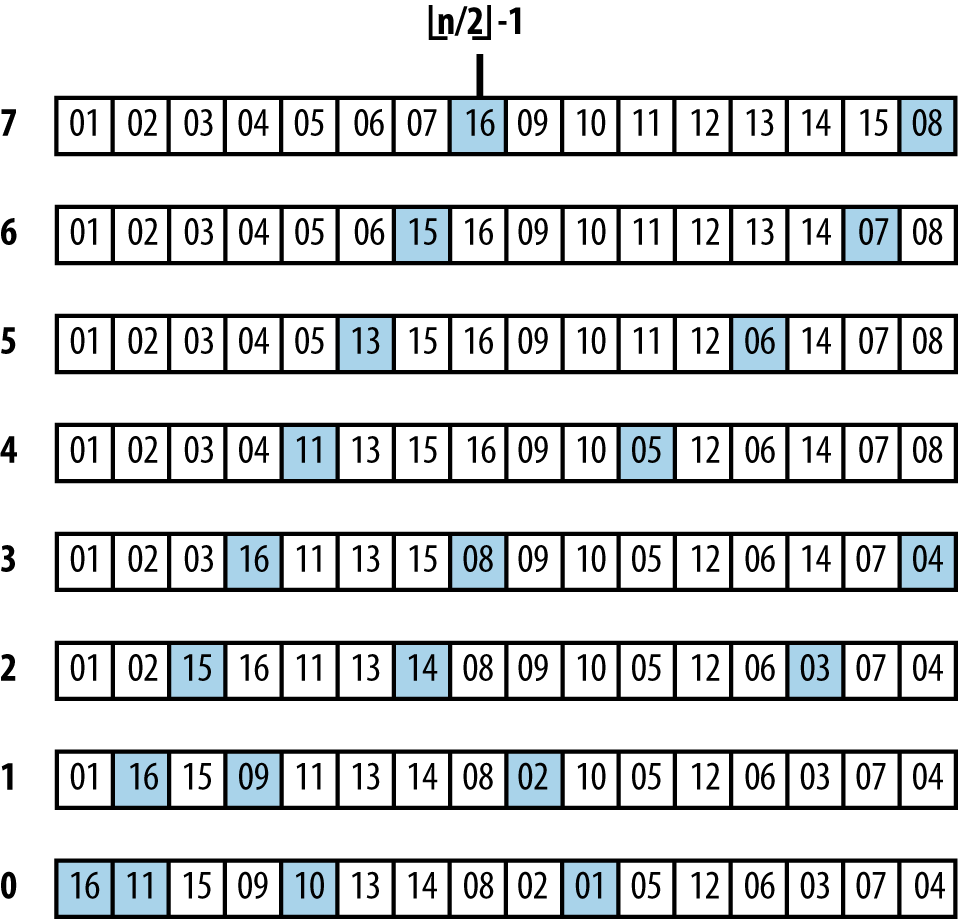
Abbildung 4-6. buildHeap verarbeitet ein anfänglich sortiertes Array

Heap Sort verarbeitet ein Array A der Größe n, indem es es als zwei verschiedene Unterarrays behandelt, A[0, m) und A[m, n), die jeweils einen Heap der Größe m und ein sortiertes Unterarray mit n - m Elementen darstellen. Wenn i von n - 1 auf 1 absteigt, vergrößert Heap Sort den sortierten Teilbereich A[i, n) nach unten, indem es das größte Element im Heap (an der Position A[0]) mit A[i] vertauscht; anschließend rekonstruiert es A[0, i) zu einem gültigen Heap, indem es heapify ausführt. Der daraus resultierende nicht leere Teilbereich A[i, n) wird sortiert, weil das größte Element im Heap, das in A[0, i) repräsentiert wird, garantiert kleiner oder gleich einem Element im sortierten Teilbereich A[i, n) ist.

Kontext

Heap Sort ist keine stabile Sortierung. Heap Sort vermeidet viele der unangenehmen (fast peinlichen!) Fälle, in denen Quicksort schlecht abschneidet. Trotzdem schneidet Quicksort im Durchschnitt besser ab als Heap Sort.

Lösung

Ein Beispiel für eine Implementierung in C ist in Beispiel 4-4 zu sehen.

Beispiel 4-4. Heap Sort Implementierung in C

static void heapify (void **ar, int (*cmp)(const void *, const void *),
                     int idx, int max) {
  int left = 2*idx + 1;
  int right = 2*idx + 2;
  int largest;

  /* Find largest element of A[idx], A[left], and A[right]. */
  if (left < max && cmp (ar[left], ar[idx]) > 0) {
    largest = left;
  } else {
    largest = idx;
  }

  if (right < max && cmp (ar[right], ar[largest]) > 0) {
    largest = right;
  }

  /* If largest is not already the parent then swap and propagate. */
  if (largest != idx) {
    void *tmp;
    tmp = ar[idx];
    ar[idx] = ar[largest];
    ar[largest] = tmp;

    heapify (ar, cmp, largest, max);
   }
}

static void buildHeap (void **ar,
                       int (*cmp)(const void *, const void *), int n) {
  int i;
  for (i = n/2-1; i>=0; i--) {
    heapify (ar, cmp, i, n);
  }
}

void sortPointers (void **ar, int n,
                   int (*cmp)(const void *, const void *)) {
  int i;
  buildHeap (ar, cmp, n);
  for (i = n-1; i >= 1; i--) {
    void *tmp;
    tmp = ar[0];
    ar[0] = ar[i];
    ar[i] = tmp;

    heapify (ar, cmp, 0, i);
  }
}

Analyse

heapify ist die zentrale Operation bei Heap Sort. In buildHeap wird sie⌊(n/2)⌋ - 1 Mal aufgerufen, und während des eigentlichen Sortierens wird sie n - 1 Mal aufgerufen, also insgesamt⌊(3*n/2)⌋ - 2 Mal. Aufgrund der Formeigenschaft ist die Tiefe des Heaps immer ⌊ log n ⌋, wobei n die Anzahl der Elemente im Heap ist. Wie du siehst, handelt es sich um eine rekursive Operation mit nicht mehr als log n rekursiven Aufrufen, bis der Heap korrigiert oder das Ende des Heaps erreicht ist. heapify hört jedoch vorzeitig auf, sobald der Heap korrigiert ist. Wie sich herausstellt, sind insgesamt nicht mehr als 2*n Vergleiche erforderlich (Cormen et al., 2009), was bedeutet, dass buildHeap sich in linearer Zeit oder O(n) verhält.

Variationen

Das Code-Repository enthält eine nicht-rekursive Heap-Sort-Implementierung. Tabelle 4-4 zeigt einen Benchmark-Vergleich, bei dem 1.000 zufällige Versuche mit beiden Implementierungen durchgeführt wurden, wobei die beste und die schlechteste Leistung der beiden Implementierungen verworfen wurden.

Tabelle 4-4. Vergleich zwischen Heap Sort und nicht-rekursivem Heap Sort (in Sekunden)

n	Nicht rekursiv Heap-Sortierung	Rekursiv Heap-Sortierung
16,384	0.0048	0.0064
32,768	0.0113	0.0147
65,536	0.0263	0.0336
131,072	0.0762	0.0893
262,144	0.2586	0.2824
524,288	0.7251	0.7736
1,048,576	1.8603	1.9582
2,097,152	4.566	4.7426

Zunächst gibt es eine spürbare Verbesserung bei der Beseitigung von Rekursionen in Heap Sort, aber dieser Unterschied verringert sich mit zunehmendem n.

Sortierung auf Basis von Partitionen

Eine Divide-and-Conquer-Strategie löst ein Problem, indem sie es in zwei unabhängige Teilprobleme aufteilt, die jeweils etwa halb so groß sind wie das ursprüngliche Problem. Du kannst diese Strategie beim Sortieren wie folgt anwenden: Finde das mittlere Element in der Sammlung A und tausche es mit dem mittleren Element von A. Nun tausche Elemente in der linken Hälfte, die größer als A[Mitte] sind, mit Elementen in der rechten Hälfte, die kleiner oder gleich A[Mitte] sind. Dadurch wird das ursprüngliche Array in zwei verschiedene Unterarrays unterteilt, die rekursiv sortiert werden können, um die ursprüngliche Sammlung A zu sortieren.

Die Umsetzung dieses Ansatzes ist eine Herausforderung, denn es ist vielleicht nicht offensichtlich, wie man das mittlere Element einer Sammlung berechnet, ohne die Sammlung vorher zu sortieren! Es stellt sich heraus, dass du jedes beliebige Element in A verwenden kannst, um A in zwei Teilfelder zu partitionieren. Wenn du jedes Mal "klug" wählst, sind beide Teilfelder mehr oder weniger gleich groß und du erreichst eine effiziente Umsetzung.

Angenommen, es gibt eine Funktion p = partition(A, left, right, pivotIndex), die einen speziellen Pivot-Wert in A, A[pivotIndex], verwendet, um A zu verändern und die Stelle p in A so zurückzugeben, dass

• A[p] = Pivot

• Alle Elemente in A[links, p) sind kleiner oder gleich dem Pivot

• Alle Elemente in A[p + 1, rechts] sind größer als Pivot

Wenn du Glück hast, ist die Größe dieser beiden Subarrays nach Abschluss der Partitionierung etwa halb so groß wie die der ursprünglichen Sammlung. Beispiel 4-5 zeigt eine C-Implementierung von partition.

Beispiel 4-5. C-Implementierung zur Partitionierung von ar[left,right] um ein gegebenes Pivotelement

/**
 * In linear time, group the subarray ar[left, right] around a pivot
 * element pivot=ar[pivotIndex] by storing pivot into its proper
 * location, store, within the subarray (whose location is returned
 * by this function) and ensuring all ar[left,store) <= pivot and
 * all ar[store+1,right] > pivot.
 */
int partition (void **ar, int (*cmp)(const void *, const void *),
               int left, int right, int pivotIndex) {
  int idx, store;
  void *pivot = ar[pivotIndex];

  /* move pivot to the end of the array */
  void *tmp = ar[right];
  ar[right] = ar[pivotIndex];
  ar[pivotIndex] = tmp;

  /* all values <= pivot are moved to front of array and pivot inserted
   * just after them. */
  store = left;
  for (idx = left; idx < right; idx++) {
    if (cmp (ar[idx], pivot) <= 0) {
      tmp = ar[idx];
      ar[idx] = ar[store];
      ar[store] = tmp;
      store++;
    }
  }

  tmp = ar[right];
  ar[right] = ar[store];
  ar[store] = tmp;
  return store;
}

Der Quicksort-Algorithmus, der 1960 von C. A. R. Hoare eingeführt wurde, wählt ein Element aus der Sammlung aus (manchmal zufällig, manchmal das ganz linke, manchmal das mittlere), um ein Array in zwei Unterarrays zu teilen. Quicksort besteht also aus zwei Schritten. Zuerst wird das Array partitioniert und dann wird jedes Subarray rekursiv sortiert.

Quicksort Zusammenfassung

Beste, Durchschnittlich: O(n log n), Schlechteste: O(ⁿ²)

sort (A)
  quicksort (A, 0, n-1)
end

quicksort (A, left, right)
  if left < right then
    pi = partition (A, left, right)
    quicksort (A, left, pi-1)
    quicksort (A, pi+1, right)
end

In diesem Pseudocode wird die Strategie für die Auswahl des Pivot-Index absichtlich nicht angegeben. Im zugehörigen Code gehen wir davon aus, dass es eine selectPivotIndex Funktion gibt, die einen geeigneten Index auswählt. Wir gehen hier nicht auf die fortgeschrittenen mathematischen Analysewerkzeuge ein, die nötig sind, um zu beweisen, dass Quicksort ein O(n log n)-Durchschnittsverhalten aufweist; weitere Details zu diesem Thema findest du in Cormen (2009).

Abbildung 4-7 zeigt Quicksort in Aktion. Jedes der schwarzen Quadrate steht für eine Pivot-Auswahl. Der erste ausgewählte Pivot ist "2", was sich als schlechte Wahl herausstellt, da er zwei Unterfelder der Größe 1 und 14 erzeugt. Beim nächsten rekursiven Aufruf von Quicksort auf dem rechten Subarray wird "12" als Pivot ausgewählt (in der vierten Zeile unten dargestellt), was zwei Subarrays der Größe 9 bzw. 4 ergibt. Du kannst bereits den Vorteil der Partitionierung erkennen, da die letzten vier Elemente im Array tatsächlich die größten vier Elemente sind, obwohl sie immer noch ungeordnet sind. Da die Auswahl der Pivots zufällig erfolgt, sind verschiedene Verhaltensweisen möglich. In einer anderen Ausführung, die in Abbildung 4-8 gezeigt wird, unterteilt der erste ausgewählte Pivot das Problem in zwei mehr oder weniger vergleichbare Aufgaben.

Kontext

Quicksort verhält sich im schlimmsten Fall quadratisch, wenn die Partitionierung bei jedem rekursiven Schritt eine Sammlung von n Elementen nur in eine "leere" und eine "große" Menge aufteilt, wobei eine dieser Mengen keine Elemente und die andere n - 1 hat (beachte, dass das Pivotelement das letzte der n Elemente liefert, also kein Element verloren geht).

Abbildung 4-7. Beispiel für die Ausführung von Quicksort

Lösung

Die in Beispiel 4-6 gezeigte Quicksort-Implementierung enthält eine Standardoptimierung, um Insertion Sort zu verwenden, wenn die Größe des zu sortierenden Subarrays unter eine bestimmte Mindestgröße fällt.

Beispiel 4-6. Quicksort-Implementierung in C

/**
 * Sort array ar[left,right] using Quicksort method.
 * The comparison function, cmp, is needed to properly compare elements.
 */
void do_qsort (void **ar, int (*cmp)(const void *, const void *),
               int left, int right) {
  int pivotIndex;
  if (right <= left) { return; }

  /* partition */
  pivotIndex = selectPivotIndex (ar, left, right);
  pivotIndex = partition (ar, cmp, left, right, pivotIndex);

  if (pivotIndex-1-left <= minSize) {
    insertion (ar, cmp, left, pivotIndex-1);
  } else {
    do_qsort (ar, cmp, left, pivotIndex-1);
  }
  if (right-pivotIndex-1 <= minSize) {
    insertion (ar, cmp, pivotIndex+1, right);
  } else {
    do_qsort (ar, cmp, pivotIndex+1, right);
  }
}

/**  Qsort straight */
void sortPointers (void **vals, int total_elems,
                   int (*cmp)(const void *, const void *)) {
  do_qsort (vals, cmp, 0, total_elems-1);
}

Die externe Methode selectPivotIndex(ar, left, right) wählt den Pivot-Wert aus, an dem das Feld aufgeteilt wird.

Analyse

Überraschenderweise kann Quicksort durch die Verwendung eines Zufallselements als Pivot eine durchschnittliche Leistung erzielen, die in der Regel besser ist als die anderer Sortieralgorithmen. Darüber hinaus gibt es zahlreiche Verbesserungen und Optimierungen, die für Quicksort erforscht wurden und die von allen Sortieralgorithmen die höchste Effizienz erreicht haben.

Im Idealfall teilt partition das ursprüngliche Array in zwei Hälften und Quicksort hat eine Leistung von O(n log n). In der Praxis ist Quicksort mit einem zufällig gewählten Pivot effektiv.

Im schlimmsten Fall wird das größte oder kleinste Element als Pivot ausgewählt. Wenn das passiert, macht Quicksort einen Durchlauf über alle Elemente im Array (in linearer Zeit), um nur ein einziges Element im Array zu sortieren. Wenn dieser Vorgang n - 1 Mal wiederholt wird, ergibt sich im schlimmsten Fall ein O(ⁿ²)-Verhalten.

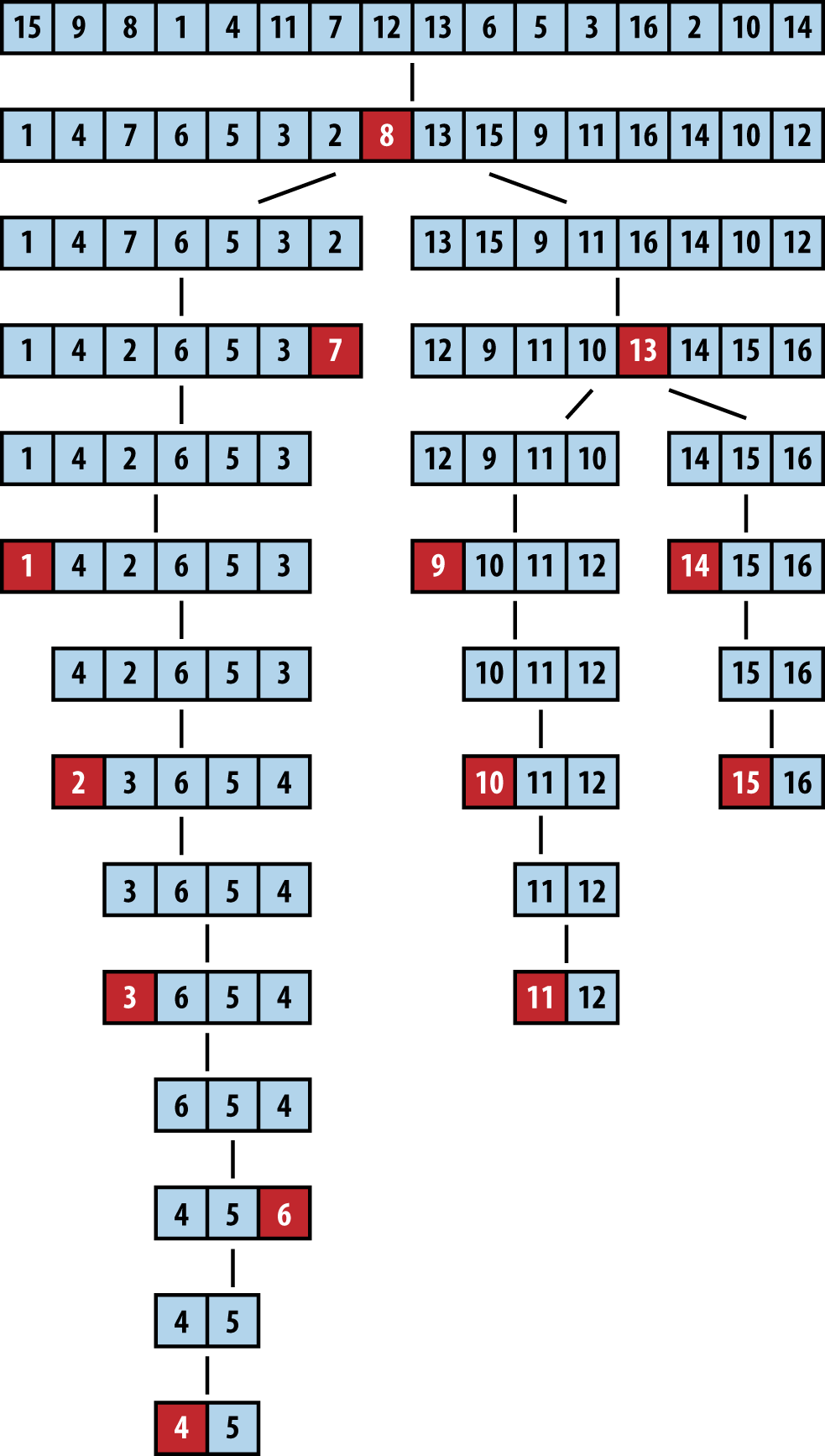
Abbildung 4-8. Ein anderes Quicksort-Verhalten

Variationen

Quicksort ist auf den meisten Systemen die bevorzugte Sortiermethode. Auf Unix-basierten Systemen gibt es eine eingebaute Bibliotheksfunktion namens qsort. Oft verwendet das Betriebssystem optimierte Versionen des Standard-Quicksort-Algorithmus. Zwei der am häufigsten zitierten Quellen für Optimierungen sind Sedgewick (1978) und Bentley und McIlroy (1993). Es ist aufschlussreich, dass einige Versionen des Linux-Betriebssystems qsort mit Heap Sort implementieren.

Zu den verschiedenen Optimierungen gehören:

• Erstelle einen Stapel, der die zu bearbeitenden Teilaufgaben speichert, um Rekursionen zu vermeiden

• Wähle den Pivot basierend auf der Median-der-Drei-Strategie

• Legen Sie die Mindestgröße der Partition fest, unterhalb derer Insertion Sort verwendet werden soll. Dieser Wert variiert je nach Implementierung und Maschinenarchitektur; im JDK 1.8 ist der Schwellenwert auf 7 gesetzt.

• Wenn du die beiden Teilprobleme bearbeitest, minimiere die Gesamtgröße des rekursiven Stapels, indem du das kleinere Teilproblem zuerst löst

Keine dieser Optimierungen wird jedoch das O(ⁿ²)-Worst-Case-Verhalten von Quicksort beseitigen. Die einzige Möglichkeit, eine O(n log n)-Leistung im schlimmsten Fall zu gewährleisten, ist die Verwendung einer Partitionsfunktion, die garantiert eine "vernünftige Annäherung" an den tatsächlichen Median der Menge findet. Der Blum-Floyd-Pratt-Rivest-Tarjan (BFPRT)-Partitionsalgorithmus (Blum et al., 1973) ist ein Algorithmus mit nachweislich linearer Zeit, hat aber nur theoretischen Wert. Eine Implementierung von BFPRT ist im Code Repository enthalten.

Einen Drehpunkt wählen

Die Auswahl des Pivotelements aus einem Subarray A[left, left + n) muss eine effiziente Operation sein ; sie sollte nicht die Überprüfung aller n Elemente des Subarrays erfordern. Einige Alternativen sind:

• Wähle zuerst oder zuletzt: A[links] oder A[links + n - 1]

• Wähle ein zufälliges Element in A[links, links + n - 1]

• Wähle den Median von k: den mittleren Wert von k Elementen aus A[links, links + n - 1].

Sedgewick berichtet, dass dieser Ansatz eine Verbesserung von 5 % bringt, aber es ist zu beachten, dass manche Datenarrangements selbst diese Alternative zu einer unterdurchschnittlichen Leistung zwingen (Musser, 1997). Es wurde auch ein Median von fünf Pivots gewählt. Die Durchführung weiterer Berechnungen zur Ermittlung des richtigen Pivotpunkts bringt aufgrund der zusätzlichen Rechenkosten nur selten positive Ergebnisse.

Bearbeitung der Partition

Bei der in Beispiel 4-5 gezeigten Methode partition werden Elemente, die kleiner oder gleich dem ausgewählten Pivot sind, an der Vorderseite des Subarrays eingefügt. Dieser Ansatz könnte die Größe der Subarrays für den rekursiven Schritt verzerren, wenn der ausgewählte Pivot viele doppelte Elemente im Array hat. Eine Möglichkeit, das Ungleichgewicht zu verringern, besteht darin, Elemente, die gleich dem Pivot sind, abwechselnd im ersten und zweiten Subarray zu platzieren.

Verarbeitung von Subarrays

Quicksort ergibt zwei rekursive Aufrufe von Quicksort auf kleineren Subarrays. Während die eine verarbeitet wird, wird der Aktivierungssatz der anderen auf den Ausführungsstapel gelegt. Wenn das größere Subarray zuerst verarbeitet wird, ist es möglich, eine lineare Anzahl von Aktivierungsdatensätzen gleichzeitig auf dem Stack zu haben (obwohl moderne Compiler diesen beobachteten Overhead eliminieren können). Um die mögliche Tiefe des Stapels zu minimieren, bearbeite zuerst das kleinere Subarray. Wenn die Tiefe der Rekursion ein vorhersehbares Problem darstellt, ist Quicksort vielleicht nicht für deine Anwendung geeignet.

Einfachere Insertion-Sort-Technik für kleine Subarrays verwenden

Bei kleinen Arrays ist Insertion Sort schneller als Quicksort, aber selbst bei großen Arrays zerlegt Quicksort das Problem letztlich so, dass zahlreiche kleine Unterarrays sortiert werden müssen. Eine gängige Methode, um die rekursive Leistung von Quicksort zu verbessern, besteht darin, Quicksort nur für große Subarrays aufzurufen und Insertion Sort für kleine Subarrays zu verwenden, wie in Beispiel 4-6 gezeigt.

Sedgewick (1978) schlägt vor, dass eine Kombination aus Median-of-Three und Insertion Sort für kleine Subarrays eine Beschleunigung von 20%-25% gegenüber reinem Quicksort bietet.

IntroSort

Das Umschalten auf Insertion Sort für kleine Subarrays ist eine lokale Entscheidung, die auf der Grundlage der Größe des Subarrays getroffen wird. Musser (1997) führte eine Quicksort-Variante namens IntroSort ein, die die Rekursionstiefe von Quicksort überwacht, um eine effiziente Verarbeitung zu gewährleisten. Wenn die Tiefe der Quicksort-Rekursion log(n)-Stufen überschreitet, schaltet IntroSort auf Heap Sort um. Die SGI-Implementierung der C++ Standard Template Library verwendet IntroSort als Standard-Sortiermechanismus.

Sortieren ohne Vergleiche

Am Ende dieses Kapitels werden wir zeigen, dass kein vergleichsbasierter Sortieralgorithmus n Elemente mit einer besseren Leistung als O(n log n) sortieren kann. Überraschenderweise gibt es potenziell schnellere Möglichkeiten, Elemente zu sortieren, wenn du etwas über diese Elemente im Voraus weißt. Wenn du zum Beispiel eine schnelle Hash-Funktion hast, die eine Sammlung von Elementen gleichmäßig in verschiedene, geordnete Eimer unterteilt, kannst du den folgenden Bucket-Sort-Algorithmus mit linearer O(n)-Leistung verwenden.

Eimer sortieren

Bei einer Menge von n Elementen konstruiert Bucket Sort eine Menge von n geordneten Eimern, in die die Elemente der Eingabemenge aufgeteilt werden; Bucket Sort reduziert seine Verarbeitungskosten auf Kosten dieses zusätzlichen Platzes. Wenn eine Hash-Funktion, hash(A[i]), die Eingabemenge von n Elementen gleichmäßig in diese n Bereiche aufteilen kann, kann Bucket Sort im schlimmsten Fall in O(n)-Zeit sortieren. Verwende Bucket Sort, wenn die folgenden zwei Eigenschaften zutreffen:

Gleichmäßige Verteilung

Die Eingabedaten müssen für einen bestimmten Bereich gleichmäßig verteilt sein. Auf der Grundlage dieser Verteilung werden n Buckets erstellt, um den Eingabebereich gleichmäßig aufzuteilen.

Geordnete Hash-Funktion

Die Eimer sind geordnet. Wenn i < j ist, sind die in den Eimer _bi eingefügten Elemente lexikografisch kleiner als die Elemente im Eimer _bj.

Zusammenfassung der Eimersortierung

Am besten, durchschnittlich, am schlechtesten: O(n)

sort (A)
  create n buckets B
  for i = 0 to n-1 do 
    k = hash(A[i])
    add A[i] to the k-th bucket B[k]
  extract (B, A) 
end

extract (B, A)
  idx = 0
  for i = 0 to n-1 do
    insertionSort (B[i]) 
    foreach element e in B[i] 
      A[idx++] = e
end

Erstelle eine Bucket-Liste und ordne alle Elemente dem richtigen Bucket zu.

Verarbeite alle Buckets, um die Werte in sortierter Reihenfolge zurück nach A zu extrahieren.

Wenn mehr als ein Element im Eimer ist, sortiere zuerst.

Kopiere die Elemente wieder an die richtige Stelle in A.

Bucket Sort eignet sich zum Beispiel nicht zum Sortieren beliebiger Zeichenketten, weil es normalerweise unmöglich ist, eine Hash-Funktion mit den erforderlichen Eigenschaften zu entwickeln. Sie kann jedoch verwendet werden, um eine Menge gleichmäßig verteilter Fließkommazahlen im Bereich [0, 1] zu sortieren.

Sobald alle zu sortierenden Elemente in die Buckets eingefügt sind, extrahiert Bucket Sort die Werte von links nach rechts, indem es den Inhalt der einzelnen Buckets mit Insertion Sort bearbeitet. Dadurch werden die Elemente in den jeweiligen Buckets geordnet, während die Werte aus den Buckets von links nach rechts extrahiert werden, um das ursprüngliche Array wieder aufzufüllen. Ein Ausführungsbeispiel ist in Abbildung 4-9 dargestellt.

Abbildung 4-9. Kleines Beispiel zur Demonstration von Bucket Sort

Lösung

In der C-Implementierung von Bucket Sort, die in Beispiel 4-7 gezeigt wird, speichert jeder Bucket eine verknüpfte Liste von Elementen, die in diesen Bucket gehasht wurden. Die Funktionen numBuckets und hash werden extern bereitgestellt und basieren auf der Eingabemenge.

Beispiel 4-7. Bucket Sort Implementierung in C

extern int hash (void *elt);
extern int numBuckets (int numElements);

/* linked list of elements in bucket. */
typedef struct entry {
  void          *element;
  struct entry  *next;
} ENTRY;

/* maintain count of entries in each bucket and pointer to its first entry */
typedef struct {
  int        size;
  ENTRY      *head;
} BUCKET;

/* Allocation of buckets and the number of buckets allocated */
static BUCKET *buckets = 0;
static int num = 0;

/** One by one remove and overwrite ar */
void extract (BUCKET *buckets, int (*cmp)(const void *, const void *),
              void **ar, int n) {
  int i, low;
  int idx = 0;
  for (i = 0; i < num; i++) {
    ENTRY *ptr, *tmp;
    if (buckets[i].size == 0) continue;   /* empty bucket */

    ptr = buckets[i].head;
    if (buckets[i].size == 1) {
      ar[idx++] = ptr->element;
      free (ptr);
      buckets[i].size = 0;
      continue;
    }

    /* insertion sort where elements are drawn from linked list and
     * inserted into array. Linked lists are released. */
    low = idx;
    ar[idx++] = ptr->element;
    tmp = ptr;
    ptr = ptr->next;
    free (tmp);

    while (ptr != NULL) {
     int i = idx-1;
     while (i >= low && cmp (ar[i], ptr->element) > 0) {
        ar[i+1] = ar[i];
        i--;
      }
      ar[i+1] = ptr->element;
      tmp = ptr;
      ptr = ptr->next;
      free (tmp);
      idx++;
    }
    buckets[i].size = 0;
  }
}

void sortPointers (void **ar, int n,
                   int (*cmp)(const void *, const void *)) {
  int i;
  num = numBuckets (n);
  buckets = (BUCKET *) calloc (num, sizeof (BUCKET));
  for (i = 0; i < n; i++) {
    int k = hash(ar[i]);

    /** Insert each element and increment counts */
    ENTRY *e = (ENTRY *) calloc (1, sizeof (ENTRY));
    e->element = ar[i];
    if (buckets[k].head == NULL) {
      buckets[k].head = e;
    } else {
      e->next = buckets[k].head;
      buckets[k].head = e;
    }

    buckets[k].size++;
  }

  /* now sort, read out, and overwrite ar. */
  extract (buckets, cmp, ar, n);

  free (buckets);
}

Für Zahlen, die gleichmäßig aus [0, 1) gezogen werden, enthält Beispiel 4-8 Beispielimplementierungen der Funktionen hash und numBuckets, die du verwenden kannst.

Beispiel 4-8. Hash- und numBuckets-Funktionen für den Bereich [0, 1].

static int num;

/** Number of buckets to use is the same as the number of elements. */
int numBuckets (int numElements) {
  num = numElements;
  return numElements;
}

/**
 * Hash function to identify bucket number from element. Customized
 * to properly encode elements in order within the buckets. Range of
 * numbers is from [0, 1), so we subdivide into buckets of size 1/num;
 */
int hash (double *d) {
  int bucket = num*(*d);
  return bucket;
}

Die Buckets könnten auch in festen Arrays gespeichert werden, die neu zugewiesen werden, wenn die Buckets voll sind, aber die Implementierung mit verknüpften Listen ist etwa 30-40% schneller.

Analyse

Die Funktion sortPointers aus Beispiel 4-7 sortiert jedes Element aus der Eingabe in den zugehörigen Bereich auf der Grundlage der angegebenen Funktion hash; dies benötigt O(n) Zeit. Aufgrund des sorgfältigen Designs der hash Funktion wissen wir, dass alle Elemente in Bucket _bi kleiner sind als die Elemente in Bucket _bj, wenn i < j.

Da die Werte aus den Buckets extrahiert und zurück in das Eingabefeld geschrieben werden, wird Insertion Sort verwendet, wenn ein Bucket mehr als ein einzelnes Element enthält. Damit Bucket Sort ein O(n)-Verhalten aufweist, müssen wir garantieren, dass die Gesamtzeit für das Sortieren jedes dieser Buckets ebenfalls O(n) ist. Definieren wir _ni als die Anzahl der Elemente, die in Bucket _bi aufgeteilt sind. Wir können _ni wie eine Zufallsvariable behandeln (mit Hilfe der statistischen Theorie). Betrachte nun den Erwartungswert E[_ni] für jeden Eimer _bi. Jedes Element in der Eingabemenge hat die Wahrscheinlichkeit p = 1/n, in einen bestimmten Bereich eingefügt zu werden, da jedes dieser Elemente gleichmäßig aus dem Bereich [0, 1) gezogen wird. Daher ist E[_ni] = n*p = n*(1/n) = 1, während die Varianz Var[_ni] = n*p*(1 - p) = (1 - 1/n) ist. Es ist wichtig, die Varianz zu berücksichtigen, weil einige Eimer leer sein werden und andere mehr als ein Element haben können; wir müssen sicher sein, dass kein Eimer zu viele Elemente hat. Auch hier greifen wir auf die statistische Theorie zurück, die die folgende Gleichung für Zufallsvariablen liefert:

E[ⁿⁱ²] = Var[_ni] + ^E2[_ni]

Aus dieser Gleichung können wir den erwarteten Wert von ⁿⁱ² berechnen. Dieser Wert ist entscheidend, denn er bestimmt die Kosten der Einfügesortierung, die im schlimmsten Fall O(ⁿ²) beträgt. Wir berechnen E[ⁿⁱ²] = (1 - 1/n) + 1 = (2 - 1/n), was zeigt, dass E[ⁿⁱ²] als eine Konstante betrachtet werden kann. Das heißt, wenn wir die Kosten für die Ausführung von Insertion Sort für alle n Buckets zusammenzählen, bleiben die erwarteten Leistungskosten O(n).

Variationen

Anstatt n Buckets zu erstellen, erstellt Hash Sort eine entsprechend große Anzahl von Buckets k, in die die Elemente aufgeteilt werden; je größer k wird, desto besser wird die Leistung von Hash Sort. Der Schlüssel zu Hash Sort ist eine Hash-Funktion hash(e), die für jedes Element e eine ganze Zahl zurückgibt, die hash(_ai) ≤ hash(_aj) ist, wenn _ai lexikografisch kleiner als _aj ist.

Die in Beispiel 4-9 definierte Hash-Funktion hash(e) arbeitet mit Elementen, die nur Kleinbuchstaben enthalten. Sie wandelt die ersten drei Zeichen der Zeichenkette (in der Darstellung zur Basis 26) in einen ganzzahligen Wert um. Für die Zeichenkette "abcdefgh" werden die ersten drei Zeichen ("abc") extrahiert und in den Wert 0*676 + 1*26 + 2 = 28 umgewandelt. Dieser String wird also in den Bucket mit der Bezeichnung 28 eingefügt.

Beispiel 4-9. hash und numBuckets Funktionen für Hash Sort

/** Number of buckets to use. */
int numBuckets (int numElements) {
  return 26*26*26;
}

/**
 * Hash function to identify bucket number from element. Customized
 * to properly encode elements in order within the buckets.
 */
int hash (void *elt) {
  return (((char*)elt)[0] - 'a')*676 +
         (((char*)elt)[1] - 'a')*26 +
         (((char*)elt)[2] - 'a');
}

Die Leistung von Hash Sort für verschiedene Bucket-Größen und Eingabemengen ist in Tabelle 4-5 dargestellt. Wir zeigen vergleichbare Sortierzeiten für Quicksort unter Verwendung des Median-of-three-Ansatzes für die Auswahl der pivotIndex.

Tabelle 4-5. Leistungsbeispiele für Hash Sort mit unterschiedlicher Anzahl von Buckets, verglichen mit Quicksort (in Sekunden)

n	26 Eimer	676 Eimer	17.576 Eimer	Quicksort
16	0.000005	0.000010	0.000120	0.000004
32	0.000006	0.000012	0.000146	0.000005
64	0.000011	0.000016	0.000181	0.000009
128	0.000017	0.000022	0.000228	0.000016
256	0.000033	0.000034	0.000249	0.000033
512	0.000074	0.000061	0.000278	0.000070
1,024	0.000183	0.000113	0.000332	0.000156
2,048	0.000521	0.000228	0.000424	0.000339
4,096	0.0016	0.000478	0.000646	0.000740
8,192	0.0058	0.0011	0.0011	0.0016
16,384	0.0224	0.0026	0.0020	0.0035
32,768	0.0944	0.0069	0.0040	0.0076
65,536	0.4113	0.0226	0.0108	0.0168
131,072	1.7654	0.0871	0.0360	0.0422

Beachte, dass Hash Sort mit 17.576 Buckets bei n > 8.192 Elementen besser abschneidet als Quicksort (und dieser Trend setzt sich mit zunehmendem n fort). Bei nur 676 Buckets, sobald n > 32.768 ist (bei durchschnittlich 48 Elementen pro Bucket), wird Hash Sort jedoch unweigerlich langsamer, da sich die Kosten für die Ausführung von Insertion Sort bei immer größeren Mengen summieren. Bei nur 26 Eimern vervierfacht sich die Leistung von Hash Sort, sobald n > 256 ist und sich die Problemgröße verdoppelt.

Sortieren mit zusätzlicher Speicherung

Die meisten Sortieralgorithmen sortieren eine Sammlung an Ort und Stelle, ohne dass eine nennenswerte zusätzliche Speicherung erforderlich ist. Wir stellen jetzt Merge Sort vor, das im schlimmsten Fall O(n log n) Verhalten bietet und dabei O(n) zusätzliche Speicherung benötigt. Er kann verwendet werden, um Daten, die extern in einer Datei gespeichert sind, effizient zu sortieren.

Zusammenführen Sortieren

Um eine Sammlung A zu sortieren, teilst du sie gleichmäßig in zwei kleinere Sammlungen auf, die dann jeweils sortiert werden. In einer letzten Phase werden die beiden sortierten Sammlungen wieder zu einer einzigen Sammlung der Größe n zusammengeführt. Eine naive Implementierung dieses Ansatzes, die hier gezeigt wird, verbraucht viel zu viel zusätzliche Speicherung:

sort (A)
  if A has less than 2 elements then
    return A
  else if A has 2 elements then
    swap elements of A if out of order
    return A

  sub1 = sort(left half of A)
  sub2 = sort(right half of A)

  merge sub1 and sub2 into new array B
  return B
end

Jeder rekursive Aufruf von sort benötigt Speicherplatz, der der Größe des Arrays oder O(n) entspricht, und es gibt O(log n) solche rekursiven Aufrufe; daher ist der Speicherbedarf für diese naive Implementierung O(n log n). Glücklicherweise gibt es eine Möglichkeit, nur O(n) Speicherung zu verwenden, wie wir jetzt diskutieren.

Input/Output

Das Ergebnis der Sortierung wird anstelle der ursprünglichen Sammlung A zurückgegeben. Die Kopie der internen Speicherung wird verworfen.

Zusammenfassung der Merge-Sortierung

Bester, Durchschnitt, Schlechtester: O(n log n)

sort (A)
  copy = copy of A 
  mergeSort (copy, A, 0, n)
end

mergeSort (A, result, start, end) 
  if end - start < 2 then return
  if end - start = 2 then
    swap elements of result if out of order
    return

  mid = (start + end)/2
  mergeSort (result, A, start, mid) 
  mergeSort (result, A, mid, end)

  merge left and right halves of A into result 
end

Mache eine vollständige Kopie aller Elemente.

Platziere die Elemente von A[start,end) in result[start,end) in sortierter Reihenfolge.

Sortiere results[start,mid) in A[start,mid).

Führe sortierte Subarrays in A wieder in result zusammen.

Lösung

Merge Sort führt die links- und rechtssortierten Subarrays zusammen, indem es zwei Indizes i und j verwendet, um über die linken (und rechten) Elemente zu iterieren. Dabei kopiert es immer das kleinere von A[i] und A[j] an die richtige Stelle result[idx]. Es gibt drei Fälle zu berücksichtigen:

• Die rechte Seite ist erschöpft(j ≥ end), in diesem Fall werden die verbleibenden Elemente von der linken Seite genommen

• Die linke Seite ist erschöpft(i ≥ mid), in diesem Fall werden die verbleibenden Elemente von der rechten Seite genommen

• Die linke und rechte Seite haben Elemente; wenn A[i] < A[j], füge A[i] ein, sonst füge A[j] ein

Wenn die Schleife for abgeschlossen ist, enthält das Ergebnis die zusammengeführten (und sortierten) Elemente aus dem ursprünglichenA[start, end). Beispiel 4-10 enthält die Python-Implementierung von Merge Sort.

Beispiel 4-10. Merge Sort Implementierung in Python

def sort (A):
  """merge sort A in place."""
  copy = list (A)
  mergesort_array (copy, A, 0, len(A))

def mergesort_array (A, result, start, end):
   """Mergesort array in memory with given range."""
  if end - start < 2:
    return
  if end - start == 2:
    if result[start] > result[start+1]:
      result[start],result[start+1] = result[start+1],result[start]
    return

  mid = (end + start) // 2
  mergesort_array (result, A, start, mid)
  mergesort_array (result, A, mid, end)

  # merge A left- and right- side
  i = start
  j = mid
  idx = start
  while idx < end:
    if j >= end or (i < mid and A[i] < A[j]):
      result[idx] = A[i]
      i += 1
    else:
      result[idx] = A[j]
      j += 1

    idx += 1

Analyse

Merge Sort schließt die "Merge"-Phase in O(n)-Zeit ab, nachdem es die linke und rechte Hälfte des Bereichs A[start, end) rekursiv sortiert und die richtig geordneten Elemente in das als Ergebnis referenzierte Array platziert hat.

Da copy eine echte Kopie des gesamten Arrays A ist, funktionieren die abschließenden Basisfälle der Rekursion , weil sie die ursprünglichen Elemente des Arrays direkt an ihren jeweiligen Indexpositionen referenzieren. Diese Beobachtung ist sehr raffiniert und der Schlüssel zum Algorithmus. Außerdem erfordert der abschließende Zusammenführungsschritt nur O(n) Operationen, so dass die Gesamtleistung O(n log n) bleibt. Da der Algorithmus nur für das Kopieren zusätzlichen Platz benötigt, ist der gesamte Platzbedarf O(n).

Variationen

Von allen Sortieralgorithmen lässt sich Merge Sort am einfachsten auf die Arbeit mit externen Daten übertragen. Beispiel 4-11 enthält eine vollständige Java-Implementierung, die das Memory Mapping von Daten nutzt, um eine Datei mit binär kodierten ganzen Zahlen effizient zu sortieren. Dieser Sortieralgorithmus setzt voraus, dass die Elemente alle die gleiche Größe haben. Daher kann er nicht so einfach angepasst werden, um beliebige Strings oder andere Elemente mit variabler Länge zu sortieren.

Beispiel 4-11. Externe Merge Sort Implementierung in Java

public static void mergesort (File A) throws IOException {
  File copy = File.createTempFile ("Mergesort", ".bin");
  copyFile(A, copy);

  RandomAccessFile src = new RandomAccessFile (A, "rw");
  RandomAccessFile dest = new RandomAccessFile (copy, "rw");
  FileChannel srcC = src.getChannel();
  FileChannel destC = dest.getChannel();
  MappedByteBuffer srcMap = srcC.map (FileChannel.MapMode.READ_WRITE,
                                      0, src.length());
  MappedByteBuffer destMap = destC.map (FileChannel.MapMode.READ_WRITE,
                                      0, dest.length());

  mergesort (destMap, srcMap, 0, (int) A.length());

  // The following two invocations are only needed on Windows platform:
  closeDirectBuffer (srcMap);
  closeDirectBuffer (destMap);
  src.close();
  dest.close();
  copy.deleteOnExit();
}

static void mergesort (MappedByteBuffer A, MappedByteBuffer result,
                       int start, int end) throws IOException {
  if (end - start < 8) {
    return;
  }

  if (end - start == 8) {
    result.position (start);
    int left = result.getInt();
    int right = result.getInt();
    if (left > right) {
      result.position (start);
      result.putInt (right);
      result.putInt (left);
    }
    return;
  }

  int mid = (end + start)/8*4;
  mergesort (result, A, start, mid);
  mergesort (result, A, mid, end);

  result.position (start);
  for (int i = start, j = mid, idx=start; idx < end; idx += 4) {
    int Ai = A.getInt (i);
    int Aj = 0;
    if (j < end) { Aj = A.getInt (j); }
    if (j >= end || (i < mid && Ai < Aj)) {
      result.putInt (Ai);
      i += 4;
    } else {
      result.putInt (Aj);
      j += 4;
    }
  }
}

Die Struktur ist identisch mit der Merge Sort-Implementierung, aber sie verwendet eine Memory-Mapping-Struktur, um die im Dateisystem gespeicherten Daten effizient zu verarbeiten. Unter Windows-Betriebssystemen kann es zu Problemen kommen, wenn die Daten von MappedByteBuffer nicht richtig geschlossen werden. Das Repository enthält eine Umgehungsmethode closeDirectBuffer(MappedByteBuffer), die diese Aufgabe übernimmt.

String Benchmark Ergebnisse

Um den passenden Algorithmus für verschiedene Daten auszuwählen, musst du einige Eigenschaften deiner Eingabedaten kennen. Wir haben mehrere Benchmark-Datensätze erstellt, um zu zeigen, wie die in diesem Kapitel vorgestellten Algorithmen im Vergleich zueinander abschneiden. Beachte, dass die tatsächlichen Werte der erzeugten Tabellen weniger wichtig sind, da sie die spezifische Hardware widerspiegeln, auf der die Benchmarks ausgeführt wurden. Stattdessen solltest du auf die relative Leistung der Algorithmen auf den entsprechenden Datensätzen achten:

Zufällige Zeichenfolgen

In diesem Kapitel haben wir die Leistung von Sortieralgorithmen beim Sortieren von 26-stelligen Zeichenketten gezeigt, die Permutationen der Buchstaben des Alphabets sind. Da es n! solche Zeichenfolgen gibt, also ungefähr 4,^03*1026 Zeichenfolgen, gibt es in unseren Beispieldatensätzen nur wenige doppelte Zeichenfolgen. Außerdem sind die Kosten für den Vergleich von Elementen nicht konstant, da gelegentlich mehrere Zeichen verglichen werden müssen.

Doppelt genaue Gleitkommawerte

Mithilfe von Pseudozufallsgeneratoren, die auf den meisten Betriebssystemen verfügbar sind, erzeugen wir eine Reihe von Zufallszahlen aus dem Bereich [0, 1). In dem Beispieldatensatz gibt es im Wesentlichen keine doppelten Werte und die Kosten für den Vergleich zweier Elemente sind eine feste Konstante. Die Ergebnisse dieser Datensätze sind hier nicht enthalten, können aber im Code-Repository nachgelesen werden.

Die den Sortieralgorithmen zur Verfügung gestellten Eingabedaten können vorverarbeitet werden, um einige der folgenden Eigenschaften zu gewährleisten (nicht alle sind kompatibel):

Sortiert

Die Eingabeelemente können in aufsteigender Reihenfolge (das eigentliche Ziel) oder in absteigender Reihenfolge vorsortiert werden.

Killer-Median-von-Drei

Musser (1997) entdeckte eine Ordnung, die sicherstellt, dass Quicksort O(ⁿ²) Vergleiche benötigt, wenn der Median von drei zur Auswahl eines Pivots verwendet wird.

Beinahe sortiert

Bei einem sortierten Datensatz können wir k Paare von Elementen zum Tauschen und den Abstand d, mit dem getauscht werden soll, auswählen (oder 0, wenn zwei beliebige Paare getauscht werden können). Mit dieser Fähigkeit kannst du Eingabemengen konstruieren, die deiner Eingabemenge besser entsprechen.

Die folgenden Tabellen sind von links nach rechts geordnet, je nachdem, wie gut die Algorithmen in der letzten Zeile der Tabelle abschneiden. Um die Ergebnisse in den Tabellen 4-6 bis 4-8 zu erhalten, haben wir jeden Versuch 100 Mal durchgeführt und die besten und schlechtesten Ergebnisse aussortiert. Der Durchschnitt der verbleibenden 98 Versuche ist in diesen Tabellen angegeben. Die Spalten mit der Bezeichnung "Quicksort ^BFPRT4 minSize = 4" beziehen sich auf eineQuicksort-Implementierung, die BFPRT (mit 4er-Gruppen) verwendet, um den Partitionswert auszuwählen, und auf Insertion Sort umschaltet, wenn ein zu sortierendes Subarray vier oder weniger Elemente hat.

Weil die Leistung von Quicksort Median-of-Three so schnell abnimmt, wurden in Tabelle 4-8 nur 10 Versuche durchgeführt.

Tabelle 4-6. Leistungsergebnisse (in Sekunden) bei zufälligen 26-Buchstaben-Permutationen des Alphabets

n	Hash Sort 17.576 Eimer	Quicksort median-of-three	Zusammenführen Sortieren	Heap Sort	Quicksort BFPRT4 minSize = 4
4,096	0.000631	0.000741	0.000824	0.0013	0.0028
8,192	0.0011	0.0016	0.0018	0.0029	0.0062
16,384	0.0020	0.0035	0.0039	0.0064	0.0138
32,768	0.0040	0.0077	0.0084	0.0147	0.0313
65,536	0.0107	0.0168	0.0183	0.0336	0.0703
131,072	0.0359	0.0420	0.0444	0.0893	0.1777

Tabelle 4-7. Leistung (in Sekunden) bei sortierten zufälligen 26-Buchstaben-Permutationen des Alphabets

n	Einfügen Sortieren	Zusammenführen sortieren	Quicksort median-of-three	Hash Sort 17.576 Eimer	Heap Sort	Quicksort BFPRT4 minSize = 4
4,096	0.000029	0.000434	0.00039	0.000552	0.0012	0.0016
8,192	0.000058	0.000932	0.000841	0.001	0.0026	0.0035
16,384	0.000116	0.002	0.0018	0.0019	0.0056	0.0077
32,768	0.000237	0.0041	0.0039	0.0038	0.0123	0.0168
65,536	0.000707	0.0086	0.0085	0.0092	0.0269	0.0364
131,072	0.0025	0.0189	0.0198	0.0247	0.0655	0.0834

Tabelle 4-8. Leistung (in Sekunden) bei Killer-Median-Daten

n	Zusammenführen sortieren	Hash Sort 17.576 Eimer	Heap Sort	Quicksort BFPRT4 minSize = 4	Quicksort median-of-three
4,096	0.000505	0.000569	0.0012	0.0023	0.0212
8,192	0.0011	0.0010	0.0026	0.0050	0.0841
16,384	0.0023	0.0019	0.0057	0.0108	0.3344
32,768	0.0047	0.0038	0.0123	0.0233	1.3455
65,536	0.0099	0.0091	0.0269	0.0506	5.4027
131,072	0.0224	0.0283	0.0687	0.1151	38.0950

Analyse-Techniken

Wenn wir einen Sortieralgorithmus analysieren, müssen wir seine Best-Case-, Worst-Case- und Average-Case-Leistung erklären (wie in Kapitel 2 beschrieben). Der durchschnittliche Fall ist in der Regel am schwierigsten zu quantifizieren und beruht auf fortgeschrittenen mathematischen Techniken und Schätzungen. Er setzt außerdem voraus, dass die Wahrscheinlichkeit, dass die Eingabe teilweise sortiert ist, einigermaßen bekannt ist. Selbst wenn ein Algorithmus nachweislich wünschenswerte Durchschnittskosten hat, kann seine Umsetzung einfach unpraktisch sein. Jeder Sortieralgorithmus in diesem Kapitel wird sowohl anhand seines theoretischen Verhaltens als auch anhand seines tatsächlichen Verhaltens in der Praxis analysiert.

Ein grundlegendes Ergebnis in der Informatik ist, dass kein Algorithmus, der durch den Vergleich von Elementen sortiert, im durchschnittlichen oder schlimmsten Fall eine bessere Leistung als O(n log n) erzielen kann. Wir skizzieren jetzt einen Beweis. Bein Elementen gibt es n! Permutationen dieser Elemente. Jeder Algorithmus, der durch paarweise Vergleiche sortiert, entspricht einem binären Entscheidungsbaum. Die Blätter des Baums entsprechen einer zugrundeliegenden Permutation, und jede Permutation muss mindestens ein Blatt im Baum haben. Die Knoten auf einem Pfad von der Wurzel zu einem Blatt entsprechen einer Folge von Vergleichen. Die Höhe eines solchen Baums ist die Anzahl der Vergleichsknoten auf dem längsten Pfad von der Wurzel zu einem Blattknoten. Die Höhe des Baums inAbbildung 4-10 ist zum Beispiel 5, weil in allen Fällen nur fünf Vergleiche nötig sind (obwohl in vier Fällen nur vier Vergleiche nötig sind).

Konstruiere einen binären Entscheidungsbaum, bei dem jeder interne Knoten des Baums einen Vergleich _ai ≤ _aj darstellt und die Blätter des Baums eine der n! Um eine Menge von n Elementen zu sortieren, beginne bei der Wurzel und werte die Aussagen in jedem Knoten aus. Wenn die Aussage wahr ist, gehst du zum linken Kind, andernfalls gehst du zum rechten Kind. Abbildung 4-10 zeigt einen beispielhaften Entscheidungsbaum für vier Elemente.

Abbildung 4-10. Binärer Entscheidungsbaum für die Ordnung von vier Elementen

Wir könnten viele verschiedene binäre Entscheidungsbäume konstruieren. Wir behaupten jedoch, dass wir bei einem beliebigen binären Entscheidungsbaum für den Vergleich von n Elementen seine minimale Höhehberechnen können- das heißt, es muss einen Blattknoten geben, der hVergleichsknoten im Baum von der Wurzel bis zu diesem Blatt erfordert. Betrachte einen vollständigen binären Baum mit der Höhe h, in dem alle Nicht-Blatt-Knoten sowohl ein linkes als auch ein rechtes Kind haben. Dieser Baum enthält insgesamtn = ^2h - 1 Knoten und die Höhe h = log(n + 1); wenn der Baum nicht vollständig ist, könnte er auf seltsame Weise unausgeglichen sein, aber wir wissen, dassh ≥ ⌈log(n + 1)⌉ ist. Jeder binäre Entscheidungsbaum mit n! Blattknoten beweist bereits, dass er insgesamt mindestens n! Wir müssen nur h = ⌈log(n!)⌉ berechnen, um die Höhe eines solchen binären Entscheidungsbaums zu bestimmen. Wir machen uns die folgenden Eigenschaften von Logarithmen zunutze: log(a*b) = log(a) + log(b) und log(x^y) = y*log(x).

h = log(n!) = log(n *(n - 1) *(n - 2) * ... * 2 * 1)

h > log(n *(n - 1) *(n - 2) * ... * n/2)

h > log ((n/2^)n/2)

h >(n/2) * log(n/2)

h >(n/2) *(log(n) - 1)

Daher ist h >(n/2)*(log(n) - 1). Was bedeutet das? Bei nzu sortierenden Elementen gibt es mindestens einen Pfad von der Wurzel zu einem Blatt der Größe h. Das bedeutet, dass ein Algorithmus, der durch Vergleich sortiert, mindestens so viele Vergleiche benötigt, um die nElemente zu sortieren. Beachte, dass h durch eine Funktion f(n) berechnet wird; in diesem Fall ist f(n) = (1/2)*n*log(n) - n/2, was bedeutet, dass jeder Sortieralgorithmus, der Vergleiche verwendet, O(n log n) Vergleiche zum Sortieren benötigt.

Referenzen

Bentley, J. und M. McIlroy, "Engineering a sort function", Software-Practice and Experience, 23(11): 1249-1265, 1993, http://dx.doi.org/10.1002/spe.4380231105.

Blum, M., R. Floyd, V. Pratt, R. Rivest, und R. Tarjan, "Time bounds for selection," Journal of Computer and System Sciences, 7(4): 448–461, 1973, http://dx.doi.org/10.1016/S0022-0000(73)80033-9.

Cormen, T. H., C. Leiserson, R. Rivest, and C. Stein, Introduction to Algorithms. Dritte Auflage. MIT Press, 2009.

Davis, M. und K. Whistler, "Unicode Collation Algorithm, Unicode Technical Standard #10," June 2015, http://unicode.org/reports/tr10/.

Gilreath, W., "Hash sort: A linear time complexity multiple-dimensional sort algorithm," Proceedings, First Southern Symposium on Computing, 1998, http://arxiv.org/abs/cs.DS/0408040.

Musser, D., "Introspective sorting and selection algorithms," Software-Practice and Experience, 27(8): 983-993, 1997.

Sedgewick, R., "Implementing Quicksort programs," Communications ACM, 21(10): 847-857, 1978, http://dx.doi.org/10.1145/359619.359631.

Trivedi, K. S., Probability and Statistics with Reliability, Queueing, and Computer Science Applications. Zweite Auflage. Wiley-Blackwell Publishing, 2001.