Think DSP

Chapter 8. Filtering and Convolution

In this chapter I present one of the most important and useful ideas related to signal processing: the Convolution Theorem. But before we can understand the Convolution Theorem, we have to understand convolution. I’ll start with a simple example, smoothing, and we’ll go from there.

The code for this chapter is in chap08.ipynb, which is in the repository for this book (see “Using the Code”). You can also view it at http://tinyurl.com/thinkdsp08.

Smoothing

Smoothing is an operation that tries to remove short-term variations from a signal in order to reveal long-term trends. For example, if you were to plot daily changes in the price of a stock, it would look noisy; a smoothing operator might make it easier to see whether the price was generally going up or down over time.

A common smoothing algorithm is a moving average, which computes the mean of the previous n values, for some value of n.

For example, Figure 8-1 shows the daily closing price of Facebook stock from May 17, 2012 to December 8, 2015. The gray line is the raw data, and the darker line shows the 30-day moving average. Smoothing removes the most extreme changes and makes it easier to see long-term trends.

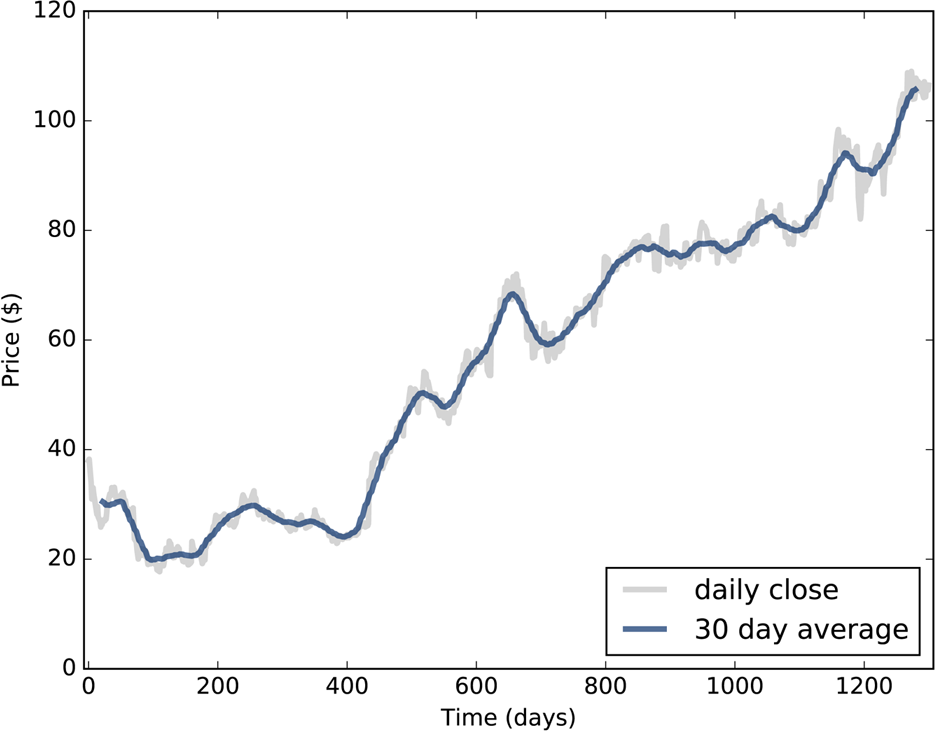
Figure 8-1. Daily closing price of Facebook stock and a 30-day moving average.

Smoothing operations also apply to sound signals. As an example, I’ll start with a square wave at 440 Hz. As ...