Think Bayes, 2. Auflage

Kapitel 4. Schätzung der Proportionen

Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: [e-mail]

Im vorigen Kapitel haben wir das 101-Schalen-Problem gelöst, und ich habe zugegeben, dass es nicht wirklich darum geht, zu erraten, aus welcher Schale die Kekse stammen, sondern darum, Proportionen zu schätzen.

In diesem Kapitel machen wir einen weiteren Schritt in Richtung Bayes'sche Statistik, indem wir das Euro-Problem lösen. Wir beginnen mit der gleichen Prioritätsverteilung und werden sehen, dass die Aktualisierung mathematisch gesehen die gleiche ist. Ich werde jedoch argumentieren, dass es sich philosophisch gesehen um ein anderes Problem handelt, und ich werde es nutzen, um zwei entscheidende Elemente der Bayes'schen Statistik vorzustellen: die Auswahl von Prior-Verteilungen und die Verwendung von Wahrscheinlichkeitsrechnungen zur Darstellung des Unbekannten.

Das Euro-Problem

In Information Theory, Inference, and Learning Algorithms stellt David MacKay dieses Problem dar:

Am Freitag, den 4. Januar 2002, erschien in The Guardian eine statistische Erklärung:

Eine belgische Ein-Euro-Münze, die 250 Mal auf den Rand gedreht wurde, zeigte 140 Mal Kopf und 110 Mal Zahl. "Das sieht für mich sehr verdächtig aus", sagt Barry Blight, ein Statistikdozent an der London School of Economics. "Wenn die Münze unvoreingenommen wäre, läge die Wahrscheinlichkeit für ein so extremes Ergebnis bei weniger als 7 %.

Aber sind diese Daten ein Beweis dafür, dass die Münze nicht fair, sondern verzerrt ist?

Um diese Frage zu beantworten, gehen wir in zwei Schritten vor. Zuerst verwenden wir die Binomialverteilung, um herauszufinden, woher die 7 % stammen. Dann verwenden wir den Satz von Bayes, um die Wahrscheinlichkeit zu schätzen, dass diese Münze Kopf zeigt.

Die Binomialverteilung

Angenommen, ich sage dir, dass eine Münze "fair" ist, d.h. die Wahrscheinlichkeit, dass Kopf ist, beträgt 50%. Wenn du sie zweimal wirfst, gibt es vier Ergebnisse: HH, HT,TH und TT. Alle vier Ergebnisse haben die gleiche Wahrscheinlichkeit, nämlich 25%.

Wenn wir die Gesamtzahl der Köpfe zusammenzählen, gibt es drei mögliche Ergebnisse: 0, 1 oder 2. Die Wahrscheinlichkeiten für 0 und 2 sind 25% und die Wahrscheinlichkeit für 1 ist 50%.

Allgemeiner ausgedrückt: Nehmen wir an, die Wahrscheinlichkeit von Köpfen ist $p$ und wir werfen die Münze $n$ mal. Die Wahrscheinlichkeit, dass wir insgesamt $k$ Köpfe erhalten, ist durch die Binomialverteilung gegeben:

$$\left(\genfrac{}{}{0pt}{}{n}{k}\right)p^k{(1-p)}^{n-k}$$

für jeden Wert von $k$ von 0 bis $n$einschließlich beider Werte. Der Term $\left(\genfrac{}{}{0pt}{}{n}{k}\right)$ ist derBinomialkoeffizient, der normalerweise als "n wähle k" ausgesprochen wird.

Wir könnten diesen Ausdruck selbst auswerten, aber wir können auch die SciPy-Funktion binom.pmf verwenden. Wenn wir zum Beispiel eine Münze n=2 werfen und die Wahrscheinlichkeit für Kopf ist p=0.5, dann ist die Wahrscheinlichkeit für k=1 Kopf:

from scipy.stats import binom

n = 2
p = 0.5
k = 1

binom.pmf(k, n, p)

0.5

Anstatt einen einzelnen Wert für k anzugeben, können wirbinom.pmf auch mit einem Array von Werten aufrufen:

import numpy as np
ks = np.arange(n+1)

ps = binom.pmf(ks, n, p)
ps

array([0.25, 0.5 , 0.25])

Das Ergebnis ist ein NumPy-Array mit der Wahrscheinlichkeit von 0, 1 oder 2 Köpfen. Wenn wir diese Wahrscheinlichkeiten in ein Pmf setzen, ist das Ergebnis die Verteilung vonk für die gegebenen Werte von n und p.

So sieht es aus:

from empiricaldist import Pmf

pmf_k = Pmf(ps, ks)
pmf_k

	Probs
0	0.25
1	0.50
2	0.25

Die folgende Funktion berechnet die Binomialverteilung für gegebene Werte von n und p und gibt ein Pmf zurück, das das Ergebnis darstellt:

def make_binomial(n, p):
    """Make a binomial Pmf."""
    ks = np.arange(n+1)
    ps = binom.pmf(ks, n, p)
    return Pmf(ps, ks)

So sieht es bei n=250 und p=0.5 aus:

pmf_k = make_binomial(n=250, p=0.5)

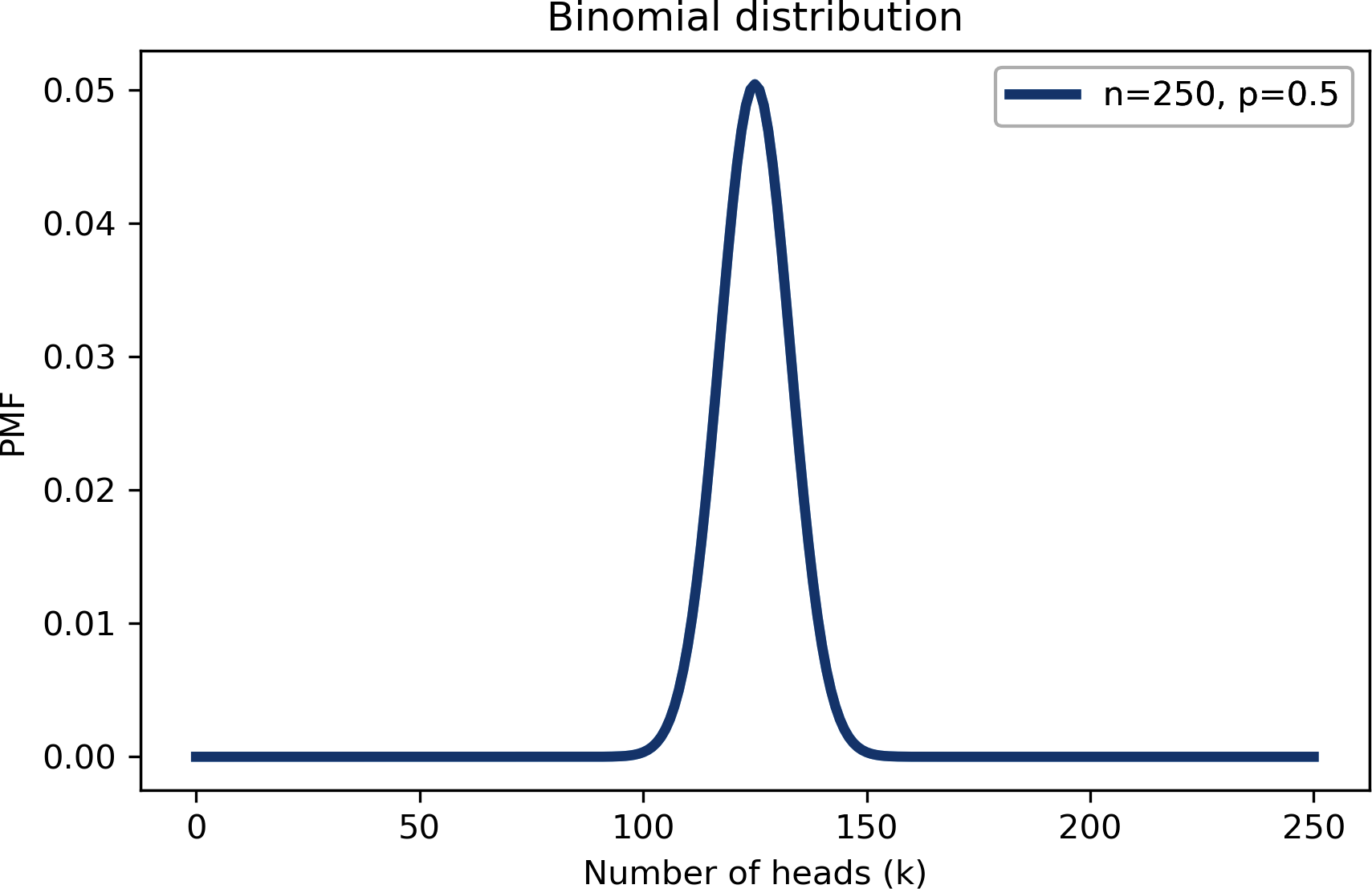
Die wahrscheinlichste Menge in dieser Verteilung ist 125:

pmf_k.max_prob()

125

Aber auch wenn es die wahrscheinlichste Menge ist, beträgt die Wahrscheinlichkeit, dass wir genau 125 Köpfe bekommen, nur etwa 5%:

pmf_k[125]

0.05041221314731537

In MacKays Beispiel haben wir 140 Köpfe, was noch unwahrscheinlicher ist als 125:

pmf_k[140]

0.008357181724917673

In dem Artikel, den MacKay zitiert, sagt der Statistiker: "Wenn die Münze unvoreingenommen wäre, läge die Chance auf ein so extremes Ergebnis bei weniger als 7 %."

Wir können die Binomialverteilung verwenden, um seine Berechnungen zu überprüfen. Die folgende Funktionnimmt eine PMF und berechnet die Gesamtwahrscheinlichkeit von Mengen, die größer oder gleich sind threshold:

def prob_ge(pmf, threshold):
    """Probability of quantities greater than threshold."""
    ge = (pmf.qs >= threshold)
    total = pmf[ge].sum()
    return total

Hier ist die Wahrscheinlichkeit, 140 Köpfe oder mehr zu bekommen:

prob_ge(pmf_k, 140)

0.033210575620022706

Pmf bietet eine Methode, die die gleiche Berechnung durchführt:

pmf_k.prob_ge(140)

0.033210575620022706

Das Ergebnis liegt bei 3,3 % und damit unter den angegebenen 7 %. Der Grund für die Differenz ist, dass der Statistiker alle Ergebnisse "so extrem wie" 140 einbezieht, was Ergebnisse kleiner oder gleich 110 einschließt.

Um zu verstehen, woher das kommt, erinnere dich daran, dass die erwartete Anzahl der Köpfe 125 beträgt. Wenn wir 140 erhalten, haben wir diese Erwartung um 15 übertroffen. Und wenn wir 110 bekommen, liegen wir 15 Punkte darunter.

7% ist die Summe dieser beiden "Schwänze", wie in der folgenden Abbildung dargestellt:

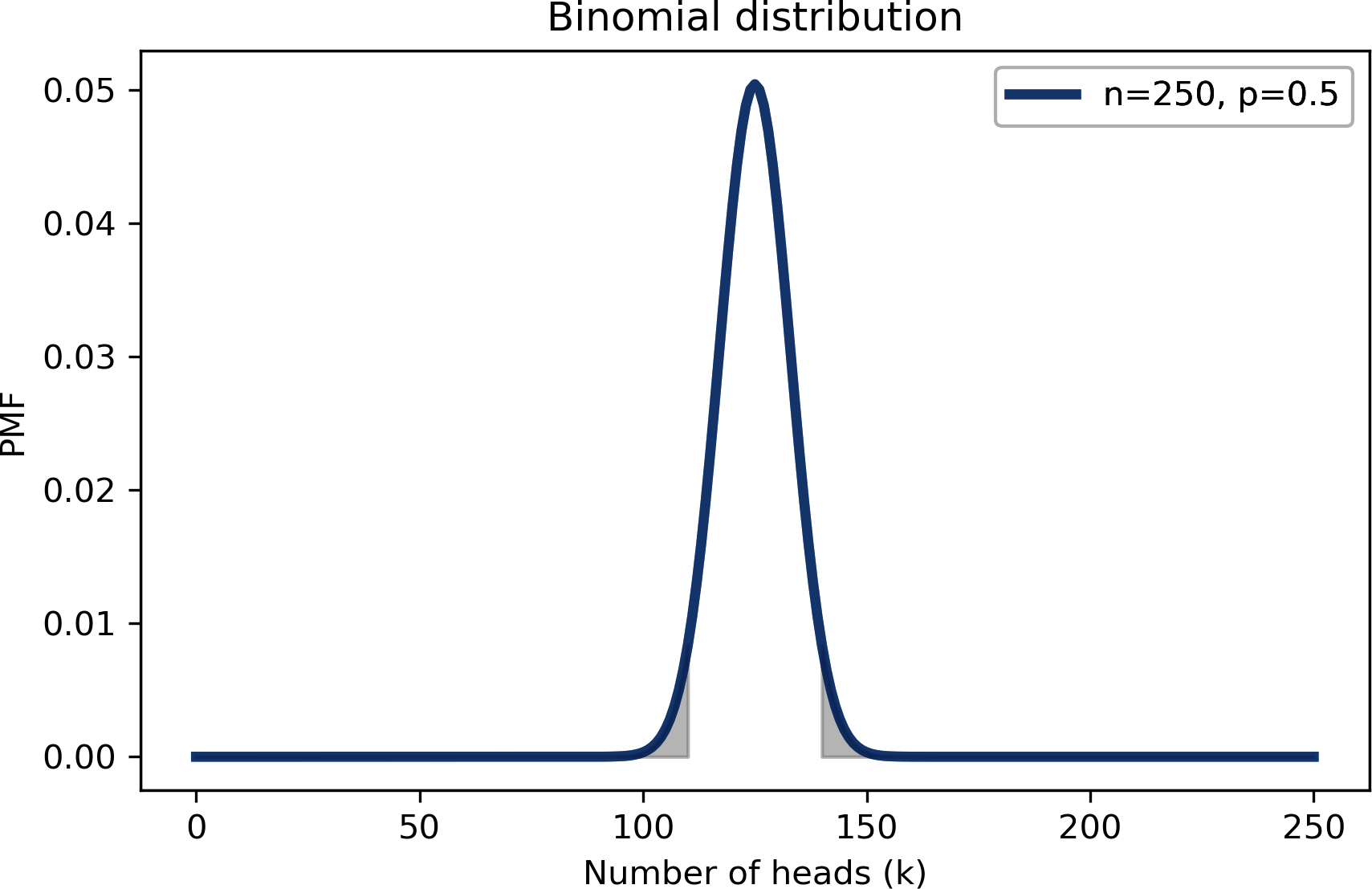
So berechnen wir die Gesamtwahrscheinlichkeit des linken Schwanzes:

pmf_k.prob_le(110)

0.033210575620022706

Die Wahrscheinlichkeit von Ergebnissen, die kleiner oder gleich 110 sind, beträgt ebenfalls 3,3 %, so dass die Gesamtwahrscheinlichkeit von Ergebnissen, die "so extrem" wie 140 sind, 6,6 % beträgt.

Der Punkt bei dieser Berechnung ist, dass diese extremen Ergebnisse unwahrscheinlich sind, wenn die Münze fair ist.

Das ist interessant, aber es beantwortet nicht MacKays Frage. Schauen wir mal, ob wir es können.

Bayes'sche Schätzung

Jede Münze hat eine gewisse Wahrscheinlichkeit, Kopf zu bekommen, wenn sie auf Kanten geworfen wird; ich nenne diese Wahrscheinlichkeit x. Es liegt nahe zu glauben, dass x von den physikalischen Eigenschaften der Münze abhängt, z. B. von der Gewichtsverteilung. Wenn eine Münze perfekt ausbalanciert ist, erwarten wir, dassx in der Nähe von 50 % liegt, aber bei einer schiefen Münze könnte x wesentlich anders sein. Mithilfe des Bayes'schen Theorems und der beobachteten Daten können wir x schätzen.

Der Einfachheit halber beginne ich mit einem einheitlichen Prior, der davon ausgeht, dass alle Werte von x gleich wahrscheinlich sind. Das ist vielleicht keine vernünftige Annahme, also werden wir später noch andere Prioritäten in Betracht ziehen.

So können wir eine einheitliche Prioritätenliste erstellen:

hypos = np.linspace(0, 1, 101)
prior = Pmf(1, hypos)

hypos ist ein Feld mit gleichmäßig verteilten Werten zwischen 0 und 1.

Wir können die Hypothesen verwenden, um die Wahrscheinlichkeiten zu berechnen, etwa so:

likelihood_heads = hypos
likelihood_tails = 1 - hypos

Ich werde die Wahrscheinlichkeiten für Kopf und Zahl in ein Wörterbuch schreiben, um die Aktualisierung zu vereinfachen:

likelihood = {
    'H': likelihood_heads,
    'T': likelihood_tails
}

Um die Daten darzustellen, konstruiere ich eine Zeichenkette mit H, die 140 Mal wiederholt wird, und T, die 110 Mal wiederholt wird:

dataset = 'H' * 140 + 'T' * 110

Die folgende Funktion führt die Aktualisierung durch:

def update_euro(pmf, dataset):
    """Update pmf with a given sequence of H and T."""
    for data in dataset:
        pmf *= likelihood[data]

    pmf.normalize()

Das erste Argument ist eine Pmf, die den Prior darstellt. Das zweite Argument ist eine Folge von Zeichenketten. Jedes Mal, wenn wir die Schleife durchlaufen, multiplizieren wir pmf mit der Wahrscheinlichkeit eines Ergebnisses, H für Kopf oder Tfür Zahl.

Beachte, dass normalize außerhalb der Schleife liegt, sodass die posterioreVerteilung nur einmal, am Ende, normalisiert wird. Das ist effizienter als die Normalisierung nach jedem Spin (obwohl wir später sehen werden, dass dies auch Probleme mit der Fließkommaarithmetik verursachen kann).

So nutzen wir update_euro:

posterior = prior.copy()
update_euro(posterior, dataset)

Und so sieht das Hinterteil aus:

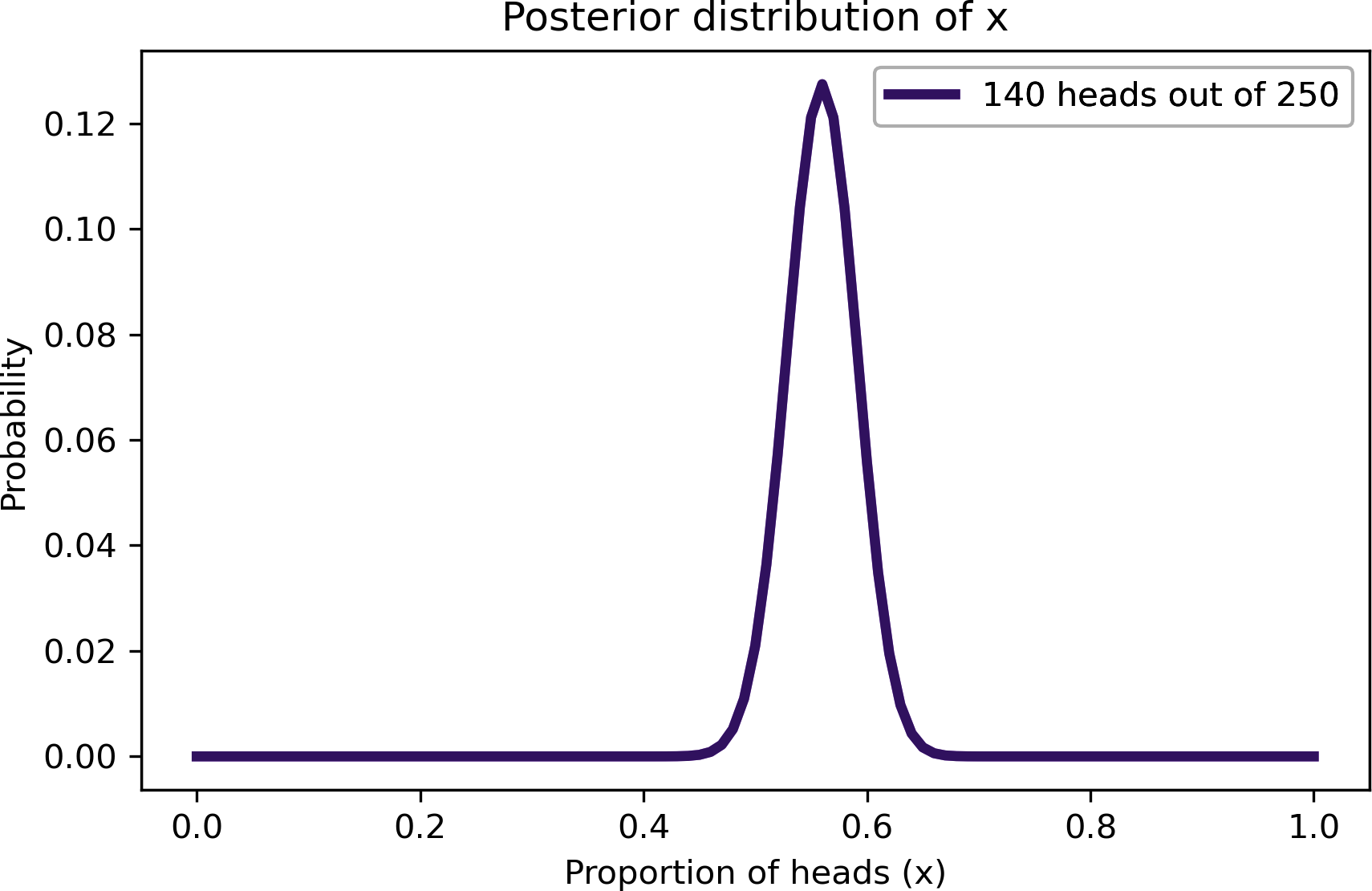
Diese Abbildung zeigt die nachträgliche Verteilung von x, d.h. den Anteil der Köpfe bei der beobachteten Münze.

Die nachträgliche Verteilung stellt unsere Vermutungen über x dar, nachdem wir die Daten gesehen haben. Sie zeigt an, dass Werte kleiner als 0,4 und größer als 0,7 unwahrscheinlich sind; Werte zwischen 0,5 und 0,6 sind am wahrscheinlichsten.

In der Tat ist der wahrscheinlichste Wert für x 0,56, was dem Anteil der Köpfe im Datensatz entspricht, 140/250.

posterior.max_prob()

0.56

Triangle Prior

Bis jetzt haben wir einen einheitlichen Prior verwendet:

uniform = Pmf(1, hypos, name='uniform')
uniform.normalize()

Aber nach dem, was wir über Münzen wissen, ist das vielleicht keine vernünftige Wahl. Ich kann mir vorstellen, dass x bei einer schiefen Münze erheblich von 0,5 abweichen könnte, aber es scheint unwahrscheinlich, dass die belgische Euro-Münze so unausgewogen ist, dass x 0,1 oder 0,9 beträgt.

Es könnte sinnvoller sein, einen Prior zu wählen, der eine höhere Wahrscheinlichkeit für Werte von x nahe 0,5 und eine geringere Wahrscheinlichkeit für Extremwerte bietet.

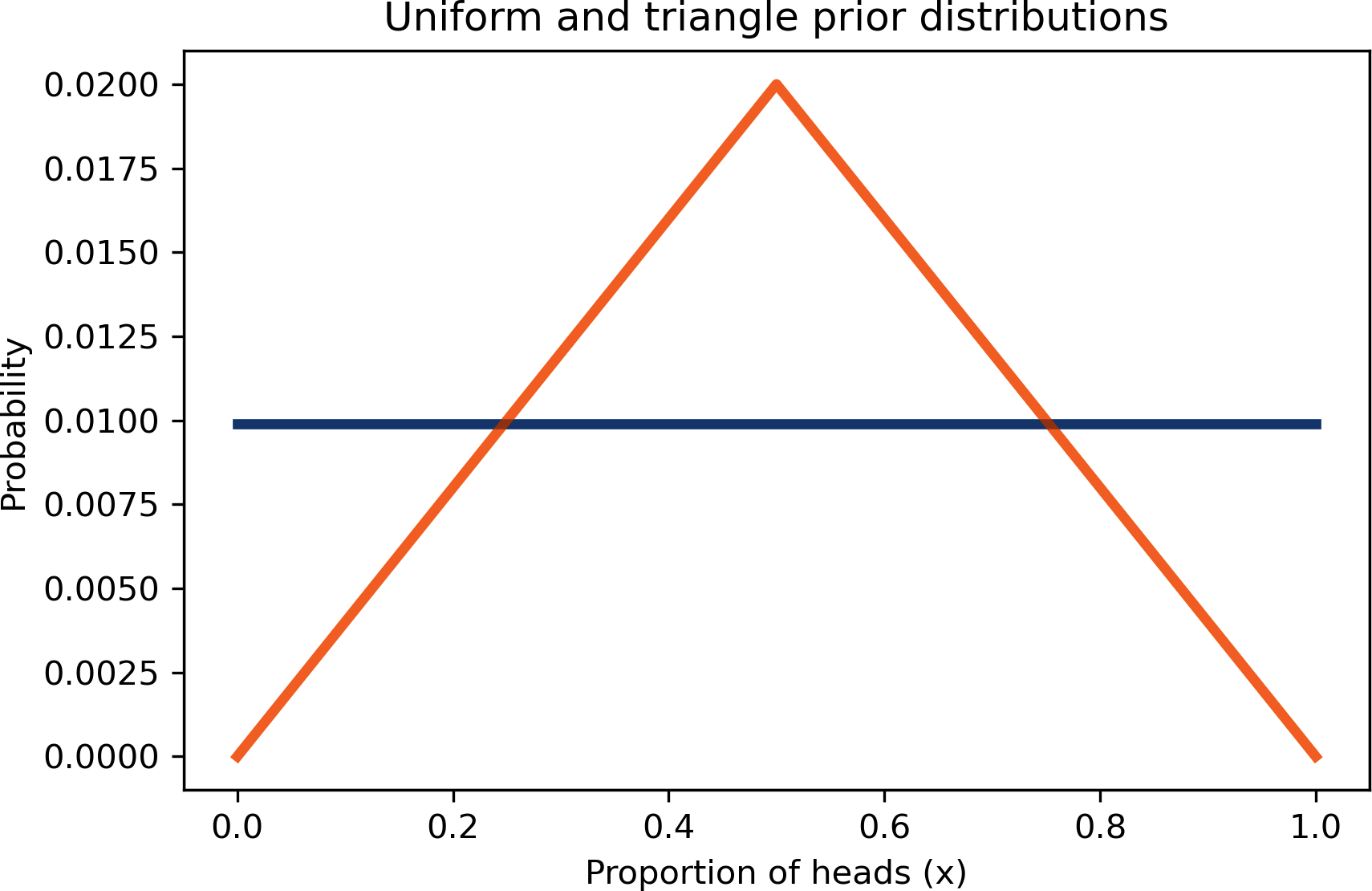
Als Beispiel wollen wir einen dreieckigen Prior ausprobieren. Hier ist der Code, der ihn konstruiert:

ramp_up = np.arange(50)
ramp_down = np.arange(50, -1, -1)

a = np.append(ramp_up, ramp_down)

triangle = Pmf(a, hypos, name='triangle')
triangle.normalize()

2500

arange gibt ein NumPy-Array zurück, so dass wir np.append verwenden können, umramp_down an das Ende von ramp_up anzuhängen. Dann verwenden wir a und hypos, um Pmf zu erstellen.

Die folgende Abbildung zeigt das Ergebnis, zusammen mit dem einheitlichen Prior:

Jetzt können wir beide Prioritäten mit denselben Daten aktualisieren:

update_euro(uniform, dataset)
update_euro(triangle, dataset)

Hier sind die Hinterteile:

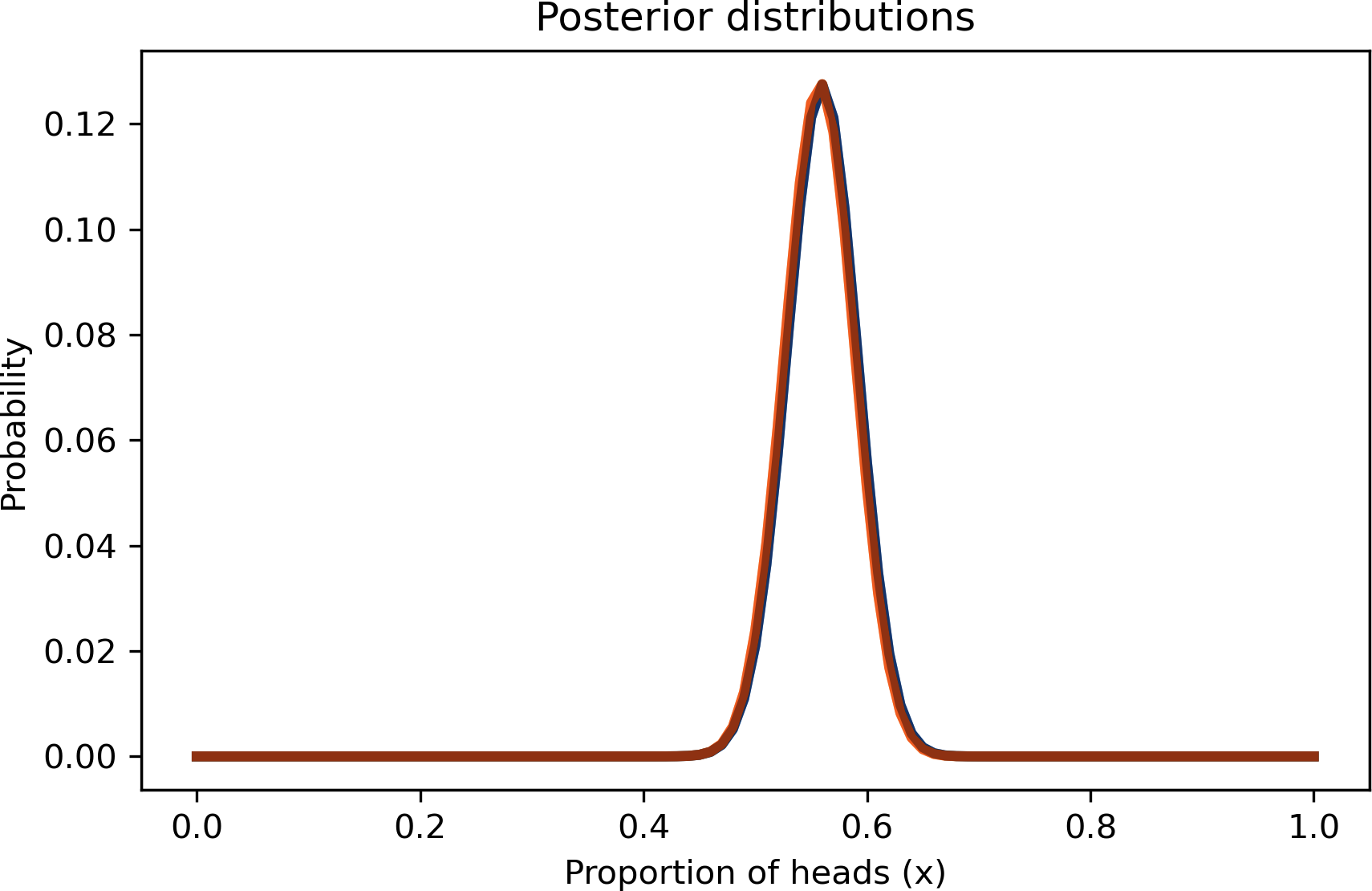
Die Unterschiede zwischen den Posterior-Verteilungen sind kaum sichtbar und so gering, dass sie in der Praxis kaum eine Rolle spielen würden.

Und das ist eine gute Nachricht. Um zu verstehen, warum das so ist, stell dir zwei Menschen vor, die sich wütend darüber streiten, welcher Prior besser ist: Uniform oder Dreieck. Jeder von ihnen hat Gründe für seine Vorliebe, aber keiner von ihnen kann den anderen überzeugen, seine Meinung zu ändern.

Aber nehmen wir an, sie einigen sich darauf, die Daten zu nutzen, um ihre Überzeugungen zu aktualisieren. Wenn sie ihre Posterior-Verteilungen vergleichen, stellen sie fest, dass es fast nichts mehr zu streiten gibt.

Dies ist ein Beispiel für das Überschwemmen der Prioritäten: Bei genügend Daten konvergieren Menschen, die mit unterschiedlichen Prioritäten starten, tendenziell auf dieselbe Posteriorverteilung.

Die Binomial-Wahrscheinlichkeitsfunktion

Bisher haben wir die Aktualisierungen nacheinander berechnet, also müssen wir für das Euro-Problem 250 Aktualisierungen vornehmen.

Eine effizientere Alternative ist es, die Wahrscheinlichkeit für den gesamten Datensatz auf einmal zu berechnen. Für jeden hypothetischen Wert von x müssen wir die Wahrscheinlichkeit berechnen, bei 250 Drehungen 140 Mal Kopf zu bekommen.

Nun, wir wissen, wie man das macht; das ist die Frage, die die Binomialverteilung beantwortet. Wenn die Wahrscheinlichkeit für Kopf gleich $p$ist, ist die Wahrscheinlichkeit von $k$ Köpfe in $n$ Drehungen ist:

$$\left(\genfrac{}{}{0pt}{}{n}{k}\right)p^k{(1-p)}^{n-k}$$

Und wir können SciPy verwenden, um sie zu berechnen. Die folgende Funktion nimmt eine Pmf, die eine Prioritätsverteilung darstellt, und ein Tupel von ganzen Zahlen, die die Daten repräsentieren:

from scipy.stats import binom

def update_binomial(pmf, data):
    """Update pmf using the binomial distribution."""
    k, n = data
    xs = pmf.qs
    likelihood = binom.pmf(k, n, xs)
    pmf *= likelihood
    pmf.normalize()

Die Daten werden mit einem Tupel von Werten für k und n dargestellt, anstatt mit einer langen Kette von Ergebnissen. Hier ist das Update:

uniform2 = Pmf(1, hypos, name='uniform2')
data = 140, 250
update_binomial(uniform2, data)

Wir können allclose verwenden, um zu bestätigen, dass das Ergebnis bis auf eine kleine Fließkommarundung dasselbe ist wie im vorherigen Abschnitt.

np.allclose(uniform, uniform2)

True

Aber diese Art der Berechnung ist viel effizienter.

Bayessche Statistik

Vielleicht hast du schon die Ähnlichkeiten zwischen dem Euro-Problem und dem 101 Bowls-Problem in "101 Bowls" bemerkt . Die Prioritätsverteilungen sind dieselben, die Wahrscheinlichkeiten sind dieselben, und mit denselben Daten würden die Ergebnisse auch dieselben sein. Aber es gibt zwei Unterschiede.

Die erste ist die Wahl des Priors. Bei 101 Schüsseln wird der gleichmäßige Priordurch die Aufgabenstellung impliziert, die besagt, dass wir eine der Schüsseln mit gleicher Wahrscheinlichkeit zufällig auswählen.

Beim Euro-Problem ist die Wahl des Priors subjektiv, d. h., vernünftige Menschen können unterschiedlicher Meinung sein, weil sie vielleicht unterschiedliche Informationen über Münzen haben oder weil sie dieselben Informationen unterschiedlich interpretieren.

Da die Prioritäten subjektiv sind, sind auch die Posterioren subjektiv.Und das finden manche Leute problematisch.

Der andere Unterschied ist die Art dessen, was wir schätzen. Beim 101-Schalen-Problem wählen wir die Schale nach dem Zufallsprinzip aus, sodass es unproblematisch ist, die Wahrscheinlichkeit für die Wahl jeder Schale zu berechnen. Beim Euro-Problem ist der Anteil der Köpfe eine physikalische Eigenschaft einer bestimmten Münze. Bei manchen Auslegungen der Wahrscheinlichkeit ist das ein Problem, weil physikalische Eigenschaften nicht als zufällig angesehen werden.

Nehmen wir zum Beispiel das Alter des Universums. Unsere beste Schätzungliegt derzeit bei 13,80 Milliarden Jahren, kann aber um 0,02 Milliarden Jahre in die eine oder andere Richtung abweichen.

Nehmen wir nun an, wir möchten wissen, wie hoch die Wahrscheinlichkeit ist, dass das Alter des Universums tatsächlich größer als 13,81 Milliarden Jahre ist. Nach einigen Auslegungen der Wahrscheinlichkeitsrechnung können wir diese Frage nicht beantworten. Wir müssten dann etwas sagen wie: "Das Alter des Universums ist keine Zufallsgröße, also hat es keine Wahrscheinlichkeit, einen bestimmten Wert zu überschreiten.

Nach der Bayes'schen Interpretation der Wahrscheinlichkeit ist es sinnvoll und nützlich, physikalische Größen so zu behandeln, als wären sie zufällig und Wahrscheinlichkeiten über sie zu berechnen.

Beim Euro-Problem stellt die Prioritätsverteilung dar, was wir über Münzen im Allgemeinen glauben, und die Posterioritätsverteilung stellt dar, was wir über eine bestimmte Münze glauben, nachdem wir die Daten gesehen haben. Wir können also die Posterior-Verteilung verwenden, um Wahrscheinlichkeiten über die Münze und ihren Anteil an Köpfen zu berechnen.

Die Subjektivität des Priors und die Interpretation des Postors sind die Hauptunterschiede zwischen der Anwendung des Bayes'schen Theorems und der Bayes'schen Statistik.

Das Bayes'sche Theorem ist ein mathematisches Wahrscheinlichkeitsgesetz, gegen das kein vernünftiger Mensch etwas einzuwenden hat. Aber die Bayes'sche Statistik ist überraschend umstritten. In der Vergangenheit haben sich viele Menschen an ihrer Subjektivität gestört und daran, dass sie die Wahrscheinlichkeit für Dinge verwendet, die nicht zufällig sind.

Wenn du dich für diese Geschichte interessierst, empfehle ich dir das Buch von Sharon Bertsch McGrayne,The Theory That Would Not Die.

Zusammenfassung

In diesem Kapitel habe ich das Euro-Problem von David MacKay gestellt und wir haben begonnen, es zu lösen. Anhand der Daten berechneten wir die Posterior-Verteilung für x, die Wahrscheinlichkeit, dass eine Euro-Münze Kopf zeigt.

Wir haben zwei verschiedene Prioritäten ausprobiert, sie mit denselben Daten aktualisiert und festgestellt, dass die Posterioren fast identisch waren. Das ist eine gute Nachricht, denn es deutet darauf hin, dass sich zwei Personen, die mit unterschiedlichen Überzeugungen starten und dieselben Daten sehen, in ihren Überzeugungen annähern.

In diesem Kapitel wird die Binomialverteilung vorgestellt, mit der wir die Posterior-Verteilung effizienter berechnen können. Außerdem habe ich die Unterschiede zwischen der Anwendung des Satzes von Bayes, wie beim 101 Bowls Problem, und der Anwendung der Bayes'schen Statistik, wie beim Euro Problem, erläutert.

Die Frage von MacKay haben wir aber immer noch nicht beantwortet: "Sind diese Daten ein Beweis dafür, dass die Münze nicht fair, sondern verzerrt ist?" Ich werde diese Frage noch etwas länger offen lassen; wir werden in Kapitel 10 darauf zurückkommen.

Im nächsten Kapitel lösen wir Probleme, die mit dem Zählen zu tun haben, wie Züge, Panzer und Kaninchen.

Aber zuerst solltest du an diesen Übungen arbeiten.

Übungen

Beispiel 4-1.

In der Major League Baseball (MLB) haben die meisten Spieler einen Batting Average zwischen .200 und .330, was bedeutet, dass die Wahrscheinlichkeit, einen Hit zu erzielen, zwischen 0,2 und 0,33 liegt.

Angenommen, ein Spieler, der in seinem ersten Spiel antritt, erzielt 3 Treffer aus 3 Versuchen. Wie lautet die Nachher-Verteilung für die Wahrscheinlichkeit, einen Treffer zu erzielen?

Beispiel 4-2.

Wenn du Menschen zu sensiblen Themen befragst, musst du dich mit derVerzerrung durch soziale Erwünschtheit auseinandersetzen, d. h. mit der Tendenz der Menschen, ihre Antworten so anzupassen, dass sie sich selbst in einem möglichst positiven Licht darstellen. Eine Möglichkeit, die Genauigkeit der Ergebnisse zu verbessern, ist dierandomisierte Beantwortung.

Ein Beispiel: Angenommen, du willst wissen, wie viele Menschen bei ihren Steuern betrügen. Wenn du sie direkt fragst, ist es wahrscheinlich, dass einige der Betrüger lügen werden. Du kannst eine genauere Schätzung erhalten, wenn du sie indirekt fragst, etwa so: Bitte jede Person, eine Münze zu werfen und das Ergebnis nicht zu verraten,

• Wenn sie Köpfe bekommen, melden sie JA.

• Wenn sie Schwänze bekommen, beantworten sie die Frage "Betrügst du bei deinen Steuern?" ehrlich.

Wenn jemand JA sagt, wissen wir nicht, ob er tatsächlich bei den Steuern betrügt; er könnte den Kopf geschüttelt haben. Wenn man das weiß, ist man vielleicht eher bereit, ehrlich zu antworten.

Angenommen, du befragst 100 Personen auf diese Weise und erhältst 80 JA- und 20 NEIN-Stimmen. Wie sieht auf der Grundlage dieser Daten die hintere Verteilung für den Anteil der Personen aus, die bei ihren Steuern betrügen? Welches ist die wahrscheinlichste Menge in der hinteren Verteilung?

Beispiel 4-3.

Angenommen, du willst testen, ob eine Münze fair ist, aber du willst sie nicht hunderte Male werfen. Also baust du eine Maschine, die die Münze automatisch wirft und das Ergebnis mit Hilfe von Computer Vision ermittelt.

Du entdeckst jedoch, dass die Maschine nicht immer genau ist. Nehmen wir an, die Wahrscheinlichkeit ist y=0.2, dass ein tatsächlicher Kopf als Zahl oder eine tatsächliche Zahl als Kopf gemeldet wird.

Wenn wir eine Münze 250 Mal werfen und die Maschine 140 Köpfe meldet, wie lautet dann die Nachverteilung von x? Was passiert, wenn du den Wert vony variierst?

Beispiel 4-4.

In Vorbereitung auf eine außerirdische Invasion hat die Earth Defense League (EDL) an neuen Raketen gearbeitet, um Eindringlinge aus dem All abzuschießen. Natürlich sind einige Raketendesigns besser als andere; nehmen wir an, dass jedes Design eine gewisse Wahrscheinlichkeit hat, ein außerirdisches Schiff zu treffen, x.

Die bisherigen Tests haben ergeben, dass die Verteilung von x in der Grundgesamtheit der Muster ungefähr gleichmäßig zwischen 0,1 und 0,4 liegt.

Nehmen wir an, der neue ultrageheime Alien Blaster 9000 wird getestet. In einer Pressekonferenz berichtet ein EDL-General, dass das neue Design zweimal getestet wurde und bei jedem Test zwei Schüsse abgegeben wurden. Die Ergebnisse des Tests sind vertraulich, deshalb will der General nicht sagen, wie viele Ziele getroffen wurden, aber er berichtet: "Bei den beiden Tests wurde die gleiche Anzahl von Zielen getroffen, also haben wir Grund zu der Annahme, dass dieses neue Design stimmig ist."

Sind diese Daten gut oder schlecht? Das heißt, erhöhen oder verringern sie deine Einschätzung von x für den Alien Blaster 9000?