Technical Mathematics, Sixth Edition

11.3. Factoring Trinomials

A trinomial, you may recall, is a polynomial having three terms, and a quadratic trinomial in x has an x² term, an x term, and a constant term. The coefficient of x² is called the leading coefficient and the coefficient of x is called the middle coefficient.

Example 14: 4x2 + 3x − 5 is a quadratic trinomial. The leading coefficient is 4, the middle coefficient is 3, and the constant term is −5.

▪ Exploration:

Try this. Multiply the two binomials (2x + 1) and (3x + 4).

What kind of expression did you get? What are the values of the two coefficients and the constant term? How are they related to the numbers in the given binomials? Can you state it as a general rule?

When we multiply the two binomials (ax + b) and (cx + d), we get a trinomial with a leading coefficient of ac, a middle coefficient of (ad + bc), and a constant term of bd.

NOTE

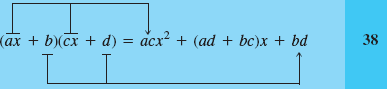
11.3.1. Test for Factorability

Not all quadratic trinomials can be factored. We test for factorability as follows:

NOTE

The trinomial ax² + bx + c (where a, b, and c are constants) is factorable if b² − 4ac is a perfect square.

Example 15: Can the trinomial 6x2 + x − 12 be factored? Solution: Using the test for factorability, Eq. 44, with a = 6, b = 1, and c = −12, we have b2 − 4ac = 12 − 4(6)(−12) = 289 By taking the square root of 289 on the calculator, we see that it is a perfect square (289 = 172), so the ...