Technical Mathematics, Sixth Edition

11.2. Difference of Two Squares

The next type of expression that we will factor is a binomial in which one square is subtracted from another.

▪ Exploration:

Try this. Multiply (2x + 3) by (2x − 3).

Examine the product you just obtained. How many terms does it have? When you multiply two binomials, do you usually get that number of terms? How are the terms related to those in the two original binomials? Can you express your results in general terms?

An expression of the form

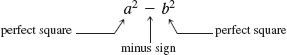
where one perfect square is subtracted from another, is called a difference of two squares. It arises when (a − b) and (a + b) are multiplied together.

NOTE

This is one example of what is called a special product.

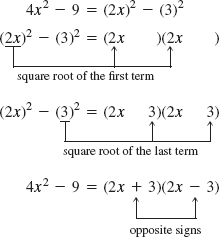
11.2.1. Factoring the Difference of Two Squares

Once we recognize its form, the difference of two squares is easily factored.

Example 8: This example shows how to factor a difference of two squares.

Example 9: Here are more examples of the factoring of a difference of two squares. y2 − 1 = (y + 1)(y − 1) 9a2 − 16b2 = (3a + 4b)(3a − 4b) 49x2 − 9a2y2 = (7x − 3ay)(7x + 3ay) 1 − a2b2c2 = (1 − abc)(1 + abc)

NOTE

There is no similar rule for factoring the sum of two squares, such as

a² + b²

TI-89 calculator ...