Technical Mathematics, Sixth Edition

16.6. CHAPTER 16 REVIEW PROBLEMS

Prove.

Solve for all positive values of θ less than 360°.

1. 1 + 2 sin² θ = 3 sin θ

2. 3 + 5 cos θ = 2 cos² θ 120°, 240°

   15. 30°, 90°, 150°

   17. 45°, 90°, 135°, 225°, 270°, 315°

3. cos θ − 2 cos³ θ = 0

4. sin θ + cos 2θ = 1 0°, 30°, 150°, 180°

5. sin θ = 1 − 3 cos θ 90°, 306.9°

6. sin² θ = 1 + 6 sin θ 189.3°, 350.7°

7. 

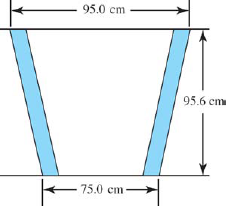
Figure 16.26. A hopper. Compound cuts are sometimes called "hopper cuts."

Evaluate each trigonometric expression to three significant digits.

1. 63.4 cos 4.11 + 72.4 tan 5.73 −80.6

2. 3.85(cos 52.5° + sin 22.6°) 3.82

3. cos² 46.2° 0.479

4. sin² 3.53 + cos² 1.77 0.183

5. Find the compound cut angles for the rectangular hopper, Fig. 16-26. bevel = 44.7°: miter = 5.94°

6. Project: We have proven that the identities in this chapter were true for acute angles. They are, in fact, true for any angles, obtuse or acute. Choose any identity and prove this assertion.

7. Project, Area of a Segment of a Circle: Prove that the area of the segment that subtends an angle θ in a circle of radius r, Fig. 16-27, is

   NOTE

   

   Hint: From the area of sector OACB subtract the area of triangle OAB, and simplify. You ...