Statistical Tableau

Chapter 4. Understanding Normal Distribution Using Histograms

When it comes to statistics, there are a few core concepts to know and understand. I’ve introduced you to some of these ideas in Chapter 1, including statistical significance, p-values, and hypothesis testing. However, one of the most important concepts to know and understand is the different ways data can be distributed. If you don’t know how your data is distributed, you could be making some wrong assumptions in your analysis, which can lead to erroneous conclusions and false assumptions.

In this chapter, I will walk you through some ways your data can be distributed, provide examples of some different types of distribution, and then show you how to visualize distribution in Tableau using histograms.

Types of Distribution

In business or in most everyday analysis, you will run across different ways data is distributed. For example, if I flipped a coin 1,000 times, recorded the data, and visualized it, I would probably have two columns (heads and tails) that would be almost exactly evenly distributed because of the 50/50 chance to get either side. Another example: if I record the altitude of an airliner taking off and reaching 36,000 feet, the data would grow exponentially over time and slowly plateau at some point. And another example: if I recorded the height of every adult in a large lecture hall, I would probably end up with a normally distributed dataset.

All around us, we can record data and visualize it to reveal unique distributions. In business, it is just the same. If you visualize the distribution of profit by product, sales over time, orders by customer, etc., you will find and observe different distributions for each dataset. Here are some common examples.

Uniform Distribution

Uniform distribution is when your data is distributed equally across your dataset, as shown in Figure 4-1.

Figure 4-1. Uniform distribution

Most of the time, when data is collected, it will come with some sort of variance. That is why this form of distribution is unlikely to occur in most situations. However, to give you an example, imagine you were recording how many minutes occur every hour or plotting the probability of rolling a number 1 through 6 on a six-sided die. In these cases, you would end up with an equally distributed dataset.

Bernoulli Distribution

A Bernoulli distribution is when you collect data with only two possible outcomes, as shown in Figure 4-2. The Bernoulli distribution plays a pivotal role in probability theory and statistics. Named after the Swiss mathematician Jacob Bernoulli, this distribution forms the foundation of many statistical models and serves as a fundamental concept in various fields.

Figure 4-2. Bernoulli distribution

Data is often collected in very simple formats like this. Clinical trials, surveys, or server status can all be recorded in this Boolean format. Boolean means something has two outcomes: 0 or 1 in binary, yes or no, true or false, server is running or server is not running, etc.

Exponential Distribution

Exponential distribution occurs when your data grows exponentially as it’s collected, then starts to taper off, as shown in Figure 4-3.

Figure 4-3. Exponential distribution

Exponential distribution can occur in a dataset when the data collected has a rapid increase or decrease and then stabilizes. Think of the altitude of an airplane as it climbs to its cruising altitude. The plane starts by climbing fast on takeoff and then tapers off as it levels out.

Normal Distribution

Normal distribution follows a bell-shaped curve, as shown in Figure 4-4. It is often referred to as a normal distribution, bell curve, or Gaussian distribution.

Figure 4-4. Normal distribution

This type of distribution occurs when the data is symmetrical in shape with no skew. To give you an example, if you measured the height of college students on a campus, you would see this pattern play out. There would be a few students that are shorter than average, but the majority would be around the national average, and some students would be taller than average.

To give you a mathematical explanation of a normal distribution, let’s look at the empirical rule: 68–95–99.7. In a normal distribution, approximately 68% of the data falls within 1 standard deviation of the mean, 95% falls within 2 standard deviations, and 99.7% falls within three standard deviations, as illustrated in Figure 4-5.

Figure 4-5. The normal distribution 68–95–99.7 (empirical rule)

This rule is very important to understand and will play a big part in outlier detection in Chapters 6 and 7. Also, many of the models that are built natively in Tableau are employed under the assumption that the data is normally distributed.

Normal Distribution and Skewness

To cover normal distribution in more depth, let’s analyze what it means to have a normal distribution. If a dataset is perfectly normal, it means the mean, mode, and median are all equal to each other. Here are the definitions of those terms:

Mean

The average of the numbers within our dataset

Mode

The number that appears most frequently in our dataset

Median

The middle number in a dataset when ordered lowest to highest

Consider this dataset: 3,4,5,5,6,6,7,7,7,8,8,9,9,10,11. Following the definitions of mean, mode, and median, you would have a perfectly distributed normal distribution, where the mean would equal 7, the mode would equal 7, and the median would equal 7.

If you visualize that dataset, you would have a normal distribution similar to Figure 4-6.

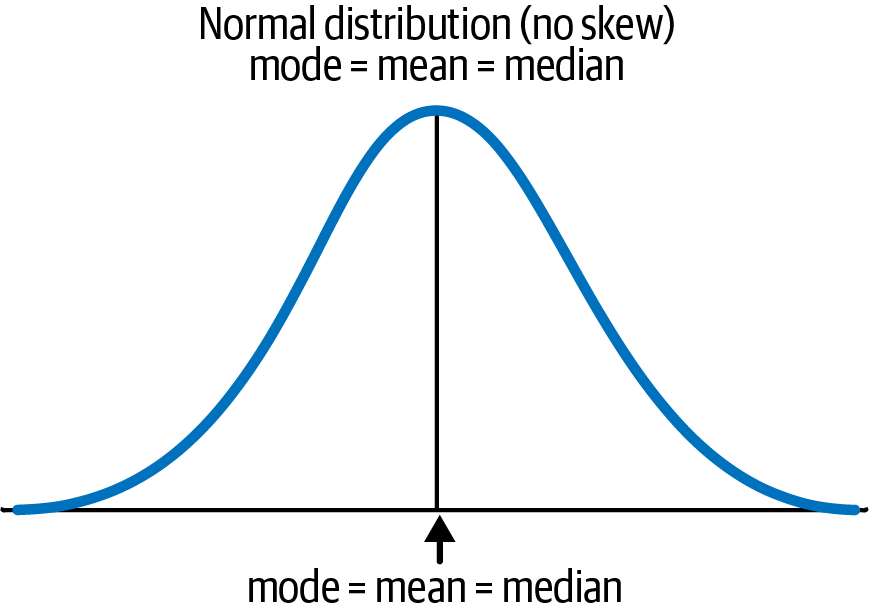
Figure 4-6. Visualizing a normal distribution

As you can see in Figure 4-6, mode = mean = median, so all of those values fall directly in the middle of the symmetrical curve. To make this concept clearer, think of the example I gave earlier about sampling the height of college students on a campus. You would have some students that would be extremely tall (like those on the basketball team) and others who were naturally shorter. However, the majority of students would be around the national average height.

Also, think of your own personal environments at school or work. If you recorded a decent number of adult heights, you would likely end up with a dataset with a normal distribution. While normal distribution happens often, it would be rare to see your data perfectly distributed like this simply due to natural variances. Instead, you will most likely see some skewness.

Understanding Skewness

Skewness is when you see the majority of the data consolidated toward one side of the curve. To give you a visual example, let’s first analyze a left-skewed distribution, as shown in Figure 4-7.

Figure 4-7. Left-skewed distribution

Mathematically, to be left skewed, the mean is less than the median, which is less than the mode. Naturally your eyes are probably drawn to the data on the right side of Figure 4-7. You may be asking yourself, Isn’t this right skewed? When it comes to skewness, you should be more interested in what is causing the data to be skewed. In this case, there is some extreme value (or values) on the left side that are causing the data to be skewed. That is why there is a long “tail” to the left side and why you would refer to this type of skewness as left-skewed.

Now let’s analyze the opposite of this, which is to be right skewed, as shown in Figure 4-8.

Figure 4-8. Right-skewed distribution

To be right skewed, the mode is less than the median, which is less than the mean. As you can see, the majority of the data is bunched to the left side with a long tail on the right side. To give you an example, imagine if the data you collected was the price of cars sold in the United States. You would probably observe some very cheap cars, but the majority of cars sold would be around the national average price ($30,000–$50,000). However, you would also have some cars sold at extremely high prices that would give you this long tail effect. Most likely, there wouldn’t be a lot of vehicles sold at those high prices; however, the prices would drag our mean away from the median.

Remember that when you are thinking about skewness, you should be more concerned about what is causing the skewness. This will also help you remember the correct name for both left- and right-skewness.

Accounting for Skewness

Many models operate with the assumption that the data you have is normally distributed. With that said, skewed data can throw off the results of these models, giving statistically significant results when there aren’t or suggesting there isn’t a statistically significant result when indeed there is one. For this reason, you need to know how to account for skewness by transforming the data in some way.

Hopefully, you can understand how skewness can happen, and maybe you are already thinking of ways you could clean your data to make it more normally distributed. For instance, in the car example, you could simply exclude the more expensive cars from your analysis or segment them out into a separate analysis.

There are many ways you can account for skewness, and each of them has its own pros and cons. Here are a few techniques that you can apply to skewed data to make it normally distributed for your analysis:

Log transformation

A common transformation is to take the log of the data. This returns the log values for the data and essentially pushes the extreme values closer to each other. This will usually give you a normal distribution you can work with for modeling. In Tableau, you can use the LOG function and apply it to the measure you are analyzing.

Pros: You may not have to remove any of your data, as this technique will get the values close enough to each other to leave everything in most cases.

Cons: It is difficult to explain and interpret your data after the transformation.

Remove extreme values

This would entail filtering all the extreme values or outliers from your analysis. In Tableau, you can simply use a conditional filter to do this. Or you can use the Explain Data feature in Tableau to find the exact observations that are causing the extreme values and remove them.

Pros: This is very easy to explain to your stakeholders and document for your colleagues.

Cons: You could exclude extremely valuable information from your analysis or create bias.

Other statistical transformations

There are many more transformation techniques that are more methodical and scientific. Some examples include winsorization and Box–Cox transformations.

Pros: The assumptions you are making are clearly defined and expected in the industry.

Cons: Providing details of these transformation techniques can be difficult for some stakeholders to understand.

How to Visualize Distributions in Tableau Using Histograms

Now that you have an understanding of different types of distributions, let me show you how to visualize the distribution of your data in Tableau.

To get started, connect to the Sample - Superstore dataset. This is the default example data that comes with any version of Tableau and will be displayed at the bottom-left corner of the data source connection screen as a data source. Once connected, you need to create a bin in Tableau. Bins are primarily used to turn measures into discrete dimension members. This is key when trying to determine the distribution of data because you want each bar in the histogram to represent a group of values.

To give you an example, Table 4-1 is a table of data that has been binned by increments of 20.

Table 4-1. Example of bins

Order	Profit	Profit bin
US-0001	$5.00	0
US-0002	$10.00	0
US-0003	$15.00	0
US-0004	$25.00	20
US-0005	$35.00	20
US-0006	($5.00)	–20
US-0007	($25.00)	–40

In each order, Tableau is assigning a bin to the raw value in increments of 20. So the first three values fall between 0 and 20, meaning their bin is 0. Orders 4 and 5 have profit that falls between 21 and 40, so they are assigned to bin 20, and so on.

Tableau actually helps you along by providing a preconstructed bin to use in the Sample - Superstore dataset called Profit (bin). I am going to walk you through how to create one from scratch, but if you would rather use that bin and jump ahead, then feel free to do so.

To create a bin, right-click on Profit and hover over the Create option to choose Bins from the menu (see Figure 4-9).

Figure 4-9. Creating a bin in Tableau

This will open a new dialog box with information about the profit measure, as shown in Figure 4-10.

Figure 4-10. Edit Bins menu in Tableau

You can see that Tableau will assign a “Size of bins” value automatically. In this case, it is 283, which means that each bar in the histogram will “bin” the profit values in these increments. As a better example, if a product generated $200 in profit, then it would get binned together with values ranging from $0 to $283. If a product generated $400 in profit, it would get binned together with values ranging from $284 to $567.

As you can imagine, the larger the bin size, the wider and fewer the bars will be, whereas the smaller bin sizes give you thinner and more abundant bars. It may be useful to test various bin sizes to get a better view of your data’s distribution.

For now, let’s use the suggested bin amount and refine it later. Before I move on, I want to explain the other information displayed in this menu. You can see a Min and Max value; these are the minimum and maximum profit values of all the records in the dataset. You can also see a CntD value, which stands for count distinct. This is a distinct count of all the individual profit amounts in the data, so I have 7,545 distinct values in this dataset. The Diff value is just the difference from the min and max values.

When you’re done, click OK. This is going to create a new dimension named “Profit (bin) 2” in the Data pane. Drag that dimension to the Columns shelf and then drag the Orders (Count) measure to the Rows shelf, which you can see in Figure 4-11.

Figure 4-11. Dragging “Profit (bin) 2” and Orders (Count) to the canvas

This gives you a nice histogram that appears to have a normal distribution, which you can see in Figure 4-12.

You can see that the majority of the CNT(Orders) generate profits ranging from about –$849 to $849. At a high level, this looks very informative, but let’s examine it a bit closer. Let’s edit the bin size from 283 to 20. This will bin the data at a more granular level. To do this, right-click on the “Profit (bin) 2” dimension and change the “Size of bins” to 20, as shown in Figure 4-13, then click OK.

Figure 4-12. Histogram of profit by orders in Tableau

Figure 4-13. Editing “Size of bins” to 20

As I mentioned earlier, the smaller the bin size, the thinner and more abundant the bars will be. By editing the size of the profit bin, you can now compare Figure 4-12 to what is shown in Figure 4-14.

Figure 4-14. Histogram after editing the bin size to 20

You can see that some orders generated profit bins to either extreme on both the left and right sides. As an analyst, you may want to exclude these extreme values and check the bins in closer detail to ensure they are calculated correctly.

To demonstrate this, let’s focus on the orders that are between –$300 and $300. Filter to these bins by clicking on the –$300 bin in the x-axis; then, while holding Shift, click on the $300 bin, which will highlight that bin and everything in between. With those bins selected, click on Keep Only from the tooltip command buttons, as shown in Figure 4-15.

Figure 4-15. Selecting a smaller range of bins

There are multiple other ways to apply this filter. As an example, you could also drag “Profit (bin) 2” to the Filters shelf and apply a dimension filter. That should give you a view that looks like Figure 4-16.

Figure 4-16. Normally distributed profit values in Tableau

You can see that the data follows a normal distribution here. In this dataset, there are some orders that generated negative profit and some that generated positive profit. What would the data look like if it were skewed, though? To show you a good example of this, let’s create a bin of sales.

Start by right-clicking on Sales, navigate to Create, and then select Bins, as shown in Figure 4-17).

This will open the Edit Bins menu, as shown in Figure 4-18.

Figure 4-17. Creating a bin of sales in Tableau

Figure 4-18. Edit Bins menu for Sales (bin)

For this example, change the “Size of bins” to 100 and then click OK to close the menu. Now create a new sheet and drag the new “Sales (bin)” field to the Columns shelf and Orders (Count) to the Rows shelf, as shown in Figure 4-19.

Figure 4-19. Histogram of sales by order count

You can see that changing the bin size to 100 has given you a right-skewed distribution. If you think about the sales data logically, this makes sense. There are few cases when a business would have negative sales from an order. That would essentially mean the business paid the customer for the product. With that said, it wouldn’t make sense to try to apply a transformation to this data either. You would need to apply a nonparametric model or a model that does not assume a normal distribution to get the best results when working with this measure.

As I’ve mentioned previously, there are some models that require the data to be normally distributed to function properly. However, there are also other models that function properly even if your data is not normally distributed. I will cover some of those models in Chapter 7. To introduce the idea to you, let’s briefly discuss parametric models and nonparametric models.

Parametric Models

Parametric models are statistical models that make assumptions about the distribution of the data. In parametric modeling, the goal is to estimate the parameters of the chosen distribution based on the available data. Once the parameters are estimated, the model can be used to make inferences and predictions or generate new data. The term parametric refers to the estimation of those parameters.

Some examples of parametric models include:

• Linear regression

• Exponential regression

• Poisson regression

• Logistic regression

The benefit of these models is that they are easy to interpret and explain to stakeholders. This makes them ideal models that a business can easily take action on and incorporate into their operations.

Nonparametric Models

Nonparametric models are statistical models that do not make strong assumptions about the underlying population distribution or its parameters. Unlike parametric models, which specify a fixed form for the distribution and estimate its parameters, nonparametric models aim to estimate the underlying data distribution directly from the data itself.

Nonparametric models are flexible and can handle a wide range of data distributions without assuming a specific functional form. They are particularly useful when the data does not adhere to the assumptions of parametric models or when there is limited prior knowledge about the data distribution. These models often focus on estimating the patterns, relationships, or rankings in the data rather than estimating specific parameters.

Some examples of nonparametric models include:

• K-nearest neighbors (k-NN)

• Decision tree

• Random forest

• Support vector machine (SVM)

The benefit of these models is their flexibility, but they are more challenging to interpret and communicate to stakeholders.

Throughout the next chapters, I will show you examples of these different types of models.

Summary

In this chapter, you learned about different types of distributions, what skewness is, and how to visualize histograms in Tableau. Being able to apply these techniques is a foundational skill you need to know before you can begin modeling.

This chapter also introduced the idea of parametric and nonparametric models. Knowing this information will help you decide which model to apply to certain data, depending on the distribution of your data.