Sparse Optimization Theory and Methods

where [𝒮𝒟(x^k)]_i0 is the ioth component of 𝒮𝒟(x^k) (which sorts the components of |x^k| into decreasing order) and i₀ is the nearest integer number to m/[4log(n/m)]. Let us replace the updating scheme ε^k+1= ε^k/2 by (7.30), and redo the aforementioned experiments. The results (for p = 0.5) were summarized in Figure 7.2, from which it can be seen that reweighted algorithms still outperform the standard ℓ₁-minimization, but this time CWB, NW1, and NW4 are quite comparable to each other, and they perform better than NW2, NW3, and Wlp under the updating scheme (7.30).

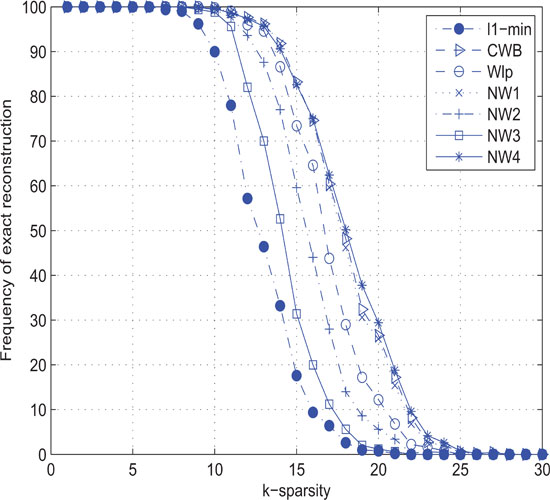
Figure 7.2: Success rates of seven algorithms in finding k-sparse solutions of linear ...