Silicon Photonics: Fundamentals and Devices

2.3 Density-of-States Function

The knowledge of the number of available energy states in the conduction and valence bands in a semiconductor is needed to obtain the expressions for many physical parameters. Let us assume that the crystal is a cube of dimension L in each of the x, y, and z directions. The electron wave function given by Eq. (2.1) must vanish at the crystal boundaries. This condition is fulfilled if

(2.7)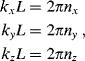

where n_x, n_y, and n_z are integers. The difference between two adjacent k_x values is (2π/L). Thus, each allowed value of k (= k_x,k_y,k_z) occupies a volume (2π/L)³ in k-space.

We now determine the density-of-states in k space. Consider a differential volume 4πk²dk bounded by radii k and k + dk. The number of quantum states is then

(2.8)

Factor 2 takes into account the two spin states. To simplify matters, let us first consider an isotropic semiconductor having a spherical constant energy surface for electrons. A common example is GaAs. The dispersion relation for the conduction band electrons is given by

(2.9)

where m_c is the electron effective mass. One obtains from Eq. (2.9)

Using these in Eq. (2.8) and noting that the crystal volume V = L³, one readily obtains

(2.10) ...