March 2020
Intermediate to advanced
608 pages
14h 31m
English
Content preview from Robot Modeling and Control, 2nd Edition
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Appendix ATRIGONOMETRY
A.1 The Two-Argument Arctangent Function
The usual inverse tangent function returns an angle in the range ( − π/2, π/2). In order to express the full range of angles we will find it useful to define the so-called two-argument arctangent function, Atan2(x, y), which is defined for all (x, y) ≠ (0, 0) and equals the unique angle θ ∈ [ − π, π] such that
(A.1)
This function uses the signs of x and y to select the appropriate quadrant for the angle θ. For example, 
, while 
. If both x and y are zero, then Atan2 is undefined.
A.2 Useful Trigonometric Formulas
Below is a list of trigonometric identities that are used to derive various expressions related to forward, inverse, and velocity kinematics.
Pythagorean Identities
Reduction Formulas
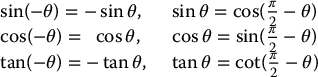
Sum-Difference Identities
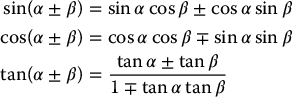
Double-Angle Identities
Half-Angle Identities
Law of Cosines
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.