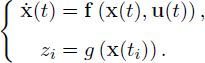Reliable Robot Localization

2Constraints Over Sets of Trajectories

2.1. Towards dynamic state estimation

2.1.1. Overall motivations

The example of the range-only robot localization presented in Chapter 1 was only a static state estimation problem. In practice, state observations are asynchronous and the system evolves between each measurement. To take into account all this information over time can be challenging, especially when dealing with nonlinearities and strong uncertainties. Figure 2.1 illustrates an extension of the range-only problem we were considering until now.

Therefore, we need to soundly deal with state estimations by considering both evolution and observation state equations:

[2.1a] [2.1b]

We emphasize that any uncertainty must be considered, for example, in the initial state x₀, in the evolution model represented by the function f and even in the measurements times t_i.

About state evolutions…

The first equation [2.1a] is an ordinary differential equation (ODE). The resolution of these equations remains an open question as they do not have analytical solutions, apart from some special cases such as in linear systems. Of course, several numerical methods exist that allow the computation of approximations of the solutions (Hairer et al. 1993). In particular, considerable work has been done to solve the so-called initial value problem (IVP) that consists of estimating the temporal evolution ...