Kapitel 1. Quantenschaltungen und Operationen
Diese Arbeit wurde mithilfe von KI übersetzt. Wir freuen uns über dein Feedback und deine Kommentare: translation-feedback@oreilly.com
In Qiskit werden Quantenprogramme normalerweise durch Quantenschaltungen ausgedrückt, die Quantenoperationen enthalten. Quantenschaltungen werden durch die Klasse QuantumCircuit dargestellt, und Quantenoperationen werden durch Unterklassen der KlasseInstruction.
Konstruktion von Quantenschaltungen
Ein Quantenschaltkreis kann erstellt werden, indem ein Argument angibt, das die Anzahl der gewünschten Quantendrähte (Qubits) für diesen Schaltkreis angibt. Dies wird oft als ganze Zahl angegeben:
fromqiskitimportQuantumCircuitQuantumCircuit(2)
Optional kann auch die Anzahl der gewünschten klassischen Drähte (Bits) angegeben werden. Das erste Argument bezieht sich auf die Anzahl der Quantendrähte, das zweite Argument auf die Anzahl der klassischen Drähte:
QuantumCircuit(2,2)
Die Anzahl der gewünschten Quanten- und klassischen Drähte kann auch ausgedrückt werden, indem du Instanzen von QuantumRegister und ClassicalRegister als Argumente für QuantumCircuit angibst. Diese Klassen werden in "Verwendung der Klasse QuantumRegister" und "Verwendung der Klasse ClassicalRegister" behandelt.
Verwendung der Klasse QuantumCircuit
Die Klasse QuantumCircuit enthält eine große Anzahl von Methoden und Attributen. Der Zweck vieler ihrer Methoden ist es, Quantenoperationen auf einen Quantenschaltkreis anzuwenden. Die meisten anderen Methoden und Attribute manipulieren oder geben Informationen über einen Quantenschaltkreis aus.
Häufig verwendete Gates
Tabelle 1-1 enthält einige häufig verwendete Ein-Qubit-Tore und Codebeispiele. Die Variable qc bezieht sich auf eine Instanz von QuantumCircuit, die mindestens vier Quantendrähte enthält.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
H, Hadamard |
|
Wendet das H-Gate auf das Qubit 0 an. Siehe "HGate". |
I, Identität |
|
Wendet das I-Gate auf Qubit 2 an. Siehe "IGate". |
P, Phase |
|
Wendet P-Gate mit π/2 Phasendrehung auf Qubit 0 an. Siehe "PhaseGate". |
RX |
|
Wendet RX-Gate mit π/4-Drehung auf Qubit 2 an. Siehe "RXGate". |
RY |
|
Wendet das RY-Gate mit π/8 Drehung auf das Qubit 0 an. Siehe "RYGate". |
RZ |
|
Wendet RZ-Gate mit π/2-Drehung auf Qubit 1 an. Siehe "RZGate". |
S |
|
Wendet das S-Gatter auf das Qubit 3 an. Entspricht dem P-Gate mit π/2 Phasendrehung. Siehe "SGate". |
S† |
|
Wendet das S†-Gatter auf das Qubit 3 an. Äquivalent zum P-Gate mit 3π/2 Phasendrehung. Siehe "SdgGate". |
SX |
|
Wendet das SX-Gatter (Quadratwurzel aus X) auf Qubit 2 an. Äquivalent zum RX-Gate mit π/2-Drehung. Siehe "SXGate". |
T |
|
Wendet das T-Gatter auf Qubit 1 an. Äquivalent zum P-Gate mit π/4 Phasendrehung. Siehe "TGate". |
T† |
|
Wendet das T†-Gatter auf Qubit 1 an. Äquivalent zum P-Gate mit 7π/4 Phasendrehung. Siehe "TdgGate". |
U |
|
Wendet eine Drehung mit 3 Euler-Winkeln auf Qubit 1 an. Siehe "UGate". |
X |
|
Wendet das X-Gate auf das Qubit 3 an. Siehe "XGate". |
Y |
|
Wendet Y-Gates auf die Qubits 0, 2 und 3 an. Siehe "YGate". |
Z |
|
Wendet das Z-Gatter auf Qubit 2 an. Äquivalent zum P-Gate mit π-Phasendrehung. Siehe "ZGate". |
Abbildung 1-1 enthält eine unsinnige Schaltung mit allen Ein-Qubit-Gatterbeispielen aus Tabelle 1-1.
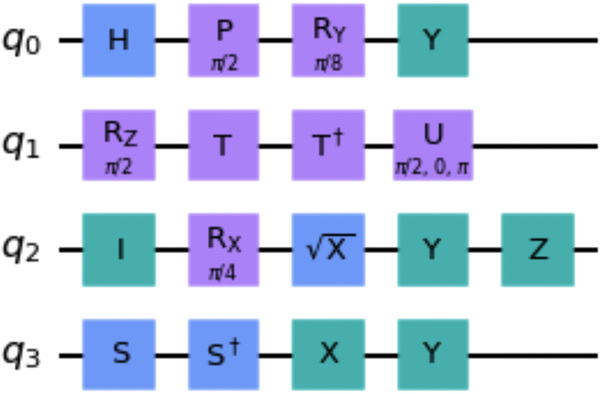
Abbildung 1-1. Unsinnige Schaltung mit Ein-Qubit-Gatterbeispielen
Tabelle 1-2 enthält einige häufig verwendete Multiqubit-Tore und Codebeispiele. Die Variable qc bezieht sich auf eine Instanz von QuantumCircuit, die mindestens vier Quantendrähte enthält.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
CCX, Toffoli |
|
Wendet das X-Gate auf den Quantendraht 2 an, abhängig vom Zustand der Kontrollqubits auf den Drähten 0 und 1. Siehe "CCXGate". |
CH |
|
Wendet das H-Gate auf die Quantenleitung 1 an, abhängig vom Zustand des Kontrollqubits auf Leitung 0. Siehe "CHGate". |
CP, Control-Phase |
|
Wendet das Phasengatter auf das Quantenkabel 1 an, abhängig vom Zustand des Steuerqubits auf Kabel 0. Siehe "CPhaseGate". |
CRX, Control-RX |
|
Wendet das RX-Gate auf das Quantenkabel 3 an, abhängig vom Zustand des Kontrollqubits auf Kabel 2. Siehe "CRXGate". |
CRY, Control-RY |
|
Wendet das RY-Gate auf das Quantenkabel 3 an, abhängig vom Zustand des Kontrollqubits auf Kabel 2. Siehe "CRYGate". |
CRZ |
|
Wendet das RZ-Gate auf das Quantenkabel 1 an, abhängig vom Zustand des Kontrollqubits auf Kabel 0. Siehe "CRZGate". |
CSwap, Fredkin |
|
Vertauscht die Zustände der Qubits an den Drähten 2 und 3, abhängig vom Zustand des Steuerqubits an Draht 0. Siehe "CSwapGate". |
CSX |
|
Wendet das SX-Gate (Quadratwurzel aus X) auf das Quantenkabel 1 an, abhängig vom Zustand des Kontrollqubits auf Kabel 0. Siehe "CSXGate". |
CU |
|
Wendet das U-Gate mit einem zusätzlichen globalen Phasenargument auf das Quantenkabel 1 an, abhängig vom Zustand des Kontrollqubits auf Kabel 0. Siehe "CUGate". |
CX, CNOT |
|
Wendet das X-Gate auf das Quantenkabel 3 an, abhängig vom Zustand des Kontrollqubits auf Kabel 2. Siehe "CXGate". |
CY, Steuerung-Y |
|
Wendet das Y-Gate auf das Quantenkabel 3 an, abhängig vom Zustand des Steuerqubits auf Kabel 2. Siehe "CYGate". |
CZ, Steuerung-Z |
|
Wendet das Z-Gate auf das Quantenkabel 2 an, abhängig vom Zustand des Kontrollqubits auf Kabel 1. Siehe "CZGate". |
DCX |
|
Wendet zwei CNOT-Gates an, deren Steuerqubits auf den Leitungen 2 und 3 liegen. Siehe "DCXGate". |
iSwap |
|
Vertauscht die Qubit-Zustände der Drähte 0 und 1 und ändert die Phase der und Amplituden durch |
MCP, Multi-Steuerungsphase |
|
Wendet das Phasengatter auf den Quantendraht 3 an, abhängig vom Zustand der Kontroll-Qubits auf den Drähten 0, 1 und 2. Siehe "MCPhaseGate". |
MCX, Multi-Control X |
|
Wendet das X-Gate auf den Quantendraht 3 an, abhängig vom Zustand der Kontrollqubits auf den Drähten 0, 1 und 2. Siehe "MCXGate". |
Tausche |
|
Vertauscht die Qubit-Zustände der Drähte 2 und 3. Siehe "SwapGate". |
Abbildung 1-2 enthält eine unsinnige Schaltung mit allen Multi-Qubit-Gatterbeispielen aus Tabelle 1-2.
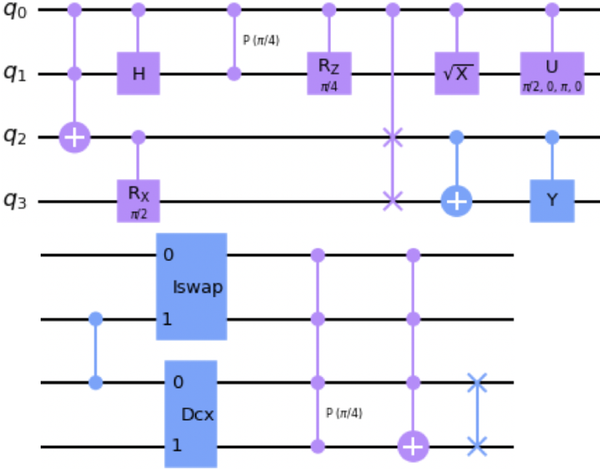
Abbildung 1-2. Unsinnige Schaltung mit Multiqubit-Gatterbeispielen
Zeichnen eines Quantenkreises
Die Methode draw() zeichnet einen Quantenkreis in verschiedenenFormaten.
Verwendung der Methode draw()
Der folgende Codeschnipsel verwendet die Methode draw() im Standardformat:
qc=QuantumCircuit(3)qc.h(0)qc.cx(0,1)qc.cx(0,2)qc.draw()
Abbildung 1-3 zeigt die gezeichnete Schaltung.
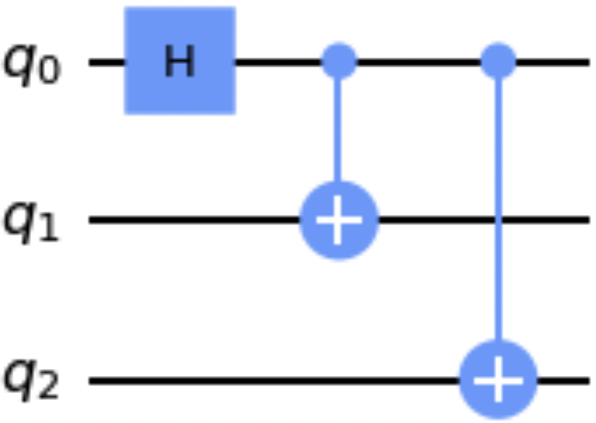
Abbildung 1-3. Beispiel einer Schaltungsvisualisierung mit der Methode draw()
Eine Barriere schaffen
Bei der Methode barrier() wird eine Barriere auf einen Schaltkreis gesetzt (siehe Abbildung 1-4), die sowohl eine visuelle als auch eine funktionale Trennung zwischen den Gattern eines Quantenschaltkreises ermöglicht. Gatter auf beiden Seiten einer Barriere sind keine Kandidaten für eine gemeinsame Optimierung, wenn die Schaltung für den Betrieb auf Quantenhardware oder einem Simulator umgewandelt wird.
Hinweis
Die Gatter, die mit Qiskit ausgedrückt werden, stellen eine Abstraktion der tatsächlichen Gatter dar, die auf einem bestimmten Quantencomputer oder Simulator implementiert sind. Qiskit überträgt die Gatter in die Gatter, die auf der Zielplattform implementiert sind, und kombiniert die Gatter nach Möglichkeit, um die Schaltung zu optimieren.
Verwendung der Methode barrier()
Die Methode barrier() benötigt als optionales Argument die Qubit-Drähte, auf denen eine Barriere platziert werden soll. Wenn kein Argument angegeben wird, wird eine Barriere über alle Quantendrähte gelegt. Diese Methode erstellt eine Barrier Instanz (siehe "Barriere").
Der folgende Codeschnipsel demonstriert die Verwendung der Methode barrier() mit und ohne Argumente:
qc=QuantumCircuit(2)qc.h([0,1])qc.barrier()qc.x(0)qc.x(0)qc.s(1)qc.barrier([1])qc.s(1)qc.draw()
Abbildung 1-4 zeigt die resultierende Schaltung.
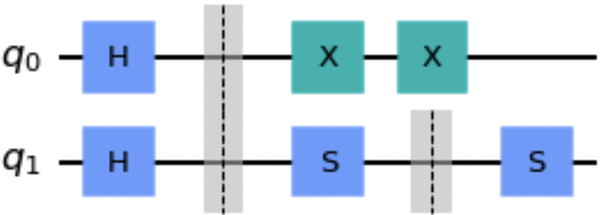
Abbildung 1-4. Beispielschaltung mit der Methode barrier()
Beachte, dass die S-Tore in der Schaltung durch eine Barriere getrennt sind und daher nicht zu einem Z-Tor kombiniert werden können. Die X-Gatter können jedoch kombiniert werden, indem beide entfernt werden, da sie sich gegenseitig aufheben.
Messung eines Quantenschaltkreises
Die gebräuchlichsten Methoden zur Messung von Quantenschaltungen sind measure() und measure_all(). Erstere ist nützlich, wenn der Quantenschaltkreis klassische Drähte enthält, an denen das Ergebnis einer Messung empfangen werden kann. Die zweite Methode ist nützlich, wenn der Quantenschaltkreis keine klassischen Drähte hat. Diese Methoden erstellen Measure Instanzen (siehe "Messen").
Verwendung der Methode measure()
Die Methode measure() benötigt zwei Argumente:
-
Die zu messenden Qubit-Drähte
-
Die klassischen Drähte, auf denen die resultierenden Bits gespeichert werden sollen
Dieser Codeschnipsel verwendet die Methode measure() und Abbildung 1-5 zeigt eine Zeichnung des resultierenden Stromkreises:
qc=QuantumCircuit(3,3)qc.h([0,1,2])qc.measure([0,1,2],[0,1,2])qc.draw()
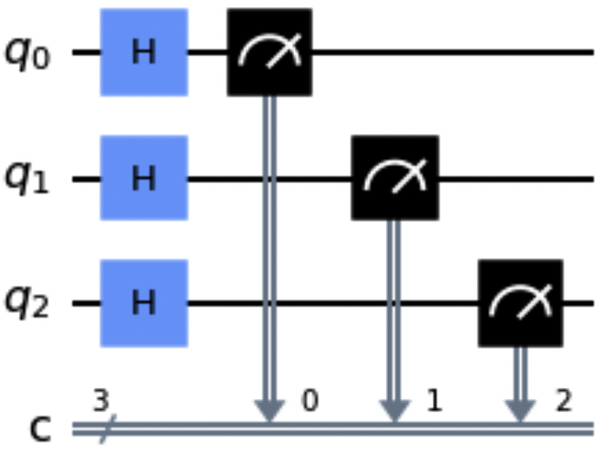
Abbildung 1-5. Beispielschaltung mit der Methode measure()
Beachte, dass die Methode measure() die geforderten Messvorgänge an den Stromkreis angehängt hat.
Verwendung der Methode measure_all()
Die Methode measure_all() kann mit ohne Argumente aufgerufen werden. In diesem Codeschnipsel wird die Methode measure_all() verwendet, und Abbildung 1-6 zeigt eine Zeichnung des resultierenden Stromkreises:
qc=QuantumCircuit(3)qc.h([0,1,2])qc.measure_all()qc.draw()
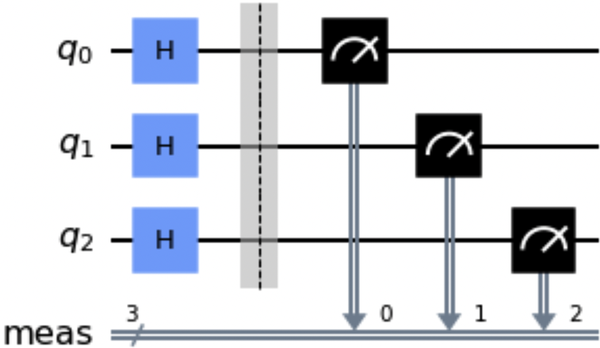
Abbildung 1-6. Beispielschaltung mit der Methode measure_all()
Beachte, dass die Methode measure_all() drei klassische Drähte erstellt und eine Barriere in den Stromkreis eingefügt hat, bevor die Operationen zur Messung hinzugefügt wurden.
Gewinnung von Informationen über einen Quantenschaltkreis
Zu den gängigen Methoden, um Informationen über einen Quantenkreis zu erhalten, gehören depth(), size() und width(). Diese sind in Tabelle 1-3 aufgeführt. Beachte, dass sich die Variable qc auf eine Instanz von QuantumCircuit bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Gibt die Tiefe (kritischer Pfad) eines Schaltkreises zurück, wenn Direktiven wie Barriere entfernt wurden |
|
|
Gibt die Gesamtzahl der Gatteroperationen in einer Schaltung zurück |
|
|
Gibt die Summe der Qubit-Drähte und der klassischen Drähte in einem Stromkreis zurück |
Zu den Attributen, die häufig verwendet werden, um Informationen über einen Quantenkreis zu erhalten, gehören clbits, data, global_phase, num_clbits, num_qubits und qubits. Diese sind in Tabelle 1-4 aufgeführt. Beachte, dass sich die Variable qc auf eine Instanz von QuantumCircuit bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Ermittelt die Liste der klassischen Bits in der Reihenfolge, in der die Register hinzugefügt wurden |
|
|
Erhält eine Liste der Operationen (z. B. Gatter, Barrieren und Messoperationen) in der Schaltung |
|
|
Ermittelt die globale Phase des Stromkreises in Radiant |
|
|
Ermittelt die Anzahl der klassischen Drähte in der Schaltung |
|
|
Ermittelt die Anzahl der Quantendrähte in der Schaltung |
|
|
Ermittelt die Liste der Quantenbits in der Reihenfolge, in der die Register hinzugefügt wurden |
Manipulation eines Quantenschaltkreises
Zu den gängigen Methoden zur Manipulation von Quantenschaltungen gehören append(), bind_parameters(), compose(), copy(), decompose(), from_qasm_file(), from_qasm_str(), initialize(), reset(), qasm(), to_gate() und to_instruction().
Verwendung der Methode append()
Die Methode append() fügt eine Anweisung oder ein Gatter an das Ende der Schaltung auf den angegebenen Drähten an und verändert die Schaltung an Ort und Stelle. Der folgende Codeschnipsel verwendet die Methode append() und Abbildung 1-7 zeigt eine Zeichnung der entstandenen Schaltung:
fromqiskit.circuit.libraryimportCXGateqc=QuantumCircuit(2)qc.h(1)cx_gate=CXGate()qc.append(cx_gate,[1,0])qc.draw()
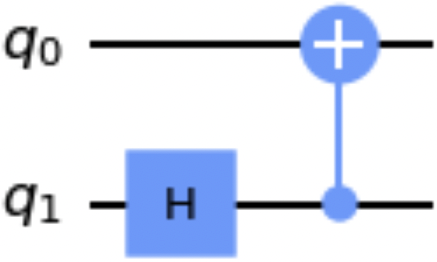
Abbildung 1-7. Beispiel für eine Schaltung nach der Methode append()
Hinweis
Die hier verwendete Klasse CXGate (siehe "CXGate") ist eines der Gates, die im Paket qiskit.circuit.library definiert sind. Wir empfehlen dir, die entsprechenden import Anweisungen zu den Codeschnipseln in diesem Buch hinzuzufügen.
Verwendung der Methode bind_parameters()
Die Methode bind_parameters() bindet Parameter (siehe "Erstellen einer Parameterinstanz") an einen Quantenkreis. Der folgende Codeschnipsel erstellt einen Schaltkreis, der drei parametrisierte Phasentore enthält. Beachte, dass die Argumente für die Parameter Konstruktoren in diesem Codeschnipsel Zeichenketten sind, in diesem Fall solche, die Theta-Zeichen enthalten. Abbildung 1-8 zeigt eine Zeichnung der Schaltung:
fromqiskit.circuitimportQuantumCircuit,\Parametertheta1=Parameter('θ1')theta2=Parameter('θ2')theta3=Parameter('θ3')qc=QuantumCircuit(3)qc.h([0,1,2])qc.p(theta1,0)qc.p(theta2,1)qc.p(theta3,2)qc.draw()
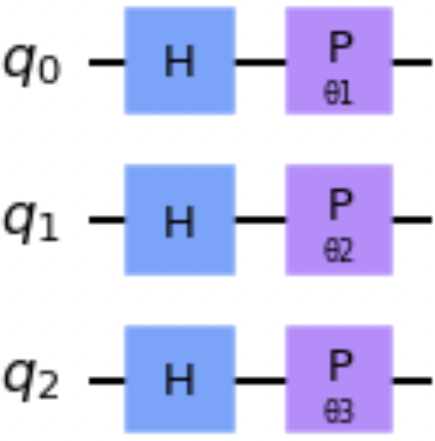
Abbildung 1-8. Beispiel einer parametrisierten Schaltung
Um die Parameterwerte an einen neuen Stromkreis zu binden, übergeben wir der Methode bind_parameters() ein Wörterbuch, das die Parameterreferenzen und die gewünschten Werte enthält. Der folgende Codeschnipsel verwendet diese Technik. Abbildung 1-9 zeigt den gebundenen Schaltkreis, in dem die Parameter des Phasentors durch die angegebenen Werte ersetzt werden:
b_qc=qc.bind_parameters({theta1:math.pi/8,theta2:math.pi/4,theta3:math.pi/2})b_qc.draw()
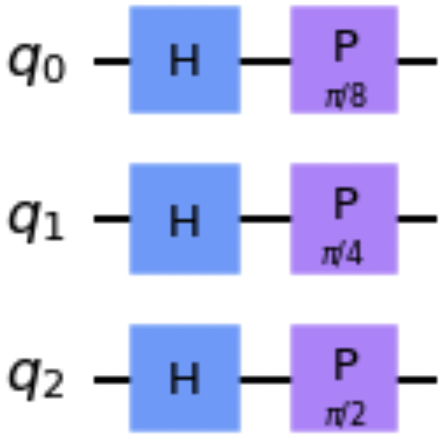
Abbildung 1-9. Beispiel für eine gebundene Schaltung mit den gelieferten Werten für die Phasendrehung
Verwendung der Methode compose()
Die Methode compose() liefert einen neuen Stromkreis, der aus dem ursprünglichen und einem weiteren Stromkreis besteht. Der folgende Codeschnipsel verwendet die Methode compose() und Abbildung 1-10 zeigt eine Zeichnung des resultierenden Stromkreises:
qc=QuantumCircuit(2,2)qc.h(0)another_qc=QuantumCircuit(2,2)another_qc.cx(0,1)bell_qc=qc.compose(another_qc)bell_qc.draw()
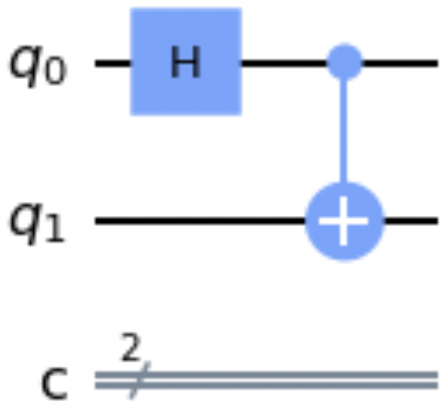
Abbildung 1-10. Beispiel für eine Schaltung nach der Methode compose()
Beachte, dass ein Schaltkreis, der in die compose() Methode übernommen wird, weniger Quanten- oder klassische Drähte haben darf als der ursprüngliche Schaltkreis.
Verwendung der Methode decompose()
Die Methode decompose() liefert einen neuen Schaltkreis, nachdem der ursprüngliche Schaltkreis um eine Stufe zerlegt wurde. Der folgende Codeschnipsel verwendet die Methode decompose(). Abbildung 1-11 zeigt eine Zeichnung der resultierenden Schaltung, in der die S-, H- und X-Gatter in die grundlegenderen U-Gatter-Operationen zerlegt werden (siehe "UGate"):
qc=QuantumCircuit(2)qc.h(0)qc.s(0)qc.x(1)decomposed_qc=qc.decompose()decomposed_qc.draw()
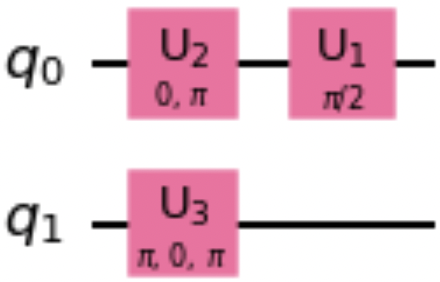
Abbildung 1-11. Beispiel für eine Schaltung nach der Methode decompose()
Verwendung der Methode from_qasm_str()
Die Methode from_qasm_str() liefert einen neuen Schaltkreis aus einem String, der ein OpenQASM-Programm enthält. Der folgende Codeschnipsel verwendet die Methode from_qasm_str() und Abbildung 1-12 zeigt eine Zeichnung des resultierenden Stromkreises:
qasm_str="""OPENQASM 2.0;include "qelib1.inc";qreg q[2];creg c[2];h q[0];cx q[0],q[1];measure q[0] -> c[0];measure q[1] -> c[1];"""new_qc=QuantumCircuit.from_qasm_str(qasm_str)new_qc.draw()
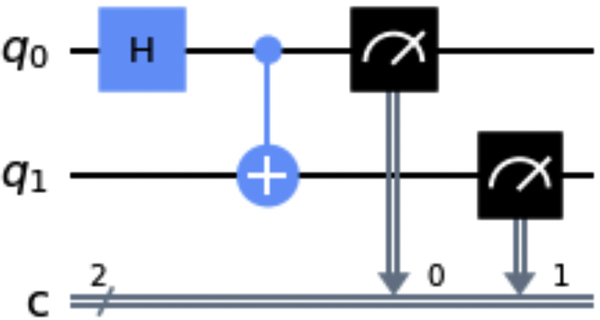
Abbildung 1-12. Beispiel für eine Schaltung nach der Methode from_qasm_str()
Verwendung der Methode initialize()
Die Methode initialize() initialisiert die Qubits eines Quantenschaltkreises auf einen bestimmten Zustand und ist keine unitäre Operation. Der folgende Code verwendet dieinitialize() Methode, und Abbildung 1-13 zeigt eine Zeichnung des resultierenden Schaltkreises. In diesem Codeschnipsel wird der Schaltkreis mit dem normalisierten Zustandsvektor initialisiert :
qc=QuantumCircuit(2)qc.initialize([0,0,0,1])qc.draw()
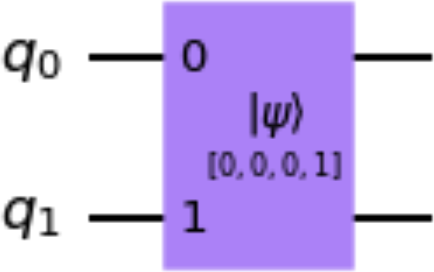
Abbildung 1-13. Beispiel für eine Schaltung nach der Methode initialize()
Verwendung der reset()-Methode
Die Methode reset() setzt ein Qubit in einer Quantenschaltung auf die Zustand zurück und ist keine unitäre Operation. Der folgende Codeschnipsel verwendet die Methode reset(), und Abbildung 1-14 zeigt eine Zeichnung der resultierenden Schaltung. Beachte, dass der Zustand des Qubits ist, bevor er zurückgesetzt wird. Diese Methode erstellt eine Reset Instanz (siehe "Reset"):
qc=QuantumCircuit(1)qc.x(0)qc.reset(0)qc.draw()
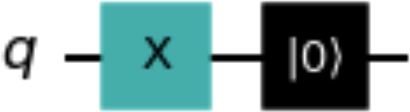
Abbildung 1-14. Beispiel für eine Schaltung nach der Methode reset()
Verwendung der Methode qasm()
Die Methode qasm() gibt ein OpenQASM-Programm zurück, das den Quantenkreis darstellt. Der folgende Codeschnipsel verwendet die Methode qasm(), und Beispiel 1-1 zeigt das daraus resultierende OpenQASM-Programm:
qc=QuantumCircuit(2,2)qc.h(0)qc.cx(0,1)qasm_str=qc.qasm()(qasm_str)
Beispiel 1-1. OpenQASM-Programm, das aus der Verwendung der Methode qasm() resultiert
OPENQASM2.0;include"qelib1.inc";qregq[2];cregc[2];hq[0];cxq[0],q[1];
Verwendung der Methode to_gate()
Die Methode to_gate() erstellt ein benutzerdefiniertes Gatter (siehe "Die Gatterklasse") aus einer Quantenschaltung. Der folgende Codeschnipsel erstellt eine Schaltung, die in ein Gatter umgewandelt wird, und Abbildung 1-15 zeigt eine Zeichnung der Schaltung:
anti_cnot_qc = QuantumCircuit(2) anti_cnot_qc.x(0) anti_cnot_qc.cx(0,1) anti_cnot_qc.x(0) anti_cnot_qc.draw()
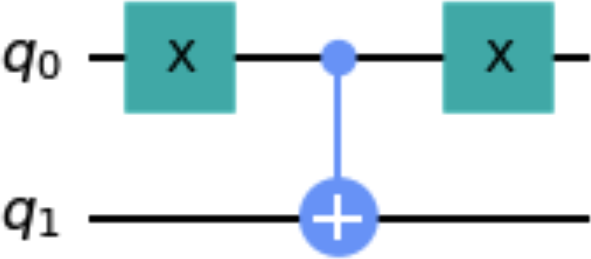
Abbildung 1-15. Beispielschaltung, die in ein Gatter umgewandelt wird
Dieses benutzerdefinierte Gatter wird ein Anti-Kontroll-NOT-Gatter implementieren, bei dem das X-Gatter nur dann angewendet wird, wenn das Kontroll-Qubit . Der folgende Codeschnipsel erstellt eine Schaltung, die dieses benutzerdefinierte Gatter verwendet. Abbildung 1-16 zeigt eine zerlegte Zeichnung dieser Schaltung:
anti_cnot_gate = anti_cnot_qc.to_gate() qc = QuantumCircuit(3) qc.x([0,1,2]) qc.append(anti_cnot_gate, [0,2]) qc.decompose().draw()
Hinweis
Ein Tor stellt eine einheitliche Operation dar. Um eine benutzerdefinierte Operation zu erstellen, die nicht einheitlich ist, verwendest du die Methode to_instruction(), die unter "Verwendung der Methode to_instruction()" beschrieben wird .
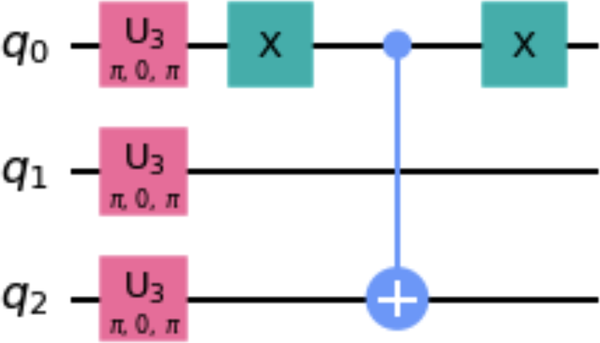
Abbildung 1-16. Zerlegte Schaltung, die ein mit der Methode to_gate() erstelltes Gatter verwendet
Verwendung der Methode to_instruction()
Die Methode to_instruction() erstellt eine benutzerdefinierte Anweisung (siehe "Die Anweisungsklasse") aus einer Quantenschaltung. Das folgende Codeschnipsel erzeugt eine Schaltung, die in eine Anweisung umgewandelt wird, und Abbildung 1-17 zeigt eine Zeichnung der Schaltung:
reset_one_qc = QuantumCircuit(1) reset_one_qc.reset(0) reset_one_qc.x(0) reset_one_qc.draw()
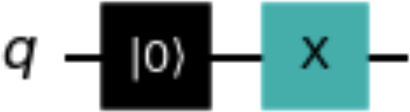
Abbildung 1-17. Beispielschaltung, die in einen Befehl umgewandelt wird
Hinweis
Eine Anweisung stellt eine Operation dar, die nicht unbedingt einheitlich ist. Um eine benutzerdefinierte Operation zu erstellen, die einheitlich ist, verwendest du die Methode to_gate(), die unter "Verwendung der Methode to_gate()" beschrieben wird .
Diese benutzerdefinierte Anweisung setzt ein Qubit zurück und wendet ein X-Gatter an, wodurch das Qubit in den Zustand zurückgesetzt wird . Der folgende Codeschnipsel erstellt eine Schaltung, die diesen Befehl verwendet. Abbildung 1-18 zeigt eine zerlegte Zeichnung dieser Schaltung:
reset_one_inst = reset_one_qc.to_instruction() qc = QuantumCircuit(2) qc.h([0,1]) qc.reset(0) qc.append(reset_one_inst, [1]) qc.decompose().draw()
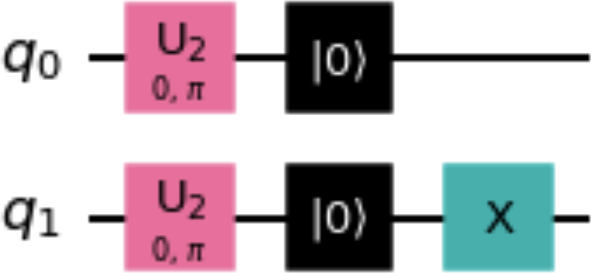
Abbildung 1-18. Schaltkreis, der eine mit der Methode to_instruction() erstellte Anweisung verwendet
Speichern des Status beim Ausführen einer Schaltung im AerSimulator
Wenn du eine Schaltung auf einem AerSimulator Backend laufen lässt (siehe "Verwendung der Aer Simulatoren"), kann der Simulatorstatus in der Schaltungsinstanz gespeichert werden, indem du die QuantumCircuit Methoden in Tabelle 1-5 verwendest. Bitte beachte, dass diese Methoden erst verfügbar sind, nachdem du ein AerSimulator Backend erhalten hast.
Verwendung der Klasse QuantumRegister
Manchmal ist es sinnvoll, Gruppen von Quanten- oder klassischen Drähten als eine Einheit zu behandeln. Zum Beispiel erwarten die Steuer-Qubits der CNOT-Gatter in der Quantenschaltung, die im folgenden Codeschnipsel und in Abbildung 1-19 dargestellt ist, drei Qubits in gleicher Überlagerung. Der zusätzliche Quantendraht in der Schaltung wird als Scratch-Bereich verwendet, dessen Ausgang nicht beachtet wird:
from qiskit import QuantumRegister, \
ClassicalRegister
qr = QuantumRegister(3, 'q')
scratch = QuantumRegister(1, 'scratch')
cr = ClassicalRegister(3, 'c')
qc = QuantumCircuit(qr, scratch, cr)
qc.h(qr)
qc.x(scratch)
qc.h(scratch)
qc.cx(qr[0], scratch)
qc.cx(qr[2], scratch)
qc.barrier(qr)
qc.h(qr)
qc.measure(qr, cr)
qc.draw()
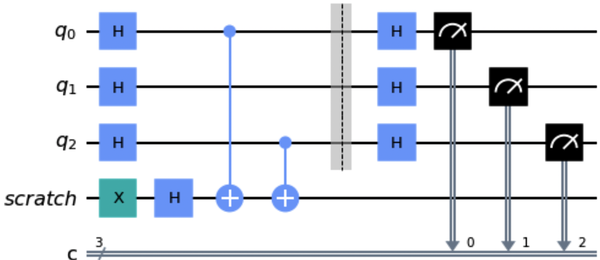
Abbildung 1-19. Beispielschaltung unter Verwendung der QuantumRegister undClassicalRegister Klassen
Wenn du ein QuantumRegister definierst, das aus drei Qubits besteht, können Methoden wie h(), barrier() und measure() auf alle drei Drähte angewendet werden, indem du eine QuantumRegister Referenz übergibst. Wenn du ein ClassicalRegister (siehe "Die Klasse ClassicalRegister verwenden") definierst, das aus drei Bits besteht, kann die Methode measure() alle drei klassischen Drähte spezifizieren, indem du eine ClassicalRegister Referenz übergibst. Außerdem werden die Namen, die den Konstruktoren QuantumRegister und ClassicalRegister übergeben werden, in der Schaltkreiszeichnung angezeigt.
Verwendung der QuantumRegister-Attribute
Zu den häufig verwendeten QuantumRegister Attributen gehören name und size. Diese sind in Tabelle 1-6 aufgeführt. Beachte, dass sich die Variable qr auf eine Instanz von QuantumRegister bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Ermittelt den Namen des Quantenregisters |
|
|
Ermittelt die Anzahl der Qubit-Drähte im Quantenregister |
Verwendung der Klasse ClassicalRegister
Unter "Verwendung der Klasse QuantumRegister" findest du Gründe für die Verwendung der Klasse ClassicalRegister.
Verwendung der ClassicalRegister-Attribute
Zu den häufig verwendeten ClassicalRegister Attributen gehören name und size. Diese sind in Tabelle 1-7 aufgeführt. Beachte, dass sich die Variable cr auf eine Instanz von ClassicalRegister bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Ermittelt den Namen des klassischen Registers |
|
|
Anweisungen und Gates
In Qiskit werden alle Operationen, die auf einen Quantenkreis angewendet werden können, von der Klasse Instruction abgeleitet. Unitäre Operationen werden von der Klasse Gate abgeleitet, die eine Unterklasse von Instruction ist. Kontrolliert-unitäre Operationen werden von der Klasse ControlledGate abgeleitet, die eine Unterklasse von Gate ist. Diese Klassen können verwendet werden, um neue Anweisungen, unitäre Gatter bzw. kontrolliert-unitäre Gatter zu definieren.
Die Unterrichtsklasse
Die nicht-einheitlichen Operationen in Qiskit (wie Measure und Reset) sind direkte Unterklassen von Instruction. Obwohl es möglich ist, eigene Anweisungen zu definieren, indem du Instruction unterklassifizierst, ist eine andere Möglichkeit, die Methode to_instruction() der Klasse QuantumCircuit zu verwenden (ein Beispiel dafür findest du unter in "Verwenden der Methode to_instruction()").
Zu den Methoden der Klasse Instruction gehören copy(), repeat() und reverse_ops(). Diese sind in Tabelle 1-8 aufgeführt. Beachte, dass die Variable inst auf eine Instanz von Instruction verweist.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Gibt eine Kopie der Anweisung zurück und gibt der Kopie den angegebenen Namen |
|
|
Gibt eine Anweisung zurück, bei der diese Anweisung eine bestimmte Anzahl von Malen wiederholt wird |
|
|
Gibt eine Anweisung mit ihren Operationen in umgekehrter Reihenfolge zurück |
Zu den häufig verwendeten Attributen in der Klasse Instruction gehören definition und params. Diese sind in Tabelle 1-9 aufgeführt. Beachte, dass sich die Variable inst auf eine Instanz von Instruction bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Gibt die Definition in Form von Basic Gates zurück |
|
|
Ermittelt die Parameter für die Anweisung |
Die Tor-Klasse
Die unitären Operationen in Qiskit (z.B. HGate und XGate) sind Unterklassen von Gate. Obwohl es möglich ist, eigene Gates zu definieren, indem du Gate unterklassifizierst, ist eine andere Möglichkeit, die to_gate() Methode der Klasse QuantumCircuit zu verwenden (siehe ein Beispiel dafür in "Verwendung der to_gate() Methode").
Zu den häufig verwendeten Methoden in der Klasse Gate gehören die in Tabelle 1-8 aufgeführten Methoden Instruction sowie control(), inverse(), power() und to_matrix(). Sie sind alle in Tabelle 1-10 aufgelistet. Beachte, dass sich die Variable gate auf eine Instanz von Gate bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Gibt eine Anzahl von Kontroll-Qubits an und liefert eine kontrollierte Version des Gatters |
|
|
Gibt eine Kopie des Gatters zurück und gibt der Kopie den angegebenen Namen |
|
|
Gibt die Inverse des Gatters zurück |
|
|
Gibt das Gatter hochgerechnet auf eine bestimmte Fließkommapotenz zurück |
|
|
Gibt ein Tor zurück, bei dem dieses Tor eine bestimmte Anzahl von Malen wiederholt wird. |
|
|
Gibt ein Gatter mit seinen Operationen in umgekehrter Reihenfolge zurück |
|
|
Gibt ein Array für die unitäre Matrix des Gatters zurück |
Zu den häufig verwendeten Attributen in der Klasse Gate gehören die in Tabelle 1-9 aufgeführten Attribute Instruction und label. Diese sind alle in Tabelle 1-11 aufgeführt. Beachte, dass sich die Variable gate auf eine Instanz von Gate bezieht.
| Namen | Beispiel | Anmerkungen |
|---|---|---|
|
|
Gibt die Definition in Form von Basic Gates zurück |
|
|
Erhält das Etikett für die Anweisung |
|
|
Ermittelt die Parameter für die Anweisung |
Die Klasse ControlledGate
Die kontrolliert-unitären Operationen in Qiskit (wie CZGate und CCXGate) sind Unterklassen von ControlledGate, das eine Unterklasse von Gate ist.
Häufig verwendete Methoden in der Klasse ControlledGate sind die in Tabelle 1-10 aufgeführten Gate Methoden
Zu den häufig verwendeten Attributen der Klasse ControlledGate gehören die in Tabelle 1-11 aufgeführten Attribute Gate sowie num_ctrl_qubits und ctrl_state.
Verwendung des Attributs num_ctrl_qubits
Das Attribut num_ctrl_qubits enthält eine ganze Zahl , die die Anzahl der Kontroll-Qubits in einem ControlledGate darstellt. Der folgende Codeschnipsel, dessen gedruckte Ausgabe 2 wäre, verwendet das Attribut num_ctrl_qubits eines Toffoli-Gatters:
fromqiskit.circuit.libraryimportCCXGatetoffoli=CCXGate()(toffoli.num_ctrl_qubits)
Verwendung der Methode ctrl_state()
Ein ControlledGate kann ein oder mehrere Kontroll-Qubits haben, von denen jedes entweder ein Kontroll- oder ein Anti-Kontroll-Qubit sein kann (siehe das Anti-Kontroll-Beispiel in "Verwendung der to_gate()-Methode"). Das Attribut ctrl_state enthält eine ganze Zahl, deren Binärwert angibt, welche Qubits Control-Qubits und welche Anticontrol-Qubits sind. Die Binärziffer 1 steht für ein Kontroll-Qubit und die Binärziffer 0 für ein Anti-Kontroll-Qubit.
Das Attribut ctrl_state unterstützt sowohl den Zugriff auf seinen Wert als auch dessen Änderung. Der folgende Codeschnipsel verwendet das Attribut ctrl_state, wobei der Binärwert 10 das oberste Kontroll-Qubit zu einem Anti-Kontroll-Qubit macht. Abbildung 1-20 zeigt eine Zeichnung der resultierenden Schaltung:
toffoli=CCXGate()toffoli.ctrl_state=2toffoli.definition.draw()
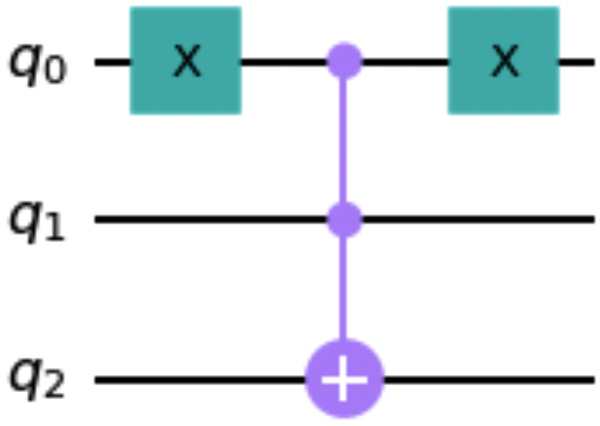
Abbildung 1-20. Toffoli-Gatter mit einem Kontroll-Qubit und einem Anti-Kontroll-Qubit
Definieren eines benutzerdefinierten kontrollierten Gates
Obwohl es möglich ist, deine eigenen kontrollierten Gates zu definieren, indem du ControlledGate unterklassifizierst, ist eine andere Möglichkeit, diese beiden Schritte zu befolgen:
-
Erstelle ein benutzerdefiniertes Tor mit der Methode
to_gate()der KlasseQuantumCircuit(ein Beispiel dafür findest du in "Verwendung der Methode to_gate()"). -
Füge deinem benutzerdefinierten Gate Kontrollqubits hinzu, indem du die
control()Methode, die in Tabelle 1-10 gezeigt wird.
Wir folgen diesen beiden Schritten, um ein benutzerdefiniertes kontrolliertes Gate zu definieren, das eine π/16-Phasendrehung anwendet, wenn beide Kontrollqubits . Zunächst definiert der folgende Codeschnipsel eine Schaltung, die ein π/16-P-Gatter enthält, und wandelt sie in ein benutzerdefiniertes Gatter um. Abbildung 1-21 zeigt eine Zeichnung des benutzerdefinierten Gatters:
fromqiskitimportQuantumCircuitimportmathp16_qc=QuantumCircuit(1)p16_qc.p(math.pi/16,0)p16_gate=p16_qc.to_gate()p16_gate.definition.draw()
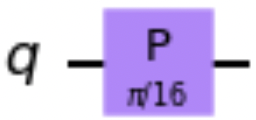
Abbildung 1-21. Kundenspezifische π/16-Phasentorzeichnung
Zweitens verwendet der folgende Code die Methode control(), um ein ControlledGate aus unserem benutzerdefinierten Tor zu erstellen, und Abbildung 1-22 zeigt eine Zeichnung des benutzerdefinierten kontrollierten Tors:
ctrl_p16=p16_gate.control(2)ctrl_p16.definition.draw()
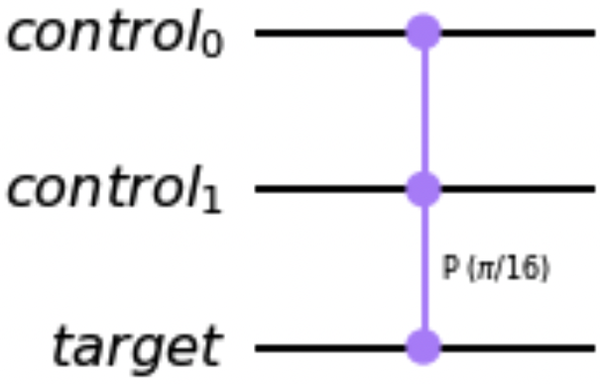
Abbildung 1-22. Zeichnung des kundenspezifisch gesteuerten π/16-Phasentors
Im folgenden Codeschnipsel nutzen wir die Methode append() (siehe "Verwenden der Methode append()"), um unser benutzerdefiniertes kontrolliertes Gatter in einer Quantenschaltung zu verwenden. Abbildung 1-23 zeigt eine Zeichnung des Schaltkreises:
qc=QuantumCircuit(4)qc.h([0,1,2,3])qc.append(ctrl_p16,[0,1,3])qc.decompose().draw()
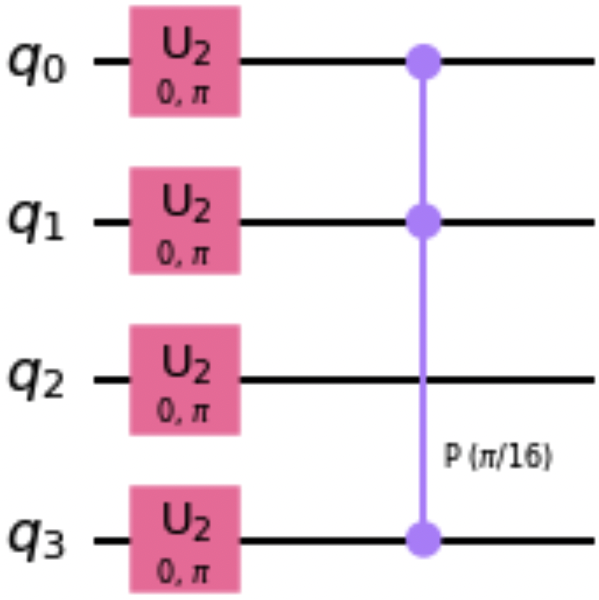
Abbildung 1-23. Zerlegte Schaltung, die das benutzerdefinierte gesteuerte Gatter verwendet
Parametrisierte Quantenschaltungen
Manchmal ist es sinnvoll, eine Quantenschaltung zu erstellen, in der Werte zur Laufzeit angegeben werden können. Diese Möglichkeit steht in Qiskit mit parametrisierten Schaltkreisen zur Verfügung, die zum Teil von den Klassen Parameter und ParameterVector implementiert werden.
Erstellen einer Parameterinstanz
Die Klasse Parameter wird verwendet, um einen Parameter in einem Quantenkreis darzustellen. Unter "Verwendung der Methode bind_parameters()" findest du ein Beispiel für die Definition und Verwendung eines parametrisierten Schaltkreises. Wie in diesem Beispiel gezeigt, kann ein Parameter erstellt werden, indem ein Unicode-String wie folgt an den Konstruktor übergeben wird:
theta1 = Parameter("θ1")
Die Parameter Objektreferenz namens theta1 kann anschließend in der bind_parameters() oder alternativ in der assign_parameters() Methode der QuantumCircuit Klasse verwendet werden.
Verwendung der ParameterVector-Klasse
Die Klasse ParameterVector kann genutzt werden, um Parameter als Sammlung zu erstellen und zu verwenden, anstatt einzelne Variablen. Der folgende Codeschnipsel erstellt einen Schaltkreis mit drei parametrisierten Phasentoren. Abbildung 1-24 zeigt eine Zeichnung der Schaltung:
fromqiskit.circuitimportQuantumCircuit,\ParameterVectortheta=ParameterVector('θ',3)qc=QuantumCircuit(3)qc.h([0,1,2])qc.p(theta[0],0)qc.p(theta[1],1)qc.p(theta[2],2)qc.draw()
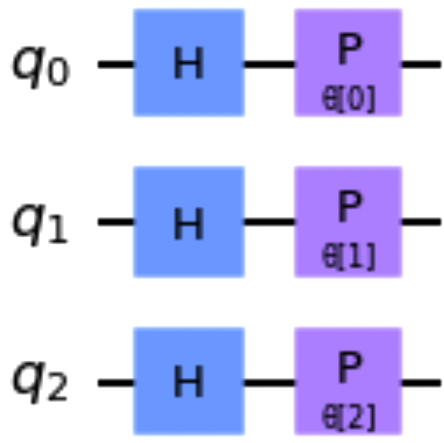
Abbildung 1-24. Beispiel für eine parametrisierte Schaltung, die ParameterVector
Um die Parameterwerte an einen neuen Stromkreis zu binden, übergeben wir der Methode bind_parameters() ein Wörterbuch, das die Referenz ParameterVector und die gewünschte Liste der Werte enthält.
Der folgende Codeschnipsel zeigt diese Technik, und Abbildung 1-25 zeigt die gebundene Schaltung, in der die Parameter des Phasentors durch die von gelieferten Werte ersetzt werden:
importmathb_qc=qc.bind_parameters({theta:[math.pi/8,math.pi/4,math.pi/2]})b_qc.draw()
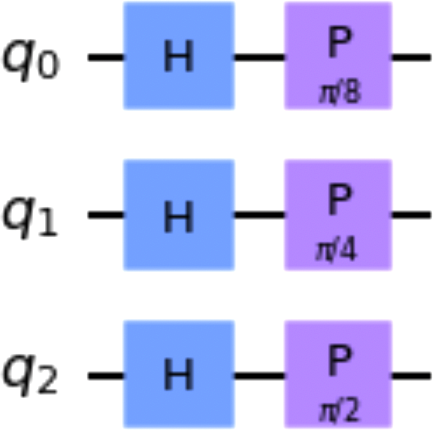
Abbildung 1-25. Beispiel für eine gebundene Schaltung mit den gelieferten Werten für die Phasendrehung
Get Qiskit Pocket Guide now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

