Programming Bitcoin

Chapter 2. Elliptic Curves

In this chapter we’re going to learn about elliptic curves. In Chapter 3, we will combine elliptic curves with finite fields to make elliptic curve cryptography.

Like finite fields, elliptic curves can look intimidating if you haven’t seen them before. But again, the actual math isn’t very difficult. Most of what you need to know about elliptic curves could have been taught to you after algebra. In this chapter, we’ll explore what these curves are and what we can do with them.

Definition

Elliptic curves are like many equations you’ve seen since pre-algebra. They have y on one side and x on the other, in some form. elliptic curves have a form like this:

• y² = x³ + ax + b

You’ve worked with other equations that look similar. For example, you probably learned the linear equation back in pre-algebra:

• y = mx + b

You may even remember that m here has the name slope and b is the y-intercept. You can also graph linear equations, as shown in Figure 2-1.

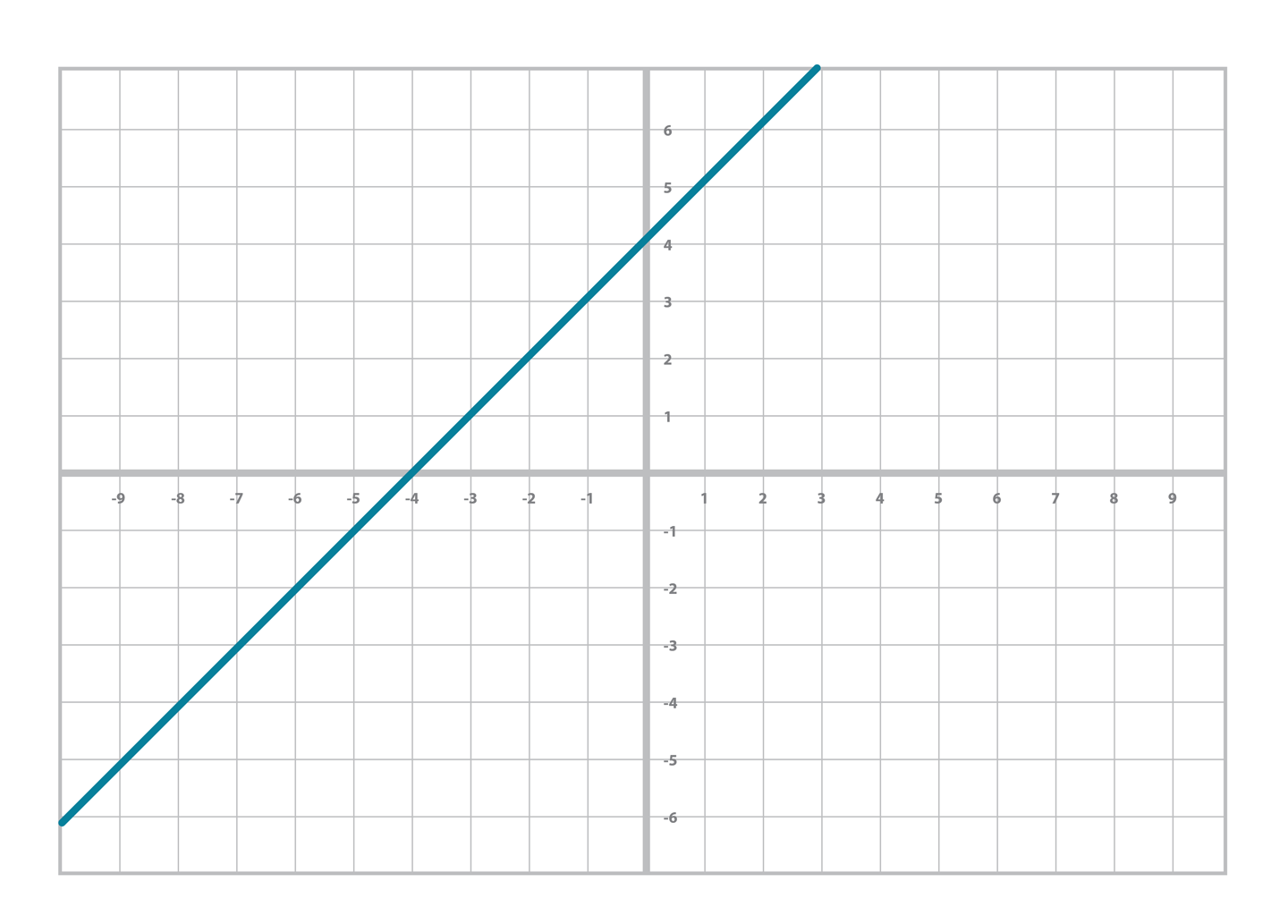
Figure 2-1. Linear equation

Similarly, you’re probably familiar with the quadratic equation and its graph (Figure 2-2):

• y = ax² + bx + c

And sometime around algebra, you did even higher orders of x—something called the cubic equation and its graph (Figure 2-3):

• y = ax³ + bx² + cx + d

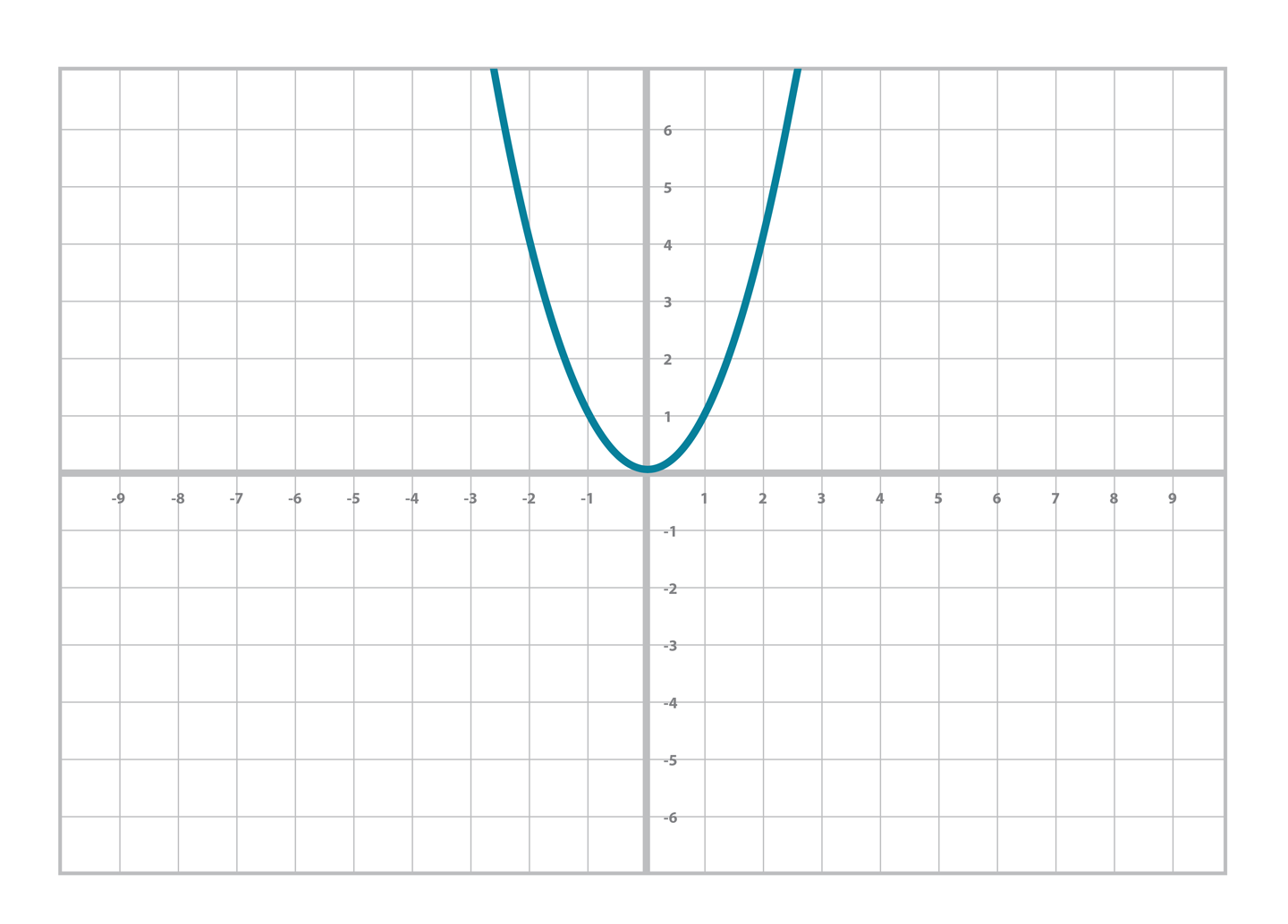
Figure 2-2. Quadratic ...