Capítulo 4. Aprendizaje por transferencia y otros trucos
Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: translation-feedback@oreilly.com
Después de haber examinado las arquitecturas en el capítulo anterior, quizá te preguntes si puedes descargar un modelo ya entrenado y entrenarlo aún más. Y la respuesta es ¡sí! Se trata de una técnica increíblemente potente en los círculos del aprendizaje profundo denominada aprendizaje por transferencia, mediante la cual una red entrenada para una tarea (por ejemplo, ImageNet) se adapta a otra (peces frente a gatos).
¿Por qué harías esto? Resulta que una arquitectura entrenada en ImageNet ya sabe muchísimo sobre imágenes y, en particular, bastante sobre si algo es un gato o un pez (o un perro o una ballena). Como ya no partes de una red neuronal esencialmente en blanco, con el aprendizaje por transferencia es probable que emplees mucho menos tiempo en el entrenamiento, y puedes salirte con la tuya con un conjunto de datos de entrenamiento mucho más pequeño. Los métodos tradicionales de aprendizaje profundo requieren enormes cantidades de datos para generar buenos resultados. Con el aprendizaje por transferencia, puedes crear clasificadores de nivel humano con unos cientos de imágenes.
Aprendizaje por transferencia con ResNet
Ahora, lo obvio es crear un modelo ResNet como hicimos en el Capítulo 3 e introducirlo en nuestro bucle de entrenamiento existente. ¡Y puedes hacerlo! No hay nada mágico en el modelo ResNet; se construye a partir de los mismos bloques de construcción que ya has visto. Sin embargo, es un modelo grande, y aunque verás alguna mejora respecto a una ResNet de referencia con tus datos, necesitarás muchos datos para asegurarte de que la señal de entrenamiento llega a todas las partes de la arquitectura y las entrena significativamente hacia tu nueva tarea de clasificación. Intentamos evitar el uso de muchos datos en este enfoque.
Pero aquí está la cuestión: no estamos tratando con una arquitectura que se ha inicializado con parámetros aleatorios, como hemos hecho en el pasado. Nuestro modelo ResNet preentrenado ya tiene codificada un montón de información para las necesidades de reconocimiento y clasificación de imágenes, así que ¿para qué molestarse en volver a entrenarlo? En lugar de eso, afinamos la red. Alteramos ligeramente la arquitectura para incluir un nuevo bloque de red al final, sustituyendo las capas lineales estándar de 1.000 categorías que normalmente realizan la clasificación de ImageNet. A continuación, congelamos todas las capas ResNet existentes, y cuando entrenamos, actualizamos sólo los parámetros de nuestras nuevas capas, pero seguimos tomando las activaciones de nuestras capas congeladas. Esto nos permite entrenar rápidamente nuestras nuevas capas preservando la información que ya contienen las capas preentrenadas.
En primer lugar, vamos a crear un modelo ResNet-50 preentrenado:
fromtorchvisionimportmodelstransfer_model=models.ResNet50(pretrained=True)
A continuación, tenemos que congelar las capas. La forma de hacerlo es sencilla: evitamos que acumulen gradientes utilizando requires_grad() . Tenemos que hacer esto para cada parámetro de la red, pero, afortunadamente, PyTorch proporciona un método parameters() que lo hace bastante fácil:
forname,paramintransfer_model.named_parameters():param.requires_grad=False
Consejo
Puede que no quieras congelar las capas de BatchNorm en un modelo, ya que se entrenarán para aproximarse a la media y la desviación típica del conjunto de datos con el que se entrenó originalmente el modelo, no con el conjunto de datos que quieres afinar. Parte de la señal de tus datos puede acabar perdiéndose a medida que BatchNorm corrige su entrada. Puedes mirar la estructura del modelo y congelar sólo las capas que no sean BatchNorm como ésta:
forname,paramintransfer_model.named_parameters():if("bn"notinname):param.requires_grad=False
Luego tenemos que sustituir el bloque de clasificación final por uno nuevo que entrenaremos para detectar gatos o peces. En este ejemplo, lo sustituimos por un par de capas Linear , una ReLU , y Dropout , pero también podrías tener capas CNN adicionales aquí. Afortunadamente, la definición de la implementación de ResNet en PyTorch almacena el bloque clasificador final como una variable de instancia, fc, así que todo lo que tenemos que hacer es sustituirla por nuestra nueva estructura (otros modelos suministrados con PyTorch utilizan fc o classifier , así que probablemente querrás comprobar la definición en el código fuente si estás intentando esto con un tipo de modelo diferente):
transfer_model.fc=nn.Sequential(nn.Linear(transfer_model.fc.in_features,500),nn.ReLU(),nn.Dropout(),nn.Linear(500,2))
En el código anterior, aprovechamos la variable in_features que nos permite coger el número de activaciones que entran en una capa (2.048 en este caso). También puedes utilizar out_features para descubrir las activaciones que salen. Se trata de funciones útiles para cuando encajas redes como si fueran ladrillos de construcción; si las funciones entrantes de una capa no coinciden con las salientes de la capa anterior, obtendrás un error en tiempo de ejecución.
Por último, volvemos a nuestro bucle de entrenamiento y entrenamos el modelo como de costumbre. Deberías ver algunos saltos grandes en la precisión, incluso en unas pocas épocas.
El aprendizaje por transferencia es una técnica clave para mejorar la precisión de tu aplicación de aprendizaje profundo, pero podemos emplear un montón de trucos más para aumentar el rendimiento de nuestro modelo. Veamos algunos de ellos.
Encontrar ese ritmo de aprendizaje
Tal vez recuerdes del Capítulo 2 que introduje el concepto de tasa de aprendizaje para el entrenamiento de redes neuronales, mencioné que era uno de los hiperparámetros más importantes que puedes alterar y, a continuación, me desentendí de lo que debías utilizar para ella, sugiriendo un número bastante pequeño y que experimentaras con distintos valores. Bueno... la mala noticia es que, en realidad, así es como mucha gente descubre la tasa de aprendizaje óptima para sus arquitecturas, normalmente con una técnica llamada grid search, buscando exhaustivamente su camino a través de un subconjunto de valores de tasa de aprendizaje, comparando los resultados con un conjunto de datos de validación. Esto lleva muchísimo tiempo, y aunque hay gente que lo hace, muchos otros se inclinan por la sabiduría popular. Por ejemplo, un valor de la tasa de aprendizaje que se ha observado empíricamente que funciona con el optimizador Adam es 3e-4. Esto se conoce como la constante de Karpathy, después de que Andrej Karpathy (actualmente director de IA en Tesla) tuiteara sobre ello en 2016. Por desgracia, menos gente leyó su siguiente tuit: "Sólo quería asegurarme de que la gente entiende que esto es una broma". Lo gracioso es que 3e-4 suele ser un valor que a menudo puede dar buenos resultados, así que es una broma con un toque de realidad.
Por un lado, tienes una búsqueda lenta y engorrosa, y por otro, conocimientos oscuros y arcanos adquiridos a base de trabajar con innumerables arquitecturas hasta que consigues hacerte una idea de lo que sería un buen ritmo de aprendizaje, incluso redes neuronales artesanales. ¿Hay alguna forma mejor que estos dos extremos?
Afortunadamente, la respuesta es sí, aunque te sorprenderá cuánta gente no utiliza este método mejor. Un artículo algo oscuro de Leslie Smith, científico investigador del Laboratorio de Investigación Naval de EE.UU., contenía un enfoque para encontrar una tasa de aprendizaje adecuada.1 Pero no fue hasta que Jeremy Howard puso de relieve la técnica en su curso fast.ai que empezó a ponerse de moda en la comunidad del aprendizaje profundo. La idea es bastante sencilla: en el transcurso de una época, empieza con una tasa de aprendizaje pequeña y aumenta a una tasa de aprendizaje más alta en cada mini-lote, dando como resultado una tasa alta al final de la época. Calcula la pérdida para cada tasa y luego, mirando un gráfico, elige la tasa de aprendizaje que dé el mayor descenso. Por ejemplo, observa el gráfico de la Figura 4-1.
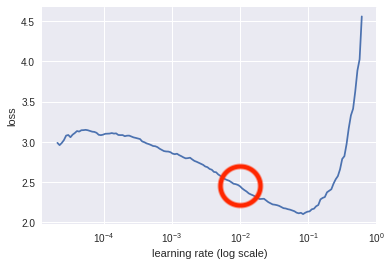
Figura 4-1. Tasa de aprendizaje frente a pérdidas
En este caso, deberíamos considerar utilizar una tasa de aprendizaje de alrededor de 1e-2 (marcado dentro del círculo), ya que ése es aproximadamente el punto en el que el gradiente del descenso es más pronunciado.
Nota
Ten en cuenta que no estás buscando la parte inferior de la curva, que podría ser el lugar más intuitivo; estás buscando el punto que está llegando a la parte inferior más rápidamente.
He aquí una versión simplificada de lo que hace la biblioteca fast.ai bajo cuerda:
importmathdeffind_lr(model,loss_fn,optimizer,init_value=1e-8,final_value=10.0):number_in_epoch=len(train_loader)-1update_step=(final_value/init_value)**(1/number_in_epoch)lr=init_valueoptimizer.param_groups[0]["lr"]=lrbest_loss=0.0batch_num=0losses=[]log_lrs=[]fordataintrain_loader:batch_num+=1inputs,labels=datainputs,labels=inputs,labelsoptimizer.zero_grad()outputs=model(inputs)loss=loss_fn(outputs,labels)# Crash out if loss explodesifbatch_num>1andloss>4*best_loss:returnlog_lrs[10:-5],losses[10:-5]# Record the best lossifloss<best_lossorbatch_num==1:best_loss=loss# Store the valueslosses.append(loss)log_lrs.append(math.log10(lr))# Do the backward pass and optimizeloss.backward()optimizer.step()# Update the lr for the next step and storelr*=update_stepoptimizer.param_groups[0]["lr"]=lrreturnlog_lrs[10:-5],losses[10:-5]
Lo que ocurre aquí es que iteramos a través de los lotes, entrenando casi como de costumbre; pasamos nuestras entradas a través del modelo y luego obtenemos la pérdida de ese lote. Registramos cuál es nuestra best_loss hasta ahora, y comparamos la nueva pérdida con ella. Si nuestra nueva pérdida es más de cuatro veces la de best_loss, salimos de la función, devolviendo lo que tenemos hasta ahora (ya que la pérdida probablemente tiende a infinito). En caso contrario, seguimos añadiendo la pérdida y los registros de la tasa de aprendizaje actual, y actualizamos la tasa de aprendizaje con el siguiente paso a lo largo del camino hasta la tasa máxima al final del bucle. El gráfico puede mostrarse entonces utilizando la función matplotlib plt :
logs,losses=find_lr()plt.plot(logs,losses)found_lr=1e-2
Observa que devolvemos trozos de los registros y pérdidas de lr. Lo hacemos simplemente porque los primeros trozos del entrenamiento y los últimos (sobre todo si la tasa de aprendizaje se hace muy grande con bastante rapidez) no suelen darnos mucha información.
La implementación en la biblioteca de fast.ai también incluye suavizado ponderado, por lo que obtendrás líneas suaves en tu gráfico, mientras que este fragmento produce un resultado irregular. Por último, recuerda que, dado que esta función entrena realmente el modelo y juega con los ajustes de la tasa de aprendizaje del optimizador, debes guardar y recargar tu modelo antes para volver al estado en el que estaba antes de llamar a find_lr() y también reinicializar el optimizador que hayas elegido, lo que puedes hacer ahora, ¡pasando la tasa de aprendizaje que hayas determinado al mirar el gráfico!
Eso nos da un buen valor para nuestra tasa de aprendizaje, pero podemos hacerlo aún mejor con tasas de aprendizaje diferenciales.
Tasas de aprendizaje diferenciales
En nuestro entrenamiento hasta ahora, hemos aplicado una tasa de aprendizaje a todo el modelo. Cuando se entrena un modelo desde cero, eso probablemente tiene sentido, pero cuando se trata de aprendizaje por transferencia, normalmente podemos obtener un poco más de precisión si probamos algo diferente: entrenar diferentes grupos de capas a diferentes ritmos. Anteriormente en el capítulo, congelamos todas las capas preentrenadas de nuestro modelo y entrenamos sólo nuestro nuevo clasificador, pero puede que queramos afinar algunas de las capas de, digamos, el modelo ResNet que estamos utilizando. Tal vez añadir algo de entrenamiento a las capas que preceden a nuestro clasificador haga que nuestro modelo sea un poco más preciso. Pero como esas capas anteriores ya han sido entrenadas en el conjunto de datos ImageNet, ¿quizá sólo necesiten un poco de entrenamiento en comparación con nuestras capas más recientes? PyTorch ofrece una forma sencilla de conseguirlo. Modifiquemos nuestro optimizador para el modelo ResNet-50:
optimizer=optimizer.Adam([{'params':transfer_model.layer4.parameters(),'lr':found_lr/3},{'params':transfer_model.layer3.parameters(),'lr':found_lr/9},],lr=found_lr)
Eso establece la tasa de aprendizaje para layer4 (justo antes de nuestro clasificador) en un tercio de la tasa de aprendizaje encontrada y un noveno para layer3. Esa combinación ha funcionado empíricamente bastante bien en mi trabajo, pero obviamente siéntete libre de experimentar. Sin embargo, hay una cosa más. Como recordarás del principio de este capítulo, congelamos todas estas capas preentrenadas. Está muy bien darles un ritmo de aprendizaje diferente, pero ahora mismo, el entrenamiento del modelo no las tocará en absoluto porque no acumulan gradientes. Cambiemos eso:
unfreeze_layers=[transfer_model.layer3,transfer_model.layer4]forlayerinunfreeze_layers:forparaminlayer.parameters():param.requires_grad=True
Ahora que los parámetros de estas capas vuelven a tomar gradientes, se aplicarán las tasas de aprendizaje diferencial cuando afines el modelo. Ten en cuenta que puedes congelar y descongelar partes del modelo a tu antojo y hacer más ajustes finos en cada capa por separado, ¡si quieres!
Ahora que hemos examinado los ritmos de aprendizaje, vamos a investigar un aspecto diferente del entrenamiento de nuestros modelos: los datos que introducimos en ellos.
Aumento de datos
Una de las frases más temidas en la ciencia de datos es: ¡Oh, no, mi modelo se ha sobreajustado a los datos! Como mencioné en el Capítulo 2, el sobreajuste se produce cuando el modelo decide reflejar los datos presentados en el conjunto de entrenamiento en lugar de producir una solución generalizada. A menudo oirás a la gente hablar de cómo un modelo concreto memorizó el conjunto de datos, lo que significa que el modelo aprendió las respuestas y pasó a obtener malos resultados en los datos de producción.
La forma tradicional de evitarlo es acumular grandes cantidades de datos. Al ver más datos, el modelo se hace una idea más general del problema que intenta resolver. Si consideras la situación como un problema de compresión, entonces si impides que el modelo pueda simplemente almacenar todas las respuestas (abrumando su capacidad de almacenamiento con tantos datos), se ve obligado a comprimir la entrada y, por tanto, a producir una solución que no puede ser simplemente almacenar las respuestas en sí misma. Esto está bien, y funciona bien, pero digamos que sólo tenemos mil imágenes y estamos haciendo aprendizaje por transferencia. ¿Qué podemos hacer?
Un enfoque que podemos utilizar es el aumento de datos. Si tenemos una imagen, podemos hacerle una serie de cosas que evitarán el sobreajuste y harán que el modelo sea más general. Considera las imágenes de la gata Helvética de las Figuras 4-2 y 4-3.

Figura 4-2. Nuestra imagen original

Figura 4-3. Una Helvética invertida
Obviamente, para nosotros son la misma imagen. La segunda no es más que una copia reflejada de la primera. La representación tensorial va a ser diferente, ya que los valores RGB estarán en lugares distintos de la imagen 3D. Pero sigue siendo un gato, así que es de esperar que el modelo que se entrene en esta imagen aprenda a reconocer la forma de un gato en el lado izquierdo o derecho del fotograma, en lugar de asociar simplemente toda la imagen con un gato. Hacer esto en PyTorch es sencillo. Puede que recuerdes este fragmento de código del Capítulo 2:
transforms=transforms.Compose([transforms.Resize(64),transforms.ToTensor(),transforms.Normalize(mean=[0.485,0.456,0.406],std=[0.229,0.224,0.225])])
Esto forma una tubería de transformación por la que pasan todas las imágenes cuando entran en el modelo para el entrenamiento. Pero la biblioteca torchivision.transforms contiene muchas otras funciones de transformación que pueden utilizarse para aumentar los datos de entrenamiento. Echemos un vistazo a algunas de las más útiles y veamos también qué le ocurre a la Helvética con algunas de las transformaciones menos obvias.
Antorcha de Visión Transforma
torchvision viene completo con una gran colección de posibles transformaciones que pueden utilizarse para aumentar los datos, además de dos formas de construir nuevas transformaciones. En esta sección, examinamos las más útiles que vienen incluidas, así como un par de transformaciones personalizadas que puedes utilizar en tus propias aplicaciones.
torchvision.transforms.ColorJitter(brightness=0,contrast=0,saturation=0,hue=0)
ColorJitter cambia aleatoriamente el brillo, el contraste, la saturación y el tono de una imagen. Para el brillo, el contraste y la saturación, puedes proporcionar un valor flotante o una tupla de valores flotantes, todos no negativos en el intervalo de 0 a 1, y la aleatoriedad estará entre 0 y el valor flotante proporcionado o utilizará la tupla para generar aleatoriedad entre el par de valores flotantes proporcionados. Para el matiz, se requiere un flotante o una tupla de flotantes entre -0,5 y 0,5, y generará ajustes aleatorios del matiz entre [-matiz,matiz] o[mín, máx]. Mira la Figura 4-4 para ver un ejemplo.

Figura 4-4. ColorJitter aplicado a 0,5 para todos los parámetros
Si quieres voltear tu imagen, estas dos transformaciones reflejan aleatoriamente una imagen en el eje horizontal o vertical:
torchvision.transforms.RandomHorizontalFlip(p=0.5)torchvision.transforms.RandomVerticalFlip(p=0.5)
Introduce un valor flotante de 0 a 1 para la probabilidad de que se produzca el reflejo o acepta el valor por defecto de un 50% de probabilidad de reflejo. En la Figura 4-5 se muestra un gato volteado verticalmente.

Figura 4-5. Volteo vertical
RandomGrayscale es un tipo de transformación similar, salvo que convierte aleatoriamente la imagen en escala de grises, en función del parámetro p (el valor por defecto es 10%):
torchvision.transforms.RandomGrayscale(p=0.1)
RandomCrop y , como era de esperar, realizan recortes aleatorios en la imagen de , que puede ser un int para la altura y la anchura, o una tupla que contenga diferentes alturas y anchuras. RandomResizeCrop sizeLa Figura 4-6 muestra un ejemplo de en acción. RandomCrop
torchvision.transforms.RandomCrop(size,padding=None,pad_if_needed=False,fill=0,padding_mode='constant')torchvision.transforms.RandomResizedCrop(size,scale=(0.08,1.0),ratio=(0.75,1.3333333333333333),interpolation=2)
Ahora tienes que tener un poco de cuidado aquí, porque si tus recortes son demasiado pequeños, corres el riesgo de recortar partes importantes de la imagen y hacer que el modelo se entrene en lo incorrecto. Por ejemplo, si en una imagen hay un gato jugando sobre una mesa, y el recorte elimina al gato y sólo deja parte de la mesa para clasificarla como gato, eso no está bien. Mientras que el RandomResizeCrop redimensionará el recorte para que ocupe el tamaño dado, el RandomCrop puede llevar un recorte cerca del perímetro y a la oscuridad más allá de la imagen.
Nota
RandomResizeCrop utiliza la interpolación bilineal, pero también puedes seleccionar el vecino más próximo o la interpolación bicúbica cambiando el parámetro interpolation. Consulta la página de filtros PIL para más detalles.
Como viste en el Capítulo 3, podemos añadir relleno para mantener el tamaño requerido de la imagen. Por defecto, se trata del relleno constant, que rellena los píxeles que de otro modo estarían vacíos más allá de la imagen con el valor dado en fill. Sin embargo, te recomiendo que utilices en su lugar el relleno reflect, ya que empíricamente parece funcionar un poco mejor que el simple hecho de añadir espacio constante vacío.

Figura 4-6. Cultivo aleatorio con tamaño=100
Si quieres girar aleatoriamente una imagen, RandomRotation variará entre [-degrees, degrees] si degrees es un único flotador o int, o (min,max) si es una tupla:
torchvision.transforms.RandomRotation(degrees,resample=False,expand=False,center=None)
Si expand está ajustado a True, esta función ampliará la imagen de salida para que pueda incluir toda la rotación; por defecto, está ajustada para recortar dentro de las dimensiones de entrada. Puedes especificar un filtro de remuestreo PIL y, opcionalmente, proporcionar una tupla (x,y) para el centro de rotación; de lo contrario, la transformación rotará sobre el centro de la imagen. La Figura 4-7 es una transformación RandomRotation con degrees ajustado a 45.

Figura 4-7. Rotación aleatoria con grados = 45
Pad es una transformación de relleno de uso general que añade relleno (altura y anchura adicionales) a los bordes de una imagen:
torchvision.transforms.Pad(padding,fill=0,padding_mode=constant)
Un único valor en padding aplicará relleno en esa longitud en todas las direcciones. Una dos-tupla padding producirá relleno en la longitud de (izquierda/derecha, arriba/abajo), y una cuatro-tupla producirá relleno para (izquierda, arriba, derecha, abajo). Por defecto, el relleno se establece en el modo constant, que copia el valor de fill en las ranuras de relleno. Las otras opciones son edge, que rellena los últimos valores del borde de la imagen en la longitud de relleno; reflect, que refleja los valores de la imagen (excepto el perímetro) en el borde; y symmetric, que es reflection pero incluye el último valor de la imagen en el perímetro. La Figura 4-8 muestra padding ajustado a 25 y padding_mode ajustado a reflect. Observa cómo se repite el recuadro en los perímetros.

Figura 4-8. Relleno con padding = 25 y padding_mode = reflect
RandomAffine te permite especificar traslaciones afines aleatorias de la imagen (escalado, rotaciones, traslaciones y/o cizallamiento, o cualquier combinación). La Figura 4-9 muestra un ejemplo de transformación afín.
torchvision.transforms.RandomAffine(degrees,translate=None,scale=None,shear=None,resample=False,fillcolor=0)

Figura 4-9. RandomAffine con grados = 10 y cizalladura = 50
El parámetro degrees puede ser un único flotador o int o una tupla. En forma simple, produce rotaciones aleatorias entre (-degrees, degrees). Con una tupla, producirá rotaciones aleatorias entre (min, max). degrees tiene que configurarse explícitamente para evitar que se produzcan rotaciones; no hay configuración por defecto. translate es una tupla de dos multiplicadores (horizontal_multipler, vertical_multiplier). En el momento de la transformación, se muestrea un desplazamiento horizontal, dx, en el intervalo -image_width × horizontal_multiplier < dx < img_width × horizontal_widthy el desplazamiento vertical se muestrea de la misma manera con respecto a la altura de la imagen y al multiplicador vertical.
La escala se gestiona mediante otra tupla, (min, max), de las que se extrae aleatoriamente un factor de escala uniforme. La cizalladura puede ser un único valor float/int o una tupla, y se muestrea aleatoriamente del mismo modo que el parámetro degrees. Por último, resample te permite proporcionar opcionalmente un filtro de remuestreo PIL, y fillcolor es un int opcional que especifica un color de relleno para las zonas de la imagen final que quedan fuera de la transformación final.
En cuanto a las transformaciones que debes utilizar en una cadena de aumento de datos, sin duda te recomiendo que utilices los diversos giros aleatorios, las fluctuaciones de color, la rotación y los recortes para empezar.
Hay otras transformaciones disponibles en torchvision; consulta la documentación para más detalles. Pero, por supuesto, puede que quieras crear una transformación particular para tu dominio de datos que no esté incluida por defecto, por lo que PyTorch proporciona varias formas de definir transformaciones personalizadas, como verás a continuación.
Espacios de color y transformadas lambda
Esto puede parecer un poco raro de mencionar, pero hasta ahora todo nuestro trabajo con imágenes se ha realizado en el espacio de color RGB bastante estándar de 24 bits , en el que cada píxel tiene un valor rojo, verde y azul de 8 bits para indicar el color de ese píxel. Sin embargo, ¡hay otros espacios de color disponibles!
Una alternativa popular es HSV, que tiene tres valores de 8 bits para el tono, la saturación y el valor. Algunas personas consideran que este sistema modela con más precisión la visión humana que el espacio de color RGB tradicional. Pero, ¿qué importancia tiene esto? Una montaña en RGB es una montaña en HSV, ¿no?
Bueno, hay algunas pruebas procedentes de trabajos recientes de aprendizaje profundo en coloración de que otros espacios de color pueden producir una precisión ligeramente superior a la del RGB. Una montaña puede ser una montaña, pero el tensor que se forma en la representación de cada espacio será diferente, y un espacio puede captar algo sobre tus datos mejor que otro.
Cuando se combinan con conjuntos, puedes crear fácilmente una serie de modelos que combinen los resultados del entrenamiento en los espacios de color RGB, HSV, YUV y LAB para exprimir unos cuantos puntos porcentuales más de precisión de tu canal de predicción.
Un pequeño problema es que PyTorch no ofrece una transformación que pueda hacer esto. Pero sí ofrece un par de herramientas que podemos utilizar para cambiar aleatoriamente una imagen de RGB estándar a HSV (u otro espacio de color). En primer lugar, si miramos en la documentación del PIL, veremos que podemos utilizar Image.convert() para trasladar una imagen PIL de un espacio de color a otro. Podríamos escribir una clase transform personalizada para realizar esta conversión, pero PyTorch añade una clase transforms.Lambda para que podamos envolver fácilmente cualquier función y ponerla a disposición del canal de transformación. Aquí está nuestra función personalizada:
def_random_colour_space(x):output=x.convert("HSV")returnoutput
A continuación, se envuelve en una clase transforms.Lambda y se puede utilizar en cualquier canal de transformación estándar, como hemos visto antes:
colour_transform=transforms.Lambda(lambdax:_random_colour_space(x))
Eso está bien si queremos convertir cada imagen en HSV, pero en realidad no queremos eso. Nos gustaría que cambiara aleatoriamente las imágenes en cada lote, para que sea probable que la imagen se presente en espacios de color diferentes en épocas diferentes. Podríamos actualizar nuestra función original para generar un número aleatorio y utilizarlo para generar una probabilidad aleatoria de cambiar la imagen, pero en lugar de eso somos aún más perezosos y utilizamos RandomApply :
random_colour_transform=torchvision.transforms.RandomApply([colour_transform])
Por defecto, RandomApply rellena un parámetro p con un valor de 0.5, por lo que hay una probabilidad del 50/50 de que se aplique la transformación. Experimenta añadiendo más espacios de color y la probabilidad de aplicar la transformación para ver qué efecto tiene en nuestro problema del gato y el pez.
Veamos otra transformación personalizada un poco más complicada.
Clases de transformación personalizadas
A veces una simple lambda no es suficiente; puede que tengamos alguna inicialización o estado del que queramos hacer un seguimiento, por ejemplo. En estos casos, podemos crear una transformación personalizada que opere sobre datos de imagen PIL o sobre un tensor. Una clase de este tipo tiene que implementar dos métodos __call__, que el canal de transformación invocará durante el proceso de transformación; y __repr__ , que debe devolver una representación en forma de cadena de la transformación, junto con cualquier estado que pueda ser útil a efectos de diagnóstico.
En el código siguiente, implementamos una clase de transformación que añade ruido gaussiano aleatorio a un tensor. Cuando se inicializa la clase, pasamos la media y la distribución estándar del ruido que necesitamos, y durante el método __call__, tomamos una muestra de esta distribución y la añadimos al tensor entrante:
classNoise():"""Adds gaussian noise to a tensor.>>> transforms.Compose([>>> transforms.ToTensor(),>>> Noise(0.1, 0.05)),>>> ])"""def__init__(self,mean,stddev):self.mean=meanself.stddev=stddevdef__call__(self,tensor):noise=torch.zeros_like(tensor).normal_(self.mean,self.stddev)returntensor.add_(noise)def__repr__(self):repr=f"{self.__class__.__name__ }(mean={self.mean},stddev={self.stddev})"returnrepr
Si añadimos esto a una canalización, podremos ver los resultados de la llamada al método __repr__:
transforms.Compose([Noise(0.1,0.05))])>>Compose(Noise(mean=0.1,sttdev=0.05))
Como las transformaciones no tienen restricciones y sólo heredan de la clase objeto base de Python, puedes hacer cualquier cosa. ¿Quieres sustituir completamente una imagen en tiempo de ejecución por algo de la búsqueda de imágenes de Google? ¿Pasar la imagen por una red neuronal completamente distinta y pasar ese resultado por la tubería? ¿Aplicar una serie de transformaciones de imagen que conviertan la imagen en una sombra reflectante enloquecida de su antiguo yo? Todo es posible, aunque no del todo recomendable. Aunque sería interesante ver si el efecto de transformación Remolino de Photoshop empeoraría o mejoraría la precisión. ¿Por qué no intentarlo?
Aparte de las transformaciones, hay algunas formas más de exprimir al máximo el rendimiento de un modelo. Veamos más ejemplos.
Empieza poco a poco y crece
He aquí un consejo que parece extraño, pero con el que se obtienen resultados reales: empieza por poco y ve aumentando. Lo que quiero decir es que si estás entrenando con imágenes de 256 × 256, crea unos cuantos conjuntos de datos más en los que las imágenes se hayan escalado a 64 × 64 y 128 × 128. Crea tu modelo con el conjunto de datos de 64 × 64, ajústalo como de costumbre y, a continuación, entrena exactamente el mismo modelo con el conjunto de datos de 128 × 128. No desde cero, sino utilizando los parámetros ya entrenados. Una vez que parezca que has exprimido al máximo los datos de 128 × 128, pasa a los datos de 256 × 256 que tienes como objetivo. Probablemente encontrarás uno o dos puntos porcentuales de mejora en la precisión.
Aunque no sabemos exactamente por qué funciona esto, la teoría de trabajo es que, al entrenarse con las resoluciones más bajas, el modelo aprende sobre la estructura general de la imagen y puede refinar ese conocimiento a medida que se amplían las imágenes entrantes. Pero eso es sólo una teoría. Sin embargo, eso no impide que sea un buen truco para tener en la manga cuando necesites exprimir hasta la última pizca de rendimiento de un modelo.
Si no quieres tener varias copias de un conjunto de datos almacenadas, puedes utilizar las transformaciones de torchvision para hacerlo sobre la marcha mediante la función Resize:
resize=transforms.Compose([transforms.Resize(64),…_otheraugmentationtransforms_…transforms.ToTensor(),transforms.Normalize([0.485,0.456,0.406],[0.229,0.224,0.225])
La penalización que pagas aquí es que acabas empleando más tiempo en el entrenamiento, ya que PyTorch tiene que aplicar el cambio de tamaño cada vez. Si redimensionaras todas las imágenes de antemano, probablemente conseguirías un entrenamiento más rápido, a costa de llenar tu disco duro. ¿Pero no es siempre así la compensación?
El concepto de empezar poco a poco y luego ir creciendo también se aplica a las arquitecturas. Utilizar una arquitectura ResNet como ResNet-18 o ResNet-34 para probar enfoques de transformaciones y tener una idea de cómo funciona el entrenamiento proporciona un bucle de retroalimentación mucho más estrecho que si empiezas utilizando un modelo ResNet-101 o ResNet-152. Empieza por lo pequeño, construye hacia arriba, y puedes reutilizar potencialmente las ejecuciones del modelo más pequeño en el momento de la predicción, añadiéndolas a un modelo conjunto.
Conjuntos
¿Qué hay mejor que un modelo que haga predicciones en ? Bueno, ¿qué tal un montón de ellos? El ensamblaje es una técnica bastante habitual en los métodos más tradicionales de aprendizaje automático, y también funciona bastante bien en el aprendizaje profundo. La idea es obtener una predicción a partir de una serie de modelos, y combinar esas predicciones para producir una respuesta final. Como los distintos modelos tendrán diferentes puntos fuertes en diferentes áreas, es de esperar que la combinación de todas sus predicciones produzca un resultado más preciso que un modelo por sí solo.
Hay muchos enfoques para los conjuntos, y no vamos a entrar en todos ellos aquí. En su lugar, aquí tienes una forma sencilla de empezar con los conjuntos, que en mi experiencia me ha proporcionado un 1% más de precisión: simplemente calcula la media de las predicciones:
# Assuming you have a list of models in models, and input is your input tensorpredictions=[m[i].fit(input)foriinmodels]avg_prediction=torch.stack(b).mean(0).argmax()
El método stack concatena el conjunto de tensores, así que si estuviéramos trabajando en el problema del gato/pez y tuviéramos cuatro modelos en nuestro conjunto, acabaríamos con un tensor 4 × 2 construido a partir de los cuatro tensores 1 × 2. Y mean hace lo que cabría esperar, sacar la media, aunque tenemos que introducir una dimensión 0 para asegurarnos de que saca la media de la primera dimensión en lugar de sumar simplemente todos los elementos del tensor y producir una salida escalar. Por último, argmax selecciona el índice del tensor con el elemento más alto, como has visto antes.
Es fácil imaginar enfoques más complejos. Quizá podrían añadirse ponderaciones a la predicción de cada modelo individual, y esas ponderaciones ajustarse si un modelo acierta o se equivoca en una respuesta. ¿Qué modelos deberías utilizar? He descubierto que una combinación de ResNets (por ejemplo, 34, 50, 101) funciona bastante bien, ¡y nada te impide guardar tu modelo con regularidad y utilizar diferentes instantáneas del modelo a lo largo del tiempo en tu conjunto!
Conclusión
Al llegar al final del Capítulo 4, dejamos atrás las imágenes para pasar al texto. Es de esperar que no sólo entiendas cómo funcionan las redes neuronales convolucionales en imágenes, sino que también tengas a mano una profunda bolsa de trucos, como el aprendizaje por transferencia, la búsqueda de la tasa de aprendizaje, el aumento de datos y el ensamblaje, que puedes poner en práctica en tu dominio de aplicación particular.
Otras lecturas
Si te interesa aprender más en el ámbito de la imagen, consulta el curso fast.ai de Jeremy Howard, Rachel Thomas y Sylvain Gugger. El buscador de tasas de aprendizaje de este capítulo es, como he mencionado, una versión simplificada del que ellos utilizan, pero el curso profundiza en muchas de las técnicas de este capítulo. La biblioteca fast.ai, construida sobre PyTorch, te permite aplicarlas a tus dominios de imagen (¡y texto!) fácilmente.
-
"Tasas de aprendizaje cíclicas para entrenar redes neuronales", por Leslie N. Smith (2015)
-
"ColorNet: Investigando la importancia de los espacios de color para la clasificación de imágenes" de Shreyank N. Gowda y Chun Yuan (2019)
1 Véase "Tasas de aprendizaje cíclicas para entrenar redes neuronales" de Leslie Smith (2015).
Get Programación de PyTorch para Aprendizaje Profundo now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

