¿Primero ordenado?

Capítulo 32. Cohesión

Este trabajo se ha traducido utilizando IA. Agradecemos tus opiniones y comentarios: [e-mail]

Los elementos acoplados deben ser subelementos del mismo elemento contenedor. Ésa es la primera implicación de la cohesión. Echa todo el estiércol en un solo montón. La segunda implicación de la cohesión es que los elementos que no son estiércol (bueno, que no están acoplados) deben ir a otra parte.

Por ejemplo, supongamos que tenemos un módulo que contiene 10 funciones. Tres de esas funciones están acopladas. ¿Dónde van las otras siete? Tenemos dos opciones(Figura 32-1).

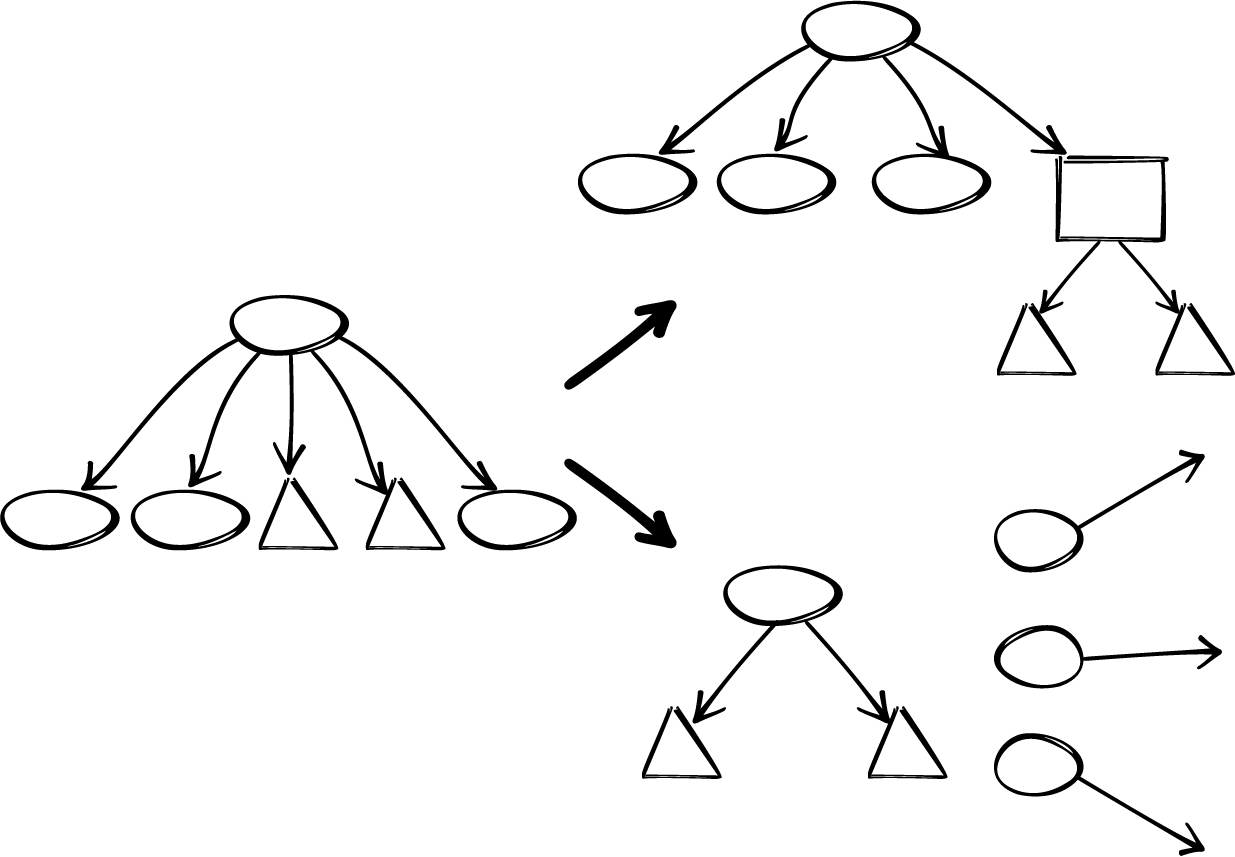
Figura 32-1. Elemento incohesivo mejorado mediante (arriba) la extracción de un subelemento cohesivo o mediante (abajo) el desplazamiento de los subelementos incohesivos a otro lugar

La primera es agrupar los elementos acoplados en su propio subelemento. Podríamos crear en un submódulo que sólo contuviera las tres funciones. Ese submódulo sería cohesivo porque sus elementos estarían acoplados. El módulo original podría ser menos cohesivo porque ahora ninguno de sus elementos estaría acoplado, pero no estaríamos peor que antes.

Extraer una función de ayuda es este tipo de enfoque de "extraer un subelemento cohesivo". Si las líneas de la función de ayuda tienen que cambiarse juntas, entonces la ayuda es cohesiva, con todas las ventajas que se derivan de la cohesión: análisis ...