Chapter 4. Building a Reverse Image Search Engine: Understanding Embeddings
Bob just bought a new home and is looking to fill it up with some fancy modern furniture. He’s flipping endlessly through furniture catalogs and visiting furniture showrooms, but hasn’t yet landed on something he likes. Then one day, he spots the sofa of his dreams—a unique L-shaped white contemporary sofa in an office reception. The good news is that he knows what he wants. The bad news is that he doesn’t know where to buy it from. The brand and model number is not written on the sofa. Asking the office manager doesn’t help either. So, he takes a few photos from different angles to ask around in local furniture shops, but tough luck: no one knows this particular brand. And searching on the internet with keywords like “white L-shaped,” “modern sofa” gives him thousands of results, but not the one he’s looking for.
Alice hears Bob’s frustration and asks, “Why don’t you try reverse image search?” Bob uploads his images on Google and Bing’s Reverse Image Search and quickly spots a similar-looking image on an online shopping website. Taking this more perfect image from the website, he does a few more reverse image searches and finds other websites offering the same sofa at cheaper prices. After a few minutes of being online, Bob has officially ordered his dream sofa!
Reverse image search (or as it is more technically known, instance retrieval) enables developers and researchers to build scenarios beyond simple keyword search. From discovering visually similar objects on Pinterest to recommending similar songs on Spotify to camera-based product search on Amazon, a similar class of technology under the hood is used. Sites like TinEye alert photographers on copyright infringement when their photographs are posted without consent on the internet. Even face recognition in several security systems uses a similar concept to ascertain the identity of the person.
The best part is, with the right knowledge, you can build a working replica of many of these products in a few hours. So let’s dig right in!
Here’s what we’re doing in this chapter:
-
Performing feature extraction and similarity search on Caltech101 and Caltech256 datasets
-
Learning how to scale to large datasets (up to billions of images)
-
Making the system more accurate and optimized
-
Analyzing case studies to see how these concepts are used in mainstream products
Image Similarity
The first and foremost question is: given two images, are they similar or not?
There are several approaches to this problem. One approach is to compare patches of areas between two images. Although this can help find exact or near-exact images (that might have been cropped), even a slight rotation would result in dissimilarity. By storing the hashes of the patches, duplicates of an image can be found. One use case for this approach would be the identification of plagiarism in photographs.
Another naive approach is to calculate the histogram of RGB values and compare their similarities. This might help find near-similar images captured in the same environment without much change in the contents. For example, in Figure 4-1, this technique is used in image deduplication software aimed at finding bursts of photographs on your hard disk, so you can select the best one and delete the rest. Of course, there is an increasing possibility of false positives as your dataset grows. Another downside to this approach is that small changes to the color, hue, or white balance would make recognition more difficult.

Figure 4-1. RGB histogram-based “Similar Image Detector” program
A more robust traditional computer vision-based approach is to find visual features near edges using algorithms like Scale-Invariant Feature Transform (SIFT), Speeded Up Robust Features (SURF), and Oriented FAST and Rotated BRIEF (ORB) and then compare the number of similar features that are common between the two photos. This helps you go from a generic image-level understanding to a relatively robust object-level understanding. Although this is great for images with rigid objects that have less variation like the printed sides of a box of cereal, which almost always look the same, it’s less helpful for comparing deformable objects like humans and animals, which can exhibit different poses. As an example, you can see the features being displayed on the camera-based product search experience on the Amazon app. The app displays these features in the form of blue dots (Figure 4-2). When it sees a sufficient number of features, it sends them to the Amazon servers to retrieve product information.
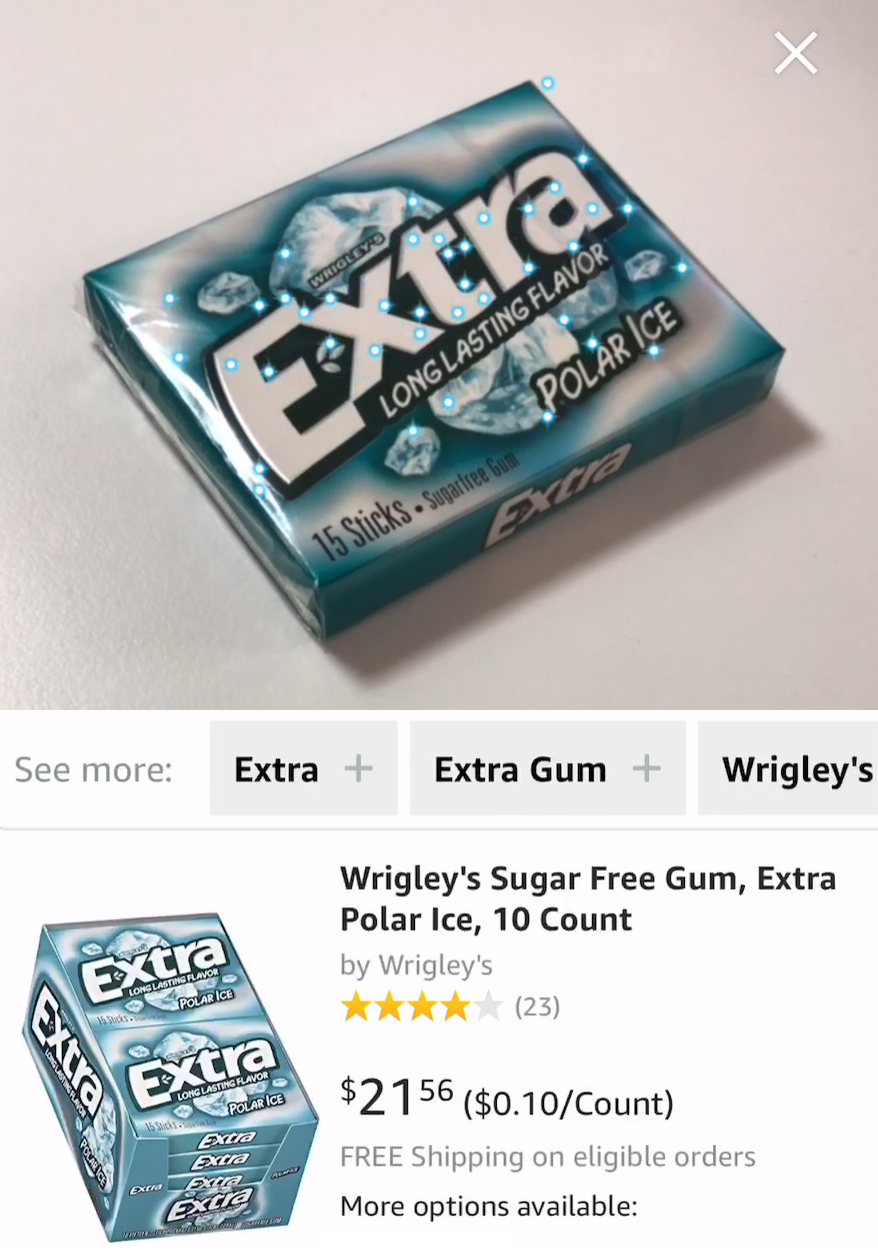
Figure 4-2. Product scanner in Amazon app with visual features highlighted
Going deeper, another approach is to find the category (e.g., sofa) of an image using deep learning and then find other images within the same category. This is equivalent to extracting metadata from an image so that it can then be indexed and used in a typical text query-based search. This can be easily scaled by using the metadata in open source search engines like ElasticSearch. Many ecommerce sites show recommendations based on tags extracted from an image while performing a query-based search internally. As you would expect, by extracting the tags, we lose certain information like color, pose, relationships between objects in the scene, and so on. Additionally, a major disadvantage of this approach is that it requires enormous volumes of labeled data to train the classifier for extracting these labels on new images. And every time a new category needs to be added, the model needs to be retrained.
Because our aim is to search among millions of images, what we ideally need is a way to summarize the information contained in the millions of pixels in an image into a smaller representation (of say a few thousand dimensions), and have this summarized representation be close together for similar objects and further away for dissimilar items.
Luckily, deep neural networks come to the rescue. As we saw in Chapter 2 and Chapter 3, the CNNs take an image input and convert it into feature vectors of a thousand dimensions, which then act as input to a classifier that outputs the top identities to which the image might belong (say dog or cat). The feature vectors (also called embeddings or bottleneck features) are essentially a collection of a few thousand floating-point values. Going through the convolution and pooling layers in a CNN is basically an act of reduction, to filter the information contained in the image to its most important and salient constituents, which in turn form the bottleneck features. Training the CNN molds these values in such a way that items belonging to the same class have small Euclidean distance between them (or simply the square root of the sum of squares of the difference between corresponding values) and items from different classes are separated by larger distances. This is an important property that helps solve so many problems where a classifier can’t be used, especially in unsupervised problems because of a lack of adequate labeled data.
An ideal way to find similar images would be to use transfer learning. For example, pass the images through a pretrained convolutional neural network like ResNet-50, extract the features, and then use a metric to calculate the error rate like the Euclidean distance.
Feature Extraction
An image is worth a thousand words features.
In this section, we play with and understand the concepts of feature extraction, primarily with the Caltech 101 dataset (131 MB, approximately 9,000 images), and then eventually with Caltech 256 (1.2 GB, approximately 30,000 images). Caltech 101, as the name suggests, consists of roughly 9,000 images in 101 categories, with about 40 to 800 images per category. It’s important to note that there is a 102nd category called “BACKGROUND_Google” consisting of random images not contained in the first 101 categories, which needs to be deleted before we begin experimenting. Remember that all of the code we are writing is also available in the GitHub repository.
Please note (as of 01 September 2020) the Caltech 101 dataset has moved locations and now has to be downloaded through Google Drive using gdown:
$ gdown https://drive.google.com/uc?id=137RyRjvTBkBiIfeYBNZBtViDHQ6_Ewsp --output 101_ObjectCategories.tar.gz $ tar -xvf 101_ObjectCategories.tar.gz $ mv 101_ObjectCategories caltech101 $ rm -rf caltech101/BACKGROUND_Google
Now, import all of the necessary modules:
importnumpyasnpfromnumpy.linalgimportnormimportpicklefromtqdmimporttqdm,tqdm_notebookimportosimporttimefromtf.keras.preprocessingimportimagefromtf.keras.applications.resnet50importResNet50,preprocess_input
Load the ResNet-50 model without the top classification layers, so we get only the bottleneck features. Then define a function that takes an image path, loads the image, resizes it to proper dimensions supported by ResNet-50, extracts the features, and then normalizes them:
model=ResNet50(weights='imagenet',include_top=False,input_shape=(224,224,3))defextract_features(img_path,model):input_shape=(224,224,3)img=image.load_img(img_path,target_size=(input_shape[0],input_shape[1]))img_array=image.img_to_array(img)expanded_img_array=np.expand_dims(img_array,axis=0)preprocessed_img=preprocess_input(expanded_img_array)features=model.predict(preprocessed_img)flattened_features=features.flatten()normalized_features=flattened_features/norm(flattened_features)returnnormalized_features
The function defined in the previous example is the key function that we use for almost every feature extraction need in Keras.
That’s it! Let’s see the feature-length that the model generates:
features=extract_features('../../sample_images/cat.jpg',model)(len(features))
> 2048
The ResNet-50 model generated 2,048 features from the provided image. Each feature is a floating-point value between 0 and 1.
If your model is trained or fine tuned on a dataset that is not similar to ImageNet, redefine the “preprocess_input(img)” step accordingly. The mean values used in the function are particular to the ImageNet dataset. Each model in Keras has its own preprocessing function so make sure you are using the right one.
Now it’s time to extract features for the entire dataset. First, we get all the filenames with this handy function, which recursively looks for all the image files (defined by their extensions) under a directory:
extensions=['.jpg','.JPG','.jpeg','.JPEG','.png','.PNG']defget_file_list(root_dir):file_list=[]counter=1forroot,directories,filenamesinos.walk(root_dir):forfilenameinfilenames:ifany(extinfilenameforextinextensions):file_list.append(os.path.join(root,filename))counter+=1returnfile_list
Then, we provide the path to our dataset and call the function:
# path to the datasetsroot_dir='../../datasets/caltech101'filenames=sorted(get_file_list(root_dir))
We now define a variable that will store all of the features, go through all filenames in the dataset, extract their features, and append them to the previously defined variable:
feature_list=[]foriintqdm_notebook(range(len(filenames))):feature_list.append(extract_features(filenames[i],model))
On a CPU, this should take under an hour. On a GPU, only a few minutes.
To get a better sense of time, use the super handy tool tqdm, which shows a progress meter (Figure 4-3) along with the speed per iteration as well as the time that has passed and expected finishing time. In Python, wrap an iterable with tqdm; for example, tqdm(range(10)). Its Jupyter Notebook variant is tqdm_notebook.

Figure 4-3. Progress bar shown with tqdm_notebook
Finally, write these features to a pickle file so that we can use them in the future without having to recalculate them:
pickle.dump(feature_list, open('data/features-caltech101-resnet.pickle', 'wb'))
pickle.dump(filenames, open('data/filenames-caltech101.pickle','wb'))
That’s all folks! We’re done with the feature extraction part.
Similarity Search
Given a photograph, our aim is to find another photo in our dataset similar to the current one. We begin by loading the precomputed features:
filenames = pickle.load(open('data/filenames-caltech101.pickle', 'rb'))
feature_list = pickle.load(open('data/features-caltech101-resnet.pickle', 'rb'))
We’ll use Python’s machine learning library scikit-learn for finding nearest neighbors of the query features; that is, features that represent a query image. We train a nearest-neighbor model using the brute-force algorithm to find the nearest five neighbors based on Euclidean distance (to install scikit-learn on your system, use pip3 install sklearn):
fromsklearn.neighborsimportNearestNeighborsneighbors=NearestNeighbors(n_neighbors=5,algorithm='brute',metric='euclidean').fit(feature_list)distances,indices=neighbors.kneighbors([feature_list[0]])
Now you have both the indices and distances of the nearest five neighbors of the very first query feature (which represents the first image). Notice the quick execution of the first step—the training step. Unlike training most machine learning models, which can take from several minutes to hours on large datasets, instantiating the nearest-neighbor model is instantaneous because at training time there isn’t much processing. This is also called lazy learning because all the processing is deferred to classification or inference time.
Now that we know the indices, let’s see the actual image behind that feature. First, we pick an image to query, located at say, index = 0:
importmatplotlib.pyplotaspltimportmatplotlib.imageasmpimg%matplotlibinline# Show the plots as a cell within the Jupyter Notebooksplt.imshow(mpimg.imread(filenames[0]))
Figure 4-4 shows the result.

Figure 4-4. The query image from the Caltech-101 dataset
Now, let’s examine the nearest neighbors by plotting the first result.
plt.imshow(mpimg.imread(filenames[indices[0]]))
Figure 4-5 shows that result.

Figure 4-5. The nearest neighbor to our query image
Wait, isn’t that a duplicate? Actually, the nearest index will be the image itself because that is what is being queried:
foriinrange(5):(distances[0][i])
0.0 0.8285478 0.849847 0.8529018
This is also confirmed by the fact that the distance of the first result is zero. Now let’s plot the real first nearest neighbor:
plt.imshow(mpimg.imread(filenames[indices[1]]))
Take a look at the result this time in Figure 4-6.

Figure 4-6. The second nearest neighbor of the queried image
This definitely looks like a similar image. It captured a similar concept, has the same image category (faces), same gender, and similar background with pillars and vegetation. In fact, it’s the same person!
We would probably use this functionality regularly, so we have already built a helper function plot_images() that visualizes several query images with their nearest neighbors. Now let’s call this function to visualize the nearest neighbors of six random images. Also, note that every time you run the following piece of code, the displayed images will be different (Figure 4-7) because the displayed images are indexed by a random integer.
foriinrange(6):random_image_index=random.randint(0,num_images)distances,indices=neighbors.kneighbors([featureList[random_image_index]])# don't take the first closest image as it will be the same imagesimilar_image_paths=[filenames[random_image_index]]+[filenames[indices[0][i]]foriinrange(1,4)]plot_images(similar_image_paths,distances[0])
Visualizing Image Clusters with t-SNE
Let’s step up the game by visualizing the entire dataset!
To do this, we need to reduce the dimensions of the feature vectors because it’s not possible to plot a 2,048-dimension vector (the feature-length) in two dimensions (the paper). The t-distributed stochastic neighbor embedding (t-SNE) algorithm reduces the high-dimensional feature vector to 2D, providing a bird’s-eye view of the dataset, which is helpful in recognizing clusters and nearby images. t-SNE is difficult to scale to large datasets, so it is a good idea to reduce the dimensionality using Principal Component Analysis (PCA) and then call t-SNE:
# Perform PCA over the featuresnum_feature_dimensions=100# Set the number of featurespca=PCA(n_components=num_feature_dimensions)pca.fit(featureList)feature_list_compressed=pca.transform(featureList)# For speed and clarity, we'll analyze about first half of the dataset.selected_features=feature_list_compressed[:4000]selected_class_ids=class_ids[:4000]selected_filenames=filenames[:4000]tsne_results=TSNE(n_components=2,verbose=1,metric='euclidean').fit_transform(selected_features)# Plot a scatter plot from the generated t-SNE resultscolormap=plt.cm.get_cmap('coolwarm')scatter_plot=plt.scatter(tsne_results[:,0],tsne_results[:,1],c=selected_class_ids,cmap=colormap)plt.colorbar(scatter_plot)plt.show()
We discuss PCA in more detail in later sections. In order to scale to larger dimensions, use Uniform Manifold Approximation and Projection (UMAP).
Figure 4-8 shows clusters of similar classes, and how they are spread close to one another.

Figure 4-8. t-SNE visualizing clusters of image features, where each cluster represents one object class in the same color
Each color in Figure 4-8 indicates a different class. To make it even more clear, we can use another helper function, plot_images_in_2d(), to plot the images in these clusters, as demonstrated in Figure 4-9.

Figure 4-9. t-SNE visualization showing image clusters; similar images are in the same cluster
Neat! There is a clearly demarcated cluster of human faces, flowers, vintage cars, ships, bikes, and a somewhat spread-out cluster of land and marine animals. There are lots of images on top of one another, which makes Figure 4-9 a tad bit confusing, so let’s try to plot the t-SNE as clear tiles with the helper function tsne_to_grid_plotter_manual(), the results of which you can see in Figure 4-10.
tsne_to_grid_plotter_manual(tsne_results[:,0],tsne_results[:,1],selected_filenames)

Figure 4-10. t-SNE visualization with tiled images; similar images are close together
This is definitely much clearer. We can see similar images are colocated within the clusters of human faces, chairs, bikes, airplanes, ships, laptops, animals, watches, flowers, tilted minarets, vintage cars, anchor signs, and cameras, all close to their own kind. Birds of a feather indeed do flock together!
2D clusters are great, but visualizing them in 3D would look stellar. It would be even better if they could be rotated, zoomed in and out, and manipulated using the mouse without any coding. And bonus points if the data could be searched interactively, revealing its neighbors. The TensorFlow Embedding projector does all this and more in a browser-based GUI tool. The preloaded embeddings from image and text datasets are helpful in getting a better intuition of the power of embeddings. And, as Figure 4-11 shows, it’s reassuring to see deep learning figure out that John Lennon, Led Zeppelin, and Eric Clapton happen to be used in a similar context to the Beatles in the English language.

Figure 4-11. TensorFlow Embedding projector showing a 3D representation of 10,000 common English words and highlighting words related to “Beatles”
Improving the Speed of Similarity Search
There are several opportunities to improve the speed of the similarity search step. For similarity search, we can make use of two strategies: either reduce the feature-length, or use a better algorithm to search among the features. Let’s examine each of these strategies individually.
Length of Feature Vectors
Ideally, we would expect that the smaller the amount of data in which to search, the faster the search should be. Recall that the ResNet-50 model gives 2,048 features. With each feature being a 32-bit floating-point, each image is represented by an 8 KB feature vector. For a million images, that equates to nearly 8 GB. Imagine how slow it would be to search among 8 GB worth of features. To give us a better picture of our scenario, Table 4-1 gives the feature-lengths that we get from different models.
| Model | Bottleneck feature-length | Top-1% accuracy on ImageNet |
|---|---|---|
| VGG16 | 512 | 71.5% |
| VGG19 | 512 | 72.7% |
| MobileNet | 1024 | 66.5% |
| InceptionV3 | 2048 | 78.8% |
| ResNet-50 | 2048 | 75.9% |
| Xception | 2048 | 79.0% |
Under the hood, many models available in tf.keras.applications yield several thousand features. For example, InceptionV3 yields features in the shape of 1 x 5 x 5 x 2048, which translates to 2,048 feature maps of 5 x 5 convolutions, resulting in a total of 51,200 features. Hence, it becomes essential to reduce this large vector by using an average or max-pooling layer. The pooling layer will condense each convolution (e.g., 5 x 5 layer) into a single value. This can be defined during model instantiation as follows:
model=InceptionV3(weights='imagenet',include_top=False,input_shape=(224,224,3),pooling='max')
For models that yield a large number of features, you will usually find that all code examples make use of this pooling option. Table 4-2 shows the before and after effect of max pooling on the number of features in different models.
| Model | # features before pooling | # features after pooling |
|---|---|---|
| ResNet-50 | [1,1,1,2048] = 2048 | 2048 |
| InceptionV3 | [1,5,5,2048] = 51200 | 2048 |
| MobileNet | [1,7,7,1024] = 50176 | 1024 |
As we can see, almost all the models generate a large number of features. Imagine how much faster the search would be if we could reduce to a mere 100 features (a whopping reduction of 10 to 20 times!) without compromising the quality of the results. Apart from just the size, this is an even bigger improvement for big data scenarios, for which the data can be loaded into RAM all at once instead of periodically loading parts of it, thus giving an even bigger speedup. PCA will help us make this happen.
Reducing Feature-Length with PCA
PCA is a statistical procedure that questions whether features representing the data are equally important. Are some of the features redundant enough that we can get similar classification results even after removing those features? PCA is considered one of the go-to techniques for dimensionality reduction. Note that it does not eliminate redundant features; rather, it generates a new set of features that are a linear combination of the input features. These linear features are orthogonal to one another, which is why all the redundant features are absent. These features are known as principal components.
Performing PCA is pretty simple. Using the scikit-learn library, execute the following:
importsklearn.decomposition.PCAasPCAnum_feature_dimensions=100pca=PCA(n_components=num_feature_dimensions)pca.fit(feature_list)feature_list_compressed=pca.transform(feature_list)
PCA can also tell us the relative importance of each feature. The very first dimension has the most variance and the variance keeps on decreasing as we go on:
# Explain the importance of first 20 features(pca.explained_variance_ratio_[0:20])
[ 0.07320023 0.05273142 0.04310822 0.03494248 0.02166119 0.0205037 0.01974325 0.01739547 0.01611573 0.01548918 0.01450421 0.01311005 0.01200541 0.0113084 0.01103872 0.00990405 0.00973481 0.00929487 0.00915592 0.0089256 ]
Hmm, why did we pick 100 dimensions from the original 2,048? Why not 200? PCA is representing our original feature vector but in reduced dimensions. Each new dimension has diminishing returns in representing the original vector (i.e., the new dimension might not explain the data much) and takes up valuable space. We can balance between how well the original data is explained versus how much we want to reduce it. Let’s visualize the importance of say the first 200 dimensions.
pca=PCA(200)pca.fit(feature_list)matplotlib.style.use('seaborn')plt.plot(range(1,201),pca.explained_variance_ratio_,'o--',markersize=4)plt.title('Variance for each PCA dimension')plt.xlabel('PCA Dimensions')plt.ylabel('Variance')plt.grid(True)plt.show()
Figure 4-12 presents the results.

Figure 4-12. Variance for each PCA dimension
The individual variance will tell us how important the newly added features are. For example, after the first 100 dimensions, the additional dimensions don’t add much variance (almost equal to 0) and can be neglected. Without even checking the accuracy it is safe to assume that the PCA with 100 dimensions will be a robust model. Another way to look at this is to visualize how much of the original data is explained by the limited number of features by finding the cumulative variance (see Figure 4-13).
plt.plot(range(1,201),pca.explained_variance_ratio_.cumsum(),'o--',markersize=4)plt.title('Cumulative Variance with each PCA dimension')plt.xlabel('PCA Dimensions')plt.ylabel('Variance')plt.grid(True)plt.show()
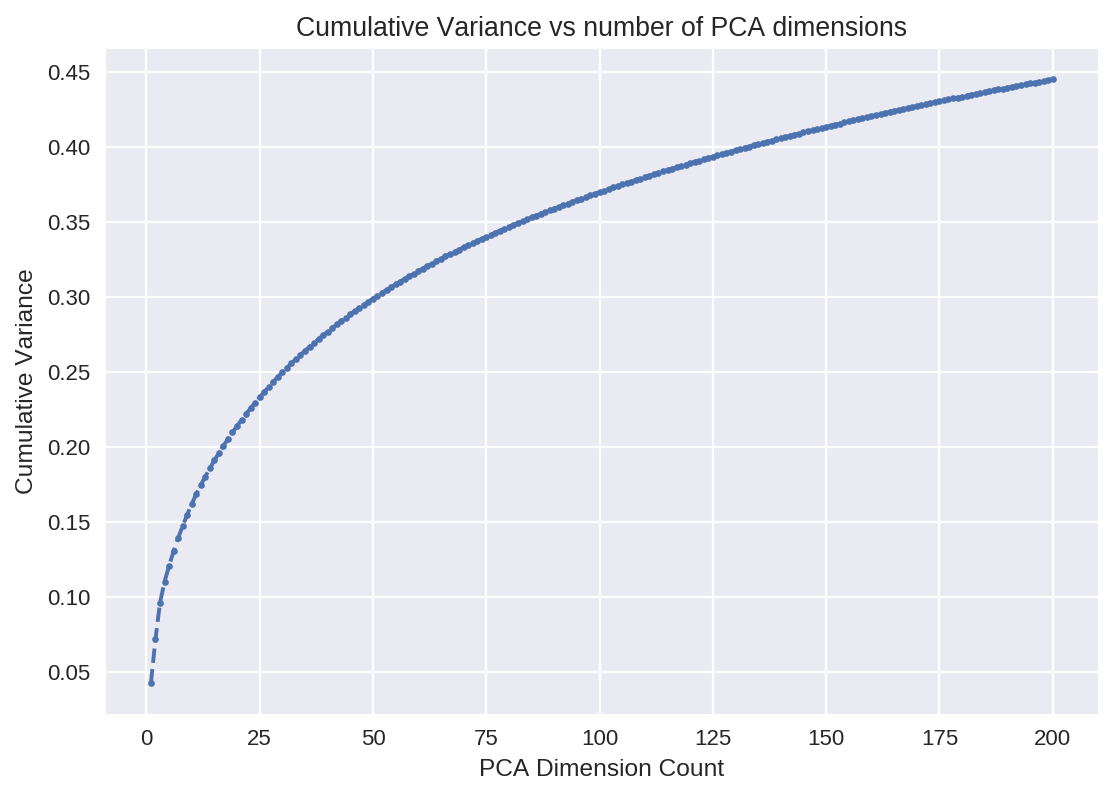
Figure 4-13. Cumulative variance with each PCA dimension
As expected, adding 100 dimensions (from 100 to 200) adds only 0.1 variance and begins to gradually plateau. For reference, using the full 2,048 features would result in a cumulative variance of 1.
The number of dimensions in PCA is an important parameter that we can tune to the problem at hand. One way to directly justify a good threshold is to find a good balance between the number of features and its effect on accuracy versus speed:
pca_dimensions=[1,2,3,4,5,10,20,50,75,100,150,200]pca_accuracy=[]pca_time=[]fordimensionsinpca_dimensions:# Perform PCApca=PCA(n_components=dimensions)pca.fit(feature_list)feature_list_compressed=pca.transform(feature_list[:])# Calculate accuracy over the compressed featuresaccuracy,time_taken=accuracy_calculator(feature_list_compressed[:])pca_time.append(time_taken)pca_accuracy.append(accuracy)("For PCA Dimensions =",dimensions,",\tAccuracy =",accuracy,"%",",\tTime =",pca_time[-1])
We visualize these results using the graph in Figure 4-14 and see that after a certain number of dimensions an increase in dimensions does not lead to higher accuracy:
plt.plot(pca_time,pca_accuracy,'o--',markersize=4)forlabel,x,yinzip(pca_dimensions,pca_time,pca_accuracy):plt.annotate(label,xy=(x,y),ha='right',va='bottom')plt.title('Test Time vs Accuracy for each PCA dimension')plt.xlabel('Test Time')plt.ylabel('Accuracy')plt.grid(True)plt.show()

Figure 4-14. Test time versus accuracy for each PCA dimension
As is visible in the graph, there is little improvement in accuracy after increasing beyond a feature-length of 100 dimensions. With almost 20 times fewer dimensions (100) than the original (2,048), this offers drastically higher speed and less time on almost any search algorithm, while achieving similar (and sometimes slightly better) accuracy. Hence, 100 would be an ideal feature-length for this dataset. This also means that the first 100 dimensions contain the most information about the dataset.
There are a number of benefits to using this reduced representation, like efficient use of computational resources, noise removal, better generalization due to fewer dimensions, and improved performance for machine learning algorithms learning on this data. By reducing the distance calculation to the most important features, we can also improve the result accuracy slightly. This is because previously all the 2,048 features were contributing equally in the distance calculation, whereas now, only the most important 100 features get their say. But, more importantly, it saves us from the curse of dimensionality. It’s observed that as the number of dimensions increases, the ratio of the Euclidean distance between the two closest points and the two furthest points tends to become 1. In very high-dimensional space, the majority of points from a real-world dataset seem to be a similar distance away from one another, and the Euclidean distance metric begins to fail in discerning similar versus dissimilar items. PCA helps bring sanity back.
You can also experiment with different distances like Minkowski distance, Manhattan distance, Jaccardian distance, and weighted Euclidean distance (where the weight is the contribution of each feature as explained in pca.explained_variance_ratio_).
Now, let’s turn our minds toward using this reduced set of features to make our search even faster.
Scaling Similarity Search with Approximate Nearest Neighbors
What do we want? Nearest neighbors. What is our baseline? Brute-force search. Although convenient to implement in two lines, it goes over each element and hence scales linearly with data size (number of items as well as the number of dimensions). Having PCA take our feature vector from a length of 2,048 to 100 will not only yield a 20-times reduction in data size, but also result in an increase in speed of 20 times when using brute force. PCA does pay off!
Let’s assume similarity searching a small collection of 10,000 images, now represented with 100 feature-length vectors, takes approximately 1 ms. Even though this looks fast for 10,000 items, in a real production system with larger data, perhaps 10 million items, this will take more than a second to search. Our system might not be able to fulfill more than one query per second per CPU core. If you receive 100 requests per second from users, even running on multiple CPU cores of the machine (and loading the search index per thread), you would need multiple machines to be able to serve the traffic. In other words, an inefficient algorithm means money, lots of money, spent on hardware.
Brute force is our baseline for every comparison. As in most algorithmic approaches, brute force is the slowest approach. Now that we have our baseline set, we will explore approximate nearest-neighbor algorithms. Instead of guaranteeing the correct result as with the brute-force approach, approximation algorithms generally get the correct result because they are...well, approximations. Most of the algorithms offer some form of tuning to balance between correctness and speed. It is possible to evaluate the quality of the results by comparing against the results of the brute-force baseline.
Approximate Nearest-Neighbor Benchmark
There are several approximate nearest-neighbor (ANN) libraries out there, including well-known ones like Spotify’s Annoy, FLANN, Facebook’s Faiss, Yahoo’s NGT, and NMSLIB. Benchmarking each of them would be a tedious task (assuming you get past installing some of them). Luckily, the good folks at ann-benchmarks.com (Martin Aumueller, Erik Bernhardsson, and Alec Faitfull) have done the legwork for us in the form of reproducible benchmarks on 19 libraries on large public datasets. We’ll pick the comparisons on a dataset of feature embeddings representing words (instead of images) called GloVe. This 350 MB dataset consists of 400,000 feature vectors representing words in 100 dimensions. Figure 4-15 showcases their raw performance when tuned for correctness. Performance is measured in the library’s ability to respond to queries each second. Recall that a measure of correctness is the fraction of top-n closest items returned with respect to the real top-n closest items. This ground truth is measured by brute-force search.

Figure 4-15. Comparison of ANN libraries (data from ann-benchmarks.com)
The strongest performers on this dataset return close to several thousand queries per second at the acceptable 0.8 recall. To put this in perspective, our brute-force search performs under 1 query per second. At the fastest, some of these libraries (like NGT) can return north of 15,000 results per second (albeit at a low recall, making it impractical for usage).
Which Library Should I Use?
It goes without saying that the library you use will end up depending heavily on your scenario. Each library presents a trade-off between search speed, accuracy, size of index, memory consumption, hardware use (CPU/GPU), and ease of setup. Table 4-3 presents a synopsis of different scenarios and recommendations as to which library might be work best for each scenario.
| Scenario | Recommendation |
|---|---|
| I want to experiment quickly in Python without too much setup but I also care about fast speed. | Use Annoy or NMSLIB |
| I have a large dataset (up to 10 million entries or several thousand dimensions) and care utmost about speed. | Use NGT |
| I have a ridiculously large dataset (100 million-plus entries) and have a cluster of GPUs, too. | Use Faiss |
| I want to set a ground-truth baseline with 100% correctness. Then immediately move to a faster library, impress my boss with the orders of magnitude speedup, and get a bonus. | Use brute-force approach |
We offer much more detailed examples in code of several libraries on the book’s GitHub website (see http://PracticalDeepLearning.ai), but for our purposes here, we’ll showcase our go-to library, Annoy, in detail and compare it with brute-force search on a synthetic dataset. Additionally, we briefly touch on Faiss and NGT.
Creating a Synthetic Dataset
To make an apples-to-apples comparison between different libraries, we first create a million-item dataset composed of random floating-point values with mean 0 and variance 1. Additionally, we pick a random feature vector as our query to find the nearest neighbors:
num_items=1000000num_dimensions=100dataset=np.random.randn(num_items,num_dimensions)dataset/=np.linalg.norm(dataset,axis=1).reshape(-1,1)random_index=random.randint(0,num_items)query=dataset[random_index]
Brute Force
First, we calculate the time for searching with the brute-force algorithm. It goes through the entire data serially, calculating the distance between the query and current item one at a time. We use the timeit command for calculating the time. First, we create the search index to retrieve the five nearest neighbors and then search with a query:
neighbors=NearestNeighbors(n_neighbors=5,algorithm='brute',metric='euclidean').fit(dataset)%timeitdistances,indices=neighbors.kneighbors([query])
> 177 ms ± 136 μs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
The timeit command is a handy tool. To benchmark the time of a single operation, prefix it with this command. Compared to the time command, which runs a statement for one time, timeit runs the subsequent line multiple times to give more precise aggregated statistics along with the standard deviation. By default, it turns off garbage collection, making independent timings more comparable. That said, this might not reflect timings in real production loads where garbage collection is turned on.
Annoy
Annoy (Approximate Nearest Neighbors Oh Yeah) is a C++ library with Python bindings for searching nearest neighbors. Synonymous with speed, it was released by Spotify and is used in production to serve its music recommendations. In contrast to its name, it’s actually fun and easy to use.
To use Annoy, we install it using pip:
$ pip install annoy
It’s fairly straightforward to use. First, we build a search index with two hyperparameters: the number of dimensions of the dataset and the number of trees:
fromannoyimportAnnoyIndexannoy_index=AnnoyIndex(num_dimensions)# Length of item vector that will beindexedforiinrange(num_items):annoy_index.add_item(i,dataset[i])annoy_index.build(40)# 40 trees
Now let’s find out the time it takes to search the five nearest neighbors of one image:
%timeitindexes=t.get_nns_by_vector(query,5,include_distances=True)
> 34.9 μs ± 165 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
Now that is blazing fast! To put this in perspective, even for our million-item dataset, this can serve almost 28,000 requests on a single CPU core. Considering most CPUs have multiple cores, it should be able to handle more than 100,000 requests on a single system. The best part is that it lets you share the same index in memory between multiple processes. Thus, the biggest index can be equivalent to the size of your overall RAM, making it possible to serve multiple requests on a single system.
Other benefits include that it generates a modestly sized index. Moreover, it decouples creating indexes from loading them, so you can create an index on one machine, pass it around, and then on your serving machine load it in memory and serve it.
Wondering about how many trees to use? More trees give higher precision, but larger indexes. Usually, no more than 50 trees are required to attain the highest precision.
NGT
Yahoo Japan’s Neighborhood Graph and Tree (NGT) library currently leads most benchmarks and is best suited for large datasets (in millions of items) with large dimensions (in several thousands). Although the library has existed since 2016, its real entry into the industry benchmark scene happened in 2018 with the implementation of the ONNG algorithm (short for Optimization of indexing based on k-Nearest Neighbor Graph for proximity). Considering multiple threads might be running NGT on a server, it can place the index in shared memory with the help of memory mapped files, helping to reduce memory usage as well as increase load time.
Faiss
Faiss is Facebook’s efficient similarity search library. It can scale to billions of vectors in RAM on a single server by storing a compressed representation of the vectors (compact quantization codes) instead of the original values. It’s especially suited for dense vectors. It shines particularly on machines with GPUs by storing the index on GPU memory (VRAM). This works on both single-GPU and multi-GPU setups. It provides the ability to configure performance based on search time, accuracy, memory usage, and indexing time. It’s one of the fastest known implementations of ANN search on GPU. Hey, if it’s good enough for Facebook, it’s good enough for most of us (as long as we have enough data).
While showing the entire process is beyond the scope of this book, we recommend installing Faiss using Anaconda or using its Docker containers to quickly get started.
Improving Accuracy with Fine Tuning
Many of the pretrained models were trained on the ImageNet dataset. Therefore, they provide an incredible starting point for similarity computations in most situations. That said, if you tuned these models to adapt to your specific problem, they would perform even more accurately at finding similar images.
In this portion of the chapter, we identify the worst-performing categories, visualize them with t-SNE, fine tune, and then see how their t-SNE graph changes.
What is a good metric to check whether you are indeed getting similar images?
- Painful option 1
-
Go through the entire dataset one image at a time, and manually score whether the returned images indeed look similar.
- Happier option 2
-
Simply calculate accuracy. That is, for an image belonging to category X, are the similar images belonging to the same category? We will refer to this similarity accuracy.
So, what are our worst-performing categories? And why are they the worst? To answer this, we have predefined a helper function worst_classes. For every image in the dataset, it finds the nearest neighbors using the brute-force algorithm and then returns six classes with the least accuracy. To see the effects of fine tuning, we run our analysis on a more difficult dataset: Caltech-256. Calling this function unveils the least-accurate classes:
names_of_worst_classes_before_finetuning,accuracy_per_class_before_finetuning=worst_classes(feature_list[:])
Accuracy is 56.54
Top 6 incorrect classifications
059.drinking-straw Accuracy: 11.76%
135.mailbox Accuracy: 16.03%
108.hot-dog Accuracy: 16.72%
163.playing-card Accuracy: 17.29%
195.soda-can Accuracy: 19.68%
125.knife Accuracy: 20.53%
To see why they are performing so poorly on certain classes, we’ve plotted a t-SNE graph to visualize the embeddings in 2D space, which you can see in Figure 4-16. To prevent overcrowding on our plot, we use only 50 items from each of the 6 classes.
To enhance the visibility of the graph we can define different markers and different colors for each class. Matplotlib provides a wide variety of markers and colors.
markers=["^",".","s","o","x","P"]colors=['red','blue','fuchsia','green','purple','orange']

Figure 4-16. t-SNE visualization of feature vectors of least-accurate classes before fine tuning
Aah, these feature vectors are all over the place and on top of one another. Using these feature vectors in other applications such as classification might not be a good idea because it would be difficult to find a clean plane of separation between them. No wonder they performed so poorly in this nearest neighbor–based classification test.
What do you think will be the result if we repeat these steps with the fine-tuned model? We reckon something interesting; let’s take a look at Figure 4-17 to see.

Figure 4-17. t-SNE visualization of feature vectors of least-accurate classes after fine tuning
This is so much cleaner. With just a little bit of fine tuning as shown in Chapter 3, the embeddings begin to group together. Compare the noisy/scattered embeddings of the pretrained models against those of the fine-tuned model. A machine learning classifier would be able to find a plane of separation between these classes with much more ease, hence yielding better classification accuracy as well as more similar images when not using a classifier. And, remember, these were the classes with the highest misclassifications; imagine how nicely the classes with originally higher accuracy would be after fine tuning.
Previously, the pretrained embeddings achieved 56% accuracy. The new embeddings after fine tuning deliver a whopping 87% accuracy! A little magic goes a long way.
The one limitation for fine tuning is the requirement of labeled data, which is not always present. So depending on your use case, you might need to label some amount of data.
There’s a small unconventional training trick involved, though, which we discuss in the next section.
Fine Tuning Without Fully Connected Layers
As we already know, a neural network comprises three parts:
-
Convolutional layers, which end up generating the feature vectors
-
Fully connected layers
-
The final classifier layer
Fine tuning, as the name suggests, involves tweaking a neural network lightly to adapt to a new dataset. It usually involves stripping off the fully connected layers (top layers), substituting them with new ones, and then training this newly composed neural network using this dataset. Training in this manner will cause two things:
-
The weights in all the newly added fully connected layers will be significantly affected.
-
The weights in the convolutional layers will be only slightly changed.
The fully connected layers do a lot of the heavy lifting to get maximum classification accuracy. As a result, the majority of the network that generates the feature vectors will change insignificantly. Thus, the feature vectors, despite fine tuning, will show little change.
Our aim is for similar-looking objects to have closer feature vectors, which fine tuning as described earlier fails to accomplish. By forcing all of the task-specific learning to happen in the convolutional layers, we can see much better results. How do we achieve that? By removing all of the fully connected layers and placing a classifier layer directly after the convolutional layers (which generate the feature vectors). This model is optimized for similarity search rather than classification.
To compare the process of fine tuning a model optimized for classification tasks as opposed to similarity search, let’s recall how we fine tuned our model in Chapter 3 for classification:
fromtf.keras.applications.resnet50importResNet50model=ResNet50(weights='imagenet',include_top=False,input_shape=(224,224,3))input=Input(shape=(224,224,3))x=model(input)x=GlobalAveragePooling2D()(x)x=Dense(64,activation='relu')(x)x=Dropout(0.5)(x)x=Dense(NUM_CLASSES,activation='softmax')(x)model_classification_optimized=Model(inputs=input,outputs=x)
And here’s how we fine tune our model for similarity search. Note the missing hidden dense layer in the middle:
fromtf.keras.applications.resnet50importResNet50model=ResNet50(weights='imagenet',include_top=False,input_shape=(224,224,3))input=Input(shape=(224,224,3))x=model(input)x=GlobalAveragePooling2D()(x)# No dense or dropout layersx=Dense(NUM_CLASSES,activation='softmax')(x)model_similarity_optimized=Model(inputs=input,outputs=x)
After fine tuning, to use the model_similarity_optimized for extracting features instead of giving probabilities for classes, simply pop (i.e., remove) the last layer:
model_similarity_optimized.layers.pop()model=Model(model_similarity_optimized.input,model_similarity_optimized.layers[-1].output)
The key thing to appreciate here is if you used the regular fine-tuning process, we would get lower similarity accuracy than model_similarity_optimized. Obviously, we would want to use model_classification_optimized for classification scenarios and model_similarity_optimized for extracting embeddings for similarity search.
With all this knowledge, you can now make both a fast and accurate similarity system for any scenario you are working on. It’s time to see how the giants in the AI industry build their products.
Siamese Networks for One-Shot Face Verification
A face verification system is usually trying to ascertain—given two images of faces—whether the two images are of the same person. This is a high-precision binary classifier that needs to robustly work with different lighting, clothing, hairstyles, backgrounds, and facial expressions. To make things more challenging, although there might be images of many people in, for instance an employee database, there might be only a handful of images of the same person available. Similarly, signature identification in banks and product identification on Amazon suffer the same challenge of limited images per item.
How would you go about training such a classifier? Picking embeddings from a model like ResNet pretrained on ImageNet might not discern these fine facial attributes. One approach is to put each person as a separate class and then train like we usually train a regular network. Two key issues arise:
-
If we had a million individuals, training for a million categories is not feasible.
-
Training with a few images per class will lead to overtraining.
Another thought: instead of teaching different categories, we could teach a network to directly compare and decide whether a pair of images are similar or dissimilar by giving guidance on their similarity during training. And this is the key idea behind Siamese networks. Take a model, feed in two images, extract two embeddings, and then calculate the distance between the two embeddings. If the distance is under a threshold, consider them similar, else not. By feeding a pair of images with the associated label, similar or dissimilar, and training the network end to end, the embeddings begin to capture the fine-grained representation of the inputs. This approach, shown in Figure 4-18, of directly optimizing for the distance metric is called metric learning.

Figure 4-18. A Siamese network for signature verification; note that the same CNN was used for both input images
We could extend this idea and even feed three images. Pick one anchor image, pick another positive sample (of the same category), and another negative sample (of a different category). Let’s now train this network to directly optimize for the distance between similar items to be minimized and the distance between dissimilar items to be maximized. This loss function that helps us achieve this is called a triplet loss function. In the previous case with a pair of images, the loss function is called a contrastive loss function. The triplet loss function tends to give better results.
After the network is trained, we need only one reference image of a face for deciding at test time whether the person is the same. This methodology opens the doors for one-shot learning. Other common uses include signature and logo recognition. One remarkably creative application by Saket Maheshwary and Hemant Misra is to use a Siamese network for matching résumés with job applicants by calculating the semantic similarity between the two.
Case Studies
Let’s look at a few interesting examples that show how what we have learned so far is applied in the industry.
Flickr
Flickr is one of the largest photo-sharing websites, especially popular among professional photographers. To help photographers find inspiration as well as showcase content the users might find interesting, Flickr produced a similarity search feature based on the same semantic meaning. As demonstrated in Figure 4-19, exploring a desert pattern leads to several similarly patterned results. Under the hood, Flickr adopted an ANN algorithm called Locally Optimized Product Quantization (LOPQ), which has been open sourced in Python as well as Spark implementations.
![Similar patterns of a desert photo (image source: code.flickr.com]](/api/v2/epubs/9781492034858/files/assets/pdlc_0419.png)
Figure 4-19. Similar patterns of a desert photo (image source)
Pinterest is an application used widely for its visual search capabilities, more specifically in its features called Similar Pins and Related Pins. Other companies like Baidu and Alibaba have launched similar visual search systems. Also, Zappos, Google Shopping, and like.com are using computer vision for recommendation.
Within Pinterest “women’s fashion” is one of the most popular themes of pins and the Similar Looks feature (Figure 4-20) helps people discover similar products. Additionally, Pinterest also reports that its Related Pins feature increased its repin rate. Not every pin on Pinterest has associated metadata, which makes recommendation a difficult cold-start problem due to lack of context. Pinterest developers solved this cold-start problem by using the visual features for generating the related pins. Additionally, Pinterest implements an incremental fingerprinting service that generates new digital signatures if either a new image is uploaded or if there is feature evolution (due to improvements or modifications in the underlying models by the engineers).

Figure 4-20. The Similar Looks feature of the Pinterest application (image source: Pinterest blog)
Celebrity Doppelgangers
Website applications like Celebslike.me, which went viral in 2015, look for the nearest neighbor among celebrities, as shown in Figure 4-21. A similar viral approach was taken by the Google Arts & Culture app in 2018, which shows the nearest existing portrait to your face. Twins or not is another application with a similar aim.

Figure 4-21. Testing our friend Pete Warden’s photo (technical lead for mobile and embedded TensorFlow at Google) on the celebslike.me website
Spotify
Spotify uses nearest neighbors for recommending music and creating automatic playlists and radio stations based on the current set of songs being played. Usually, collaborative filtering techniques, which are employed for recommending content like movies on Netflix, are content agnostic; that is, the recommendation happens because large groups of users with similar tastes are watching similar movies or listening to similar songs. This presents a problem for new and not yet popular content because users will keep getting recommendations for existing popular content. This is also referred to as the aforementioned cold-start problem. The solution is to use the latent understanding of the content. Similar to images, we can create feature vectors out of music using MFCC features (Mel Frequency Cepstral Coefficients), which in turn generates a 2D spectrogram that can be thought of as an image and can be used to generate features. Songs are divided into three-second fragments, and their spectrograms are used to generate features. These features are then averaged together to represent the complete song. Figure 4-22 shows artists whose songs are projected in specific areas. We can discern hip-hop (upper left), rock (upper right), pop (lower left), and electronic music (lower right). As already discussed, Spotify uses Annoy in the background.

Figure 4-22. t-SNE visualization of the distribution of predicted usage patterns, using latent factors predicted from audio (image source: “Deep content-based music recommendation” by Aaron van den Oord, Sander Dieleman, Benjamin Schrauwen, NIPS 2013)
Image Captioning
Image captioning is the science of translating an image into a sentence (as illustrated in Figure 4-23). Going beyond just object tagging, this requires a deeper visual understanding of the entire image and relationships between objects. To train these models, an open source dataset called MS COCO was released in 2014, which consists of more than 300,000 images along with object categories, sentence descriptions, visual question-answer pairs, and object segmentations. It serves as a benchmark for a yearly competition to see progress in image captioning, object detection, and segmentation.

Figure 4-23. Image captioning feature in Seeing AI: the Talking Camera App for the blind community
A common strategy applied in the first year of the challenge (2015) was to append a language model (LSTM/RNN) with a CNN in such a way that the output of a CNN feature vector is taken as the input to the language model (LSTM/RNN). This combined model was trained jointly in an end-to-end manner, leading to very impressive results that stunned the world. Although every research lab was trying to beat one another, it was later found that doing a simple nearest-neighbor search could yield state-of-the-art results. For a given image, find similar images based on similarity of the embeddings. Then, note the common words in the captions of the similar images, and print the caption containing the most common words. In short, a lazy approach would still beat the state-of-the-art one, and this exposed a critical bias in the dataset.
This bias has been coined the Giraffe-Tree problem by Larry Zitnick. Do an image search for “giraffe” on a search engine. Look closely: in addition to giraffe, is there grass in almost every image? Chances are you can describe the majority of these images as “A giraffe standing in a grass field.” Similarly, if a query image like the photo on the far left in Figure 4-24 contains a giraffe and a tree, almost all similar images (right) can be described as “a giraffe standing in the grass, next to a tree.” Even without a deeper understanding of the image, one would arrive at the correct caption using a simple nearest-neighbor search. This shows that to measure the real intelligence of a system, we need more semantically novel/original images in the test set.

Figure 4-24. The Giraffe-Tree problem (image source: Measuring Machine Intelligence Through Visual Question Answering, C. Lawrence Zitnick, Aishwarya Agrawal, Stanislaw Antol, Margaret Mitchell, Dhruv Batra, Devi Parikh)
In short, don’t underestimate a simple nearest-neighbor approach!
Summary
Now we are at the end of a successful expedition where we explored locating similar images with the help of embeddings. We took this one level further by exploring how to scale searches from a few thousand to a few billion documents with the help of ANN algorithms and libraries including Annoy, NGT, and Faiss. We also learned that fine tuning the model to your dataset can improve the accuracy and representative power of embeddings in a supervised setting. To top it all off, we looked at how to use Siamese networks, which use the power of embeddings to do one-shot learning, such as for face verification systems. We finally examined how nearest-neighbor approaches are used in various use cases across the industry. Nearest neighbors are a simple yet powerful tool to have in your toolkit.
Get Practical Deep Learning for Cloud, Mobile, and Edge now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.


