Optical Communications, 2nd Edition

PROBLEMS

4.1

• (a) Using Figure 4.2, show that β in Eq. (4.1.2) is equal to the ratio Δ/I_sm_p, where Δ is the range of output power that defines the linear range of the modulator and m_P is the peak value of m(t).
• (b) (b) Assuming maximum linear range around I_s, write β in terms of the maximum and minimum values of the output intensity that define the linear range of the modulator.

4.2

• (a) Given the circuit loading in Figure P4.2 at the output of a photo-detector, show that the processor input current is a low-pass filtered version of the detector output current.

  

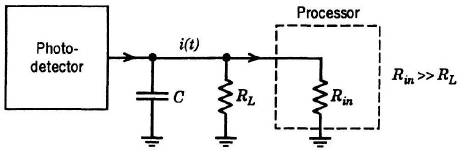
  Figure P4.2.

• (b) Determine the 3-dB bandwidth of this filter.
• (c) Show that if the bandwidth of this filter is to be set at B Hz for any capacitance value C, the noise current spectral level due to R_L in Eq. (4.2.2) increases with B.

4.3 Consider two independent, zero mean, complex random processes

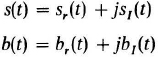
each with uncorrelated real and imaginary parts, with the individual spectral densities

Let S(ω) and B(ω) have transforms R_s(τ) and R_B (τ). Define a new process

1. (a) Compute the correlation of y(t) in terms of R_s(τ) and R_B (τ). ...