October 2022
Intermediate to advanced
448 pages
12h 24m
English
book
Nonparametric Statistics with Applications to Science and Engineering with R, 2nd Edition
by Paul Kvam, Brani Vidakovic, Seong-joon Kim
Content preview from Nonparametric Statistics with Applications to Science and Engineering with R, 2nd Edition
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
10Estimating Distribution Functions
The harder you fight to hold on to specific assumptions, the more likely there's gold in letting go of them.
John Seely Brown (1997), former Chief Scientist at Xerox Corporation
10.1 Introduction
Let 
be a sample from a population with continuous cumulative distribution function (CDF) 
In Chapter 3, we defined the empirical (cumulative) distribution function (EDF) based on a random sample as
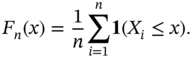
Because 
, for a fixed 
, has a sampling distribution directly related to the binomial distribution, its properties are readily apparent, and it is easy to work with as an estimating function.
The EDF provides a sound estimator for the CDF, but not through any methodology that can be extended to general estimation problems in nonparametric statistics. For example, what if the sample is right truncated? Or censored? What if the sample observations are not independent or identically distributed? In standard statistical analysis, the method of maximum likelihood ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.