Natural Language Processing with Spark NLP

Chapter 4. Deep Learning Basics

In this chapter we will cover the basics of deep learning. The goal of this chapter is to create a foundation for us to discuss how to apply deep learning to NLP. There are new deep learning techniques being developed every month, and we will cover some of the newer techniques in later chapters, which is why we need this foundation. In the beginning of this chapter we will cover some of the history of the artificial neural network, and we will work through some example networks representing logical operators. This will help us build a solid foundation for thinking about artificial neural networks.

Fundamentally, deep learning is a field of study of artificial neural networks, or ANNs. The first appearance of artificial neural networks in academic literature was in a paper called A Logical Calculus of the Ideas Immanent in Nervous Activity, by Warren S. McCulloch and Walter Pitts in 1943. Their work was an attempt to explain how the brain worked from a cyberneticist perspective. Their work would become the root of modern neuroscience and modern artificial neural networks.

An ANN is a biologically inspired algorithm. ANNs are not realistic representations of how a brain learns, although from time to time news stories still hype this. We are still learning many things about how the brain processes information. As new discoveries are made, there is often an attempt to represent real neurological structures and processes in terms of ANNs, like the concept of receptive fields inspiring convolutional neural networks. Despite this, it cannot be overstated how far we are from building an artificial brain.

In 1957, Frank Rosenblatt created the perceptron algorithm. Initially, there were high hopes about the perceptron. When evaluating, the single layer perceptron does the following:

1. $n$ inputs, $x_1,...,x_n$
2. Each input is multiplied by a weight, $x_i{w}_i$
3. These products are then summed with the bias term, $s=b+{\sum }_{i=1}^n{x}_i{w}_i$

4. This sum is then run through an activation function, which returns 0 or 1, $\widehat{y}=f\left(s\right)$

   • The Heaviside step function, $H$, is often used

$H\left(x\right):=\left\{\begin{array}{cc}0,\hfill & \text{if}x<0\hfill \\ 1,\hfill & \text{if}x>0\hfill \end{array}\right.$

This can also be expressed through linear algebra.

$\begin{array}{cc}\hfill \overrightarrow{x}& =<x_1,...,x_n>\hfill \\ \hfill \overrightarrow{w}& =<w_1,...,w_n>\hfill \\ \hfill y& =H(\overrightarrow{x}·\overrightarrow{w}+b)\hfill \end{array}$

This can be visualized with the diagram in Figure 4-1.

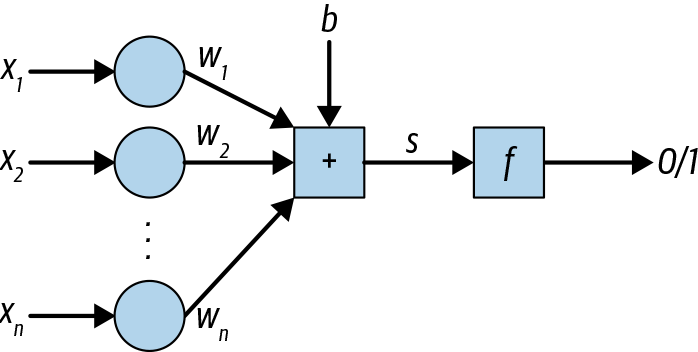
Figure 4-1. Perceptron

In 1969, Marvin Minsky and Seymour Papert showed the limitations of the algorithm. The perceptron could not represent the exclusive “or” operator XOR. The difficulty here is that a simple perceptron cannot solve problems that do not have linear separability. In terms of binary classification, a linearly separable problem is one in which the two classes can be separated by a single line, or plane in higher dimensions. To better understand this in terms of neural networks, let’s look at some examples.

We will try and create some perceptrons representing logical functions by hand, to explore the XOR problem. Imagine that we want to train networks to perform some basic logical functions. The inputs will be 0s and 1s.

If we want to implement the NOT operator, what would we do? In this case, there is no $x_2$. We want the following function:

$NOT\left(x\right):=\left\{\begin{array}{cc}0,\hfill & \text{if}x=1\hfill \\ 1,\hfill & \text{if}x=0\hfill \end{array}\right.$

This gives us two equations to work with.

$\begin{array}{cc}\hfill H(0·w_1+b)& =1\hfill \\ \hfill H(1·w_1+b)& =0\hfill \end{array}$

So let’s see if we can find values that satisfy these equations.

$\begin{array}{cc}\hfill H(0·w_1+b)& =1\hfill \\ \hfill 0·w_1+b& >0\hfill \\ \hfill b& >0\hfill \end{array}$

So we know b must be positive.

$\begin{array}{cc}\hfill H(1·w_1+b)& =0\hfill \\ \hfill 1·w_1+b& <0\hfill \\ \hfill w_1& <-b\hfill \end{array}$

So $w_1$ must be a negative number less than $-b$. An infinite number of values fit this, so the perceptron can easily represent NOT.

Now let’s represent the OR operator. This requires two inputs. We want the following function:

$OR(x_1,x_2):=\left\{\begin{array}{cc}1,\hfill & \text{if}{x}_1=1,x_2=1\hfill \\ 1,\hfill & \text{if}{x}_1=1,x_2=0\hfill \\ 1,\hfill & \text{if}{x}_1=0,x_2=1\hfill \\ 0,\hfill & \text{if}{x}_1=0,x_2=0\hfill \end{array}\right.$

We have a few more equations here; let’s start with the last case.

$\begin{array}{cc}\hfill H(0·w_1+0·w_2+b)& =0\hfill \\ \hfill 0·w_1+0·w_2+b& <0\hfill \\ \hfill b& <0\hfill \end{array}$

So $b$ must be negative. Now let’s handle the second case.

$\begin{array}{cc}\hfill H(1·w_1+0·w_2+b)& =1\hfill \\ \hfill 1·w_1+0·w_2+b& >0\hfill \\ \hfill w_1& >-b\hfill \end{array}$

So $w_1$ must be larger than $-b$, and so it is a positive number. The same will work for case 3. For case 1, if $w_1+b>0$ and $w_2+b>0$ then $w_1+w_2+b>0$. So again, there are an infinite number of values. A perceptron can represent $OR$.

Let’s look at $XOR$ now.

$XOR(x_1,x_2):=\left\{\begin{array}{cc}0,\hfill & \text{if}{x}_1=1,x_2=1\hfill \\ 1,\hfill & \text{if}{x}_1=1,x_2=0\hfill \\ 1,\hfill & \text{if}{x}_1=0,x_2=1\hfill \\ 0,\hfill & \text{if}{x}_1=0,x_2=0\hfill \end{array}\right.$

So we have four equations:

$\begin{array}{cc}\hfill H(1·w_1+1·w_2+b)& =0\hfill \\ \hfill H(1·w_1+0·w_2+b)& =1\hfill \\ \hfill H(0·w_1+1·w_2+b)& =1\hfill \\ \hfill H(0·w_1+0·w_2+b)& =0\hfill \end{array}$

Cases 2 to 4 are the same as for $OR$, so this implies the following:

$\begin{array}{cc}\hfill b& <0\hfill \\ \hfill w_1& >-b\hfill \\ \hfill w_2& >-b\hfill \end{array}$

However, when we look at case 1, it falls apart. We cannot add the two weights, either of which are larger than $-b$ to $b$ and get a negative number. So XOR is not representable with the perceptron. In fact, the perceptron can solve only linearly separable classification problems. Linearly separable problems are problems that can be solved by drawing a single line (or plane for higher dimensions). XOR is not linearly separable.

However, this problem can be solved by having multiple layers, but this was difficult given the computational capability of the time. The limitations of the single-layer perceptron network caused research to turn toward other machine-learning approaches. In the 1980s there was renewed interest when hardware made multilayer perceptron networks more feasible (see Figure 4-2).

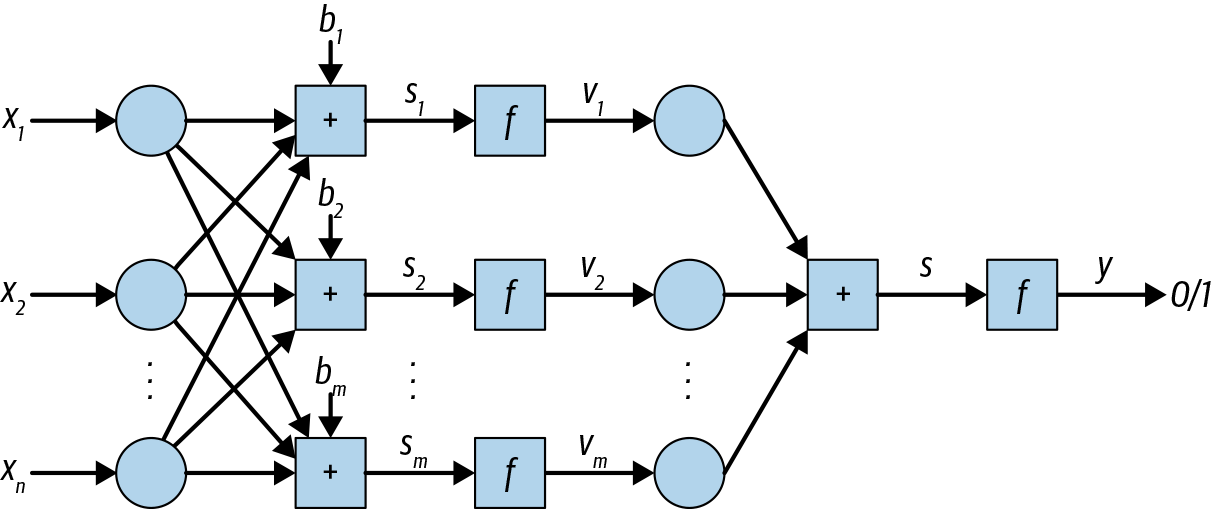
Figure 4-2. Multilayer perceptron

Now that we are dealing with modern neural networks there are some more options for us to consider:

1. The output is not necessarily 0 or 1. It could be real valued, or even a vector of values.
2. There are several activation functions to choose from.
3. Now that we have hidden layers, we will have a matrix of weights between each layer.

Look at how we would calculate the output for a neural network with one hidden layer:

$\widehat{y}=g(W^{\left(2\right)}·f(W^{\left(1\right)}·\overrightarrow{x}+{\overrightarrow{b}}^{\left(1\right)})+{\overrightarrow{b}}^{\left(2\right)})$

We could repeat this for many layers if we wish. And now that we have hidden layers, we’re going to have a lot more parameters—so solving for them by hand won’t do. We are going to need to talk about gradient descent and backpropagation.

Gradient Descent

In gradient descent, we start with a loss function. The loss function is a way of assigning a loss, also referred to as a cost, to an undesired output. Let’s represent our model with the function $F(\overrightarrow{x};\Theta )$, where $\Theta$ represents our parameters ${\theta }_1,...,{\theta }_k$, and $\overrightarrow{x}$ is an input. There are many options for a loss function; let’s use squared error for now.

$SE\left(\Theta \right)={\left(y-F(\overrightarrow{x};\Theta )\right)}^2$

Naturally, the higher the value the worse the loss. So we can also imagine this loss function as a surface. We want to find the lowest point in this surface. To find it, we start from some point and find the slope along each dimension—the gradient $\nabla$. We then want to adjust each parameter so that it decreases the error. So if parameter ${\theta }_i$ has a positive slope, we want to decrease the parameter, and if it has a negative slope we want to increase the parameter. So how do we calculate the gradient? We take the partial derivative for each parameter.

$\nabla SE\left(\Theta \right)=<\frac{\partial }{\partial {\theta }_1}E\left(\Theta \right),...,\frac{\partial }{\partial {\theta }_k}SE\left(\Theta \right)>$

We calculate partial derivatives for \theta__i by holding the other parameters constant and taking the derivative with respect to ${\theta }_i$. This will give us the slope for each parameter. We can use these slopes to update the parameters by subtracting the slope from the parameter value.

If we overcorrect a parameter we might overshoot the minimal point, but the weaker our updates, the slower we learn from examples. To control the learning rate we use a hyperparameter. I’ll use $r$ for this learning rate, but you may also see it represented by other characters (often Greek). The update looks like this:

${\theta }_j={\theta }_j-r\frac{\partial }{\partial {\theta }_j}SE\left(\Theta \right)$

If we do this for each example, training on a million examples will take a prohibitively long time, so let’s use an error function based on a batch of examples—a mean squared error.

$\begin{array}{cc}\hfill MSE\left(\Theta \right)& =\frac{1}{n}\sum _{i=1}^{M}SE\left(\Theta \right)\hfill \\ & =\frac{1}{n}\sum _{i=1}^M{\left(y-F({\overrightarrow{x}}_i;\Theta )\right)}^2\hfill \end{array}$

$\begin{array}{cc}\hfill {\theta }_j& ={\theta }_j-r\frac{\partial }{\partial {\theta }_j}MSE\left(\Theta \right)\hfill \\ & ={\theta }_j-r\frac{\partial }{\partial {\theta }_j}\frac{1}{n}\sum _{i=1}^{M}SE\left(\Theta \right)\hfill \end{array}$

The gradient is a linear operator, so we can distribute it under the sum.

$\begin{array}{cc}\hfill {\theta }_j& ={\theta }_j-r\frac{\partial }{\partial {\theta }_j}MSE\left(\Theta \right)\hfill \\ & ={\theta }_j-r\frac{1}{n}\sum _{i=1}^M\frac{\partial }{\partial {\theta }_j}\frac{1}{n}SE\left(\Theta \right)\hfill \\ & ={\theta }_j-r\frac{1}{n}\sum _{i=1}^M\frac{\partial }{\partial {\theta }_j}\frac{1}{n}{\left(y-F(\overrightarrow{x};\Theta )\right)}^2\hfill \\ & ={\theta }_j-r\frac{1}{n}\sum _{i=1}^M\frac{2}{n}\left(y-F(\overrightarrow{x};\Theta )\right)\frac{\partial }{\partial {\theta }_j}F(\overrightarrow{x};\Theta )\hfill \end{array}$

This will change if you use a different loss function. We will go over loss functions as we come across them in the rest of the book. The value of $\frac{\partial }{\partial {\theta }_j}F(\overrightarrow{x};\Theta )$ will depend on your model. If it is a neural network, it will depend on your activation function.

Backpropagation

Backpropagation is an algorithm for training neural networks. It is essentially an implementation of chain rule from calculus. To talk about backpropagation, we must first talk about forward propagation.

To build a solid intuition, we will proceed with two parallel descriptions of neural networks: mathematical and numpy. The mathematical description will help us understand what is happening on a theoretical level. The numpy description will help us understand how this can be implemented.

We will again be using the Iris data set. This data is really too small for a realistic use of deep learning, but it will help us explore backpropagation. Let’s remind ourselves about the Iris data set (see Table 4-1).

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from scipy.special import softmax

df = pd.read_csv('data/iris/iris.data', names=[
    'sepal_length',
    'sepal_width',
    'petal_length',
    'petal_width',
    'class',
])

df.head()

Table 4-1. Iris data

	sepal_length	sepal_width	petal_length	petal_width	class
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa

Now, let’s define our network.

We know we will have 4 inputs (the number of our features), so our input layer has a length of 4. There are 3 outputs (the number of our classes), so our output layer must have a length of 3. We do whatever we want for the layers in between, and we will use 6 and 5 for the first and second hidden layers, respectively. A lot of research has gone into how to construct your network. You will likely want to explore research for different use cases and approaches. As is so common in NLP and machine learning in general, one size does not fit all.

layer_sizes = [4, 6, 5, 3]

We will define our inputs, X, and our labels, Y. We one-hot encode the classes. In short, one-hot encoding is when we represent a categorical variable as a collection of binary variables. Let’s look at the one-hot–encoded DataFrame. The results are in Tables 4-2 and 4-3.

X = df.drop(columns=['class'])
Y = pd.get_dummies(df['class'])

X.head()

Table 4-2. Iris features matrix

	sepal_length	sepal_width	petal_length	petal_width
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

Y.head()

Table 4-3. Iris labels matrix

	Iris-setosa	Iris-versicolor	Iris-virginica
0	1	0	0
1	1	0	0
2	1	0	0
3	1	0	0
4	1	0	0

As we can see, each possible value of the class column has become a column itself. For a given row, if the value of class was, say, iris-versicolor, then the iris-versicolor column will have value 1, and the others will have 0.

In mathematical terms, this is what our network looks like:

$\begin{array}{cc}\hfill W^{\left(1\right)}& =5\times 4\text{matrix}\hfill \\ \hfill b^{\left(1\right)}& =5\times 1\text{vector}\hfill \\ \hfill f_1& =tanh\hfill \\ \hfill W^{\left(2\right)}& =6\times 5\text{matrix}\hfill \\ \hfill b^{\left(2\right)}& =6\times 1\text{vector}\hfill \\ \hfill f_2& =tanh\hfill \\ \hfill W^{\left(3\right)}& =3\times 5\text{matrix}\hfill \\ \hfill b^{\left(3\right)}& =3\times 1\text{vector}\hfill \\ \hfill f_3& =tanh\hfill \end{array}$

There are many ways to initialize parameters. It might seem easy to set all the parameters to 0, but this does not work. If all the weights are 0, then the output of forward propagation is unaffected by the input, making learning impossible. Here, we will be randomly initializing them. If you want to learn about more sophisticated initialization techniques, there are links in the “Resources”. We can, however, set the bias terms to 0, since they are not associated with an input.

np.random.seed(123)
W_1 = np.random.randn(layer_sizes[1], layer_sizes[0])
b_1 = np.zeros((layer_sizes[1], 1))
f_1 = np.tanh
W_2 = np.random.randn(layer_sizes[2], layer_sizes[1])
b_2 = np.zeros((layer_sizes[2], 1))
f_2 = np.tanh
W_3 = np.random.randn(layer_sizes[3], layer_sizes[2])
b_3 = np.zeros((layer_sizes[3], 1))
f_3 = lambda H: np.apply_along_axis(softmax, axis=0, arr=H)

layers = [
    (W_1, b_1, f_1),
    (W_2, b_2, f_2),
    (W_3, b_3, f_3),
]

Now, we will implement forward propagation.

Mathematically, this is what our network is doing:

$$\begin{array}{cc}\hfill X& =3\times Mmatrix\hfill \\ \hfill H^{\left(1\right)}& =W^{\left(1\right)}·X+b^{\left(1\right)}\hfill \\ \hfill V^{\left(1\right)}& =f_1\left(H^{\left(1\right)}\right)=\text{tanh}\left(H^{\left(1\right)}\right)\hfill \\ \hfill H^{\left(2\right)}& =W^{\left(2\right)}·V^{\left(1\right)}+b^{\left(2\right)}\hfill \\ \hfill V^{\left(2\right)}& =f_2\left(H^{\left(2\right)}\right)=\text{tanh}\left(H^{\left(2\right)}\right)\hfill \\ \hfill H^{\left(3\right)}& =W^{\left(3\right)}·V^{\left(2\right)}+b^{\left(3\right)}\hfill \\ \hfill \widehat{Y}& =f_3\left(H^{\left(3\right)}\right)=\text{softmax}\left(H^{\left(1\right)}\right)\hfill \\ \\ \hfill \text{softmax}\left(\overrightarrow{x}\right)=<\begin{array}{c}...\\ \frac{e^{x_j}}{{\sum }_{i=0}^K{e}^{x_i}}\\ ...\end{array}>\end{array}$$

The following code shows how forward propagation works with an arbitrary number of layers. In this function, X is the input (one example per row). The argument layers is a list of weight matrix, bias term, and activation function triplets.

def forward(X, layers):
    V = X.T
    Hs = []
    Vs = []
    for W, b, f in layers:
        H = W @ V
        H = np.add(H, b)
        Hs.append(H)
        V = f(H)
        Vs.append(V)
    return V, Hs, Vs

Now we need to talk about our loss function. As we described previously, the loss function is the function we use to calculate how the model did on a given batch of data. We will be using log-loss.

$\begin{array}{cc}\hfill L& =-\sum _k^K(Y\circ log\left(\widehat{Y}\right))\hfill \end{array}$

The symbol ∘ represents elementwise multiplication, also known as the Hadamard product. The following function safely calculates the log-loss. We need to make sure that our predicted probabilities are between 0 and 1, but neither 0 nor 1. This is why we need the eps argument.

def log_loss(Y, Y_hat, eps=10**-15):
    # we need to protect against calling log(0), so we seet an 
    # epsilon, and define our predicted probabilities to be between
    # epsilon and 1 - epsilon
    min_max_p = np.maximum(np.minimum(Y_hat, 1-eps), eps)
    log_losses = -np.sum(np.multiply(np.log(min_max_p), Y), axis=0)
    return np.sum(log_losses) / Y.shape[1]

Y_hat, Hs, Vs = forward(X, layers)
loss = log_loss(Y.T, Y_hat)
loss

1.4781844247149367

Now we see how forward propagation works and how to calculate the loss. To use gradient descent, we need to be able to calculate the gradient of the loss with respect to the individual parameters.

$\begin{array}{cc}\hfill \frac{\partial L}{\partial W^{\left(3\right)}}& =\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial W^{\left(3\right)}}\hfill \\ & =\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial H^{\left(3\right)}}·\frac{\partial H^{\left(3\right)}}{\partial W^{\left(3\right)}}\hfill \end{array}$

The combination of log-loss and softmax gives us a friendly expression for $\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial H^{\left(3\right)}}$.

$\begin{array}{cc}\hfill \frac{\partial L}{\partial W^{\left(3\right)}}& =\frac{1}{M}(\widehat{Y}-Y)·\frac{\partial H^{\left(3\right)}}{\partial W^{\left(3\right)}}\hfill \\ & =\frac{1}{M}(\widehat{Y}-Y)·V^{\left(2\right)T}\hfill \end{array}$

The gradient for the bias term is derived in the same way. Instead of taking the output from the earlier layer, it is multiplied (dot product) by a vector of all 1s.

$\begin{array}{cc}\hfill \frac{\partial L}{\partial b^{\left(3\right)}}& =\frac{1}{M}(\widehat{Y}-Y)·\overrightarrow{1}\hfill \\ & =\frac{1}{M}\sum _j^M{\widehat{y}}_j-y_j\hfill \end{array}$

Let’s see what this looks like in code. We will use names that parallel the mathematical terms. First we can define $\frac{\partial L}{\partial H^{\left(3\right)}}$. We need to remember to transpose Y, so it has the same dimensions as Y_hat.

Let’s look at the gradient values for $\frac{\partial L}{\partial W^{\left(3\right)}}$ (see Table 4-4).

dL_dH_3 = Y_hat - Y.values.T
dH_3_dW_3 = Vs[1]
dL_dW_3 = (1 / len(Y)) * dL_dH_3 @ dH_3_dW_3.T
print(dL_dW_3.shape)
dL_dW_3

(3, 5)

Table 4-4. Gradient values for \frac{\partial L}{\partial W^{(3)}}

	0	1	2	3	4
0	0.010773	-0.008965	0.210314	-0.210140	0.207157
1	-0.084970	-0.214219	0.123530	-0.122504	0.126386
2	0.074197	0.223184	-0.333843	0.332644	-0.333543

Now let’s calculate the gradient for the bias term (see Table 4-5).

dH_3_db_3 = np.ones(len(Y))
dL_db_3 = (1 / len(Y)) * dL_dH_3 @ dH_3_db_3
print(dL_db_3.shape)
dL_db_3

(3,)

Table 4-5. Gradient values for \frac{\partial L}{\partial b^{(3)}}

	0
0	-0.210817
1	-0.123461
2	0.334278

Let’s look a layer further. To calculate the gradient for the $\frac{\partial L}{\partial W_{\left(2\right)}}$, we will need to continue applying the chain rule. As you can see, this derivation gets complicated quickly.

$\begin{array}{cc}\hfill \frac{\partial L}{\partial W^{\left(2\right)}}& =\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial W^{\left(2\right)}}\hfill \\ & =\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial H^{\left(3\right)}}·\frac{\partial H^{\left(3\right)}}{\partial W^{\left(2\right)}}\hfill \\ & =\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial H^{\left(3\right)}}·\frac{\partial H^{\left(3\right)}}{\partial V^{\left(2\right)}}·\frac{\partial V^{\left(3\right)}}{\partial W^{\left(2\right)}}\hfill \\ & =\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial H^{\left(3\right)}}·\frac{\partial H^{\left(3\right)}}{\partial V^{\left(2\right)}}·\frac{\partial V^{\left(2\right)}}{\partial H^{\left(2\right)}}·\frac{\partial H^{\left(2\right)}}{\partial W^{\left(2\right)}}\hfill \end{array}$

We know part of this.

$\begin{array}{cc}\hfill \frac{\partial L}{\partial W^{\left(2\right)}}& =\frac{1}{M}(\widehat{Y}-Y)·\frac{\partial H^{\left(3\right)}}{\partial V^{\left(2\right)}}·\frac{\partial V^{\left(2\right)}}{\partial H^{\left(2\right)}}·\frac{\partial H^{\left(2\right)}}{\partial W^{\left(2\right)}}\hfill \\ & =\frac{1}{M}(\widehat{Y}-Y)·W^{\left(3\right)}·(1-V^{\left(2\right)}\circ V^{\left(2\right)})·V^{\left(1\right)T}\hfill \end{array}$

We can calculate this. Notice here that we need to keep track of intermediate values. Use these values returned from the forward propagation step.

dH_3_dV_2 = W_3
dV_2_dH_2 = 1 - np.power(Vs[1], 2)
dH_2_dW_2 = Vs[0]
dL_dH_2 = np.multiply((dL_dH_3.T @ dH_3_dV_2).T, dV_2_dH_2)
dL_dW_2 = (1 / len(Y)) * dL_dH_2 @ dH_2_dW_2.T
print(dL_dW_2.shape)
dL_dW_2

(5, 6)

Now we can look at the gradient values, shown in Table 4-6.

Table 4-6. Gradient values for \frac{\partial L}{\partial W^{(2)}}

	0	1	2	3	4	5
0	-0.302449	-0.194403	0.314719	0.317461	0.317539	0.317538
1	0.049117	-0.001843	-0.055560	-0.055613	-0.055634	-0.055636
2	0.000722	0.000503	-0.000734	-0.000747	-0.000747	-0.000747
3	0.003561	0.002604	-0.003723	-0.003732	-0.003732	-0.003732
4	0.016696	-0.006639	-0.017758	-0.018240	-0.018247	-0.018247

For the bias term it is similar (see Table 4-7).

$\begin{array}{cc}\hfill \frac{\partial L}{\partial b^{\left(2\right)}}& =\frac{1}{M}(\widehat{Y}-Y)·\frac{\partial H^{\left(3\right)}}{\partial V^{\left(2\right)}}·\frac{\partial V^{\left(2\right)}}{\partial H^{\left(2\right)}}·\frac{\partial H^{\left(2\right)}}{\partial b^{\left(2\right)}}\hfill \\ & =\frac{1}{M}(\widehat{Y}-Y)·W^{\left(3\right)}·(1-V^{\left(2\right)}\circ V^{\left(2\right)})·\overrightarrow{1}\hfill \end{array}$

dH_2_db_2 = np.ones(len(Y))
dL_db_2 = (1 / len(Y)) * dL_dH_2 @ dH_2_db_2.T
print(dL_db_2.shape)
dL_db_2

(5,)

Table 4-7. Gradient values for \frac{\partial L}{\partial b^{(2)}}

	0
0	0.317539
1	-0.055634
2	-0.000747
3	-0.003732
4	-0.018247

I’ll leave deriving the next layer as an exercise. It should be straightforward because layer 1 is so similar to layer 2 (see Tables 4-8 and 4-9).

dH_2_dV_1 = W_2
dV_1_dH_1 = 1 - np.power(Vs[0], 2)
dL_dH_1 = np.multiply((dL_dH_2.T @ dH_2_dV_1).T, dV_1_dH_1)
dH_1_dW_1 = X.values.T
dL_dW_1 = (1 / len(Y)) * dL_dH_1 @ dH_1_dW_1.T
print(dL_dW_1.shape)
dL_dW_1

(6, 4)

Table 4-8. Gradient values for \frac{\partial L}{\partial W^{(1)}}?

	0	1	2	3
0	-1.783060e-01	-1.253225e-01	-5.240050e-02	-7.952154e-03
1	4.773021e-01	3.260914e-01	1.394070e-01	2.328259e-02
2	1.808615e-02	3.469462e-02	-4.649400e-02	-2.300012e-02
3	-7.880986e-04	-5.902413e-04	-3.475747e-05	8.403521e-05
4	-4.729628e-16	-2.866947e-16	-1.341379e-16	-2.326840e-17
5	-4.116040e-06	-2.487064e-06	7.311565e-08	4.091940e-07

dH_1_db_1 = np.ones(len(Y))
dL_db_1 = (1 / len(Y)) * dL_dH_1 @ dH_1_db_1.T
print(dL_db_1.shape)
dL_db_1

(6,)

Table 4-9. Gradient values for \frac{\partial L}{\partial b^{(1)}}

	0
0	-3.627637e-02
1	9.832581e-02
2	7.392729e-03
3	-1.758950e-04
4	-1.066024e-16
5	-1.025423e-06

Now that we have calculated the gradients for our first iteration, let’s build a function for doing these calculations.

params = [[W_1, W_2, W_3], [b_1, b_2, b_3]]

We need a function for calculating our gradients. This method will need the following: the inputs $X$, the labels $Y$, the predicted probabilities $\widehat{Y}$, the parameters $W^{\left(i\right)}$ and $b^{\left(i\right)}$, and the intermediate values $V^{\left(i\right)}$.

def gradients(X, Y, Y_hat, params, Vs):
    Ws, bs = params
    assert len(Ws) == len(bs)
    dL_dHs = [None] * len (layers)
    dL_dWs = [None] * len (layers)
    dL_dbs = [None] * len (layers)
    dL_dHs[2] = Y.T - Y_hat
    for layer in np.arange(len(layers), 0, -1) - 1:
        dL_dH = dL_dHs[layer]
        dH_dW = Vs[layer - 1] if layer > 0 else X.T
        dL_dW = (1 / len(Y)) * dL_dH @ dH_dW.T
        dH_db = np.ones(len(Y))
        dL_db = (1 / len(Y)) * dL_dH @ dH_db
        dL_dWs[layer] = dL_dW
        dL_dbs[layer] = dL_db.reshape(len(dL_db), 1)
        if layer > 0:
            dH_dV = Ws[layer]
            # just supporting tanh
            dV_dH_next = 1 - np.power(Vs[layer - 1], 2)
            dL_dHs[layer - 1] = \
                np.multiply((dL_dH.T @ dH_dV).T, dV_dH_next)
        
    return dL_dWs, dL_dbs

We need a method that will evaluate the model then calculate the loss and gradients.

def update(X, Y, params, learning_rate=0.1):
    Ws, bs = params
    Y_hat, Hs, Vs = forward(X, layers)
    loss = log_loss(Y.T, Y_hat)
    dWs, dbs = gradients(X, Y, Y_hat, params, Vs)
    for i in range(len(Ws)):
        Ws[i] += learning_rate * dWs[i]
        bs[i] += learning_rate * dbs[i]
    return Ws, bs, loss

Finally, we will have a method for training the network.

def train(X, Y, params, learning_rate=0.1, epochs=6000):
    X = X.values
    Y = Y.values
    Ws = [W for W in params[0]]
    bs = [b for b in params[1]]
    for i in range(epochs):
        Ws, bs, loss = update(X, Y, [Ws, bs], learning_rate)
        if i % (epochs // 10) == 0:
            print('epoch', i, 'loss', loss)
    print('epoch', i, 'loss', loss)
    return Ws, bs

Let’s train our network. The results are shown in Table 4-10.

Ws, bs = train(X, Y, params)

epoch 0 loss 1.4781844247149367
epoch 600 loss 0.4520794985146122
epoch 1200 loss 0.29327186345356115
epoch 1800 loss 0.08517606119594413
epoch 2400 loss 0.057984381652688245
epoch 3000 loss 0.05092154382167823
epoch 3600 loss 0.04729254314395461
epoch 4200 loss 0.044660097961296365
epoch 4800 loss 0.038386971515831474
epoch 5400 loss 0.03735081006838356
epoch 5999 loss 0.036601105223619555

Y_hat, _, _ = forward(X, layers)
Y_hat = pd.DataFrame(Y_hat.T, columns=[c + '_prob' for c in Y.columns])
Y_hat['pred'] = np.argmax(Y_hat.values, axis=1)
Y_hat['pred'] = Y_hat['pred'].apply(Y.columns.__getitem__)
Y_hat['truth'] = Y.idxmax(axis=1)
Y_hat.head()

Table 4-10. Predictions from the trained model

	Iris-setosa_prob	Iris-versicolor_prob	Iris-virginica_prob	pred	truth
0	0.999263	0.000737	2.394229e-07	Iris-setosa	Iris-setosa
1	0.998756	0.001244	3.903808e-07	Iris-setosa	Iris-setosa
2	0.999256	0.000744	2.416573e-07	Iris-setosa	Iris-setosa
3	0.998855	0.001145	3.615654e-07	Iris-setosa	Iris-setosa
4	0.999376	0.000624	2.031758e-07	Iris-setosa	Iris-setosa

Let’s see the proportion we got right.

(Y_hat['pred'] == Y_hat['truth']).mean()

0.9933333333333333

This is good, but we have likely overfit. When we try actual training models, we will need to create train, validation, and test data sets. The train data set will be for learning our parameters (e.g., weights), validation for learning our hyperparameters (e.g., number and sizes of layers), and finally the test data set for understanding how our model will perform on unseen data.

Let’s look at the errors our model makes (see Table 4-11).

Y_hat[Y_hat['pred'] != Y_hat['truth']]\
  .groupby(['pred', 'truth']).size()

pred            truth          
Iris-virginica  Iris-versicolor    1
dtype: int64

Table 4-11. Erroneous predictions

pred	truth	count
Iris-virginica	Iris-versicolor	1

It looks like the only mistake we made was misidentifying an Iris versicolor as an Iris virginica. So it looks like we have learned from this data—though we most likely have overfit to the data.

Training the model is done in batches. These batches are generally small sets of your training data. There are tradeoffs to the size of the batches: if you pick a smaller batch size, you require less computation. However, you are using less data to perform an update, which may be noisy. If you pick a larger batch size, you get a more reliable update, but this requires more computation and can lead to overfitting. The overfitting is possible because you are using more of your data to calculate the updates.

Once we have these gradients, we can use them to update our parameters and so perform gradient descent. This is a very simplified introduction to a rich and complicated topic. I encourage you to do additional learning on the topic. As we go on, I will cover deep learning topics to the depth necessary to understand how the techniques are implemented. A thorough explanation of deep learning topics is outside the scope of this book.

Now let’s look at some developments on top of neural networks.

Convolutional Neural Networks

In 1959 David H. Hubel and Torsten Wiesel conducted experiments on cats that showed the existence of specialized neurons that detected edges, position, and motion. This inspired Kunihiko Fukushima to create the “cognitron” in 1975 and later the “neocognitron” in 1980. This neural network, and others based on it, included early notions of pooling layers and filters. In 1989, the modern convolutional neural network, or CNN, with weights learned fully by backpropagation, was created by Yann LeCun.

Generally, CNNs are explained with images as an example, but it’s just as easy to apply these techniques to one-dimensional data.

Filters

Filters are layers that take a continuous subset of the previous layer (e.g., a block of a matrix) and feed it into a neuron in the next layer. This technique is inspired by the idea of a receptive field in the human eye, where different neurons are responsible for different regions and shapes in vision.

Imagine you have a $6\times 6$ matrix coming into a layer. We can use a filter of size $4\times 4$ to feed into 9 neurons. We do this by doing an element-wise multiplication between a subsection of the input matrix and the filter and then summing the products. In this example we use elements (1,1) to (4,4) with the filter for the first element of the output vector. We then multiply the elements (1,2) to (4,5) with the filter for the second element. We can also change the stride, which is the number of columns/rows for which we move the filter for each output neuron. If we have our $6\times 6$ matrix with $4\times 4$ filter and a stride of 2, we can feed into 4 neurons. With padding, we can add extra rows and columns of 0s to our input matrix, so that the values at the edge get the same treatment as the interior values. Otherwise, elements on the edge are used less than inner elements.

Pooling

Pooling works similarly to filters—except, instead of using weights that must be learned, simple aggregate is used. Max pooling, taking the max of the continuous subset, is the most commonly used. Though, one can use average pooling or other aggregates.

This is often useful for reducing the size of the input data without adding new parameters.

Recurrent Neural Networks

In the initial research into modeling biological neural networks, it has been assumed that memory and learning have some dependence on time. However, none of the techniques covered so far take that into account.

In a multilayer perceptron, we get one example and produce one output. The forward propagation step for one example is not affected by another example. In a recurrent neural network, or RNN, we need to be aware of the previous, and sometimes later, examples. For example, if I am trying to translate a word, it is important that I know its context.

Now, the most common type of RNN uses long short-term memory, or LSTM. To understand LSTMs, let’s talk about some older techniques.

Backpropagation Through Time

The primary training algorithm for RNNs is backpropagation through time, or BPTT. This works by unfolding the network. Let’s say we have a sequence of k items. Conceptually, unfolding works by copying the recurrent part of the network k times. Practically, it works by calculating the partial derivate of each intermediate output with respect to the parameters of the recurrent part of the network.

We will go through BPTT in depth in Chapter 8 when we cover sequence modeling.

Elman Nets

Also known as simple RNNs, or SRNNs, an Elman network reuses the output of the previous layer. Jeffrey Elman invented the Elman network in 1990. The idea is relatively straightforward. We want the output of the previous example to represent the context. We combine that output with current input, using different weights.

$\begin{array}{cc}\hfill V^{\left(0\right)}& =0\hfill \\ \hfill 1& \le t\le T\hfill \\ \hfill V^{\left(t\right)}& =f_{input}(W_{input}·X^{\left(t\right)}+U_{input}·V^{(t-1)}+b_{input})\hfill \\ \hfill Y^{\left(t\right)}& =f_{output}(W_{output}·V^{\left(t\right)}+b_{output})\hfill \end{array}$

As you can see, the context is represented by $V^{(t-1)}$. This will provide information from all previous elements in the sequence to some degree. This means that the longer the sequence, the more terms there are in the gradient for the parameters. This can make the parameters change chaotically. To reduce this concern, we could use a much smaller learning rate at the cost of increased training time. We still have the chance of a training run resulting in exploding or vanishing gradients. Exploding/vanishing gradients are when the gradients for a parameter increase rapidly or go to 0. This problem can occur in any sufficiently deep network, but RNNs are particularly susceptible.

$\frac{\partial L}{\partial W_{input}^{\left(i\right)}}=\frac{\partial L}{\partial \widehat{Y}}·...·\frac{\partial L}{\partial V^{(i,T)}}·{\prod }_{t=2}^T\frac{\partial V^{(i,t)}}{\partial V^{(i,t-1)}}·\frac{\partial V^{(i,1)}}{\partial W_{input}^{\left(i\right)}}$

For long sequences, this could make our gradient go very high or very low quickly.

LSTMs

The LSTM was invented by Sepp Hochreiter and Jürgen Schmidhuber in 1997 to address the exploding/vanishing gradients problem. The idea is that we can learn how long to hold on to information by giving our recurrent units state. We can store an output produced from an element of the sequence and use this to modify the output. This state can also be connected with a notion of forgetting, so we can allow some gradients to vanish when appropriate. Here are the components of the LSTM:

$\begin{array}{cc}\hfill v_0& =0\hfill \\ \hfill c_0& =0\hfill \\ \hfill 1& \le t\le T\hfill \\ \hfill f_t& =\sigma (W_f·{\overrightarrow{x}}_t+U_f·v^{(t-1)}+b_f)\hfill \\ \hfill i_t& =\sigma (W_i·{\overrightarrow{x}}_t+U_i·v^{(t-1)}+b_i)\hfill \\ \hfill o_t& =\sigma (W_o·{\overrightarrow{x}}_t+U_o·v^{(t-1)}+b_o)\hfill \\ \hfill {\tilde{c}}_t& =\text{tanh}(W_c·{\overrightarrow{x}}_t+U_c·v^{(t-1)}+b_c)\hfill \\ \hfill c_t& =f_t\circ c_{t-1}+i_t\circ {\tilde{c}}_t\hfill \\ \hfill v_t& =o_t\circ \text{tanh}\left(c_t\right)\hfill \end{array}$

There is a lot to unpack here. We will go into more depth, including covering variants, when we get to Chapter 8, in which we present a motivating example.

Exercise 1

Being able to reason mathematically about what is happening in a neural network is important. Derive the updates for the first layer in the network mentioned in this chapter.

$\frac{\partial L}{\partial W^{\left(1\right)}}=\frac{1}{M}\frac{\partial L}{\partial \widehat{Y}}·\frac{\partial \widehat{Y}}{\partial W^{\left(1\right)}}$

Exercise 2

A common exercise when studying deep learning is to implement a classifier on the Modified National Institute of Standards and Technology (MNST) data set. This classifier takes in an image of a handwritten digit and predicts which digit it represents.

There are thousands of such tutorials available, so I will not retread that overtrodden ground. I recommend doing the TensorFlow tutorial.

Resources

• Andrew Ng’s Deep Learning Specialization: this course is a great way to become familiar with deep learning concepts.
• TensorFlow tutorials: TensorFlow has a number of great resources. Their tutorials are a way to get familiar with deep learning and the TensorFlow API.
• Deep Learning, by Ian Goodfellow, Yoshua Bengio, and Aaron Courville (MIT Press): this is a free online book that goes over the theory of deep learning.
• Natural Language Processing with PyTorch, by Delip Rao and Brian McMahan (O’Reilly)
  • This book covers NLP with PyTorch, which is another popular deep learning library. This book won’t cover PyTorch, but if you want to have a good understanding of the field, learning about PyTorch is a good idea.
• Hands-On Machine Learning with Scikit-Learn, Keras and TensorFlow, by Aurélien Géron (O’Reilly)
  • This book covers many machine learning techniques in addition to deep learning.