Matrix Differential Calculus with Applications in Statistics and Econometrics, 3rd Edition

Chapter 9First‐order differentials and Jacobian matrices

1 INTRODUCTION

We begin this chapter with some notational issues. We shall strongly argue for a particular way of displaying the partial derivatives ∂f_st(X)/∂x_ij of a matrix function F(X), one which generalizes the notion of a Jacobian matrix of a vector function to a Jacobian matrix of a matrix function.

For vector functions there is no controversy. Let f : S → ℝ^m be a vector function, defined on a set S in ℝⁿ with values in ℝ^m. We have seen that if f is differentiable at a point x ∈ S, then its derivative Df(x) is an m × n matrix, also denoted by ∂f(x)/∂x′:

(1)

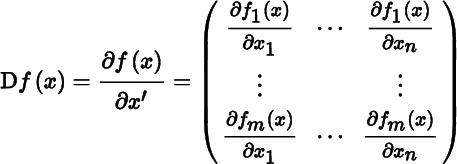
with, as a special case, for the scalar function ϕ (where m = 1):

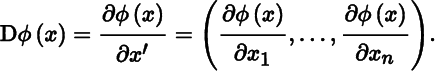
The notation ∂f(x)/∂x′ has the advantage of bringing out the dimension: we differentiate m elements of a column with respect to n elements of a row, and the result is an m × n matrix. This is just handy notation, it is not conceptual.

However, the fact that the partial derivatives ∂f_s(x)/∂x_i are organized in an m × n matrix and not, for example, in an n × m matrix or an mn‐vector is conceptual and it matters. All mathematics texts define vector derivatives in this way. There is no controversy about vector derivatives; there is, however, some controversy about matrix derivatives and this needs to be resolved. ...