SVD is one of the most useful tools in linear algebra. Beltrami and Jordan published several papers on its use. SVD is used in a wide variety of applications, such as computer vision and signal processing.
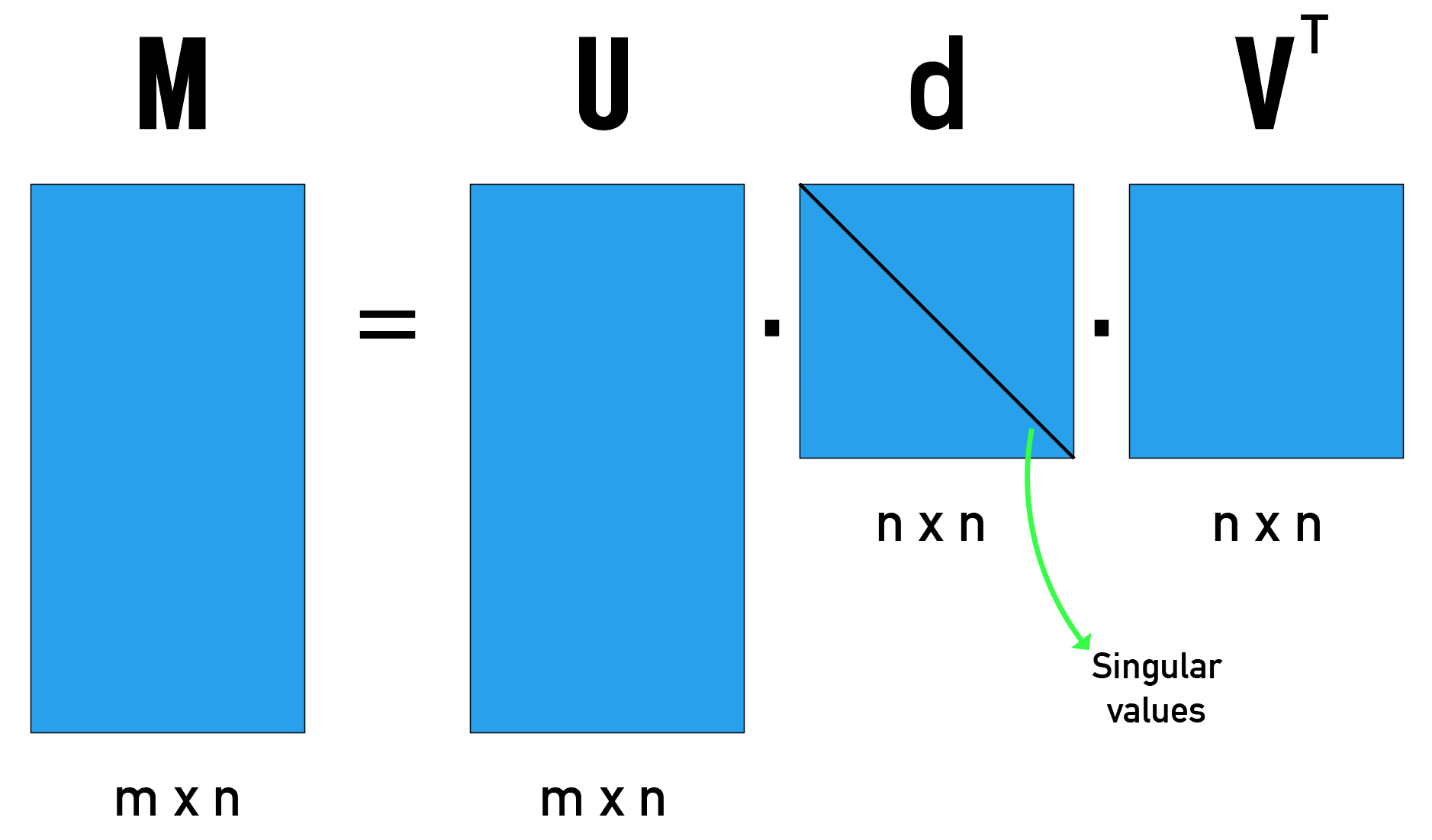
If you have a square or rectangular matrix (M), you can decompose it into matrix (U), matrix (V) (using the transpose of the matrix in the calculation), and the singular value (d).
Your ultimate formula will look like the following:

The following is an illustration of singular-value decomposition:
A simple data-reduction ...

