Martingales and Financial Mathematics in Discrete Time

8Solutions to Exercises and Practical Work

8.1. Solutions to exercises in Chapter 1

8.1.1. Exercise 1.1

1. 1) Let us describe all the σ-algebras of Ω = {a, b, c} based on their cardinal. The smallest is ₀ = {∅, Ω}. Those generated by an element are
   

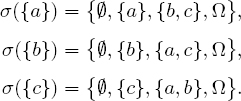
   The largest σ-algebra is that generated by two elements that corresponds to the set of subsets of Ω:

   
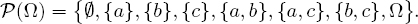
2. 2) The only inclusions are
   

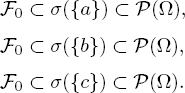
The trivial σ-algebra is contained in all the σ-algebras and all the σ-algebras are sub-σ-algebras of (Ω).

8.1.2. Exercise 1.2

1. 1) The family 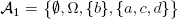is indeed a σ-algebra: it contains Ω, it is stable under complement and it is stable under countable union.
2. 2) The family 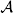₂ = {∅, Ω, {b, c, d}, {c, d}} is not a σ-algebra. For example, it does not contain the complement {a} of {b, c, d}. The σ-algebra that it generates is